当前位置：文档之家 › 第一章潮汐与潮流详解

第一章潮汐与潮流详解

  • 格式：ppt
  • 大小：4.89 MB
  • 文档页数：428

下载文档原格式

  / 172

合集下载

航海学3潮汐与潮流作业

航海学3潮汐与潮流作业

第一章第一节潮汐基本成因及潮流一、简答题：1、潮汐产生的基本原因是什么？答：潮汐产生的原动力是天体引潮力，主要是月球引潮力，其次是太阳引潮力。

2、潮汐周日不等有哪些具体表现？答：当月球赤纬不等于零、纬度不为零时，在同一太阴日中所发生的两次高潮或两次低潮的潮高以及相邻的高、低潮的时间间隔不相等。

3、潮汐的周日不等、半月不等和视差不等的基本原因各是什么？答：周日不等：月球赤纬不等于零，测者纬度不为零；半月不等：月球、太阳和地球在空间的相对位置不同；视差不等：地球和月球之间的距离发生变化。

二、名词解释1、平均高（低）潮间隙：每天月中天时刻至高（低）潮时的时间间隔的长期平均值。

2、回归潮：当月球赤纬最大时的潮汐称为回归潮，此时，潮汐周日不等现象最显著。

3、大潮升：从潮高基准面到平均大潮高潮面的高度。

4、停潮：当低潮发生后，海面有一段时间呈现停止升降的现象。

第二节中版《潮汐表》与潮汐推算一、名词解释1、高（低）潮时差：主港与附港高（低）潮潮时之差。

、高（低）潮时差：主港与附港高（低）潮潮时之差。

2、潮差比：对半日潮港来说，是指附港的平均潮差与主港的平均潮差之比；对日潮港来说，是指附港的回归潮大的潮差与主港的回归潮大的潮差之比。

二、计算题二、计算题1、我国某主港某日高潮潮时为11381138，，其附港的潮时差为01500150，，改正值为1515。

则该附港日的高潮潮时是多少？则该附港日的高潮潮时是多少？解：附港高潮时解：附港高潮时==主港高潮时主港高潮时++高潮时差高潮时差=1138+0150=1328 =1138+0150=13282、我国某主港某日潮高为3.6m 3.6m，，某附港的潮差比为1.201.20，，主港平均海面220厘米，附港平均海面222厘米，主附港平均海面季节改正值均为厘米，主附港平均海面季节改正值均为+18+18厘米，求该附港的潮高。

求该附港的潮高。

解：附港潮高解：附港潮高=[=[=[主港潮高主港潮高主港潮高--（主港平均海面（主港平均海面++主港季节改正值）主港季节改正值）]]×潮差比×潮差比++（附港平均海面（附港平均海面++附港季节改正值）=[3.6-（2.2+0.182.2+0.18））] ] ××1.20+（2.22+0.182.22+0.18））=3.864m3、从潮信表查得某海区的平均低潮间隔MLWI 为11471147，则，则8月28日（农历二十六）的低潮潮大约是多少？二十六）的低潮潮大约是多少？解：月上中天时解：月上中天时==（农历日期（农历日期-16-16-16）×）×）×0.8=0.8=0.8=（（26-1626-16）×）×）×0.8=8 h 0.8=8 h低潮时t1=t1=低潮间隙低潮间隙低潮间隙++格林尼治月上中天时格林尼治月上中天时=1147+0800=1947 =1147+0800=1947低潮时t2=1947-1225=0722t2=1947-1225=0722（注：（注：（注：12251225为潮汐周期）为潮汐周期）4、我国某地高潮间隔10501050，概算农历，概算农历8月21日该地的高潮时。

第一章 潮汐和潮流

第一章 潮汐和潮流


四、潮汐的类型和潮汐术语

潮汐的影响因素 上述对潮汐成因、潮汐不等问题的讨论，都是根据牛顿的 潮汐静力学理论，在理想的假设条件（整个地球被等深的大洋 所覆盖，所有自然地理因素对潮汐不起作用；海水没有摩擦力 和惯性力，外力使海水在任何时刻都处于平衡状态 。）下进行 的。事实上，海水有粘滞性，海洋深浅不一，海底崎岖不平， 海水与地面有很大的摩擦力，因此实际上的潮汐并非向以上简 单，高潮并不发生在月上（下）中天之时，而是滞后一段时间 才发生。从月上（下）中天时到出现第一次低潮的时间间隔称 低潮间隙；从月上（下）中天时到当地出现第一次高潮的时间 间隔称高潮间隙；大潮也不发生在朔望之日，而往往发生在朔 望后的1－3天。朔望日到发生大潮的间隔天数称为潮龄（Tide age）。潮汐还受到以下因素的影响： 1 地形和水深；沿岸海区地理条件较大洋更加复杂 。 2 受大风、气压变化（如台风）、洪水、结冰等影响。
二、利用中版《潮汐表》推算潮汐
1.求主港潮汐 主港高、低潮的潮时和潮高，以及部分主港的每整点时刻的 潮高，直接按日期查《潮汐表》的主表求得。注意船时与表列标 准时是否一致。 例1．求1984年10月1日大连港潮汐。 解：《潮汐表》第一册的封里找得大连港为主港，其潮汐预报刊 于10页；10月1日的潮汐资料为： 高潮时 0200 1411 高潮潮高 317 239 低潮时 0832 2048 低潮潮高 089 051 注意：若船时与表列标准时不一致，应将求得的潮时修正到相应 的船时。
二、潮汐的半月不等
就潮汐而言，月球的作用 是主要的，但是太阳的引 潮力也回产生周日不等的 现象。月球、太阳、和地 球在空间周期性的变化相 对位置，发生了潮汐半月 不等的现象。（初一、十 五，大潮；初七、初八， 小潮）
复习和小结
厦门大学-潮汐学原理-复习

厦门大学-潮汐学原理-复习


!!引潮力产生的原因!! 地球上任何一点的惯性离心力两只相等，方向一致。 地球的惯性离心力：������������
月球对地球的万有引力：������0
������������ ������2
由于������������
=
������0
���������������2���，得������
=
������0
(3������������������2������
−
1)，���������′���
=
3 ������0������������ 2 ���������3���
sin 2
������
第三章 引潮势和平衡潮
引潮势
在保守力场中，力矢���⃗���和势������之间的关系为：���⃗��� = −∇������
主要是由月球引起的。
平衡潮
理论假定： 1. 地球表面完全被海水覆盖 2. 海水无限深，不考虑摩擦和惯性 3. 在引潮力的作用下，海面离开原先的平衡位置，并假定在任一瞬间海面处处随时与引潮
力和重力的合力相垂直，从而达到新的平衡。 合理之处： 1. 对潮汐类型的解释 2. 对大、小潮现象的解释 3. 对高潮时逐日推迟的解释（高潮时每天推迟 50 分钟） 理论缺陷： 1. 实际上，地球上的海水被陆地所分割; 2. 现实中，海水不是无限深; 3. 海水不是静止的，而是运动着的; 4. 产生潮汐的力并不只有重力和引潮力，还有压强梯度力和科氏力。 不足： 1. 平衡潮理论认为当月球位于观测点上中天时，当地应该出现高潮，但实际上高潮要落后
平衡潮的达尔文展开 仅对引潮势的������2项进行展开，需要修正。 太阴主要半日分潮：������2 太阳主要半日分潮：������2 太阴主要全日分潮：������1 太阳主要全日分潮：������1 太阴主要椭圆率全日分潮：������1 太阴主要椭圆率半日分潮：������2 太阴太阳赤纬半日分潮：������2 太阴太阳赤纬全日分潮：������1
航海学潮汐与潮流课件

航海学潮汐与潮流课件

详细描述
潮汐的形成是一个复杂的过程，除了天体引力对其产生影响。这些因素相互作用，导致地球上不同地 区的潮汐特征各不相同。
03
潮流的形成原理
地球自转与潮流
地球自转导致地转偏向力，引 起海水在运动过程中产生旋转
，形成潮流。
由于地球自西向东自转，赤 道地区的水流方向与地球自 转方向相同，而高纬度地区
海洋科学研究
潮汐与潮流的研究对于深入了解地球气候系统、全球变化等方面 具有重要意义，有助于推动海洋科学的发展。
THANKS
感谢观看
02
潮汐的形成原理
天体引力与潮汐
总结词
天体引力是潮汐形成的主要因素，月球和太阳的引力作用对地球上的水体产生 周期性的拉伸和压缩，导致潮汐现象的产生。
详细描述
月球和太阳对地球的引力作用在地球上的水体（海洋、湖泊等）产生周期性的 拉伸和压缩，形成潮汐现象。这种引力变化导致水体在不同位置产生不同的水 位涨落，形成潮汐。
海洋水体流动与潮流
01
02
03
04
海洋水体的流动受到多种因素 的影响，包括风、地转偏向力
、海水温度和盐度等。
风力作用是形成潮流的主要因 素之一，风力推动海水产生运
动，形成潮流。
地转偏向力对海洋水体的流动 产生影响，使水流方向发生偏
转，形成潮流。
海水温度和盐度对海洋水体的 密度和流动性产生影响，从而
02
在制定航行计划时，应充分考虑潮汐和潮流的影响，采取必要
的安全措施，确保航行安全。
潮汐与潮流的预报
03
利用现代科技手段获取潮汐和潮流的实时数据和预报信息，为
航行提供决策依据。
06
航海学潮汐与潮流的未来发展
潮汐与潮流的研究现状
潮汐与潮流

潮汐与潮流

潮汐与潮流2008-04-02 22:28:09| 分类：自然地理| 标签：|字号大中小订阅潮汐与潮流潮汐（Tide）是海面周期性的升降运动。

与潮汐现象同时发生的还有海水周期性的水平流动，即潮流（Tidal Stream）。

潮汐与渔业、盐业、港口建筑、以及海水动力利用有着十分密切的关系。

潮汐与航海的关系也非常重要，将直接影响船舶的航行计划的实施和航海安全，如需要通过浅水区，须预先依据潮汐资料计算出当地潮高、潮时，并正确调整吃水差；为了保证船舶安全地航行在计划航线上，须随时掌握当的潮汐与潮流资料，观测船位，调整航向。

即使是在港内，也不容忽视潮汐、潮流对船舶安全的影响。

在沿岸航行中，船长的航行命令、公司的航行规章制度、国际性机构对航行值班驾驶员的指导性文件中，都将掌握当时和未来的潮汐和潮流列为确保航行安全的驾驶台工作的重要内容。

潮汐学有着丰富的内容，本章仅从航海应用实际出发，阐述潮汐的基本成因、潮汐术语、潮流的计算方法等内容。

§13—1 潮汐的基本成因和潮汐术语一、潮汐的成因海水的涨落现象是由诸多复杂因素决定的，经研究表明，潮汐产生的原动力，是天体的引潮力，即天体的引力、地球与天体相对运动所需的惯性离心力的向量和。

其中最主要的是月球的引潮力，其次是太阳的引潮力。

本章仅从航海实际需要出发，扼要地利用平衡潮理论（静力学理论）分析潮汐的基本成因，并对调和常数分析法作简单扼要的介绍。

平衡潮理论是牛顿创立的，所谓平衡潮是指海水在引潮力和重力作用下，达到平衡时的潮汐。

为了使问题简化，作以下两个假设：1、整个地球被等深的海水所覆盖，所有自然地理因素对潮汐不起作用；2、海水没有摩擦力、惯性力，外力使海水在任何时候都处于平衡状态。

下面以月引潮力为例来分析潮汐的成因：㈠月球的引力根据万有引力定律，有：式中：mM ——月球质量；mE——地球质量；R——地月中心距离；k——万有引力系数。

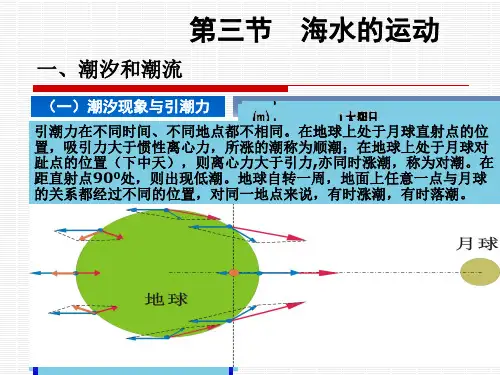
而地球表面上至月球中心距离为X的单位质点P所受的引力为：所以：（如图5-1-1所示）月球引力的方向：均指向月心；大小：与天体的距离的平方成反比。

海洋潮汐课件

海洋潮汐课件

M V 0 M H 0 M co s( ) 2 D M sin ( ) 2 D
继续
返回
引潮力 与
引潮力势
• 特点：引潮力为矢量、引潮力势为标量
• 引潮力与引潮力势的关系：
U U U FX ; FY ; FZ X Y Z F gr adU
继续
返回
2。为什么要研究海洋潮汐？ • 海洋潮汐在军事上.海洋工程上.科研上等各个 方面都存在及其重要的意义。随着现代利用海 洋和开发海洋的需要对海洋潮汐有深刻的了解 和认识。（举例） • 众所周知，海道测量是在运动的海面上进行的。 测量载体利用测深仪器或其他测深工具在测深 时，在同一地点不同的时刻得到的水深值是不 同的值。这主要是载体在运动的海面上受到各 种因素的影响，特别是海洋潮汐的影响。如何 获取稳定的水深值，供使用着使用而不产生误 解，是我们海道测量人员工作中一项重要工作。 所以，需要系统地学习它。
继续
返回
３. 海洋潮汐研究的内容与方法？ 本书学习的主要目的是； 研究，了解潮汐运动的规律，掌握其规律 性。
本书学习的主要内容是： 进行潮汐分析和预报 计算深度基准面 求取水位改正值 绪论结束
返回
第一章 潮汐和潮流现象及其 观测
继续
返回
1.描述潮汐现象的有关术语？
潮高 潮高（低）潮 、涨（落）潮 、 平潮与潮时 、 潮差与周期、涨（落）潮时间 、月中天 高（低）潮 间隙
继续
返回
2.引潮力
EM r F o r2 r
万有引力定律（牛顿1687年） 地、月相对运动与惯性离心力
E X
r
M
公共质心：
当两个物体当为一个物体时，其质心为公共质心，地 --月公共质心，地-日公共质心。
航海学3--潮汐经典课件

航海学3--潮汐经典课件



地面各点惯性离心力 大小相等，相互平行 且皆背离月球 （END） M
A4 E4 A1 G1 E3 E1 G A2 E2 M1 A3
3
M4
地球的平动运动6
4、月引潮力与月潮椭圆体
D

月球引力
A M
E
B
C
D
月球引力

惯性离心力
A M E B
C
D

月球引力 惯性离心力 月引潮力 地心： 地面：
TD与CD是否一致：实际水深=海图水深＋潮高＋（CD－TD） 中国沿岸三册《潮汐表》预报误差: 一般情况下--潮时预报误差：20～30min；潮高预报误差：20～30cm。 特殊情况下--台风增水(max: 1m)；寒潮减水(max: 1m)；江河口汛 期实际水位往往高于预报水位；南海日潮混合潮港平潮时间较长， 潮时预报误差M4
地球：E4
M3 E1
E4 A1 E3 G A2 E2 M1 A3


A点：A4
M4
地球的平动运动4
M2
A4

A点与地心E作同质量、 同半径（0.73r）、同 角速度（27.3d）的平 M 动。
E4 A1 G1 E3 E1 G A2 E2 M1 A3
3
M4
地球的平动运动5
M2
• 低高潮（lower high water，LHW）：在一个太阴日中发生的两次高潮 中潮高较低的高潮。 • 高低潮（higher low water，HLW）：在一个太阴日中发生的两次低潮 中潮高较高的低潮。 • 低低潮（lower low water，LLW）：在一个太阴日中发生的两次低潮中 潮高较低的低潮。 • 潮龄（tidal age）：由朔望至实际大潮发生的时间间隔称为潮龄。潮龄 一般为1天～3天。 • 平均高（低）潮间隙（mean high／low water interval，MHWI／ MLWI）：每天月中天时刻至高（低）潮时的时间间隔的长期平均值称 为平均高（低）潮间隙。
海水的运动

海水的运动


随冲流而下的是借助于重力的退流。
（二）波浪的折射
波浪在港湾海岸也发生折 波峰线在深水区是和引起 射。港湾海岸附近海底等 波浪的力的方向，即波浪 深线基本上与海岸平行， 前进的方向相垂直的。但 波浪前进方向与海岸 港湾中海浪因水深而保持 当波浪进入浅水区后，波 斜交常常造成水体沿 原速前进，在伸向海中的 浪的传播方向不再垂直于 海岸流动，这种纵向 岬角上则因即仍然与海岸 海岸，而是常与海岸斜交， 水流称为沿岸流。虽 线平行。图中波峰线上的 这样，同一波列两端的水 AB与BC两段分别在 ab与 然沿岸流的流速一般 bc两段相遇，因而bc段即 深就可能有较大差异。近 不超过1-1.5m/s，但 岬角部分所受的力比ab段 岸较浅一端因受摩擦而减 它携带和搬运泥沙， 即湾内部分强。岬角上波 速，离岸远而较深一端在 对海岸地貌的形成发 能集中而港湾内波能分散， 育也有一定影响。 深水处继续保持原速前进， 故港湾成为船舶的庇护所。 最后波峰线将发生转折而 与海岸平行，这种现象称 为波浪的折射。
个太阴日内，水流则往复只有一次。）
（二）潮 流
潮流在一个周期里出现两次最大流速和最小流速。 地形愈狭窄，最大与最小流速的差值愈大。潮流的 一般流速为4-5km/h，但在狭窄的海峡或海湾中， 如我国的杭州湾，时速可达18-22km/h。 喇叭形海湾或河口湾可以激起怒潮，如我国的钱塘 江口、亚洲的波斯湾、南美的麦哲伦海峡、北美的 芬地湾都是以潮高闻名天下，其特点是涨潮时潮波 来势迅猛，潮端陡立，水花飞溅，潮流上涌，声闻 数十里，如万马奔腾，排山倒海，异常壮观。
（二）潮 流
潮汐现象在国民经济中具有重要的意义，各种海洋事 业都与潮汐涨落密切相关。人们根据潮汐涨落的规律， 张网捕鱼，引水晒盐；利用广阔的海涂，发展水产养 殖事业。潮汐还是取之不尽、用之不竭的动力资源， 可以利用它发出强大的、廉价的电力。 潮汐涨落对海洋航运事业至为重要。世界上许多浅水 港口，诸如我国的上海，英国的伦敦和德国的汉堡等， 在很大程度上都是依赖潮汐而存在的。巨型的远洋航 轮，只有利用涨潮时的较高水位，才能进出海港。倘 若月球一旦停止对地球的引潮作用，那么，这些海港 将减低或丧失它们在海运上的地位。
潮汐概述

潮汐概述


十五，满月 高潮最高，低潮最低 “大潮”(spring tide)
初七、八，上弦月 高潮最低，低潮最高 “小潮” （neap tide）
月潮椭圆体
廿二、三，下弦月 高潮最低，低潮最高 “小潮”（neap tide）
初一，新月 高潮最高，低潮最低 “大潮” (spring tide)
太阳潮椭圆体
（END）
从高潮时到低潮时的时间间隔称为落潮时间。（END）
潮汐术语 2
航海学院
NAVIGATION COLLEGE
➢平潮（Slack）
高潮发生后，海面有一段时间呈现停止升降的现象。
➢停潮（Stand）
低潮发生后，海面有一段时间呈现停止升降的现象。
➢潮龄（Tidal age）
由朔望至实际大潮发生日的时间间隔天数。1～3天
航海学（3）
2009年4月
课程内容
航海学院
NAVIGATION COLLEGE
潮汐与潮流 航标与《航标表》 航海图书资料 航线与航行方法 （END）
第一章 潮汐与潮流
航海学院
NAVIGATION COLLEGE
概述 潮汐的基本成因与潮汐不等 潮汐调和分析简介 潮汐类型与潮汐术语 中版《潮汐表》与潮汐推算 英版《潮汐表》与潮汐推算 潮流推算（END）
潮汐的基本成因
成因：月引潮力 + 地球自转 现象：
➢ A1(上中天)：HW1； A2(转90O)：LW1 ➢ A3(下中天)：HW2 ；A4(转90O)：LW2
太阴日：24h50m 潮汐周期：12h25m(半日潮)
（END）
A1
航海学院
NAVIGATION COLLEGE
A4
Pn
A3
潮汐与潮流

潮汐与潮流


潮汐和潮流
潮汐和潮流
潮汐的基本成因
潮汐由天体的引潮力产生的。
引潮力：天体的 引力和惯性离心力 的合力。
对潮汐影响较大的是月球和太阳的引潮力，其 中月球引潮力 是产生潮汐的主要因素 ，包括月 球的引力和地球绕月地公共质心进行平动运动 所产生的惯性离心力。
潮汐和潮流
引潮力的性质
A：涨潮方向与月
球引力方向一致，
潮汐和潮流
?
钱塘潮的成因？
潮汐和潮流
钱塘潮的成因：
? 天文：农历八月十六日至十八日，太阳、月 球、地球几乎在一直线上，所以这天海水受到 的潮引力最大。（大潮） ? 地形：跟钱塘江口状似喇叭形有关，潮水易 进难退。当大量潮水从钱塘江口涌进来时，由 于江面迅速缩小，使潮水来不及均匀上升，就 只好后浪推前浪，层层相叠。
精品资料潮汐与潮流精品资料潮汐和潮流4b517孙晓张颖乔如娟胡婉君精品资料潮汐和潮流一线潮精品资料潮汐和潮流交叉潮精品资料潮汐和潮流回头潮精品资料潮汐和潮流一潮汐概念二潮汐成因三潮汐变化潮汐和潮流精品资料潮汐和潮流?潮汐与潮流在月球太阳和其他天体引潮力的作用下地表海水发生周期性运动的现象为潮汐
潮汐和潮流
逢朔、望，月、日、地三 个天体中心大致在同一条 直线上，由于月球和太阳 的引潮力叠加，因而所形 成的引潮力在一个月内是 最大的。
此时，高潮潮位特高，低 潮潮位特低，潮差最大。 称为大潮
逢上（下）弦（初 八、二十三），月 、日、地三者的位 置形成直角，月、 日的引潮力相互抵 消一部分，故此时 合成引潮力最小。
4b517孙晓 张颖 乔如娟胡婉君
潮汐和潮流
一线潮
交叉潮
潮汐和潮流
回头潮
潮汐和潮流
潮汐和潮流
潮汐和潮流
航海学潮汐教案

航海学潮汐教案

第一章潮汐与潮流一．概述潮汐(Tide)高潮(High Water/HW)低潮(Low Water/LW)涨潮(Flood Tide)落潮(Ebb Tide)潮流往复流(Alternating Current)回转流(Rotary Current)潮汐的基本成因与潮汐不等二．潮汐基本成因1. 平衡潮理论两个假设整个地球被等深的大洋所覆盖，所有自然因素对潮汐不起作用；海水无摩擦力和惯性力，外力使海水在任何时候都处于平衡状态。

2. 月球引力月球对地球的吸引力：地球表面某水质点所受引力➢公式：➢特点：➢大小➢方向3. 惯性离心力地-月公共质心地球各点惯性离心力➢地球的平动运动➢地心E：➢地面各点：相等、平行、背离月球4. 月引潮力与月潮椭圆体月球引力惯性离心力月引潮力➢地心：➢地面：月潮椭圆体5. 潮汐基本成因成因：月引潮力+ 地球自转现象：A1(上中天)：HW1A2(转90O)：LW1A3(下中天)：HW2A4(转90O)：LW2太阴日：24h48m潮汐周期：12h24m（半日潮）（END）三．潮汐不等（周日不等、半月不等、视差不等）1.周日不等成因：δ≠0 且ϕ≠0现象：ϕ≠0 ：两次HW(LW)潮高不等；涨(落)潮时间间隔不等；ϕ=0 ：无不等现象。

ϕ >90o- δ：一次高潮与一次低潮。

特点：ϕ、δ愈大，现象愈显著。

2. （1）半月不等成因：太阳引潮力太阳引潮力特点：➢比月引潮力小2.17倍；➢半日潮周期约为12h。

现象：➢新月/满月：引潮力相互叠加->大潮➢上弦/下弦：引潮力部分抵销->小潮（2）潮汐半月变化规律：新月/满月时潮汐现象：太阳引潮力和月引潮力相互叠加高潮最高，低潮最低->大潮（END）上弦/下弦时潮汐现象月引潮力与太阳引潮力部分抵销高潮最低，低潮最高->小潮（END）新月(朔)->上弦->满月(望)->下弦-> 新月潮汐大潮小潮大潮小潮大潮高潮高max min max min max低潮高min max min max min潮差max min max min max四. 潮汐调和分析简介潮汐静力学理论不足（两个假设、实际情况、原因）潮汐预报法：潮汐调和分析法（潮汐静力学理论＋潮汐动力学理论）潮汐调和分析法：原理：方法：常见分潮（半日分潮、日分潮、浅海分潮）两个假设：整个地球被等深的大洋所覆盖，所有自然因素对潮汐不起作用；海水无摩擦力和惯性力，外力使海水在任何时候都处于平衡状态。

第一章--潮汐与潮流


A. 0点 B. 12点
C. 月中天时刻 D. A、B、C都对
思考练习
13、大潮的变化周期约为：
A. 半个太阳月 B. 一个太阴月 C. 半个朔望月 D. 以上都不对
14、地球表面上在受引潮力的作用下，其上指向球心的各点组成的水圈称之为：
______。
A. 真子午圈
B. 照耀圈
C. 卯酉圈
D. 向心圈
潮流
➢ 往复流(Alternating Current) ➢ 回转流(Rotary Current)
潮汐与潮流的意义
潮汐(tide):
潮汐(tide):
海面周期性的升降运动。其中，海面上升的过程称为 涨潮(flood tide)，当海面升到最高时，称为高潮(high water，HW)；海面下降的过程称为落潮(ebb tide)， 当海面降到最低时，称为低潮(low water，LW)。
上弦/下弦时潮汐现象
❖ 月引潮力与太 阳引潮力部分 抵销
上弦月 小潮 太阳潮椭圆体
❖ 高潮最低，低
潮最高->小潮
（END）
太阳引潮力
地球
月引潮力
太阳
月潮椭圆体
下弦月
潮汐半月变化规律
❖
新月(朔)->上弦->满月(望)->下弦-> 新月
❖ 潮 汐 大潮 小潮 大潮 小潮 大潮
❖ 高潮高 max min max
❖ 各地潮差不等，甚至非常悬殊。相邻 两地可能发生不同性质的潮汐。
（END）
潮汐静力学理论不足成因
“迟到、高潮间隙、潮龄”的产生
❖ 大陆对海水阻隔阻碍了理想的潮汐椭圆体的 形成；
❖ 海洋深浅不一，海底崎岖不平海水受较大摩 擦力；

海洋工程水文


(4)无潮点
在一些半封闭的海湾中，常常出现没有潮汐涨落的无潮点(区)，并 且同潮时线绕无潮点按顺时针或逆时针方向旋转，海湾两岸的潮差也常 不等。这一现象只有从潮汐动力学理论才能解释，潮波在传播过程中， 既受地形影响亦受利· 氏力影响，在海湾内常有潮波反射，与前进潮波 相会，出观纵、横向驻颧液运动，在两个振动的节线交点上，潮汐涨落 才为冬，此交点称为无潮点。
第二节 潮位观测与潮汐预报
一、潮位观测 近岸潮汐的变化不但与引潮力有关，还常受到水文气象因素、海岸 形态以及水下地形等影响，各地的差异甚大。到目前为止，无论是 应用潮汐静力学理论还是动力学理论的计算结果，都无法达到满足 实际工程应用的程度，尤其是对于地形复杂的边缘海域差距更大。 因此，按我国《港口工程技术规范》规定，港口工程建设须有20年 以上的实测潮位资料，对于远离验潮站的新建港口也必须至少具有 1年以上的实测潮位资料，用于推求设计潮位。我国沿海海洋站和 港口都设有验潮柱(水尺)和浮筒式验潮仪，长期地、系统地记录潮 位资料。在缺少潮位资料的海域进行工程设计时，应尽早设立临时 水尺或验潮仪进行短期潮位观测。 水位＝水尺读数+水尺零点高程
潮汐不等现象
除了上述的潮汐日不等、半月不等现象外，还有月不等、年不等与 多年不等现象．因为月球绕地球旋转的轨道为一椭圆，地球位于其内 一个焦点上。月球位于近地点时的引潮力比位于远地点时大40％，这 就形成了潮汐的月不等现象。同样，在1年周期中，地球绕太阳轨道 的近日点引潮力比远日点大10％，这样使潮汐大小有年周期的变化。
二、潮汐分析与预报
1 潮汐调和分析
潮汐调和分析的目的就是根据实测潮位过程推求当地各组成分潮的调和常数。
由实测潮位资料可以看出，各地潮位变化都具有较好的周期性，但各测站潮 位变化过程干差万别，这是因为潮汐的变化除了受到日、月引潮力的作用外，还 受到地区性的气象、水文、地形和深度等多种因素的影响．数学分析已经证明， 潮位曲线可以近似地用许多余弦曲线的叠加来表示，故海洋潮汐可以看作是由许 多振幅、周期、位相不同的分潮叠加组成，每一分潮都是由天球赤道面上作等速 圆周运动的某一假想天体所引起的。以月球引力为例，可以设想在天球上有许多 运动速度各异．和地球的距离各不相同的“假想月球”，它们围绕地球运动的轨 道都是圆，由这些假想月球对地球引潮力的合力应和实际月球的引潮力相同。每 一个假想天体对应一个分潮，例如主太阴半日分潮(M2)，就是由一个假想的理想 月球的引潮力所引起的，其绕地球周期和月球的周期相同，但它是在赤道平面上， 以地球为圆心作阅周运动。对于天球上的太阳和其它天体引力都可以参照应用。

航海学_潮汐与潮流


潮汐的基本成因
潮汐由天体的引潮力产生的。 引潮力：天体的引力和惯性离心力的合力。 对潮汐影响较大的是月球和太阳的引潮力，其中月球引潮力 是产生潮汐的主要因素，包括月球的引力和地球绕月地公共 质心进行平动运动所产生的惯性离心力。 两个假设 整个地球被等深的大洋所覆盖，所有自然因素对潮 汐不起作用； 海水无摩擦力和惯性力，外力使海水在任何时候都 处于平衡状态。
平潮（Slack Tide）：高潮前后的一段时间内，海面处于停止 状态，称为平潮。
高潮时（Time of High Water）：简记THW，平潮的中间时刻。 涨潮时间（Duration of Rise）：从低潮到高潮的时间间隔。 落潮时间（Duration of Fall）：从高潮到低潮的时间间隔。
潮汐与潮汐推算
潮汐的基本成因与潮汐不等 中版《潮汐表》与潮汐推算 英版《潮汐表》与潮汐推算 潮流推算
潮汐的基本成因和潮汐术语
用下产生的周期性的升降现象。
白天的海面上升为潮，晚上的海面上升为汐。 涨潮（Rising tide或Flood tide）：海面上升的过程。 落潮（Falling tide或Ebb tide ）：海面下降的过程。 高潮（High Water）：海面涨到最高位置时，称为高潮。 低潮（Low Water）：海面落到最低位置时，称为低潮。 潮流（Tidal Stream）：伴随海面周期性的升降运动而产生 的海水周期性的水平方向的流动。
月亮的赤纬为零时称为分点潮。
月球赤纬增大，周日不等的现象更为显著，且与测者的地理 纬度有关，即 、愈大，现象愈显著。 。 当测者纬度很高( >90- ) ，月亮赤纬又较大时，某相邻的 低高潮和高低潮的高度可能相差无几，形成一天只有一次高潮、 一次低潮，称为日潮现象。 当月赤纬达到最大时，潮汐周日不等现象最为显著，月赤纬 最大时的潮汐称为回归潮。

航海学潮汐教案

附港潮汐推算（中版）
差比数表预报内容
公式
附港高(低)潮潮时＝主港高(低)潮潮时＋高(低)潮潮时差
附港高(低)潮潮高＝[主港高(低)潮潮高－（主港MSL＋主港SC）]×潮差比＋（附港MSL＋附港SC）
或：附港高(低)潮＝主港高(低)潮潮高×潮差比＋改正值
步骤
实例1、实例2（END）
高潮时差、低潮时差、潮差比、改正值；
铜沙2月1日潮时（中版）
高潮潮时低潮潮时
吴凇（2月1日）0327 1539 1127 2358
潮时差＋) -0157 -0157 -0221 -0221
铜沙（2月1日）0130 1342 0906 2137
（END）
高潮潮高低潮潮高
吴凇潮高315 328 059 059
季改后MSL - ) 177 177 177 177
低高潮（Lower high water, LHW）
平均大潮高潮面
（Mean high water spring, MHWS）
平均大潮低潮面
（Mean low water spring, MLWS）
平均小潮高潮面
（Mean high water neap, MHWN）
平均小潮低潮面
（Mean low water neap, MLWN）
号、差比数；
2.港口编号、月份－平均海面季节改正表
主附港平均海面MSL和季节改正SC；
3.主港名、日期－主港潮汐预报表主港当日
潮汐资料；
4.按相应公式计算。
附港潮汐推算实例1（中版）
例1：求铜沙94年2月1日高(低)潮潮时、潮高。
解：查1994年第一册《潮汐表》差比数表得：
铜沙编号：5012；MSL：260cm

潮汐与潮流

第一章潮汐与潮流一﹑简答题1.试述潮汐的成因。

2.何谓潮汐的周日不等?其产生的原因?3.试述潮汐的半月不等。

4.试述潮汐类型。

5.何谓潮差和潮差比。

6.何谓分点潮和回归潮。

7.试述中版<<潮汐表>>由几册组成?各册范围和主要内容?8.试写出应用差比数进行潮汐推算的公式。

9.试述英版<<潮汐表>>由几卷组成?各卷范围和主要内容?二﹑计算题1.某轮X日要过A浅滩,已知该轮吃水8米,要求安全富裕水深0.7米,A浅滩海图水深5米.海图深度基准面在平均海面下2.5米,潮高基准面在平均海面下1.5米,求该日过浅滩时所需潮高.2.某水道海图最小水深6.5米,潮高基准面在平均海面下220cm,海图基准面在平均海面下200cm.某轮吃水7.8米,要求安全富裕水深1米.又该水道上空有一架空电缆高33米,该轮水线上最大高度30米,要求安全余量2米.求该轮应在多少潮高范围内通过该水道.(该地大潮升330cm,小潮升110cm)3.求铜沙X年10月20日的高、低潮时和潮高.(利用附表9“潮汐表”﹑附表10“差比数和潮信表”及附表11“平均海面季节改正值”)4.X年5月22日0100某轮抵长江口锚地抛锚.锚地距铜沙24n mile,船速12kn,吃水8.5m,要求保留安全富裕水深0.7m,铜沙航道最浅海图水深6.2m,试求该轮最早何时起锚方可安全通过铜沙.5.X年7月5日1500某轮预计抵达铜沙，试求当时铜沙潮高是多少？6.某轮吃水8m,预计某日上午0800抵达某浅滩,已知该处海图水深6.0m,海图基准面在平均海面下300cm,潮高基准面在平均海面下280cm,要求保留富裕水深0.7m,若该地当日潮汐为: 0630 110cm 1250 450cm, 试问:该轮是否需要候潮? 若需候潮,该轮当日上午最早能安全通过浅滩的时机.7.某轮从秦皇岛装煤运上海,拟在12月5日上午进长江南水道.满载吃水为8.6m,铜沙浅滩在深度基准面下 6.7m,要求保留富裕水深0.7m,求该轮过浅滩的时间范围?该轮航速16kn,从秦皇岛到铜沙浅滩的航程是697n mile.如果选择白天高潮前1小时过浅滩,该轮应在何日何时之前离开秦皇岛港?附:12月5日浅滩附近的潮汐: 0236 0.5m 0812 3.5m 1448 0.9m 2024 3.3m8.海图上有图式得知该处当天潮汐为1230 395；1850 125，求1530该障碍物上的水面高度或水下的深度是多少？9.海图上一图式 15，并得知该处当天潮汐为1230 395；1850 125，求1530该障碍物上的水面高度或水下的深度是多少？10.我国沿海某地大潮升4.4米，小潮升3.0米，平均海面2.5米,求农历初五的高、低潮潮高。

潮汐和潮流


二、潮汐不等现象
2、潮汐半月不等 在朔（农历初一，也称新月）或望（农历 十五，也称满月）日，太阳、月亮和地球的位 置几乎在一条线上，这时太阳引潮力和月球引 潮力几乎作用于潮汐同一方向，互相叠加，因 而出现了高潮最高和低潮最低的潮汐现象，这 时高潮潮高与低潮潮高之差也最大即潮差最大， 称为大潮。
二、潮汐不等现象
在上弦（农历初七、初八）或下弦（农历二十二、 二十三）日，太阳、月亮和地球三者在空间位置几 乎成直角，太阳的引潮力与月亮引潮力方向几乎垂 直，最大限度相互削弱，因而出现高潮最低和低潮 最高的潮汐现象，这时潮差最小，称为小潮。 大潮和小潮在农历一个月中各出现两次，因此潮 差是以半个太阳月（14.5天）为周期变化的，故称 为潮汐半月不等。
二、潮汐不等现象
（2）月球赤纬不等于0度时的潮汐现象 a、在一个潮汐的周期中，在纬度小于90度减 去赤纬的地区出现混合潮（也称不规则半日 潮），在赤道地区出现半日潮；在纬度大于90 度减去赤纬的地区出现日潮。 b、除赤道地区外，各地区的高潮与低潮之间 的时间间隔均不等于6h12min ； c、除赤道地区外，各地两次的高潮潮高均不 等。
潮汐和潮流
潮汐与潮流
潮汐：海面在周期性外力作用下产生的周期性升 降运动。 涨潮：海面上升的过程。 高潮：当海面升到最高时。 落潮：海面下降的过程。 低潮：海面下降的过程。 潮流：伴随海水周期性的涨落现象，还同时产生海 水周期性的水平方向流动，即产生潮流。 我国古代将白天海水上涨称为潮；晚上上涨称为汐。
一、潮汐的成因
潮汐是因天体的引潮力而产生的。 天体的引力与惯性离心力的矢量和称为引潮力。 其中月球的引潮力是形成潮汐的主要力量。 1、月球的引潮力 （1）月球的引力 （2）地球绕月球和地球的公有质心旋转时所 产生的惯性离心力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


月球引力 惯性离心力 月引潮力

D
地心： 地面：
A M
E
B

月潮椭圆体
（END）
C
潮汐基本成因
成因：月引潮力 + 地球自转 现象： A1(上中天)：HW1 A2(转90O)：LW1 M A3(下中天)：HW2 A4(转90O)：LW2 太阴日：24h48m 潮汐周期：12h24m（半日潮）

（END）
A 4
A 1
P A 2 E
A 3
潮汐周日不等
成因：0 现象：
且 0
Z 1
1
P N D 1 L Z 2 Q 2 L ' P S D 2 Z 3 Q 3
M 0 ： Q 两次HW(LW)潮高不等； 涨(落)潮时间间隔不等； =0 ：无不等现象。 >90o- ：一次高潮与一次低潮。 特点： 、愈大，现象愈显著。

新月 太阳引潮力
太阳
太阳引潮力和月引潮力相互叠加 高潮最高，低潮最低->大潮（END）
上弦/下弦时潮汐现象
上弦月
月引潮力与太 阳引潮力部分 抵销 高潮最低，低 潮最高->小潮

（END）
小潮 太阳潮椭圆体 太阳引潮力 地球 月引潮力 月潮椭圆体 太阳
下弦月
潮汐半月变化规律


mM 1 地心E： f E k 2 R
（END）
地面各点：相等、平行、背离月球
月引潮力与月潮椭圆体

月球引力
D
A M
E
B
C
月引潮力与月潮椭圆体


月球引C
月引潮力与月潮椭圆体


月球引力 惯性离心力 月引潮力

D
地心： 地面：
A M
E
B
C
月引潮力与月潮椭圆体
思考练习
1、产生大潮小潮的原因主要由于： A、月球、太阳赤纬较大引起的。 B、月球、太阳地球相互位置不同引起的。 C、月引潮力与太阳引潮力的合力不同引起的。 D、B、C都对。 2、潮汐半月不等的潮汐现象是： A、从新月到上弦潮差逐渐增大。 B、从新月到满月潮差逐渐减小。 C、潮差的变化是以半个太阴月为周期。 D、A、B、C都不对。 3、潮汐半月不等主要是由于______引起的。 A、月亮赤纬较大 B、太阳赤纬较大 C、日、月与地球相互位置不同 D、日、月对地球的距离的变化 4、潮汐产生的原动力是______，其中主要是______。 A. 月球引潮力、太阳引潮力 B. 天体引潮力、太阳引潮力 C. 天体引潮力、月球引潮力 D. 太阳引潮力、月球引潮力 5、潮汐的视差不等主要是由于： A、太阳、月球与地球相对位置的不同引起的 B、月球赤纬不同引起 C、太阳、月球与地球的距离变化引起的 D、太阳赤纬的不同引起的
（END）
潮汐半月不等


成因：太阳引潮力 太阳引潮力特点：
比月引潮力小2.17倍； 半日潮周期约为12h。


现象：

新月/满月：引潮力相互叠加->大潮 上弦/下弦：引潮力部分抵销->小潮

（END）
潮汐半月变化规律
新月/满月时潮汐现象
月潮椭圆体 太阳潮椭圆体 大潮 P 满月 月引潮力
潮流(tidal stream):
伴随海水周期性涨落现象，同时产生的海水周 期性的水平方向流动。
潮汐与潮流的意义
潮汐与渔业、盐业、港口建筑以及海水动力利用有 着十分密切的关系。潮汐与航海的关系也非常重要，将 直接影响船舶航行计划的实施和航海安全，如需要通过 浅水区，需预先依据潮汐资料计算出当地潮高，并正确 调整货载和吃水差；为了保证船舶安全地行驶在计划航 线上，需随时掌握当地潮汐与潮流资料，观测船位，调 整航向，即使在港内也不容忽视潮汐、潮流对船舶安全 的影响。
第一章 潮汐与潮流




概述 潮汐的基本成因与潮汐不等 潮汐调和分析简介 潮汐类型与潮汐术语 中版《潮汐表》与潮汐推算 英版《潮汐表》与潮汐推算 潮流推算
（END）
潮汐概述
潮汐(Tide)



高潮(High Water/HW) 低潮(Low Water/LW) 涨潮(Flood Tide) 落潮(Ebb Tide)
潮流


往复流(Alternating Current) 回转流(Rotary Current)
潮汐与潮流的意义
潮汐(tide):
潮汐(tide): 海面周期性的升降运动。其中，海面上升的过程称为 涨潮(flood tide)，当海面升到最高时，称为高潮(high water，HW)；海面下降的过程称为落潮(ebb tide)， 当海面降到最低时，称为低潮(low water，LW)。
潮汐基本成因与潮汐不等

潮汐基本成因



平衡潮理论两个假设 月球引力 惯性离心力 月引潮力与月潮椭圆体 潮汐基本成因

潮汐不等（周日不等、半月不等、视差不等）
（END）
平衡潮理论假设

天体引力（月球*、太阳） 潮汐 引潮力 惯性离心力

两个假设
整个地球被等深的大洋所覆盖，所有自然 因素对潮汐不起作用； 海水无摩擦力和惯性力，外力使海水在任何 时候都处于平衡状态。
新月(朔)->上弦->满月(望)->下弦-> 新月
潮 汐 大潮 小潮 大潮 小潮 大潮
高潮高 max
低潮高 min
min
max
max
min
min
max
max
min
潮 差
（END）
max
min
max
min
max
潮汐的视差不等
由于月球是沿椭圆轨道绕地球转动的，地球在椭圆轨道 的一个焦点上。当月球位于近地点时(距离约为57个地球半径) 其引潮力要比位于远地点(距离约为63.7个地球半径)时大40％， 这种由于地球和月球距离变化而产生的潮汐不等，称为潮汐 视差不等(parallax inequality of tide)，其周期为一个恒星月， 约27.3天。太阳潮中也同样存在视差不等的现象。每年1月3 日前后，地球离太阳最近，此点为近日点，此时日、地相距 14.71╳l08km，而每年7月4日前后，地球离太阳最远，此点为 远日点，此时日、地相距15．21╳l08km ,近日点的引潮力比 远日点的引潮力大10％，其周期为一个回归年，约365.24日。

（END）
月球引力


mM m E 月球对地球的吸引力：f k R2
公式： f p k mM 1 2 x 特点： 大小 M 方向

地球表面某水质点所受引力
x R
E
（END）
惯性离心力

地-月公共质心
M
07 .3 r
G
E

地球各点惯性离心力

地球的平动运动