2010学年第二学期七年级数学独立作业_7

321七年级（下学期）数学独立作业 学生姓名一、填空题：1、()=-⋅⎪⎭⎫ ⎝⎛n n221 ；=÷-++112n n y y；=-23])[(m . 2、如图，直线a ∥b ，那么∠A= .第6题图3、如果一个等腰三角形的两条边长分别为2、4，那么这个三角形的周长是 .4、图中阴暗部分的面积是 .5、如图，平面镜A 与B 之间的夹角为120°，光线经平面镜A 反射后射在平面镜B 上，再反射出去，若∠1＝∠2，则∠1的度数为 .6、如图，给出了过直线外一点作已知直线的平行线的方法，其依据是 .7、若(x-m)2=x 2+4x+a ,则 a ｍ＝ ．8、若多项式225x kx ++是一个完全平方式，则k ＝ .9、(1)当a 时，1)3(0=+a ． (2)已知210,t t +-=则322t t ++2008= .10、 已1nm=10-9m ，花粉的直径为35 000nm ，那么这种花粉的直径用科学记数法可记为___________m 。

11、右图为6个边长等的正方形的组合图形，则123∠+∠+∠= ．（第11题）12、如图，边长为4cm 的正方形ABCD 先向上平移2cm ，再向右平移1cm ，得到正方形A′B′C′D′，此时阴影部分的面积为_______cm 2．13、如图，它是由6个面积为1的小正方形组成的长方形，点A 、B 、C 、D 、E 、F 是小正方形的顶点，以这六个点中的任意三点为顶点，可以组成________个面积是1的三角形．14、已知在△ABC 中，已知点D 、E 、F 分别为BC 、AD 、CE 的中点，且S △ABC ＝4cm 2，则S △BEF 的值为________cm 2．15、已知1639273m m ⨯⨯=,则m= .A B C a b 28° 50° 第2题图 120° 第5题图 12aba 21 b 21 第4题图 A B D A′ D ′ C ′ B ′ （第12题） A B CD E F （第13题） A B CD E F（第14题）绿化园地 16、如果一个多边形的每个内角都相等，且内角比与它相邻的外角大100°，则这个多边形的内角和等于 度 二、选择题17、如果(),990-=a ()11.0--=b ,235-⎪⎭⎫⎝⎛-=c ,那么c b a ,,三数的大小为( )A.c b a >>B.b a c >>C.b c a >>D.a b c >> 18、下面计算中，正确的是 （ ） A 、(m+n)(-m+n)=－m 2+n 2B 、5523)()(n m n m n m +=++C 、69323)(b a b a -=-- D 、a a a =-2323 19、计算3112)(n n x x x +-⋅⋅的结果为( ) A.33+n xB.36+n xC.nx12 D.66+n x20、下列各式中，能用平方差公式计算的是（ ） A ．)3)(3(+--x x B ．)2)(2(b a b a -+ C ．)1)(1(---a aD ．2)3(-x21、如图，在一个长方形花园ABCD 中，AB=a ，AD=b ，花园中建有一条长方形道路LMPQ 及一条平行四边形道路RSKT ，若LM=RS=c ，则花园中可绿化部分的面积为 （ ）A 、2b ac ab bc ++-B 、ac bc ab a -++2C 、2c ac bc ab +--D 、ab a bc b -+-22（第21题图） （第23题图） （第24题图）22、篮子里有若干苹果，可以平均分给)1(+x 名同学，也可以平均分给)3(-x 名同学（x 为大于3的正整数），用代数式表示苹果数量不可能是 （ ）A ．322-+x xB ．322--x x C ．)3)(1(3-+x x D ．)32(2--x x x23、 如图，正方形ABCD 和CEFG 的边长分别为m 、n ，那么∆AEG 的面积的值 （ ） A ．与m 、n 的大小都有关 B ．与m 、n 的大小都无关 C ．只与m 的大小有关 D ．只与n 的大小有关24、已知 n 是大于1的自然数,则()()11+--⋅-n n c c 等于 ( )A.()12--n c B.nc 2- C.nc 2- D.nc2三、解答题： 25、计算A D GF(1) 022)14.3(3)2(4π-÷---- (2)3105322334)()2()(2a a a a a a ÷+-⋅-+29、（1）化简（2x-3y ）2 +(2x+3y)2（2）先化简，再求值：32233)21()(ab b a -+-⋅，其中441==b a ，.（3）因式分解a 2－10a ＋25 （4）a 2（x －y ）－b 2（x －y ）30、先化简，再求值(2a ＋b)2－(3a －b)2+5a(a －b) ，其中a=2，b= 1531、如图AB ∥DE ，且有∠1＝∠2，∠3＝∠4，试说明：BC ∥EF 解：∵AB ∥DE(已知)∴∠1＝_____ (两直线平行，同位角相等)∵∠1＝∠2，∠3＝∠4 (已知)∴∠2＝ (等量代换) ∴BC ∥EF (________________________)32、如图，在△ABC 中，∠BAC 是钝角，请画出AB 边上的高CD ，BC 边上的中线AE ，∠B 的平分线BF 。

七年级数学独立作业2010. 9.16班级__________姓名________一、选择题（每题只有一个答案,2分×12=24分）1．下列说法中,准确的是 （ ）A ．有理数就是正数和负数的统称B ．零不是自然数,但是正数C ．一个有理数不是整数就是分数D ．正分数、零、负分数统称分数2．下列说法中,准确的是 （ ）A 1是最小的正数B ． 最大的负数是－1C ．任何有理数的绝对值都是正数D ．任何有理数的绝对值都不可能小于03．若︱a ︱=－a ， 则a 是 （ ）A ．零B ．负数C ．非负数D ．负数或零4．如图数轴上的A 、B 两点分别表示有理数a 、b,下列式子中不准确的是 （ ）A ． a + b < 0B ． a+b =a +bC ．（－a ）＋b ＞ 0D ． b > a5．相反数等于其本身的数有 （ ）A ．1个B ．2个C ．0个D ．无数个6．下列说法准确的是 （ ）A ．）与（2)21(+-互为相反数 B ．5的相反数是5-C ．数轴上表示－a 的点一定在原点的左边D ．任何负数都小于它的相反数 7．两个有理数的和（ ）A ．一定大于其中的一个加数B ．一定小于其中的一个加数C ．大小由两个加数符号决定D ．大小由两个加数的符号及绝对值而决定8．关于数0,下列几种说法不准确的是 （ ）A ． 0既不是正数,也不是负数B ． 0的相反数是0C ． 0的绝对值是0D ． 0是整数，但不是自然数9．41-的相反数与绝对值等于41的数的和应等于 （ ）A.21B.0C.21-D.21或0 10．四个数相加，和为负，则其中负加数有 （ ）A ． 1个B ． 3个C ． 最少1个D ．最多3个11．有下列各数，0.01，10，－6.67，31-，0，－90，－（－3），2--，+（-4），其中属于非负整数的共有 （ ）A ．1个B ．2个C ．3个D ．4个12．已知013=-++b a ,则b a +的相反数是 ( )A.-4B.4C.2D.-2二、填空(每空2分，共18分)13．点A 表示数轴上的一个点,将点A 向右移动7个单位,再向左移动4个单位,终点恰好是原点,则点A 表示的数是 ．14．三个数－12、－2、＋7的和比它们的绝对值的和小 ．15．绝对值不大于421的所有整数的和为 ． 16．已知数轴上有A 、B 两点,点A 与原点的距离为2, A 、B 两点的距离为1,则满足条件的点B 所表示的数是 ．17．若某次数学考试标准成绩定为85分，规定高于标准记为正，两位学生的成绩分别记作：+9；－3，则两名学生的实际得分为_______、_______．18．按规律填数:21, 61-,121,201-,301,_________ ． 19．2008年8月8日，第29届奥运会在北京开幕，5个城市的国际标准时间(单位：时)在数轴上的表示如图所示，那么北京时间2008年8月8日20时应是 ．A ．伦敦时间2008年8月8日11时B ．巴黎时间2008年8月8日13时C ．纽约时间2008年8月8日5时D ．首尔时间2008年8月8日19时20．用●表示实心圆，用○表示空心圆，现有若干个实心圆与空心圆，按一定的规律排列如下：●○●●○●●●○●○●●○●●●○●○●●○●●●○…… 问：前2009个 圆中，有________ __个空心圆．21．用“＜”“＝”或“＞”号填空＋|－５|_____－|－４| －(＋5) _____－[－|－5|]三、解答题：( 4分×6=24分)22．⑴)25.1(++)431()43()21(++-+- （2）152()( 2.5)(5)( 2.5)1717++-+-+++（3）3557()()()212212-+-++- （4）(+3)(-21)+(-19)+(+12)+(+5)23．（共8分）把下列各数填入表示它所在的数集的大括号：－2.4，3，2.004，－310，141，－••15.0，0，－(－2.28)，3.14，－|－4|。

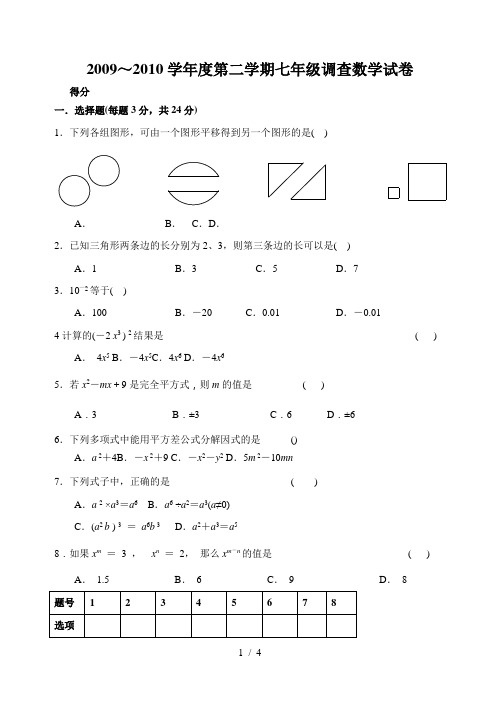
2009～2010学年度第二学期七年级调查数学试卷得分一．选择题(每题3分，共24分)1．下列各组图形，可由一个图形平移得到另一个图形的是( )A．B．C．D．2．已知三角形两条边的长分别为2、3，则第三条边的长可以是( )A．1 B．3 C．5 D．73．10—2等于( )A．100 B．－20 C．0.01 D．－0.014计算的(－2 x3 ) 2结果是( ) A．4x5 B．－4x5C．4x6 D．－4x65．若x2－mx＋9是完全平方式，则m的值是( )A．3 B．±3 C．6 D．±66．下列多项式中能用平方差公式分解因式的是()A．a 2＋4B．－x 2＋9 C．－x2－y2 D．5m 2－10mn7．下列式子中，正确的是( )A．a 2 ×a3＝a6B．a6 ÷a2＝a3(a≠0)C．(a2 b ) 3＝a6b 3D．a2＋a3＝a58．如果x m＝3 ，x n＝2，那么x m－n的值是( ) A．1.5 B．6 C．9 D．8二．填空题(每空3分，共30分) 9．计算：(1)(－3)0＝；(2)(a 2)3＝．10．在△ABC 中，∠A=120度,∠B=∠C ，则∠C=度 11．已知二元一次3x+2y=4,且x,y 互为相反数，则xy=.12． 2009年我省为335万名农村中小学生免费提供教科书，减轻了农民的负担。

335万用科学计数法可表示为。

13．计算3x 3·(－2x 2y)的结果是．14．如下图，圆环形绿地的面积是m 2(结果保留π)． 15．一副三角板放置如下图，则图中∠ABC ＝°．(第14题图) (第15题图) (第16题图)16．如上图，添加一个条件，可以得到l 1∥l 2，理由是．三．解答题（共46分） 17．（5×2）分）计算或解方程组 （1）(－3)2－2×22 + 0.50 （2）32528x y x y +=⎧⎨-=⎩ 54312l 2l 118.(7分)如图，已知∠CFD =∠BEA ，BE=CF ，AE=DF ，求AB=DC .19．( 7分)如图，三角形ABC 中，已知∠C ＝45°，∠ADB ＝90°，DE 为的∠ADB 平分线，DE 与CA 平行吗？说明你的理由．20．(6分)已知：如图，在△ABC 中，∠BAC=900,AB=AC 。

县杨汛桥镇中学2021-2021学年七年级数学下学期第二次HY 作业试题一、选择题〔每一小题2分，满分是20分〕1.为理解全校学生的课外作业量，你认为抽样方法比拟适宜的是〔 〕A 调查全体女生B 调查全体男生C 调查九年级学生D 调查七、八、九年级各100名学生2.以下现象中，属于平移现象的为〔 〕A ．方向盘的转动B ．自行车行驶时车轮的转动C ．钟摆的运动D ．电梯的升降3. 以下运算正确的选项是 ( )A ．2a a a +=B ．325()a a -= C. 34a a a = D. 22(2)2a a =4. 假设分式121x x -+无意义，那么x 的取值范围是〔 〕 A ．1x ≠ B ．12x ≠- C ．1x = D ．12x =- 5. 方程是二元一次方程，那么的取值为〔 〕 A ．0a ≠ B ．1a ≠- C ．1a ≠ D ．2a ≠6. 假设224x Mxy y -+是一个完全平方式，那么M 的值是〔 〕A ．2B ． ±2C ．4D ．±4221121a a a a a--÷++的结果是〔 〕 A.12 B.1a a + C.1a a + D.12a a ++ 8.一个样本一共有20个数据：28，29，30，26，28，25，18，20，35，25，29，27，21，25，24，26，24，22，23，28，假如取组距为3，那么这组数据可以分成〔 〕A. 4组B. 5组C. 6组D. 7组9. 楠溪江某景点门票价格：成人票每张70元，儿童票每张35元．小明买20张门票一共花了1225元，设其中有x 张成人票，y 张儿童票，根据题意，以下方程组正确的选项是〔 〕A ．B ．C ．D ．10. 如图，AB ∥EF ，∠C=90°，那么α、β、γ的关系为〔 〕A.βαγ∠=∠+∠B. 0180αβγ∠+∠+∠=C.090βγα∠+∠-∠=D. 090αβγ∠+∠-∠=二、填空题〔每一小题3分，满分是30分〕11、10(1)(2)--+-= 。

2019-2020年七年级（下）第二次独立作业数学试卷一、选择题：（本大题共有8小题，每小题2分，共16分．）1．下列计算结果正确的是（）A．（2x5）3=6x15 B．（﹣x4）3=﹣x12C．（2x3）2=2x6D．[（﹣x）3]4=x72．如果a＞b，那么下列各式中一定正确的是（）A．a﹣3＜b﹣3 B．3a＞3b C．﹣3a＞﹣3b D．3．下列等式由左边到右边的变形中，属于因式分解的是（）A．（a+1）（a﹣1）=a2﹣1 B．a2﹣6a+9=（a﹣3）2C．x2+2x+1=x（x+2）+1 D．﹣18x4y3=﹣6x2y2•3x2y4．四根长度分别为3cm、4cm、7cm、10cm的木条，以其中三根的长为边长钉成一个三角形框架，那么这个框架的周长可能是（）A．14cm B．17cm C．20cm D．21cm5．如果不等式组有解，那么m的取值范围是（）A．m＞8 B．m＜8 C．m≥8 D．m≤86．为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地抽查了10000人，并进行统计分析．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人．如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（）A．B．C．D．7．已知4x2+mxy+25y2是完全平方式，则m的值为（）A．10 B．±10 C．20 D．±208．如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个长方形的两边长（x＞y），观察图案及以下关系式：①x﹣y=n；②xy=；③x2﹣y2=mn；④x2+y2=．其中正确的关系式的个数有（）A．1个B．2个C．3个D．4个二、填空题：（本大题共10小题，每空2分，共20分.）9．已知一粒米的质量是0.0000021千克，用科学记数法表示为2.1×10﹣6千克．10．若（x+2）（x﹣n）=x2+mx﹣12，则m﹣n=．11．方程3x m﹣2﹣2y2n﹣1=7是关于x、y的二元一次方程，则m=；n=．12．若x，y满足|x﹣y+1|+（x+y+3）2=0，则x2﹣y2=．13．已知方程3x+y=1的一个解是（a≠0），那么9a+3b﹣2的值为．14．如图，BC⊥ED于O，∠A=45°，∠D=20°，则∠B=°．15．不等式mx﹣2＜3x+4的解集是x＞，则m的取值范围是．16．某种商品的进价为800元，出售标价为1 200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则最低可打折．17．已知关于x的不等式组的整数解共有5个，则a的取值范围是．18．若方程组的解是，则方程组的解为．三、解答题（共64分）19．计算（1）（3.14﹣π）0﹣32+|﹣4|+（）﹣2（2）（﹣2a2b3）4+（﹣a）8•（2b4）3．20．分解因式（1）﹣8ax2+16axy﹣8ay2（2）16（a﹣b）2﹣9（a+b）2．21．解方程组或不等式（1）（2）﹣＜4．22．解不等式组并在数轴上表示出解集．23．先化简，再求值：（2a+b）2+5a（a+b）﹣（3a﹣b）2，其中a=3，b=﹣．24．如图，BD是△ABC的角平分线，DE∥BC，交AB于点E，∠A=45°，∠BDC=60°，求∠BED的度数．25．若不等式组的解集是﹣1＜x＜3，（1）求代数式（a+1）（b﹣1）的值；（2）若a，b，c为某三角形的三边长，试求|c﹣a﹣b|+|c﹣3|的值．26．xx年巴西世界杯正如火如荼的进行着，带给了全世界的球迷25个不眠之夜，足球比赛规则规定：每队胜一场得3分，平一场得1分，负一场得0分．（1）若夺冠热门巴西队如愿登顶，手捧大力神杯，在本届世界杯上巴西队共比赛7场，并且保持不败，共得分17分，求巴西队赢了几场比赛？（2）若A、B两队一共比赛了10场，A队保持不败且得分超过22分，A队至少胜多少场？27．对x，y定义一种新运算T，规定：（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：，已知T（1，﹣1）=﹣2，T（4，2）=1（1）求a，b的值；（2）若关于m的不等式组恰好有4个整数解，求实数p的取值范围．28．直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，AD、BC的延长线交于点F，点A、B在运动的过程中，∠F=；DE、CE又分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小也不发生变化，其大小为∠CED=．（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF=；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．xx学年江苏省泰州市靖江市靖城中学七年级（下）第二次独立作业数学试卷参考答案与试题解析一、选择题：（本大题共有8小题，每小题2分，共16分．）1．下列计算结果正确的是（）A．（2x5）3=6x15B．（﹣x4）3=﹣x12C．（2x3）2=2x6D．[（﹣x）3]4=x7【考点】幂的乘方与积的乘方．【分析】运用幂的乘方与积的乘方的法则判定即可．【解答】解：A、（2x5）3=8x15，故A选项错误；B、（﹣x4）3=﹣x12，故B选项正确；C、（2x3）2=4x6，故C选项错误；D、[（﹣x）3]4=x12，故D选项错误．故选：B．2．如果a＞b，那么下列各式中一定正确的是（）A．a﹣3＜b﹣3 B．3a＞3b C．﹣3a＞﹣3b D．【考点】不等式的性质．【分析】看各不等式是加（减）什么数，或乘（除以）哪个数得到的，用不用变号【解答】解：a＞b，A、a﹣3＞b﹣3，故A选项错误；B、3a＞3b，故B选项正确；C、﹣3a＜﹣3b，故C选项错误；D、﹣1＞﹣1，故D选项错误．故选：B．3．下列等式由左边到右边的变形中，属于因式分解的是（）A．（a+1）（a﹣1）=a2﹣1 B．a2﹣6a+9=（a﹣3）2C．x2+2x+1=x（x+2）+1 D．﹣18x4y3=﹣6x2y2•3x2y【考点】因式分解的意义．【分析】把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，由此判断即可．【解答】解：A、右边不是整式积的形式，不是因式分解，故本选项错误；B、属于因式分解，故本选项正确；C、右边不是整式积的形式，不是因式分解，故本选项错误；D、等号左边不是多项式，单项式不涉及因式分解，故本选项错误；故选B．4．四根长度分别为3cm、4cm、7cm、10cm的木条，以其中三根的长为边长钉成一个三角形框架，那么这个框架的周长可能是（）A．14cm B．17cm C．20cm D．21cm【考点】三角形三边关系．【分析】首先写出所有的组合情况，再进一步根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．【解答】解：其中的任意三条组合有4cm、7cm、10cm；3cm、4cm、7cm；3cm、7cm、10cm；3cm、4cm、10cm共四种情况，根据三角形的三边关系，则只有4cm、7cm、10cm符合，故周长是21cm．故选D．5．如果不等式组有解，那么m的取值范围是（）A．m＞8 B．m＜8 C．m≥8 D．m≤8【考点】不等式的解集．【分析】解出不等式组的解集，根据已知解集比较，可求出m的取值范围．【解答】解：∵不等式组有解∴m＜x＜8∴m＜8m的取值范围为m＜8．故选B．6．为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地抽查了10000人，并进行统计分析．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人．如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（）A．B．C．D．【考点】由实际问题抽象出二元一次方程组．【分析】根据“吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人，以及在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，”分别得出等式方程组成方程组，即可得出答案．【解答】解：设吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意得：．故选：B．7．已知4x2+mxy+25y2是完全平方式，则m的值为（）A．10 B．±10 C．20 D．±20【考点】完全平方式．【分析】先展开（2x±5y）2，再求出m的值．【解答】解：∵（2x±5y）2=4x2±20xy+25y2，∴m=±20，故选：D．8．如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个长方形的两边长（x＞y），观察图案及以下关系式：①x﹣y=n；②xy=；③x2﹣y2=mn；④x2+y2=．其中正确的关系式的个数有（）A．1个B．2个C．3个D．4个【考点】整式的混合运算；因式分解的应用．【分析】根据长方形的长和宽，结合图形进行判断，即可得出选项．【解答】解：①x﹣y等于小正方形的边长，即x﹣y=n，正确；②∵xy为小长方形的面积，∴xy=，故本项正确；③x2﹣y2=（x+y）（x﹣y）=mn，故本项正确；④x2+y2=（x+y）2﹣2xy=m2﹣2×=，故本项错误．则正确的有3个．故选C．二、填空题：（本大题共10小题，每空2分，共20分.）9．已知一粒米的质量是0.0000021千克，用科学记数法表示为2.1×10﹣6千克．【考点】科学记数法—表示较小的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：0.0000021=2.1×10﹣6，故答案为2.1×10﹣6，10．若（x+2）（x﹣n）=x2+mx﹣12，则m﹣n=﹣10．【考点】多项式乘多项式．【分析】先将左边展开，再根据等式的性质，得到关于m和n的方程组，求得m和n的值即可．【解答】解：∵（x+2）（x﹣n）=x2+mx﹣12，∴x2﹣nx+2x﹣2n=x2+mx﹣12，即x2+（2﹣n）x﹣2n=x2+mx﹣12，∴解得∴m﹣n=﹣4﹣6=﹣10故答案为：﹣1011．方程3x m﹣2﹣2y2n﹣1=7是关于x、y的二元一次方程，则m=3；n=1．【考点】二元一次方程的定义．【分析】根据二元一次方程的定义分别列出关于m、n的方程，通过解方程求得它们的值即可．【解答】解：根据题意，得m﹣2=1，2n﹣1=1，解得m=3，n=1．故答案是：3，1．12．若x，y满足|x﹣y+1|+（x+y+3）2=0，则x2﹣y2=3．【考点】因式分解-运用公式法；非负数的性质：绝对值；非负数的性质：偶次方．【分析】利用绝对值以及偶次方的意义得出关于x，y的方程组，求出即可．【解答】解：∵|x﹣y+1|+（x+y+3）2=0，∴，解得：，∴x2﹣y2=（x+y）（x﹣y）=（﹣2﹣1）×（﹣2+1）=3．故答案为：3．13．已知方程3x+y=1的一个解是（a≠0），那么9a+3b﹣2的值为1．【考点】二元一次方程的解．【分析】根据方程的解的定义，将方程的解代入得到3a+b的值，然后整体代入代数式计算即可得解．【解答】解：∵方程3x+y=1的一个解是（a≠0），∴3a+b=1，∴9a+3b﹣2=3（3a+b）﹣2=3×1﹣2=3﹣2=1．故答案为：1．14．如图，BC⊥ED于O，∠A=45°，∠D=20°，则∠B=25°．【考点】三角形的外角性质；三角形内角和定理．【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠A+∠D，根据垂直的定义可得∠BOE=90°，然后根据三角形的内角和定理列式计算即可得解．【解答】解：∵∠A=45°，∠D=20°，∴∠BED=∠A+∠D=45°+20°=65°，∵BC⊥ED，∴∠BOE=90°，∴∠B=90°﹣65°=25°．故答案为：25．15．不等式mx﹣2＜3x+4的解集是x＞，则m的取值范围是m＜3．【考点】解一元一次不等式．【分析】将不等式mx﹣2＜3x+4移项合并同类项得，（m﹣3）x＜6，由于其解为x＞，不等号的方向发生了改变，故m﹣3＜0，即可求得m的取值范围．【解答】解：不等式mx﹣2＜3x+4移项合并同类项得，（m﹣3）x＜6，又知不等式的解集为x＞，∴m﹣3＜0，∴m＜3．16．某种商品的进价为800元，出售标价为1 200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则最低可打七折．【考点】一元一次不等式的应用．【分析】设打x折，利用销售价减进价等于利润得到1200•﹣800≥800×5%，然后解不等式求出x的范围，从而得到x的最小值即可．【解答】解：设打x折，根据题意得1200•﹣800≥800×5%，解得x≥7．所以最低可打七折．故答案为七．17．已知关于x的不等式组的整数解共有5个，则a的取值范围是﹣3＜a≤﹣2．【考点】一元一次不等式组的整数解．【分析】将a看做已知数，求出不等式组的解集，根据解集中整数解有5个，即可确定出a 的范围．【解答】解：不等式组解得：a≤x≤2，∵不等式组的整数解有5个为2，1，0，﹣1，﹣2，∴﹣3＜a≤﹣2．故答案为：﹣3＜a≤﹣2．18．若方程组的解是，则方程组的解为．【考点】解二元一次方程组．【分析】把后面的方程组整理为关于，此方程与前面的方程组一样，它是关于x和y的方程组，所以x=21，y=﹣10，然后求出x和y即可．【解答】解：把方程组变形为，而方程组的解是，所以x=21，y=﹣10，解得x=6，y=﹣4，所以方程组的解为．故答案为．三、解答题（共64分）19．计算（1）（3.14﹣π）0﹣32+|﹣4|+（）﹣2（2）（﹣2a2b3）4+（﹣a）8•（2b4）3．【考点】单项式乘单项式；实数的运算；幂的乘方与积的乘方；零指数幂；负整数指数幂．【分析】（1）首先分别计算零次幂、乘方、绝对值、负整数指数幂，然后再计算有理数的加减即可；（2）首先计算积的乘方，然后再合并同类项即可．【解答】解：（1）原式=1﹣9+4+9=5；（2）原式=16a8b12+a8•8b12=16a8b12+8a8b12=24a8b12．20．分解因式（1）﹣8ax2+16axy﹣8ay2（2）16（a﹣b）2﹣9（a+b）2．【考点】提公因式法与公式法的综合运用．【分析】（1）首先提公因式﹣8a，再利用完全平方公式进行分解；（2）直接利用平方差进行分解即可．【解答】解：（1）原式=﹣8a（x2﹣2xy+y2）=﹣8a（x﹣y）2；（2）原式=[4（a﹣b）+3（a+b）][4（a﹣b）﹣3（a+b）]=（7a﹣b）（a﹣7b）．21．解方程组或不等式（1）（2）﹣＜4．【考点】解一元一次不等式；解二元一次方程组．【分析】（1）整理原方程组后利用加减消元法求解即可得；（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．【解答】解：（1）原方程组整理，得：，①﹣②，得：2x=﹣6，解得：x=﹣3，将x=﹣3代入①，得：﹣12﹣3y=﹣5，解得：y=﹣，∴方程组的解为：；（2）去分母，得：3（2x+3）﹣（x﹣2）＜24，去括号，得：6x+9﹣x+2＜24，移项、合并同类项，得：5x＜13，系数化为1，得：x＜．22．解不等式组并在数轴上表示出解集．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．【解答】解：，由①得，x＜3，由②得，x≥﹣1，故不等式组的解集为：﹣1≤x＜3．在数轴上表示为：．23．先化简，再求值：（2a+b）2+5a（a+b）﹣（3a﹣b）2，其中a=3，b=﹣．【考点】整式的混合运算—化简求值．【分析】先算乘法，再合并同类项，最后代入求出即可．【解答】解：（2a+b）2+5a（a+b）﹣（3a﹣b）2=4a2+4ab+b2+5a2+5ab﹣9a2+6ab﹣b2=15ab，当a=3，b=﹣时，原式=15×3×（﹣）=﹣30．24．如图，BD是△ABC的角平分线，DE∥BC，交AB于点E，∠A=45°，∠BDC=60°，求∠BED的度数．【考点】三角形的外角性质；角平分线的定义；平行线的性质．【分析】求∠BED的度数，应先求出∠ABC的度数，根据三角形的外角的性质可得，∠ABD=∠BDC﹣∠A=60°﹣45°=15°．再根据角平分线的定义可得，∠ABC=2∠ABD=2×15°=30°，根据两直线平行，同旁内角互补得∠BED的度数．【解答】解：∵∠BDC是△ABD的外角，∴∠ABD=∠BDC﹣∠A=60°﹣45°=15°．∵BD是△ABC的角平分线，∴∠DBC=15°∵DE∥BC，∴∠BDE=15°．∴∠BED=180°﹣∠BDE﹣∠DBE=180°﹣15°﹣15°=150°．25．若不等式组的解集是﹣1＜x＜3，（1）求代数式（a+1）（b﹣1）的值；（2）若a，b，c为某三角形的三边长，试求|c﹣a﹣b|+|c﹣3|的值．【考点】解一元一次不等式组；三角形三边关系．【分析】先把a，b当作已知条件求出不等式组的解集，再与已知解集相比较求出a，b的值．（1）直接把ab的值代入即可得出代数式的值；（2）根据三角形的三边关系判断出c﹣a﹣b的符号，再去绝对值符号．合并同类项即可．【解答】解：，由①得，x＜，由②得，x＞2b﹣3，∵不等式组的解集是﹣1＜x＜3，∴=3，2b﹣3=﹣1，∴a=5，b=1．（1）（a+1）（b﹣1）=（5+1）（2﹣1）=6；（2）∵a，b，c为某三角形的三边长，∴5﹣1＜c＜5+1，即4＜c＜6，∴c﹣a﹣b＜0，c﹣3＞0，∴原式=a+b﹣c+c﹣3=a+b﹣3=5+1﹣3=3．26．xx年巴西世界杯正如火如荼的进行着，带给了全世界的球迷25个不眠之夜，足球比赛规则规定：每队胜一场得3分，平一场得1分，负一场得0分．（1）若夺冠热门巴西队如愿登顶，手捧大力神杯，在本届世界杯上巴西队共比赛7场，并且保持不败，共得分17分，求巴西队赢了几场比赛？（2）若A、B两队一共比赛了10场，A队保持不败且得分超过22分，A队至少胜多少场？【考点】一元一次不等式的应用；一元一次方程的应用．【分析】（1）表示出巴西队的胜利场数和平局场数，进而根据题意得出等式即可；（2）利用已知表示出A队胜y场，进而得出不等式求出即可．【解答】解：（1）设巴西队赢了x场比赛，则平了（7﹣x）场，根据题意可得：3x+7﹣x=17解得：x=5，答：巴西队赢了5场比赛；（2）设A队胜y场，根据题意可得：3y+（10﹣y）＞22，解得：y＞6，答：A队至少胜7场比赛．27．对x，y定义一种新运算T，规定：（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：，已知T（1，﹣1）=﹣2，T（4，2）=1（1）求a，b的值；（2）若关于m的不等式组恰好有4个整数解，求实数p的取值范围．【考点】解二元一次方程组；一元一次不等式组的整数解．【分析】（1）根据题中的新定义列出关于a与b的方程组，求出方程组的解即可得到a与b 的值；（2）根据题中的新定义列出不等式组，根据不等式组恰好有4个正整数解，确定出p的范围即可．【解答】解：（1）根据题中的新定义得：，整理得：，①+②得：3a=3，即a=1，把a=1代入①得：b=3；（2）根据题中的新定义化简得：，整理得：，即﹣≤m＜，由不等式组恰好有4个整数解，即0，1，2，3，∴3＜≤4，即15＜9﹣3p≤20，解得：﹣≤p＜﹣2．28．直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，AD、BC的延长线交于点F，点A、B在运动的过程中，∠F=45°；DE、CE又分别是∠ADC 和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小也不发生变化，其大小为∠CED=67.5°．（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF=90°；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．【考点】三角形内角和定理；三角形的角平分线、中线和高；三角形的外角性质．【分析】（1）根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=∠OAB，∠ABE=∠ABO，由三角形内角和定理即可得出结论；（2）延长AD、BC交于点F，根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°，进而得出∠OAB+∠OBA=90°，故∠PAB+∠MBA=270°，再由AD、BC分别是∠BAP和∠ABM的角平分线，可知∠BAD=∠BAP，∠ABC=∠ABM，由三角形内角和定理可知∠F=45°，再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°，进而得出结论；（3））由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=∠BAO，∠EOQ=∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．【解答】解：（1）∠AEB的大小不变，∵直线MN与直线PQ垂直相交于O，∴∠AOB=90°，∴∠OAB+∠OBA=90°，∵AE、BE分别是∠BAO和∠ABO角的平分线，∴∠BAE=∠OAB，∠ABE=∠ABO，∴∠BAE+∠ABE=（∠OAB+∠ABO）=45°，∴∠AEB=135°；（2）∠CED的大小不变．延长AD、BC交于点F．∵直线MN与直线PQ垂直相交于O，∴∠AOB=90°，∴∠OAB+∠OBA=90°，∴∠PAB+∠MBA=270°，∵AD、BC分别是∠BAP和∠ABM的角平分线，∴∠BAD=∠BAP，∠ABC=∠ABM，∴∠BAD+∠ABC=（∠PAB+∠ABM）=135°，∴∠F=45°，∴∠FDC+∠FCD=135°，∴∠CDA+∠DCB=225°，∵DE、CE分别是∠ADC和∠BCD的角平分线，∴∠CDE+∠DCE=112.5°，∴∠E=67.5°；（3）∵∠BAO与∠BOQ的角平分线相交于E，∴∠EAO=∠BAO，∠EOQ=∠BOQ，∴∠E=∠EOQ﹣∠EAO=（∠BOQ﹣∠BAO）=∠ABO，∵AE、AF分别是∠BAO和∠OAG的角平分线，∴∠EAF=90°．在△AEF中，∵有一个角是另一个角的3倍，故有：①∠EAF=3∠E，∠E=30°，∠ABO=60°；②∠EAF=3∠F，∠E=60°，∠ABO=120°（舍去）；③∠F=3∠E，∠E=22.5°，∠ABO=45°；④∠E=3∠F，∠E=67.5°，∠ABO=135°（舍去）．∴∠ABO为60°或45°．xx年8月27日34352 8630 蘰{23274 5AEA 嫪22828 592C 夬39710 9B1E 鬞1S824167 5E67 幧30865 7891 碑33990 84C6 蓆29525 7355 獕21935 55AF 喯&。

第9章不等式与不等式组检测（§9.1）（时间45分钟满分100分）班级学号姓名得分一、填空题（每小题3分，共30分）1．用不等号连接下列各对数．（1）－1－2.1；(2)π 3.142；（3）－（－3）2―（―2）2．2．在式子：①－3＜0；②4x＋3y＞0；③x＝3；④x2＋xy＋y2；⑤x≠5中是不等式的有．（填序号）3．在数：4，5，6，－1中，是不等式x－2＜3的解的有．4．一个不等式的解集在数轴上表示如右图所示，则它的解集为．5．用“＞”或“＜”填空（1）若a－1＜b－1，则a b；（2）若－3a＜－3b，则a b；（3）若3a＋1＜3b＋1，则a b．6．使不等式x－5＞4x－1成立的值中最大整数是．7．某数的3倍与2的差是非正数，如果设某数为x，则得不等式．8．关于x的不等式2a－3x＜6的解集为x＞2，则a值为．9．刘天借到一本有72页的图书，要在10天之内读完，开始两天每天只读5页，那么以后几天里每天至少要读多少页？设以后几天里每天至少要读x页，所列不等式为．10．关于x的不等式（n－m）x＞0，其中m＞n，则其解集为．二、选择题（每小题3分，共24分）11．下列说法错误的是（）．A．x＜2的负整数解有无数个B．x＜2的整数解有无数个C．x＜2的正整数解有1和2D．x＜2的正整数解只有112．若关于x 的不等式mx ＜n 的解集为x ＞mn ，则m 的取值范围是（ ）． A ．m≥0 B ．m ＞0 C ．m≤0 D ．m ＜013．不等式17－3x≥2的正整数解的个数为（ ）．A ．5B ．4C ．3D ．214．如图，当输入x ＝－2时，则输出的y 的值为（ ）．A ．45 B ．－11 C ．1 D ．不能确定 15．若关于x 的方程11=+x m 的解是负数，则m 的取值范围是（ ）． A ．m ＜1 B ．m ＜1且m ≠0 C ．m ≤1 D ．m ≤1且m ≠016．有理数数a ．b ．c 在数轴上的位置如图所示，下列各不等关系中正确的是（ ）．A ．a ＋b ＜b ＋cB ．a c ＞bcC ．b －a ＜b －cD ．c a ＞c b 17．若243x -的值不大于6，则x 的取值范围是（ ）. A ．15x > B ．15x < C ．15x ≥ D ．15x ≤18．在四川抗震救灾中，某抢险地段需实行爆破．操作人员点燃导火线后，要在炸药爆炸前跑到400米以外的安全区域．已知导火线的燃烧速度是1.2厘米/秒，操作人员跑步的速度是5米/秒．为了保证操作人员的安全，导火线的长度要超过（ ）A ．66厘米B ．76厘米C ．86厘米D ．96厘米三、解答题（共46分）19．（6分）某班同学去春游，花了230元包租了一辆客车，如果参加春游的同学每人交7元租车费，还不够，怎样表示上述关系．20．（10分）有理数m ，n 在数轴上如图，用不等号填空．（1）m ＋n 0； （2）m －n 0；（3）m·n 0； （4）m 2 n ；（5）|m| |n|．21．（6分）解不等式321x ≥1，并将它的解集在数轴上表示出来．22．（6分）若不等式3x －（2k －3）＜4x ＋3k ＋6的解集为x ＞1，试确定k 的值．23．（8分）x 为何值时，代数式31232+-+x x 的值分别满足以下条件： （1）是负数 （2）不大于124．（10分）已知不等式5x －2＜6x ＋1的最小正整数解是方程3x －23a x ＝6的解，求a 的值．（§9.1）一、填空题1．（1）＞，（2）＞，（3）＜ 2．①②⑤ 3．4 4．x≥－4 5．（1）＜；（2）＞；（3）＜ 6．－2 7．3x －2≤0 8．6 9．（10－2）x ＋5×2≥72 10．x ＜0二、选择题11．C 12．D 13．A 14．B 15．D 16．C 17．D 18．D三、解答题19．设该班去春游的同学有x 人，则上述关系可表示为：7x ＜230 20．（1）＜；（2）＜；（3）＞；（4）＞；（5）＞ 21．x≤－1 22．k ＝－54 23．（1）x ＜74 的值时；（2）x≤－41 24．a ＝－2。

七年级（下）期中数学独立作业一、精心选一选（本题有10小题，每小题3分，共30分）1、下列运算正确的是……………………………………………………（ ）A. a 5·a 6=a 30B. a 5+a 6=a 11C. (a 5)6=a 30D. a 5÷a 6=562、现有两根长为40cm 和50cm 的直木条，要钉一个三角形木架，应在下面直木条中选取…………………………………………………………………（ ） A. 10cm B. 40cm C. 90cm D. 100cm3、已知如图∠A=∠A ′，∠B=∠B ′，若要说明△ABC ≌△A ′B ′C ′，•则下列条件不能满足的是……（ ）A ．AB=A ′B ′ B ．BC=B ′C ′ C ．AC=A ′C ′D ．∠C=∠C ′4、已知63=-y x ，则用含x 的代数式表示y 为………………………（ ）A. 36y x +=B. x y 36-=C. 36yx -= D. 63-=x y 5、 如图是一个由黑白小方块组成的长方形，小惠用一个小球在上面随意滚动，球停在黑色方块（黑白小方块的大小相同） 的概率是………………………………………………（ ）A. 14B. 124C. 118D. 166、 下列四个代数式：(1) (x+y )(-x-y )； (2) (x-y )(y-x )；(3) （2a+3b ）(3b-2a )；(4) (2x -3y ) (2y +3x ). 其中能用平方差公式计算的有………………（ ） A. 1个 B.2个 C . 3个 D. 4个 7、如图，将四边形AEFG 变换到四边形ABCD ，其中E 、G 分别是AB ，AD 的中点，下列叙述不正确的是……………………………………（ ）A 、这种变换是相似变换B 、对应边扩大到原来的2倍C 、各对应角度数不变D 、面积扩大到原来的2倍8、已知2x y m=⎧⎨=⎩是二元一次方程5x+3y=1的一组解，则m 的值是(A) 3 (B) 3- (C)113 (D) 113- 9、．下列因式分解不正确的是(A)3322422(2)a b ab ab a b -+=-+ (B) 224(2)(2)x y x y x y -=+-(C) 2211(1)42x x x -+=- (D) 2223(231)m n mn mn mn m n -+=+- 第7题图10、《九章算术》是我国东汉初年编订的一部数学经典著作．•在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图（1）、图（2）．图中各行从左到右列出的算筹数分别表示未知数x ，y 系数与相应的常数项，把图（1）所示的算筹图用我们现在所熟悉的方程组形式表述出来就是3219423x y x y +=⎧⎨+=⎩类似地，图（2）所示的算筹图我们可以表述为……………………………………………（ ）(1) (2)A ．211211321926 (432743224234327)x y x y x y x y B C D x y x y x y x y +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨+=+=+=+=⎩⎩⎩⎩ 二、耐心填一填（本题有8小题，每小题3分，共24分）11、1纳米=000000001.0米，则200纳米用科学记数法表示为_____________米. 12、若53x x x m =÷，则______=m .13、如图AB=AD ，CB=CD ， AC 与BD 相交于E ，请根据这些条件写出一个．．正确的结论：__________________________ (不再添加辅助线，不标注其它字母，不写推理过程)14、 若)3)((++x m x 的乘积中不含x 的一次项，则m 的值为________.15、 按完全平方公式填空：()()2210a a -+=16、 如右图所示，把⊿ABC 绕C 点顺时针旋转35°，得⊿A′B′C ，此时恰好A′B′⊥AC 于D ，则∠A′=_______度.17、解二元一次方程组275(1)32(2)m n n m +=⎧⎨=-⎩，则把②代人①中消去n ，得到关于m 的一元一次方程为 .18、 已知3223222⨯=+，8338332⨯=+，154415442⨯=+， ……若bab a ⨯=+21010（a 、b 均为正整数），则________=+b a .三、细心解一解（本题有6小题，共46分）19、（本题6分）计算或化简： （1）022)313()3()31(-+----； （2）43)()(a a a -⋅⋅-；______________ E _ D _ C_ B_ A _ D _ B _’ _ A_ ‘ _ C_ B_ A20、（本题6分）解方程组:（1） ⎪⎩⎪⎨⎧-=--=421y x x y （2）3262317x y x y -=⎧⎨+=⎩21、（本题4分）如图，在正方形网格上有一个△ABC。

靖城中学2021-2021学年七年级数学下学期第二次HY 作业试题一．选择题：〔每一小题2分，一共18分〕1.以下计算：〔1〕n n n a a a 2=⋅，〔2〕1266a a a =+，〔3〕55c c c =⋅，〔4〕766222=+，〔5〕93339)3(y x xy =中正确的个数为 〔 〕A. 0个B. 1个C. 2个D. 3个2.如图，不一定能推出b a //的条件是： 〔 〕A ．31∠=∠B ．42∠=∠C ．41∠=∠D ． 18032=∠+∠ 3.三角形的三边分别为2，a -1，4，那么a 的取值范围是 〔 〕A ．3<a <7B ．2<a <6C ．1<a <5D ．4<a <614-=-x y ax 是二元一次方程，那么a 的取值为( ) A ．a ≠0 B ．a ≠－1 C ．a ≠1 D ．a ≠25.不等式组2201x x +>⎧⎨--⎩≥的解集在数轴上表示为〔 〕6.为了美化城，经统一规划，将一正方形草坪的南北方向增加3m ，东西方向缩短3m ，那么改造后的长方形草坪面积与原来正方形草坪面积相比〔 〕A ．减少9m 2B ．增加9m 2C ．保持不变D ．增加6m 27.把面值20元的纸币换成1元或者5元的纸币，那么换法一共有 〔 〕 A ． 4种 B. 5种 C .6种 D. 7种8.以下多项式, 在有理数范围内不能．．用平方差公式分解的是：〔 〕A ．22y x +—B ．()224b a a +—C ． 228b a —D ． —22y x 19.以下表达中，正确的有： 〔 〕 ①任意一个三角形的三条中线．．．．．．．．都相交于一点；②任意一个三角形的三条高．．．．．．．都相交于一点；③任意一个三角形的三条角平分线．．．．．．．．．．都相交于一点；④一个五边形最多．．有3个内角．．是直角 A. 0个 B. 1个 C. 2个 D. 3个二．填空题：〔每一小题2分，一共20分〕 度，外角和是 度.11.某种细菌的存活时间是只有0.000 012秒，假设用科学记数法表示此数据应为___________秒.16.边长为a 、b 的矩形，它的周长．．22a b ab += ．17将ABC ∆经过平移得到111A B C ∆,假如53,8BAC AB ︒∠==,那么111B AC ∠= ,11A B = 。

第7章 三角形检测（整章测试）（时间90分钟 满分100分）班级 学号 姓名 得分一、填空题（每小题2分，共20分）1．用7根火柴棒首尾顺次连接摆成一个三角形，能摆成的不同的三角形的个数为 ．2．工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的 性．3．如图，三角形纸片ABC 中，∠A ＝65°，∠B ＝75°，将纸片的一角折叠，使点C 落在△ABC 内，若∠1＝20°，则∠2的度数为______．4．如图，已知AB ∥CD ，∠A=55°，∠C=20°，则∠P=___________．5．如图，在△ABC 中，AB ＝AC ，∠A ＝50°，BD 为∠ABC 的平分线，则∠BDC ＝ °． 6．如图，小亮从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A 点时，一共走了 米．7．如用同一种正多边形地砖镶嵌成平整的地面，那么这种正多边形地砖的形状可以是 ． （写出两种即可）（第2题）（第4题）（第6题） 30° 30°30°A （第7题） G FE D C BA（第9题）E D C BA（第3题）（第5题）DCBA9．如图，△ABC中，BD平分∠ABC，CD平分∠ACE，请你写出∠A与∠D的关系：．10．一个多边形，除了一个内角外，其余各角的和为2750°，则这一内角为．二、选择题（每题3分，共24分）11．三角形的三条高所在的直线相交于一点，这个交点的位置在（）A．三角形内B．三角形外C．三角形边上D．要根据三角形的形状才能定12．下列长度的各组线段中，能组成三角形的是（）A．1、2、3 B．1、4、2 C．2、3、4 D．6、2、313．一批相同的正六边形地砖铺满地面的图案中，每个顶点处由几块正六边形组成A．2块B．3块C．4块D．6块14．一个多边形只有27条对角线，则这个多边形的边数为（）A．8 B．9 C．10 D．1115．下列正多边形的组合中，能够铺满地面（即平面镶嵌）的是A．正三角形和正四边形B．正四边形和正五边形C．正五边形和正六边形D．正六边形和正八边形16．已知一个多边形的内角和为540°，则这个多边形为A．三角形B．四边形C．五边形D．六边形17．某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖, 有人提出了4种地砖的形状供设计选用：①正三角形，②正四边形，③正五边形，④正六边形．其中不能进行密铺的地砖的形状是（）．A．①B．②C．③D．④18．一个三角形的两边的长分别为3和8，第三边的长为奇数，则第三边的长为（）A．①5或7 B．7 C．9 D．7或9三、解答题（共56分）19．（5分）在△ABC中，∠C=900，BD是∠ABC的平分线，∠A=200，求∠BDC的度数．20．（5分）小明在求一个多边形的内角和时，由于疏忽，把一个内角加了两遍，而求出的结果为20040，请问这个内角是多少度？这个多边形是几边形？21．（5分）一个凸多边形的内角的度数从小到大排列，恰好依次增加相同的度数，其中最小角是1000，最大角是1400，求这个多边形的边数．22．（5分）如图所示，在△ABC 中，O 是高AD 和BE 的交点，观察图形，试猜想∠C 和∠DOE 之间具有怎样的数量关系？并证明你的猜想结论．23．（5分）分别测量如图所示的△ABC 和△DEF 的内角 （1）你发现了什么？ （2）你有何猜想？ （3）通过什么途径说明你的猜想？第23题A D EF24．（5分）如果一个凸多边形的所有内角从小到大排列起来，恰好依次增加的度数相同，设最小角为100°，最大角为140°，那么这个多边形的边数为多少？ 25．（6分）如图所示，BE 、CD 交于A 点，∠C 和∠E 的平分线相交于F ． （1）试求：∠F 与∠B ，∠D 有何等量关系？ （2）当∠B ﹕∠D ﹕∠F=2﹕4﹕x 时，x 为多少？∠4∠3∠2∠1FEABCD第25题图26．（6分）如图所示，求∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数．27．（6分）已知，如图，∠XOY =900，点A 、B 分别在射线OX 、OY 上移动，BE 是∠ABY的平分线，BE 的反向延长线与∠OAB 的平分线相交于点C ，试问∠ACB 的大小是否发生变化．如果保持不变，请给出证明，如果随点A 、B 移动发生变化，请求出变化范围．YXOABCE第26题图F ED CB A28．（8分）（1）AD 是△ABC 的中线，那么△ABD 与△ACD 的面积有什么关系？为什么？ （2）你能用三种不同的方法把一个三角形的面积四等分吗？请画出图形．第7章 整章测试一、填空题1．2 2．稳定 3．60° 4．35° 5．82.5 6．120 7．答案不唯一 8．540° 9．∠A=2∠D 10．130°二、选择题11．D 12．C 13．B 14．B 15．A 16．C 17．C 18．D 三、解答题19．550 20．240，十三边形 21．6 22．∠C+∠DOE=1800 23．（1）两个三角形的内角和都等于或接近1800；（2）任意三角形的内角和等于1800；（3）方法很多（略） 24．六边形 25．（1）∠F=21（∠B+∠D ）；（2）3 26．360° 27．∠C 的大小保持不变 28．（1）相等；（2）略。