初一数学独立作业2010。9。16

第13题O 西 北南 A B东 江苏省泰兴市南新低级中学 学年七年级数学上学期第二次独立作业试题一、选择题（每题3分，共18分）1.以下四个算式中，有一个算式与其他三个算式的计算结果不同，那么该算式是 【 】 A ．()21- B ．21- C ．()31- D ．1--2.已知水星的半径约为米，用科学记数法表示为（ ▲ ）米 【 】 A ．80.24410⨯ B ．61044.2⨯ C ．71044.2⨯ D ．624.410⨯5.若是∠α和∠β互补，且∠α＞∠β，那么以下表示∠β的余角的式子中：①90°－∠β；②∠α－90°；③180°－∠α；④12（∠α－∠β）．正确的选项是： 【 】A.①②③④B. ①②④C. .①②③D. ①②6.黄桥镇对定慧路进行绿化，打算把某一段公路的一侧全数栽上香樟树，要求路的两头各栽一棵，而且每两棵树的距离相等．若是每隔5米栽1棵，那么树苗缺21棵；若是每隔6米栽1棵，那么树苗正好用完．那么原有树苗 棵． 【 】二、填空题（本大题共10小题，每题3分，共30分）7.假设3x m +5y 与x 3y 是同类项，那么m = _________ ． 8.已知∠A =30°36′，它的余角 = ．9.若是a －3与a ＋1互为相反数，那么a ＝ ．10.如图所给的三视图表示的几何体是 _________ ．11.若∠1+∠2=180°，∠2+∠3=180°，那么∠1=∠3．理由是 ．12.如图，假设添上一个正方形，使之能折叠成一个正方体，且使相对面上的两个数字之和相等，那么添上的正方形上的数字应为 ．13.如图，A 、O 、B 在同一条直线上，若是OA 的方向是北偏西7437'︒，那么OB 的方向是 .第12题第15题第14题14.如图，直线AB 、CD 相交于点O ，OE 平分∠BOD ，假设∠BOE =36°，那么∠AOC 的度数为 . 15.小明同窗在某月的日历上圈出2×2个数（如图），正方形方框内的4个数的和是28，那么这4个数是 .16.点C 在直线AB 上，AC = 8 cm ，CB = 6 cm ，点M 、N 别离是AC 、BC 的中点, 那么线段MN 的长为 .三、解答题（本大题共10小题，共102分）. 17.（此题12分）计算：（1）)9()8()4()3(--+--+- （2）20143)1(|52|)3(2)2(---+-⨯--18.（此题12分）解以下方程：（1）x x 25.0125.0-=- （2）673422--=--x x 错误！未找到引用源。

2016学年第一学期七年级数学学科独立作业一、选择题（本题有10小题，每小题2分，共20分. 请选出一个符合题意的正确选项, 不选、多选、错选，均不给分）1. 下列具有相反意义的量是 （ ▲ ）A 、向西走2米与向南走3米B 、胜2局与负3局C 、气温升高3°C 与气温为—3°CD 、盈利3万元与支出3万元2．121的算术平方根是 （ ▲ ）A 、11 B 、±11 C 、 D 、±3．在4-，3.14 ，0.3131131113，π，10，1.51•• ，001.0-，72中无理数的个数有 （ ▲ ） A 、 2个 B 、3个 C 、4个 D 、5个4．尽管受到国际金融危机的影响，但绍兴市经济依然保持了平稳增长.据统计，截止到今年9月底，该市金融机构存款余额约为1193亿元，用科学记数法应记为 （ ▲ ）A 、1.193×1010元B 、1.193×1011元C 、1.193×1012元D 、1.193×1013元5．如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数。

从轻重的角度看，最接近标准的是 （ ▲ ）6．下列各式中,正确的是（ ▲ ）A 、 ―5―5＝0B 、 1( 1.25)(1)04--+= C 、222(5)(12)(13)-+-=- D 、25371()1()3725÷+=⨯+ 7. 下列说法中正确的是 （ ▲ ）①若两数的差是正数，则这两个数都是正数。

②任何数的绝对值一定是正数。

③零减去任何一个有理数，其差是该数的相反数。

④正数的倒数是正数，负数的倒数是负数，任何数都有倒数。

A、①B、②C、③D、④8．甲、乙、丙三家超市为了促销一种定价为100元的商品，甲超市连续两次降价20%，乙超市一次性降价40%，丙超市第一次降价30%，第二降价10%，此时顾客要购买这种商品，若想最划算应到的超市是（▲）A.甲B.乙C.丙D.三个超市一样划算9．如果x＜0，y＞0，x+y＜0，那么下列关系式中正确的是（▲）A、x＞y＞﹣y＞﹣xB、﹣x＞y＞﹣y＞xC、y＞﹣x＞﹣y＞xD、﹣x＞y＞x＞﹣y10.正方形ABCD在数轴上的位置如图所示，点D、A对应的数分别为0和1，若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为2；则翻转2016次后，数轴上数2016所对应的点是（▲）A、点CB、点BC、点AD、点D二、填空题（本题有10小题，每小题3分，共30分）11．－32的相反数为________，倒数为________，绝对值为________。

新人教版七年级数学上册第一章独立作业考试时间120分钟一、选择题(每小题2分，共计20分)1．在﹣，0，，﹣1这四个数中，最小的数是（）A．﹣ B．0 C． D．﹣12． 2015的相反数是（）A．12015B．12015C．2015 D．﹣20153．某地一天的最高气温是12℃，最低气温是-2℃，则该地这天的温差是（）A．﹣10℃ B．10℃ C．14℃ D．﹣14℃4．下列说法正确的是（）A．一个数的绝对值一定比0大 B．一个数的相反数一定比它本身小C．绝对值等于它本身的数一定是正数 D．最小的正整数是15．如图，数轴上点A、B分别对应实数a、b，则下列结论正确的是（）A．a＞b B．|a|＞|b| C．a+b＞0 D．-a＞b6．已知|x|=3，y=2，且x＜y，则x+y的值为（）A．5 B．﹣1 C．5或1 D．1或﹣17．若（）﹣（﹣2）=3，则括号内的数是（）A．1 B．﹣1 C．5 D．﹣58．下列各组数中，相等的一组是（）A．23和32 B．|﹣2|3和|2|3C．﹣（+2）和|﹣2| D．（﹣2）2和﹣22 9．下列各数据中，准确数是（）A.王楠体重为45．8kgB.大同市矿区某中学七年级有322名女生C.珠穆朗玛峰高出海平面8844.43mD.中国约有13亿人口10．小明想上十阶楼梯，他想：我可以一步上一阶楼梯，也可以一步上两阶楼梯，也可以两种走法混用．①台阶为1阶时，上法有1种②台阶为2阶时，可以一步一阶上，也可以一步上两阶上，因此上法有2种．③台阶为3阶时，可以一步一阶上，也可以先一步上一阶，再一步上两阶上，还可以先一步上两阶，再一步上一阶，这样上法有3种④台阶为10阶时，上法有种．（）A. 21B. 34C. 55D. 89二、填空题（每小题3分，共计30分）11. -13的倒数是．12．数轴上到原点的距离等于4的数是．13．绝对值不大于2的所有的整数是________________14．有一数值转换器，原理如图所示，若开始输入x的值是14，可发现第1次输出的结果是7，第2次输出的结果是12，依次继续下去，则第2015次输出的结果是．15．小惠测量一根木棒的长度，由四舍五入得到的近似数为2．8米，则这根木棒的实际长度的范围是 __________________16．地球七大洲的总面积约为149 480 000km²，如对这个数据精确到百万位可表示为2km.17．一把标有0至10的直尺，如图所示放在数轴上，且直尺上的刻度0、1、2、3、4和数轴上的-1、-2、-3、-4、-5分别对应。

七年级（下）期中数学独立作业一、精心选一选（本题有10小题，每小题3分，共30分）1、下列运算正确的是……………………………………………………（ ）A. a 5·a 6=a 30B. a 5+a 6=a 11C. (a 5)6=a 30D. a 5÷a 6=562、现有两根长为40cm 和50cm 的直木条，要钉一个三角形木架，应在下面直木条中选取…………………………………………………………………（ ） A. 10cm B. 40cm C. 90cm D. 100cm3、已知如图∠A=∠A ′，∠B=∠B ′，若要说明△ABC ≌△A ′B ′C ′，•则下列条件不能满足的是……（ ）A ．AB=A ′B ′ B ．BC=B ′C ′ C ．AC=A ′C ′D ．∠C=∠C ′4、已知63=-y x ，则用含x 的代数式表示y 为………………………（ ）A. 36y x +=B. x y 36-=C. 36yx -= D. 63-=x y 5、 如图是一个由黑白小方块组成的长方形，小惠用一个小球在上面随意滚动，球停在黑色方块（黑白小方块的大小相同） 的概率是………………………………………………（ ）A. 14B. 124C. 118D. 166、 下列四个代数式：(1) (x+y )(-x-y )； (2) (x-y )(y-x )；(3) （2a+3b ）(3b-2a )；(4) (2x -3y ) (2y +3x ). 其中能用平方差公式计算的有………………（ ） A. 1个 B.2个 C . 3个 D. 4个 7、如图，将四边形AEFG 变换到四边形ABCD ，其中E 、G 分别是AB ，AD 的中点，下列叙述不正确的是……………………………………（ ）A 、这种变换是相似变换B 、对应边扩大到原来的2倍C 、各对应角度数不变D 、面积扩大到原来的2倍8、已知2x y m=⎧⎨=⎩是二元一次方程5x+3y=1的一组解，则m 的值是(A) 3 (B) 3- (C)113 (D) 113- 9、．下列因式分解不正确的是(A)3322422(2)a b ab ab a b -+=-+ (B) 224(2)(2)x y x y x y -=+-(C) 2211(1)42x x x -+=- (D) 2223(231)m n mn mn mn m n -+=+- 第7题图10、《九章算术》是我国东汉初年编订的一部数学经典著作．•在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图（1）、图（2）．图中各行从左到右列出的算筹数分别表示未知数x ，y 系数与相应的常数项，把图（1）所示的算筹图用我们现在所熟悉的方程组形式表述出来就是3219423x y x y +=⎧⎨+=⎩类似地，图（2）所示的算筹图我们可以表述为……………………………………………（ ）(1) (2)A ．211211321926 (432743224234327)x y x y x y x y B C D x y x y x y x y +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨+=+=+=+=⎩⎩⎩⎩ 二、耐心填一填（本题有8小题，每小题3分，共24分）11、1纳米=000000001.0米，则200纳米用科学记数法表示为_____________米. 12、若53x x x m =÷，则______=m .13、如图AB=AD ，CB=CD ， AC 与BD 相交于E ，请根据这些条件写出一个．．正确的结论：__________________________ (不再添加辅助线，不标注其它字母，不写推理过程)14、 若)3)((++x m x 的乘积中不含x 的一次项，则m 的值为________.15、 按完全平方公式填空：()()2210a a -+=16、 如右图所示，把⊿ABC 绕C 点顺时针旋转35°，得⊿A′B′C ，此时恰好A′B′⊥AC 于D ，则∠A′=_______度.17、解二元一次方程组275(1)32(2)m n n m +=⎧⎨=-⎩，则把②代人①中消去n ，得到关于m 的一元一次方程为 .18、 已知3223222⨯=+，8338332⨯=+，154415442⨯=+， ……若bab a ⨯=+21010（a 、b 均为正整数），则________=+b a .三、细心解一解（本题有6小题，共46分）19、（本题6分）计算或化简： （1）022)313()3()31(-+----； （2）43)()(a a a -⋅⋅-；______________ E _ D _ C_ B_ A _ D _ B _’ _ A_ ‘ _ C_ B_ A20、（本题6分）解方程组:（1） ⎪⎩⎪⎨⎧-=--=421y x x y （2）3262317x y x y -=⎧⎨+=⎩21、（本题4分）如图，在正方形网格上有一个△ABC。

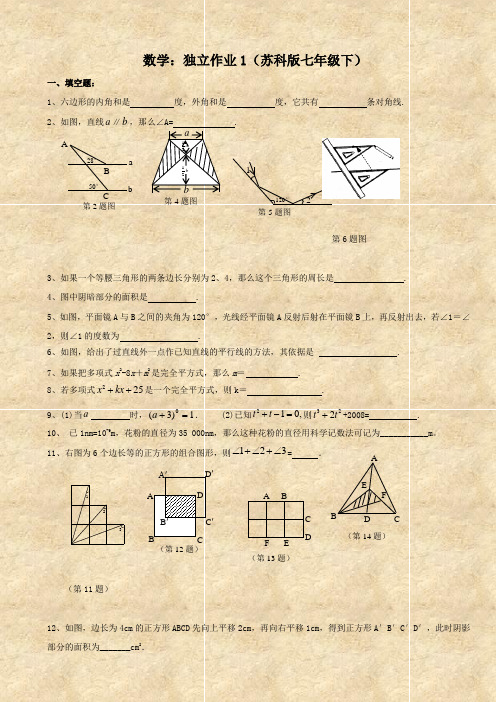
321数学：独立作业1（苏科版七年级下）一、填空题：1、六边形的内角和是 度，外角和是 度，它共有 条对角线.2、如图，直线a ∥b ，那么∠A= .第6题图3、如果一个等腰三角形的两条边长分别为2、4，那么这个三角形的周长是 .4、图中阴暗部分的面积是 .5、如图，平面镜A 与B 之间的夹角为120°，光线经平面镜A 反射后射在平面镜B 上，再反射出去，若∠1＝∠2，则∠1的度数为 .6、如图，给出了过直线外一点作已知直线的平行线的方法，其依据是 .7、如果把多项式x 2-8x ＋m 2是完全平方式，那么m ＝ . 8、若多项式225x kx ++是一个完全平方式，则k ＝ .9、(1)当a 时，1)3(0=+a ． (2)已知210,t t +-=则322t t ++2008= .10、 已1nm=10-9m ，花粉的直径为35 000nm ，那么这种花粉的直径用科学记数法可记为___________m 。

11、右图为6个边长等的正方形的组合图形，则123∠+∠+∠= ．（第11题）12、如图，边长为4cm 的正方形ABCD 先向上平移2cm ，再向右平移1cm ，得到正方形A′B′C′D′，此时阴影部分的面积为_______cm 2．A BCa b28°50°第2题图120°第5题图12a ba 21b 21第4题图ABCDA′D ′ C ′ B ′ （第12题）ABCDEF（第13题）A BCDEF （第14题）绿化园13、如图，它是由6个面积为1的小正方形组成的长方形，点A 、B 、C 、D 、E 、F 是小正方形的顶点，以这六个点中的任意三点为顶点，可以组成________个面积是1的三角形．14、已知在△ABC 中，已知点D 、E 、F 分别为BC 、AD 、CE 的中点，且S △ABC ＝4cm 2，则S △BEF 的值为________cm 2． 15、已知1639273m m ⨯⨯=,则m= .16、如果一个多边形的每个内角都相等，且内角比与它相邻的外角大100°，则这个多边形的内角和等于 度 二、选择题17、已知△ABC 中， 2∠A=3∠B= 4∠C，则此三角形是（ ）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、以上都有可能18、下面计算中，正确的是 （ ） A 、(m+n)(-m+n)=－m 2+n 2B 、5523)()(n m n m n m +=++C 、69323)(b a b a -=-- D 、a a a =-232319、为了美化城市，经统一规划，将一正方形．．．草坪的南北方向增加3m ，东西方向缩短3m ，则改造后的长方形草坪面积与原来正方形草坪面积相比 （ ） Ａ、增加6m 2 Ｂ、增加9m 2 Ｃ、保持不变 Ｄ、减少9m 2 20、下列各式中，能用平方差公式计算的是（ ） A ．)3)(3(+--x x B ．)2)(2(b a b a -+ C ．)1)(1(---a aD ．2)3(-x21、如图，在一个长方形花园ABCD 中，AB=a ，AD=b ，花园中建有一条长方形道路LMPQ 及一条平行四边形道路RSKT ，若LM=RS=c ，则花园中可绿化部分的面积为 （ ）A 、2b ac ab bc ++-B 、ac bc ab a -++2C 、2c ac bc ab +--D 、ab a bc b -+-22（第21题图） （第23题图） （第24题图）22、篮子里有若干苹果，可以平均分给)1(+x 名同学，也可以平均分给)3(-x 名同学（x 为大于3的正整数），用代数式表示苹果数量不可能是 （ ）A ．322-+x xB ．322--x xC ．)3)(1(3-+x xD ．)32(2--x x x23、 如图，正方形ABCD 和CEFG 的边长分别为m 、n ，那么∆AEG 的面积的值 （ ）A BC D GEFA ．与m 、n 的大小都有关B ．与m 、n 的大小都无关C ．只与m 的大小有关D ．只与n 的大小有关24、如图，一块四边形绿化园地，四角都做有半径为R 的圆形喷水池，则这四个喷水池占去的绿化园地的面积为 （ ） A 、22R π B 、24R π C 、2R π D 、不能确定 三、解答题： 25、计算(1) （π-3.14）0－(12)－1+ ()200820092 1.53⎛⎫⨯- ⎪⎝⎭(2)3105322334)()2()(2a a a a a a ÷+-⋅-+29、化简（1）（2x-3y ）2(2x+3y)2（2）（3） （4）30、先化简，再求值2(21)(21)(2)a a a +-+-4(1)a -+(2)a -，其中2=a ．31、如图AB ∥DE ，且有∠1＝∠2，∠3＝∠4，试说明：BC ∥EF 解：∵AB ∥DE(已知)∴∠1＝_____ (两直线平行，同位角相等)∵∠1＝∠2，∠3＝∠4 (已知)∴∠2＝ (等量代换) ∴BC ∥EF (________________________)32、如图，在△ABC 中，∠BAC 是钝角，请画出AB 边上的高CD ，BC 边上的中线AE ，∠B 的平分线BF 。

独立作业1202406.6-101.已知{x=1y=−2，是方程2mx+y=−1的一组解，则m的值为( )A.−23 B.2 C.−32D.122.若m>n，下列不等式不一定成立的是（）A.−2m<−2nB.m2>n2C.m+8>n+8D.m3>n33.《九章算术》中的方程问题：“五只雀六燕共重1斤（等于16两），雀重燕轻，互换其中一只，恰好一样重，问：每只雀、燕的重量各为多少？”设每只雀、燕的重量各为x两，y两，列方程组为( )A.{x+y=164x+y=x+5y B.{5x+6y=165x+y=x+6y C.{5x+6y=164x+y=x+5y D.{6x+5y=165x+y=x+6y4.若干辆载重的卡车来运载货物，若每辆卡车装4t，则剩下18货物；若每辆卡车装61，则最后一辆汽车有货物但不足4t，则可能有( )辆汽车.A.9B.10C.11D.125.若关于x的不等式组{x−12≥2kx−k≤4k+6有解，且关于x的方程kx=2(x-2)-(3x+2)有非负整数解，则符合条件的所有整数k的和为( )A.-5B.-9C.-12D.-166.如图,第一象限内有两点P(a-5，b)，Q(a,b-4)，将线段PQ平移，使点P、Q分别落在两条坐标轴上，则点P平移后的对应点的坐标是____7.如图，已知：在四边形ABCD中，AB//CD，AD//BC,点E为线段BC延长线上一点，连接AE交CD于F，∠1=∠2.(1)求证：∠DAC=∠BAE；(2)若CD是∠ACE的角平分线，∠1=80°，求∠DAE的度数.8. “全民阅读”深入人心，读书好，好读书，读好书，让人终身受益.为满足同学们的读书需求，学校图书馆准备到新华书店采购文学名著和动漫书两类图书，经了解，30本文学名著和60本动漫书共需3000元，15本文学名著与20本动漫书的费用一样(注：所采购的文学名著价格都一样，所采购的动漫书价格都一样).(1)求每本文学名著和动漫书各多少元？(2)若学校要求购买文学名著比动漫书多50本，动漫书和文学名著总数不低于90本，总费用不超过3610元，请问有几种购书方案？(3)在(2)的条件下，若学校实际购买时，文学名著单价上调m元/本，动漫书单价下调了3m元/本，此时购买这两种书籍所需最少费用为3450元，则m的值为9.如图1，已知△ABC，E是BC延长线上一点，射线CD//AB.(1)求证：∠ACE=∠A+∠B;(2)如图2，过点A 作AH//BC 交CD 于点H ，连接AE 交CD 于点G ，AF 平分∠EAH，CF 平分∠DCE，若∠BAE=80°，求∠F 的度数；(3)如图3，点M 为线段AC 上一点，∠QMP 的两边分别交线段BA 延长线于点Q ，射线CD 于点P ，连接BP ，其中∠QMP=2∠CMP，∠ABP=2∠CBP，则∠BQM，∠MPB 与∠ACB 的数量关系 是 图1 图2 图310.如图，平面直角坐标系中，A(a ，0)，B(0，b)，C(0，c)，√a +3+(4−b)2=0，c=-a-b.(1)求A 、B 、C 的坐标和△ABC 的面积；(2)如图2，①点D(p ，q)在线段AC 上，求q 与p 之间的数量关系；②将点D 向上平移2个单位长度至E 点(点E 在△ABC 内部)，若△ABE 的面积等于2，求点E 的坐标；(3)在(2)的条件下，将线段BE 向右平移m 个单位(m>0)；得到线段B ′E ′，其中点B ，点E 的对应点分别为点B ′，点E ′.若点N(1，n)在射线B ′E ′上，连接ON ，OE ，EN 得到△OEN，若32<S ∆OEN <52，则m 的取值范围是11.关于x ，y 的二元一次方程(a-1)x+(a+2)y+5-2a=0，当a 取一个确定的值时就得到一个方程，所有这些方程有一个公共解，则这个公共解是（ ）A.{x =3y =−1B.{x =2y =0C.{x =−3y =1D.{x =1y =212对于任意实数，通常用[x]表示不超过x 的最大整数，如：[π]=3，[2]=2，[-2.1]=-3，给出如下结论：①[-x]=-x ；②若[x]=n,则x 的取值范围是n≤x＜n+1；③当-1＜x ＜1时，[1+x]+[1-x]的值为1或2；④若[x +12]=3，且[3−2x]=−4，则x 的取值范围为52≤x <72.其中正确的结论有（ ）个A.1B.2C.3D.413.已知{x +y =2k 2x −y =12k −1，且2<−y <3，则k 的取值范围是 14.已知2x−13+1≥x −5−3x 2，则代数式|2-x|-|x+4|最大值与最小值的差是 15.某小区准备开发一块长为32m ，宽为21m 的长方形空地.(1)方案一：如图，将这块空地种上草坪，中间修一条弯曲的小路，小路的左边线向右平移am 就是它的右边线，则这块草地的面积为 m 2（用含有a 的式子表示）：(2)方案二：在空地上修建一个面积为450m 2的正方形游泳池，这个游泳池能修起来吗？并说明理由.16.已知A(1，2)、B(3，1).(1)画出线段CD ，使A 、B 刚好是CD 的三等分点，C 、A 、B 、D 依次排列，请直接写出点C 坐标 ，点D 坐标 ；(2)平移线段AB ，使A 的对应点A 1刚好落在x 轴上，B 的对应点B 1刚好落在y 轴上，在图上画出四边形AA 1BB 1，并直接写出该四边形的面积为(3)在（2）的条件下，若AA 1交y 轴于点E ，直接写出线段EB 1的长为17.某工艺品店购进A ，B 两种工艺品，已知这两种工艺品的单价之和为100元，购进2个A 种工艺品和3个B 种工艺品需花费260元.(1)求A 、B 两种工艺品的单价；(2)该店主欲用4800元用于进货，且最多购进A 种工艺品37个，B 种工艺品的数量不超过A 种工艺品的2倍，求共有几种进货方案？(不需要写出每种进货方案)(3)已知每个A 种工艺品售价为54元，每个B 种工艺品售价为78元，该店主决定每售出一个A 种工艺品就为希望工程捐款m 元.在(2)的条件下，若A 、B 两种工艺品全部售出后所有方案获利均相同，求m 的值.18.已知AB//MN.(1)如图1，求证：∠N+∠E=∠B;∠EFB，BG平分∠ABF交MN于点G，EF交MN (1)若F为直线MN、AB之间的一点，∠E=14于点C.①如图2，若∠N=54°，且BG//EN，求∠E的度数；∠ENM，若∠NKB=∠EFB,∠E:∠FBD=3：4，②如图3，若点K在射线BG上，且满足∠KNM=45直求∠E的度数.②图1 图2 图319.在平面直角坐标系中，已知点A(a，0)、B(a，6)、C(a-3，2).(1)求△ABC的面积；(2)将线段BC向右平移m个单位，使△ABC的面积大于17，求m的取值范围；(3)若点D(a+10，10)，连结AD，将线段BC向右平移n个单位.若线段BC与线段AD有公共点，求n的取值范围。

某某省靖江市靖城中学2015-2016学年七年级数学下学期第一次独立作业试题一、选择题1．下列线段能构成三角形的是( )A．2，2，4 B．3，4，5 C．1，2，3 D．2，3，62．一个多边形的内角和是外角和的2倍，则这个多边形是( )A．四边形B．五边形C．六边形D．八边形3．如图，CD是△ABC的角平分线，DE∥BC．若∠A=60°，∠B=80°，则∠CDE的度数是( ) A．20° B．30° C．35° D．40°4．如果3a=5，3b=10，那么3a+b的值为( )A．15 B．50 C．5 D．不能确定5．下列计算：（1）a n•a n=2a n，（2）a6+a6=a12，（3）c•c5=c5，（4）26+26=27，（5）（3xy3）3=9x3y9中，正确的个数为( )A．0个B．1个C．2个D．3个6．如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于( )A．90° B．180°C．210°D．270°7．如图，将周长为8的△ABC 沿BC 方向平移1个单位得到△DEF ，则四边形ABFD 的周长为( )A ．6B ．8C ．10D ．128．如图，在△ABC 中，已知点D 、E 、F 分别是边BC 、AD 、CE 上的中点，且S △ABC =4，则S △BFF =( )A ．2cm 2B ．1cm 22 D ．0.25 cm 2二、填空题9．若（x ﹣2）0=1，则x 应满足条件__________． 10．求值：20132014522125⎛⎫⎛⎫-⨯ ⎪ ⎪⎝⎭⎝⎭=．n 28232=÷，则n 的值为__________．23-=a ，23--=b ，231-⎪⎭⎫ ⎝⎛-=c ，051⎪⎭⎫ ⎝⎛-=d ，用 “>”将a 、b 、c 、d 按大到小排列__________． 13．在△ABC 中，三个内角的度数比为2∶3∶4，则相应的外角度数的比是.14．已知等腰三角形的两边长分别为5cm 和9cm ，则此三角形的周长为______________cm ．15.一个十边形所有内角都相等，它的每一个外角等于__________．16．如图，则∠A+∠B+∠C+∠D+∠E+∠F 的度数为．17．如图，小明在操场上从A 点出发，沿直线前进15米后向左转45°，再沿直线前进15米后，又向左转45°，照这样走下去，他第一次回到出发地A 点时，一共走了__________米．18．如图，BE 是∠ABD 的平分线，CF 是∠ACD 的平分线，BE 与CF 交于G ，若∠BDC=140°，∠BGC=110°，则∠A 为__________．七年级数学独立作业答案一、选择BCABBBCB二、填空9、2≠x 10、512- 11、7- 12、a b d c >>> 13、5:6:7 14、2319或 15、 36 16、 36017、120 18、 80三、解答19（1）12t （2）24-x（3）821a - （4）()3b a - （5）1 （6） -920（1）（2）（3）略 （4）821略22（1）DG 与BC 平行，证明略（2）70°23（1）161 （2）2 m 24（1）54 （2）1500 25（1）16 （2）9026（1）∵四边形ABCD 中，∠A=145°，∠D=75°，∴∠B+∠C=360°﹣（145°+75°）=140°，∵∠B=∠C，∴∠C=70°；（2）∵BE∥AD，∴∠ABE=180°﹣∠A=180°﹣145°=35°，∵∠ABC 的角平分线BE 交DC 于点E ，∴∠ABC=70°，∴∠C=360°﹣（145°+75°+70°）=70°；（3）①∵四边形ABCD 中，∠A=145°，∠D=75°，∴∠B+∠C=360°﹣（145°+75°）=140°，∵∠ABC 和∠BCD 的角平分线交于点E ，∴∠EBC+∠ECB=70°，∴∠BEC=180°﹣70°=110°；②不变．∵∠F=40°，∴∠FBC+∠BCF=180°﹣40°=140°，∵∵∠ABC 和∠BCD 的角平分线交于点E ，∴∠EBC+∠ECB=70°，∴∠BEC=180°﹣70°=110°．。

2016-2017学年某某省某某市靖江市靖城中学七年级（上）第一次数学独立作业一、选择题1．﹣2的相反数是（）A．﹣ B．C．2 D．±22．下列说法中，正确的是（）A．1是最小的正数B．任何有理数的绝对值都不可能小于0C．任何有理数的绝对值都是正数D．最大的负数是﹣13．若b＜0，则a，a﹣b，a+b，最大的是（）A．a B．a﹣bC．a+b D．还要看a的符号，才能判定4．下列各组数中，互为相反数的是（）A．2与B．﹣（+3）与+（﹣3）C．﹣1与﹣（﹣1）D．2与|﹣2|5．绝对值大于π而不大于6的所有正整数之和为（）A．0 B．9 C．10 D．156．如图，数轴上的A、B两点分别表示有理数a、b，下列式子中不正确的是（）A．a+b＜0 B．a﹣b＜0 C．﹣a+b＞0 D．|b|＞|a|7．若a+b＜0，ab＜0，则下列判断正确的是（）A．a，b都是正数B．a，b都是负数C．a，b异号且负数的绝对值大D．a，b异号且正数的绝对值大8．一潜水艇所在的海拔高度是﹣70米，一条海豚在潜水艇上方20米，则海豚所在的高度是海拔（）A．﹣90米B．﹣70米C．﹣50米D．50米9．下列说法正确的有（）①0是绝对值最小的数②绝对值等于本身的数是非正数③数轴上原点两侧的数互为相反数④两个数比较，绝对值大的反而小．A．1个B．2个C．3个D．4个10．已知：|x|=3，|y|=2，且x＜y，则x+y的值为（）A．﹣5 B．﹣1 C．5或1 D．﹣5或﹣1二、填空题11．绝对值等于3的数有个，它们分别是．12．三个数﹣5、﹣2、+7的和比它们的绝对值的和小．13．比较大小：﹣﹣，﹣（﹣5）﹣|﹣5|14．有一列数﹣，，﹣，，…，那么第7个数是．15．一个数从数轴上表示2的点开始，先向左移动3个单位长度，再向右移动6个单位长度，这个点最终所对应的数是．16．下面四个三角形内的数有共同的规律，请找出这个规律，确定A为．17．若a+1与5互为相反数，则a=．18．某公交车上原有20人，经过4个站点时的上下车情况如下（上车为正，下车为负）：（+4，﹣8），（﹣5，+6），（﹣3，+2），（+1，﹣7），则现在车上还有人．19．若|a|=5，|b|=3，则a+b的值=；若a+b＜0，则a﹣b的值=．20．数轴上表示整数的点称为整点，某数轴的单位长度为1cm，若在这个数轴上随意划出一条长2016cm的线段AB，则它盖住的整点有个．三、解答题（共44分）21．把下列各数填入相应的数集合中﹣21，，﹣||，0，2016，﹣（﹣9），12%，，﹣，自然数{ …}；分数 { …}正数 { …}；非负整数 { …}．22．计算（1）（﹣8）+47+8+（﹣27）（2）﹣2﹣（﹣4）﹣（+5）+（﹣8）﹣（﹣9）（3）﹣21﹣12+33+12﹣67（4）|﹣4|+|﹣5|﹣|（﹣）+（﹣0.5）|23．在数轴上表示下列各数：+6，﹣||，，﹣1，0，2.5，并用“＞”将它们连接起来．24．某检修小组从O地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西为负，一天中七次行驶纪录如表．（单位：km）第一次A 第二次B 第三次C 第四次D 第五次E 第六次F 第七次G ﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2（1）画数轴表示出每次结束时的点的位置（用表格中的字母表示），并求出收工时距A地多远？（2）在第次纪录时距A地最远．（3）若每千米耗油，问共耗油多少升？25．我们知道，在数轴上，|a|表示数a表示的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上两个点A、B，分别用a，b表示，那么A、B两点间的距离为：AB=|a﹣b|．利用此结论，回答以下问题：（1）数轴上表示2和5的两点的距离是，数轴上表示﹣2和﹣5的两点之间的距离是，数轴上表示1和﹣3的两点之间的距离是；（2）若|a+1|=2，则a=；若|a+2|+|a﹣1|=6，则a=；（3）当|a+2|+|a﹣1|取最小值时，此时a符合条件是；（4）当a=时，|a+5|+|a﹣1|+|a﹣3|的值最小，最小值是．2016-2017学年某某省某某市靖江市靖城中学七年级（上）第一次数学独立作业参考答案与试题解析一、选择题1．﹣2的相反数是（）A．﹣ B．C．2 D．±2【考点】相反数．【专题】存在型．【分析】根据相反数的定义进行解答即可．【解答】解：∵﹣2＜0，∴﹣2相反数是2．故选C．【点评】本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．2．下列说法中，正确的是（）A．1是最小的正数B．任何有理数的绝对值都不可能小于0C．任何有理数的绝对值都是正数D．最大的负数是﹣1【考点】绝对值；有理数．【分析】根据有理数、绝对值对各选项进行逐一判断即可．【解答】解：A、没有最小的正数，故本选项错误；B、0的绝对值是0，故本选项错误；C、0的绝对值是0，故本选项错误；D、最大的负数是﹣1，故本选项正确；故选D．【点评】本题考查了有理数、绝对值，熟知有理数、绝对值的性质是解答此题的关键．3．若b＜0，则a，a﹣b，a+b，最大的是（）A．a B．a﹣bC．a+b D．还要看a的符号，才能判定【考点】有理数大小比较．【专题】推理填空题．【分析】由于b＜0，所以﹣b＞0，因此即可得到a，a﹣b，a+b，最大的数．【解答】解：∵b＜0，∴﹣b＞0，∴a，a﹣b，a+b，最大的是a﹣b．故选B．【点评】此题主要考查了有理数的大小的比较，解决此类问题的关键是找出最大最小有理数和对减法法则的理解．4．下列各组数中，互为相反数的是（）A．2与B．﹣（+3）与+（﹣3）C．﹣1与﹣（﹣1）D．2与|﹣2|【考点】绝对值；相反数．【分析】根据相反数的概念：只有符号不同的两个数叫做互为相反数进行分析即可．【解答】解：A、2与互为倒数，故此选项错误；B、﹣（+3）=﹣3与+（﹣3）=﹣3相等，故此选项错误；C、﹣1与﹣（﹣1）=1互为相反数，故此选项正确；D、2与|﹣2|相等，故此选项错误；故选：C．【点评】此题主要考查了相反数的定义，关键是正确掌握相反数定义．5．绝对值大于π而不大于6的所有正整数之和为（）A．0 B．9 C．10 D．15【考点】有理数的加法；有理数大小比较．【分析】首先确定绝对值大于π而不大于6的所有正整数，然后再求和即可．【解答】解：绝对值大于π而不大于6的所有正整数是4，5，6，4+5+6=15，故选：D．【点评】此题主要考查了有理数的加法和绝对值，关键是正确确定绝对值大于π而不大于6的所有正整数．6．如图，数轴上的A、B两点分别表示有理数a、b，下列式子中不正确的是（）A．a+b＜0 B．a﹣b＜0 C．﹣a+b＞0 D．|b|＞|a|【考点】数轴；绝对值．【分析】根据数轴得出a＜0＜b，且|a|＞|b|，根据有理数的大小比较法则即可判断各个选项．【解答】解：由数轴可知：a＜0＜b，且|a|＞|b|，A、a+b＜0，正确，故本选项错误；B、a﹣b=a+（﹣b）＜0，正确，故本选项错误；C、﹣a+b＞0，正确，故本选项错误；D、|b|＜|a|，错误，故本选项正确，故选D．【点评】本题考查了绝对值，数轴，有理数的大小比较等知识点，主要考查学生的观察能力和辨析能力．7．若a+b＜0，ab＜0，则下列判断正确的是（）A．a，b都是正数B．a，b都是负数C．a，b异号且负数的绝对值大D．a，b异号且正数的绝对值大【考点】有理数的乘法；有理数的加法．【专题】计算题．【分析】依据有理数的加法和乘法法则，即可得到答案．【解答】解：因为ab＜0，所以a，b异号，又a+b＜0，所以负数的绝对值比正数的绝对值大．故选C．【点评】本题考查了有理数的加法和乘法法则．有理数的加法法则：同号两数相加，取相同的符号，并把绝对值相加；绝对值不等的异号两数加加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0；一个数同0相加，仍得这个数．有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．任何数同零相乘，都得0．8．一潜水艇所在的海拔高度是﹣70米，一条海豚在潜水艇上方20米，则海豚所在的高度是海拔（）A．﹣90米B．﹣70米C．﹣50米D．50米【考点】有理数的加法．【分析】根据正负数具有相反的意义，由已海豚所在的高度是海拔多少米实际就是求﹣70与20的和．【解答】解：由已知，得﹣70+20=﹣50．故选C．【点评】本题考查的是正负数的意义，关键是要明确所求为﹣70与20的和．9．下列说法正确的有（）①0是绝对值最小的数②绝对值等于本身的数是非正数③数轴上原点两侧的数互为相反数④两个数比较，绝对值大的反而小．A．1个B．2个C．3个D．4个【考点】绝对值；数轴；相反数．【分析】根据绝对值具有非负性可得0是绝对值最小的数；绝对值的性质：①当a是正有理数时，a 的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数﹣a；③当a是零时，a的绝对值是零可得绝对值等于本身的数是非负数；互为相反数的两个数，它们分别在原点两旁且到原点距离相等；两个负数相比较，绝对值大的反而小进行分析即可．【解答】解：①0是绝对值最小的数，说法正确；②绝对值等于本身的数是非正数，说法错误，应是非负数；③数轴上原点两侧的数互为相反数，说法错误；④两个数比较，绝对值大的反而小，说法错误；正确的说法有1个，故选：A．【点评】此题主要考查了绝对值、相反数、有理数的比较大小，关键是掌握绝对值的性质，相反数的定义．10．已知：|x|=3，|y|=2，且x＜y，则x+y的值为（）A．﹣5 B．﹣1 C．5或1 D．﹣5或﹣1【考点】有理数的加法；绝对值．【分析】先求出x，y的值，再求出x+y的值即可．【解答】解：∵|x|=3，|y|=2，且x＜y，∴x=﹣3，y=2或﹣2，∴x+y=﹣3+2=﹣1，x+y=﹣3+（﹣2）=﹣5．故选：D．【点评】本题主要考查了有理数的加法及绝对值，解题的关键是求出x，y的值．二、填空题11．绝对值等于3的数有 2 个，它们分别是±3 ．【考点】绝对值．【分析】根据绝对值的概念可求出答案．【解答】解：绝对值等于3的数为±3，故答案为：2；±3．【点评】本题考查绝对值的概念，属于基础题型．12．三个数﹣5、﹣2、+7的和比它们的绝对值的和小14 ．【考点】绝对值．【专题】计算题；实数．【分析】根据题意列出算式，计算即可得到结果．【解答】解：根据题意得：|﹣5|+|﹣2|+|+7|﹣（﹣5﹣2+7）=5+2+7﹣0=14，故答案为：14【点评】此题考查了绝对值，熟练掌握绝对值的代数意义是解本题的关键．13．比较大小：﹣＞﹣，﹣（﹣5）＞﹣|﹣5|【考点】有理数大小比较；正数和负数；绝对值．【专题】探究型．【分析】（1）先通分，再根据负数比较大小的法则进行比较；（2）先去括号、去绝对值符号，再根据有理数比较大小的法则进行比较．【解答】解：（1）∵﹣=﹣＜0，﹣=﹣＜0，|﹣|＜|﹣|，∴﹣＞﹣；（2）∵﹣（﹣5）=5＞0，﹣|﹣5|=﹣5＜0，∴﹣（﹣5）＞﹣|﹣5|．故答案为：＞、＞．【点评】本题考查的是有理数的大小比较，解答此类题目时要先把各数化为最简形式，再根据有理数大小比较的法则进行比较．14．有一列数﹣，，﹣，，…，那么第7个数是．【考点】规律型：数字的变化类．【专题】规律型．【分析】先看符号，奇数个为负数，偶数个为正数，再看绝对值，第一个数的分子是1，分母是12+1；第二个数的分子是2，分母是22+1；那么第7个数的分子是7，分母是72+1=50．【解答】解：第7个数的分子是7，分母是72+1=50．则第7个数为﹣．【点评】应从符号，分子，分母分别考虑与数序之间的联系．关键是找到第7个数的分子是7，分母是72+1=50．15．一个数从数轴上表示2的点开始，先向左移动3个单位长度，再向右移动6个单位长度，这个点最终所对应的数是 5 ．【考点】数轴．【分析】根据题意画出数轴，进而得出符合题意的答案．【解答】解：如图所示：从2的点开始，先向左移动3个单位长度到达﹣1，再向右移动6个单位长度，到达5，这个点最终所对应的数是：5．故答案为：5．【点评】此题主要考查了数轴，正确结合数轴分析是解题关键．16．下面四个三角形内的数有共同的规律，请找出这个规律，确定A为55 ．【考点】规律型：数字的变化类．【分析】观察前三个三角形可知，里面的数的规律是：10÷2=2+3；21÷3=3+4；36÷4=4+5；则有A ÷5=5+6=11，故A=11×5．【解答】解：通过分析：A=（5+6）×5=55．故答案为：55．【点评】此题考查数据的变化规律，关键是找出前三组数据的规律，利用规律，解决问题．17．若a+1与5互为相反数，则a= 4 ．【考点】相反数．【分析】直接利用相反数的定义进而得出答案．【解答】解：∵a+1与5互为相反数，∴a+1=5，解得：a=4．故答案为：4．【点评】此题主要考查了相反数的定义，正确把握定义是解题关键．18．某公交车上原有20人，经过4个站点时的上下车情况如下（上车为正，下车为负）：（+4，﹣8），（﹣5，+6），（﹣3，+2），（+1，﹣7），则现在车上还有10 人．【考点】正数和负数．【分析】根据有理数的加法运算，可得车上人数．【解答】解：20+4﹣8﹣5+6﹣3+2+1﹣7=10（人），故答案为：10．【点评】本题考查了正数和负数，有理数的加法运算是解题关键．19．若|a|=5，|b|=3，则a+b的值=±8或±2 ；若a+b＜0，则a﹣b的值= 8或2 ．【考点】有理数的减法；绝对值；有理数的加法．【分析】根据题意，利用绝对值的代数意义确定出a与b的值，即可求出a+b，a﹣b的值．【解答】解：∵|a|=5，|b|=3，∴a=±5，b=±3，∴a=﹣5，b=﹣3时，a+b=﹣5﹣3=﹣8；a=﹣5，b=3时，a+b=﹣5+3=﹣2；a=5，b=﹣3时，a+b=5﹣3=2；a=5，b=3时，a+b=5+3=8；∵a+b＜0，∴a=5，b=±3，∴a=5，b=﹣3时，a﹣b=5+3=8；a=5，b=3时，a﹣b=5﹣3=2．故答案为：±8或±2；8或2．【点评】此题考查了有理数的加法，绝对值，以及有理数的减法，熟练掌握运算法则是解本题的关键．20．数轴上表示整数的点称为整点，某数轴的单位长度为1cm，若在这个数轴上随意划出一条长2016cm的线段AB，则它盖住的整点有2016或2017 个．【考点】数轴．【分析】分类讨论：线段的两端点是整数点，线段的两端点不是整数点，根据线段的长度，可得答案【解答】解：当线段的两端点是整数点时，一条长2016cm的线段AB，则被线段AB盖住的整数有2017个，当线段的两端点不是整数点时，一条长2016cm的线段AB，则被线段AB盖住的整数有2016个，则它盖住的整点有2016或2017个；故答案为：2016或2017．【点评】本题考查的是数轴，在学习中要注意培养学生数形结合的思想，本题画出数轴解题非常直观，且不容易遗漏，体现了数形结合的思想．三、解答题（共44分）21．（8分）把下列各数填入相应的数集合中﹣21，，﹣||，0，2016，﹣（﹣9），12%，，﹣，自然数{ …}；分数 { …}正数 { …}；非负整数 { …}．【考点】绝对值；有理数．【分析】利用有理数的分类即可写出答案．【解答】解：自然数{0，2016，﹣（﹣9）…}；分数{，﹣||，12%，，﹣…}；正数{，2016，﹣（﹣9），12%，…}；非负整数{0，2016，﹣（﹣9）…}；【点评】本题考查有理数的分类，涉及绝对值，符号化简等知识，属于基础题型．22．计算（1）（﹣8）+47+8+（﹣27）（2）﹣2﹣（﹣4）﹣（+5）+（﹣8）﹣（﹣9）（3）﹣21﹣12+33+12﹣67（4）|﹣4|+|﹣5|﹣|（﹣）+（﹣0.5）|【考点】有理数的加减混合运算．【分析】根据有理数的加减混合运算，即可解答．【解答】解：（1）（﹣8）+47+8+（﹣27）=﹣8+8+47﹣27=0+20=20．（2）﹣2﹣（﹣4）﹣（+5）+（﹣8）﹣（﹣9）=﹣2+4﹣5﹣8+9=﹣2﹣5﹣8+4+9=﹣15+13=﹣2．（3）﹣21﹣12+33+12﹣67=﹣33+33+12﹣67=12﹣67=﹣55．（4）|﹣4|+|﹣5|﹣|（﹣）+（﹣0.5）|=4+5﹣|﹣1|=9﹣1=8．【点评】本题考查了有理数的加减混合运算，解决本题的关键是熟记有理数的加减法．23．在数轴上表示下列各数：+6，﹣||，，﹣1，0，2.5，并用“＞”将它们连接起来．【考点】有理数大小比较；数轴．【分析】把各个数在数轴上表示出来，根据数轴上的数右边的数总是大于左边的数，即可把各个数按从大到小的顺序用“＞”连接起来．【解答】解：在数轴上表示为：按从大到小的顺序排列为：+6＞＞＞0＞＞﹣||．【点评】此题考查了数轴，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．24．某检修小组从O地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西为负，一天中七次行驶纪录如表．（单位：km）第一次A 第二次B 第三次C 第四次D 第五次E 第六次F 第七次G ﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2（1）画数轴表示出每次结束时的点的位置（用表格中的字母表示），并求出收工时距A地多远？（2）在第五次纪录时距A地最远．（3）若每千米耗油，问共耗油多少升？【考点】数轴；正数和负数．【分析】（1）把所有行驶记录相加，再根据正数和负数的意义解答；（2）分别写出各次记录时距离A地的距离，然后判断即可；【解答】解：（1）﹣4+7﹣9+8+6﹣5﹣2，=7+8+6﹣4﹣9﹣5﹣2，=21﹣20，=1千米，1﹣（﹣4）=5答：收工时检修小组在距O地东边5千米处；（2）第1次到第7次记录时距离A的分别为：0、3、6、2、8、3、1，所以，距A地最远时是第5次；（3）|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|，=4+7+9+8+6+5+2，=41千米，41×0.3=．答：从出发到收工时共耗油【点评】此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示25．我们知道，在数轴上，|a|表示数a表示的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上两个点A、B，分别用a，b表示，那么A、B两点间的距离为：AB=|a﹣b|．利用此结论，回答以下问题：（1）数轴上表示2和5的两点的距离是 3 ，数轴上表示﹣2和﹣5的两点之间的距离是 3 ，数轴上表示1和﹣3的两点之间的距离是 4 ；（2）若|a+1|=2，则a= ﹣3或1 ；若|a+2|+|a﹣1|=6，则a= ﹣或；（3）当|a+2|+|a﹣1|取最小值 3 时，此时a符合条件是﹣2≤a≤1 ；（4）当a= 1 时，|a+5|+|a﹣1|+|a﹣3|的值最小，最小值是8 ．【考点】绝对值；数轴．【分析】利用AB=|a﹣b|，即可求出答案．【解答】解：（1）5﹣2=3，﹣2﹣（﹣5）=3，1﹣（﹣3）=4；（2）∵|a+1|=2，∴a+1=±2，∴a=﹣3或a=1，∵|a+2|+|a﹣1|=6，当a＜﹣2时，∴﹣（a+2）﹣（a﹣1）=6，∴a=﹣，当﹣2≤a≤1时，∴a+2﹣（a﹣1）=6，∴3=6，此时矛盾，当a＞1时，∴a+2+a﹣1=6，∴a=，综上所述，a=﹣或a=；（3）当a在数轴上表示﹣2和1之间时，此时|a+2|+|a﹣1|的最小值为3，此时﹣2≤a≤1，（4）由于当﹣5≤a≤3时，此时|a+5|+|a﹣3|最小值为8，∴若要|a+5|+|a﹣1|+|a﹣3|的值最小，只需要|a﹣1|的值最小即可，此时a=1，|a﹣1|=0，∴|a+5|+|a﹣1|+|a﹣3|最小是为8，故答案为：（1）3，3，4；（2）﹣3或1，﹣或；（3）3，﹣2≤a≤1；（4）1，8．【点评】本题考查数轴，涉及绝对值，解方程等知识，综合程度较高．。

2010学年第二学期七年级数学独立作业一:选择题(每题3分,共30分)1.下列长度的三条线段,能组成三角形的是( )A.2,2,4B.2,2,5C. 2,3,6D.2,4,52.从1到10,这10个数中任选一个数是2的倍数的概率是( ) A. 101 B. 21 C. 31 D.51 3.如图,若△DEF 是由△ABC 经过平移后得到的,则平移的距离是( )A. 线段BC 的长度B. 线段EC 的长度C. 线段BE 的长度D.线段EF 的长度4． x=1 是方程ax-y=3的解,则a 的取值( ) y=2A. 5B.-5C. 2D.15.如图,已知AC 与BD 相交于则图中全等三角形有( ) A. 1对 B.2对 C. 3对 D.4对6.下列事件是不确定事件的是( )A.购买一张彩票,中奖B.在一个标准大气压下,水加热到100℃沸腾C.在奥运会上,百米赛跑的成绩是5秒D.掷一枚普通骰子,朝上一面的点数是87.已知AB=A ′B ′,∠A=∠A ′,则补充下列条件,仍然不能．．说明 △ABC 和△A ′B ′C ′全等的是( )A.∠B=∠B ′B. ∠C=∠C ′C.AC=A ′C ′D.BC=B ′C ′8.一副三角板,如图所示叠放在一起,则图中∠α的度数是( )A. 75°B. 60°C.65 °D.55°9三人同行，两人性别相同的概率是（ ）A ．13 B. 23 C. 1 D.3410．如图，在Rt △ABC 中，∠B=60°，将△ABC 绕点A 逆时针旋转70°后得到△A ′B ′C ′，则∠CA B ′为（ ）A ． 60 ° B. 70°C. 100°D.120°二.填空题(每空4分,共24分)11．若 x+2y=6 ，则x+y=＿＿＿＿＿2x+y=912．在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间是＿＿13.在△ABC 中∠A=130°-∠B ，则∠C=＿＿＿＿＿14．已知23x y +=，则用含x 的代数式表示y=＿＿＿＿＿15．如图Rt △ABC ，∠C=90°，BD 平分∠CBA ，交AC 于点D ，AC=6，CD=2，则D 到AB 的距离是＿＿＿＿＿16.从3点15分开始,到时针与分针第一次成30度角需要时间是＿＿＿分钟三.解答题(共66分)17．（共6分）解方程组： y-x+2=03x-2y=118．（共6分）在下面的方格中,先画出△ABC 向右平移三个单位长度的像△A ′B ′C ′,再画出△A ′B ′C ′关于直线LB A EC F D对称的像19．（共7分）如图，△ABC中，AD平分∠BAC，AD⊥BC，垂足为D。