下载文档原格式
VII 符号计算（4课时）一、符号对象：1. 建立符号变量和符号常数(1)sym函数sym函数用来建立单个符号量，例如，a=sym('a')建立符号变量a，此后，用户可以在表达式中使用变量a进行各种运算。
例考察符号变量和数值变量的差别。
在 MATLAB命令窗口，输入命令：a=sym('a');b=sym('b');c=sym('c');d=sym('d'); %定义4个符号变量w=10;x=5;y=-8;z=11; %定义4个数值变量A=[a,b;c,d] %建立符号矩阵AB=[w,x;y,z] %建立数值矩阵Bdet(A) %计算符号矩阵A的行列式det(B) %计算数值矩阵B的行列式例比较符号常数与数值在代数运算时的差别。
在 MATLAB命令窗口，输入命令：pi1=sym('pi');k1=sym('8');k2=sym('2');k3=sym('3'); % 定义符号变量pi2=pi;r1=8;r2=2;r3=3; % 定义数值变量sin(pi1/3) % 计算符号表达式值sin(pi2/3) % 计算数值表达式值sqrt(k1) % 计算符号表达式值sqrt(r1) % 计算数值表达式值sqrt(k3+sqrt(k2)) % 计算符号表达式值sqrt(r3+sqrt(r2)) % 计算数值表达式值(2)syms函数syms函数的一般调用格式为：syms var1 var2 … varn函数定义符号变量var1,var2,…,varn等。
用这种格式定义符号变量时不要在变量名上加字符分界符(')，变量间用空格而不要用逗号分隔。
2. 建立符号表达式例用两种方法建立符号表达式。
在MATLAB窗口，输入命令：(1) 直接用sym函数建立符号表达式U=sym('3*x^2+5*y+2*x*y+6') %定义符号表达式U (2) 先用syms函数定义符号变量，然后再建立符号表达式syms x y; %建立符号变量x、yV=3*x^2+5*y+2*x*y+6 %定义符号表达式V（3）符号表达式的值2*U-V+6 %求符号表达式的值例计算3阶范得蒙矩阵行列式的值。
第二章Matlab 初步（12课时）一、初等运算和初等函数（0.5课时）１、简单指令：（P5/6）例1．算术运算 a=2^2+(12+2*(7-4))/3^2-2^(1/2) %注意算术运算的运算符例2. 简单矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A 的 输入。
A = [1,2,3; 4,5,6; 7,8,9]A = [1 2 3; 4 5 6; 7 8 9]A=[1,2,34,5,67,8,9] %分行输入例3．指令的续行输入S=1–1/2+1/3–1/4+1/5–1/6+1/7 …-1/8２、数值、变量和表达式（１）数值的记述MATLAB 的数值采用习惯的十进制（或科学计数法）表示，可以带小数点或负号。
（２）变量命名规则变量名、函数名是对字母大小写敏感的。
变量名的第一个字符必须是英文字母，最多可包含63个字符（英文、数字和下连符）。
（３）MATLAB 默认的预定义变量：（P7/8）３、有关复数的函数：(P8/9)real(a) %给出复数a 的实部imag(a) %给出复数a 的虚部abs(a) %给出复数a 的模angle(a) %以弧度为单位给出复数a 的相位角例4．复数的运算——表达复数ie z i z i z 63212,21,43π=+=+=，及计算321z z z z =。
z1=3+4i %经典教科书的直角坐标表示法z2=1+2*i %运算符构成的直角坐标表示法z3=2*exp(i*pi/6) %运算符构成的极坐标表示法z=z1*z2/z3例5．复数矩阵的生成与计算(P15/10)A=[1,3;2,4]-[5,8;6,9]*iB=[1+5i,2+6i;3+8*i,4+9*i]C=A*B例6．求复数矩阵的实部、虚部、模和相角（接例5）C_real=real(C)C_imag=imag(C)C_magnitude=abs(C)C_phase=angle(C)*180/pi例7．复数的运算 ——计算-8的3次方根 (P10/11)(1) 直接计算时，得到的是处于第一象限的方根a=-8;r=a^(1/3)(2) 全部方根的计算% 先构造一个多项式a r r p -=3)(p=[1,0,0,-a]; %p 是多项式)(r p 的系数向量%指令末尾的“英文状态分号”使该指令运行后，不显示结果。
第1章MATLAB操作基础1.1 MATLAB概述1.2 MATLAB的运行环境与安装1.3 MATLAB集成环境1.4 MATLAB帮助系统1.1 MATLAB概述•1.1.1 MATLAB的发展1984年，MATLAB第1版(DOS版)1992年，MATLAB4.0版1994年，MATLAB 4.2版1997年，MATLAB 5.0版1999年，MATLAB 5.3版2000年，MATLAB 6.0版2001年，MATLAB 6.1版2002年，MATLAB 6.5版2004年，MATLAB 7.0版•1.1.2 MATLAB的主要功能1．数值计算和符号计算功能MATLAB以矩阵作为数据操作的基本单位，还提供了十分丰富的数值计算函数。
MATLAB和著名的符号计算语言Maple相结合，使得MATLAB具有符号计算功能。
2．绘图功能MATLAB提供了两个层次的绘图操作：一种是对图形句柄进行的低层绘图操作，另一种是建立在低层绘图操作之上的高层绘图操作。
•3．编程语言MATLAB具有程序结构控制、函数调用、数据结构、输入输出、面向对象等程序语言特征，而且简单易学、编程效率高。
4．MATLAB工具箱MATLAB包含两部分内容：基本部分和各种可选的工具箱。
MATLAB工具箱分为两大类：功能性工具箱和学科性工具箱。
•1.1.3 初识MATLAB例1-1 绘制正弦曲线和余弦曲线。
x=[0:0.5:360]*pi/180;plot(x,sin(x),x,cos(x));•例1-2 求方程3x4+7x3 +9x2-23=0的全部根。
p=[3,7,9,0,-23]; %建立多项式系数向量x=roots(p) %求根•例1-3 求积分quad('x.*log(1+x)',0,1)•例1-4 求解线性方程组。
a=[2,-3,1;8,3,2;45,1,-9];b=[4;2;17];x=inv(a)*b1.2 MATLAB的运行环境与安装•1.2.1 MATLAB的运行环境硬件环境：(1) CPU(2) 内存(3) 硬盘(4) CD-ROM驱动器和鼠标。
（完整版）matlab电子教案（2）第二章Matlab初步（12课时）四、字符串数组与图形标注1、字符串数组及其基本操作：(P275/70)字符串是用单引号括起来的字符序列。
例如，'Central South University'。
若字符串中的字符含有单引号，则该单引号字符应用两个单引号来表示。
字符串是以ASCII码形式存储的。
abs和double函数都可以用来获取字符串矩阵所对应的ASCII码数值矩阵。
相反，char函数可以把ASCII码矩阵转换为字符串矩阵。
size函数可以得到数组的大小。
a='This is a example. ' %创建一维串数组size(a)b='这是一个例子。
'c=[a b];subc=c(1:21) %提取a的子串revc=c(end:-1:1) %翻转字符串a, end是最后一个元素的下标asciic=double(c) %取a中字符的ascii码zi=asciic(21) %取a中第21个字符的ascii码char(asciic) %char()和double()是一对反函数char(zi) %取ascii码对应的字符２、转换函数产生数码字符串：(P276/74，76)a=[1 2;3 4]int2str(a) %整型数据转换成字符串num2str(rand(2),3) %数值型数据转换成字符串，保持3位有效数字b=mat2str(rand(3),3) %数值数组转换成“数组输入形式”字符串，保持3位有效数字，该字符串可以通过eval函数执行。
eval(b)与字符串有关的另一个重要函数是eval，其调用格式为：eval(t) 其中t为字符串。
它的作用是把字符串的内容作为对应的MATLAB语句来执行。
例如t=pi;m='[t,sin(t),cos(t)]';y=eval(m)３、用字符串数组给图形标注：(P277/75)clear %以下是图形标注a=2;w=3;t=0:0.001:10; %取初值y=exp(-a*t).*sin(w*t); %计算函数值，得到函数数组[y_m,i_m]=max(y); %取函数数组的最大元素t_x=['t=',num2str(t(i_m))]; %num2str()将数t(i_m)转为字符t_y=['y=',num2str(y_m)];max_text=char('maximum',t_x,t_y);tit=['y=exp(-',num2str(a),'t)*sin(',num2str(w),'t)'];plot(t,zeros(size(t)),'k') %画基准线0hold onplot(t,y,'b') %画y(t)曲线plot(t(i_m),y_m,'r.','MarkerSize',20) %用红点标注最大值点text(t(i_m)+0.3,y_m+0.05,max_text) %标注最大值点处的值title(tit),xlabel('t'),ylabel('y') %标注图形标题hold off点评：●数组是Matlab中最常用的数据类型，它的元素是数，主要用于计算。
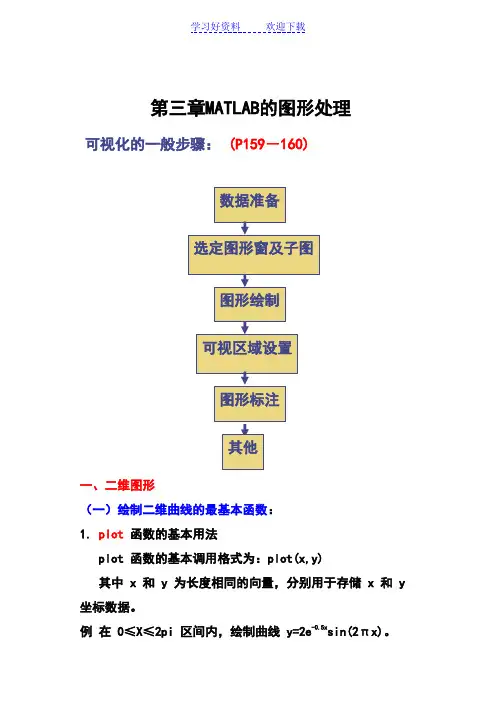
第三章MATLAB的图形处理可视化的一般步骤：(P159－160)一、二维图形（一）绘制二维曲线的最基本函数：1. plot 函数的基本用法plot 函数的基本调用格式为：plot(x,y)其中 x 和 y 为长度相同的向量，分别用于存储 x 和 y 坐标数据。
例在 0≤X≤2pi 区间内，绘制曲线 y=2e-0.5x sin(2πx)。
x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y)说明：（1）当 x,y 是同维矩阵时，则以 x,y 对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
（2）当 x 是向量，y 是有一维与 x 同维的矩阵时，则绘制出多根不同色彩的曲线。
曲线条数等于 y 矩阵的另一维数，x 被作为这些曲线共同的横坐标。
（3）plot 函数最简单的调用格式是只包含一个输入参数：plot(x)。
例某工厂 2000 年各月总产值（单位：万元）分别为22、60、88、95、56、23、9、10、14、81、56、23，试绘制折线图以显示出该厂总产值的变化情况。
p=[22,60,88,95,56,23,9,10,14,81,56,23];plot(p)2．含多个输入参数的 plot 函数含多个输入参数的 plot 函数调用格式为：plot(x1,y1,x2,y2,…,xn,yn)3．含选项的 plot 函数含选项的 plot 函数调用格式为：plot(x1,y1,选项 1,x2,y2, 选项 2,…,xn,yn,选项 n)为了对所绘多条曲线作进一步区分，需要对曲线的线型、点型、色彩(P177-179/162-163)及其他属性(help)作相应说明。
例用不同线型和颜色在同一坐标内绘制曲线 y=2e-0.5x sin(2πx)及其包络线。
x=(0:pi/100:2*pi)';y1=2*exp(-0.5*x)*[1,-1];y2=2*exp(-0.5*x).*sin(2*pi*x);x1=(0:12)/2;y3=2*exp(-0.5*x1).*sin(2*pi*x1);plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');4．双纵坐标函数 plotyyplotyy 函数是 MATLAB 5.X 新增的函数。
《MATLAB教案》PPT课件第一章：MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义（Matrix Laboratory）强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章：MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章：MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章：MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章：MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章：MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用：模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章：MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式，包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章：MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章：MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章：MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章：MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用：快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章：MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章：MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章：MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章：MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件，内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。
第二章Matlab 初步（12课时）一、初等运算和初等函数（0.5课时）１、简单指令：（P5/6）例1．算术运算a=2^2+(12+2*(7-4))/3^2-2^(1/2) %注意算术运算的运算符例2. 简单矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A 的 输入。
A = [1,2,3; 4,5,6; 7,8,9]A = [1 2 3; 4 5 6; 7 8 9]A=[1,2,34,5,67,8,9] %分行输入例3．指令的续行输入S=1–1/2+1/3–1/4+1/5–1/6+1/7 …-1/8２、数值、变量和表达式（１）数值的记述MATLAB 的数值采用习惯的十进制（或科学计数法）表示，可以带小数点或负号。
（２）变量命名规则变量名、函数名是对字母大小写敏感的。
变量名的第一个字符必须是英文字母，最多可包含63个字符（英文、数字和下连符）。
（３）MATLAB 默认的预定义变量：（P7/8）３、有关复数的函数：(P8/9)real(a) %给出复数a 的实部imag(a) %给出复数a 的虚部abs(a) %给出复数a 的模angle(a) %以弧度为单位给出复数a 的相位角例4．复数的运算——表达复数ie z i z i z 63212,21,43π=+=+=，及计算321z z z z =。
z1=3+4i %经典教科书的直角坐标表示法z2=1+2*i %运算符构成的直角坐标表示法z3=2*exp(i*pi/6) %运算符构成的极坐标表示法z=z1*z2/z3例5．复数矩阵的生成与计算(P15/10)A=[1,3;2,4]-[5,8;6,9]*iB=[1+5i,2+6i;3+8*i,4+9*i]C=A*B例6．求复数矩阵的实部、虚部、模和相角（接例5）C_real=real(C)C_imag=imag(C)C_magnitude=abs(C)C_phase=angle(C)*180/pi例7．复数的运算 ——计算-8的3次方根 (P10/11)(1) 直接计算时，得到的是处于第一象限的方根a=-8;r=a^(1/3)(2) 全部方根的计算% 先构造一个多项式a r r p -=3)(p=[1,0,0,-a]; %p 是多项式)(r p 的系数向量%指令末尾的“英文状态分号”使该指令运行后，不显示结果。
R=roots(p) %求多项式的根问题1：rrr 给出-8的3个3次方根，如何求一个数的n 次方根？（3）图形表示MR=abs(R(1)); %计算复根的模t=0:pi/20:2*pi; %产生参变量在0到2*pi间的一组采样点x=MR*sin(t);y=MR*cos(t);plot(x,y,'b:'),grid on %画一个半径为R的圆%注意“英文状态逗号”在不同位置的作用hold onplot(R(2),'.','MarkerSize',30,'Color','r') %画第一象限的方根plot(R([1,3]),'o','MarkerSize',15,'Color','b')%画另两个方根axis([-3,3,-3,3]),axis square %保证屏幕显示呈真圆hold off点评：●数值计算是Matlab最简单的运算，它格式和符号以及初等函数与习惯基本相同●后面还会学习Matlab的符号计算●数值计算有精度问题。
计算的精度可以由format()函数设置，但不能超过最小精度eps，这里我们略去这些问题（参P17/14）。
学习要点：●变量名的命名规则（与C语言相似）●注意预定义变量i与pi含义，ans,inf,nan也是预定义变量。
复习、自学内容（第一章）：１、了解有关表格：表1.4-2, 1.4-3, 1.4-4, 1.5-1, 1.6-1。
２、当前目录、搜索路径及其设置：(P23-25/20-23)MATLAB的所有（M、MAT、MEX）文件都被存放在一组结构严整的目录树上。
MATLAB把这些目录按优先次序设计为“搜索路径”上的各个节点。
此后，MATLAB工作时，就沿着此搜索路径，从各目录上寻找所需的文件、函数、数据。
MATLAB的基本搜索过程大抵如下：当用户从指令窗送入一个名为cont的指令后，●检查MATLAB内存，看cont是不是变量；假如不是变量，则进行下一步。
●检查cont是不是内建函数（Built-in Function）；假如不是，再往下执行。
●在当前目录上，检查是否有名为cont的M文件存在；假如不是，再往下执行。
●在MATLAB搜索路径的其他目录中，检查是否有名为cont的M文件存在。
３、工作空间及有关命令：(P28-31/23-29)４、帮助系统及其使用：(P32)实习一：1、熟悉MATLAB环境；2、做例题；二、Matlab数据及Matlab运算（0.5课时）１、Matlab数据的特点矩阵是MATLAB最基本、最重要的数据对象。
单个数据(标量)可以看成是矩阵的特例。
在Matlab中使用变量时不需要说明变量的数据类型，系统将根据赋给变量的值来确定变量的数据类型。
２、Matlab数据类型数值数据：双精度型、单精度数、带符号整数和无符号整数。
字符数据。
结构(Structure)和元胞（或细胞或单元）(Cell)。
多维矩阵和稀疏矩阵(Sparse)。
３、变量和赋值（1）变量的命名●在MATLAB中，变量名是以字母开头，后接字母、数字或下划线的字符序列，最多63个字符。
●在MATLAB中，变量名区分字母的大小写。
MATLAB提供的标准函数名以及命令名必须用小写字母。
（2）赋值语句MATLAB赋值语句有两种格式：①变量=表达式②表达式一般情况下，运算结果在命令窗口中显示出来。
如果在语句的最后加分号，那么，MATLAB仅仅执行赋值操作，不再显示运算的结果。
在MATLAB语句后面可以加上注释，注释以%开头，后面是注释的内容。
4、Matlab运算(1) 算术运算(a) 基本算术运算：＋(加)、－(减)、*(乘)、/(右除)、\(左除)、^(乘方)。
（P8/9）注意:运算是在矩阵意义下进行的，单个数据的算术运算只是一种特例。
(b) 点运算：点运算符有.*、./、.\和.^。
两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维数相同。
(c) MATLAB常用数学函数:(P110/48)注意：数学函数exp( ),abs( ),angle( )的意义和用法。
这样的函数还有很多，如：sqrt(x)—平方根, round(x)—取整数部分, rem(x,y)—求余, gcd(x,y)—最大公约数, log(x), tan(x), sign(x)—符号函数等，它们可查帮助获得。
(2) 关系运算：MATLAB提供了6种关系运算符：<(小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、= =(等于)、～=(不等于)。
(3)逻辑运算：MATLAB提供了3种逻辑运算符：&(与)、|(或)和～(非)。
三、矩阵(数组)及其运算：（1课时）内容：输入矩阵进行矩阵的各种运算，观察运算结果，学习Matlab 的使用方法。
（第３章／第２章）（一）、矩阵（数组）的创建（P97-102/41-44）1. 直接输入法:将矩阵的元素用方括号括起来，按矩阵行的顺序输入各元素，同一行的各元素之间用空格或逗号分隔，不同行的元素之间用分号分隔。
例如A=[1 2 3;4 5 6;7 8 9]２、冒号生成法：只生成一维数组（行向量）。
一般格式： e1:e2:e3例９x1=1:0.2:5%创建一维向量x1，步长0.2；1和5为两个终点A=-4:5%创建一维向量A，步长1；-4和5为两个终点３、线性定点法：只生成一维数组（行向量）。
一般格式：linspace(a,b,n)linspace(a,b,n)与a:(b-a)/(n-1):b等价。
４、利用MATLAB函数建立矩阵：(P98,101/50)●几个产生特殊矩阵的函数：zeros、ones、 eye、rand、randn。
●这几个函数的调用格式相似，下面以产生零矩阵的zeros函数为例进行说明。
其调用格式是：zeros(m) 产生m×m零矩阵zeros(m,n) 产生m×n零矩阵。
zeros(size(A)) 产生与矩阵A同样大小的零矩阵例10.利用MATLAB函数建立矩阵B=ones(3), B1=ones(3,2) %全1矩阵C=zeros(3), C1=zeros(3,2) %全零阵rand('state',0) %将随机数产生器置为初始状态D=rand(3), D1=rand(3,2)D2=100*rand(3) %随机矩阵的输入格式E=eye(3) %单位对角阵diag(D) %取D的对角元素（D未必是方阵），生成一维数组diag(diag(D)) %以D的主对角线构造对角阵５、利用M文件建立矩阵：对于比较大且比较复杂的矩阵，可以为它专门建立一个M文件。
例如利用M文件建立MYMAT矩阵。
(1)启动有关编辑程序或MATLAB文本编辑器，并输入待建矩阵.(2)把输入的内容以纯文本方式存盘(设文件名为mymatrix.m)。
(3)运行该M文件，就会自动建立一个名为MYMAT的矩阵，可供以后使用。
６、建立大矩阵大矩阵可由方括号中的小矩阵建立起来。
例如A=[1 2 3;4 5 6;7 8 9];C=[A,eye(size(A)); ones(size(A)),A]（二）、矩阵的标识与寻访（P103/45）1. 矩阵元素●MATLAB允许用户对一个矩阵的单个元素进行赋值和操作。
例如A(3,2)=200●也可以采用矩阵元素的序号来引用矩阵元素。
矩阵元素按列编号，先第一列，再第二列，依次类推。
以m×n矩阵A为例，矩阵元素A(i,j)的序号为 (j-1)*m+i。
其相互转换关系也可利用sub2ind和ind2sub函数求得（单下标和双下标的转换函数）。
IND = sub2ind(size(A),3,2)[I,J] = ind2sub(size(A),IND)2. 子矩阵标识(1)利用冒号表达式获得子矩阵①A(i,j) 表示取A矩阵第i行、第j列的元素。
A(:,j) 表示取A矩阵的第j列全部元素；A(i,:) 表示A矩阵第i行的全部元素；②A(i:i+m,:) 表示取A矩阵第i～i+m行的全部元素；A(:,k:k+m) 表示取A矩阵第k～k+m列的全部元素，A(i:i+m,k:k+m) 表示取A矩阵第i～i+m行内，并在第k～k+m列中的所有元素。
