利用函数单调性证明不等式的难点_构造辅助函数_贺学海

利用导数与辅助函数解决有关不等式问题的探讨摘要：数学课堂拥有着极为独特的魅力，但是学生在学习数学时往往会遇到很多困难。

这些困难主要是导数及辅助函数问题，通过合理利用导数以及辅助函数教师可帮助学生突破难点、完成学习激发。

为做好此点在课堂上教师应用导数的单调性导数的定义进行讲解，着重突破应用导数处理不等式的相关问题。

过后再利用构建一次函数、二次函数、三角函数等来帮助学生了解高中阶段的不等式问题，深化课堂教学。

关键词：导数;辅助函数;不等式一、引言不等式是高中阶段教学的一大难点，不少学生在学习不等式时往往会遇到很多困难。

这时教师需要去做的也是利用好导数以及辅助函数来突破不等式学习难点，用好相关定理完成不等式的证明理解。

为做好这一点，教师也要改革整个数学课堂的教学方式。

了解学生在不等式学习过程中的薄弱之处，积极做好评价总结。

对不等式的相关问题完成了解，最终成功突破不等式解题的难点。

二、利用导数解决不等式问题（一）应用导数的单调性证明不等式（三）利用导数来处理不等式的恒成立问题不等式的恒成立问题就是指不等式中的未知量，无论取最大值还是最小值时它都能够被当作不等式成立。

将不等式恒成立问题转化为函数的最值问题可以简化教学思路，完成学生学习的再次创造。

在教学不等式恒成立问题时教师可由参数问题进行出发，将不等式恒成立问题转换为参数的转变思考。

将变量进行分离之后把整个函数式转成M>f（x）的形式，这样整个题目就变成了M>f（x）最大值了。

之后教师再把不等式的恒成立问题转化为函数的最值问题，但是在使用导数来解决不等式恒成立问题时教师也要注重好教学的一些细节点比如该不等式的区间端点是否可取。

不等式问题在高考中占有着非常重要的比重，这也是教师应该注重的一点。

三、构造函数在不等式证明中的应用（一）善于构造一次函数不等式的证明是一项技巧性很強的题目类型，由此它也很容易成为学生学习的难点部分。

但是通过合理构造函数，教师却可以实现不等式复杂问题的简单化。

函数单调性在不等式证明中的应用冯永奎[摘要] 不等式是我们从初中就开始接触，一直在整个数学研究中占有一定的比例，它包括不等式的解法，不等式的构造，不等式的证明.其中不等式的证明是不等式学习的重点之一，本文讨论了利用函数单调性来证明不等式。

[关键词] 函数 单调性 不等式 证明不等式的证明是中学数学的重要内容之一，也是高等数学的重要工具。

它的题型广泛，技巧多变，思路灵活，涉及的知识面也较广。

我们可以用构造函数的方法，通过函数的单调性来刻画不等式的性质，也可以用来证明不等式，下面结合具体的例子来说明函数单调性在不等式证明中的应用。

[5] 设函数)(x f 在区间),(b a 内可导。

（1） 如果在),(b a 内恒有0)('>x f ， 则函数)(x f 在),(b a 内单调增加； （2） 如果在),(b a 内恒有0)('<x f ， 则函数)(x f 在),(b a 内单调减少。

[6] 设函数)(x f 在点0x 处的一个领域可导，且0)('0=x f ，或)('0x f 不存在，但)(x f 在0x x =处连续，若)(x f 在点0x 的两侧邻近导数异号，则)(0x f 是函数)(x f 的极值。

当导数符号由正变负时，)(0x f 是极大值，由负变正时，)(0x f 是极小值，若)(x f 在点0x 处的两侧邻近导数不变号，则)(0x f 不是极值。

根据题目所给的不等式和条件，对不等式作适当变形，选取适当的函数)(x f 及区间],[b a ，再利用[5]来判断)(x f 在),(b a 内的单调性，然后取函数)(x f 在区间端点处的值，则得不等关系，当)(x f 单调增加时，)()()(b f x f a f <<当)(x f 单调减少时，)()()(b f x f a f >>.从而有)()(b f a f <或)()(b f a f >再确定不等式。

浅谈高等数学在高中阶段的应用作者简介：田帅，（1990.12-），男，籍贯：河南淮阳，单位：周口师范学院研究方向：信息与计算科学，职业：学生。

摘要：本文介绍高中数学和高等数学的概念，然后总结了它们之间的关系，重点探讨了高等数学中导数、极限思想、柯西不等式在高中数学题中的应用，并给出了例子进行详细说明。

关键词：导数；极限思想；向量方法1.中学数学和高等数学的关系高等数学与中学数学之间无论在观点上还是在方法上都有着很大的区别，正因为这个原因，有许多学者认为，学生不需要懂得高等数学知识。

其实，这是一种误解。

因为高等数学是在中学数学的基础上发展起来的，是中学数学的继续和提高，利用高等数学知识揭示中学数学的解题方法，有利于提高学生的数学思维能力，帮助学生学会以高等数学的思想、方法为工具从不同的角度去研究中学数学问题，还可以借助于高等数学的方法来统一处理和解决中学数学中一些或一类问题等等。

中学数学里很多理论遗留问题必须在高等数学中才能澄清，很多数学题都因为高等知识的运用才得以扩展，才让我们对题的本质有更透彻的了解，所以二者有着密切的关系。

我们应该将高等数学思想方法全面渗入到中学数学中，寻找高等数学与中学数学的结合点。

2.高等数学知识在中学数学题中的应用高等数学中有许多方法和中学数学相通，有些可以适当迁移到中学数学中来。

高等数学的方法不仅可以使我们居高临下地去观察中学数学问题，帮助我们确定解题思路，有时还能够帮助我们剖析某些问题实质，寻求简捷的解法。

中学数学中常用的高等数学方法有极限法、求导法、向量法、概率法等。

下面以中学中常见的问题为例来说明高等数学方法在中学数学中的应用。

2.1导数的应用导数是中学数学与高等数学的重要衔接点，在中学数学里导数的应用很广泛，比传统的方法有许多优越性，给传统的数学内容注入了新的生机和活力。

2.1.1求函数的极值、最值求导是数学中非常重要的一种方法，求极值、最值问题是是中学数学里很普遍的，用一般的方法比较复杂，利用导数求函数的极大（小）值，求函数在连续区间a，b上的最大（小）值，能使问题变得简单化。

龙源期刊网
函数最值方法在不等式证明中的应用
作者：吴子生
来源：《文理导航》2018年第05期
【摘要】本文主要研究函数的最值方法在不等式证明中的应用。

结合不等式的不同特点，对不等式做恰当的变形，找出规律，构造不同的辅助函数，然后根据函数的单调性找出定义域上最大值或者最小值，便可以建立不等式关系，通过整理得到不等式结果。

【关键词】不等式；函数的极值；函数的最值；辅助函数
引言
不等式的证明不仅是高中数学非常重要的一部分内容，还是将来学习高等数学微积分的重要基础。

所以我们有必要研究总结证明不等式的若干方法，从而使学习更具有系统性。

本文介绍了不等式证明的八种方法，有比较好的参照性，但是由于高中阶段学生所学习的知识有限，文章所介绍的许多方法，例如微分中值定理方法、凹凸性方法和积分中值定理方法，并不能在高中教学中大力推广。

文主要结合高中所学习的函数单调性来证明一些不等式。

事实上，高中数学中函数的最值在不等式的证明中也有很好的作用，本文将利用函数的极值最值问题再结合函数单调性的相关结论来总结不等式证明的方法。

1.利用导数判定函数的极值
我们在讨论函数最值的时候，其实需要先找出函数的极值，下面先给出极值点与函数的导数的关系：。

不等式证明中辅助函数的构造方法与技巧大庆师范学院本科生毕业论文不等式证明中辅助函数的构造方法与技巧学院教师教育学院专业数学与应用数学研究方向数学教育学生姓名刘雨琳学号201101051311指导教师姓名李秀丽指导教师职称副教授2015年5月25日摘要不等式的证明问题是高等数学学习中一类很重要的问题，有些不等式的证明问题可以运用我们所学的基础知识直接解决，但有些不等式成立需要借助于构造辅助函数，构造辅助函数证明不等式成立的方法有很多。

本文简单介绍了几种在证明不等式时可以运用的构造辅助函数的方法和技巧，并且给出了在常见的几种不等式类型中这些方法的应用，主要就是通过构造出适合的辅助函数，将复杂的问题转变为基础的、简单的问题，提高解题的效率。

关键词：不等式；构造；辅助函数；方法；技巧；AbstractProving inequalities is a class of very important problems in learning Higher Mathematics. The proof of some inequalities can be solved directly using what we have learned the basic knowledge , but some inequalities can be established by constructing an auxiliary function , constructing an auxiliary function that inequality into the established method has much . This article simply introduces the methods and skills of several in proving inequalities can be used to construct the auxiliary function , and gives the application of these methods in several common types of inequality , mainly is by constructing a suitable auxiliary function , transformation of the complex issues as basis , a simple problem , improve their problem solving efficiency .Keywords: inequality; structure; auxiliary function; methods; techniques;目录第一章前言 (1)第二章几种构造辅助函数的方法与技巧 (2)2.1利用单调性法 (2)2.2参数变易法 (3)2.3变形法 (4)2.4利用凸函数定义 (5)2.5利用詹森不等式 (6)2.6借助中值定理 (7)第三章构造辅助函数证明几类常见不等式 (9)3.1一般不等式的证明 (9)3.2含积分符号的不等式的证明 (10)3.3含微分符号的不等式的证明 (11)第四章总结 (12)参考文献 (13)第一章前言不等式证明是数学中一类十分重要的问题，它可以运用到许多相关的知识，比如函数的性质，微积分等。

导数与构造函数证明不等式的技巧【摘要】本文首先介绍了导数与构造函数的基本概念，以及不等式证明的重要性。

接着详细阐述了利用导数证明不等式的一般步骤和常见的技巧，包括化简不等式时的常用策略和特殊不等式的处理方法。

通过实例分析，展示了如何利用导数与构造函数证明常见不等式。

结尾部分强调了导数与构造函数在不等式证明中的应用价值，并总结了证明不等式的技巧。

本文旨在帮助读者了解如何运用导数与构造函数来证明不等式，提高数学推理能力，以及加深对不等式证明方法的理解和掌握。

【关键词】导数、构造函数、不等式、证明、技巧、重要性、步骤、常见、策略、特殊、实例分析、应用价值、总结。

1. 引言1.1 导数与构造函数的基本概念导数是微积分中非常重要的概念，它描述了函数在某一点上的变化率。

在不等式证明中，导数可以帮助我们证明某个函数在某个区间内的增减性，从而推导出不等式的情况。

导数的定义是函数在某一点上的斜率，它可以用极限的概念来定义。

如果一个函数在某一点的导数存在，那么这个函数在这一点是可导的，也就是说在这一点上有切线。

导数可以用符号f'(x)或\frac{dy}{dx}表示，其中y是函数f(x)的值。

构造函数是指通过一定的方法构建出符合特定性质的函数。

在不等式证明中，构造函数的技巧是非常重要的，通过构造出合适的函数来推导不等式，使得证明变得更加简单。

构造函数的过程需要我们对函数的性质有一定的了解，需要灵活运用函数的各种性质来构造出满足条件的函数。

导数和构造函数是不等式证明中常用的工具，它们可以帮助我们更好地理解和推导各种不等式。

在接下来的正文中，我们将介绍如何利用导数和构造函数来证明不等式，以及常见的技巧和策略。

1.2 不等式证明的重要性不等式在数学中具有非常重要的意义，不仅在理论研究中有着重要的地位，也在实际问题中发挥着重要作用。

不等式证明作为数学推理的一种形式，是数学学习中的重要内容之一，它不仅培养了学生的逻辑思维能力和数学推理能力，还拓展了他们的数学思维。

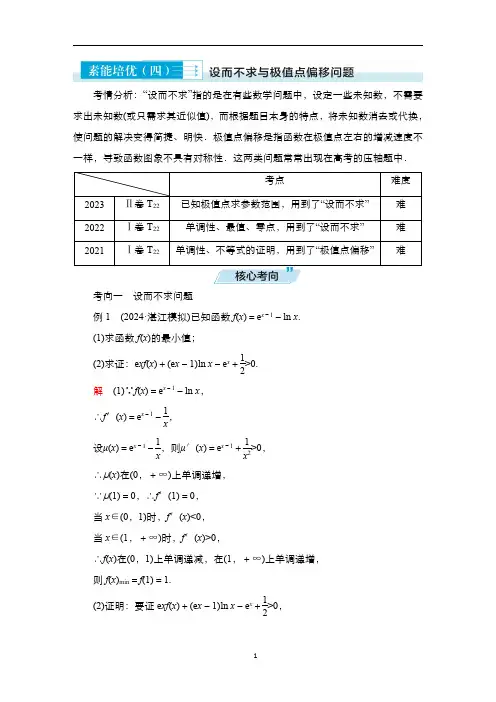
考情分析：“设而不求”指的是在有些数学问题中，设定一些未知数，不需要求出未知数(或只需求其近似值)，而根据题目本身的特点，将未知数消去或代换，使问题的解决变得简捷、明快．极值点偏移是指函数在极值点左右的增减速度不一样，导致函数图象不具有对称性．这两类问题常常出现在高考的压轴题中．考点难度2023Ⅱ卷T22已知极值点求参数范围，用到了“设而不求”难2022Ⅰ卷T22单调性、最值、零点，用到了“设而不求”难2021Ⅰ卷T22单调性、不等式的证明，用到了“极值点偏移”难考向一设而不求问题例1(2024·湛江模拟)已知函数f(x)＝e x－1－ln x.(1)求函数f(x)的最小值；(2)求证：e xf(x)＋(e x－1)ln x－e x＋12>0.解(1)∵f(x)＝e x－1－ln x，∴f′(x)＝e x－1－1x，设μ(x)＝e x－1－1x ，则μ′(x)＝e x－1＋1x2>0，∴μ(x)在(0，＋∞)上单调递增，∵μ(1)＝0，∴f′(1)＝0，当x∈(0，1)时，f′(x)<0，当x∈(1，＋∞)时，f′(x)>0，∴f(x)在(0，1)上单调递减，在(1，＋∞)上单调递增，则f(x)min＝f(1)＝1.(2)证明：要证e xf(x)＋(e x－1)ln x－e x＋12>0，只需证e x(e x－1－ln x)＋(e x－1)ln x－e x＋12>0，即证(x－1)e x－ln x＋12>0.令g(x)＝(x－1)e x－ln x＋12，则g′(x)＝x e x－1x(x>0)，当x>0时，令h(x)＝g′(x)＝x e x－1x，则h′(x)＝(x＋1)e x＋1x2>0，∴h(x)在(0，＋∞)上单调递增，即g′(x)＝x e x－1x在(0，＋∞)上为增函数，又g ＝23e23－32＝23e23－，g′(1)＝e－1>0，∴存在x0g′(x0)＝0.由g′(x0)＝x0e x0－1x0＝x20e x0－1x0＝0，得x20e x0＝1，即e x0＝1x20，即－2ln x0＝x0，∴当x∈(0，x0)时，g′(x)＝x e x－1x<0，g(x)单调递减，当x∈(x0，＋∞)时，g′(x)＝x e x－1x>0，g(x)单调递增，∴g(x)min＝g(x0)＝(x0－1)e x0－ln x0＋12＝x0－1x20＋x02＋12＝x30＋x20＋2x0－22x20.令φ(x)＝x3＋x2＋2x－2，则当xφ′(x)＝3x2＋2x＋2＝＋53>0，∴φ(x)∴φ(x0)>＝227>0，∴g (x )>0，∴(x －1)e x －ln x ＋12>0，即e xf (x )＋(e x －1)ln x －e x ＋12>0.隐零点问题解题策略我们把函数或其导函数存在零点，但零点不可求出的问题称为隐零点问题，具体求解步骤如下：(1)用零点存在定理判定导函数零点的存在性，列出零点方程，f ′(x )＝0，并结合f (x )的单调性得到零点的范围(有时范围可根据具体情况适当缩小)．(2)以零点为分界点，说明导函数f ′(x )的正负，进而得到f (x )的最值表达式．(3)将零点方程f ′(x )＝0适当变形，整体代入f (x )最值式子进行化简，可以消除f (x )最值式子中的指对项，也可以消除其中的参数项，再将得到的f (x )最值式子进行化简证明．(2024·湖北部分学校联考)已知函数f (x )＝(x －4)ln x ＋x 2＋ax －2.(1)证明：f (x )有唯一的极值点；(2)若f (x )≥0恒成立，求实数a 的取值范围．解(1)证明：f (x )的定义域为(0，＋∞)，因为f ′(x )＝ln x ＋x －4x＋2x ＋a ＝ln x －4x ＋2x ＋a ＋1，所以f ′(x )在定义域内单调递增，且值域为R ，所以f ′(x )有唯一的零点x 0∈(0，＋∞)，使得f ′(x 0)＝0，当x ∈(0，x 0)时，f ′(x )<0，f (x )单调递减；当x ∈(x 0，＋∞)时，f ′(x )>0，f (x )单调递增，所以f (x )有唯一的极值点．(2)由(1)知，f (x )在x ＝x 0处取得极小值，也是最小值，由f ′(x 0)＝0，得a ＝－ln x 0－2x 0＋4x 0－1，所以f (x 0)＝(x 0－4)ln x 0＋x 20＋ax 0－2＝(x 0－4)ln x 0＋x 20ln x 0－2x 0＋4x 0－0－2＝－4ln x 0－x 20－x 0＋2＝－4ln x0－(x0＋2)(x0－1)，当0<x0≤1时，－4ln x0≥0，－(x0＋2)(x0－1)≥0，所以f(x0)≥0；当x0>1时，－4ln x0<0，－(x0＋2)(x0－1)<0，所以f(x0)<0，因为f(x0)≥0，所以0<x0≤1.设h(x)＝－ln x－2x＋4x－1(0<x≤1)，因为h(x)单调递减，所以a＝h(x0)≥h(1)＝1，即a≥1.所以实数a的取值范围是[1，＋∞)．考向二极值点偏移问题例2(2021·新高考Ⅰ卷改编)已知函数f(x)＝x(1－ln x)在(0，1)上单调递增，在(1，＋∞)上单调递减．借助函数f(x)的单调性解决下列问题．(1)设x1，x2是两个不相等的正数，且x1(1－ln x1)＝x2(1－ln x2)，证明：2<x1＋x2<e；(2)设a，b为两个不相等的正数，且b ln a－a ln b＝a－b，证明：2<1a ＋1 b<e.证明(1)∵f(x)在(0，1)上单调递增，在(1，＋∞)上单调递减，∴f(x)max＝f(1)＝1，且f(e)＝0.由x1(1－ln x1)＝x2(1－ln x2)知，x1，x2是f(x)＝k的两根，其中k∈(0，1)，不妨令x1∈(0，1)，x2∈(1，e)，则2－x1>1，先证2<x1＋x2，即证x2>2－x1，即证f(x1)＝f(x2)<f(2－x1)．令h(x)＝f(x)－f(2－x)，x∈(0，1)，则h′(x)＝f′(x)＋f′(2－x)＝－ln x－ln(2－x)＝－ln[x(2－x)]>0，故函数h(x)单调递增，∴h(x)<f(1)－f(2－1)＝0，∴f(x1)<f(2－x1)，故2<x1＋x2得证．下面证明x1＋x2<e.∵0<x1<1<x2<e，∴1－ln x1>1，∴x1(1－ln x1)>x1.∵x1(1－ln x1)＝x2(1－ln x2)，∴x2(1－ln x2)>x1.要证x1＋x2<e，只要证x2(1－ln x2)＋x2<e，即证2x2－x2ln x2<e，x2∈(1，e)．设g(x)＝2x－x ln x，x∈(1，e)，则g′(x)＝1－ln x>0.∴g(x)在(1，e)上单调递增．∴g(x)<2e－e＝e.∴2x2－x2ln x2<e成立．∴原命题成立，即x1＋x2<e.综上可知，2<x1＋x2<e.(2)由b ln a－a ln b＝a－b得－1a ln1a＋1bln1b＝1b－1a，－ln－ln借助(1)的结论知2<1a ＋1 b<e.函数极值点偏移问题的解题策略(1)(对称化构造法)构造辅助函数：对结论x1＋x2>(<)2x0型，构造函数F(x)＝f(x)－f(2x0－x)；对结论x1x2>(<)x20型，构造函数F(x)＝f(x)－F(x)的单调性证明不等式．(2)(比值代换法)将所证的双变量不等式通过代换t＝x1x2化为单变量的函数不等式，利用函数的单调性证明不等式．(2023·张家口模拟)已知函数f (x )＝x 2＋2cos x ，f ′(x )为函数f (x )的导函数．(1)讨论函数f (x )的单调性；(2)已知函数g (x )＝f ′(x )－5x ＋5a ln x ，存在x 1，x 2且x 1≠x 2，使得g (x 1)＝g (x 2)，证明：x 1＋x 2>2a .解(1)f (x )的定义域为R ，f ′(x )＝2x －2sin x ，令h (x )＝2x －2sin x ，则h ′(x )＝2－2cos x ≥0，所以函数h (x )在R 上单调递增，又因为h (0)＝0，所以h (x )<0⇒x <0，h (x )>0⇒x >0，即f ′(x )<0⇒x <0，f ′(x )>0⇒x >0，所以函数f (x )在(－∞，0)上单调递减，在(0，＋∞)上单调递增．(2)证明：由(1)，得g (x )＝2x －2sin x －5x ＋5a ln x ＝－2sin x －3x ＋5a ln x ，x >0，又g (x 1)＝g (x 2)，即－2sin x 1－3x 1＋5a ln x 1＝－2sin x 2－3x 2＋5a ln x 2，所以5a (ln x 2－ln x 1)＝2(sin x 2－sin x 1)＋3(x 2－x 1)．不妨设x 2>x 1>0，所以ln x 2>ln x 1.由(1)得当x >0时，函数f ′(x )单调递增，所以2x 1－2sin x 1<2x 2－2sin x 2，故2(sin x 2－sin x 1)<2(x 2－x 1)，所以5a (ln x 2－ln x 1)＝2(sin x 2－sin x 1)＋3(x 2－x 1)<5(x 2－x 1)，所以a <x 2－x 1ln x 2－ln x 1，故2a <2（x 2－x 1）ln x 2－ln x 1.下证2（x 2－x 1）ln x 2－ln x 1<x 2＋x 1.即证2（x 2－x 1）x 2＋x 1<ln x 2－ln x 1＝lnx 2x 1，设x2x 1＝t >1，h (t )＝ln t －2（t －1）t ＋1，t >1，则h′(t)＝（t－1）2t（t＋1）2>0，所以函数h(t)在区间(1，＋∞)上单调递增，所以h(t)>ln1－2×（1－1）1＋1＝0，故ln t>2（t－1）t＋1，即ln x2x1>x2x1＋1所以2（x2－x1）x2＋x1<ln x2－ln x1，即2（x2－x1）ln x2－ln x1<x2＋x1，所以x2＋x1>2a，得证．。

高考数学必杀技系列之导数5构造函数证明不等式
专题5 构造函数证明不等式
一、考情分析
函数与导数一直是高考中的热点与难点, 利用导数证明不等式在近几年高考中出现的频率比较高．求解此类问题关键是要找出与待证不等式紧密联系的函数,然后以导数为工具来研究该函数的单调性、极值、最值(值域),从而达到证明不等式的目的．
二、解题秘籍
(一) 把证明转化为证明
此类问题一般是有最小值且比较容易求,或者有最小值,
但无法具体确定,这种情况下一般是先把的最小值转化为关于极值点的一个函数,再根据极值点所在范围,确定最小值所在范围
此类问题是证明不等式中最基本的一类问题,把两个函数通过作差转化为一个函数,再利用导数研究该函数的性质,通过函数性质证明该不等式.
(五) 改变不等式结构,重新构造函数证明不等式
此类问题要先对待证不等式进行重组整合,适当变形,找到其等价的不等式,观察其结构,根据结构构造函数.常见的变形方法有：
①去分母,把分数不等式转化为整式不等式；
②两边取对数,把指数型不等式转化为对数型不等式；
③两边同时除以,此方法适用于以下两类问题：
(i)不等式为类型,且的符号确定；
(ii)不等式中含有,有时为了一次求导后不再含有对数符号,可考虑此法.
(六) 通过减元法构造函数证明不等式
对于多变量不等式,一般处理策略为消元或是把一个看作变量其他看作常量；当都不能处理的时候,通过变形,再换元产生一个新变量,从而构造新变量的函数.
(七) 与数列前n项和有关的不等式的证明
此类问题一般先由已知条件及导数得出一个不等式,再把该不等式中的自变量依次用1,2,3,,n代换,然后用叠加法证明.
完整电子版可关注下载。

构造辅助函数证明不等式辅助函数证明不等式的思路是通过构造一个与原问题相关的函数，在该函数中利用特定的性质或者算术关系，来证明原问题中的不等式成立。

以下将详细介绍如何通过构造辅助函数来证明不等式。

在不等式的证明中，我们可以通过构造辅助函数来简化问题。

辅助函数通常具有比原不等式更具有特殊性质的问题。

通过对辅助函数进行一系列等式或不等式推导，最终可以得到原不等式的证明。

具体的步骤如下：1.确定证明的对象：在不等式证明中，首先需要明确要证明的不等式是什么。

例如，要证明一组数的不等式a≥b成立。

2.构造辅助函数：根据问题的特点，可以通过构造一个与原不等式相关的辅助函数，来简化问题或者将原问题转化为更易证明的形式。

例如，可以构造辅助函数f(x)=a-b。

3.分析辅助函数的性质：分析辅助函数的特点和性质，找到能够帮助证明原不等式成立的关系或者算术操作。

4.推导辅助函数的等式或不等式：利用辅助函数的性质，通过一系列等式或不等式推导，逐步将辅助函数简化为更易处理的形式。

例如，可以利用辅助函数的性质将不等式f(x)≥0推导为a-b≥0。

以下通过一个具体的例子来解释如何使用辅助函数证明不等式。

例：证明对于任意实数x，有x^2≥0。

1.由于要证明的是一个不等式，我们需要构造一个与该不等式相关的辅助函数。

2.我们可以构造辅助函数f(x)=x^23.辅助函数的性质是平方总是非负的，即f(x)≥0。

4.根据辅助函数的性质，我们可以得到等式f(x)=x^2=0。

这个等式表明，辅助函数的取值范围为非负数。

以上就是使用辅助函数证明不等式的一般步骤。

在具体的证明中，可以根据问题的特点和要证明的不等式的形式，选择合适的辅助函数，然后通过推导和链接辅助函数与原不等式，来得出最终的结论。

高等数学中不等式证明的方法示例作者：杨雪来源：《科技风》2020年第18期摘要：不等式证明问题是高等数学中的重要内容，针对不等式的证明问题，本文分析并总结了高等数学中证明不等式的主要方法及其解题思路，并辅以典型例题，使学生能够系统地掌握不等式的证明方法。

关键词：高等数学;不等式;证明不等式是研究数学问题的重要工具，也是高等数学中的重要内容。

不等式的证明也是考研试题中的重要考点，也是难点。

很多学生对不等式问题缺乏系统的思考和总结。

本文举例说明了不等式证明的常用方法及适用情况，使学生更好地掌握不等式的证明技巧。

1 利用函数的单调性利用函数的单调性证明不等式，常将不等式进行恒等变形以便于构造辅助函数f（x），在判断辅助函数f（x）的单调性时，若判断f′（x）的符号困难，则可考虑求f″（x）甚至f（x）来递推确定。

当然，若此时无法确定导数符号，则说明此方法失效，应改用其他方法。

3 利用拉格朗日中值定理利用拉格朗日中值定理证明不等式的关键在于满足定理的两个条件，通过观察不等式经过恒等变形可以化成函数值之差的形式，可考虑用拉格朗日中值定理，并合理设定f（x），再根据ξ的取值范围对f′（ξ）进行估计，进而推导出所证不等式。

4 利用泰勒公式这种方法适合于题中所给（或能推导出）条件f″（x）存在且>0（或<0）的命题，此时只能利用带拉格朗日余项的泰勒公式证明不等式，关键是在哪一个点将函数用泰勒公式展开，通常展开点一般选取已知导数信息最多的点。

然后根据题设对展开式的余项进行适当的放缩，导出所证不等式。

种方法是高等数学中证明不等式的常用方法，不等式的证法因题而异，灵活多变，我们应该具体问题具体分析。

要想熟练掌握其中的技巧，我们要多思考多总结，才能快捷地解决不等式的证明问题。

参考文献：[1]同济大学数学教研室.高等数学（第七版）[M].北京：高等教育出版社，2014.[2]夏靜.高等数学中不等式证明的常用方法[J].赤峰学院学报（自然科学版），2015（10）：19-20.[3]李永乐，王式安，武忠祥，季文铎.2019考研数学复习全书[M].北京：国家行政学院出版社，2017.12.作者简介：杨雪（1982-），女，吉林长春人，长春工业大学硕士研究生，吉林工商学院助教，研究方向：最优化理论与应用。

利用函数的单调性证明不等式1、利用导数研究函数的单调性，再由单调性来证明不等式(函数、导数、不等式综合)2、解题技巧是构造辅助函数，把不等式的证明转化为利用导数研究函数的单调性或求最值，从而证得不等式，而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。

一、利用题目所给函数证明例：x>0时,求证；x 2x 2-－ln(1+x)＜0证明：设f(x)= x 2x 2-－ln(1+x) (x ≥0),则f '(x)=2x 1x -+∵x>0时,∴f '(x)<0,故f(x)在（0，+∞）上递减， 所以x>0时,f(x)<f(0)=0，即x 2x 2-－ln(1+x)<0成立。

例、求证：n ∈N *,n ≥3时，2n >2n+1证明：要证原式，即需证：2n －2n －1>0,n ≥3时成立 设f(x)=2x －2x －1(x ≥3),则f '(x)=2x ln2－2(x ≥3), ∵x ≥3,∴f '(x)≥23ln3－2>0 ∴f(x)在[3，+∞ )上是增函数，∴f(x)的最小值为f(3)=23－2×3－1=1>0所以，n ∈N *,n ≥3时，f(n)≥f(3)>0, 即n ≥3时,2n －2n －1>0成立，例：f(x)=13x 3－x, x 1,x 2∈[－1,1]时，求证：|f(x 1)－f(x 2)|≤43证明：∵f '(x)=x 2－1, x ∈[－1,1]时,f '(x)≤0,∴f(x)在[－1,1]上递减.故f(x)在[－1,1]上的最大值为f(－1)=23最小值为f(1)=23-,即f(x)在 [－1,1]上的值域为22[,]33-；所以x 1,x 2∈[－1,1]时，|f(x 1)|23≤, |f(x 2)|23≤,即有 |f(x 1)－f(x 2)|≤|f(x 1)|+ |f(x 2)|224333≤+=【例1】求证：当1->x 时，恒有11ln(1)1x x -≤++分析：构造函数111)1ln()(-+++=x x x g ，从其导数入手即可证明。

利用导数证明不等式的常见题型及解题技巧
发布时间：2022-05-07T11:31:58.110Z 来源：《中国教师》2022年1月2期作者：丁华娟[导读] 利用导数研究函数的单调性，再由单调性来证明不等式是函数、导数、不等式综合中的一个难点，也是近几年高考的热点。

丁华娟
绍兴市柯桥区鉴湖中学高三数学组技巧精髓
1、利用导数研究函数的单调性，再由单调性来证明不等式是函数、导数、不等式综合中的一个难点，也是近几年高考的热点。

2、解题技巧是构造辅助函数，把不等式的证明转化为利用导数研究函数的单调性或求最值，从而证得不等式，而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。

一、利用题目所给函数证明
【警示启迪】如果是函数在区间上的最大（小）值，则有（或），那么要证不等式，只要求函数的最大值不超过就可得证．2、直接作差构造函数证明
【警示启迪】本题首先根据题意构造出一个函数（可以移项，使右边为零，将移项后的左式设为函数），并利用导数判断所设函数的单调性，再根据函数单调性的定义，证明要证的不等式。

读者也可以设做一做，深刻体会其中的思想方法。

3、换元后作差构造函数证明
也就是说，在可导的前提下，只要证明０即可．
4、从条件特征入手构造函数证明。

利用函数的单调性证不等式
周德明
【期刊名称】《数学教学通讯：教师阅读》
【年(卷),期】1995(000)001
【总页数】2页(P32-33)
【作者】周德明
【作者单位】湖北大悟县新城中学 432800
【正文语种】中文
【中图分类】G634.6
【相关文献】
1.利用函数的单调性解方程或解(证)不等式 [J], 吴厚荣
2.利用函数的单调性巧解抽象函数的不等式 [J], 李其华
3.利用函数单调性证明不等式的难点——构造辅助函数 [J], 贺学海
4.利用函数单调性（证）解证不等式举例 [J], 张铭
5.利用函数单调性求不等式问题的三种技巧 [J], 孙光元
因版权原因，仅展示原文概要，查看原文内容请购买。