R语言 Markov Switching马尔科夫转化模型 附代码数据
- 格式:docx
- 大小:454.39 KB
- 文档页数:8

马尔可夫链蒙特卡洛方法及其r实现马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法是一种统计推断方法,主要用于解决难以直接计算的问题。
它的基本思想是通过构造一个马尔可夫链,使其平稳分布为所要求解的分布,然后通过迭代这个马尔可夫链来得到所要求解的分布的样本。
在R语言中,我们可以使用`rstan`包来实现MCMC方法。
下面是一个简单的例子,说明如何使用MCMC方法来估计一个简单模型的参数。
首先,你需要安装和加载`rstan`包:```r("rstan")library(rstan)```然后,定义一个Stan模型。
这里我们使用一个简单的线性回归模型作为例子:model_code <- "data {int<lower=0> N; // number of data pointsvector[N] y; // response variablevector[N] x; // predictor variable};parameters {real mu; // mean of yreal beta; // slope of the regression line};model {y ~ normal(mu, 1); // normal distribution for ymu ~ normal(0, 1); // normal distribution for mu beta ~ normal(0, 1); // normal distribution for beta };"```接着,使用`stan`函数来拟合模型:Generate some fake dataN <- 100 number of data pointsx <- rnorm(N) predictor variabley <- 3x + rnorm(N) response variable with added noiseFit the model using MCMC methodfit <- stan(model_code, data = list(N = N, y = y, x = x))```最后,你可以使用`print`函数来查看模型拟合的结果:```rprint(fit)```这只是一个非常简单的例子。

马尔可夫区制转换向量自回归模型随着大数据时代的到来,统计学和数据科学领域的研究和应用也取得了长足的发展。
马尔可夫区制转换向量自回归模型(Markov regime-switching vector autoregressive model)作为一种重要的时间序列模型,在金融市场预测、宏观经济分析等领域得到了广泛的应用。
本文将对马尔可夫区制转换向量自回归模型进行介绍和分析,包括其基本概念、模型假设、参数估计方法等内容。
一、马尔可夫区制转换向量自回归模型的基本概念马尔可夫区制转换向量自回归模型是一种描述时间序列变量之间动态关系的模型,它考虑了不同时间段内数据的不同特征,并能够在不同状态下描述不同的关系。
具体来说,该模型假设时间序列在不同的时间段内处于不同的状态(或区域),而状态之间的转换满足马尔可夫链的性质,即未来状态的转换仅与当前状态有关,与过去状态无关。
二、马尔可夫区制转换向量自回归模型的模型假设马尔可夫区制转换向量自回归模型的主要假设包括以下几点:1. 状态转移性:时间序列的状态转移满足马尔可夫链的性质,未来状态的转移仅与当前状态相关。
2. 向量自回归性:时间序列变量之间的关系可以用向量自回归模型描述,即当前时间点的向量可以由过去时间点的向量线性组合而成。
3. 区制转换性:时间序列的状态在不同时期具有不同的动态特征,模型需要考虑不同状态下的向量自回归关系。
以上假设为马尔可夫区制转换向量自回归模型的基本假设,这些假设使得模型能够较好地描述时间序列数据的动态演化。
三、马尔可夫区制转换向量自回归模型的参数估计方法马尔可夫区制转换向量自回归模型的参数估计是一个重要且复杂的问题,一般可以通过以下几种方法进行估计:1. 极大似然估计:假设时间序列的概率分布形式,通过最大化似然函数来得到模型参数的估计值。
这种方法需要对概率分布进行合理的假设,并且通常需要通过迭代算法来求解。
2. 贝叶斯方法:利用贝叶斯统计理论,结合先验分布和似然函数,通过马尔科夫链蒙特卡洛(MCMC)等方法得到模型参数的后验分布,进而得到参数的估计值。

r语言马科维茨模型求股票收益率(原创实用版)目录1.R 语言简介2.马科维茨模型简介3.使用 R 语言实现马科维茨模型4.应用马科维茨模型求股票收益率5.总结正文1.R 语言简介R 语言是一种功能强大的数据处理和统计分析语言,广泛应用于各个领域,如金融、生物、社会科学等。
R 语言的优势在于其丰富的库和扩展包,可以方便地处理和分析各种类型的数据。
2.马科维茨模型简介马科维茨模型是一种用于投资组合优化的经典模型,由美国经济学家哈里·马科维茨于 1952 年提出。
该模型主要通过计算投资组合的预期收益率和标准差,以最大化收益或最小化风险为目标,为投资者提供有效的投资建议。
3.使用 R 语言实现马科维茨模型在 R 语言中,可以使用诸如“portfolio”和“mvtnorm”等库来实现马科维茨模型。
以下是一个简单的示例:首先,安装并加载所需的库:```Rinstall.packages("portfolio")install.packages("mvtnorm")library(portfolio)library(mvtnorm)```然后,设置投资组合的权重和资产收益率:```Rweights <- c(0.5, 0.3, 0.2)returns <- c(0.1, 0.05, -0.02)```接下来,使用马科维茨模型计算投资组合的预期收益率和标准差:```Rmv_optimal_portfolio <- mvtnorm(returns, weights=weights, type="mean")mv_optimal_portfolio$meanmv_optimal_portfolio$var```4.应用马科维茨模型求股票收益率在实际应用中,我们可以使用马科维茨模型来计算股票的预期收益率。
例如,假设我们有三只股票,其收益率分别为 0.1、0.05 和 -0.02,权重分别为 0.5、0.3 和 0.2。

马尔可夫区制转移模型r语言代码概述及解释说明1. 引言1.1 概述马尔可夫区制转移模型是一种常用的数学工具,用于描述系统在不同状态之间的转移规律。
它基于随机过程理论,可以应用于各个领域的研究和实践中。
在本文中,我们将介绍马尔可夫链的概念以及区制转移模型的定义和特点,并重点关注R语言在该模型中的应用。
通过R语言代码的实现,我们可以有效地建立马尔可夫矩阵和状态空间模型,并进行模型训练与参数估计。
1.2 文章结构本文分为五个部分,每个部分都有特定的目标和内容。
以下是各个部分的概要:- 第一部分为引言部分,主要介绍了文章的背景和目的,以及整体结构。
- 第二部分详细介绍了马尔可夫链的概念,并对区制转移模型进行了定义和特点解释。
- 第三部分着重介绍了R语言在马尔可夫区制转移模型中的应用,并逐步讲解了实现过程。
- 第四部分通过选择一个具体案例并导入相关数据集,展示了如何使用R语言代码进行马尔可夫区制转移模型分析。
- 第五部分为结论与展望部分,总结了本文的研究成果,并提出了目前存在的问题以及未来的改进方向。
1.3 目的本文旨在介绍马尔可夫区制转移模型的原理和R语言代码实现过程,帮助读者深入了解该模型,并能够运用R语言进行相关数据分析。
通过实例分析和结果解释,读者可以更好地理解该模型的应用价值和意义。
此外,本文还将探讨当前马尔可夫区制转移模型存在的问题,并展望未来的改进方向,以期为后续研究提供参考。
2. 马尔可夫区制转移模型概述及原理解释2.1 马尔可夫链概念介绍马尔可夫链是一种随机过程,它具有马尔可夫性质,即未来的状态只依赖于当前状态而与过去的状态无关。
马尔可夫链由一组离散的状态以及这些状态之间的转移概率所定义。
在时间步长递进的过程中,通过转移概率可以预测和描述系统从一个状态到另一个状态的演变过程。
2.2 区制转移模型定义和特点区制转移模型是马尔可夫链的一种扩展形式,在传统马尔可夫链中只有一个全局的转移矩阵,而在区制转移模型中,根据不同的时间或空间划分将系统分为多个子区域,并针对每个子区域建立相应的转移矩阵。

咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogR语言使用马尔可夫链Markov Chain, MC来模拟抵押违约数据分析报告来源:大数据部落| 有问题百度一下“”就可以了原文/?p=3603这篇文章的目的是将我学习的材料与我的日常工作和R相结合。
如果我们有一些根据固定概率随时间在状态之间切换的对象,我们可以使用马尔可夫链 * 来模拟该对象的长期行为。
一个很好的例子是抵押贷款。
在任何给定的时间点,贷款都有违约概率,保持最新付款或全额偿还。
总的来说,我们将这些称为“转移概率”。
假设这些概率在贷款期限内是固定的**。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog举个例子,我们将看一下传统的固定利率30年期抵押贷款。
让我们假设每个当前贷款的时间T有75%的可能性保持最新,10%的违约机会,15%的机会在T + 1时间内获得回报。
这些转换概率在上图中列出。
显然,一旦贷款违约或获得偿还,它将保持默认或支付。
我们称这些国家为“吸收国家”。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog由于我们知道转移概率,我们所需要的只是贷款的初始分配,我们可以预测在30年期间任何给定点的每个州的贷款百分比。
假设我们从T = 0开始,有100个当前贷款,0个违约和已付清贷款。
在时间T + 1,我们知道(根据我们的转换概率),这100个中的75个将保持最新的付款。
但是,15笔贷款将被清偿,10笔贷款将被违约。
由于我们假设转移概率在贷款期限内是不变的,我们可以用它们来查找当前贷款的时间t = 2。
在目前T + 1的75笔贷款中,56.25笔贷款将保持在T + 2(75 * .75 = 56.25)。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog如果我们重复这个过程28次(在代码中完成)并绘制点,我们得到上面绘制的时间序列。

马尔可夫区制转换向量自回归模型马尔可夫区制转换向量自回归模型(Vector Autoregression Model with Markov Regime Switching, VAR-MS),结合了马尔可夫区制转换模型和向量自回归模型的特点,可用于对多变量时间序列数据进行建模和预测。
传统的向量自回归模型(Vector Autoregression Model, VAR)假设观测数据具有平稳性,且变量之间的关系是线性的。
然而,在实际的金融、经济和社会领域中,经常会出现时间序列数据在不同时间段呈现不同的模式或状态,如金融市场的牛熊转换、经济周期的波动等。
为了更准确地捕捉这种转变过程,VAR-MS模型引入了马尔可夫区制转换的思想。
马尔可夫区制转换是指时间序列数据的状态在不同的时间段随机地发生转换。
这种转换可以用马尔可夫链来表示,其中每个时间段被定义为一个状态,而状态之间的转换概率由状态转移矩阵表示。
在VAR-MS模型中,时间序列数据被整体分为多个区域,并假设每个区域内的数据服从一个固定的向量自回归模型。
根据当前的状态,根据转移概率矩阵,模型会在不同的区域之间进行切换。
VAR-MS模型可以用以下的数学表达式表示:Y_t = μ_Z + A_ZY_{t-1} + ε_t其中,Y_t是一个n维向量,表示时间t时刻的观测数据;μ_Z是一个n维向量,表示在状态为Z时的截距项;A_Z是一个n×n的矩阵,表示在状态为Z时的系数矩阵;ε_t是一个n维向量,表示误差项,满足ε_t ∼ N(0, Σ_Z),其中Σ_Z是在状态为Z时的协方差矩阵。
VAR-MS模型的参数估计通常采用最大似然估计或贝叶斯估计方法。
在实际应用中,首先需要通过一些判别方法(如似然比检验或信息准则)来确定马尔可夫区制转换的状态数。
然后,使用EM算法或Gibbs采样等方法来估计模型的参数和状态序列。
VAR-MS模型在金融和经济领域具有广泛的应用。


马尔可夫转移场方法,python
马尔可夫转移概率矩阵(Markov Transition Probability Matrix,MTPM)是一种描述状态转移的方法,常用于时间序列分析、机器学习等领域。
Python中的马尔可夫转移概率矩阵可以使用多种方法实现,下面是一个简
单的示例代码:
```python
import numpy as np
定义状态转移矩阵
P = ([[, ], [, ]])
生成随机初始状态
current_state = ([0, 1], p=P[0])
模拟状态转移过程
states = [current_state]
for i in range(10):
next_state = ([0, 1], p=P[current_state])
current_state = next_state
(current_state)
输出模拟结果
print(states)
```
在这个示例中,我们首先定义了一个2x2的马尔可夫转移概率矩阵P,表示状态0和状态1之间的转移概率。
然后,我们随机选择一个初始状态,并使用循环模拟状态转移过程,直到达到指定的步数。
在每次循环中,我们根据当前状态和转移概率矩阵P选择下一个状态,并将当前状态更新为下一个状态。
最后,我们输出模拟结果。
需要注意的是,在实际应用中,状态转移矩阵P通常是未知的,需要通过数据训练得到。
常用的训练方法包括Baum-Welch算法、Viterbi算法等。

马尔可夫模型实例python全文共四篇示例,供读者参考第一篇示例:马尔可夫模型是一种统计学模型,用于描述一个系统在连续时间之间的状态转移概率。
它基于马尔可夫过程,即未来状态仅仅取决于当前状态,与过去状态无关。
马尔可夫模型在自然语言处理、金融市场预测、天气预测等领域有着广泛的应用。
在这篇文章中,我们将使用Python来实现一个简单的马尔可夫模型实例。
我们将从头开始构建一个简单的文本生成模型,以便展示马尔可夫模型如何工作。
我们需要定义一个包含文本数据的样本数据集。
在这个例子中,我们将使用莎士比亚的《罗密欧与朱丽叶》作为我们的文本数据集。
我们将读取文本文件,并将其转换为一个字符串。
```pythonwith open('romeo_and_juliet.txt', 'r') as file:text = file.read().replace('\n', ' ')```接下来,我们需要预处理我们的文本数据,以便于后续的分析。
我们将使用nltk库来进行文本分词和清洗。
```pythonimport nltknltk.download('punkt')from nltk.tokenize import word_tokenize然后,我们可以构建我们的马尔可夫模型。
我们将创建一个字典,其中键值对为当前单词和下一个单词的组合。
这样我们就可以根据当前单词来预测下一个单词。
```pythondef build_markov_model(tokens):markov_model = {}for i in range(len(tokens) - 1):current_word = tokens[i]next_word = tokens[i + 1]return markov_modelreturn text通过运行上述代码,我们就可以生成一个基于马尔可夫模型的文本。
详解R语⾔MCMC:Metropolis-Hastings采样⽤于回归的贝叶斯估计MCMC是从复杂概率模型中采样的通⽤技术。
1. 蒙特卡洛2. 马尔可夫链3. Metropolis-Hastings算法问题如果需要计算有复杂后验pdf p(θ| y)的随机变量θ的函数f(θ)的平均值或期望值。
您可能需要计算后验概率分布p(θ)的最⼤值。
解决期望值的⼀种⽅法是从p(θ)绘制N个随机样本,当N⾜够⼤时,我们可以通过以下公式逼近期望值或最⼤值将相同的策略应⽤于通过从p(θ| y)采样并取样本集中的最⼤值来找到argmaxp(θ| y)。
解决⽅法1.1直接模拟1.2逆CDF1.3拒绝/接受抽样如果我们不知道精确/标准化的pdf或⾮常复杂,则MCMC会派上⽤场。
马尔可夫链为了模拟马尔可夫链,我们必须制定⼀个过渡核T(xi,xj)。
过渡核是从状态xi迁移到状态xj的概率。
马尔可夫链的收敛性意味着它具有平稳分布π。
马尔可夫链的统计分布是平稳的,那么它意味着分布不会随着时间的推移⽽改变。
Metropolis算法对于⼀个Markov链是平稳的。
基本上表⽰处于状态x并转换为状态x'的概率必须等于处于状态x'并转换为状态x的概率或者⽅法是将转换分为两个⼦步骤;候选和接受拒绝。
令q(x'| x)表⽰候选密度,我们可以使⽤概率α(x'| x)来调整q 。
候选分布 Q(X'| X)是给定的候选X的状态X'的条件概率,和接受分布α(x'| x)的条件概率接受候选的状态X'-X'。
我们设计了接受概率函数,以满⾜详细的平衡。
该转移概率可以写成:插⼊上⼀个⽅程式,我们有Metropolis-Hastings算法A的选择遵循以下逻辑。
在q下从x到x'的转移太频繁了。
因此,我们应该选择α(x | x')=1。
但是,为了满⾜细致平稳,我们有下⼀步是选择满⾜上述条件的接受。
R语言中实现马尔可夫链蒙特卡罗MCMC模型原文链接:/?p=2687什么是MCMC,什么时候使用它?MCMC只是一个从分布抽样的算法。
这只是众多算法之一。
这个术语代表“马尔可夫链蒙特卡洛”,因为它是一种使用“马尔可夫链”(我们将在后面讨论)的“蒙特卡罗”(即随机)方法。
MCMC只是蒙特卡洛方法的一种,尽管可以将许多其他常用方法看作是MCMC的简单特例。
正如上面的段落所示,这个话题有一个引导问题,我们会慢慢解决。
我为什么要从分配中抽样?你可能没有意识到你想(实际上,你可能并不想)。
但是,从分布中抽取样本是解决一些问题的最简单的方法。
可能MCMC最常用的方法是从贝叶斯推理中的某个模型的后验概率分布中抽取样本。
通过这些样本,你可以问一些问题:“参数的平均值和可信度是多少?”。
如果这些样本是来自分布的独立样本,则估计均值将会收敛在真实均值上。
假设我们的目标分布是一个具有均值m和标准差的正态分布s。
显然,这种分布的意思是m,但我们试图通过从分布中抽取样本来展示。
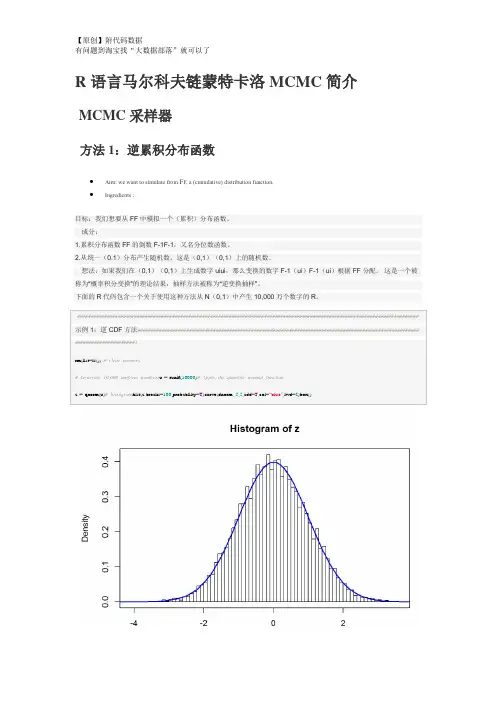
作为一个例子,考虑用均值m和标准偏差s来估计正态分布的均值(在这里,我将使用对应于标准正态分布的参数):我们可以很容易地使用这个rnorm 函数从这个分布中抽样•seasamples<-rn 000,m,s)样本的平均值非常接近真实平均值(零):•••••mean(sa es)## [1] -0. 537事实上,在这种情况下,$ n $样本估计的预期方差是$ 1 / n $,所以我们预计大部分值在$••••••\ pm 2 \,/ \ sqrt {n} = 0.02 $ 10000分的真实意思。
summary(re 0,mean(rnorm(10000,m,s))))## Min. 1st Qu. Median Mean 3rd Qu. Max. ## -0.03250 -0.00580 0.00046 0.00042 0.00673 0.03550这个函数计算累积平均值(即元素$ k $,元素$ 1,2,\ ldots,k $除以$ k $)之和。
以下是一个简单的马尔可夫模型的R语言代码示例,用于计算给定状态转移矩阵的稳态概率分布:
```r
# 定义状态转移矩阵
transition_matrix <- matrix(c(0.9, 0.1, 0.5, 0.5), nrow = 2)
# 计算稳态概率分布
steady_state <-eigen(transition_matrix)$vectors[, 1] / sum(eigen(transition_matrix)$vectors[, 1])
# 输出稳态概率分布
print(steady_state)
```
在这个例子中,我们定义了一个2x2的状态转移矩阵,其中第一行表示状态1的转移概率,第二行表示状态2的转移概率。
然后,我们使用R语言的eigen函数计算状态转移矩阵的特征值和特征向量,并取第一个特征向量作为稳态概率分布。
最后,我们将稳态概率分布输出到控制台。
请注意,这只是一个简单的示例,实际的马尔可夫模型可能更加复杂。
根据具体问题,您可能需要调整状态转移矩阵的大小和形状,以及计算稳态概率分布的方法。
马尔可夫链是一种在概率论和统计学中常用的模型,用来描述状态空间中,从一个状态到另一个状态的概率转移过程。
这种模型在许多领域都有着广泛的应用,比如金融、生物学、计算机科学等。
本文将介绍matlab中如何使用马尔可夫链来建立转换模型。
一、马尔可夫链的基本概念1. 马尔可夫链的定义马尔可夫链是指一个随机过程,具有马尔可夫性质,即在给定当前状态的情况下,未来的状态只依赖于当前状态,而与过去状态无关。
数学上可以用条件概率的形式表示为P(Xn+1|Xn,Xn-1,...,X1) =P(Xn+1|Xn)。
2. 马尔可夫链的状态空间马尔可夫链的状态空间可以是有限的,也可以是无限的。
有限状态空间的马尔可夫链通常可以用状态转移矩阵来描述,而无限状态空间的马尔可夫链则需要用到更为复杂的数学工具。
二、在matlab中建立马尔可夫链转换模型的方法1. 生成随机马尔可夫链在matlab中,我们可以使用随机矩阵生成函数rand来生成一个随机的状态转移矩阵,然后利用这个状态转移矩阵来模拟马尔可夫链的转移过程。
```Matlab生成状态转移矩阵P = rand(n,n); n为状态空间的维度for i = 1:nP(i,:) = P(i,:)/sum(P(i,:)); 将每一行的元素归一化,使得每一行的和为1end模拟马尔可夫链的转移过程state = randi(n); 随机选择一个初始状态ch本人n = [state]; 用数组ch本人n来记录整个转移过程for i = 1:1000 模拟1000次状态转移state = randsample(1:n,1,true,P(state,:)); 根据状态转移矩阵P进行状态转移ch本人n = [ch本人n,state]; 将新的状态添加到数组ch本人n中end```通过上述代码,我们可以生成一个随机的马尔可夫链,并模拟其状态转移过程。
这种方法可以帮助我们更好地理解马尔可夫链的基本概念和特性。
R语言隐马尔科夫模型(HMM)模型股指预测代码了解不同的股市状况,改变交易策略,对股市收益有很大的影响。
有些策略在波澜不惊的股市中表现良好,而有些策略可能适合强劲增长或长期下跌的情况。
弄清楚何时开始或合适止损,调整风险和资金管理技巧,都取决于股市的当前状况。
在本文中,我们将通过使用一类强大的机器学习算法“隐马尔可夫模型”(HMM)来探索如何识别不同的股市状况。
▍隐马尔可夫模型马尔科夫模型是一个概率过程,查看当前状态来预测下一个状态。
一个简单的例子就是看天气。
假设我们有三种天气情况:下雨、多云、阳光明媚。
如果今天下雨,马尔科夫模型就会寻找每种不同天气的概率。
例如,明天可能会持续下雨的可能性较高,变得多云的可能性略低,而会变得晴朗的几率很小。
▍构建模型基于以上背景,然后我们可以用来找到不同的股市状况优化我们的交易策略。
我们使用2004年至今的上证指数(000001.ss)来构建模型。
首先,我们得到上证指数的收盘价数据,计算得到收益率数据,并建立HMM模型比较模型的预测结果。
library(depmixS4)library(TTR)library(ggplot2)library(reshape2)library(plotly)# create the returns stream from thisshdata<-getSymbols( "000001.ss", from="2004-01-01",auto.assign=F )gspcRets = diff( log( Cl( shdata ) ) )returns = as.numeric(gspcRets)write.csv(as.data.frame(gspcRets),"gspcRets.csv")shdata=na.omit(shdata)df <- data.frame(Date=index(shdata),coredata(shdata))p <- df %>%plot_ly(x = ~Date, type="candlestick",open = ~X000001.SS.Open, close = ~X000001.SS.Close,high = ~X000001.SS.High, low = ~X000001.SS.Low, name = "000001.SS",increasing = i, decreasing = d) %>%add_lines(y = ~up , name = "B Bands",line = list(color = '#ccc', width = 0.5),legendgroup = "Bollinger Bands",hoverinfo = "none") %>%add_lines(y = ~dn, name = "B Bands",line = list(color = '#ccc', width = 0.5),legendgroup = "Bollinger Bands",showlegend = FALSE, hoverinfo = "none") %>%add_lines(y = ~mavg, name = "Mv Avg",line = list(color = '#E377C2', width = 0.5),hoverinfo = "none") %>%layout(yaxis = list(title = "Price"))绘制上证指数的收盘价和收益率数据,我们看到2004年和2017年期间股市的波动情况。