北师大版2019年秋学期七年级数学上册第一章单元复习检测卷附答案解析
- 格式:docx
- 大小:333.17 KB
- 文档页数:8

北师大版七年级上册数学第一章测试题(附答案)一、单选题(共12题;共36分)1.如图,有一个正方体,乐乐用了一个平面去截这个正方体,截面形状不可能是()A. B. C. D.2.如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是()A. B. C. D.3.某几何体的三视图如图所示,则这个几何体是()A. 圆柱B. 正方体C. 球D. 圆锥4.如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是()A. B. C. D.5.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( )A. B. C. D.6.如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是()A. 和B. 谐C. 社D. 会7.如图所示的几何体是由五个小正方体组合而成的,它的主视图是()A. B. C. D.8.在下面的四个几何图形中,左视图与主视图不相同的几何体是()A. 长方体B. 正方体C. 球D. 圆锥9.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是()A. 主视图的面积为5B. 左视图的面积为3C. 俯视图的面积为3D. 三种视图的面积都是410.一个几何体是由若干个相同的立方体组成,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是()A. 15个B. 13个C. 11个D. 5个11.一些完全相同的小正方形搭成一个几何体,这个几何体从正面和左面看所得的平面图形均如图所示,小正方体的块数可能有()A. 7种B. 8种C. 9种D. 10种12.某三棱锥的三视图如图所示,该三棱锥的体积是()A. B. 4 C. 2 D.二、填空题(共5题;共15分)13.一个几何体是由一些完全相同的小立方块搭成的,从三个不同的方向看到的情形如图所示,则搭成这个几何体共需这样的小方块________个.14.长方体纸盒的长、宽、高分别是,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是________ .15.如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为________ .16.一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,m+n=________.17.长方体的主视图与俯视图如图所示,则这个长方体的体积是________.三、解答题(共3题;共15分)18.一个几何体的三视图如图,求这个几何体的侧面积19.长方体的主视图与俯视图如图所示,这个长方体的体积是多少?20.如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.(1)设原大正方体的表面积为S,图②中几何体的表面积为S1,那么S1与S的大小关系是A.S1>S B.S1=S C.S1<S D.无法确定(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1,那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.四、作图题(共1题;共8分)21.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.五、综合题(共2题;共26分)22.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.(1)如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有________.(2)从已知正确的纸样中选出一种,在原图上标注上尺寸.(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)23.如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:(1)如果面A在多面体的上面,那么哪一面会在下面?(2)如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面?(3)从右面看是面A,从上面看是面E,那么哪一面会在前面?答案一、单选题1. D2. D3. D4. B5. C6. D7. A8. A9. B 10. A 11. C 12.B二、填空题13. 5 14. 92 15. 8116. 16 17. 24三、解答题18. 解:根据三视图可得:这个几何体是圆柱,∵圆柱的直径为2,高为3,∴侧面积为2×""×2×3π=6π.答:这个几何体的侧面积是6π.19. 解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24.答:这个长方体的体积是24.20. 解:(1)设原大正方体的表面积为S,图②中几何体的表面积为S1,那么S1与S的大小关系是相等;故选:B;(2)设大正方体棱长为1,小正方体棱长为x,那么l1﹣l=6x.只有当x=时,才有6x=3,所以小明的话是不对的;(3)如图所示:四、作图题21. 解:如图所示:五、综合题22. (1)甲.丙;(2)标注尺寸只需在甲图或丙图标出一种即可(3)S侧=(b+a+b+a)h=2ah+2bh;S表=S侧+2S底=2ah+2bh+2ab .23. (1)解:如果面A在多面体的上面,那么C面会在下面(2)解:如果面在多面体的后面,从左面看是面C,那么向外折时面C会在上面,向里折时面A会在上面。

期末练习一.选择题(共12小题)1. A2. C3. B4. D5. B6. D7. C8. D9. B 10. C11. C 12. B二.填空题(共4小题)13.【答案】2314.【答案】315.【答案】100016.【答案】17,3n +2三.解答题(共7小题)17. 解:(-3) 3 ÷ (-9)+22 × |(-4)+1|= (-27) ÷ (-9)+4×3= 3+12= 15.18. 解:2(a 2b +ab 2)-2(a 2b -1) -3(ab 2+1)= 2a 2b +2ab 2-2a 2b +2-3ab 2-3=-ab 2-1.当a =-2,b =2时,原式=-(-2)×22-1=8-1=7.19. 解:(1)去括号,得x -7=10-4x -2,移项、合并同类项,得5x =15,方程两边同除以5,得 x =3.(2)去分母,得 2(5x +1)-(2x -1) =6,移项、合并同类项,得 8x =3,方程两边同除以8,得 x =83.20. 解:(1)如图:(2)点C 与点A 的距离为:2+4=6km .(3)邮递员骑行了:2+3+9+4=18km ,所以耗油量为:18×0.03=0.54(升)答:这趟路共耗油0.54升.21. 解:(1)20,15%,35%(2)因为D 组的人数为:400×35%=140,(3)D 部分扇形所对应的圆心角是360°×35%=126°.22. 解:(1)设成人人数为x 人,则学生人数为(12-x )人.依题意,得()3501223535=-+x x解得:x =8,所以12-x =4,故小明他们一共去了8个成人,4个学生.(2)如果买团体票,按16人计算,共需费用:35×0.6×16=336(元). 336<350,所以,购买团体票更省钱.23. 解:(1)因为∠NOC ∶∠MOC =2∶1,所以∠MOC =90°×121+=30°,所以∠AOC =∠AOM +∠MOC= 90°+30°=120°.(2)∠AOM =2∠NOC .理由如下:设∠NOC 为α,∠AOM 为β,则∠MOC =∠BOC = 90°-α,因为∠AOM +∠MOC +∠BOC = 180°,所以 β + (90°-α) + (90°-α) = 180°,所以 β-2α =0,即β =2α,所以∠AOM =2∠NOC .。

2019年秋七年级数学上册期第一章单元复习测试卷(时间100分钟:满分120分)•、选择题(本大题10小题,毎小题3分,共30分)L下列几何体中,没冇曲面的是()』・圆锥B.圆柱a球D.棱柱2.下面几何体的柢血图可能是圆的是()札止方体圆铢C K方体D.棱柱3.如图,在四个儿何体中,从左面看与从正面看不相同的几何体是()1E方体8 Ki方体G球D.圆锥4.把图①中的图形绕着点线旋转一周后形成的立体图形是图②中的()□1 S 1 0图①7, 将下图折拄成正方体后,与“义”字相对而上的汉/是(礼&智。
信D.学从E 面看,第9题图)5. 如图,不能折成无盖的正方体的是(ET06. B如图①,用一个水平的平面去截长方体, 吁IJ则截面的形状为图②中的(8.—个儿何体的展开图如图'这个儿何体是()A.三棱柱B.三枝锥C.四棱柱D.四棱锥9. —个H 方体,从左血、上面看得到的图形及相关数据如图,则从正面看该儿何体所得到的图形 的面积为()A. 6B. 8C. 12D. 910. 有一个三稜柱,底面是边K 为3 m 的小三角形,侧棱的氐为 g 则该枝柱的侧面展开图是 ( )』・惶为9 宽为3 m 的位方形B.氏为27质,宽为3皿的氏方形C 边K 为9 w 的止方形D.边K 为3 M 的止方形二、填空题(本大题6小题,每小题1分,共24分) 11. 流星划过天空时留下一道明亮的光线,用数学知讥解释为.12. 圖锥是由2个面围成的,它们的交线为13.如图,它是八棱柱的表面展开图,展开前的几何图形共有—茶枝,—个顶点, 个面.14.如果K 方体的长、宽、高分别为5 cm, 4 m, 3 g 那么至少需要K 的铁姪•才能做成 这样的K:方体架「・圆锥得到.(壊序号)16. 如图,左辺是一个由5个棱长为1的小正方体组合而成的几何体,现在増加一个小正方体,15.在如图的四个图形中,图形②③ 可以用平面栈长方体得到;图形可以用平而截矗丑。
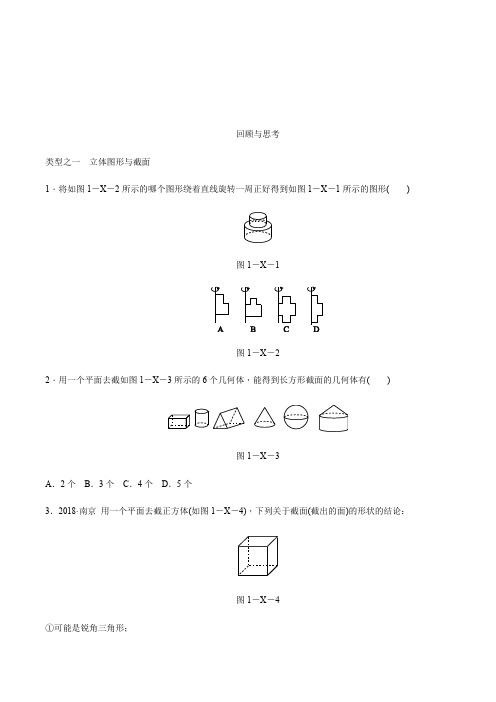
回顾与思考类型之一立体图形与截面1.将如图1-X-2所示的哪个图形绕着直线旋转一周正好得到如图1-X-1所示的图形()图1-X-1图1-X-22.用一个平面去截如图1-X-3所示的6个几何体,能得到长方形截面的几何体有()图1-X-3A.2个B.3个C.4个D.5个3.2018·南京用一个平面去截正方体(如图1-X-4),下列关于截面(截出的面)的形状的结论:图1-X-4①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是()A.①②B.①④C.①②④D.①②③④4.如图1-X-5所示,截去正方体一角变成一个新的多面体,这个新多面体有7个顶点,有________条棱,有________个面,截面形状是____________.图1-X-55.如图1-X-6所示的五棱柱的底面边长都是5 cm,侧棱长为12 cm,它有多少个面?它的所有侧面的面积之和是多少?图1-X-6类型之二立体图形的展开与折叠6.2018·陕西如图1-X-7是一个几何体的展开图,则该几何体是()图1-X-7A.正方体B.长方体C.三棱柱D.四棱锥7.2018·内江如图1-X-8是正方体的一种展开图,则与“前”字相对的字是()图1-X-8A.认B.真C.复D.习8.把如图1-X-9所示的纸片折叠成一个正方体.与点H重合的点是________,与棱AB重合的线段是________.图1-X-99.在图1-X-10中剪去一个正方形,使剩余部分恰好能折成一个正方体,可能剪去的小正方形的编号为__________.图1-X-1010.如图1-X-11,回答下列问题:(1)将该图形折叠能得到什么几何体?(2)要把这个几何体重新展开,最少需要剪开几条棱?图1-X-11类型之三从三个方向观察立体图形11.2018·随州改编如图1-X-12是由4个相同的小立方块组成的一个几何体,从左面看到的它的形状图是图1-X-13中的()图1-X-12图1-X-1312.[2017·鄂州改编]一个几何体是由几个大小相同的小立方块搭成的,从上面看到的形状图如图1-X-14,小正方形中的数字表示该位置上小立方块的个数,则从左面看到的这个几何体的形状图是图1-X-15中的()图1-X-14图1-X-1513.一个几何体是由若干个棱长为3 cm的小立方块搭成的,从正面、左面、上面看到的几何体的形状图如图1-X-16所示:图1-X-16(1)在“从上面看”的图中标出各个位置上小立方块的个数;(2)求该几何体的体积.类型之四综合与实践14.一个多面体的面数a和这个多面体的展开图的顶点数b、边数c之间存在一定规律.正三棱柱有5个面,如图1-X-17①是正三棱柱的展开图,展开后有10个顶点(重合的顶点只算一个),14条边.图1-X-17【探索发现】(1)请在图②中用实线画出正方体的一种展开图;(2)请根据图②中你所画的展开图和如图③所示的某几何体的展开图填写下表:(3)发现:多面体的面数a和展开图的顶点数b、边数c之间存在的关系式是____________.详解详析1.A2.B[解析] 圆锥、球和圆柱与圆锥的组合体不可能得到长方形截面,故能得到长方形截面的几何体有:长方体、圆柱、三棱柱,一共有3个.3.B[解析] 用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,而三角形只能是锐角三角形,不能是直角三角形或钝角三角形.4.127等边三角形[解析] 截去正方体一角变成一个新的多面体,这个新多面体有7个面,有12条棱,有7个顶点,图中的截面形状是等边三角形.5.解:这个五棱柱有7个面,沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是长方形,面积为5×12×5=300(cm2).答:这个五棱柱有7个面,所有侧面的面积之和是300 cm2.6.C7.B8.B,D IH9.1,2,310.解:(1)拼图存在问题.多出一个正方形,如图所示.(2)修正后所折叠而成的长方体的表面积为52×2+8×5×4=50+160=210(cm2).11.[解析] 由平面图形的折叠及立体图形的展开图的特点解题.三个长方形和两个三角形能围成三棱柱.结合三棱柱的展开图的特征可知,要把这个几何体重新展开,最少需要剪开5条棱.解:(1)将它折叠能得到三棱柱.(2)要把三棱柱重新展开,最少需要剪开5条棱.12.D13.D[解析] 从左面看,一共有3列,左侧一列有2层,中间一列有2层,右侧一列有1层,故选D. 14.解:(1)如图所示:(2)该几何体的体积为33×(2+3+2+1+1+1)=27×10=270(cm3).15.解:(1)答案不唯一,如图:(2)如下表:(3)a+b-c=1。

北师大版七年级数学上册第一章测试题(一)(时间:90分钟分值:120分)一.填空(每空1分,共21分).1.(3分)圆柱体是由个面围成,其中个平面,个曲面.2.(2分)面与面相交成,线与线相交成.3.(1分)把下列展开图的立体图形名称分别写在图的下边横线上:、、、.4.(5分)如图,六棱柱的底面边长都是5厘米,侧棱长为4厘米,则(1)这个六棱柱一共有个面,有个顶点;(2)这个六棱柱一共有条棱,它们的长度分别是.(3)这个六棱柱:顶点数+面数﹣棱数=.5.(2分)如图中的截面分别是(1)(2).6.(3分)如图所示,截去正方体一角变成一个多面体,这个多面体有个面,有条棱,有个顶点.7.(2分)若要使图中平面展开图折叠成正方体后,使得相对面的数的和相等,则 x=,y=.二、选择题(每题3分,共33分)8.(3分)下列几何体的截面形状不可能是圆的是()A.圆柱B.圆锥C.球D.棱柱9.(3分)用平面去截图中的正方体,截面形状不可能是()A.B.C.D.10.(3分)下列图形中,不是正方体平面展开图的是()A.B.C.D.11.(3分)如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是()A.4个B.5个C.6个D.7个12.(3分)若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个图形可能是()A.圆台B.圆柱C.三棱柱D.圆锥13.(3分)如图是由四个小正方体叠成的一个立体图形,那么它的俯视图是()A. B. C. D.14.(3分)观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来()A.B.C.D.15.(3分)几何体的下列性质:①侧面是平行四边形;②底面形状相同;③底面平行;④棱长相等.其中棱柱具有的性质有()A.1个B.2个C.3个D.4个16.(3分)埃及金字塔类似于几何体()A.圆锥B.圆柱C.棱锥D.棱柱17.(3分)一个正方形,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7、10、11,则六个整数的和为()A.51 B.52 C.57 D.5818.(3分)小丽制作了一个如图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是()A.B.C.D.三.解答题:(共46分)19.(9分)分别画如图几何体的主视图、左视图、俯视图.20.(8分)如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.21.(10分)用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.22.(10分)将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)23.(9分)如图是一个几何体从三个方向看所得到的形状图.(1)写出这个几何体的名称;(2)画出它的一种表面展开图;(3)若从正面看的高为3cm,从上面看三角形的边长都为2cm,求这个几何体的侧面积.参考答案一.填空(每空1分,共21分).1.(3分)圆柱体是由3个面围成,其中2个平面,1个曲面.【考点】认识立体图形.【分析】根据圆柱的概念和特性即可求解.【解答】解:圆柱是由三个面组成,其中两底面是平面,侧面是一个曲面.故答案为:3、2、1.【点评】本题考查几何体的面的组成情况和立体图形的侧面展开图的特征,属于基础题型.2.(2分)面与面相交成线,线与线相交成点.【考点】点、线、面、体.【分析】根据面和面相交线和线相交的定义即可解.【解答】解:由线和点的定义知,面与面相交成线,线与线相交成点.故答案为线,点.【点评】面有平的面和曲的面两种.3.(1分)把下列展开图的立体图形名称分别写在图的下边横线上:长方体、三棱柱、圆锥、圆柱.【考点】几何体的展开图.【分析】根据几何体的平面展开图的特征分别进行判定即可.【解答】解:第一个是长方体的展开图;第二个是三棱柱的展开图;第三个是圆锥的展开图;第四个是圆柱的展开图.故答案为:长方体,三棱柱,圆锥,圆柱.【点评】本题考查几何体展开图,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.4.(5分)如图,六棱柱的底面边长都是5厘米,侧棱长为4厘米,则(1)这个六棱柱一共有8个面,有12个顶点;(2)这个六棱柱一共有18条棱,它们的长度分别是侧棱4cm,底边5cm.(3)这个六棱柱:顶点数+面数﹣棱数=2.【考点】认识立体图形.【分析】(1)根据n棱柱的面是(n+2),顶点数是(2n),可得答案;(2))根据n棱柱的3n,可得答案.(3)根据顶点数+面数﹣棱数=2n+(n+2)﹣3n=2,可得答案.【解答】解:(1)这个六棱柱一共有 8个面,有 12个顶点;(2)这个六棱柱一共有 18条棱,它们的长度分别是侧棱4cm,底边5cm.(3)这个六棱柱:顶点数+面数﹣棱数=2,故答案为:8,12;18,侧棱4cm,底边5cm;2.【点评】本题考查了认识立体图形,顶点数+面数﹣棱数=2n+(n+2)﹣3n=2是解题关键.5.(2分)如图中的截面分别是(1)圆(2)长方形.【考点】截一个几何体.【分析】根据几何体的形状特点和截面的角度判断即可.【解答】解:(1)当截面平行于圆柱底面截取圆柱时得到截面图形是圆;(2)截面截取经过四个顶点的截面时可以截得长方形,故答案为:(1)圆;(2)长方形.【点评】此题主要考查了截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.6.(3分)如图所示,截去正方体一角变成一个多面体,这个多面体有7个面,有12条棱,有7个顶点.【考点】截一个几何体;认识立体图形.【分析】截去正方体一角变成一个多面体,这个多面体多了一个面、棱不变,少了一个顶点.【解答】解:仔细观察图形,正确地数出多面体的面数、棱数及顶点数,它们分别是7,12,7.【点评】本题结合截面考查多面体的相关知识.对于一个多面体:顶点数+面数﹣棱数=2.7.(2分)若要使图中平面展开图折叠成正方体后,使得相对面的数的和相等,则 x=4,y=5.【考点】专题:正方体相对两个面上的文字.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“3”与“y”是相对面,“x”与“4”是相对面,∵相对面的数的和相等,∴x=4,y=5,故答案为4,5.【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.二、选择题(每题3分,共33分)8.(3分)下列几何体的截面形状不可能是圆的是()A.圆柱B.圆锥C.球D.棱柱【考点】截一个几何体.【分析】根据圆柱、圆锥、球、棱柱的形状特点判断即可.【解答】解:棱柱无论怎么截,截面都不可能有弧度,自然不可能是圆,故选D.【点评】本题考查几何体的截面,关键要理解面与面相交得到线.9.(3分)用平面去截图中的正方体,截面形状不可能是()A.B.C.D.【考点】截一个几何体.【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.无论如何去截,截面也不可能有弧度,因此截面不可能是圆.【解答】解:无论如何去截,截面也不可能有弧度,因此截面不可能是圆.故选D.【点评】本题考查正方体的截面.正方体有六个面,截面与其六个面相交最多得六边形,不可能是七边形或多于七边的图形或其他的弧形.10.(3分)下列图形中,不是正方体平面展开图的是()A.B.C.D.【考点】几何体的展开图.【专题】应用题.【分析】由平面图形的折叠及正方体的展开图解题.【解答】解:由四棱柱四个侧面和上下两个底面的特征可知,A,B,C选项可以拼成一个正方体;而D选项,上底面不可能有两个,故不是正方体的展开图.故选D.【点评】本题主要考查了四棱柱的特征及正方体展开图的各种情形,难度适中.11.(3分)如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是()A.4个B.5个C.6个D.7个【考点】由三视图判断几何体.【分析】根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.【解答】解:由三视图可得,需要的小正方体的数目:1+2+1=4.如图:故选:A.【点评】本题考查了几何体的三视图及空间想象能力.12.(3分)若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个图形可能是()A.圆台B.圆柱C.三棱柱D.圆锥【考点】由三视图判断几何体;等腰三角形的性质.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:A、圆台是三视图分别是等腰梯形,等腰梯形,同心圆,不符合题意;B、圆柱的三视图分别是长方形,长方形,圆,不符合题意;C、三棱柱的三视图分别为三角形,矩形,矩形,不符合题意.D、圆锥的三视图分别是等腰三角形,等腰三角形,圆及一点,符合题意;故选D.【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.13.(3分)如图是由四个小正方体叠成的一个立体图形,那么它的俯视图是()A. B. C. D.【考点】简单组合体的三视图.【分析】找到从上面看所得到的图形即可.【解答】解:从上面可看到第二层有2个正方形,第一层右下角有一个正方形.故选B.【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.14.(3分)观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来()A.B.C.D.【考点】点、线、面、体.【分析】根据面动成体的原理以及空间想象力即可解.【解答】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.故选D.【点评】考查学生立体图形的空间想象能力及分析问题,解决问题的能力.15.(3分)几何体的下列性质:①侧面是平行四边形;②底面形状相同;③底面平行;④棱长相等.其中棱柱具有的性质有()A.1个B.2个C.3个D.4个【考点】认识立体图形.【分析】根据棱柱的概念即可得到结论.【解答】解:棱柱具有下列性质:①侧面是平行四边形;②底面形状相同;③底面平行;④棱长相等.故选D.【点评】本题考查了认识立体图形,棱柱的性质,熟练掌握棱柱的性质是解题的关键.16.(3分)埃及金字塔类似于几何体()A.圆锥B.圆柱C.棱锥D.棱柱【考点】认识立体图形.【专题】几何图形问题.【分析】根据埃及金字塔的形状及棱锥的定义分析即可求解.【解答】解:埃及金字塔底面是多边形,侧面是有公共顶点的三角形,所以是棱锥.故选C.【点评】本题主要考查棱锥的概念的掌握情况.棱锥的定义:如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.17.(3分)一个正方形,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7、10、11,则六个整数的和为()A.51 B.52 C.57 D.58【考点】整数问题的综合运用;几何体的展开图.【分析】由平面图形的折叠及立体图形的表面展开图的特点解题,根据题意分析可得:六个面上分别写着六个连续的整数,故六个整数可能为7,8,9,10,11,12或6,7,8,9,10,11,然后分析符合题意的一组数即可.【解答】解:根据题意分析可得:六个面上分别写着六个连续的整数,故六个整数可能为或7,8,9,10,11,12,或6,7,8,9,10,11;且每个相对面上的两个数之和相等,10+9=1911+8=197+12=19故只可能为7,8,9,10,11,12其和为57.故选C.【点评】本题主要考查整数问题的综合运用和几何体的展开图的知识点,解答本题的关键是对几何图形的观察能力和空间想象能力,此题难度不大.18.(3分)小丽制作了一个如图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是()A.B.C.D.【考点】几何体的展开图.【分析】本题考查了正方体的展开与折叠.可以动手折叠看看,充分发挥空间想象能力解决也可以.【解答】解:根据题意及图示只有A经过折叠后符合.故选:A.【点评】本题着重考查学生对立体图形与平面展开图形之间的转换能力,与课程标准中“能以实物的形状想象出几何图形,由几何图形想象出实物的形状”的要求相一致,充分体现了实践操作性原则.要注意空间想象哦,哪一个平面展开图对面图案都相同三.解答题:(共46分)19.(9分)分别画如图几何体的主视图、左视图、俯视图.【考点】作图-三视图.【分析】从正面看从左往右3列正方形的个数依次为1,3,2;从左面看从左往右2列正方形的个数依次为2,1;从上面看从左往右3列正方形的个数依次为1,2,1.【解答】解:如图所示:【点评】本题考查了三视图的画法,得到从各个方向看得到的每列正方形的个数是解决本题的关键.20.(8分)如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.【考点】作图-三视图;由三视图判断几何体.【分析】主视图有3列,每列小正方形数目分别为2,3,4;左视图有2列,每列小正方形数目分别为4,2;依此画出图形即可求解.【解答】解:如图所示:【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图.21.(10分)用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.答:最多8个,最少7个.【考点】由三视图判断几何体.【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,相加即可.【解答】解:有两种可能;有主视图可得:这个几何体共有3层,由俯视图可得:第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,故:最多为3+4+1=8个小立方块,最少为个2+4+1=7小立方块.最多时的左视图是:最少时的左视图为:【点评】此题主要考查了由三视图判断几何体,关键是掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就很容易得到答案.22.(10分)将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)【考点】圆柱的计算.【专题】分类讨论.【分析】圆柱体的体积=底面积×高,注意底面半径和高互换得圆柱体的两种情况.【解答】解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.【点评】本题考查圆柱体的体积的求法,注意分情况探讨.23.(9分)如图是一个几何体从三个方向看所得到的形状图.(1)写出这个几何体的名称;(2)画出它的一种表面展开图;(3)若从正面看的高为3cm,从上面看三角形的边长都为2cm,求这个几何体的侧面积.【考点】由三视图判断几何体;几何体的表面积;几何体的展开图.【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;(2)应该会出现三个长方形,两个三角形;(3)侧面积为3个长方形,它的长和宽分别为3cm,2cm,计算出一个长方形的面积,乘3即可.【解答】解:(1)正三棱柱;(2)如图所示:;(3)3×3×2=18cm2.答:这个几何体的侧面积18cm2.【点评】本题主要考查由三视图确定几何体和求几何体的面积等相关知识,考查学生的空间想象能力.注意:棱柱的侧面都是长方形,上下底面是几边形就是几棱柱.北师大版七年级数学上册第一章测试题(二)(时间:90分钟分值:120分)一.选择题(共12小题)1.下列图形中,属于立体图形的是()A.B.C.D.2.如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是()A.V甲>V乙 S甲=S乙B.V甲<V乙 S甲=S乙C.V甲=V乙 S甲=S乙D.V甲>V乙 S甲<S乙3.将四个棱长为1的正方体如图摆放,则这个几何体的表面积是()A.3 B.9 C.12 D.184.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是()A.遇B.见C.未D.来5.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是()A.①B.②C.③D.④6.下面平面图形中能围成三棱柱的是()A.B.C. D.7.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是()A.丽B.连C.云D.港8.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是()A.B.C.D.9.一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是()A.B.C.D.10.如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是()A.B.C.D.11.一个几何体的三视图如图所示,则该几何体的表面积为()A.4πB.3πC.2π+4 D.3π+412.如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距()A.0 B.1 C. D.二.填空题(共4小题)13.如图,在长方体ABCD﹣EFGH中,平面ABFE与平面DCGH的位置关系是平行.14.如图,一个长方体的表面展开图中四边形ABCD是正方形,则根据图中数据可得原长方体的体积是12cm3.15.如图,一个表面涂满颜色的正方体,现将每条棱三等分,再把它切开变成若干个小正方体,两面都涂色的有12个;只有一面涂色的小正方体有6个.16.如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为24π.(结果保留π)三.解答题(共6小题)17.如图,上面的平面图形绕轴旋转一周,可以得出下面的立方图形,请你把有对应关系的平面图形与立体图形连接起来.18.把19个边长为2cm的正方体重叠起来,作成如图那样的立体图形,求这个立体图形的表面积.19.小明用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小明看来看去觉得所拼图形似乎存在问题.(1)请你帮小明分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;(2)若图中的正方形边长6cm,长方形的长为8cm,宽为6cm,请求出修正后所折叠而成的长方体的表面积和体积.20.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和相等,请你求出y﹣x的值.21.如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2,那么这根木料本来的体积是多少?22.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)参考答案一.选择题(共12小题)1.下列图形中,属于立体图形的是()A.B.C.D.【考点】认识立体图形.【分析】根据平面图形所表示的各个部分都在同一平面内,立体图形是各部分不在同一平面内的几何,由一个或多个面围成的可以存在于现实生活中的三维图形,可得答案.【解答】解:A、角是平面图形,故A错误;B、圆是平面图形,故B错误;C、圆锥是立体图形,故C正确;D、三角形是平面图形,故D错误.故选:C.【点评】本题考查了认识立体图形,立体图形是各部分不在同一平面内的几何,由一个或多个面围成的可以存在于现实生活中的三维图形.2.如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是()A.V甲>V乙 S甲=S乙B.V甲<V乙 S甲=S乙C.V甲=V乙 S甲=S乙D.V甲>V乙 S甲<S乙【考点】点、线、面、体.【分析】根据圆柱体的体积=底面积×高求解,再利用圆柱体侧面积求法得出答案.【解答】解:V甲=π•b2×a=πab2,V乙=π•a2×b=πba2,∵πab2<πba2,∴V甲<V乙,∵S甲=2πb•a=2πab,S乙=2πa•b=2πab,∴S甲=S乙,故选:B.【点评】此题主要考查了面动成体,关键是掌握圆柱体的体积和侧面积计算公式.3.将四个棱长为1的正方体如图摆放,则这个几何体的表面积是()A.3 B.9 C.12 D.18【考点】几何体的表面积.【分析】观察几何体,得到这个几何体向前、向后、向上、向下、向左、向右分别有3个正方形,则它的表面积=6×3×1.【解答】解:这个几何体的表面积=6×3×1=18.故选:D.【点评】本题考查了几何体的表面积:正方体表面积为6a2 (a为正方体棱长).4.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是()A.遇B.见C.未D.来【考点】几何体的展开图.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“遇”与“的”是相对面,“见”与“未”是相对面,“你”与“来”是相对面.故选D.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.5.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是()A.①B.②C.③D.④【考点】展开图折叠成几何体.【分析】由平面图形的折叠及正方体的表面展开图的特点解题.【解答】解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,故选:A.【点评】本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.6.下面平面图形中能围成三棱柱的是()A.B.C. D.【考点】展开图折叠成几何体.【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.【解答】解:A、能围成三棱柱,故选项正确;B、折叠后有两个面重合,不能围成三棱柱,故选项错误;C、不能围成三棱柱,故选项错误;D、折叠后有两个侧面重合,不能围成三棱柱,故选项错误.故选:A.【点评】考查了展开图折叠成几何体,解题时勿忘记三棱柱的特征及正方体展开图的各种情形.7.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是()A.丽B.连C.云D.港【考点】专题:正方体相对两个面上的文字.【分析】正方体的平面展开图中,相对面的特点是必须相隔一个正方形,据此作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“美”与“港”是相对面,“丽”与“连”是相对面,“的”与“云”是相对面.故选D.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.8.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形。
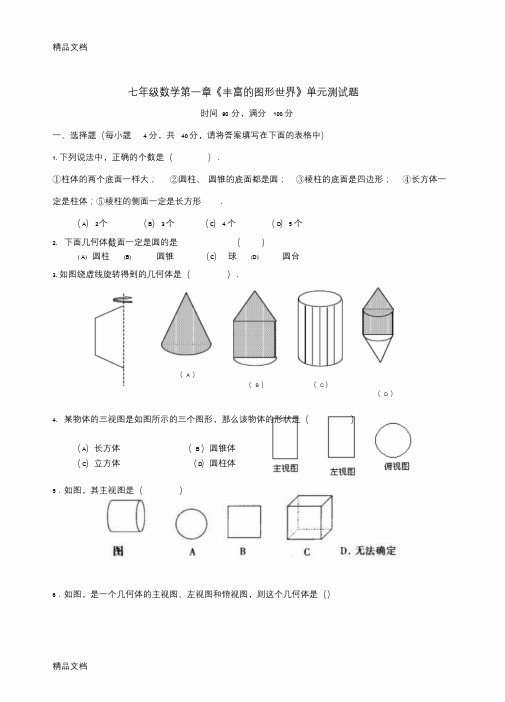
七年级数学第一章《丰富的图形世界》单元测试题时间90 分,满分100 分一、选择题(每小题 4 分,共40 分,请将答案填写在下面的表格中)1. 下列说法中,正确的个数是().①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.(A)2个(B)3个(C)4个(D)5个2. 下面几何体截面一定是圆的是()( A) 圆柱(B) 圆锥(C)球(D) 圆台3. 如图绕虚线旋转得到的几何体是().(A )(B )(C )(D )4. 某物体的三视图是如图所示的三个图形,那么该物体的形状是()(A)长方体(B )圆锥体(C)立方体(D)圆柱体5.如图,其主视图是()6.如图,是一个几何体的主视图、左视图和俯视图,则这个几何体是()精品文档7. 下列各个平面图形中,属于圆锥的表面展开图的是( )(A)(B)(C)(D)8.如图是由一些相同的小正方体构成的立体图形的三种视图:构成这个立体图形的小正方体的个数是().A.5 B .6 C .7 D .89.下面每个图形都是由 6 个全等的正方形组成的,其中是正方体的展开图的是()A B C D10.如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是()(A)35、、(B)23、5、2 3(C)5、、(D)2 5、、32精品文档第10 题图11、在下面的图形中,()是正方体的表面展开图.12、如图 1 所示的立方体,如果把它展开,可以是下列图形中的()图113、圆锥的侧面展开图是()A、三角形B、矩形C、圆D、扇形14、下列图形中,属于棱柱的是()15、如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有()A、4 个B、5 个C、6 个D、7 个1 6、如图是一个生日蛋糕盒,A、6 条B、12 条C、18 条D、24 条17、如图所示的图形绕虚线旋转一周,所形成体是()精品文档18、下列图形中,不属于三棱柱的展开图的是()19、如图,用一个平面去截圆锥,得到的截面是()二、填空题(每小题3分,共18分)第二部分:填空题1、如图 2 所示的几何体由_____个面围成,面与面相交成_____条线,其中直的线有_____条,曲线有_____条.图2 10 题图2、用一个平面去截一个圆柱,图甲中截面的形状是_____,图乙中截面的形状是_____.3、将一个有底无盖的长方形盒子沿某些棱剪开,展成一个平面图形,至少要剪开_____条棱。
2018-2019学年七年级数学上册第一章检测卷时间:100分钟满分:120分一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.下列几何体中,没有曲面的是()2.如图中的图形绕虚线旋转一周,可得到的几何体是()3.如图所示是由六个相同的小正方体搭成的几何体,从正面看该几何体得到的平面图形是()4.如图所示是某几何体从三个方向看到的图形,则这个几何体是()A.三棱锥B.圆柱C.球D.圆锥第4题图第6题图5.三棱柱的侧面展开图是下列图形中的()6.一个几何体由几个大小相同的小正方体搭成,其从左面看和从上面看得到的图形如图所示,则搭成这个几何体的小正方体的个数是()A.3个B.4个C.5个D.6个二、填空题(本大题共6小题,每小题3分,共18分)7.在朱自清的《春》中有描写春雨的语句“像牛毛,像细丝,密密地斜织着”,这里把雨滴看成了点,用数学知识解释这一现象:.8.如果某六棱柱的一条侧棱长为5cm,那么所有侧棱之和为.9.用一个平面去截正方体,截面是三角形(填“可能”或“不可能”).10.如图,某长方体的底面是长为4cm、宽为2cm的长方形,如果从左面看这个长方体时看到的图形面积为6cm2,则这个长方体的体积等于.第10题图第11题图第12题图11.如图所示是一个正方体的展开图,它所有相对的面上两数之和相等,则x 的值为.12.一个圆柱的侧面展开图为如图所示的长方形,则这个圆柱的底面面积为.三、(本大题共5小题,每小题6分,共30分)13.如图,上面是一些实物,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).14.如图所示,将下列几何体分类.15.如图所示,说出下列几何体截面(阴影部分)的形状.16.由7个相同的小立方块搭成的几何体如图所示,请画出从正面、左面、上面看到的几何体的形状图.17.小毅设计了某个产品的包装盒(如图所示),由于粗心少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子.(1)共有种添补的方法;(2)任意画出一种成功的设计图.四、(本大题共3小题,每小题8分,共24分)18.在如图所示的长方形纸中,剪出两个圆和一个长方形恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).19.一个几何体从三个方向看到的图形如图所示(单位:cm).(1)写出这个几何体的名称:;(2)若其从上面看为正方形,根据图中数据计算这个几何体的体积.20.如图所示是一个多面体的展开图形,每个面(外表面)都标注了字母,请你根据要求回答问题:(1)这个多面体是什么常见几何体?(2)如果D是多面体的底部,那么哪一面在上面?(3)如果B在前面,C在左面,那么哪一面在上面?五、(本大题共2小题,每小题9分,共18分)21.如图①,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.(1)甲三角形(如图②)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?(2)乙三角形(如图③)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米(π取3.14)?22.用5个相同的正方体搭出如图所示的组合体.(1)分别画出从正面、左面、上面看这个组合体时看到的图形;(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.六、(本大题共12分)23.如图,图①为一个正方体,其棱长为10,图②为图①的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:(1)如果正方体相对面上的两个数字之和相等,则x=,y =;(2)如果面“2”是右面,面“4”在后面,则上面是(填“6”“10”“x”或“y”);(3)如图①所示,M,N为所在棱的中点,试在图②中找出点M,N的位置.参考答案与解析1.B2.B3.B4.D5.B6.B 解析:由图可知,底层有3个小正方体,第2层有1个小正方体.故搭成这个几何体的小正方体的个数是3+1=4(个).7.点动成线 8.30cm 9.可能 10.24cm 3 11.4 12.4π或π 解析:分以下两种情形:(1)当底面周长为4π时,半径为4π÷π÷2=2,底面圆的面积为π×22=4π;(2)当底面周长为2π时,半径为2π÷π÷2=1,底面圆的面积为π×12=π.故其底面圆的面积为4π或π.13.解:如图所示.(6分)14.解:①③⑤⑥属于柱体,(2分)④属于锥体,(4分)②属于球体.(6分) 15.解:图①②截面形状均为三角形,(4分)图③截面形状为四边形.(6分) 16.解:如图所示.(每个图2分)17.解:(1)4(4分)(2)答案不唯一,如图所示.(6分)18.解:由图可知圆柱的半径r =12.56÷2π=2(dm),高h =4r =8dm.(4分)则体积V =πr 2h =3.14×22×8=100.48(dm 3).(7分)答:这个圆柱的体积是100.48dm 3.(8分) 19.解:(1)长方体(3分)(2)由题可知,长方体的底面是边长为3cm 的正方形,高是4cm ,则这个几何体的体积是3×3×4=36(cm 3).(7分)答:这个几何体的体积是36cm 3.(8分) 20.解:(1)这个多面体是一个长方体.(2分) (2)B 面在上面.(5分) (3)E 面在上面.(8分)21.解:(1)甲三角形旋转一周可以形成一个圆锥,(2分)它的体积是13×3.14×62×10=376.8(立方厘米).(4分)(2)乙三角形旋转一周可以形成一个空心的圆柱,(6分)它的体积是3.14×62×10-13×3.14×62×10=753.6(立方厘米).(9分)22.解:(1)画出的图形如图①所示.(3分)(2)能实现.(5分)添加正方体后从上面看到的图形如图②所示,有两种情况.(9分)23.解:(1)128(4分)(2)y(6分)(3)点N在与DC相对的棱上,点M的位置有两种情况,如图甲、图乙所示.(12分)。
一、选择题1.如图是由5个大小相同的正方体组成的几何体,则该几何体从正面看得到的平面图形是()A.B.C.D.2.如图,是一个正方体的表面展开图,则“2”所对的面是()A.0 B.9 C.快D.乐3.如图,从上向下看几何体,得到的图形是()A.B.C.D.4.下列图是由一些相同的小正方体搭成的几何体的三视图,则组成该几何体的小正方体的个数为( )A.7 B.8 C.9 D.105.如图是一个正方体的展开图,把展开图折叠成正方体后,标有“☆“的一面相对面上的字是()A.神B.奇C.数D.学6.在一个有盖的正方体玻璃容器内装了一些水(约占一半),把容器按不同方式倾斜,容器内水面的形状不可能是()A.B.C.D.7.下列四个立体图形中,从正面和左面看到的形状图有可能不同的是()A.B.C.D.8.下列哪个选项的图形经过折叠能围成一个正方体()A.B.C.D.9.图①是正方体的平面展开图,六个面的点数分别为1点、2点、3点、4点、5点、6点,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图②所示,若骰子初始位置为图②所示的状态,将骰子向右翻滚90 ,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻折后,骰子朝下一面的点数是3点;连续完成2019次翻折后,骰子朝下一面的点数是()A.2 B.3 C.4 D.510.如图,经过折叠后不能围成正方体的是( )A .B .C .D . 11.如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A 、B 、C 表示的数依次是( )A . 35,,2π--B .3,5,2π- C .35,,2π-D .352π-,, 12.下列语句中错误的是( ) A .正方体的截面可能是三角形、四边形、五边形、六边形B .正方体的截面可能是长方形,长方体的截面不可能是正方形C .正方体的截面不可能出现七边形D .正方体的截面可能是梯形二、填空题13.如图是一个正方体的表面展开图,则折成正方体后,与点M 重合的点是点______.14.乐乐发现三个大小相同的球可以恰好放在一个圆柱形盒子里(底和盖的厚度均忽略不计),如图所示,则三个球的体积之和占整个盒子容积的__________.(球的体积计算公式为343V r π=)15.如图是一个正方形的展开图,则这个正方体与“诚”字所在面相对的面上的字是_______.++ 16.若要使图中的平面展开图折叠成正方体后,相对面上的两个数之和为6,则x y z 的值为_____.17.从上面看圆柱和从上面看圆锥,其形状是一样的,都是圆,但是它们的俯视图是有区别的,其区别是________________.18.一个几何体的三种视图如图所示,这个几何体的表面积是__.(结果保留π)19.如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为________ .20.如图是一个由若干个小正方体组合而成的几何体的三视图,请问组成该组合体的小正方体个数是______.三、解答题21.如图所示是一个几何体的表面展开图.(1)该几何体的名称是.(2)根据图中所给信息,求该几何体的体积(结果保留π)22.如图是由一些棱长为单位1的相同的小正方体组合成的简单几何体,请在图中的方格子中分别画出从几何体正面看、左面看、上面看得到的图形。
基础复习七年级数学(上)第一章:丰富的图形世界知识要求:1 •经历展开与折叠,切截以及“从不同的方向看”等数学活动,积累数学活动经验.2 •在平面图形与空间几何体相互转换等的活动过程中,发展空间观念.3.认识常见几何体的基本特性,能对这些几何体进行正确的识别和简单的分类.4•通过丰富的实例,进一步认识点、线、面,了解有关点、线及某些基本图形的一些简单性质.5. 初步体会从不同方向观察同一物体可能看到不同的图形,能识别简单物体的三视图,会画立方体及其简单组合体的三视图. 6•了解直棱柱、。
圆柱、圆锥的侧面展开图,能根据展开图想象和制作立体模型.7•进一步丰富数学学习的成功体验,激发对空间与图形学习的好奇心,初步形成积极参与数学活动,主动与他人合作交流的意识.★ ★★ (I)考点突破★★★考点1:几何体的三视图及常见几何体的侧面展开图一、考点讲解:1. 视图:(1 )直三(四)棱柱、球体、圆柱、圆锥的三视图(主视图、左视图、俯视图人门)简单几何体的组合体的三视图.(2 )由三视图猜想物体的形状.(3)圆柱的侧面展开图是矩形,圆锥的侧面展开图为一扇形,其中扇形的半径为圆锥的母线,扇形的弧长为圆锥的底面周长.注意:在画视图时,看得见的各部分的轮廓通常画成实线,看不见的部分的轮廓通常画成虚线.2. 三视图的投影关系:由三视图可以看出,俯视图反映物体的长和宽,主视图反映它的长和高,左视图反映它的宽和高,因此物体的三视图之间有如下对应关系:(1)主视图和俯视图的长度相等,且相互对正,即“长对正” .(3)主视图和左视图的高度相等,且相互平齐,即“高平齐”.(4)俯视图与左视图的宽度相等,即“宽相等”.在三视图中,无论是物体的总长,总宽,总高,还是局部的长、宽、高都必须符合“长对正”,“高平齐”、“宽相等”的对应关系,因此,这“九字令” 是绘制和阅读三视图必须遵循的对应关系二、经典考题剖析:【考题1 —1】如图1—1 —1。
综合内容与测试A卷(共100分)一、选择题(每小题3分,共30分)1.若规定收入为“+”,那么-50元表示( )A.收入了50元B.支出了50元C.没有收入也没有支出D.收入了100元2.地球上的陆地面积约为149 000 000平方千米,这个数用科学记数法表示应为( ) A.0.149×106 B.1.49×107C.1.49×108 D.14.9×1073.如图是由几个相同的小正方体搭成的一个几何体,从右边看,得到的平面图形是( )A BC D4.如果数轴上表示2和-4的两点分别是点A和点B,那么点A和点B之间的距离是( )A.-2 B.2 C.-6 D.65.阜阳某企业今年1月份产值为a万元,2月份比1月份减少了8%,预计3月份比2月份增加12%.则3月份的产值将达到( )A.(a-8%)(a+12%)万元B.(a-8%+12%)万元C.a(1-8%)(1+12%)万元D.a(1-8%+12%)万元6.如果2m9-x n y和-3m8n4是同类项,则2m9-x n y+(-3m2y n3x+1)=( )A.-m8n4 B.mn4C.-m9n D.5m3n27.下列说法中,正确的是( )A.两点之间的连线中,直线最短B.若AP=BP,则P是线段AB的中点C.若P是线段AB的中点,则AP=BPD.两点之间的线段叫做这两点之间的距离8.已知∠A O B=70°,以O为端点作射线O C,使∠A O C=42°,则∠B O C的度数为( ) A.28° B.112°C.28°或112° D.68°9.下列方程的变形中,正确的是( )A .方程3x -2=2x +1,移项,得3x -2x =-1+2B .方程3-x =2-5(x -1),去括号,得3-x =2-5x -1C .方程23x =32,未知数系数化为1,得x =1D .方程x -12-x5=1化成5(x -1)-2x =1010.积极行动起来,共建节约型社会!我市某居民小区400户居民参加了节水行动,现统计了10估计该小区400户家庭这个月节约用水的总量是( ) A .360吨 B .400吨 C .480吨 D .720吨 二、填空题(每小题4分,共16分)11.如图是一个长方体的表面展开图,四边形ABCD 是正方形,则根据图中数据可得原长方体的体积是____ cm 3.12.已知|a +2|+|b -1|=0,则(a +b )-(b -a )=____.13.学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他采集数据后,绘制出一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有____人.14.定义运算:ab =⎩⎪⎨⎪⎧a -b (a≤b),a +b (a>b ),则(-3)(-2)=____.三、解答题(本大题共6小题,共54分)15.(9分)计算:(1)⎣⎢⎡⎦⎥⎤2-5×⎝ ⎛⎭⎪⎫-122÷⎝ ⎛⎭⎪⎫-14;(2)(-24)×⎝ ⎛⎭⎪⎫12-123-38; (3)-14-(1-0.4)÷13×[(-2)2-6].16.(8分)解方程: (1)7x -4=3(x +2); (2)2x +53-4=x -32.17.(8分)化简并求值:2(a 2-ab )-3⎝ ⎛⎭⎪⎫23a 2-ab -5.其中a =-2,b =3.18.(9分)如图,直线AB ,CD ,EF 交于点O ,O G 平分∠B O F ,且CD ⊥EF ,∠A O E =70°,求∠D O G 的度数.19.(10分)甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行110公里.(1)两车同时开出,背向而行,多少小时后两车相距800公里?(2)两车同时开出,同向而行,出发时快车在慢车的后面,多少小时后两车相距40公里?20.(10分)为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:(1)若A 组的频数比B 组小24,求频数分布直方图中a ,b 的值;(2)扇形统计图中,D 部分所对的圆心角为n °,求n 的值并补全频数分布直方图; (3)若成绩在80分以上为优秀,全校共有2 000名学生,估计成绩优秀的学生有多少名.B 卷(共50分)四、填空题(本大题共5个小题,每小题4分,共20分)21.如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为____.22.设a ,b 为实数,且a ≠0,方程|x +a |+|2b |=4,恰有三个不相等的解,则b =_______.23.观察下列等式:12=1-12=12,12+14=1-14=34,12+14+18=1-18=78,…,则12+14+18+…+12n =______.(用含n 的代数式表示,n 是正整数,且n ≥1) 24.已知a ,b ,c 为有理数,且满足-a >b >|c |,a +b +c =0,则|a +b |+|a -2b |-|a +2b |=_______.(结果用含a ,b 的代数式表示)25.如图,数轴上,点A 的初始位置表示的数为1,现点A 作如下移动:第1次点A 向左移动3个单位长度至点A 1,第2次从点A 1向右移动6个单位长度至点A 2,第3次从点A 2向左移动9个单位长度至点A 3,…,按照这种移动方式进行下去,如果点A n 与原点的距离不小于20,那么n 的最小值是______.五、解答题(本大题共3个小题,共30分)26.(10分)如图,点O 是直线AB 上一点,射线O A 1,O A 2均从O A 的位置开始绕点O 顺时针旋转,O A 1旋转的速度为每秒30°,O A 2旋转的速度为每秒10°.当O A 2旋转6秒后,O A 1也开始旋转.当其中一条射线与O B 重合时,另一条也停止.设O A 1旋转的时间为t 秒.(1)用含有t 的式子表示∠A 1O A =______°,∠A 2O A =_______°; (2)当t =______时,O A 1是∠A 2O A 的角平分线; (3)若∠A 1O A 2=30°时,求t 的值. 27.(8分)观察下面三行数:①-2,4,-8,16,-32,64,… ②0,6,-6,18,-30,66,… ③-1,2,-4,8,-16,32,…(1)第①、②、③行第n 个数分别为_______,_______,_______. (2)取每行数的第九个数,计算这三个数的和.28.(12分)某制造企业有一座对生产设备进行水循环冷却的冷却塔,冷却塔的顶部有一个进水口,3小时恰好可以注满这座空塔,底部有一个出水口,7小时恰好可以放完满塔的水.为了保证安全,塔内剩余水量不得少于全塔水量的14,出水口一直打开,保证水的循环,进水口根据水位情况定时对冷却塔进行补水.假设每次恰好在剩余水量为满水量的m 倍时开始补水,补满后关闭进水口.(1)当m =14时,请问:两次补水之间相隔多长时间?每次补水需要多长时间?(2)能否找到适当的m 值,使得两次补水的间隔时间和每次的补水时间一样长?如果能,请求出m 值;如果不能,请你分析两次补水的间隔时间和每次的补水时间之间的数量关系,并表示出来.参考答案1. B2. C3. C4. D5. C6. A7. C8. C9. D 10. C11. 96 12. -4 13.8 14. -115. 解:(1)原式=⎝ ⎛⎭⎪⎫2-54×(-4)=-8+5=-3. (2)原式=-12+40+9=37.(3)原式=-1-35×3×(-2)=-1+185=135.16. 解:(1)去括号,得7x -4=3x +6,移项、合并,得4x =10, 解得x =2.5.4分(2)去分母,得2(2x +5)-24=3(x -3), 去括号,得4x +10-24=3x -9, 移项、合并,得x =5.17. 解:原式=2a 2-2ab -2a 2+3ab -5=ab -5,当a =-2,b =3时,原式=(-2)×3-5=-6-5=-11. 18. 解:∵∠A O E =70°,∴∠B O F =∠A O E =70°. 又∵O G 平分∠B O F ,∴∠G O F =12∠B O F =35°.又∵CD ⊥EF ,∴∠D O F =90°,∴∠D O G =∠D O F -∠G O F =90°-35°=55°. 19. 解:(1)设x 小时后两车相距800公里.依题意,得90x +480+110x =800, 解得x =1.6,∴1.6小时后两车相距800公里. (2)设y 小时后两车相距40公里. 若相遇之前两车相距40公里, 则90y +480-110y =40, 解得y =22.若相遇后两车相距40公里, 则110y -90y -480=40, 解得y =26,∴22或26小时后两车相距40公里.20. 解:(1)学生总数是24÷(20%-8%)=200(人),则a =200×8%=16,b =200×20%=40.(2)n =360×70200=126.C 组的人数是200×25%=50(人).补全频数分布直方图如答图.答图(3)样本D ,E 两组的百分数的和为1-25%-20%-8%=47%, ∴2 000×47%=940(名),则成绩优秀的学生约有940名. 21.20° 22. 2或-2【解析】 ∵方程|x +a |+|2b |=4,∴|x +a |=4-|2b |=4±2b .∵有三个不相等的解,∴4+2b 与4-2b ,其中一个为0,则得3个解,如果都不是零,则得4个解,故b =2或-2. 23. 2n-12n24. -3a -b【解析】 ∵-a >b >|c |,a +b +c =0,∴a <0,b >c >0,|a |>|b |>|c |,∴a +b <0,a -2b <0,a +2b >0,∴|a +b |+|a -2b |-|a +2b |=-a -b +2b -a -a -2b =-3a -b . 25. 【解析】 由题意及图可知,A 1表示-2,A 2表示4, A 3表示-5,A 4表示7, 依次类推,可得A 5表示-8,A 6表示10, A 7表示-11,A 8表示13, A 9表示-14,A 10表示16, A 11表示-17,A 12表示19, A 13表示-20,…故A 13与原点的距离不小于20.26.(1)(30t) (10t +60) (2)1.2【解析】(2)由(1)知,∠A 1O A =(30t )°,∠A 2O A =(10t +60)°.∵O A 1是∠A 2O A 的角平分线,∴∠A 2O A =2∠A 1O A ,10t +60=60t ,∴t =1.2.解:(3)由(1)知,∠A 1O A =(30t )°,∠A 2O A =(10t +60)°, ∵∠A 1O A 2=30°,∴|30t -(10t +60)|=30,∴t =32或t =92.27. (1) (-2)n (-2)n +2 12(-2)n(2)-1 278.【解析】 (1)∵第1行中,第1个数=(-2)1=-2,第2个数=(-2)2=4,第3个数=(-2)3=-8,…,故第n 个数=(-2)n.第2行数等于第1行相应的数加2. 第3行数等于第1行相应的数的一半.解:(2)当n =9时,(-2)n =-512;(-2)n +2=-510;12(-2)n=-256,∴这三个数的和=-512-510-256=-1 278.28. 解:(1)设两次补水之间相隔x 小时,每次补水需要y 小时,满塔水量记为1,进水速度为13,出水速度为17.根据题意,得17x +14=1,解得x =214,13y -17y +14=1,解得y =6316, 则两次补水之间相隔214小时,每次补水需要6316小时.(2)∵两次补水间隔时间t 1=(1-m )÷17=7(1-m )小时,每次的补水时间为t 2=(1-m )÷⎝ ⎛⎭⎪⎫13-17=214(1-m )小时,∴t 1≠t 2,即不能找到适当的m 值,使得两次补水的间隔时间和每次的补水时间一样长.∴两次补水的间隔时间和每次的补水时间之比为4∶3.。