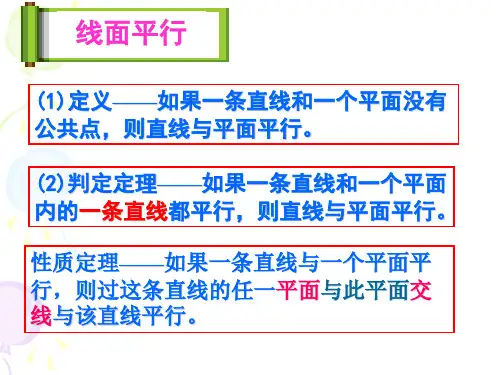
平行关系的判定定理

平行1．直线与平面平行的判定(1)直线与平面平行的定义：如果一条直线与一个平面没有公共点，我们就说这条直线与这个平面平行．(2)直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．符号表示为：．注意：这个定理是证明直线与平面平行最常用的一个定理，也就是说欲证明一条直线与一个平面平行，一是说明这条直线不在这个平面内，二是要证明已知平面内有一条直线与已知直线平行．2．两个平面平行的判定(1)两个平面平行的定义：两个平面没有公共点，则两个平面平行．(2)平面与平面的平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行．符号表示为：．注意：这个定理的另外一种表达方式为“如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行，那么这两个平面平行”．(3)平行于同一平面的两个平面互相平行．即．3．直线与平面平行的性质(1) 直线与平面平行的性质定理：一条直线和一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．符号表示为：．注意：如果一条直线和一个平面平行，那么这条直线和平面内的无数条直线平行，但不能误解为“如果一条直线与一个平面平行，那么这条直线就和平面内的任意一条直线平行”．(2)直线与平面平行的性质：过平面内一点的直线与该平面平行的一条直线平行，则这条直线在这个平面内．符号表示为：若，点，且，则．4．平面与平面平行的性质(1)如果两个平面平行，那么其中一个平面内的任意直线均平行与另一个平面．此结论可以作为定理用，可用来判定线面平行．(2)两个平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．(3)夹在两个平行平面间的平行线段相等．垂直1．直线与平面垂直的判定(1)直线与平面垂直的定义如果一条直线和一个平面内的任意一条直线都垂直，我们就说这条直线和这个平面垂直，其中直线叫作平面的垂线，平面叫作直线的垂面．注意：①定义中的“任意一条直线”和“所有直线”是同义语，不能改成“无穷多条直线”．②如果或，那么直线l不可能与平面内的任意一条直线都垂直．由此可知，当时，直线l和一定相交，它们唯一的交点叫做垂足．(2)直线和平面垂直的判定定理如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直与这个平面．(3)关于垂直的存在唯一性命题1：过一点有且只有一条直线和已知平面垂直．命题2：过一点有且只有一个平面和已知直线垂直．2．平面与平面垂直的判定(1)平面与平面垂直的定义：两个平面相交，如果所成的二面角是直二面角，则称这两个平面互相垂直．(2)两个平面垂直的判定定理如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直． 符号表示为：．3．直线与平面垂直的性质如果两条直线同垂直于一个平面，那么这两条直线平行． 符号表示：． 作用：可作线线平行的判定定理． 4．平面与平面垂直的性质(1)两个平面垂直的性质定理如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面． 符号表示为：．(2)如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面． (3)三个两两垂直的平面的交线两两垂直．(4)如果两个平面垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内．空间几何定理公理总结：1.平面的基本性质公理1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点，有且只有一个平面. 推论1 经过一条直线和这条直线外一点，有且只有一个平面. 推论2 经过两条相交直线，有且只有一个平面. 推论3 经过两条平行直线，有且只有一个平面. 公理4 同平行于一条直线的两条直线互相平行。

直线平行的判定定理
直线平行的判定定理是指，当两条直线与另一条直线交错相交时，若交错相交的内角相等，则这两条直线平行。

具体来说，设有两条直线L1和L2，它们都与另一条直线L相交，交点分别为A、B和C、D。

如果∠BAC=∠DCB，则L1与L2平行。

这个定理可以通过角的对应关系进行证明。

因为∠BAC=∠DCB，
所以∠ABC和∠CBD互补，∠ABD和∠CBA互补。

由于L1与L2分别与L相交，所以∠ABC和∠ABD是同旁内角，∠CBD和∠CBA也是同旁内角，根据同旁内角定理可知∠ABC=∠ABD，∠CBD=∠CBA。

而由于∠ABC 和∠CBD互补，所以∠ABD和∠CBA也互补，即L1与L2平行。

这个定理在几何证明中有着重要的应用，对于平面几何的学习也有着不可替代的作用。

- 1 -。

线和平面平行的判定定理
1. 垂直平行线定理，如果一条直线和平面上的两条平行线垂直
相交，那么这条直线与该平面平行。

2. 平行线的截距定理，如果一条直线与两条平行线分别相交，
且这两个交点到两条平行线的距离相等，那么这条直线与这两条平
行线平行。

3. 平行线的倾斜定理，如果一条直线与两条平行线分别相交，
且这两个交点到两条平行线的距离之比相等于一个常数k，那么这
条直线与这两条平行线平行。

4. 平行线的夹角定理，如果一条直线与两条平行线分别相交，
那么这两个交点所成的两个内角互为对应角，即它们相等。

这些定理提供了判定线和平面是否平行的方法，通过这些定理
我们可以在几何问题中判断线和平面的平行关系，从而解决相关问题。

这些定理在实际问题中有着广泛的应用，例如在建筑设计、工
程测量和地理空间分析等领域都有着重要的作用。

通过深入理解和
灵活运用这些定理，我们可以更好地理解空间关系，解决实际问题。

平行线的判定定理6条平行线的判定定理有六条，这个听上去是不是有点复杂？咱们把它们想得简单点，就会发现其实它们就像生活中的一些规律，挺有趣的。

咱们得明白，平行线就是那种永远不相交的两条线，就像两个好朋友，无论怎么走，始终保持一定的距离，不会碰上。

这第一条，咱们可以说是“同位角相等”，这就像两个人穿了相同的衣服，走在一起，显得特别默契，对吧？只要角度相等，大家就可以放心大胆地说，这俩线肯定是平行的。

再说说第二条，“内错角相等”。

这就像是一对情侣，一个在左边，一个在右边，虽然他们不站在同一条线上，但总有些互动，一聊起来就知道心意相通。

就像你和朋友一起去看电影，你们虽然坐得远，但心里却都是那部影片的粉丝。

这条定理提醒我们，只要内错角相等，线也是不可能相交的。

接下来是第三条，“同侧内角互补”。

嘿，这个可有意思了，想象一下，两个好朋友在同一条线上，分别面对着两边，一个在左，一个在右，他们的内角就像是手中各拿着一杯饮料，刚好加在一起等于180度，这可真是绝配！只要他们互补，就说明两条线相互间的距离保持不变，自然就不碰头。

咱们再来聊聊第四条，叫做“外错角相等”。

这就像两个邻居，虽然家里隔着一道墙，但总能隔空聊天，偶尔还一起喝茶，外面交流得特别好。

只要外错角相等，这两条线就可以安心做自己的事情，不用担心会发生意外。

然后第五条，“同侧外角互补”。

这就有点像足球赛上，两个球员在场边策划战术，一个拿着战术板，一个在旁边认真听，虽然离得远，但脑子里想的却是一样的事情，想好了配合。

这两条线只要同侧外角互补，根本不需要担心相遇的问题，都是在自己的路上奔跑。

我们来到第六条，这条可不简单，叫做“平行线的切线”。

这就像一条独行侠的道路，虽然周围有许多线，但他依然坚定地走自己的路，不被其他线影响。

只有那些真正的平行线，才会与切线形成一个美妙的交点，而这个交点就是它们的底线，平行的力量就藏在其中。

这六条判定定理，像是生活中各种关系的缩影，让我们明白无论是朋友、情侣，还是工作伙伴，互相的角度和位置都很重要。

1、一个平面内的两条相交直线平行于另一个平面，则这两平面平行；
2、垂直于同一直线的两平面平行；
3、一个平面内的两条相交直线与另一个平面内的两条相交直线平行，则这两个平面平行。

两平面平行简介
两平面平行是两平面间的一种位置关系，如果两个平面没有公共点，则称这两
个平面有平行位置关系，简称两平面相互平行，一个平面称为另一个平面的平行平面。

平面与平面平行的性质定理
如果两个平行平面都和第三个平面相交，那么它们的交线平行，由两个平面平行，我们还有：
1、如果两个平面平行，那么其中一个平面内的直线平行于另一个平面；
2、和两个平行平面同时垂直的直线，叫做这两个平行平面的公垂线。

它夹在
这两个平行平面间的部分叫这两个平行平面的公垂线段。

公垂线段的长度叫做两个平行平面的距离。

注意：①两个平面平行，其中一个平面内的直线必平行于另一个平面。

但这两
个平面内的所有直线并不一定相互平行。

它们可能是平行直线，也可能是异面直线，但不可能是相交直线。

②两个平面平行的性质定理指出两个平面平行时所具有的性质：如果两个平面
平行同时与第三个平面相交，那么它们的交线平行。

③一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

考点一平行线的判定：1．两直线被第三条直线所截，如果同位角相等，那么这两条直线平行．2．两直线被第三条直线所截，如果内错角相等，那么这两条直线平行．3. 两直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．注意：证明两直线平行，关键是找到与特征结论相关的角.例1．如下图，当∠1=∠3时，直线a、b平行吗？当∠2+∠3=180°时，直线a、b平行吗？为什么？你有几种方法。

例2．请将下面的空补充完整1．如右图，若∠1=∠2，则_______∥_______（）若∠3=∠4，则_________∥_________（）若∠5=∠B，则_________∥_________（）若∠D+∠DAB=180°，则______∥_______（）2．如右图，∠1+∠2=180°（已知）∠3+∠2=180°（）∴∠1=_________∴AB∥CD（）课堂练习：1．如图6－21，已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证：AB∥C D．2．已知，如下图（1），（2），直线AB∥ED．求证：∠ABC+∠CDE=∠BCD．（1） （2） 3．如图，如果AB∥CD，求角α、β、γ与180º之间的关系式．4．如图，已知CD 是∠ACB 的平分线，∠ACB = 500，∠B = 700，DE ∥BC，求：∠EDC 和 ∠BDC 的度数。

达标训练： 一．选择题1．下列命题中，不正确的是( )A ．两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行B ．两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行C ．两条直线被第三条直线所截，那么这两条直线平行D ．如果两条直线都和第三条直线平行，那么这两条直线也互相平行2．如右图，直线a 、b 被直线c 所截，现给出下列四个条件： ( ) (1)∠1=∠2，(2)∠3=∠6，(3)∠4+∠7=180°，(4)∠5+∠8=180°， 其中能判定a ∥b 的条件是( ) A ．(1)(3) B ．(2)(4) C ．(1)(3)(4) D ．(1)(2)(3)(4) 3．如右图，如果∠1=∠2，那么下面结论正确的是( ) A ．AD ∥BC B ．AB ∥CD C ．∠3=∠4 D ．∠A =∠C4．一辆汽车在笔直的公路上行驶，两次拐弯后，行驶的方向与原来 的方向相同，这两次拐弯的角度可能是( ) A ．第一次向右拐40°，第二次向左拐40° B ．第一次向右拐50°，第二次向左拐130° C ．第一次向右拐50°，第二次向右拐130° D ．第一次向左拐50°，第二次向左拐130° 二．填空题αγβED C BAAB D E12FOCABDE5．如右图，∠1=∠2=∠3，则直线l 1、l 2、l 3的关系是________．6．如果两条直线被第三条直线所截，一组同旁内角的度数之比为3∶2，差为36°，那么这两条直线的位置关系是________ ． 7．同垂直于一条直线的两条直线________． 8．根据图形及上下文的含义推理并填空． （1）∵∠A =_______（已知）∴AC ∥ED （ ） （2）∵∠2=_______（已知）∴AC ∥ED （ ） （3）∵∠A +_______=180°（已知） ∴AB ∥FD （ ） 三．解答题9．已知：如图7，∠1=∠2，且BD 平分∠ABC ． 求证．AB ∥CD ．10、.如图，∠A BC =∠BCD, ∠1=∠2,求证：BE ∥CF.11．如图，是大众汽车的标志图案,其中蕴涵着许多几何知识． 根据下面的条件完成证明．已知：如图，BC//AD ，BE//AF ． (1) 求证：B A ∠=∠；(2) 若︒=∠135DOB ，求A ∠的度数．12.已知:如图,∠3与∠1互余,∠3与∠2互余.求证:AB ∥CD.考点二：1．平行线的性质．公理：两直线平行，同位角相等. 定理：两直线平行，内错角相等.CFDEBAOHG321ED C BA定理：两直线平行，同旁内角互补.例1．如图，BE∥DF，∠B =∠D，求证．AD∥BC．课堂作业：1．如上图，AB∥CD，AD∥BC则下列结论成立的是( )A．∠A+∠C=180°B．∠A+∠B=180°C．∠B+∠D=180°D．∠B=∠D2．若两个角的一边在同一条直线上，另一边互相平行，那么这两个角的关系是( )A．相等B．互补C．相等或互补D．相等且互补3．如右图，已知∠1=∠2，∠BAD=57°，则∠B=________．4．已知：如图，AD⊥BC，EF⊥BC，∠4=∠C．求证：∠1=∠2．5．如图所示，已知AB⊥BD于点B，ED⊥BD于点D，且AB=CD，BC=DE，那么AC与CE有什么关系？写你的猜想，并说明理由6、如图所示：已知：AB∥DE。

直线、平面平行的判定与性质1．直线与平面平行的判定定理和性质定理(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β； (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b ； (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.判断正误(正确的打“√”，错误的打“×”)(1)若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面．( )(2)若一条直线平行于一个平面，则这条直线平行于这个平面内的任一条直线．( )(3)若直线a 与平面α内无数条直线平行，则a ∥α.( )(4)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行．( )(5)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．( )答案：(1)× (2)× (3)× (4)× (5)√(教材习题改编)如果直线a ∥平面α，那么直线a 与平面α内的( )A ．一条直线不相交B ．两条直线不相交C ．无数条直线不相交D ．任意一条直线都不相交解析：选D.因为a ∥平面α，直线a 与平面α无公共点，因此a 和平面α内的任意一条直线都不相交，故选D.a 、b 、c 为三条不重合的直线，α、β、γ为三个不重合的平面，现给出四个命题： ①⎭⎪⎬⎪⎫c ∥αc ∥β⇒α∥β ②⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β ③⎭⎪⎬⎪⎫c ∥αa ∥c ⇒a ∥α ④⎭⎪⎬⎪⎫a ∥γα∥γ⇒a ∥α其中正确的命题是________．解析：②正确．①错在α与β可能相交．③④错在a 可能在α内． 答案：②(教材习题改编)在正方体ABCD -A1B 1C 1D 1中，E 是DD 1的中点，则BD 1与平面ACE 的位置关系为________．解析：如图，连接AC ，BD 交于O 点，连接OE ，因为OE ∥BD 1，而OE ⊂平面ACE ，BD 1⊄平面ACE ，所以BD 1∥平面ACE .答案：平行线面平行的判定与性质(高频考点)平行关系是空间几何中的一种重要关系，包括线线平行、线面平行、面面平行，其中线面平行在高考试题中出现的频率很高，一般出现在解答题的某一问中．高考对线面平行的判定与性质的考查主要有以下三个命题角度：(1)线面位置关系的判断；(2)线面平行的证明；(3)线面平行性质的应用．[典例引领]角度一线面位置关系的判断设m，n表示不同直线，α，β表示不同平面，则下列结论中正确的是()A．若m∥α，m∥n，则n∥αB．若m⊂α，n⊂β，m∥β，n∥α，则α∥βC．若α∥β，m∥α，m∥n，则n∥βD．若α∥β，m∥α，n∥m，n⊄β，则n∥β【解析】A错误，n有可能在平面α内；B错误，平面α有可能与平面β相交；C错误，n也有可能在平面β内；D正确，易知m∥β或m⊂β，若m⊂β，又n∥m，n⊄β，所以n∥β，若m∥β，过m作平面γ交平面β于直线l，则m∥l，又n∥m，所以n∥l，又n⊄β，l⊂β，所以n∥β.【答案】 D角度二线面平行的证明在正方体ABCD-A1B1C1D1中，E，F，G，H分别是BC，CC1，C1D1，A1A的中点．求证：(1)BF∥HD1；(2)EG∥平面BB1D1D.【证明】(1)如图所示，取BB1的中点M，连接MH，MC1，易证四边形HMC1D1是平行四边形，所以HD1∥MC1.又因为在平面BCC1B1中，BM綊FC1，所以四边形BMC1F为平行四边形，所以MC1∥BF，所以BF∥HD1.(2)取BD的中点O，连接EO，D1O，则OE∥DC且OE＝12DC，又D1G∥DC且D1G＝12DC，所以OE綊D1G，所以四边形OEGD1是平行四边形，所以GE∥D1O.又D1O⊂平面BB1D1D，GE⊄平面BB1D1D，所以EG∥平面BB1D1D.角度三线面平行性质的应用B1C1D1中，E为线段AD上的任意一如图，在四棱柱ABCD-A点(不包括A，D两点)，平面CEC1与平面BB1D交于FG.证明：FG∥平面AA1B1B.【证明】在四棱柱ABCD-A1B1C1D1中，BB1∥CC1，BB1⊂平面BB1D，CC1⊄平面BB1D，所以CC1∥平面BB1D，又CC1⊂平面CEC1，平面CEC1与平面BB1D交于FG，所以CC1∥FG，因为BB1∥CC1，所以BB1∥FG，而BB1⊂平面AA1B1B，FG⊄平面AA1B1B，所以FG∥平面AA1B1B.证明直线与平面平行的常用方法(1)定义法：证明直线与平面没有公共点，通常要借助于反证法来证明．(2)判定定理法：在利用判定定理时，关键是找到平面内与已知直线平行的直线，可先直观判断题中是否存在这样的直线，若不存在，则需作出直线，常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面，找其交线进行证明．[通关练习]1．(优质试题·高考全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()解析：选A.对于选项B，如图所示，连接CD，因为AB∥CD，M，Q分别是所在棱的中点，所以MQ∥CD，所以AB∥MQ，又AB⊄平面MNQ，MQ⊂平面MNQ，所以AB∥平面MNQ.同理可证选项C，D中均有AB∥平面MNQ.故选A.2.如图，四棱锥P-ABCD中，底面ABCD为矩形，F是AB的中点，E是PD的中点．(1)证明：PB ∥平面AEC ；(2)在PC 上求一点G ，使FG ∥平面AEC ，并证明你的结论．解：(1)证明：连接BD 与AC 交于点O ，连接EO . 因为四边形ABCD 为矩形， 所以O 为BD 的中点． 又E 为PD 的中点， 所以EO ∥PB .因为EO ⊂平面AEC ，PB ⊄平面AEC ， 所以PB ∥平面AEC .(2)PC 的中点G 即为所求的点． 证明如下： 连接GE 、FG ， 因为E 为PD 的中点， 所以GE 綊12CD .又F 为AB 的中点，且四边形ABCD 为矩形， 所以F A 綊12CD . 所以F A 綊GE .所以四边形AFGE 为平行四边形，所以FG ∥AE .又FG ⊄平面AEC ，AE ⊂平面AEC ，所以FG∥平面AEC.面面平行的判定与性质[典例引领]B1C1中，E，F，G，如图所示，在三棱柱ABC-AH分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EF A1∥平面BCHG.【证明】(1)因为G，H分别是A1B1，A1C1的中点，所以GH∥B1C1，又B1C1∥BC，所以GH∥BC，所以B，C，H，G四点共面．(2)在△ABC中，E，F分别为AB，AC的中点，所以EF∥BC，因为EF⊄平面BCHG，BC⊂平面BCHG，所以EF∥平面BCHG.又因为G，E分别为A1B1，AB的中点，所以A1G綊EB，所以四边形A1EBG是平行四边形，所以A1E∥GB.因为A1E⊄平面BCHG，GB⊂平面BCHG，所以A1E∥平面BCHG.又因为A1E∩EF＝E，所以平面EF A1∥平面BCHG.1．在本例条件下，若D为BC1的中点，求证：HD∥平面A1B1BA.证明：如图所示，连接HD，A1B，因为D为BC1的中点，H为A1C1的中点，所以HD∥A1B，又HD⊄平面A1B1BA，A1B⊂平面A1B1BA，所以HD∥平面A1B1BA.2．在本例条件下，若D1，D分别为B1C1，BC的中点，求证：平面A1BD1∥平面AC1D.证明：如图所示，连接A1C交AC1于点M，因为四边形A1ACC1是平行四边形，所以M是A1C的中点，连接MD，因为D为BC的中点，所以A1B∥DM.因为A1B⊂平面A1BD1，DM⊄平面A1BD1，。

线面、面面平行的判定与性质（教师版）知识回顾1．线面平行的判定（1）直线与平面平行的定义：直线与平面无公共点． （2）直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行． 用符号表示为：a ⊄α，b ⊂α，且a ∥b ⇒a ∥α． 2．线面平行的性质直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行符号语言描述：⎭⎪⎬⎪⎫a ∥αa ⊂ββ∩α＝b ⇒a ∥b ． 3. 面面平行的判定（1）平面α与平面β平行的定义：两平面无公共点． （2）直线与平面平行的判定定理：下面的命题在“________”处缺少一个条件，补上这个条件，使其构成真命题(m ，n 为直线，α，β为平面)，则此条件应为m ，n 相交．⎭⎪⎬⎪⎫m ⊂αn ⊂αm ∥βn ∥β⇒α∥β 4．面面平行的性质平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．符号表示为：⎭⎪⎬⎪⎫α∥βα∩γ＝a β∩γ＝b ⇒a ∥b ． 题型讲解题型一 利用三角形中位线证明线面平行例1、如图，ABCD 是平行四边形，S 是平面ABCD 外一点，M 为SC 的中点.求证：SA∥平面MDB.答案:证明：连结AC交BD于N，因为ABCD是平行四边形，所以N是AC的中点.又因为M是SC的中点，所以MN∥SA.因为MN平面MDB，所以SA∥平面MDB.例2、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，求证：MN∥平面PB1C.答案证明：如图，连结AC，则P为AC的中点，连结AB1，∵M、N分别是A1A与A1B1的中点，∴MN∥AB1.又∵平面PB1C，平面PB1C，故MN∥面PB1C.例3、如图所示，P是▱ABCD所在平面外一点，E、F分别在PA、BD上，且PE∶EA＝BF∶FD．求证：EF∥平面PBC．证明连接AF延长交BC于G，连接PG．在▱ABCD中，易证△BFG∽△DFA．∴GFFA＝BFFD＝PEEA，∴EF∥PG．而EF⊄平面PBC，PG⊂平面PBC，∴EF∥平面PBC．练习在正方体ABCD－A1B1C1D1中，E为DD1的中点，则BD1与过点A，E，C的平面的位置关系是______．答案：平行题型二利用平行四边形证明线面平行例1、如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱BC、C1D1的中点．求证：EF∥平面BDD1B1．证明：取D1B1的中点O，连接OF，OB．∵OF 12B1C1，BE12B1C1，∴OF BE．∴四边形OFEB是平行四边形，∴EF∥BO．∵EF⊄平面BDD1B1，BO⊂平面BDD1B1，∴EF∥平面BDD1B1．例2、如图所示，已知正方体ABCD－A1B1C1D1中，面对角线AB1、BC1上分别有两点E、F，且B1E＝C1F．求证：EF∥平面ABCD．证明方法一过E、F分别作AB、BC的垂线，EM、FN分别交AB、BC于M、N，连接MN．∵BB1⊥平面ABCD，∴BB1⊥AB，BB1⊥BC，∴EM∥BB1，FN∥BB1，∴EM∥FN，∵AB1＝BC1，B1E＝C1F，∴AE＝BF，又∠B1AB＝∠C1BC＝45°，∴Rt△AME≌Rt△BNF，∴EM＝FN．∴四边形MNFE是平行四边形，∴EF∥MN．又MN⊂平面ABCD，EF⊄平面ABCD，∴EF∥平面ABCD．方法二过E作EG∥AB交BB1于G，连接GF，∴B1EB1A＝B1GB1B，B1E＝C1F，B1A＝C1B，∴C1FC1B＝B1GB1B，∴FG∥B1C1∥BC．又∵EG∩FG＝G，AB∩BC＝B，∴平面EFG∥平面ABCD．又EF⊂平面EFG，∴EF∥平面ABCD．题型三利用面面平行证明线面平行例. 如图，在四棱锥中，是平行四边形，，分别是，的中点．求证：平面．答案：证明：如图，取的中点，连接，，分别是，的中点，，，P ABCDABCD M N AB PCMN//PADCD E NE ME∵M N AB PCNE PD∴//ME AD//可证明平面，平面．又，平面平面，又平面，平面．题型四面面平行的证明例1、如图所示，在正方体ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO?解：当Q为CC1的中点时，平面D1BQ∥平面PAO．∵Q为CC1的中点，P为DD1的中点，∴QB∥PA．∵P、O为DD1、DB的中点，∴D1B∥PO．又PO∩PA＝P，D1B∩QB＝B，D1B∥平面PAO，QB∥平面PAO，∴平面D1BQ∥平面PAO．题型五平行性质NE//PAD ME//PADNE ME E=∴MNE//PADMN⊂MNE∴MN//PAD例1、如图所示，长方体ABCD－A1B1C1D1中，E、F分别是棱AA1和BB1的中点，过EF的平面EFGH分别交BC和AD于G、H，则HG与AB的位置关系是()A．平行 B．相交C．异面 D．平行和异面答案：A例2、ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：AP∥GH．证明如图所示，连接AC交BD于O，连接MO，∵ABCD是平行四边形，∴O是AC中点，又M是PC的中点，∴AP∥OM．根据直线和平面平行的判定定理，则有PA∥平面BMD．∵平面PAHG∩平面BMD＝GH，根据直线和平面平行的性质定理，∴AP∥GH．练习、如图，在三棱柱ABC－A1B1C1中，M是A1C1的中点，平面AB1M∥平面BC1N，AC∩平面BC1N＝N．求证：N为AC的中点．证明 ∵平面AB 1M ∥平面BC 1N ， 平面ACC 1A 1∩平面AB 1M ＝AM ， 平面BC 1N∩平面ACC 1A 1＝C 1N ， ∴C 1N ∥AM ，又AC ∥A 1C 1， ∴四边形ANC 1M 为平行四边形， ∴AN 綊C 1M ＝12A 1C 1＝12AC ，∴N 为AC 的中点．跟踪训练1．如右图所示的三棱柱ABC －A 1B 1C 1中，过A 1B 1的平面与平面ABC 交于直线DE ，则DE 与AB 的位置关系是( )A ．异面B ．平行C ．相交D ．以上均有可能 答案：B[解析] ∵A 1B 1∥AB ，AB ⊂平面ABC ，A 1B 1⊄平面ABC ， ∴A 1B 1∥平面ABC.又A 1B 1⊂平面A 1B 1ED ，平面A 1B 1ED∩平面ABC ＝DE ，∴DE ∥A 1B 1. 又AB ∥A 1B 1，∴DE ∥AB.2．已知直线l ，m ，平面α，β，下列命题正确的是( ) A ．l ∥β，l ⊂α⇒α∥βB ．l ∥β，m ∥β，l ⊂α，m ⊂α⇒α∥βC ．l ∥m ，l ⊂α，m ⊂β⇒α∥βD ．l ∥β，m ∥β，l ⊂α，m ⊂α，l ∩m ＝M ⇒α∥β 答案：D3、直线a ∥平面α，α内有n 条直线交于一点，则这n 条直线中与直线a 平行的直线( )A．至少有一条 B．至多有一条C．有且只有一条 D．没有答案：B4、给出下列结论，正确的有()①平行于同一条直线的两个平面平行；②平行于同一平面的两个平面平行；③过平面外两点，不能作一个平面与已知平面平行；④若a，b为异面直线，则过a与b平行的平面只有一个．A．1个 B．2个 C．3个 D．4个答案：B5．正方体EFGH—E1F1G1H1中，下列四对截面中，彼此平行的一对截面是()A．平面E1FG1与平面EGH1B．平面FHG1与平面F1H1GC．平面F1H1H与平面FHE1D．平面E1HG1与平面EH1G答案：A6．如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为________．答案：平行四边形[解析]∵平面ABFE∥平面CDHG，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面CDHG＝HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH的形状是平行四边形．7. 如图所示，在三棱柱ABC－A1B1C1中，AC＝BC，点D是AB的中点，求证：BC1∥平面CA1D.证明：如图所示，连接AC1交A1C于点O，连接OD，则O是AC1的中点．∵点D是AB的中点，∴OD∥BC1.又∵OD⊂平面CA1D，BC1⊄平面CA1D，∴BC1∥平面CA1D.8．如图所示，在正方体ABCD－A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、DC和SC的中点．求证：平面EFG∥平面BDD 1B1．证明如图所示，连接SB，SD，∵F、G分别是DC、SC的中点，∴FG∥SD．又∵SD⊂平面BDD1B1，FG⊄平面BDD1B1，∴直线FG∥平面BDD1B1．同理可证EG∥平面BDD1B1，又∵EG⊂平面EFG，FG⊂平面EFG，EG∩FG＝G，∴平面EFG∥平面BDD1B1．9．（本小题满分12分）在四棱锥S－ABCD中，底面ABCD是正方形， M、N分别为AB、SC的中点，SA⊥底面ABCD．求证：//MN平面SAD；答案．证明（Ⅰ）： E 为SD 中点，连接AE ，NE ，因为M 、N 分别为AB 、SC 的中点，所以AM//EN ，AM=EN ，即四边形AMNE 是平行四边形，所以MN//AE ，可得//MN 平面SAD ；10. 一个多面体的直观图及三视图如图所示：(其中M 、N 分别是AF 、BC 的中点)．(1)求证：MN ∥平面CDEF ；(2)求多面体A －CDEF 的体积．答案 由三视图可知，该多面体是底面为直角三角形的直三棱柱ADE-BCF ，且AB =BC =BF=2，DE =CF=2，∴∠CBF =. (1)证明：取BF 的中点G ，连结MG 、NG ，由M 、N 分别为AF 、BC 的中点可得，NG ∥CF ，MG ∥EF ，∴平面MNG ∥平面CDEF ，又MN ⊂平面MNG ，∴MN ∥平面CDEF .(2)取DE 的中点H .∵AD =AE ，∴AH ⊥DE ， 在直三棱柱ADE-BCF 中，平面ADE ⊥平面CDEF ，平面A DE ∩平面CDEF=DE .∴AH ⊥平面CDEF.∴多面体A-CDEF 是以AH 为高，以矩形CDE F 为底面的棱锥，在△ADE 中，AH =. S 矩形CDEF =DE ·EF =4，∴棱锥A-CDEF 的体积为2222V=·S 矩形CDEF ·AH =×4×= 解法2：13218222323A CDEF AED BFC A BFCAED V V V S AB S AB ---=-=⨯-⨯⨯=⨯⨯⨯⨯=△△BFC 11如图，在直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB ∥CD ，且AB ＝2CD ，在棱AB 上是否存在一点F ，使平面C 1CF ∥平面ADD 1A 1？若存在，求点F 的位置；若不存在，请说明理由．答案 存在这样的点F ，使平面C 1CF ∥平面ADD 1A 1，此时点F 为AB的中点，证明如下：∵AB ∥CD ，AB ＝2CD ，∴AF ∥CD ，∴四边形AFCD 是平行四边形，∴AD ∥CF ，又AD ⊂平面ADD 1A 1，CF ⊄平面ADD 1A 1，∴CF ∥平面ADD 1A 1.又CC 1∥DD 1，CC 1⊄平面ADD 1A 1，DD 1⊂平面ADD 1A 1，∴CC 1∥平面ADD 1A 1，又CC 1、CF ⊂平面C 1CF ，CC 1∩CF ＝C ，∴平面C 1CF ∥平面ADD 1A 1.12. 如图，在底面是平行四边形的四棱锥P －ABCD 中，点E 在PD 上，且PE ∶ED ＝2∶1，在棱PC 上是否存在一点F ，使BF ∥平面AEC ？证明你的结论．答案 存在．证明如下：取棱PC 的中点F ，线段PE 的中点M ，连接BD .设BD ∩AC ＝O .连接BF ，MF ，BM ，OE .13132283∵PE ∶ED ＝2∶1，F 为PC 的中点，M 是PE 的中点，E 是MD的中点，∴MF ∥EC ，BM ∥OE .∵MF ⊄平面AEC ，CE ⊂平面AEC ，BM ⊄平面AEC ，OE ⊂平面AEC ，∴MF ∥平面AEC ，BM ∥平面AEC .∵MF ∩BM ＝M ，∴平面BMF ∥平面AEC .又BF ⊂平面BMF ，∴BF ∥平面AEC .13. (北京)如图，在四面体PABC 中，PC ⊥AB ，PA ⊥BC ，点D ，E ，F ，G 分别是棱AP ，AC ，BC ，PB 的中点．(1)求证：DE ∥平面BCP ；(2)求证：四边形DEFG 为矩形；(3)是否存在点Q ，到四面体PABC 六条棱的中点的距离相等？说明理由．答案 (1)证明：因为D ，E 分别为AP ，AC 的中点，所以DE ∥PC .又因为DE ⊄平面BCP ，PC ⊂平面BCP ，所以DE ∥平面BCP .(2)证明：因为D ，E ，F ，G 分别为AP ，AC ，BC ，PB 的中点所以DE ∥PC ∥FG ，DG ∥AB ∥EF ，所以四边形DEFG 为平行四边形．又因为PC ⊥AB ，所以DE ⊥DG ，所以四边形DEFG 为矩形．(3)存在点Q 满足条件，理由如下：连接DF ，EG ，设Q 为EG 的中点．由(2)知，DF ∩EG ＝Q ，且QD ＝QE ＝QF ＝QG ＝12EG .分别取PC ，AB 的中点M ，N ，连接ME ，EN ，NG ，MG ，MN .与(2)同理可证四边形MENG 为矩形，其对象线交点为EG 的中点Q ，且QM ＝QN ＝12EG ，所以EG 的中点Q 是满足条件的点．。

专题平行关系本讲义主要内容：第一部分：【知识回顾】1．直线与平面平行的判定(1直线与平面平行的定义：如果一条直线与一个平面没有公共点，我们就说这条直线与这个平面平行．(2直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．符号表示为：．注意：这个定理是证明直线与平面平行最常用的一个定理，也就是说欲证明一条直线与一个平面平行，一是说明这条直线不在这个平面内，二是要证明已知平面内有一条直线与已知直线平行．2．两个平面平行的判定(1两个平面平行的定义：两个平面没有公共点，则两个平面平行．(2平面与平面的平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行．符号表示为：．注意：这个定理的另外一种表达方式为“如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行，那么这两个平面平行”．(3平行于同一平面的两个平面互相平行．即．3．直线与平面平行的性质(1 直线与平面平行的性质定理：一条直线和一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．符号表示为：．注意：如果一条直线和一个平面平行，那么这条直线和平面内的无数条直线平行，但不能误解为“如果一条直线与一个平面平行，那么这条直线就和平面内的任意一条直线平行”．实际上，如果一条直线和一个平面平行，这条直线和平面内的直线平行或异面，有两种位置关系．(2直线与平面平行的性质：过平面内一点的直线与该平面平行的一条直线平行，则这条直线在这个平面内．符号表示为：若，点，且，则．4．平面与平面平行的性质(1如果两个平面平行，那么其中一个平面内的任意直线均平行与另一个平面．此结论可以作为定理用，可用来判定线面平行．(2两个平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．(3夹在两个平行平面间的平行线段相等．第二部分：【经典例题】例1 下面说法正确的是（）A. 直线平行于平面内的无数条直线，则∥；B. 若直线在平面外，则∥；C. 若直线∥，直线，则∥；D. 与两条异面直线都平行的平面有无穷多个例2 下列说法中正确的是（）①若一个平面内有两条直线都与另一个平面平行，则这两个平面平行；②若一个平面内有无数条直线都与另一个平面平行，则这两个平面平行；③若一个平面内任何一条直线都平行于另一个平面，则这两个平面平行；④若一个平面内的两条内的两条相交直线分别平行于另一个平面，则这两个平面平行。