第3章 多元数据图表示法
- 格式:ppt
- 大小:372.50 KB
- 文档页数:44



多元统计学课程设计一、课程目标知识目标:1. 学生能理解多元统计学的基本概念,掌握多元数据的描述性统计分析、推断性统计分析及相应的数学模型。
2. 学生能运用多元回归分析、主成分分析、因子分析等多元统计方法对实际问题进行数据分析和解释。
3. 学生能掌握多元统计软件的使用,对实际数据集进行有效处理和分析。
技能目标:1. 学生具备运用多元统计方法解决实际问题的能力,包括数据收集、整理、分析及结果解释。
2. 学生能够熟练运用统计软件进行多元数据分析,并撰写分析报告。
3. 学生能够通过小组合作,共同探讨解决复杂数据分析问题,提高团队协作能力。
情感态度价值观目标:1. 学生能够认识到多元统计学在科学研究、社会生活中的重要作用,培养对统计学学习的兴趣和热情。
2. 学生能够树立正确的数据观,遵循科学、严谨的态度对待数据分析,避免数据误用和滥用。
3. 学生能够在多元统计分析过程中,培养批判性思维,敢于质疑,勇于探索,形成独立思考和判断的能力。
课程性质:本课程为高年级本科或研究生统计学相关专业的核心课程,旨在帮助学生掌握多元统计方法,培养数据分析能力。
学生特点:学生具备一定的统计学基础,对统计方法有一定的了解,但可能缺乏实际应用经验。
教学要求:结合学生特点,注重理论与实践相结合,强调实际案例分析和操作练习,提高学生的实际应用能力。
同时,注重培养学生的团队协作、批判性思维和独立判断能力。
通过本课程的学习,使学生能够在实际工作中运用多元统计学知识解决复杂问题。
二、教学内容1. 多元数据的描述性统计分析:包括多元数据的收集、整理、图示方法,如散点图矩阵、相关系数等;多元分布特征,如均值、协方差、协方差矩阵等。
教材章节:第一章 多元数据的描述性分析2. 多元推断性统计分析:多元正态分布、多元回归分析、多元方差分析、判别分析等。
教材章节:第二章 多元推断性分析3. 多元统计方法的应用:主成分分析、因子分析、聚类分析、时间序列分析等。


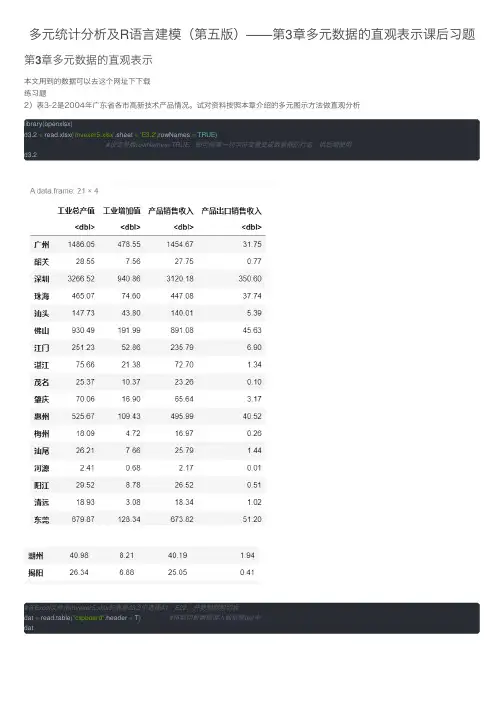
多元统计分析及R语⾔建模(第五版)——第3章多元数据的直观表⽰课后习题第3章多元数据的直观表⽰本⽂⽤到的数据可以去这个⽹址下下载练习题2)表3-2是2004年⼴东省各市⾼新技术产品情况。
试对资料按照本章介绍的多元图⽰⽅法做直观分析library(openxlsx)d3.2= read.xlsx('mvexer5.xlsx',sheet ='E3.2',rowNames =TRUE)#设定参数rowNames=TRUE,即可将第⼀列字符变量变成数据框的⾏名,供后期使⽤d3.2#在Excel⽂件中mvexer5.xlsx的表单d3.2中选择A1:E22,并复制到剪切板dat = read.table("clipboard",header = T)#将剪切板数据读⼊数据框dat中dat#数据框标记转换函数msa.X <-function(df){#将数据框第⼀列设置为数据框⾏名 X = df[,-1]#删除数据框df的第⼀列并赋给Xrownames(X)= df[,1]#将df的第⼀列值赋给X的⾏名X #返回新的数值数据框=return(X)}d3.2= msa.X(dat)d3.2barplot(apply(d3.2,2,mean))#按⾏作均值条形图barplot(apply(d3.2,1,mean),las =3)#修改横坐标标记barplot(apply(d3.2,2,mean))#按列作均值条图barplot(apply(d3.2,2,median))#按列作中位数条图barplot(apply(d3.2,2,median),col =1:8)#按列取⾊boxplot(d3.2)#按列作箱尾图boxplot(d3.2,horizontal = T)#箱尾图中图形按⽔平放置install.packages('aplpack',repos="https:///CRAN/") library(aplpack)faces(d3.2,ncol.plot =7)#按每⾏7个作脸谱图install.packages('TeachingDemos',repos="https:///CRAN/") library(TeachingDemos)faces2(d3.2,ncols =7)#作⿊⽩脸谱图install.packages('andrews',repos="https:///CRAN/") library(andrews)andrews(d3.2,clr =2,ymax =5)#⼀般调和曲线source('msaR.R')msa.andrews(d3.2)#改进调和曲线msa.andrews(d3.2[c(1,3,5,7,9,11,13,15,17),])#作第1,3,5,7,9,11,13,15,17个观测的调和曲线图。




第一章绪论§1.1 什么是多元统计分析在工业、农业、医学、气象、环境以及经济、管理等诸多领域中,常常需要同时观测多个指标。
例如,要衡量一个地区的经济发展,需要观测的指标有:总产值、利润、效益、劳动生产率、万元生产值能耗、固定资产、流动资金周转率、物价、信贷、税收等等;要了解一种岩石,需观测或化验的指标也很多,如:颜色、硬度、含碳量、含硫量等等;要了解一个国家经济发展的类型也需观测很多指标,如:人均国民收入,人均工农业产值、人均消费水平等等。
在医学诊断中,要判断某人是有病还是无病,也需要做多项指标的体检,如:血压、心脏脉搏跳动的次数、白血球、体温等等。
总之,在科研、生产和日常生活中,受多种指标共同作用和影响的现象是大量存在的,举不胜举。
上述指标,在数学上通常称为变量,由于每次观测的指标值是不能预先确定的,因此每个指标可用随机变量来表示。
如何同时对多个随机变量的观测数据进行有效的统计分析和研究呢?一种做法是把多个随机变量分开分析,一次处理一个去分析研究;另一种做法是同时进行分析研究。
显然前者做法有时是有效的,但一般来说,由于变量多,避免不了变量之间有相关性,如果分开处理不仅会丢失很多信息,往往也不容易取得好的研究结果。
而后一种做法通常可以用多元统计分析方法来解决,通过对多个随机变量观测数据的分析,来研究变量之间的相互关系以及揭示这些变量内在的变化规律,如果说一元统计分析是研究一个随机变量统计规律的学科,那么多元统计分析则是研究多个随机变量之间相互依赖关系以及内在统计规律性的一门统计学科,同时,利用多元分析中不同的方法还可以对研究对象进行分类(如指标分类或样品分类)和简化(如把相互依赖的变量变成独立的或降低复杂集合的维数等等)。
在当前科技和经济迅速发展的今天,在国民经济许多领域中特别对社会经济现象的分析,只停留在定性分析上往往是不够的。
为提高科学性、可靠性,通常需要定性与定量分析相结合。
实践证明,多元分析是实现做定量分析的有效工具。

第四章 多元数据图表示法图形有助于对所研究数据的直观了解,如果能把一些多元数据直接显示在平面图上,便可从图形一目了然地看出多元数据之间的关系,当只有一、二维数据时,可以使用通常的直角坐标系在平面上点图。
当有三维数据时,虽然可以在三维坐标系里点图,但已很不方便,而当维数大于3时,用通常的方法已不能点图。
但在许多实际问题中,多元数据的维数都大于3。
自20世纪70年代以来多元数据的图表示法一直是人们所关注的问题,人们想了不少办法,这些方法大体上分为两类:一类是使高维空间的点与平面上的某种图形对应,这种图形能反映高维数据的某些特点或数据间的某些关系;另一类是在尽可能多地保留原数据信息的原则下进行降维,若能使数据维数降至2或1,则可在平面上点图。
后者可用后面介绍的主成分法、因子分析法等去解决。
本章仅对前者介绍四种图表示法,更多的这类方法可在有关专著中找到。
设变量数为p ,观测次数为n ,第α次观测值记为n n x x x X ap a a a ,,,1,),,,(21 ='=α次观测数据组成的矩阵为p n ij x X ⨯=)(。
例 考察北京、上海、陕西、甘肃四个省市人均生活消费支出情况,选取以下五项指标,具体数据如下表(摘自1996年中国统计年鉴):此例变量个数5=p ,观测次数4=n 。
§4.1 轮廓图作图步骤为:(1)作平面坐标系,横坐标取p 个点表示p 个变量。
(2)对给定的一次观测值,在p 个点上的纵坐标(即高度)和它对应的变量取值成正比。
(3)连接p 个高度的顶点得一折线,则一次观测值的轮廓为一条多角折线形。
n 次观测值可画出n 条折线,构成轮廓图。
下面画出四条折线为北京、上海、陕西、甘肃五项指标的数据即四个省市五项指标的轮廓。
由轮廓图可以看出:北京、上海的居民生活消费较高且相似。
陕西、甘肃生活消费较低且相似。
如果考察的样品较多,画折线时图形中可能出现重复点多,不便于区分哪个样品对应哪条折线,这时最好多用几种颜色或长短虚实等标志来画出折线。
数据统计模型多变量统计分析主要用于数据分类和综合评价。
综合评价是区划和规划的基础。
从人类认识的角度来看有精确的和模糊的两种类型,因为绝大多数地理现象难以用精确的定量关系划分和表示,因此模糊的模型更为实用,结果也往往更接近实际,模糊评价一般经过四个过程:(1)评价因子的选择与简化;(2)多因子重要性指标(权重)的确定;(3)因子内各类别对评价目标的隶属度确定;(4)选用某种方法进行多因子综合。
1.主成分分析地理问题往往涉及大量相互关联的自然和社会要素,众多的要素常常给模型的构造带来很大困难,为使用户易于理解和解决现有存储容量不足的问题,有必要减少某些数据而保留最必要的信息。
主成分分析是通过数理统计分析,求得各要素间线性关系的实质上有意义的表达式,将众多要素的信息压缩表达为若干具有代表性的合成变量,这就克服了变量选择时的冗余和相关,然后选择信息最丰富的少数因子进行各种聚类分析,构造应用模型。
设有n个样本,p个变量。
将原始数据转换成一组新的特征值——主成分,主成分是原变量的线性组合且具有正交特征。
即将x1,x2,…,xp综合成m(m<p)个指标zl ,z2,…,zm,即z1=l11*x1+l12*x2+...+l1p*xpz2=l21*x1+l22*x2+...+l2p*xp..................zm=lm1*x1+lm2*x2+...+lmp*xp这样决定的综合指标z1,z2,…,zm分别称做原指标的第一,第二,…,第m主成分,且z1,z2,…,zm在总方差中占的比例依次递减。
而实际工作中常挑选前几个方差比例最大的主成分,从而简化指标间的关系,抓住了主要矛盾。
从几何上看,找主成分的问题,就是找多维空间中椭球体的主轴问题,从数学上容易得到它们是x1,x2,…,xp的相关矩阵中m个较大特征值所对应的特征向量,通常用雅可比(Jaobi)法计算特征值和特征向量。
主成分分析这一数据分析技术是把数据减少到易于管理的程度,也是将复杂数据变成简单类别便于存储和管理的有力工具。