水文随机分析第二章110914
- 格式:ppt
- 大小:624.01 KB
- 文档页数:86



基于小波分析方法的水文随机模拟摘要:本文对小波分析进行了简要介绍,包括小波分析的发展历史、分析方法、应用领域以及发展现状,在此基础之上介绍了小波分析在水文随机模拟中的应用,最后,对小波分析方法在今后水文水资源领域中的应用进行了展望。
总而言之,小波分析在水文预报、水文随机模拟、水文多时间尺度分析、水文时间序列变化特性分析等很多方面具有很大的研究价值和发展前景。
关键词:小波分析;不确定性;水文随机模拟1引言由于水文系统较为复杂,受制于气候和人为活动等多因素的影响,所以目前没有一个准确的数学物理方程能够描述并求解这一过程,而传统的随机模型结构简单、参数少,能描述水文序列的主要统计特性。
但通过数理统计方法得到的参数描述水文过程过于粗糙,信息量少。
小波分析是一种多分辨率分析方法,能充分展示水文序列的精细结构,挖掘更多的信息,可揭示水文系统的多时间尺度特性,较方便识别出水文时间序列中隐含的主要周期。
通过小波消噪技术可把高频成分有效分离,从两方面分别研究其水文序列特性。
鉴此,本文提出了基于小波分析的随机水文模型。
1.1小波分析的分析方法及发展历史小波分析或小波转换是指用有限长或快速衰减的、称为母小波的振荡波形来表示信号。
该波形被缩放和平移以匹配输入的信号。
小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的,通过物理的直观和信号处理的实际需要经验的建立了反演公式,当时未能得到数学家的认可。
随后,1986年著名数学家Y.Meyer偶然构造出一个真正的小波基,小波分析自此才开始蓬勃发展起来。
小波变换与Fourier变换、窗口Fourier变换相比,这是一个时间和频率的局域变换,因而能有效的从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,解决了Fourier变换不能解决的许多困难问题,因此,小波变化被誉为“数学显微镜”,它是调和分析发展史上里程碑式的进展。
1.2小波分析的应用领域及发展现状事实上小波分析的应用领域十分广泛,包括数学领域的许多学科、信号分析、图像处理、理论物理、医学成像与诊断、地震勘探数据处理、大型机械的故障诊断等方面;例如,在数学方面,它已用于数值分析、构造快速数值方法、曲线曲面构造、微分方程求解、控制论等;在信号分析方面的滤波、去噪声、压缩、传递等;在图像处理方面的图像压缩、分类、识别与诊断,去污等;除此之外,小波分析在工程技术等方面也有着至关重要的应用,包括计算机视觉、计算机图形学、曲线设计、湍流、远程宇宙的研究与生物医学方面等。




随机水文学以水文过程为研究对象,以随机过程理论和时间序列分析技术为手段的一门学科随机模拟法的特点1随机水文模型全面表征水文现象统计变化的特征,不同模型表征水文现象变化特性的重点有所差异。
2、由随机模型能模拟出大量的水文序列。
3、大量的模拟序列表征着未来水文现象可能出现的各种情况。
当随机函数随时间t 连续地取有限区间内的值时,称此随机函数为随机过程。
是否相依:相关和独立随机过程 按变量多少:单变量和多变量随机过程 参数是否随时间改变:平稳和非平稳随机过程据分布函数的不同性质:独立,平稳,独立增量,马尔柯夫过程非平稳随机过程一个随机过程X(t),若对任意n 与实数k ,X(t)的n 维分布函数满足关系式称X(t)为平稳随机过程(简称平稳过程),否则被称为非平稳过程。
特征:平稳随机过程的n 维分布函数不因所选开始时刻的改变而不同;平稳随机过程的统计特性不随时间原点(起点)的选取不同而变化。
各态历经性:在一定条件下,平稳随机过程的一个相当长的样本资料(一个现实)可以用来分析计算平稳随机过程的统计特性。
这样的随机过程被称为具备各态历经性或遍历性,并称为各态历经过程判断:年径流或年降水过程在人类活动影响很小时可以认为是平稳随机过程。
月降水过程和日降水过程是非平稳的。
马尔柯夫过程如果随机过程X(t)满足 则随机过程X(t)被称为马尔柯夫过程(马氏过程)。
性质1 马尔柯夫过程在时刻tn+k 所处的状态只与其在时刻tn 所处的状态有关,而与其在tn 时刻之前所处的状态无关2马尔柯夫过程的统计特性完全由它的初始分布和转移概率确定。
水文序列的组成;确定成分(周期性、非周期性)随机性成分(平稳的(相依的和独立的)非平稳的)自相关分析中:判断时间序列是否独立的方法。
① 计算样本自相关系数rk 并绘制样本自相关图。
② 计算rk 的容许限(选择显著性水平α=5%),即 之中:取“+”时为容许上限;取“-”时为容许下限③ 推断。
随机方法在水文学中的应用一、概述水文现象随时间变化的过程称为水文过程或水文序列,水文现象是一种自然现象,具有确定性变化规律和随机性变化规律。
这些确定性和随机性的变化规律通过水文过程可以较为清晰的展示出来。
水文过程中的确定性变化规律突出表现在过程中有年、日的变化。
如日、旬、月径流过程,明显存在以年为周期的变化;逐时气温和蒸发量过程存在一日为周期的变化。
这是由于影响水文过程的确定性因素——气候因素存在以年为周期的变化和某些气象因素存在以日为周期的变化之故。
水文过程在表现出确定性变化规律的同时,更多的表现出随机性变化特征。
如每一年的的月平均流量过程不相同,形状和数量相差较大;水文过程内前后期要素之间好似变化无序,时大时小,但它们之间存在相依关系,2月平均流量与1月平均流量相依,后一年与前一年径流量相依。
随机性变化特征是水文过程形成与演变中众多影响因素所致。
这些影响的无限复杂性和多样性,致使水文过程不断发生着各种各样情形,表现出随机变化特征。
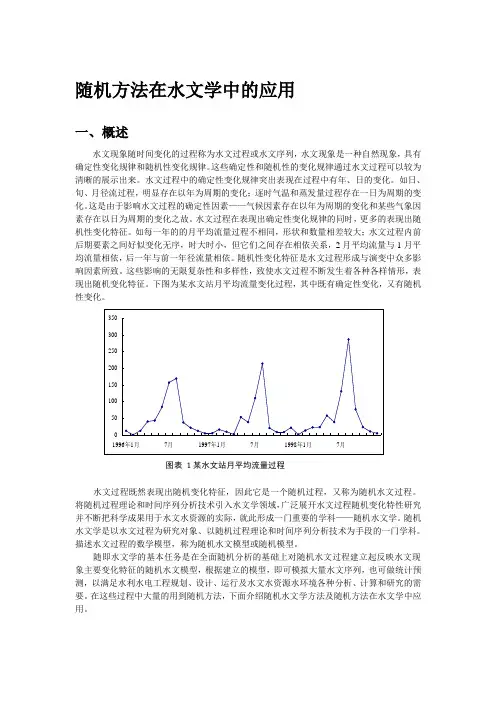
下图为某水文站月平均流量变化过程,其中既有确定性变化,又有随机性变化。
350300250200150100501996年1月7月1997年1月7月1998年1月7月图表1某水文站月平均流量过程水文过程既然表现出随机变化特征,因此它是一个随机过程,又称为随机水文过程。
将随机过程理论和时间序列分析技术引入水文学领域,广泛展开水文过程随机变化特性研究并不断把科学成果用于水文水资源的实际,就此形成一门重要的学科——随机水文学。
随机水文学是以水文过程为研究对象、以随机过程理论和时间序列分析技术为手段的一门学科。
描述水文过程的数学模型,称为随机水文模型或随机模型。
随即水文学的基本任务是在全面随机分析的基础上对随机水文过程建立起反映水文现象主要变化特征的随机水文模型,根据建立的模型,即可模拟大量水文序列,也可做统计预测,以满足水利水电工程规划、设计、运行及水文水资源水环境各种分析、计算和研究的需要。



第1篇一、实验目的本次实验旨在通过分析水文数据,了解水文频率分析的基本原理和方法,掌握如何利用现有水文资料进行水文变量的频率计算,并学会绘制频率曲线。
通过实验,加深对水文频率分析在实际工程中的应用的认识。
二、实验原理水文频率分析是水文研究中的重要方法,它通过对水文变量的统计特性进行分析,研究水文变量设计值与出现频率(或重现期)之间的定量关系。
水文频率分析主要包括以下步骤:1. 收集和整理水文资料,建立样本系列;2. 选择合适的频率曲线线型,估计其统计参数;3. 根据所绘制的频率曲线,分析水文变量的设计值与出现频率(或重现期)之间的关系;4. 利用频率曲线进行水文预报和设计洪水计算。
三、实验内容1. 收集实验数据:本次实验选用某地区20年降雨量数据作为样本系列。
2. 数据处理:将降雨量数据进行整理,去除异常值,确保数据的准确性。
3. 频率计算:采用皮尔逊Ⅲ型分布进行频率计算,计算各频率对应的降雨量值。
4. 绘制频率曲线:根据计算结果,绘制皮尔逊Ⅲ型频率曲线。
5. 分析结果:分析频率曲线,研究降雨量设计值与出现频率之间的关系。
四、实验步骤1. 数据准备:收集某地区20年降雨量数据,包括各年降雨量值。
2. 数据处理:对数据进行整理,去除异常值,确保数据的准确性。
3. 频率计算:(1)计算样本系列的总数N;(2)计算频率序列,公式为:f = n / N,其中n为出现次数,N为样本总数;(3)根据频率序列,计算皮尔逊Ⅲ型分布的参数,包括均值μ、离差系数Cv、偏态系数Cs。
4. 绘制频率曲线:(1)根据计算得到的参数,绘制皮尔逊Ⅲ型频率曲线;(2)在频率曲线上标出各频率对应的降雨量值。
5. 结果分析:(1)分析频率曲线,观察降雨量设计值与出现频率之间的关系;(2)根据频率曲线,预测未来降雨量可能出现的情况。
五、实验结果与分析1. 数据处理:经过数据整理,得到20年降雨量样本系列,共计N=20。
2. 频率计算:计算得到皮尔逊Ⅲ型分布的参数为μ=XXX,Cv=XXX,Cs=XXX。