当前位置：文档之家 › 最小二乘法程序说明及流程图

最小二乘法程序说明及流程图

  • 格式：pdf
  • 大小：526.08 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

最小二乘法过程

最小二乘法过程

最小二乘法过程嘿，朋友们！今天咱来聊聊最小二乘法过程。

这玩意儿啊，就像是一个神奇的魔法，能帮我们解决好多问题呢！想象一下，你有一堆数据点，就像一群调皮的小精灵，东一个西一个的。

那怎么才能找到一条线或者一个模型，能最好地把这些小精灵都串起来呢？这时候最小二乘法就闪亮登场啦！它的第一步呢，就是先确定我们要找的那个模型的形式。

比如说，是一条直线呢，还是一个曲线呀。

这就好比给小精灵们找一个合适的家。

然后呢，就开始计算啦！计算每个数据点到这个模型的距离。

这距离可不是随便算算的哦，就好像你要衡量你和朋友之间的亲密程度一样，得仔细着呢！接着，把这些距离都加起来，得到一个总的误差值。

这误差值就像是一个总成绩，能反映出这个模型和数据的契合程度。

可别小瞧了这个误差值哦，它可重要啦！我们的目标就是要让这个误差值尽可能地小。

就好像你挑衣服，肯定要挑最合身的那件呀！为了让误差值变小，我们就得不断地调整模型的参数。

这就像给小精灵们的家不断地装修，直到它们都舒舒服服地待在里面。

在这个过程中，可能会遇到一些困难。

有时候数据点很调皮，不太听话，让你找的模型也变得怪怪的。

但别灰心呀，我们要像勇士一样，坚持不懈地和它们战斗！而且哦，最小二乘法可不是只能用在一条直线上呢。

它可以用在各种各样的模型上，只要你能想得到！是不是很厉害？你想想看，生活中有多少地方能用到最小二乘法呀。

比如说预测天气，分析股票走势，这些都离不开它呢！所以啊，大家可别小瞧了这个最小二乘法过程。

它虽然看起来有点复杂，但只要你用心去理解，就会发现它就像一个贴心的小助手，能帮你解决好多难题呢！好好去探索它吧，说不定你会发现更多的惊喜哦！怎么样，是不是对最小二乘法过程有了更深的认识啦？哈哈！。

matlab最小二乘法

matlab最小二乘法

4. 设某物理量Y与X 满足关系式Y=aX2+bX+c，实验获得一批数据如下表，试辨识模型参数a，b和c 。

（50分）X 1.01 2.03 3.02 4.015 6.027.038.049.0310Y9.6 4.1 1.30.40.050.10.7 1.8 3.89.0单，最后给出结果及分析。

(1) 问题描述：由题意知，这是一个已知模型为Y=aX2+bX+c，给出了10组实验输入输出数据，要求对模型参数a，b，c进行辨识。

这里对该模型参数辨识采用递推最小二乘法。

(2) 参数估计原理对该模型参数辨识采用递推最小二乘法，即RLS（recurisive least square），它是一种能够对模型参数进行在线实时估计的辨识方法。

其基本思想可以概括为：新的估计值=旧的估计值+修正项下面将批处理最小二乘法改写为递推形式即递推最小二乘参数估计的计算方法。

批处理最小二乘估计为，设k时刻的批处理最小二乘估计为：令K时刻的最小二乘估计可以表示为==；式中，因为要推导出P(k)和K(k)的递推方程，因此这里介绍一下矩阵求逆引理：设A、（A+BC）和（I+）均为非奇异方阵，则通过运用矩阵求逆引理，把复杂的矩阵求逆转化为标量求倒数，大大减小了计算量。

与间的递推关系。

最终得到递推最小二乘参数递推估计公式如下：（3)程序流程图 (如右图1所示）递推最小二乘法（RLS）步骤如下：已知：、和d。

Step 1 ：设置初值和P(0)，输入初始数据；Step2 ：采样当前输出y(k)、和输入u(k)Step3 ：利用上面式计算、和；Step4 ：kk+1，返回step2，继续循环。

图1 程序流程图(4) Matlab仿真程序、输出参数估计值、参数估计变化轨迹图像、结果分析仿真程序如下：X=[1.01 2.03 3.02 4.01 5 6.02 7.03 8.04 9.03 10]; Y=[9.6 4.1 1.3 0.4 0.05 0.1 0.7 1.8 3.8 9.0];%实验输入数据、实验输出数据syms a b c % 定义待辨识参数theta=[a;b;c]; %theta包含待辨识参数a，b，ctheta1=zeros(3,1); %对象参数初始化P=10^6*eye(3) %构造初始P阵for k=1:10 %仿真步长范围1到10phi=[X(k)*X(k);X(k);1];%y=aX*X+bX+c=phi'*theta%theta=[a；b；c]；phi=[X(k)*X(k);X(k);1]K=P*phi/(1+phi'*P*phi); %递推最小二乘法K阵的递推公式theta=theta1+K*(Y(k)-phi'*theta1); %theta的递推公式P=(eye(3)-K*phi')*P; %递推最小二乘法P阵的递推公式theta1=theta; %theta的最终估计向量theta2(:,k)=theta; %theta估计向量矩阵化，目的是为了%下面的plot仿真图像输出endtheta1 %输出参数估计值plot([1:10],theta2) %输出参数逐步递推估计的轨迹图像xlabel('k'); %设置横坐标为步长kylabel('参数估计a，b，c'); %纵坐标为估计参数a，b，c legend('a','b','c'); %标示相应曲线对应的参数axis([1 10 -10 20]); %设置坐标轴范围P =1000000 0 00 1000000 00 0 1000000输出参数估计值、参数估计变化轨迹图像：theta1 =0.4575-5.073413.3711图 2 参数估计逐步变化轨迹图像结果分析：通过matlab仿真可知，由递推最小二乘法辨识到的参数为：a=0.4575；b=-5.0734；c=13.3711所以Y=0.4575-5.0734X+13.3711 。

第3章4节最小二乘法(课堂PPT)

第3章4节最小二乘法(课堂PPT)
§4 曲线拟合的最小二乘法
1 最小二乘法及其计算
在函数的最佳平方逼近中 f (x) C如[a果, b],
f (x)
只在一组离散点集 {xi , i 0,1,上给, m定}，这就是科 学实验中经常见到的实验数据 {(xi , yi ),i 0的,1, , m} 曲线拟合.
1
问题为利用 yi f (xi ),i 求0出,1一,个, m函,数 y S * (x) 与所给数据{(xi , yi ),i 0,拟1,合. , m}
7
Ga d ,
其中 a (a0 , a1, , an )T , d (d0 , d1, , dn )T ,
(0 ,0 ) (0 ,1)
G
(1
,
0
)
(1 , 1 )
(0 ,n )
(1
,
n
)
.
n (n ,0 ) (n ,1) (n ,n )
(k , j )a j dk (k 0,1, , n).
6
若记
m
( j ,k ) ( xi ) j ( xi )k ( xi ), i0 m
( f ,k ) (xi ) f (xi )k (xi ) dk i0 (k 0,1, , n).
上式可改写为
n
(k , j )a j dk
j 0
(k 0,1, , n).
这个方程称为法方程，可写成矩阵形式
要使j法0 方程有唯一解， 就要求矩阵 非奇G异，
而 0 (x),1(x),在 ,n上(x线) 性[无a,关b]不能推出
矩阵 G非奇异，必须加上另外的条件.
8
例如
（0 x) sin x,（1 x) sin 2x,显然（0 x)，（1 x)线性无关。 取X {x0,...,x4} {0, ,2 ,3 ,4}, （0 x j ) （1 x j ) 0; j 0,...,4

最小二乘法的基本步骤

最小二乘法的基本步骤

最小二乘法的基本步骤最小二乘法是一种常见的数据处理方法，主要用于寻找最优解。

在实际应用中，最小二乘法广泛应用于数据拟合、回归分析、参数估计等方面。

本文将介绍最小二乘法的基本步骤及其应用，以帮助读者更好地掌握该方法。

一、最小二乘法的基本原理最小二乘法是利用已知数据的信息，通过求解估计值和实际值之间的差的平方和的最小值，来寻找最优解的方法。

在这个过程中，我们通常需要确定一个或多个参数，使我们得到的拟合结果与实际值的误差最小。

这就是最小二乘法的基本原理。

二、最小二乘法的基本步骤最小二乘法包括以下的基本步骤：1. 确定模型首先，在最小二乘法中，我们需要确定需要拟合的模型的形式。

例如，在线性回归中，我们选择y = kx + b来描述因变量y和自变量x之间的关系，其中k和b就是需要估计的参数。

在确定估计模型后，我们就可以开始对数据进行拟合。

2. 确定误差函数在确定模型后，我们需要确定一个误差函数来衡量估计值与实际值之间的差异。

通常，误差函数可选择为平方误差函数，其计算公式为：E = Σ(yi - f(xi))^2（i=1,2,…,n）其中，yi为实际值，f(xi)为估计值，n为样本数。

3. 求解参数求解参数是最小二乘法的核心步骤。

在这一步中，我们需要通过最小化误差函数来求解参数。

对于线性回归问题，我们可以通过解析解或迭代优化方法求解。

在解析解法中，我们可以直接给出参数的求解公式，例如在二元线性回归中，参数的求解公式为：k = ((nΣxy) - (Σx)(Σy)) / ((nΣx^2) - (Σx)^2)b = (Σy - kΣx) / n其中，x和y分别为自变量和因变量的观测值，Σ表示求和符号，n为样本数。

4. 拟合数据在求解出参数后，我们可以通过估计模型得到拟合的结果，并将其与实际值进行比较。

如果误差较小，我们就可以认为模型的拟合结果是较为准确的。

三、最小二乘法的应用最小二乘法在实际应用中具有广泛的应用。

第十节+最小二乘法演示文稿

第十节+最小二乘法演示文稿
y f (t) 0.3036t 27.125
为衡量上述经验公式的优劣, 计算各点偏差如下:
机动 目录 上页 下页 返回 结束
0 1 2 3 4 56 7 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8
27.125 26.518 25.911 25.303
26.821 26.214 25.607 25.000
第十节+最小二乘法演示文稿
优选第十节+最小二乘法
特别, 当数据点分布近似一条直线时, 问题为确定 a, b
使 y ax b 满足:
n
y
M (a,b) ( yk axk b)2 min
k 0
M
令
a M
b
o
x
n
xk b
得
n
k 0
xk a
k 0
解此线性方程组 即得 a, b
机动 目录 上页 下页 返回 结束
其均方误差为
1 7
M
0.135
所求经验公式为
机动 目录 上页 下页 返回 结束
ln y m ln k (书中取的是常用对数) 令 Y ln y , X , a m, b ln k
Y a X b (线性函数)
机动 目录 上页 下页 返回 结束
因此 a , b 应满足法方程组:
8
k lyk
k 1
经计算得
解得:
y 78.57e0.104
大致在一条直线上, 故可设经验公式为
y axb
列表计算:
o
t
机动 目录 上页 下页 返回 结束
i ti 00 77
28
ti2
yi
yiti

最小二乘法

最小二乘法

其中：������������ = ������������ − ������������观测
周期误差的计算
• 测距仪轴向与标准钢卷尺平行，多次移动 棱镜，分别读取测距仪和钢卷尺读数 ������������ , ������0������
• 根据������������ = ������������ − ������0������ 可获得一组 ������������ , ������������ • 根据相位������������ =
最小二乘法
什么是参数估计？
• 最小二乘法是一种参数估计原则 • 参数估计是指从带有误差的观测值中提取我们感兴趣 • 典型的参数估计： 通过测量多条标准基线求得测距仪的加、乘常数 通过三角测量求得被测点的平面坐标 距离交会，求得被测点的坐标
欧式距离最短
• 假设某观测方程为： ������11 ������12 ������1 ������ ������2 = ������21 ������22 ������1 2 ������31 ������32 ������3 • 可写为： ������11 ������12 ������1 ������2 = ������1 ������21 + ������2 ������22 ������31 ������32 ������3
如果我们只知道A有一辆百万级豪车，而不了解 其他任何相关信息，我们更愿意相信，A的年收 入为100万，而不会倾向于相信他的年收入为20 万
• 因此，当我们只有一个观测值x的时候，我 们更愿意相信，真值就等于x，因为此时概 率密度最大
当我们进行了多次观测，得到多个观测值 （ ������1 , ������2 , ⋯ ）由于每次观测相互独立，因此 有联合概率分布（似然函数）：

第十八讲全面最小二乘法


Y
V H ，其中σ 1 ≥ σ 2 ≥ ≥ σ r > 0 。又设 0 m×n σ 1 Vn (s < r ) 则 U σs 0 m×n
z∈C rankz = s F
min X − Y= X −Z F m×n
H
首先来考虑 F-范数。设 Pm×n = UQV ,U、V 分别为 m 阶、n 阶酉
r
r
n
1 i= r +1 j =
∑ ∑ tij
m
n
2
对任意 Z 矩阵而言，各 tij 之间完全独立，则 X − Z 于零的。但是 rank ( Z )= s < r 。故 X − Z
F
F
是可能等
不可能为零。详细论证
F
可知 tij = 0(i ≠ j ), tii = 0(i > s ), tii = σ i (i = 1, 2,, s ) 时， X − Z 小 下 面 仅 考 虑 在 实 际 应 用 中 非 常 常 见 的 一 种 情 况 ： A ∈ Cn
14
= min ∆ F =
显然满足
rank ( C +∆ ) =n
rank ( C +∆ )< n +1
min
C − (C + ∆ )
F
min
= C− ( C + ∆ ) σ n+1
0 H ∆ =U 0 V σ + n 1 O
15
定理 2： 设σ n +1 为 C 的 n-k+1 重奇异值，且 vk +1 , vk + 2 , vn +1 相应的为

最小二乘法fortran应用。ppt


要求： 要求：
实验数据共200个，要求从文件（文件名： 实验数据共200个，要求从文件（文件名： Ps.in) Ps.in)读入，拟合参数，计算出饱和压与实 验数据间的误差，找出最大误差和平均误 差，并以文件（文件名：Ps.out）形式输出。 差，并以文件（文件名：Ps.out）形式输出。 温度、饱和压及相应中间变量都采取双精 度实数。
A Ax = A b
T T
可以证明如果如果A 可以证明如果如果A是列满秩的，则该方程存在 唯一解，且使得
ϕ(x1, x2 ,⋅⋅⋅, xn )
取得最小值，该解就称为超定方程组的最小二乘解。
例 1：用最小二乘法求下列超定
方程组的近似解
2x1 − x2 =1 8x + 4x = 0 2 1 2x1 + x2 =1 7x − x = 8 1 2 4x1 = 3
最小二乘法
计算地球化学
主要内容
1. 基本原理 2. 程序编写 3. 应用举例
1. 基本原理
一般m*n线性方程组 一般m*n线性方程组(m>n) 线性方程组(m>n)
a11x1 + a12 x2 +⋯+ a1n xn = b 1 a x + a x +⋯+ a x = b 21 1 22 2 2n n 2 ⋯ ⋯ ⋯ am1x1 + am2 x2 +⋯+ amn xn = bm
第一列为温度，单位为 ； 第一列为温度，单位为K； 第二列为实验的饱和压，单位为bar. 第二列为实验的饱和压，单位为
65 65.5 66 66.5 67 67.5 68 68.5 69 69.5 70 70.5 71 71.5 72 72.5 73 73.5 74 74.5

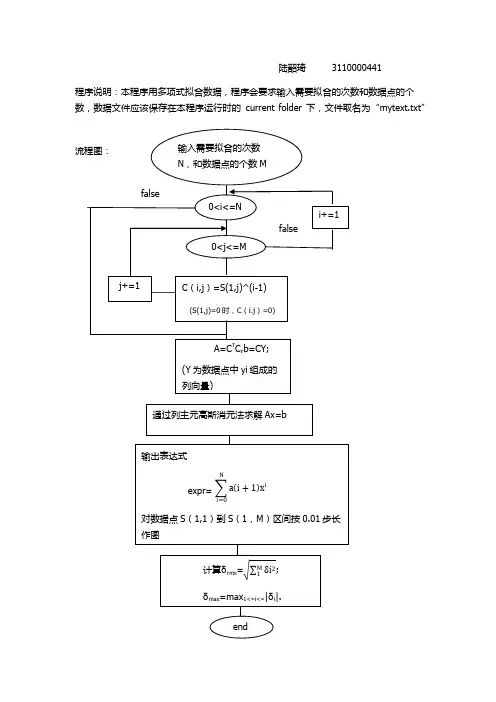
最小二乘法程序说明及流程图

陆韶琦 3110000441程序说明：本程序用多项式拟合数据，程序会要求输入需要拟合的次数和数据点的个数，数据文件应该保存在本程序运行时的current folder下，文件取名为“mytext.txt”程序代码：%多项式最小二乘法拟合数据N=input('please put in how many times the power will you overfit:'); M=input('how many couples of statistics are there in the table:');%读入数据文件f=fopen('mytxt.txt','r');S=fscanf(f,'%g',[M 2]);fclose(f);S=S';%显示数据文件，确保正确输入disp('S(x,y)=');disp(S);%建立多项式系数法方程组中间矩阵C=zeros(N+1,M);for i=1:N+1for j=1:Mif S(1,j)==0C(i,j)=0;elseC(i,j)=S(1,j).^(i-1);endendend%建立法方程组A=C*C';Y=zeros(M,1);for i=1:MY(i,1)=S(2,i);endb=C*Y;%用列主元高斯消元法接法方程组A=[A,b];for i=1:N+1max=abs(A(i,i));for j=i+1:N+1if abs(A(j,i))>maxflag=j;max=A(j,i);endendfor k=i:N+2B=A(flag,k);A(flag,k)=A(i,k);A(i,k)=B;endfor kh=i+1:N+1m=-A(kh,i)/A(i,i);A(kh,i)=0;for kl=i+1:N+2A(kh,kl)=A(kh,kl)+m*A(i,kl);endendendX=zeros(N+1,1);for i=N+1:-1:1for j=i-1:-1:1m=-A(j,i)/A(i,i);A(j,N+2)=A(j,N+2)+m*A(i,N+2);endX(i,1)=A(i,N+2)/A(i,i);enddisp(X);%根据系数求得待定曲线syms x;expr=0;for i=1:N+1expr=expr+X(i,1)*x.^(i-1);end%输出得到的曲线表达式disp(expr);%计算偏差bias=zeros(M,1);for j=1:Mfor i=1:N+1bias(j,1)=bias(j,1)+X(i,1)*S(1,j)^(i-1); endbias(j,1)=bias(j,1)-S(2,j);end%寻找最大偏差max=abs(bias(1,1));flag=1;for i=2:Mif abs(bias(i,1))>maxflag=i;max=abs(bias(i,1));endenddisp('the maximun absoulute value is:'); disp(max);%计算均方误差rms=0;for i=1:Mrms=rms+bias(i,1)^2;endrms=sqrt(rms);disp('the square bias is:');disp(rms);%制图a=S(1,1):0.01:S(1,M);y=subs(expr,x,a);plot(a,y);hold on;grid on;for i=1:Mx=S(1,i);y=S(2,i);plot(x,y,'*');hold on;end运行结果：表达式中分式难以化简，但在表达式前给出了次幂前的四位有效数字的系数。

最小二乘法-PPT课件

请用最小二乘法求出这两个变量之间的线性回归方程.
解 根据上表数据，可以计算出：x 4.5, y 25.5 其他数据如下表
-
19
i 1 2 3 4 5 6 7 8 合计
，
xi
yi
1
1
2
4
3
9
4
16
5
25
6
36
7
49
8
64
36
204
x2 i
xi yi
1
1
4
8
9
27
16
64
25
125
36
216
49
343
d bxi yi a b2 1
方法二:
xi,abix
yi a bxi 2 0 -
yabx
x
4
显然方法二能有效地表示点A与直线y=a+bx的距离， 而且比方法一计算更方便，所以我们用它来表示二者 之间的接近程度.
-
5
思考2.怎样刻画多个点与直线的接近程度？ 提示：
例如有5个样本点，其坐标分别为（x1，y1），（x2， y2），（x3，y3），（x4，y4），（x5，y5），与直 线y=a+bx的接近程度：
使上式达到最小值的直线y=a+bx就是所要求的直线， 这种方法称为最小二乘法.
-
7
思考3：怎样使 [y1 (a bx1)]2 [yn (a bxn )]2 达到最小值？
先来讨论3个样本点的情况
…………………①
-
8
3 a 2 - 2 （ a y - b x ) ( y 1 - b x 1 ) 2 ( y 2 - b x 2 ) 2 ( y 3 - b x 3 ) 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

陆韶琦 3110000441
程序说明：本程序用多项式拟合数据，程序会要求输入需要拟合的次数和数据点的个数，数据文件应该保存在本程序运行时的current folder下，文件取名为“mytext.txt”
程序代码：
%多项式最小二乘法拟合数据
N=input('please put in how many times the power will you overfit:'); M=input('how many couples of statistics are there in the table:');
%读入数据文件
f=fopen('mytxt.txt','r');
S=fscanf(f,'%g',[M 2]);
fclose(f);
S=S';
%显示数据文件，确保正确输入
disp('S(x,y)=');
disp(S);
%建立多项式系数法方程组中间矩阵
C=zeros(N+1,M);
for i=1:N+1
for j=1:M
if S(1,j)==0
C(i,j)=0;
else
C(i,j)=S(1,j).^(i-1);
end
end
end
%建立法方程组
A=C*C';
Y=zeros(M,1);
for i=1:M
Y(i,1)=S(2,i);
end
b=C*Y;
%用列主元高斯消元法接法方程组
A=[A,b];
for i=1:N+1
max=abs(A(i,i));
for j=i+1:N+1
if abs(A(j,i))>max
flag=j;
max=A(j,i);
end
end
for k=i:N+2
B=A(flag,k);
A(flag,k)=A(i,k);
A(i,k)=B;
end
for kh=i+1:N+1
m=-A(kh,i)/A(i,i);
A(kh,i)=0;
for kl=i+1:N+2
A(kh,kl)=A(kh,kl)+m*A(i,kl);
end
end
end
X=zeros(N+1,1);
for i=N+1:-1:1
for j=i-1:-1:1
m=-A(j,i)/A(i,i);
A(j,N+2)=A(j,N+2)+m*A(i,N+2);
end
X(i,1)=A(i,N+2)/A(i,i);
end
disp(X);
%根据系数求得待定曲线
syms x;
expr=0;
for i=1:N+1
expr=expr+X(i,1)*x.^(i-1);
end
%输出得到的曲线表达式
disp(expr);
%计算偏差
bias=zeros(M,1);
for j=1:M
for i=1:N+1
bias(j,1)=bias(j,1)+X(i,1)*S(1,j)^(i-1); end
bias(j,1)=bias(j,1)-S(2,j);
end
%寻找最大偏差
max=abs(bias(1,1));
flag=1;
for i=2:M
if abs(bias(i,1))>max
flag=i;
max=abs(bias(i,1));
end
end
disp('the maximun absoulute value is:'); disp(max);
%计算均方误差
rms=0;
for i=1:M
rms=rms+bias(i,1)^2;
end
rms=sqrt(rms);
disp('the square bias is:');disp(rms);
%制图
a=S(1,1):0.01:S(1,M);
y=subs(expr,x,a);
plot(a,y);
hold on;
grid on;
for i=1:M
x=S(1,i);
y=S(2,i);
plot(x,y,'*');
hold on;
end
运行结果：
表达式中分式难以化
简，但在表达式前给出
了次幂前的四位有效数
字的系数。