《流体力学》课后习题答案 PPT

第一章1、什么是流体？流体的三大特性？流体是能流动的物质。

从其力学特征看，流体是一种受任何微小剪切力都能连续变形的物质。

流体的三大特性：易流动性，可压缩性，粘性2、什么是流体的连续介质假设？对于流体质点而言，我们假定他们之间没有空隙，在空间连续分布，所以将流体视为由无数连续分布的流体质点所组成的连续介质，这就是流体的连续介质假设。

连续介质假设是流体力学的基本假设之一，我们依据了这个假设，才能把微观问题转化为宏观问题来处理。

3、什么是不可压缩流体？流体的膨胀系数和压缩系数全为零的流体叫不可压缩流体。

4、体积压缩系数、温度膨胀系数如何定义？体积压缩系数：表示当温度保持不变时，单位压强增量所引起的体积变化率。

温度膨胀系数：表示当压强不变时，单位温升所引起的流体体积的变化率。

5、什么是流体的黏性？流体的粘性是指流体质点运动发生相对滑移时产生切向阻力的性质。

6、什么是牛顿内摩擦定律？作用在流层上的切向力与速度梯度成正比，其比例系数为流体的动力粘度7、动力黏度与压强、温度有什么关系？普通压强对流体的黏度几乎没有影响，可以认为，流体的黏度只随温度变化。

温度对流体粘度的影响很大。

液体的黏度随着温度的上升而减小，气体的黏度随着温度的上升而增大。

之所以会出现这种情况，是因为构成它们黏性的机理不同。

液体分子间的吸引力是构成液体黏性的主要因素；构成气体黏性的主要因素是气体分子做随机运动时，在不同流速的流层间所进行的动量交换。

8、什么是理想流体？黏性为零的流体称为理想流体9、如何计算肥皂泡内的压强？设肥皂泡外压强为大气压强P0,表面张力系数为σ。

表面张力引起的附加压力成为毛细压力，曲面的凹面高于凸面的压强差为ΔP=2σR（R为球面的曲率半径）。

对肥皂泡，因为存在两个液体表面，故泡内高于泡外的压强差为ΔP=4σR.所以肥皂泡内压强:P1=P0+4σR1、什么是质量力、表面力，二者有何关系？质量力：指作用在流体内部每一个质点上的力，它的大小与流体的质量成正比。

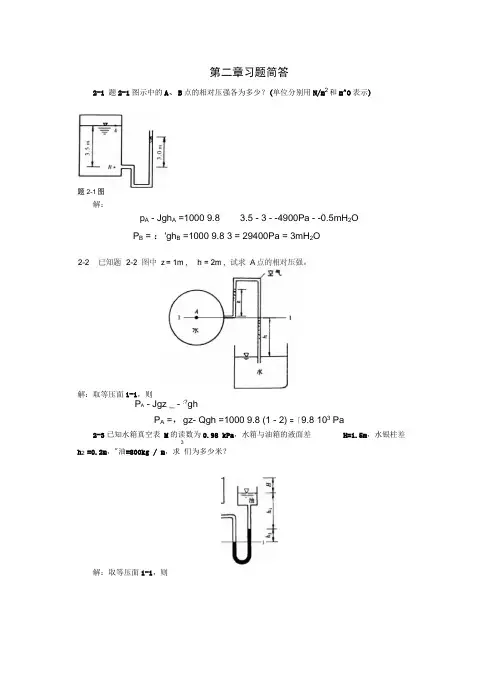
第二章习题简答2-1 题2-1图示中的A、B点的相对压强各为多少？(单位分别用N/m2和m^O表示)题2-1图解：p A - Jgh A =1000 9.8 3.5 - 3 - -4900Pa - -0.5mH2OP B = ：'gh B =1000 9.8 3 = 29400Pa = 3mH2O解：取等压面1-1，则P A - Jgz _ - :?ghP A =，gz- Qgh =1000 9.8 (1 - 2) =「9.8 103 Pa 2-3已知水箱真空表M的读数为0.98 kPa，水箱与油箱的液面差H=1.5m，水银柱差3h2=0.2m，"油=800kg / m，求们为多少米？解：取等压面1-1，则P a -PEg H h i h 2 A P aT 油ghi‘HggdPHggh 2 + P — Pg(H +h2 ) h 1亍「油g133280 0.2 980-9800 1.5 0.2 - (1000 — 800^9.8二 5.6m2-4为了精确测定密度为 匸的液体中A 、B 两点的微小压差，特设计图示微压计。

测定 时的各液面差如图示。

试求J 与r 的关系及同一高程上A 、B 两点的压差。

如图取等压面1-1，r'gb gb-a （对于a 段空气产生的压力忽略不计）得 戸_ P （b -a ）P A - 'gH = P B - "gH：p = P A _ P B = ：gH _「'gH =■2-5 图示密闭容器，压力表的示值为4900N/m ，压力表中心比 A 点高0.4m , A 点在水面下1.5m,求水面压强。

解：P 0:?gH 二 P ?ghP 0 二 P ：gh - ：gH =4900 9800 （0.4 -1.5） =「5880Pa2-6图为倾斜水管上测定压差的装置，已知z =20cm ，压差计液面之差 h =12cm ，求当（1）时=920kg/m 3的油时；（2）J 为空气时;A 、B 两点的压差分别为多少？.口解: 取等压面2-2，则a?gH b y解：(1 )取等压面1-1P A—^huPB — PgZ — HghP B -P A」i gh 勺Z- ?gh= 920 9.8 0.12 9800 (0.2 - 0.12) = 1865.92Pa = 0.19mH2O(2)同题(1)可得P A - pgh = P B - PgZP B ~■P A gZ -・"gh二9800 (0.2 - 0.12) = 784Pa 二0.08mH 2O2-7已知倾斜微压计的倾角:-30，测得丨=0.5m，容器中液面至测压管口高度h = 0.1m ,求压力P。

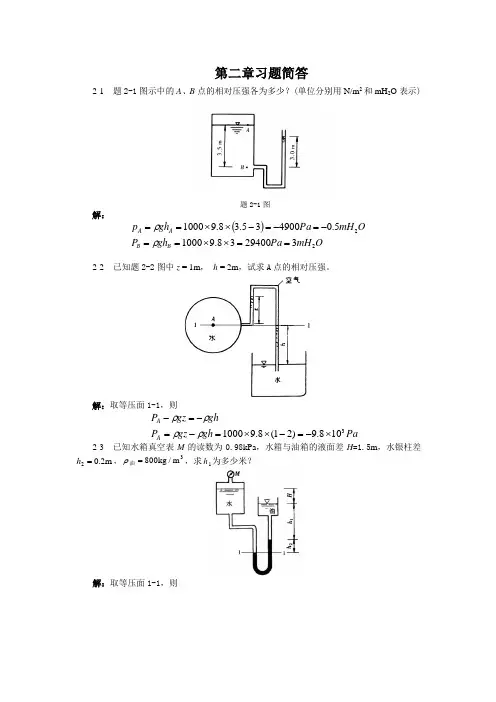
第二章习题简答2-1 题2-1图示中的A 、B 点的相对压强各为多少？(单位分别用N/m 2和mH 2O 表示)题2-1图解：()OmH Pa gh P O mH Pa gh p B B A A 2232940038.910005.0490035.38.91000==⨯⨯==-=-=-⨯⨯==ρρ2-2 已知题2-2图中z = 1m ， h = 2m ，试求A 点的相对压强。

解：取等压面1-1，则Pagh gz P ghgz P A A 3108.9)21(8.91000⨯-=-⨯⨯=-=-=-ρρρρ2-3 已知水箱真空表M 的读数为0.98kPa ，水箱与油箱的液面差H =1.5m ，水银柱差m 2.02=h ，3m /kg 800=油ρ，求1h 为多少米？解：取等压面1-1，则()()()()()mgh H g P gh h gh gh P h h H g P P Hg Hg a a 6.58.980010002.05.198009802.01332802212121=⨯-+⨯-+⨯=-+-+=++=+++-油油ρρρρρρρ2-4 为了精确测定密度为ρ的液体中A 、B 两点的微小压差，特设计图示微压计。

测定时的各液面差如图示。

试求ρ与ρ'的关系及同一高程上A 、B 两点的压差。

解：如图取等压面1-1，以3-3为基准面，则()a b g gb -=ρρ' （对于a 段空气产生的压力忽略不计）得()⎪⎭⎫ ⎝⎛-=-=b a ba b 1'ρρρ取等压面2-2，则gHbagH gH p p p gHp gH p B A B A ρρρρρ=-=-=∆-=-''2-5 图示密闭容器，压力表的示值为4900N/m 2，压力表中心比A 点高0.4m ，A 点在水面下1.5m,求水面压强。

解：PagH gh P P ghP gH P 5880)5.14.0(9800490000-=-⨯+=-+=+=+ρρρρ2-6 图为倾斜水管上测定压差的装置，已知cm 20=z ，压差计液面之差cm 12=h ，求当（1）31kg/m 920=ρ的油时;（2）1ρ为空气时;A 、B 两点的压差分别为多少？解：（1）取等压面1-1OmH Pa ghgZ gh P P gh gZ P gh P A B B A 21119.092.1865)12.02.0(980012.08.9920==-⨯+⨯⨯=-+=---=-ρρρρρρ（2）同题（1）可得OmH Pa ghgZ P P gZ P gh P A B B A 208.0784)12.02.0(9800==-⨯=-=--=-ρρρρ2-7 已知倾斜微压计的倾角︒=30α，测得0.5m =l ，容器中液面至测压管口高度m 1.0=h ,求压力p 。

第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3，求它的密度ρ。

解：由g γρ=得，3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3，运动黏度ν=0.893×10-6m 2/s ，求它的动力黏度μ。

解：ρμ=v 得，3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中，它们之间的距离为0.5mm ，可动板若以 0.25m/s 的速度移动，为了维持这个速度需要单位面积上的作用力为2N/m 2，求这两块平板间流体的动力黏度μ。

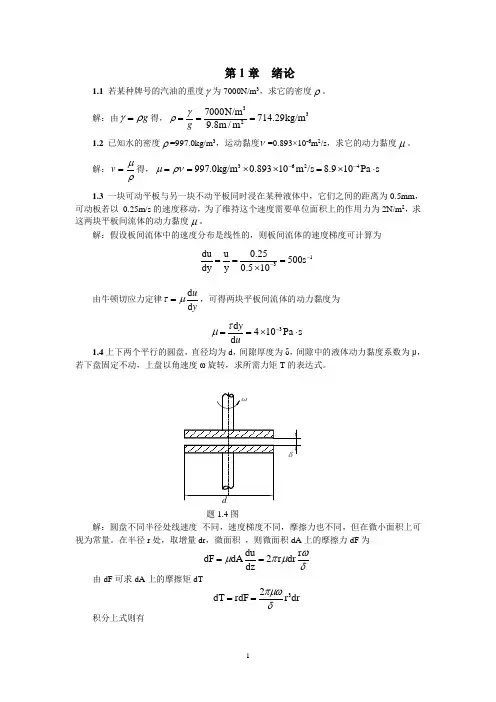
解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=，可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩T 的表达式。

题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。

在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。

（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1.5图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时，221510N/m τ-=⨯；y=2cm 时，222 2.510N/m τ-=⨯；y=4cm 时，30τ= 1.6 某流体在圆筒形容器中。

《流体力学》习题与答案周立强中南大学机电工程学院液压研究所第1章流体力学的基本概念1-1.是非题(正确的打“√”，错误的打“”)1. 理想流体就是不考虑粘滞性的、实际不存在的，理想化的流体。

（√）2. 在连续介质假设的条件下，液体中各种物理量的变化是连续的。

（√ ）3. 粘滞性是引起流体运动能量损失的根本原因。

（√ ）4. 牛顿内摩擦定律适用于所有的流体。

（）5. 牛顿内摩擦定律只适用于管道中的层流。

（）6. 有旋运动就是流体作圆周运动。

（）7. 温度升高时，空气的粘度减小。

（）8. 流体力学中用欧拉法研究每个质点的轨迹。

（）9. 平衡流体不能抵抗剪切力。

（√ ）10. 静止流体不显示粘性。

（√ ）11. 速度梯度实质上是流体的粘性。

（√ ）12. 流体运动的速度梯度是剪切变形角速度。

（√ ）13. 恒定流一定是均匀流，层流也一定是均匀流。

（）14. 牛顿内摩擦定律中，粘度系数m和v均与压力和温度有关。

（）15. 迹线与流线分别是Lagrange和Euler几何描述；它们是对同一事物的不同说法；因此迹线就是流线，流线就是迹线。

（）16. 如果流体的线变形速度θ=θx+θy+θz=0,则流体为不可压缩流体。

（√ ）17. 如果流体的角变形速度ω=ωx+ωy+ωz=0,则流体为无旋流动。

（√ ）18. 流体的表面力不仅与作用的表面积的外力有关，而且还与作用面积的大小、体积和密度有关。

（）19. 对于平衡流体，其表面力就是压强。

（√ ）20. 边界层就是流体的自由表明和容器壁的接触面。

（）1-2已知作用在单位质量物体上的体积力分布为：，物体的密度，坐标量度单位为m；其中，，，；，，。

试求：如图1-2所示区域的体积力、、各为多少？题1-2图解：答：各体积力为：、、1-3作用在物体上的单位质量力分布为：，物体的密度为，如图1-3所示，其中，，，；。

试求：作用在图示区域内的质量总力？解：题图1-3答：各质量力为：、、，总质量力。

第三章习题简答3-1 已知流体流动的速度分布为22y x u x -= ，xy u y 2-=，求通过1,1==y x 的一条流线。

解：由流线微分方程yx u dyu dx =得dy u dx u x y =则有 dy y x xydx )(222-=-两边积分可得C y y x yx +-=-3322即0623=+-C y x y将x=1,y=1代入上式，可得C=5，则 流线方程为05623=+-y x y3-3 已知流体的速度分布为⎭⎬⎫==-=-=tx x u ty y u y x 00εωεω（ω>0，0ε>0）试求流线方程，并画流线图。

解：由流线微分方程yx u dyu dx =得dy u dx u x y =则有 tydy txdx 00εε-=两边积分可得C y x +-=22流线方程为C y x =+223-5 以平均速度s m v /5.1=流入直径为D=2cm 的排孔管中的液体，全部经8个直径d=1mm 的排孔流出，假定每孔出流速度依次降低2%，试求第一孔与第八孔的出流速度各为多少？题3-5图解：由题意得：v 2=v 1(1-2%)，v 3=v 1(1-2%)2，…，v 8=v 1(1-2%)7 根据质量守恒定律可得282322212832144444dv d v d v d v D v Q Q Q Q Q πππππ⋅+⋅⋅⋅+⋅+⋅+⋅=⋅+⋅⋅⋅+++=sm d vD v v d v v v v d D v /4.80)98.01(001.002.002.05.1)98.01()98.01(98.01)98.01(4)(448228221812832122=-⨯⨯⨯=--⋅=∴--⋅=+⋅⋅⋅+++⋅=⋅πππ则 v 8=v 1(1-2%)7=80.4×(1-2%)7=69.8m/s3-6 油从铅直圆管向下流出。

管直径cm d 101=，管口处的速度为s m v /4.11=，试求管口处下方H=1.5m 处的速度和油柱直径。

习题【1】1-1 解：已知：120t =℃，1395p kPa '=，250t =℃ 120273293T K =+=，250273323T K =+= 据p RT ρ=，有：11p RT ρ'=，22p RT ρ'= 得：2211p T p T '='，则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解：受到的质量力有两个，一个是重力，一个是惯性力。

重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-3 解：已知：V=10m 3，50T ∆=℃，0.0005V α=℃-1根据1V V V Tα∆=⋅∆，得：30.000510VVV Tα∆=⋅⋅∆=⨯⨯1-4 解：已知：419.806710Pa p '=⨯，52 5.884010Pa p '=⨯，150t =℃，278t =℃得：1127350273323T t K=+=+=，G ＝mg自由落体： 加速度a ＝g2227378273351T t K =+=+=根据mRTp V=，有：111mRT p V '=，222mRT p V '=得：421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯，即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解：已知：40mm δ=，0.7Pa s μ=⋅，a =60mm ，u =15m/s ，h =10mm根据牛顿内摩擦力定律：uT Ayμ∆=∆ 设平板宽度为b ，则平板面积0.06A a b b =⋅=上表面单位宽度受到的内摩擦力：1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ，方向水平向左下表面单位宽度受到的内摩擦力： 2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ，方向水平向左平板单位宽度上受到的阻力：12216384N τττ=+=+=，方向水平向左。