二重积分的换元法

用二重积分换元法证明卷积公式卷积公式是数学中的一种运算，用于描述两个函数之间的关系。

在信号处理、图像处理和数值计算等领域中经常用到卷积公式。

本文将使用二重积分换元法来证明卷积公式。

首先，我们先了解一下二重积分换元法的基本概念。

二重积分换元法是利用变量代换的方法，将原二重积分中的变量替换为新的变量，从而简化被积函数的形式，使得计算更加容易。

设有两个实值函数 f(x) 和 g(x)，定义它们的卷积函数 (f*g)(x)如下：(f*g)(x) = ∫[-∞,∞] f(x-t)g(t) dt其中，积分运算从负无穷到正无穷。

要证明卷积公式，我们需要证明以下等式成立：∫[-∞,∞] (f*g)(x) dx = ∫[-∞,∞] f(x)g(x) dx为了方便计算，我们先对卷积公式做一个变形。

首先，我们令u = x-t，于是 t = x-u。

然后对变量 u 求导，得到 du = -dt。

将上述变换代入卷积公式中，得到：(f*g)(x) = ∫[-∞,∞] f(u)g(x-u) (-du)将上式中的积分限进行一下变换。

当 t = -∞ 时，有 u = x-(-∞)= ∞；当 t = ∞ 时，有 u = x-∞ = -∞。

所以，积分限可以变换为∞ 和 -∞。

(f*g)(x) = ∫[∞,-∞] f(u)g(x-u) (-du)现在我们开始证明卷积公式。

根据卷积公式的右边，我们有：∫[-∞,∞] f(x)g(x) dx根据二重积分换元法，我们令 v = x-u，于是 x = v+u。

对变量v 求导，得到 dv = dx。

将上述变换代入卷积公式中，得到：∫[-∞,∞] f(x)g(x) dx = ∫[-∞,∞] f(v+u)g(v) dv接下来，我们将积分限进行一下变换。

当 x = -∞ 时，有 v = -∞-u = -∞；当x = ∞ 时，有v = ∞-u = ∞。

所以，积分限可以变换为 -∞ 和∞。

∫[-∞,∞] f(x)g(x) dx = ∫[-∞,∞] f(v+u)g(v) dv我们使用换元法，并令 u = x-t，v = x，则有 x = u+v。

二重积分雅可比式换元《二重积分雅可比式换元》一、什么是二重积分雅可比式换元二重积分雅可比式换元，即多元函数的二重积分求解中，针对函数两个积分变量的换元法，也称为换根法。

在使用该方法时，先把一个高维函数通过定义域划分为若干个连续小段，利用秩一矩阵中的二重积分，用最简单的单元求解函数的积分，或者以比较好的速度求解函数的积分，从而实现对函数的求解。

二、求解积分的好处换元法是一种求解二重积分的很好的方法，求解积分的好处是可以让不同的函数的变量的求解更加简单，而且可以有效减少计算的复杂性，提高计算的效率。

换元法在求解二重积分类函数时，可以有效减少机器计算量，提高求解速度。

同时，换元法可以尽可能利用当前机器的计算速度，实现尽可能快的求解效率。

三、实际求解步骤1、将目标函数写成一般形式；2、把所有变量范围边界都明确定义；3、将要求求解的函数根据坐标系的变换变换为等价的形式；4、建立从原函数到等价函数的转换关系；5、将第四步中建立的关系引入到原函数中，得到换元后的函数；6、求出新函数的积分，建立积分关系；7、将求解的积分结果和关系引入到原函数中，得到换元前的积分结果。

四、注意事项在换元的过程中，由于函数的结构以及函数表达式的具体情况而有所不同，因此，每一步都要慎重考虑函数的结构。

因为二重积分的步骤是繁琐的，过程中存在很多的实际问题，要根据具体函数情况进行实际操作，把握住步骤，正确处理才能求得准确答案。

五、总结二重积分雅可比式换元是一种多元函数求解的方法，通过把一个高维函数分割为若干个连续小段，利用二重积分的换元法，用最简单的单元求解函数的积分，或者以比较好的速度求解函数的积分，从而实现多元函数的求解。

换元法可以有效减少机器计算量，提高求解速度，便于求解。

但在进行换元计算过程中，要根据具体函数情况进行实际操作，才能求得准确答案.。

二重积分换元法雅可比行列式 -回复雅可比行列式是一个非常有用的工具，在计算二重积分时经常会用到。

换元法就是在给定的积分上进行一定的代数变换，将其转换为另一个形式，以便更容易地计算。

二重积分换元法雅可比行列式就是其中的一种方法。

首先，我们来看一下什么是二重积分。

二重积分就是对二维空间中的某个区域内的函数进行积分。

具体来说，如果我们有一个函数f(x,y)，那么它在一个区域D上的二重积分可以表示为：∬D f(x,y) dxdy其中，dxdy表示对x和y的积分。

在进行二重积分时，我们经常会遇到需要进行换元的情况。

这时，我们可以采用雅可比行列式的方法，将原来的积分变为新的积分，以便更加方便地进行计算。

接下来，我们来看一下何为雅可比行列式。

雅可比行列式是一个矩阵的行列式，记作：J = |Δx/Δu Δx/Δv||Δy/Δu Δy/Δv|其中，Δx/Δu和Δx/Δv分别表示在u和v方向上，x的变化量。

同理，Δy/Δu和Δy/Δv分别表示在u和v方向上，y的变化量。

通过雅可比行列式，我们可以将原来的积分变为新的积分：∬R f(x(u,v), y(u,v)) |J| dudv其中，R为u和v所在的区域。

我们可以通过对R内的u和v进行积分来计算新的积分。

需要注意的是，积分范围需要通过原来的变换来进行计算。

以一个简单的例子来说明如何使用雅可比行列式。

假设我们需要计算二重积分：其中，D为一个以原点为圆心，半径为1的圆盘。

我们采用极坐标变换来进行转换。

假设x = rcosθ，y = rsinθ，那么雅可比行列式为：J = |co sθ sinθ||-rsinθ rcosθ|求出J的行列式为r，那么原积分就变成了：∬R (r^2cos^2θ + r^2sin^2θ) r dθdr其中，R为r的范围为0到1，θ的范围为0到2π。

我们可以对r和θ进行分别积分，最终得到积分结果为π/2。

第三讲 二重积分的换元法回顾上节内容直角坐标系下二重积分的计算本节教学内容1.二重积分的换元积分公式；2.极坐标系下二重积分的计算。

【教学目的与要求】1.掌握二重积分的换元积分公式；2.熟练掌握极坐标系下二重积分的计算。

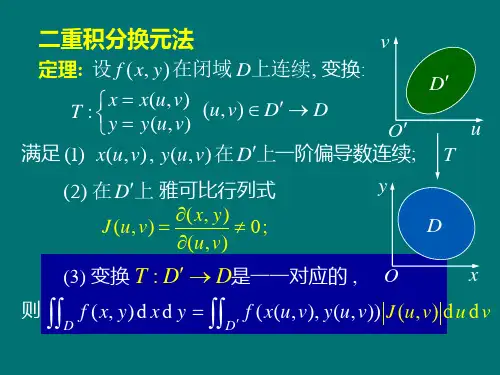
【教学重点与难点】换元公式和极坐标系下二重积分的计算§7.3 二重积分的换元法一、二重积分的换元公式在某些情况下，利用直角坐标计算二重积分很不方便，而利用其它坐标如极坐标等可能会很容易求得结果，这就需要对直角坐标系下的二重积分进行变量代换．关于二重积分的变量代换，有如下定理．定理 设),(y x f 在D 上连续，),(),,(v u y y v u x x ==在平面uOv 上的某区域*D 上具有连续的一阶偏导数且雅可比.)Jacobi,( C.G.J 行列式0≠''''=vu vu y y x x J ， *D 对应于xOy 平面上的区域D ，则⎰⎰Df dudv J v u y v u x f dxdy y x D )],(),,([),(*⎰⎰=． （１）公式（１）称为二重积分的换元公式．二、极坐标系下二重积分的计算极坐标与直角坐标的关系为θθsin cos r y r x ==⎪⎩⎪⎨⎧ ． （２）其中，r 是极径，θ是极角．由极坐标的特殊性，以坐标原点O 向外发散的区域D ，如圆、圆环、扇形等，用极坐标表示是比较方便的，而且如果二重积分的被积函数也能够用极坐标简单表示（比如被积函数为)(22y x f +等），则利用极坐标，计算更方便．利用公式（１）可给出极坐标下二重积分的计算公式．由式（２）θθy y x x J rr''''=r r r r =+=-=)s i n (c o s c o ss i n s i n c o s 22θθθθθθ． 即r r J ==，从而极坐标系下二重积分的计算公式为⎰⎰⎰⎰=*)sin ,cos (),(D Drdrd r r f dxdy y x f θθθ． （３）例１ 计算积分dxdy e Dy x⎰⎰--22，D 是圆心在原点，半径为R 的闭圆．解 这里D ={}222),(R y x y x ≤+，在极坐标系下}20,0),{(*πθθ≤≤≤≤=R r r D ，且222r y x =+，于是dxdy e Dy x⎰⎰--22为)1(212222*220R Rr r R D r e e dr red rdrd e-----=⎥⎦⎤⎢⎣⎡-==⎰⎰⎰⎰ππθθπ．例２ 计算二重积分⎰⎰Ddxdy x 2，D 是由圆122=+y x 及422=+y x 所围成的环形区域.解 环区域D 在极坐标系中可表示为}20,21),{(*πθθ≤≤≤≤=r r D ，所以⎰⎰⎰⎰=DDrdrd r dxdy x θθ222cos =⎰⎰πθθ203212cos dr r d π415=. 例3 计算⎰⎰--Ddxdy y x a 2224，D 是半圆周22x ax y -=及x 轴所围成的闭区域（图7-9）．解 在极坐标系中，域D 可表示为}20,cos 20),{(*πθθθ≤≤≤≤=a r r D ，于是⎰⎰--Ddxdy y x a 2224⎰⎰-=*224D rdrd r a θ图7－10图7－9⎰⎰-=20cos 20224πθθa rdr r a d=⎰-=-20333)322(38)sin 1(38ππθθa d a ．例4 计算⎰⎰Dxydxdy ，其中D {}x y x y y x 21,0),(22≤+≤>=．解 区域D 见图7－10（阴影部分），在极坐标下*D {}0,cos 21),(πθθθ≤≤≤≤=r r ,于是⎰⎰Dxydxdy ⎰⎰⋅⋅=*sin cos D rdrd r r θθθ⎰⎰=3cos 213sin cos πθθθθdr r dθθθθπd r cos 214041sin cos 3⎥⎦⎤⎢⎣⎡=⎰θθθθπd )41cos 4(sin cos 04⎰-=图7—11 θθθπcos )cos 41cos 4(305d --=⎰169cos 64cos 81062=⎥⎦⎤⎢⎣⎡-=πθθ． 例5 计算⎰⎰Ddxdy ，其中D 为椭圆12222=+by a x 所围成的闭区域．解 作广义极坐标变换⎩⎨⎧==.sin ,cos θθbr y ar x 其中πθ20,0,0,0≤≤≥>>r b a ，在此代换下，与D 相应的区域{}πθθ20,10),(*≤≤≤≤=r r D雅可比行列式 θθy y x x J rr ''''=abr br b ar a =-=θθθθcos sin sin cos ，从而⎰⎰Ddxdy ab abrdr d drd J D πθθπ===⎰⎰⎰⎰120*．由二重积分的几何意义，ab π即为椭圆12222=+by a x 所围成的面积．例6 计算⎰⎰Ddxdy y x 22，其中D 是由曲线2,1==xy xy 和直线xy x y 4,==所围成的第一象限的区域（图7－11）．解 该积分利用直角坐标或极坐标比较麻烦，根据积分区域，作变换.,v x y u xy ==⎩⎨⎧ 即 ⎪⎩⎪⎨⎧==.,v u x uv y 可得v J 21=． 于是⎰⎰D dxdy y x 22dv v du u dudv v u D ⎰⎰⎰⎰==41212212121*[]2ln 37ln 312141213=⎥⎦⎤⎢⎣⎡=v u ．三、广义二重积分前面我们讨论的都是有界区域D 上有界函数的二重积分．若将积分区域推广到无界区域，或者被积函数有无穷型间断点，则有广义二重积分．其定义与计算与一元函数的广义积分类似． 定义 设函数),(y x f z =在xOy 平面上的无界区域D 上连续．在D 上任取一有界区域1D ，则),(y x f z =在1D 上的二重积分存在，若此积分当D D →1时的极限存在，则称该极限为无界区域D 上的广义二重积分，即⎰⎰⎰⎰→=11),(lim ),(D DD Dd y x f d y x f σσ．可以证明，若),(y x f z =在D 上不变号，则广义二重积分的值与D D →1的方式无关．例7 证明概率积分π=⎰∞+∞--dx e x 2．证明 考虑广义二重积分σd e Dy x⎰⎰--22，其中D 是xOy 平面．取1D 为圆心在原点，半径为R 的圆，当D D →1时，+∞→R ．根据例1求得的结果，σd e Dy x ⎰⎰--22=DD →1limππ=-=-+∞→--⎰⎰)1(lim 2122R R D y x e dxdy e ．另一方面，令{}R y R x y x D ≤≤=,),(2（图7－12）， 则当D D →2时，+∞→R ．dxdy e dxdy e D y x DD Dy x⎰⎰⎰⎰--→--==222222limπ图7－12⎥⎦⎤⎢⎣⎡=⎰⎰----+∞→R R R R y x R dy e dx e 22lim2222lim ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎰⎰∞+∞----+∞→dx e dx e x R R x R ，于是 π=⎰∞+∞--dx e x 2．若函数),(y x f z =在xOy 平面上的有界区域D 上有无穷间断点，或在D 内的某一条曲线上有无穷间断点，此时，可取D D ⊂1，而),(y x f 在1D 上连续，定义广义二重积分⎰⎰⎰⎰→=11),(lim),(D DD Dd y x f d y x f σσ．例8 计算广义积分,22⎰⎰+Dyx d σ其中，{}222),(R y x y x D ≤+=．解 对于被积函数来说，点)0,0(为其无穷间断点．设R a <<0，则在环型区域1D {}2222),(R y x a y x ≤+≤=上，被积函数连续，且当D D →1时，0→a ，于是⎰⎰⎰⎰⎰⎰→→=+=+R aa D DD Drdr rd yx d yx d 22022221lim lim11πθσσR a R a ππ2)(2lim 0=-=→．小结1.二重积分的换元积分公式；2.极坐标系下二重积分的计算。