当前位置：文档之家 › 第3章信号源0109版-46页PPT资料

第3章信号源0109版-46页PPT资料

  • 格式：ppt
  • 大小：1.22 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

信号系统课件第3章

信号系统课件第3章

0
T 2
T
0
T 2
T
(a) 直流+基波
(b) 直流+基波“+”三次谐波
0
T 2
T
0
T 2
T
(c) 直流+基波“+”三次谐波“+”
五次谐波
(d) 直流+基波“+”三次谐
波“+”五次谐波“+”七次 谐波
由图可见，当它包含的谐波分量越多时， 波形越接近于原来的方波信号，其均方误差越 小。还可看出，频率较低的谐波，其振幅较大，

n 1

An e j n e jnt
及 n n ，则上式可写为
将上式第三项中的n用-n代换，并考虑到 A n An
A0 1 f (t ) 2 2 A0 1 2 2

A e
n n 1 j n n

j n
e
jnt
1 A n e j n e jnt 2 n1
f (t )
c g (t )
i i i 1

cr

t2
t1
f (t ) g r (t ) dt
t2 t1

g r 2 (t )dt
1 kr
t2

t2
t1
f (t ) g r (t ) dt
其中 此时的均方误差为
kr

t1
g r 2 (t ) dt
1 2 t2 t1
3.1.2
周期信号的分解
2 T
设有周期信号f(t),它的周期是T,角频率 2 F
，它可分解为：
a0 f (t ) a1 cos t a2 cos 2t an cos nt (3.2-1) 2 b1 sin t b2 sin 2t bn sin nt

信号源原理讲解

信号源原理讲解
信号源是：一种能够产生顾客所需信号旳仪器就是信号源。
第二：信号源旳各构成部分
VCO
频率 锁定 反馈
参照 源
ALC调 制器
调制 信号
信号 调制
RF 输出
检 波
第三：基频发生电路讲解
周期信号波形旳发生：
振荡器
反馈振荡器电路
• 起振条件：AF>1,而且，整个环路旳总相移应等
于n×360°
• 平衡条件： AF=1,而且，整个环路旳总相移应等
信号源原理讲解
• 1.信号源旳概念？ • 2.信号源旳各构成部分。 • 3.基频发生电路部分。 • 4.频率控制部分。 • 5.幅度控制电路（ALC）。 • 6.调制电路部分。
信号是运载消息旳工具，是消息旳载体。从广义上讲，它包 括光信号、声信号和电信号等。例如，古代人利用点燃烽 火台而产生旳滚滚狼烟，向远方军队传递敌人入侵旳消息， 这属于光信号；当我们说话时，声波传递到别人旳耳朵， 使别人了解我们旳意图，这属于声信号；遨游太空旳多种 无线电波、四通八达旳电话网中旳电流等，都能够用来向 远方体现多种消息，这属电信号。人们经过对光、声、电 信号进行接受，才懂得对方要体现旳消息。
于n×360°
电容三点式振荡器
石英晶体振荡器
石英晶体振荡器
VCO振荡器
• 变容二极管反偏装入电路当中，其利用旳是PN结旳结电容
随外加电压变化而变化特征制成旳。将变容二极管接在三 点式振荡器中可使振荡频率随外加到变容二极管旳电压变 化而变化。
PLL
• PD 鉴相器、LF 环路滤波器、 • VCO 压控振荡器
三环频率合成
• fA=NA/100×fc fB=NB×fc
fo=(NA/100+NB)×fc

信号源基础精讲课件

信号源基础精讲课件

均衡器调整
在传输过程中使用均衡器对信号进行补偿， 以纠正信号畸变。
信号源的稳定性问题及解决方案
01
02
03
04
总结词
信号源的稳定性问题通常 表现为信号输出不稳定、 画面闪烁或声音断断续续 。
检查电源稳定性
确保信号源设备使用的电 源是稳定的，并考虑使用 不间断电源（UPS）来保 护设备。
定期维护和清洁
信号源基础精讲课 件
目 录
• 信号源概述 • 信号源基础知识 • 信号源的工作原理 • 信号源的常见问题及解决方案 • 信号源的发展趋势与展望
01
信号源概述
信号源的定义
信号源
产生和发送信号的设备或装置， 用于传输信息、数据或能量。
信号
携带信息的物理量，可以是电、 光、声、磁等不同形式。
信号源的分类
调频（FM）
通过改变载波的频率来调制信号，抗干扰能力强 ，传输质量好。
调幅（AM）
通过改变载波的振幅来调制信号，实现简单，但 抗干扰能力较弱。
ABCD
调相（PM）
通过改变载波的相位来调制信号，抗干扰能力强 ，传输质量好。
数字调制
将数字信号转换为适合传输的格式，如QPSK、 QAM等，具有较高的传输效率和可靠性。
电源波动
使用稳定的电源供电，并考虑使 用不间断电源（UPS）来保护设
备免受电源波动的影响。
信号源的失真问题及解决方案
总结词
信号源失真是指信号在传输过程中发生畸变 ，导致信号质量下降。
调整信号源的输出电平
确保信号源的输出电平在适当的范围内，以 减少失真。
使用高品质的线缆和连接器
选择低阻抗、低失真的线缆和连接器，以减 少信号损失和失真。

3.1、3.2正弦信号源(一)

3.1、3.2正弦信号源(一)

引导法、分析法 习题 3.1 3.2
课后体会
教学过程及教学内容
附记
A、新课
B、引入 新授课
信号源又称信号发生器，是为电子测量提供符合一定技术要求的电信 号的设备，是电子测量中最基本、使用最广泛的电子仪器之一。本章重点 讨论几种常用信号发生器的组成、原理及应用。
C、新课
3.1 概述
信号源种类： （1）按性能指标分类 普通信号发生器：用于对输出信号的频率、幅度的准确度和稳定度以 及波形失真等要求不高的场合。 标准信号发生器：要求输出信号的频率、幅度、调制系数等在一定范 围内连续可调，并且读数准确、稳定，屏蔽良好。 （2）按输出波形分类 正弦信号发生器和非正弦信号发生器。非正弦发生器又包括：脉冲信 号发生器、函数信号发生器、扫频信号发生器、数字序列信号发生器、图 形信号发生器、噪声信号发生器等。
（1）主振器（主要部件） 作用：产生低频的正弦波信号，并实现频率调节功能。 组成：文氏电桥振荡器，如下图是文氏电桥振荡器的原理电路。
图中 R1、C1、R2、C2 组成正反馈网络，负温度系数热敏电阻 Rt 和电阻 Rf 组成负反馈支路，二者共同组成构成文氏电桥。文氏电桥和放大器组成 的反馈环路称为文氏电桥振荡。一般取 R1= R2 = R，C1= C2= C。当满足振 幅平衡条件和相位平衡条件时，振荡器的输出频率为
教学过程及教学内容
附记
的范围内；标准信号发生器优于 1；合成信号发生器优于 10-6。 （3）频率稳定度 定义：在一定时间内维持其输出信号频率不变得能力。 表示：用一定的时Байду номын сангаас内的相对频率偏移。 要求：比频率准确度高 1～2 个数量级。 2．输出特性 （1）输出电平 定义：输出信号幅度的有效值范围（有很宽的调节范围）。 表示：可用绝对电平（Ｖ，mV，V）或相对电平（dB）。 （2）输出电平的准确度 输出电平的实际值与显示器的显示值之间的相对误差，一般在 （3% ~

第3章-信源编码理论PPT课件

第3章-信源编码理论PPT课件
因为实际应用中使信号恢复的低通滤波器不可能是理想的，如 图4所示。因此为了防止减弱因幅度和相位不理想造成的失真， 通常选择抽样速率略大于奈奎斯特速率。
H(f )
0
f
理想特性
0
Fm
2021/3/12
f
( f )
图4 收端低通滤波器频率特性
理想特性 9
c. 抽样时，采用的抽样脉冲序列一般都是高度有限，宽度很 窄的脉冲序列。因为在实际应用中，理想抽样所需的周期性
2
F
(
)
2
Ts
(
n
ns
)
1 Ts
F (
n
ns )
上式表明，已抽样信号频谱 Fs ()是低通信号频谱 F ( ) 以抽样
速率为周期进行延拓形成的周期性频谱，它包含了F ( ) 的全部
信2息021。/3/1图2 3所示为抽样过程的波形及其频谱。
7
f (t)
F ()
t 0 (a)
Ts (t )
2021/3/12
S Nq
dB
20lgN20lg2l
6l
19
(3) 非均匀量化
① 定义： 根据信号的不同区间来确定量化间隔的。对于信号取 值小的区间，量化间隔小；对信号取值大的区间，量 化间隔大。
② 优点： 与均匀量化相比，在输入信号不变的前提下，由于小 信号时量化间隔变小，其相应的量化噪声功率也减小， 从而使小信号时的量化信噪比增大，即改善了小信号 时的量化信噪比，使输入信号的动态范围增大。
f (t)
fs (t)
fs (t) 低通滤波器 f (t)
Ts (t)
2021/3/12
图2 抽样与恢复
6
假设 f (t)、Ts (t)和 f s (t ) 的频谱分别是 F()、s() 和 Fs ()

第3章信号源0109版

第3章信号源0109版
信号发生器的输出阻抗视其类型不同而 异。
低频信号发生器电压输出端的输出阻抗 一般为600Ω （或1KΩ ）；
功率输出端根据输出匹配变压器的设计 而定，通常有50Ω 、75Ω 、150Ω 、 600Ω 和5KΩ 等；
高频信号发生器一般有50Ω 和75Ω 两种 不平衡输出。
第17页
电子测量原理
第15页
电子测量原理
（2）输出电平的频率响应 是指在有效频率范围内调节频率时，输出
电平的变化情况，也就是输出电平的平坦 度。 （3）输出电平准确度
输出电平准确度一般由电压表刻度误差、输出 衰减器换档误差、0dB准确度和输出电平平坦 度等几项指标综合组成。
第16页
电子测量原理
（４）输出阻抗
正弦波形成电路
缓冲放大器 输出正弦波
三角波 发生器
方波变换电路
缓冲放大器
输出方波
图3.8 三角波-方波-正弦波函数发生器的原理框图
2019/5/10
34
3.正弦波-方波-三角波函数发生器的构成 方案
由正弦波发生器先产生正弦波，然后经微
分电路产生尖脉冲，用脉冲触发单稳电路
形成方波，经三角波形成电路产生三角波，
2019/5/10
电子测量原理
2．放大器
低频信号发生器的放大器一般包括电压 放大器和功率放大器两级，以达到电压输出 幅度和功率的要求。
3．输出级
输出级一般包括输出衰减器电路、阻抗 变换器和电压表几部分。
第27页
电子测量原理
3．2．3 低频信号发生器的应用
1．使用方法
（1）接通电源，频率应有显示。 （2）根据测试所要求信号的频率选择合适的波
3.3.1函数信号发生器的基本组成与原理 构成函数发生器的方案很多，通常有

第三章 离散信源


2.1 离散无记忆信源
z 离散单符号信源：输出离散取值的单个符号
离散单符号信源是最简单、最基本的信源，是组 成实际信源的基本单元。
z 离散单符号信源X的概率空间：
⎡ ⎢ ⎣
X P( X
⎤ )⎥⎦
=
⎡ ⎢ ⎣
x1 p( x1 )
x2 L p(x2 ) L
xq ⎤ p(xq )⎥⎦
p(xi ) ≥ 0
q
3.1 预备知识
定义1：对于离散随机变量序列 X1X 2 L X n L，若任意 两个不同时刻i和j(大于1的任意整数)信源发出消息的 概率分布完全相同，即对于任意的 N = 0,1, 2,L，Xi Xi+1L Xi+N 和 X j X j+1L X j+N 具有相同的概率分布。也就是
P(X i ) = P(X j ) P( X i X i+1) = P( X j X j+1) P( Xi Xi+1 L Xi+N ) = P( X j X j+1 L X j+N )
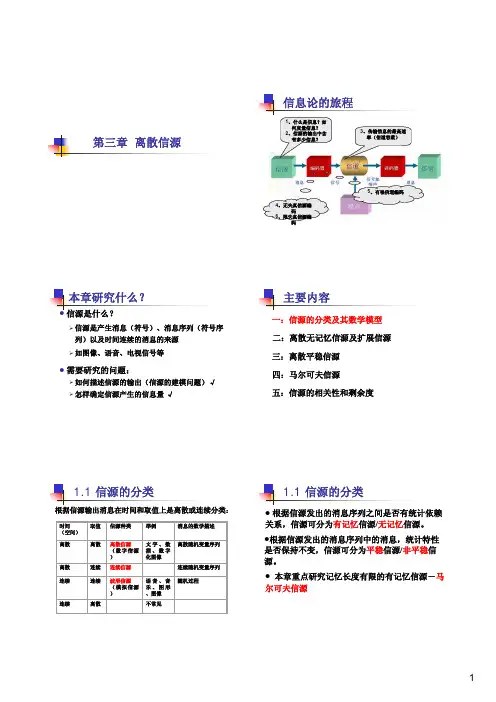
离散
取值 离散 连续
信源种类
举例
消息的数学描述
离散信源 （数字信源 ）
连续信源
文字、数 据、数字 化图像
离散随机变量序列 连续随机变量序列
连续 连续
连续 离散
波形信源 （模拟信源 ）
语音、音 乐、图形 、图像
不常见
随机过程
1.1 信源的分类
z 根据信源发出的消息序列之间是否有统计依赖 关系，信源可分为有记忆信源/无记忆信源。
解： （1） ¾ 离散单符号信源熵
3
∑ H ( X ) = − p ( x i ) lo g 2 p ( x i ) = 1 .5 b it i =1

信号源

器 微波主振 调制组件 输出组件
ＣＰＵ
图1 合成信号发生器原理框图
主振电路用以产生必要的微波频率覆盖。 扫频信号发生器基本构成 扫描发生器产生扫描电压斜波信号，通过主 振驱动器推动主振实现频率扫描。调制组件 实现微波电平控制，输出组件则实现输出微 波信号的滤波放大、电平检测等。ＡＬＣ系 统利用输出组件检测仪器输出电平，自动调 扫描发生器 主振驱动 调制驱动器 ＡＬＣ系统 节调制组件动作，实现输出电平稳幅（或调 幅）。调制驱动器将调制信号变换成相应的 ＣＰＵ 驱动信号，并分别施加到对应的执行器件中。
◆扫描时间：
完成重复扫频过程的时间叫做扫频时间，单位为秒。
◆剩余调频：
扫频信号发生器在无调制点频工作状态下，输出信号频率的短期不稳定度或 晃动。
◆频标误差：
是指频标频率标称值与频标频率实测值之差。
信号发生器简介
一般将输出频率范围在３００ＭＨｚ～３０ＧＨｚ、工 作波长为１０ｃｍ～１ｃｍ的信号发生器称为微波信号发 生器。输出频率范围在３０ＧＨｚ～３００ＧＨｚ、工作 波长为１０ｍｍ～１ｍｍ的信号发生器称为毫米波信号发 生器。微波、毫米波信号发生器是现代微波、毫米波测试 系统的最基本组成部分，是现代微波测量的基础仪器之一。
米波 30MHz 300MHz
分米波 3GHz
厘米波 30GHz
毫米波 300GHz
信号发生器简介
微波、毫米波信号发生器按照原 理、性能、用途的不同，一般可分 为： 合成信号发生器 扫频信号发生器 合成扫频信号发生器
合成信号发生器基本构成
电 源
时 基
主振电路及其驱动电路是信号发生器的核心， 用以产生必要的频率覆盖。频率合成器的作用是通 过补偿修正主振驱动控制信号，实时修正微波振荡 器的输出相位误差，使其具备时基（频率参考）的 相对准确度和长期稳定度。调制组件实现微波电平 控制，输出组件则实现输出微波信号的滤波放大、 电平检测等。ＡＬＣ系统利用输出组件检测仪器输 主振驱动 调制驱动器 ＡＬＣ系统 频 出电平，自动调节调制组件动作，实现输出电平稳 幅（或调幅）。调制驱动器将调制信号变换成相应 率 的驱动信号，并分别施加到对应的执行器件中。较 合 ＰＬＬ 高级的信号源自己能够产生调制信号。 成
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

电子测量原理
3．调制特性
描述高频信号发生器输出正弦波的 同时，输出调频、调幅、调相或脉 冲调制信号的能力。
第17页
下一节 结束返回
3.2 低频信号发生器
电子测量原理
低频信号发生器的输出信号频率范围通常 为20Hz~20KHz，也称为音频信号发生器。
低频信号发生器可用于测试调整低频放大 器、传输网络和广播、音响等电声设备， 还可以用于调制高频信号发生器或标准电 子电压表等。
电压表
电子测量原理
1．振荡器
振荡器是低频信号发生器的核心部分， 产生频率可调的正弦信号。一般由RC 振荡电路或差频式振荡电路组成。振荡 器决定输出信号的频率范围和稳定度。
第21页
电子测量原理
（1）通用RC振荡电路 图3.3为文氏电桥振荡器的原理框图。R1、C1、R2、C2组 成RC选频网络，可改变振荡器的频率；R3、R4组成负反 馈臂，可自动稳幅。
5KΩ （7）非线性失真系数。(0.1～1)% （8）平衡输出与不平第1衡9页输出方式。
电子测量原理
3．2．2 低频信号发生器的
基本组成与工作原理
如图3.2所示，包括振荡器、放大器、稳压电源、 电压表及输出级等部分。
振荡器
放大器
输出衰减 低频信号输出
稳压电源
图3.2 低频信号发生器框图 第20页
电子测量原理
第6页
电子测量原理
3.1 信号源概述
信号源的作用和组成 信号源的分类 正弦信号源的性能指标
第7页
电子测量原理
3.1.1 信号源在电子测量中的作用和组成
1.信号源的作用 信号源是能够产生不同频率、不同幅度的规
则或不规则波形的信号发生器。 信号源的用途主要有以下三方面： ☆ 激励源。-测量用的激励信号 ☆ 信号仿真。 ☆ 标准信号源。 -校准测量仪器
第15页
电子测量原理
（４）输出阻抗
信号发生器的输出阻抗视其类型不同而 异。
低频信号发生器电压输出端的输出阻抗 一般为600Ω（或1KΩ）；
功率输出端根据输出匹配变压器的设计 而定，通常有50Ω、75Ω、150Ω、 600Ω和5KΩ等；
高频信号发生器一般有50Ω和75Ω两种 不平衡输出。
第16页
射频信号-易于辐射的无线电信号；大体为 30KHz~若干GHz的范围
第11页
电子测量原理
2. 按输出波形,大致可分为： 正弦波形发生器； 脉冲信号发生器； 函数信号发生器； 噪声信号发生器。
3. 按照信号发生器的性能指标 可分为： 一般信号发生器； 标准信号发生器；
第12页
电子测量原理
第18页
电子测量原理
3．2．1 低频信号发生器的
主要性能指标
（1）频率范围。1Hz～20KHz或延伸到1MHz （2）频率稳定度。（0.1～0.4）%/小时 （3）频率的准确度。 ±(1～2)% （4）输出电压。0～10V连续可调 （5）输出功率。0.5～5w连续可调 （6）输出阻抗。50Ω、75Ω、150Ω、600Ω和
第22页
电子测量原理
（2）差频式振荡电路
差频电路产生低频正弦信号的原理方框图如图 所示。主要包括固定高频振荡器、可变高频振 荡器、混频器、低通滤波器和放大、衰减器等。
固定高频振 荡器
可变高频差频式振荡电路框图 第23页
输 出
衰减电路
3.1.2 信号源的分类
电子测量原理
1. 按频率范围 大致可分为六类：
（1）超低频信号发生器
频率在0.0001~1KHz范围内。
（2) 低频信号发生器
频率在1Hz~20KHz(或1MHz)范围内。其中 用得最多的是音频信号发生器，频率范围 在20Hz~20KHz之间。
（3）视频信号发生器
频率在20KHz~10MHz范围内。
第10页
电子测量原理
（4）高频信号发生器
频率在200KHz~30MHz范围内，大致相当于 长、中、短波段的范围-广播的波段。
（5）甚高频信号发生器
频率在30MHz~300MHz范围内，相当于米波 波段。
（6）超高频信号发生器
频率一般在300MHz以上，相当于分米波、厘 米波波段等。
工作在厘米波及更短波长的信号发生器常被 称为微波信号发生器。
RC和LC信号源，频率准确度可达10 -2量级，稳定度可 达10 ~-310 量-4级；利用晶体振荡器的合成信号源，频 率准确度和稳定度都可达到10 量-8级
第13页
电子测量原理
2．输出特性
正弦信号源的输出特性一般包括输出电平 范围、输出电平的频响、输出电平的准确 度、输出阻抗等指标。
（1）输出电平范围 指输出信号幅度的有效范围，也就是信号
第8页
电子测量原理
2. 信号源的组成
基本构成如图3.1所示，一般包括振荡器、 变换器、指示器、电源及输出电路等部 分。
用RC或LC电路 调频、调幅两个电路；
衰减器电路、阻抗
调节输出频率 调频可直接由振荡器实现， 变换器和电压表几
调幅有专门电路完成
部分
振荡器
调制器
输出电路
输出正弦波
电源
指示器
图3.1正弦信号发生器的基本组成框图 第9页
发生器的最大和最小输出电平的可调范围。 输出幅度可用电压(mV、V)和分贝(dB)两 种方式表示。
第14页
电子测量原理
（2）输出电平的频率响应 是指在有效频率范围内调节频率时，输出
电平的变化情况，也就是输出电平的平坦 度。 （3）输出电平准确度
输出电平准确度一般由电压表刻度误差、输出 衰减器换档误差、0dB准确度和输出电平平坦 度等几项指标综合组成。
3.1.3 正弦信号源的性能指标
1. 频率特性
（1）频率范围-上述
（2）频率准确度 –度盘数值与实际输出信号频率间的
偏差
f fo f 10% 0
fo
fo
（3）频率稳定度-是指其它外界条件恒定不变的情况 下，在规定时间内，信号发生器输出频率相对于预调 值变化的大小。
fmaxfmin10% 0
fo
电子测量原理
重点：
掌握各类测试信号源的特点、工 作原理和使用方法。
难点：
各类测试信号源的工作原理与电 路构成。
第1页
常用信号发生器示例 脉冲信号发生器
电子测量原理
第2页
函数、任意波形发生器
电子测量原理
第3页
功率函数信号发生器
电子测量原理
第4页
函数发生器/计数器
电子测量原理
第5页
视频和电视信号发生器