高一立体几何练习题广州市中学数学之窗
- 格式:doc
- 大小:82.50 KB
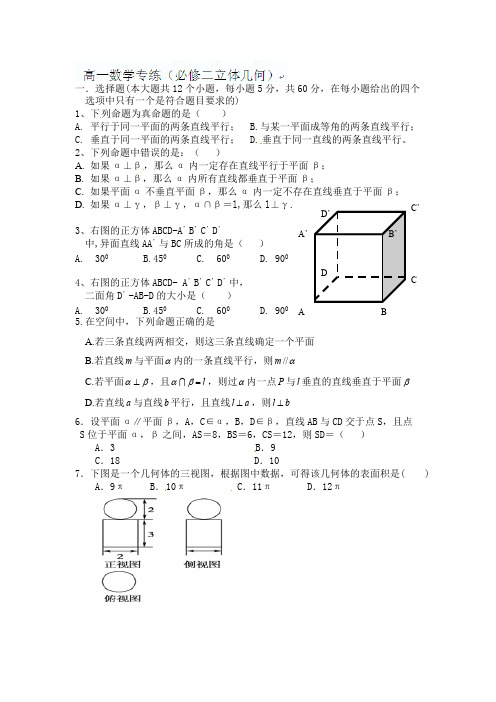
- 文档页数:5

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省高中数学人教A 版选修一空间向量与立体几何强化训练(7)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)1. 在三棱锥 中, 底面ABC , , , ,则点C 到平面PAB 的距离是( )A. B. C.D. 2.如图,在棱长为2的正方体中,点分别是棱 、的中点,则点到平面的距离等于( )A. B. C. D.3.如图所示,正方体ABCD-A'B'C'D'的棱长为1,O 是平面A'B'C'D'的中心,则O 到平面ABC'D'的距离是( )A. B. C. D.4. 已知四面体中, , , 两两垂直, , 与平面 所成角的正切值为 ,则点 到平面 的距离为( )A. B. C. D.3个4个5个6个5. 如图,在正方体ABCD ﹣A 1B 1C 1D 1中,P 为对角线BD 1的三等分点,P 到各顶点的距离的不同取值有( )A. B. C. D. 6.已知A 、B 、C 三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点A 、B 、C 一定共面的是( )A. B.C. D. 当运动时,二面角的最小值为当运动时,三棱锥体积不变当运动时,存在点使得当运动时,二面角为定值7. 如图,正方体的棱长为2,线段上有两个动点(在的左边),且 . 下列说法不正确的是()A. B. C. D. 5278. 如图,平行六面体ABCD ﹣A 1B 1C 1D 1中,侧棱B 1B 长为3,底面是边长为2的菱形,∠A 1AB=120°,∠A 1AD=60°,点E 在棱B 1B 上,则AE+C 1E 的最小值为( )A. B. C. D. 9.已知点 ,, 则( )A. B. C. D.10. 已知正方体的棱长为a , , 点N 为的中点, 则=( )A. B. C. D.+ ﹣ ﹣ + ﹣ + + ﹣ + ﹣11. 直三棱柱ABC ﹣A 1B 1C 1中,若 = , = , = ,则 =( )A. B. C. D. M 一定在直线AC 上M 一定在直线BD 上M 可能在直线AC 上,也可能在直线BD 上M 既不在直线AC 上,也不在直线BD 上12. 在空间四边形ABCD 的边AB 、BC 、CD 、DA 上分别取E 、F 、G 、H 四点,如果EF 与HG 交于点M ,那么( )A. B. C. D. 13. 已知点A (4,1,3),B (6,3,2),且,则点C 的坐标为 .14. 直三棱柱中, , 分别是的中点, , 则所成角的余弦值为15. 已知 , ,若 ,且 与 反向,则 .16. 已知 A (3,1,2),B (4,﹣2,﹣2),则= 17. 如图,在四棱锥中,底面梯形 中, ,平面 平面 , 是等边三角形,已知, .(1) 求证:平面平面 ;(2) 求二面角 的余弦值.18. 如图,三棱锥P -ABC 的顶点P 在圆柱轴线上,底面△ABC 内接于⊙O ,AB 为⊙O 的直径,且∠ABC =60°,O 1O =AB =4, 上一点D 在平面ABC 上的射影E 恰为劣弧AC 的中点.(Ⅰ)设,求证:DO⊥平面PAC;(Ⅱ)设,求二面角D-AC-P的余弦值.19. 如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1, A1D的中点.(1) 证明:MN∥平面C1DE;(2) 求二面角A-MA1-N的正弦值.20. 如图,直三棱柱的体积为4,点,分别为,的中点,的面积为.(1) 求点A到平面的距离;(2) ,平面平面,求平面与平面所成角的余弦值.21. 如图,在四棱锥中,底面是平行四边形,平面,垂足为G,G在上,且,是的中点.(1) 求异面直线与所成角的余弦值;(2) 若F点是棱上一点,且,求的值.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)18.(1)(2)20.(1)(2)21.(1)(2)。

高一数学常考立体几何证明的题目及答案预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制1、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE; (2)平面CDE ⊥平面ABC 。
2、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证: 1//A C 平面BDE 。
3、已知ABC ?中90ACB ∠=o,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .4、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D .A EDBCAED 1CB 1DCBASDCB AD 1ODB AC 1B 1A 1C5、正方体''''ABCD A B C D-中,求证:(1)''AC B D DB⊥平面;(2)''BD ACB⊥平面.6、正方体ABCD—A1B1C1D1中.(1)求证:平面A1BD∥平面B1D1C;(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.7、四面体ABCD中,,,AC BD E F=分别为,AD BC的中点,且22EF AC=,90BDC∠=o,求证:BD⊥平面ACD8、如图,在正方体1111ABCD A B C D-中,E、F、G分别是AB、AD、11C D的中点.求证:平面1D EF∥平面BDG.9、如图,在正方体1111ABCD A B C D-中,E是1AA的中点.(1)求证:1//A C平面BDE;(2)求证:平面1A AC⊥平面BDE.10、已知ABCD是矩形,PA⊥平面ABCD,2AB=,4PA AD==,E为BC的中点.(1)求证:DE⊥平面PAE;AAB1C1CD1DGEF(2)求直线DP 与平面PAE 所成的角.11、如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG ⊥平面PAD ;(2)求证:AD PB ⊥.12、如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD .13、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .14.(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.已知:如图,三棱锥S—ABC,SC∥截面EFGH,AB∥截面EFGH.求证:截面EFGH是平行四边形.15.(12分)已知正方体ABCD—A1B1C1D1的棱长为a,M、N 分别为A1B和AC上的点,A1M=AN=23 a,如图.(1)求证:MN∥面BB1C1C;(2)求MN的长.16.(12分)(2009·浙江高考)如图,DC⊥平面ABC,EB∥DC,AC =BC=EB=2DC=2,∠ACB=120°,P,Q 分别为AE,AB的中点.(1)证明:PQ ∥平面ACD ;(2)求AD 与平面ABE 所成角的正弦值.17.(12分)如图,在四面体ABCD 中,CB =CD ,AD ⊥BD ,点E 、F 分别是AB 、BD 的中点.求证:(1)直线EF ∥面ACD . (2)平面EFC ⊥平面BCD.1、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学人教A 版 必修二第八章 立体几何强化训练(12)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)平面平面PAE 平面PAE 平面平面ABC 平面平面ABC 1. 在正四面体(所有棱长都相等)中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论中不成立的是( )A. B. C. D. 2.某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.12343. 棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中,点M ,N 分别在线段AB 1 , BC 1上,且AM=BN ,给出以下结论:其中正确的结论的个数为( )①AA 1⊥MN②异面直线AB 1 , BC 1所成的角为60°③四面体B 1﹣D 1CA 的体积为④A 1C ⊥AB 1 , A 1C ⊥BC 1 .A. B. C. D.一个圆四个点两条直线双曲线的一支4.已知平面∥,直线l ,点P ∈l ,平面、间的距离为5,则在内到点P 的距离为13且到直线l 的距离为的点的轨迹是( )A. B. C. D.如果,那么内一定存在直线平行于如果不垂直于,那么内一定不存在直线垂直于如果,那么如果,l与,都相交,那么l与,所成的角互余5. 设l 是一条直线,是不同的平面,则下列说法不正确的是( )A. B. C. D. 若,则若,则若,则若,则6. 设是两条不同的直线,是两个不同的平面,则下列说法正确的是( )A. B. C. D. 平行相交平行或相交以上都不对7. 平面满足则与的位置关系为( )A. B. C. D. 四条侧棱、四个顶点八条侧棱、四个顶点四条侧棱、八个顶点六条侧棱、八个顶点8. 四棱柱有几条侧棱,几个顶点( )A. B. C. D. α内所有直线都与直线m 异面α内所有直线都与直线m 平行α内有且只有一条直线与直线m 平行α内有无数条直线与直线m 垂直9. 已知直线m ∥平面α,则下列命题中正确的是( )A. B. C. D. 10. 已知一个正三棱柱所有棱长均为3,若该正三棱柱内接于半球体,即正三棱柱的上底面的三个顶点在球面上,下底面的三个顶点在半球体的底面圆内,则该半球体的体积为( )A. B. C. D.11. 如图,正方体的棱长为 , 点是内部(不包括边界)的动点.若 , 则线段长度的取值不可能为( )A. B. C. D.12. 已知某空间几何体的三视图如图所示,每个小方格是边长为1的正方形,则该几何体的表面积为()A. B. C. D.阅卷人二、填空得分13. 若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则(写出所有正确结论编号)①四面体ABCD每组对棱相互垂直②四面体ABCD每个面的面积相等③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°④连接四面体ABCD每组对棱中点的线段互垂直平分⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.14. 在四面体中,,二面角的大小为,则四面体外接球的半径为.15. 在四棱锥P﹣ABCD中,PB⊥底面ABCD,底面ABCD是边长为2的正方形,若直线PC与平面PDB所成的角为30°,则四棱锥P﹣ABCD的外接球的表面积为.16. 一个圆锥的侧面积等于底面面积的倍,若圆锥底面半径为 cm,则圆锥的体积是 cm3.阅卷人三、解答得分17. 如图,多面体中,四边形为矩形,二面角为,,,,, .(1) 求证:平面;(2) 为线段上的点,当时,求二面角的余弦值.18. 如图,已知在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为CE的中点.(1) 求直线AF与平面ACD所成的角;(2) 求证:平面BCE⊥平面DCE.19. 在四棱锥中,四边形为正方形,平面平面为等腰直角三角形,.(1) 求证:平面平面;(2) 设为的中点,求点到平面的距离.20. 如图,在四棱锥E﹣ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.(Ⅰ)求证:BE=DE;(Ⅱ)若AB=2 ,AE=3 ,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.21. 如图,在正方体ABCD﹣A1B1C1D1中,E是AA1的中点,求证:(Ⅰ)A1C∥平面BDE;(Ⅱ)平面A1AC⊥平面BDE.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)18.(1)(2)(1)(2)20.21.。

立体几何试题一.选择题(每题 4 分,共 40 分)1. 已知 AB3003001500空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形, (2)四边相等的四边形是菱形(4)有两边及其夹角对应相等的两个三角(3)平行于同一条直线的两条直线平行 ;形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A平行B相交C在平面内D平行或在平面内4. 已知直线 m过平面外一点,作与平行的平面,则这样的平面可作()A 1 个或 2 个B 0个或1个C1个 D 0个6.如图 , 如果 MC 菱形 ABCD 所在平面 , 那么 MA与 BD的位置关系是 ( )A平行B垂直相交C异面D相交但不垂直7. 经过平面外一点和平面内一点与平面垂直的平面有()A 0 个B 1个C无数个 D 1个或无数个8.下列条件中 , 能判断两个平面平行的是 ( )B一个平面内的两条直线平行于另一个平面C一个平面内有无数条直线平行于另一个平面D一个平面内任何一条直线都平行于另一个平面9. 对于直线m ,n 和平面,, 使成立的一个条件是 ( )A m // n, n, mB m // n, n,mC m n,I m, nD m n, m //, n //)10 . 已知四棱锥 , 则中 , 直角三角形最多可以有 (A 1个B2个 C 3个D4个二.填空题(每题 4 分,共16 分)11. 已知ABC的两边 AC,BC分别交平面于点M,N,设直线AB与平面交于点O,则点 O与直线 MN的位置关系为 _________12.过直线外一点与该直线平行的平面有 ___________个,过平面外一点与该平面平行的直线有_____________条13. 一块西瓜切 3 刀最多能切 _________块14.将边长是 a 的正方形 ABCD沿对角线 AC 折起 , 使得折起后 BD得长为 a, 则三棱锥D-ABC的体积为 ___________三、解答题15(10 分)如图,已知 E,F 分别是正方形ABCD A1B1C1 D1的棱 AA1和棱 CC1上的点,且 AE C1 F 。

AC立体几何专项训练1.如图,四边形ABCD 与''ABB A 都是边长为a 的正方形,点E 是A A '的中点,'A A ⊥平面ABCD.(I )求证:CA '//平面BDE ;(II )求证:平面AC A '⊥平面BDE .2.如图,在四棱锥AB CD -P 中,底面ABCD 是矩形,侧棱PD ⊥底面ABCD , DC PD =,E 是PC 的中点,作EF ⊥PB 交PB 于点F .(1)证明:PA ∥平面EDB ; (2)证明:PB ⊥平面EFD .ABCEFP1A 1C 1B 3.在棱长为2的正方体1111DC B A ABCD -中,E 、F 分别为1DD 、DB 的中点。
(1)求证:EF//平面11D ABC ; (2)求证:EF C B 1⊥;(3)求三棱锥EFC B -1的体积V 。
4.在直三棱柱111C B A ABC -中, AC=4,CB=2,AA 1=2ο60=∠ACB ,E 、F 分别是BC C A ,11的中点。
(1)证明:平面⊥AEB 平面C C BB 11; (2)证明://1F C 平面ABE ;(3)设P 是BE 的中点,求三棱锥F C B P 11-的体积。
GFEBA5.如图,四边形ABCD 为矩形,AD ⊥平面ABE 2,AE EB BC === F 为CE 上的点,且BF ⊥平面ACE ,.BD AC G =I(1)求证:AE ⊥平面BCE ; (2)求证://AE 平面BFD ; (3)求三棱锥E ADC -的体积.6.如图,在侧棱垂直于底面的三棱柱ABC —A 1B 1C 1中,AC=3,AB=5,AA 1=BC=4,点D 是AB 的中点。
(Ⅰ)求证:1AC BC ⊥; (Ⅱ)求证:1//AC 平面CDB 1; (Ⅲ)求三棱锥A 1—B 1CD 的体积。
7.正方形ADEF 与梯形ABCD 所在的平面互相垂直, ,//,22AD CD AB CD CD AB AD ⊥==. (Ⅰ)求证:BC BE ⊥;(Ⅱ)在EC 上找一点M ,使得//BM 平面ADEF ,请确定M 点的位置,并给出证明.8.三棱柱111ABC A B C -中,侧棱与底面垂直,90ABC ∠=o ,12AB BC BB ===, ,M N 分别是AB ,1A C 的中点. (Ⅰ)求证:MN ∥平面11BCC B ; (Ⅱ)求证:MN ⊥平面11A B C ;(Ⅲ)求三棱锥M -11A B C 的体积. EBA CDFNMC 1B 1A 1CBAA 1B 1C 1D 1A B CDE9.如图,长方体1111D C B A ABCD -中,11==AA AB ,2=AD ,E 是BC 的中点. (Ⅰ)求证:直线//1BB 平面DE D 1; (Ⅱ)求证:平面AE A 1⊥平面DE D 1; (Ⅲ)求三棱锥DE A A 1-的体积.10.如图,PA 垂直于矩形ABCD 所在的平面,AD PA 2==,CD 22=,E 、F 分别是AB 、PD 的中点。

高一数学立体几何练习题一、选择题(下列各题中只有一个选项正确,每题4分,共40分)1、下列说法正确是[ D ]。
A.圆台是直角梯形绕其一边旋转而成B.圆锥是直角三角形绕其一边旋转而成C.圆柱的母线和它的底面不垂直。
D.圆台可以看作是平行于底面的平面截一个圆锥而得到的。
2、下列说法错误的是[ B ]。
A、用斜二测画法画出的直观图是在平行投影下画得的空间图形B、几何体直观图中的长、宽、高与几何体的长、宽高的比例相同。
C、水平放置的矩形的直观图一定是平行四边形。
D、水平放置的圆的直观图一定是椭圆。
3、底面放置在同一平面的一个圆柱和一个圆锥,底面积相同且体积相等, 用通过圆柱中截面的平面截圆锥和圆柱所得两个截面的面积之比是 [ A ] 。
A. 25∶36B. 9∶16C. 4∶9D. 5∶64、下列命题中,真命题的是 [ B ] 。
A.两两相交的三条直线共面B.对角线交于一点的四边形一定是平面图形C.不共面的四点中可以有三点共线D.边长相等的四边形一定是菱形5、下列条件能得到直线l1,l2互相平行的是 [ D ] 。
A.l1,l2都平行于同一个平面B.l1,l2与同一个平面所成的角相等C.l1平行于l2所在的平面D.l1,l2都垂直于同一个平面6、下列四个命题中正确的是[ B ] 。
①两个平面没有公共点,则这两个平面平行②一个平面内有三个点到另一个平面的距离(距离不为零)相等,则这两个平面平行③一个平面内任一点到另一个平面的距离(距离不为零)都相等,则这两个平面平行④一个平面内有无数个点到另一个平面的距离(距离不为零)相等,则这两个平面平行.A.①②B.①③C.①②③D.①②③④7、如果直线a平行于平面β,那么 [ D ] 。
A.平面β内不存在与a垂直的直线B.平面β内有且只有一条直线与a垂直C.平面β内有且只有一条直线与a平行D.平面β内有无数多条直线与a不平行8、已知直线l⊥平面α,直线mβ,有如下四个命题:①α∥βl⊥m,②α⊥βl∥m,③l ∥mα⊥β,l⊥mα∥β,其中正确命题是 [ C ]A.③④B.①②C.①③D.②④9、平面α内有三条相交于一点的直线, 另有一条直线与它们所成的角都相等, 则此直线与平面α的关系是 [ B ]。

高一数学立体几何练习题及部分答案汇编(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高一数学立体几何练习题及部分答案汇编(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高一数学立体几何练习题及部分答案汇编(word版可编辑修改)的全部内容。
立体几何试题一.选择题(每题4分,共40分)1。
已知AB//PQ,BC//QR,则∠PQP等于()A 0150 D 以上结论都不对30 C 030 B 02。
在空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A 平行B 相交C 在平面内D 平行或在平面内4。
已知直线m//平面α,直线n在α内,则m与n的关系为()A 平行B 相交C 平行或异面D 相交或异面5。
经过平面α外一点,作与α平行的平面,则这样的平面可作( )A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7。
经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个8。
下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学人教A 版选修一空间向量与立体几何专项提升(2)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)与斜交1. 若直线的方向向量为 , 平面的法向量为, 则( )A.B.C.D. ﹣2. 三棱锥P ﹣ABC 的四个顶点都在球O 的球面上,已知PA ,PB ,PC 两两垂直,PA=1,PB+PC=4,当三棱锥的体积最大时,球心O 到平面ABC 的距离是( )A.B.C.D.①③②③①④①③④3. 在正方体中,点E 为线段上的动点,现有下面四个命题:①直线DE 与直线AC 所成角为定值;②点E 到直线AB 的距离为定值;③三棱锥的体积为定值;④三棱锥外接球的体积为定值.其中所有真命题的序号是( )A. B. C.D. 4. 已知,,则直线AB 与平面xOz 交点的坐标是( )A. B. C.D.(12,14,10)(10,12,14)(14,10,12)(4,2,3)5. 已知点A 在基底{ ,, }下的坐标为(8,6,4),其中=+ , =+ , =+ , 则点A 在基底{ , , }下的坐标为( )A. B. C. D. 6. 如图,在四棱锥中,底面是矩形, , 为棱的中点,且,, 若点到平面的距离为, 则实数的值为( )A. B. C. D.7. 在正方体中,是的中点,则异面直线与所成角的余弦值为( )A.B.C.D.8. 若是空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是( )A. B. C. D.夹角的余弦值为A ,B ,C ,D 共面点O 到直线AB 的距离是9. 在空间直角坐标系中,已知, 则以下错误的是( )A.B.C. D. 235410. 给出下列命题,其中是真命题个数的是( )①若直线的方向向量 , 直线的方向向量, 则与平行②若直线的方向向量 , 平面的法向量, 则③若平面 , 的法向量分别为 ,, 则④若平面经过三点 ,,, 向量是平面的法向量,则⑤若点,, 点是点关于平面的对称点,则点与的距离为⑥若、、、的方差为 , 则、、、的方差为27⑦若,, 则与共线的单位向量是A. B. C. D. (1,1,1)(1,1,﹣1)(﹣1,1,1)(1,﹣1,1)11. 已知点A (0,0,0),B (1,0,1),C (0,1,1),则平面ABC 的一个法向量是( )A. B. C. D. 12. 如图,三棱柱ABC ﹣A 1B 1C 1中,侧棱AA 1⊥底面A 1B 1C 1 , AA 1=AC=BC=1,∠ACB=90°,D 是A 1B 1的中点,F 是BB 1上的点,AB 1 , DF 交于点E ,且AB 1⊥DF ,则下列结论中不正确的是( )A. B. C. D.CE与BC1异面且垂直AB1⊥C1F△C1DF是直角三角形DF的长为13. 已知向量,则.14. 若 =(2,3,m), =(2n,6,8)且,为共线向量,则m+n= .15. 在如图所示的试验装置中,四边形框架为正方形,为矩形,且,且它们所在的平面互相垂直,为对角线上的一个定点,且,活动弹子在正方形对角线上移动,当取最小值时,活动弹子到直线的距离为 .16. 正方体中不在同一表面上两顶点坐标为M(﹣1,2,﹣1),N(3,﹣2,3),则此正方体的内切球的表面积为17. 如图,四棱锥的底面为正方形,平面平面,且, .(1) 证明:平面;(2) 求点到平面的距离.18. 如图,在四棱柱中,底面和侧面都是矩形,,,是的中点,.(1) 求证:平面;(2) 求平面与平面的夹角.19. 如图,在四棱锥中,四边形是直角梯形,,,底面,,,是的中点.(1) 求证:平面;(2) 若二面角的余弦值为,求直线与平面所成角的正弦值.20. 在矩形ABCD中,,点E是线段AD的中点,将△ABE沿BE折起到△PBE位置(如图),点F是线段CP的中点.(1) 求证:DF∥平面PBE:(2) 若二面角的大小为,求点A到平面PCD的距离.21. 如图,在多面体中,四边形是边长为的正方形,,,且,,面,,N为中点.(1) 若是中点,求证:面;(2) 求二面角的正弦值.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)18.(1)(2)19.(1)(2)20.(1)(2)21.(1)(2)。

高一数学立体几何试题答案及解析1.设三棱柱的体积为,分别是侧棱上的点,且,则四棱锥的体积为()A.B.C.D.【答案】C【解析】假设重合,重合,则【考点】棱柱棱锥的体积2.如图,四棱锥中,,四边形是边长为的正方形,若分别是线段的中点.(1)求证:∥底面;(2)若点为线段的中点,求三角形的面积。
【答案】(1)见解析;(2)【解析】要想证明线面平行,只需证明出该线段与面内的任意一条线段平行即可,在本题中,需要连接辅助线进行解答,在解此问题时主要运用了三角形内中位线平行于底边的性质;首先需要掌握知识,三角形的中位线的长度为底边的一半,先求出所需边的长度,再运用余弦定理,求出角的度数,在运用三角形面积公式即可得到结果。
试题解析:(1)解:连接,由题意知,为中点,为的中位线,平面平面平面(2)连接由(1)知:,同理可得:,,【考点】空间几何的运算3.如图,在四棱台中,底面,四边形为正方形,,,平面.(1)证明:为的中点;(2)求点到平面的距离.【答案】(1)详见解析;(2)【解析】(1)根据线面平行的性质定理,线面平行则,线线平行,所以可证,可证四边形是平行四边形,即证明是中点;(2)根据等体积转化,可证是直角三角形,写出体积公式,求解距离.试题解析:解(1)连接AD1,则D1C1∥DC∥AB,∴A、E、C1、D1四点共面,∵C1E∥平面ADD1A1,则C1E∥AD1,∴AEC1D1为平行四边形,∴AE=D1C1=1,∴E为AB的中点.(6分)(2),∵AD⊥DC,AD⊥DD1,∴AD⊥平面DCC1D1,AD⊥DC1.设点E到平面ADC1的距离为h,则,解得.【考点】1.线面平行的性质定理;2.等体积转化.4.设长方体的长、宽、高分别为2,1, 1,其顶点都在同一个球面上,则该球的体积为_______.【答案】【解析】球直径为长方体的体对角线,故半径为【考点】球内接长方体的性质,球体积的计算5.(本小题12分)如图所示,三棱柱ABC-A1B1C1中,.(1)证明:;(2)若,求三棱柱ABC-A1B1C1的体积.【答案】(1)见解析;(2)3【解析】(1)取AB的中点O,连接OC,OA1,A1B,证得,,则根据线面垂直的判定定理可得,进而得出;(2)先证明,进而证出,再求出,最后利用柱体的体积公式求出体积;试题解析:(1)取AB 的中点O ,连接.因为,所以.由于,故△AA 1B 为等边三角形,所以.因为,所以.又,故.(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形,所以. 又,则,故.因为所以,为三棱柱的高.又△ABC 的面积,故三棱柱的体积.【考点】1.线面垂直的判定定理;2.线线垂直的证明方法;3.柱体的体积公式;6. 如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误的是( ).A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1D .异面直线AD 与CB 1角为60°【答案】D【解析】因为易证∥,由线面平行的判定定理可证得∥面,所以A 选项结论正确; 由正方体可得面,可证得,由为正方体得,因为,所以面,从而可证得.同理可证明,根据线面垂直的判定定理可证得面,所以B ,C 选项结论都正确; 因为∥,所以为异面直线与所成的角,由正方体可得,所以D 选项的内容不正确. 故选D 。

广州市第一中学2021届高三数学第二轮复习专题立体几何专题复广州市第一中学2021届高三数学第二轮复习专题-立体几何专题复广州市第一中学高三第二轮数学复习——三维几何何专题复习1.如图所示,已知面ABC⊥ 面部BCD,ab⊥ 公元前,公元前⊥ CD,ab=BC=CD,让AD 和面ABC之间的角度为?,ab与面acd所成角为β,则?与β的大小关系为(a)?<β(b)?=β(c)?>β(d)无法确定2.下图为立方体或四面体。
P、 Q、R和s是边的中点。
四个点中非共面的一个是spppspssppsspqqqqrrspsrrrrpppqrrpqqpqpprpssqrrqqrqqqqssssrrrrssqa、然后是三角金字塔p-bdq2(a)(b)(c)(d)3、在棱长为a的正方体abcd-a1b1c1d1中,p,q是对角线a1c上的点,且pq=体积是333333a(b)a(c)a(d)无法确定3618244、已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm,2cm和3cm,则此球的体积为(a)(a)1632123163?cm3(b)?cm3(c)?cm3(d)?cm333335.如图所示,在长度为11厘米、外周长为6厘米的圆柱的外表面上,缠绕一根细铁丝,形成10个螺旋,例如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为(a) 61厘米(b)157厘米(c)1021厘米(d)1037厘米6、设a、b是两条不同的直线,?、?是两个不同的平面,则下列四个命题:① 如果是?b、 aB然后B/?;② 如果a//和?,,然后一个??;③ 如果a,B??,,那么a/?或者一个??;④ 如果是?b、 aB那你能吗正确命题的数量为()a.0b.1c.2d.37.如果e和F分别是SC和ab的中点,则么异面直线ef与sa所成角为()a.900b.600c.450d.3008.右图是正方体的平面展开图,在这个正方体中:①bm与de平行;②cn与be是异面直线;③cn与bm成60°角本网站的部分信息来源于网络,仅用于学习、讨论和收集。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学人教A 版选修一空间向量与立体几何章节测试(3)姓名:____________班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)x=1,y=﹣11. 已知 , ,且 ,则( )A. B. C. D. 90°60°45°30°2. 在三棱柱中,侧棱垂直于底面,, , , ,点E 为 的中点,点F在的延长线上且,则异面直线与所成的角为( )A. B. C. D. 3. 若平面α的一个法向量为=(4,1,1),直线l的一个方向向量为 =(﹣2,﹣3,3),则l 与α所成角的正弦值为( )A.B.C.D.4. 在四面体 中,PA , PB , PC 两两垂直,设,则点P 到平面ABC 的距离为( )A.B.C.D.5. 如图,在长方体中, , , 为棱上一点,且 , 平面上一动点满足, 设是该长方体外接球上一点,则 , 两点间距离的最大值是( )A. B. C. D.都不可以6. 已知向量 是空间的一个基底,其中与向量, 一定构成空间另一个基底的向量是( )A.B.C.D.14127. 已知 ,若 共面,则实数 的值为( )A.B. C. D.x=1,y=1x= ,y=﹣x= ,y=﹣x=﹣ ,y=8. 若 =(2x ,1,3), =(1,﹣2y ,9),如果 与 为共线向量,则( )A. B. C. D. 9. 直三棱柱 中,侧棱 , , ,则点C 到平面的距离为( )A.B.C.D.234810. 如图,在正方体中, , 为正方形的边上一点(与点不重合),且满足, 则满足条件的点的个数为( )A. B. C. D. ﹣4﹣22411. 已知向量 =(﹣1,x ,3), =(2,﹣4,y ),且 ∥ ,那么x+y 等于( )A. B. C. D. l ∥平面αl ∥平面α或l ⊂平面αl ⊥平面αl ⊂平面α12. 已知直线l 的一个方向向量=(-2,3,1),平面α的一个法向量=(4,0,8),则直线l 与平面α的位置关系是( )A. B. C. D. 阅卷人二、填空题(共4题,共20分)得分13. 已知空间三点A(1,1,1)、B(﹣1,0,4)、C(2,﹣2,3),则与的夹角θ的大小是14. 向量=(2,-1,4),与=(-1,1,1)的夹角的余弦值为15. (理)已知平面α和平面β的法向量分别为 =(1,1,2), =(x,﹣2,3),且α⊥β,则x=16. 在棱长为1的正方体ABCD﹣A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为.17. 如图,四棱锥中,底面ABCD是边长为2的正方形,,,且.(1) 求证:面;(2) 在线段PD上是否存在点E ,使平面PAB与平面ACE所夹角的余弦值为?若存在,找出点E的位置:若不存在,请说明理由.18. 如图,已知三棱柱,,,为线段上的动点,.(1) 求证:平面平面;(2) 若, D为线段的中点,,求与平面所成角的余弦值.19. 如图,已知三棱锥D-ABC中,二面角A-BC-D的大小为90°,且∠BDC=90°,∠ABC=30°,BC=3,.(1) 求证:AC⊥平面BCD;(2) 二面角B-AC-D为45°,且E为线段BC的中点,求直线AE与平面ACD所成的角的正弦值.20. 如图,四边形是矩形,四边形是梯形,,平面平面,,点是的中点.(1) 求证:∥平面;(2) 求二面角的余弦值.21. 如图,四棱台中,底面,平面平面为的中点.(1) 证明:;(2) 若,且,求点到平面的距离.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)(1)(2)19.(1)(2)20.(1)(2)21.(1)(2)。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学苏教版 必修二立体几何初步强化训练(17)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)641.某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A. B. C.D. 2. 已知在正四面体 中,为 的中点,则直线与 所成角的余弦值为( )A.B.C.D.平面 平面3. 已知如图正方体 中,P 为棱 上异于其中点的动点,Q 为棱 的中点,设直线m 为平面 与平面的交线,以下关系中正确的是( )A. B. C. D.4. 三棱锥中, , 则三棱锥的外接球表面积的最小值为()A.B. C. D.5. 长方体中,,,,则异面直线与成角余弦值为( )A. B. C. D.6.若正三棱柱的三视图如图所示,该三棱柱的表面积是()A. B. C. D.35,2036,2035,2136,217. “端午节”为中国国家法定节假日之一,已被列入世界非物质文化遗产名录,吃粽子便是端午节食俗之一.全国各地的粽子包法各有不同.如图,粽子可包成棱长为的正四面体状的三角粽,也可做成底面半径为,高为(不含外壳)的圆柱状竹筒粽.现有两碗馅料,若一个碗的容积等于半径为的半球的体积,则这两碗馅料最多可包三角粽或最多可包竹筒粽的个数为(参考数据:)()A. B. C. D. 若l 1∥α,α∥l 2 , 则l 1∥l 2若l 1⊥α,l 2⊥α,则l 1⊥l 2若l 1∥l 2 ,,,,则l 1∥l 3若α⊥β,,,则l 1∥l 28. 设l 1 , l 2 , l 3是三条不同的直线,α,β,γ是三个不同的平面,则下列命题是真命题的是( )A. B. C. D. 与相交但不一定垂直9. 平面平面 ,, , ,则( )A.B.C.D. 10. 已知正方体 中,以下结论错误的有( )点P 在直线BC 1上运动时,三棱锥A-D 1PC 的体积不变点P 在直线BC 1上运动时,直线AP 与平面AD 1C 所成角的大小不变点P 在直线BC 1上运动时,二面角P-AD 1-C 的大小不变M 是平面上到点D 和C 1距离相等的点,则点M 的轨迹是过点D 1的直线A. B. C. D. 8πcm 212πcm 216πcm 220πcm 211. 一个体积为8cm 3的正方体的顶点都在球面上,则球的表面积是( )A. B. C. D. 12. 已知三棱锥的所有顶点都在球的表面上,是边长为的等边三角形,若三棱锥体积的最大值是, 则球的表面积是( )A. B. C. D.13. 日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬 ,则晷针与点A 处的水平面所成角的大小为 .14. 如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=4cm ,则三棱锥A 1ABD 的体积为 cm 3 .15. 在正四棱锥中,已知 , 为底面的中心,以点为球心作一半径为的球,则平面截该球的截面面积为 .16. 在正四棱柱中,底面的边长为,与底面所成角的大小为,则该正四棱柱的高等于17. 如图一,在等腰梯形中,是的中点,将沿折起,使点到点的位置,且,如图二.(1) 求证:平面平面;(2) 求平面与平面的夹角的余弦值.18. 在如图所示的多面体中,,平面.(Ⅰ)证明:平面;(Ⅱ)若,,求三棱锥的体积.19. 如图,是一个三棱锥,是圆的直径,是圆上的点,垂直圆所在的平面,,分别是棱,的中点.(1) 求证:平面;(2) 若二面角是,,求与平面所成角的正弦值.20. 如图,已知四棱锥的底面是平行四边形,侧面PAB是等边三角形,,,.(1) 求证:面面ABCD;(2) 设Q为侧棱PD上一点,四边形BEQF是过B,Q两点的截面,且平面BEQF,是否存在点Q,使得平面平面PA D?若存在,确定点Q的位置;若不存在,说明理由.21. 如图,在三棱锥中, .(1) 画出二面角的平面角,并求它的度数;(2) 求三棱锥的体积.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)18.19.(1)(2)20.(1)(2)21.(1)(2)。

高一立体几何试题及答案一、选择题(每题4分,共40分)1. 若一个长方体的长、宽、高分别为a、b、c,则该长方体的体积为()A. abcB. ab+bc+acC. a^2b^2c^2D. a^2+b^2+c^2答案:A2. 一个正方体的棱长为a,则其表面积为()A. 6a^2B. 8a^2C. 10a^2D. 12a^23. 一个圆柱的底面半径为r,高为h,则其体积为()A. πr^2hB. 2πr^2hC. πr^3D. 2πr^3答案:A4. 一个圆锥的底面半径为r,高为h,则其体积为()A. 1/3πr^2hB. 1/2πr^2hC. πr^2hD. 2πr^2h答案:A5. 一个球的半径为r,则其体积为()B. 2/3πr^3C. 1/3πr^3D. 3/4πr^3答案:A6. 若一个三棱锥的四个顶点分别为A、B、C、D,且AB=AC=AD=BC=BD=CD=a,则该三棱锥为()A. 正四面体B. 正三棱锥C. 正六棱锥D. 正八棱锥答案:A7. 若一个三棱柱的底面为等边三角形,且侧棱与底面垂直,则该三棱柱为()B. 斜三棱柱C. 直三棱柱D. 正六棱柱答案:A8. 若一个四棱锥的底面为正方形,且侧棱与底面垂直,则该四棱锥为()A. 正四棱锥B. 斜四棱锥C. 直四棱锥D. 正八棱锥答案:A9. 若一个五棱锥的底面为正五边形,且侧棱与底面垂直,则该五棱锥为()B. 斜五棱锥C. 直五棱锥D. 正十棱锥答案:A10. 若一个六棱锥的底面为正六边形,且侧棱与底面垂直,则该六棱锥为()A. 正六棱锥B. 斜六棱锥C. 直六棱锥D. 正十二棱锥答案:A二、填空题(每题4分,共20分)11. 一个长方体的长、宽、高分别为a、b、c,则该长方体的表面积为______。
答案:2(ab+bc+ac)12. 一个正方体的棱长为a,则其体积为______。
答案:a^313. 一个圆柱的底面半径为r,高为h,则其侧面积为______。

高一数学立体几何练习题及答案一、选择题1. 下列哪个图形不是立体图形?A. 立方体B. 圆锥C. 圆柱D. 正方形答案:D2. 已知一个立方体的边长为5cm,求它的表面积和体积分别是多少?A. 表面积:150cm²,体积:125cm³B. 表面积:100cm²,体积:125cm³C. 表面积:150cm²,体积:100cm³D. 表面积:100cm²,体积:100cm³答案:A3. 以下哪个选项可以形成一个正方体?A. 六个相等的长方体B. 一个正方形和一个长方体C. 六个相等的正方形D. 一个正方形和一个正方体答案:C4. 以下哪个图形可以形成一个圆柱?A. 一个正方形和一个长方体B. 一个圆和一个长方体C. 一个长方形和一个长方体D. 一个正方形和一个正方体答案:C5. 以下哪个选项可以形成一个圆锥?A. 一个圆和一个长方体B. 一个圆和一个正方体C. 一个正方形和一个长方体D. 一个正方形和一个正方体答案:B二、填空题1. 已知一个正方体的表面积为96cm²,求它的边长是多少?答案:4cm2. 已知一个圆柱的半径为3cm,高为10cm,求它的表面积和体积分别是多少?答案:表面积:198cm²,体积:90π cm³3. 以下哪个选项可以形成一个长方体?A. 六个相等的正方形B. 一个圆和一个长方形C. 六个相等的长方形D. 一个正方形和一个正方体答案:C三、解答题1. 某长方体的长、宽、高分别为3cm、4cm、5cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)表面积 = 2(长×宽 + 长×高 + 宽×高)= 2(3×4 + 3×5 + 4×5)= 2(12 + 15 + 20)= 2(47)= 94cm²(2)体积 = 长×宽×高= 3×4×5= 60cm³2. 某圆锥的半径是5cm,高是12cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)斜面积= π×半径×斜高= π×5×13≈ 204.2cm²(2)体积= (1/3)π×半径²×高= (1/3)π×5²×12≈ 314.2cm³四、解析题某正方体的表面积是96cm²,它的边长是多少?解答:设正方体的边长为x,由表面积的计算公式可得:表面积 = 6x²96 = 6x²16 = x²x = 4所以,该正方体的边长为4cm。

立体几何0215、如图 ,直三棱柱111ABC A B C -的体积为8 ,且2AB AC == ,∠=90BAC ,E 是1AA 的中点 ,O 是11C B 的中点 求异面直线1C E 与BO 所成角的大小. (结果用反三角函数值表示 )E OCAA1C1B1B【答案】解:由18V S AA =⋅=得14AA = ,………………………3分 取BC 的中点F ,联结AF ,EF ,那么1//C F BO ,所以1EC F ∠即是异面直线1C E 与BO 所成的角 ,记为θ. ………………………5分2118C F = ,218C E = ,26EF = ,………………………8分 22211115cos 26C F C E EF C F C E θ+-==⋅ ,………………………11分因而5cos 6arc θ=………………………………………………12分16、如图四棱锥ABCD P -中的底面是边长为6的正方形 ,侧棱PA 的长为8 ,且垂直于底面 ,点N M 、分别是AB DC 、的中点.求F EOBB1C1A1AC(1 )异面直线PM 与CN 所成角的大小 (结果用反三角函数值表示 );(2 )四棱锥ABCD P -的外表积 【答案】(1 )解法 一:连结AM ,可证CN ∥AM ,直线PM 与AM 所成角等于直线PM 与CN 所成角. …………………………2分 因为PA 垂直于底面,所以AM PA ⊥,点M 分别是DC 的中点, 6=DC 53=∴AM 在PAM Rt ∆中,8=PA ,53=AM ,1558538tan ==∠PMA ,1558arctan=∠∴PMA …………………………4分即异面直线PM 与CN 所成角的大小为1558arctan .…………………………6分 解法二:以A为坐标原点建立空间直角坐标系可得)0,6,3(M ,)8,0,0(P ,)0,0,3(N ,)0,6,6(C ,)8,6,3(-=∴PM ,)0,6,3(--=∴CN…………………………2分直线PM 与CN 所成角为θ ,向量CN PM 与的夹角为ϕ10954534510945cos -=⋅-==CNPM CN PM ϕ …………………………4分 又1095453cos cos ==ϕθ ,1095453arccos =θ , 即异面直线PM 与CN 所成角的大小为1095453arccos .…………………………6分 (说明:两种方法难度相当 )(2) 因为PA 垂直于底面,所以AB PA ⊥ ,AD PA ⊥即PAB Rt ∆≌PDC Rt ∆PB BC BCAB BCPA ⊥⇒⎩⎨⎧⊥⊥ ,同理PD CD ⊥PBC Rt ∆∴≌PAD Rt ∆…………8分 底面四边形ABCD 是边长为6的正方形 ,所以36=底S 又PAB S S ∆=侧PAD S ∆+PBCS ∆+PCDS ∆+1086048)21(2)21(2=+=⋅⨯+⋅⨯=BC PB AB PA14436108=+=表S所以四棱锥ABCD P -的外表积是144 …………………………………………12分16、如图 ,△ABC 中 ,090=∠ACB ,030=∠ABC ,3=BC ,在三角形内挖去一个半圆(圆心O 在边BC 上 ,半圆与AC 、AB 分别相切于点C 、M ,与BC 交于点N ) ,将△ABC绕直线BC 旋转一周得到一个旋转体 .(1 )求该几何体中间一个空心球的外表积的大小;(2 )求图中阴影局部绕直线BC 旋转一周所得旋转体的体积.【答案】解 (1 )连接OM ,那么AB OM ⊥2,1,30,30==∴=∠=AB AC ABC BC , …………3分设r OM = ,那么r OB 2= ,又r OB -=3 ,所以33,32=-=r r r ,…………6分所以 ,.34r 42ππ==球表S …………8分 (2 ).273534AC 3132πππ=-⨯⨯=-=r BC V V V 球圆锥…………12分17、如图 ,在三棱锥ABC P -中 ,⊥PA 底面ABC ,BC AC ⊥ ,2===PA BC AC .(1 )求三棱锥ABC P -的体积V ;(2 )求异面直线AB 与PC 所成角的大小.【答案】 (1 )因为⊥PA 底面ABC ,所以三棱锥ABC P -的高PA h = ,………… (3分 ) 所以 ,34213131=⋅⋅⋅⋅==PA BC AC Sh V .………… (6分 ) (2 )取PA 中点E ,PB 中点F ,BC 中点G ,连结EF ,FG ,EG ,那么EF ∥AB ,FG ∥PC ,所以EFG ∠就是异面直线AB 与PC 所成的角 (或其补角 ).………… (2分 ) 连结AG ,那么522=+=CG AC AG ,…… (3分 )622=+=AG EA EG , ………… (4分 )又22==PC AB ,所以2==FG EF .………… (5分 )在△EFG 中 ,212cos 222-=⋅-+=∠FG EF EG FG EF EFG ,…… (7分 ) PABG P ABC FE故︒=∠120EFG .所以异面直线AB 与PC 所成角的大小为︒60.………… (8分 )18、如图 ,四面体ABCD 中 ,O 、E 分别是BD 、BC 的中点 ,AO ⊥平面BCD ,2CA CB CD BD ====.(1 )求三棱锥A BCD -的体积; (2 )求异面直线AE 与CD 所成角的大小.【答案】(1 )因为CO,AO =1所以113V ==. (2 )因为O 、E 为中点 ,所以OE//CD ,所以AEO ∠的大小即为异面直线AE 与CD 所成角 . 在直角三角形AEO 中 ,=4AEO π∠ ,所以异面直线AE 与CD 所成角的大小为4πAB EODC。

立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 4 3.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( ) A 1个 或2个 B 0个或1个 C 1个 D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直 7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个 8.下列条件中,能判断两个平面平行的是( ) A 一个平面内的一条直线平行于另一个平面; B 一个平面内的两条直线平行于另一个平面 C 一个平面内有无数条直线平行于另一个平面 D 一个平面内任何一条直线都平行于另一个平面 9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( ) A //,,m n n m βα⊥⊂ B //,,m n n m βα⊥⊥ C ,,m n m n αβα⊥=⊂ D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( ) A 1个 B 2个 C 3个 D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。

立体几何011、假设一个圆锥的轴截面是边长为4cm 的等边三角形 ,那么这个圆锥的侧面积为 2cm 【答案】8π 【解析】因为圆锥的轴截面是边长为4cm 的等边三角形 ,所以母线4l = ,底面半径2r = .所以底面周长24c r ππ== ,所以侧面积为1144822lc ππ=⨯⨯= .2、如下列图 ,一个空间几何体的三视图 ,那么该几何体的体积为俯视图左视图主视图【答案】2323π+【 解析】由三视图可知该几何下面是圆柱 ,上面是四棱锥 .圆柱的底面半径为1 ,高为2 所以圆柱的体积为2π .四棱锥的高为2213-= ,四棱锥底面边长为2 ,所以四棱锥的体积为2123(2)333⨯⨯= ,所以该几何体的体积为2323π+ .3、正方体1111D C B A ABCD -中 ,异面直线C B 1与D C 1所成的角的大小为【答案】【 解析】连结11AC ,1A D ,那么11//AD B C ,所以11D BC ∠为直线1BD 与平面11B BCC 所成的角 ,所以设正方体的边长为 1 ,那么12BC = ,所以1111112tan 22D C D BC BC === ,所以11D BC ∠2arctan2= .4、 三棱锥S ABC -中 ,E 、F 、G 、H 分别为SA 、AC 、BC 、SB 的中点 ,那么截面EFGH 将三棱锥S ABC -分成两局部的体积之比为【答案】1:1【 解析】因为E 、F 、G 、H 分别为SA 、AC 、BC 、SB 的中点 ,所以四边形EFGH 为平行四边形 ,SC 平行平面EFGH 且AB 平行平面EFGH ,且SC 和AB 到平面EFGH 的距离相同 .每一局部都可以可作是一个三棱锥和一个四棱锥两局部的体积和 .如图1中连接DE 、DF ,V ADEFGH =V D ﹣EFGH +V D ﹣EFA :图2中 ,连接BF 、BG ,V BCEFGH =V B ﹣EFGH +V G ﹣CBF E ,F ,G 分别是棱AB ,AC ,CD 的中点 ,所以V D ﹣EFGH =V B ﹣EFGH V D ﹣EFA 的底面面积是V G ﹣CBF 的一半 ,高是它的2倍 ,所以二者体积相等.所以V ADEFGH :V BCEFGH =1:15、正三棱柱的底面正三角形边长为2 ,侧棱长为3 ,那么它的体积=V . 【答案】33【 解析】正三棱柱的底面面积为12222⨯⨯⨯=,所以体积为. 6、假设圆柱的侧面展开图是一个正方形 ,那么它的母线长和底面半径的比值是 .【答案】π2【解析】设圆柱的底面半径为r ,母线为l ,那么2l r π= ,所以2l rπ= .7、假设圆椎的母线cm 10=l ,母线与旋转轴的夹角030=α,那么该圆椎的侧面积为 2cm【答案】50π【 解析】因为线与旋转轴的夹角030=α ,设底面圆的半径为r ,那么010sin305r == .所以底面圆的周长210c r ππ== ,所以该圆锥的侧面积1110105022lc ππ=⨯⨯= .8、123,,l l l 是空间三条不同的直线 ,以下命题中正确的选项是 ( )A 如果1223,l l l l ⊥ ,那么13l l ⊥B 如果1223,l l l l ,那么123,,l l l 共面C 如果1223,l l l l ⊥⊥ ,那么13l l ⊥D 如果123,,l l l 共点 ,那么123,,l l l 共面【答案】A【 解析】根据线面垂直和平行的性质可知 ,A 正确 ,所以选A9、一个圆锥的侧面展开图是一个半径为R 的半圆 ,那么这个圆锥的底面积是________. 【答案】24R π【 解析】因为圆锥的侧面展开图是一个半径为R 的半圆 ,所以圆锥的 ,母线l R =,设圆锥底面圆的半径为r ,那么2r R ππ=,即2R r =,所以圆锥的底面积是222()24R R r πππ==10、,,,A B C D 是空间四点 ,命题甲:,,,A B C D 四点不共面 ,命题乙:直线AC 和BD 不相交 ,那么甲是乙成立的 [答]( )(A )充分不必要条件(B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件 【答案】A【 解析】假设,,,A B C D 四点不共面 ,那么直线AC 和BD 不共面 ,所以AC 和BD 不相交 .假设直线AC 和BD 不相交 ,AC 和BD 平行时 ,,,,A B C D 四点共面 ,所以甲是乙成立的充分不必要条件 ,选A11、长方体的三条棱长分别为1 ,1 ,2 ,并且该长方体的八个顶点都在一个球的球面上 ,那么此球的外表积为____________.【答案】6π【 解析】因为长方体的八个顶点都在一个球的球面上 ,那么长方体的体对角线为球的直径 ,2r = ,所以球半径2r = ,所以球的外表积为22446r πππ== . 12、m ,n 是两条不同直线 ,βα,是两个不同平面 ,以下命题中的假命题的是 ( )A βαβα//,,则若⊥⊥m mB αα⊥⊥n m n m 则若,,//C n m n m //,,//则若=βααD βαβα⊥⊂⊥则若,,m m【答案】C【 解析】C 中 ,当m β⊂时 ,直线//m n ,当m β⊄时 ,直线//m n 不一定成立 ,所以C 为假命题 ,选C13、假设圆锥的侧面展开图是半径为1cm 、圆心角为180︒的半圆 ,那么这个圆锥的轴截面面积等于【答案】4【 解析】因为半圆的周长为π ,所以圆锥的母线为1 .设圆锥的底面半径为r ,那么2r ππ= ,所以12r =.= ,所以圆锥的轴截面面积为11222⨯⨯= .14、半径为R 的球的球面上有三个点 ,其中任意两点间的球面距离都等于3R π ,且经过这三个点的小圆周长为4π ,那么R = .【答案】【 解析】设三点分别为A 、B 、C ,球心为O ,由题意知∠AOB =∠AOC =∠BOC =3π ,所以AB =BC =CA =R ,所以,小圆周长为24ππ= ,解得R =。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学人教A 版选修一空间向量与立体几何专项提升(19)姓名:____________班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)必要不充分条件充分不必要条件充要条件既不充分也不必要条件1. 已知空间任意一点O 和不共线的三点A ,B ,C ,若 ,则“ ”是“A ,B ,C,D 四点共面”的( )A. B. C. D.2. 如图,四面体 -,是底面△的重心,,则( )A. B. C. D.30°45°60°120°3. “阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美如图.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”,则异面直线AB 与CD 所成角的大小是( )A. B. C. D. 4. 在平面ABCD 中,A (0,1,1),B (1,2,1),C (-1,0,-1),若a =(-1,y ,z ),且a 为平面ABC 的法向量,则y 2等于( )201无意义A. B. C. D. 5. 如图,已知正方体的上底面中心为,点为上的动点,为的三等分点(靠近点),为的中点,分别记二面角,,的平面角为,则()A. B. C. D.(2,3,3)(﹣2,﹣3,﹣3)(5,﹣2,1)(﹣5,2,﹣1)6. 空间四边形ABCD 中,若向量=(﹣3,5,2),=(﹣7,﹣1,﹣4)点E ,F 分别为线段BC ,AD 的中点,则的坐标为( )A. B. C. D. 7. 已知直线, 的方向向量分别为,, 则直线, 夹角的余弦值为( )A. B. C. D.8. 已知正方形的边长为2, ,分别为 ,的中点,沿 ,将三角形 ,折起,使得点 ,恰好重合,记为点 , 则与平面所成角的正弦值为()A. B. C. D.9. 阅读材料:空间直角坐标系中,过点且一个法向量为的平面的方程为, 阅读上面材料,解决下面问题:已知平面的方程为 , 直线是两平面与的交线,则直线与平面所成角的正弦值为( )A.B.C.D.10. 点P 是棱长为1的正方体ABCD ﹣A 1B 1C 1D 1内一点,且满足=++ , 则点P 到棱AB 的距离为( )A. B. C. D.四点O ,A ,B ,C 必共面四点P ,A ,B ,C 必共面四点O ,P ,B ,C 必共面五点O ,P ,A ,B ,C 必共面11. 对于空间任意一点O 和不共线的三点A ,B ,C ,有如下关系: ,则( )A. B. C. D. A 、B 、DA 、B 、CB 、C 、DA 、C 、D12. 已知向量 、 ,且 = +2 , =-5 +6 , =7 -2 ,则一定共线的三点是( )A. B. C. D. 13. 如图,在四棱锥中, , 分别是 , 的中点,底面 , , ,, 若平面平面, 则二面角的正弦值是 .14. 已知空间向量 , ,若 ,则 .15. 已知四棱锥 的底面是边长为4的正方形, 面 ,点 、 分别是 的中点, 为上一点,且 , 为正方形 内一点,若 //面 ,则 的最小值为 .16. 已知平面 的一个法向量 , , ,且 ,则直线 与平面 所成的角为 .17. 在斜三棱柱 中, 是边长为 的正三角形,侧棱 ,顶点 在面 的射影为 边的中点 .(1) 求证:面 面 ;(2) 求面与面所成锐二面角的余弦值.18. 如图,已知矩形ABCD 所在平面外一点P ,平面ABCD , E 、F 分别是AB 、PC 的中点.(1) 求证:共面;(2) 求证:.19. 如图,在三棱柱中,侧棱底面 ,且 , 是棱的中点,点在侧棱上运动.(1) 当是棱的中点时,求证:平面;(2) 当直线与平面所成的角的正切值为时,求二面角的余弦值.20. 已知四点A(2,3,1),B(﹣5,4,1),C(6,2,﹣3),D(5,﹣2,1),求通过点A且垂直于B,C,D所确定的平面的直线方程.21. 如图,在四棱锥中,四边形ABCD是菱形,,,三棱锥是正三棱锥,E,F分别为,的中点.(1) 求证:直线平面SAC;(2) 求二面角的余弦值;(3) 判断直线SA与平面BDF的位置关系.如果平行,求出直线SA与平面BDF的距离;如果不平行,说明理由.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.16.17.(1)(2)18.(1)(2)(1)(2)20.(1)(2)(3)。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年广东省广州市高中数学人教A 版选修一空间向量与立体几何强化训练(16)姓名:____________ 班级:____________学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)341. 设 ,向量, , ,且 , ,则 ( )A. B. C. D. 2. 正四面体的内切球球心到一个面的距离等于这个正四面体高的( )A.B.C.D.3. 如图,直三棱柱底面是直角三角形,且 , E ,F ,G 分别为 , , 的中点,则EF 与平面所成角的正弦值为( )A. B. C. D.若两条直线和同一个平面所成的角相等,则这两条直线平行若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行4. 下列命题正确的是( )A. B. C.若两个平面都垂直于第三个平面,则这两个平面平行D. 5. 如图,在三棱锥中 ,点D 是棱AC 的中点 ,若,,,则等于()A. B. C. D.与夹角的余弦值为6. 已知空间向量,,则下列结论不正确的是( )A.B.C. D. --不确定,与μ值相关7. 已知,,若,则λ的值为( )A.B. C. D. 8. 在三棱锥中,底面ABC ,,,,则点C 到平面PAB 的距离是A. B. C. D.-10109. 已知空间向量 ,, 且 , 则的值为( )A. B. C. D.60°45°30°75°10. 正四棱锥中,O 为顶点在底面内的投影,P 为侧棱SD 的中点,且, 则直线BC 与平面PAC 的夹角是( )A. B. C. D. (4,﹣1,2)(﹣4,﹣1,2)(﹣4,1,2)(4,﹣1,﹣2)11. 若空间向量=(1,﹣2,1),=(1,0,2),则下列向量可作为向量 ,所在平面的一个法向量的是( )A. B. C. D. 12. 空间四边形ABCD 中,若向量,,点E,F 分别为线段BC,AD 的中点,则的坐标为()A. B. C. D.13. 已知正四面体的棱长为,为的中心,为上一点且满足、、两两垂直.过点作平面,其中、、位于平面的同一侧,是平面的单位法向量且指向另外一侧,、两点到平面的距离分别为1和 .以为坐标原点,、、为、、轴建立空间直角坐标系(如图所示),则的坐标为 .14. 如图所示,长方体中,,,点是线段的中点,点是正方形的中心,则直线与直线所成角的余弦值为15. 如图,已知, D是中点,则点B到平面的距离是 .16. 两平行平面α、β相距18cm,直线l与平面α、β分别交于A、B两点,点P∈l,若PA= PB,则点P到平面β的距离为.阅卷人三、解答得分17. 已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为,连接PB,如图2所示.(Ⅰ)求证:平面PMN⊥平面BCNM;(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.18. 如图,在三棱柱中,侧棱垂直于底面,、分别是、的中点,是边长为的等边三角形, .(1) 求证:平面;(2) 求点到平面的距离.19. 如图1,平面图形是一个直角梯形,其中,是上一点,且.将沿着折起使得平面平面,连接,分别是的中点,如图2.(1) 证明:在图2中四点共面,且平面平面;(2) 在图2中,若是线段上一个动点,当直线与平面所成角的正弦值取得最大值时,求的长.20. 如图所示,在梯形CDEF中,四边形ABCD为正方形,且,将沿着线段AD折起,同时将沿着线段BC折起.使得E,F两点重合为点P.(1) 求证:平面平面ABCD;(2) 求点D到平面PBC的距离h.21. 如图,三棱锥中,底面和侧面都是等边三角形, .(1) 若P点是线段的中点,求证:平面;(2) 点Q在线段上且满足,求与平面所成角的正弦值.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.(1)(2)(1)(2)(1)(2)(1)(2)。
高一数学立体几何练习题
一、选择题(下列各题中只有一个选项正确,每题4分,共40分)
1、下列说法正确是[ D ]。
A.圆台是直角梯形绕其一边旋转而成
B.圆锥是直角三角形绕其一边旋转而成
C.圆柱的母线和它的底面不垂直。
D.圆台可以看作是平行于底面的平面截一个圆锥而得到的。
2、下列说法错误的是[ B ]。
A、用斜二测画法画出的直观图是在平行投影下画得的空间图形
B、几何体直观图中的长、宽、高与几何体的长、宽高的比例相同。
C、水平放置的矩形的直观图一定是平行四边形。
D、水平放置的圆的直观图一定是椭圆。
3、底面放置在同一平面的一个圆柱和一个圆锥,底面积相同且体积相等, 用通过圆柱中截面的平面截圆锥和圆柱所得两个截面的面积之比是 [ A ] 。
A. 25∶36
B. 9∶16
C. 4∶9
D. 5∶6
4、下列命题中,真命题的是 [ B ] 。
A.两两相交的三条直线共面
B.对角线交于一点的四边形一定是平面图形
C.不共面的四点中可以有三点共线
D.边长相等的四边形一定是菱形
5、下列条件能得到直线l1,l2互相平行的是 [ D ] 。
A.l1,l2都平行于同一个平面
B.l1,l2与同一个平面所成的角相等
C.l1平行于l2所在的平面
D.l1,l2都垂直于同一个平面
6、下列四个命题中正确的是[ B ] 。
①两个平面没有公共点,则这两个平面平行
②一个平面内有三个点到另一个平面的距离(距离不为零)相等,则这两个平面平行
③一个平面内任一点到另一个平面的距离(距离不为零)都相等,则这两个平面平行
④一个平面内有无数个点到另一个平面的距离(距离不为零)相等,则这两个平面平行.
A.①②B.①③C.①②③D.①②③④
7、如果直线a平行于平面β,那么 [ D ] 。
A.平面β内不存在与a垂直的直线
B.平面β内有且只有一条直线与a垂直
C.平面β内有且只有一条直线与a平行
D.平面β内有无数多条直线与a不平行
8、已知直线l⊥平面α,直线mβ,有如下四个命题:①α∥βl⊥m,②α⊥βl∥m,③l∥mα⊥β,l⊥mα∥β,其中正确命题是 [ C ]
A.③④B.①②C.①③D.②④
9、平面α内有三条相交于一点的直线, 另有一条直线与它们所成的角都相等, 则此直线与平面α的关系是 [ B ]。
A.平行
B.垂直
C.斜交
D.以上答案都不对
10、已知a、b是异面直线,下面结论中不正确的是[ C ]。
A.存在着无数个平面与a、b都平行
B.存在着一个平面与a、b等距离
C.存在着一个平面与a、b都垂直
D.存在着无数条直线与a、b都垂直
二、填空题(每小题4分,共20分)
1、如图,四面体ABCD中,CD=4,AB=2,E、F分别为AC、BD的中点,EF=,则AB与CD所成角的大小
是_________.
2、平面α∥平面β,直线a与平面α所成的角和直线b与平面β所成的角相等,则直线a与直线b
的位置关系是_________.
3、如图所示,∠BAD=的等腰Rt△ABD与正三角形CBD所在面互相垂直,E是BC中点,则AE与平面BCD所成角的大小为________.
4、把半径为R的球削成长方体,这样得到的长方体体积最大值是_________.
5、一个正四棱锥底面一边的长为1,侧棱长也都是1,求它的表面积是__________,体积是_________。
三、解答题(每小题8分,共40分)
1、如图,的交线并说明理由.
2、求证:如果一条直线和两个相交平面平行,那么这条直线和这两个平面的交线平行.
3、已知a、b为异面直线,平面α过a与b平行,平面β过b与a平行.
求证α∥β.
4、如图,平面AOB,平面BOC,平面AOC两两垂直,且OA=OB=OC,求平面ABC与平面BOC的夹角的余弦.
5、解答题
如图,已知空间四边形ABCD中,AB⊥CD,EF为AB、CD的公垂线.
①求证平面ABF⊥平面BCD.②在△ABF中作AO⊥BF,求直线AO与BC所成的角。
高一数学立体几何练习题答案
一、选择题(下列各题中只有一个选项正确,每题4分,共40分)
1—5 DBABD 6—10 BDCBC
二、填空题(每小题4分,共20分)
1、2、平行、相交或异面都有可能3、
4、 5、16
三、解答题(每小题8分,共40分)
1.作图提示:作直线AB交直线a于点E。
2、如图,已知:a∥α,α∥β,α∩β=b
证明:设A∈α,且A b,过a及A作平面γ交平面α于c.∵a∥α∴a∥c
同理,过a及B作平面δ交平面β于d,则a∥d ∴c∥d
又dβ,cβ∴c∥β
又cα,α∩β=b ∴c∥b 又a∥c ∴a∥b
3.
4.提示;取BC中点E,连结AE,OE。
5、连结AD、AF.。