北京市西城区2019届高三4月统一测试(一模)数学(文)试题有答案

2018-2019学年北京市西城区高三（上）期末数学试卷（文科）一、选择题（本大题共8小题，共40.0分）1.已知集合，，那么( )A. B.C. D.【答案】B【解析】【分析】先求出集合A，B，由此能求出A∩B．【详解】解：∵集合A＝{x|x＝2k，k∈Z}，B＝{x|x2≤5}＝{x|}，∴A∩B＝{﹣2，0，2}．故选：B．【点睛】本题考查交集的求法，考查交集定义、不等式性质等基础知识，考查运算求解能力，是基础题．2.下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（）A. B. C. D.【答案】C【解析】【分析】根据题意，依次分析选项中函数的奇偶性与单调性，综合即可得答案．【详解】根据题意，依次分析选项：对于A，y＝x2+2x为二次函数，其对称轴为x＝﹣1，不是偶函数，不符合题意；对于B，y＝x3，是奇函数，不符合题意；对于C，y＝ln|x|，是偶函数又在区间（0，+∞）上单调递增，符合题意；对于D，y＝cos x为偶函数，在区间（0，+∞）上不是单调函数，不符合题意，故选：C．【点睛】本题考查函数的奇偶性与单调性的判定，关键是掌握常见函数的奇偶性与单调性，属于基础题．3.一个四棱锥的三视图如图所示，那么这个四棱锥最长棱的棱长为（）A. B. C. D.【答案】C【解析】【分析】由三视图可知：该几何体如图所示，PA⊥底面ABCD，PA=2，底面是一个直角梯形，其中BC∥AD，AB⊥AD，BC=AB=1，AD=2．即可得出．【详解】解：由三视图可知：该几何体如图所示，PA⊥底面ABCD，PA=2，底面是一个直角梯形，其中BC∥AD，AB⊥AD，BC=AB=1，AD=2．可知其最长棱长为PD2．故选：C．【点睛】本题考查了四棱锥的三视图的有关计算，考查空间想象能力，属于基础题．4.设x，y满足约束条件，则z=x+3y的最小值为（）A. B. C. 1 D. 2【答案】A由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．【详解】解：由x，y满足约束条件作出可行域如图，联立，解得A（2，﹣1），化目标函数z＝x+3y为y，由图可知，当直线y过A时，直线在y轴上的截距最小，z有最小值为﹣1．故选：A．【点睛】本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题．5.执行如图所示的程序框图，若输入的m=1，则输出数据的总个数为（）A. 5B. 6C. 7D. 8【答案】B【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】解：模拟程序的运行，可得：m=1满足条件m∈（0，100），执行循环体，n=3，输出n的值为3，m=3满足条件m∈（0，100），执行循环体，n=7，输出n的值为7，m=7满足条件m∈（0，100），执行循环体，n=15，输出n的值为15，m=15满足条件m∈（0，100），执行循环体，n=31，输出n的值为31，m=31满足条件m∈（0，100），执行循环体，n=63，输出n的值为63，m=63满足条件m∈（0，100），执行循环体，n=127，输出n的值为127，m=127此时，不满足条件m∈（0，100），退出循环，结束．可得输出数据的总个数为6．故选：B．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．6.设数列是等比数列，则“”是“为递增数列”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】当时，虽然有，但是数列不是递增数列，所以不充分；反之当数列是递增数列时，则必有，因此是必要条件，应选答案B。

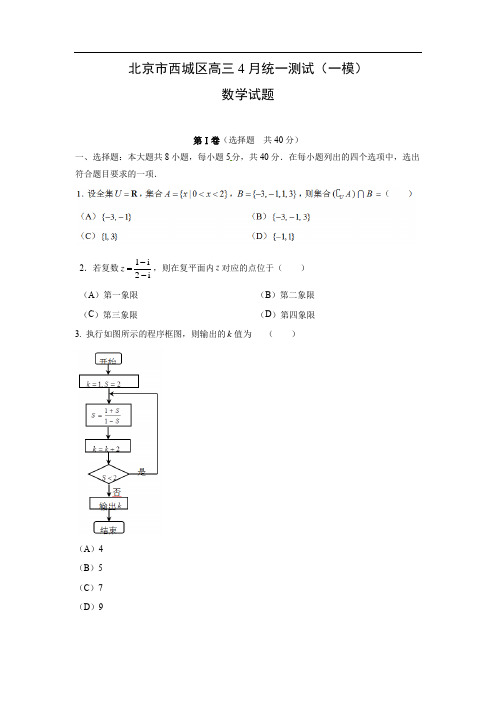
北京市西城区高三4月统一测试（一模）数学试题第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出 符合题目要求的一项．2．若复数1i2iz -=-，则在复平面内z 对应的点位于（ ） （A ）第一象限 （B ）第二象限 （C ）第三象限（D ）第四象限3. 执行如图所示的程序框图，则输出的k 值为 （ ）（A ）4 （B ）5 （C ）7 （D ）94．下列直线中，与曲线C ：12,()24x t t y t =+⎧⎨=-+⎩为参数没有公共点的是（ ） （A ）20x y += （B ）240x y +-= （C ）20x y -=（D ）240x y --=5. 设 ,,a b m 均为正数，则“b a >”是“a m ab m b+>+”的（ ） （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件 （D ）既不充分也不必要条件6．如图，阴影表示的平面区域W 是由曲线0x y -=，222x y +=所围成的. 若点(,)P x y 在W 内（含边界），则43z x y =+的最大值和最小值分别为（ ）（A）7-（B）-（C ）7，-（D ）7，7-7. 团体购买公园门票，票价如下表：11元/人现某单位要组织其市场部和生产部的员工游览该公园，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为990元，那么这两个部门的人数之差为（ ） （A ）20 （B ）30 （C ）35（D ）4013. 能说明“若sin cos αβ=，则36090k αβ+=⋅+，其中k ∈Z ”为假命题的一组α，β的值是___．14．如图所示，玩具计数算盘的三档上各有7个算珠，现将每档算珠分为左右两部分，左侧 的每个算珠表示数2，右侧的每个算珠表示数1（允许一侧无珠），记上、中、下三档的数字 和分别为a ，b ，c . 例如，图中上档的数字和9a =. 若a ，b ，c 成等差数列，则不同的 分珠计数法有____种.16．（本小题满分14分）如图，在多面体ABCDEF 中，梯形ADEF 与平行四边形ABCD 所在平面互相垂直，//AF DE ，DE AD ⊥，AD BE ⊥，112AF AD DE ===，AB =（Ⅰ）求证：//BF 平面CDE ； （Ⅱ）求二面角B EF D --的余弦值；（Ⅲ）判断线段BE 上是否存在点Q ，使得平面CDQ ⊥平面BEF ？若存在，求 出BQBE的值，若不存在，说明理由．17．（本小题满分13分）为培养学生的阅读习惯，某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动. 活动后，为了解阅读情况，学校统计了甲、乙两组各10名学生的阅读量（单位：本），统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以a 表示.（Ⅰ）若甲组阅读量的平均值大于乙组阅读量的平均值， 求图中a 的所有可能取值； （Ⅱ）将甲、乙两组中阅读量超过．．15本的学生称为“阅读达人”. 设3a ，现从所有“阅读达人”里任取3人，求其中乙组的人数X 的分布列和数学期望.（Ⅲ）记甲组阅读量的方差为20s . 在甲组中增加一名学生A 得到新的甲组，若A 的阅读量为10，则记新甲组阅读量的方差为21s ；若A 的阅读量为20，则记新甲组阅读量的方差为22s ，试比较 20s ，21s ，22s 的大小.（结论不要求证明）18．（本小题满分13分）设函数2()e 3x f x m x =-+，其中∈m R ．（Ⅰ）当()f x 为偶函数时，求函数()()h x xf x =的极值；（Ⅱ）若函数()f x 在区间[2,4]-上有两个零点，求m 的取值范围．19．（本小题满分14分）已知椭圆W :2214x y m m +=的长轴长为4，左、右顶点分别为,A B ，经过点(,0)P n 的直线与椭圆W 相交于不同的两点,C D （不与点,A B 重合）.（Ⅰ）当0n =，且直线CD ⊥x 轴时， 求四边形ACBD 的面积；（Ⅱ）设1n =，直线CB 与直线4x =相交于点M ，求证：,,A D M 三点共线.20．（本小题满分13分）如图，设A 是由n n ⨯(2)n ≥个实数组成的n 行n 列的数表，其中ij a (,1,2,,)i j n =表示位于第i 行第j 列的实数，且{1,1}ij a ∈-.[]定义1122st s t s t sn tn p a a a a a a =+++(,1,2,,)s t n =为第s 行与第t 行的积. 若对于任意,s t（st ），都有0st p =，则称数表A 为完美数表. （Ⅰ）当2n =时，试写出一个符合条件的完美数表； （Ⅱ）证明：不存在10行10列的完美数表；（Ⅲ）设A 为n 行n 列的完美数表，且对于任意的1,2,,i l =和1,2,,j k =，都有1ij a =，证明：kl n ≤.【参考答案】一、选择题：本大题共8小题，每小题5分，共40分.1．B 2．D 3．D 4．C 5．C 6．A 7．B 8．B 二、填空题：本大题共6小题，每小题5分，共30分. 9．1122n -- 10．311． π；a 12．4313．答案不唯一，如110α=，20β= 14．32注：第11题第一问3分，第二问2分.[三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）解：（Ⅰ）当3m =时，由题可知 2223a c b ac +-=，由余弦定理2222cos b a c ac B =+-， ……………… 3分得2223cos 22a cb B ac +-==． ……………… 4分这与cos [1,1]B ∈-矛盾，所以m 不可能等于3 . ……………… 6分 （Ⅱ）由（Ⅰ），得 1cos 22m B ==-，所以2π3B =. ……………… 7分因为b =4c =，222a c b ac +-=-， 所以216284a a +-=-，解得6a =-（舍）或2a =. ……………… 9分 在△ABC 中，由正弦定理sin sin a b A B=， ……………… 11分得sin2321 sin21427a BAb==⨯=. ……………… 13分16．（本小题满分14分）解：（Ⅰ）由底面ABCD为平行四边形，知//AB CD，又因为AB⊄平面CDE，CD⊂平面CDE，所以//AB平面CDE. ……………… 2分同理//AF平面CDE，又因为AB AF A=，所以平面//ABF平面CDE. ……………… 3分又因为BF⊂平面ABF，所以//BF平面CDE. ……………… 4分（Ⅱ）连接BD,因为平面ADEF⊥平面ABCD，平面ADEF平面ABCD AD=，DE AD⊥，所以DE⊥平面ABCD. 则DE DB⊥.又因为DE AD⊥，AD BE⊥，DE BE E=，所以AD⊥平面BDE，则AD BD⊥.故,,DA DB DE两两垂直，所以以,,DA DB DE所在的直线分别为x轴、y轴和z轴，如图建立空间直角坐标系，……………… 6分则(0,0,0)D ，(1,0,0)A ，(0,1,0)B ，(1,1,0)C -，(0,0,2)E ，(1,0,1)F ， 所以(0,1,2)BE =-,(1,0,1)EF =-，(0,1,0)=n 为平面DEF 的一个法向量. 设平面BEF 的一个法向量为(,,)x y z =m ， []由0BE ⋅=m ，0EF ⋅=m ，得20,0,y z x z -+=⎧⎨-=⎩令1z =，得(1,2,1)=m . ………………8分所以cos ,||||⋅<>=m n m n m n如图可得二面角B EF D --为锐角， 所以二面角B EF D --.………………10分 （Ⅲ）结论：线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF . ………………11分 证明如下：设(0,,2)([0,1])BQ BE λλλλ==-∈， 所以(0,1,2)DQ DB BQ λλ=+=-.设平面CDQ 的法向量为(,,)a b c =u ，又因为(1,1,0)DC =-，所以0DQ ⋅=u ，0DC ⋅=u ，即(1)20,0,b c a b λλ-+=⎧⎨-+=⎩……………… 12分若平面CDQ ⊥平面BEF ，则0⋅=m u ，即20a b c ++=， ……………… 13分 解得1[0,1]7λ=∈.所以线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF ，且此时17BQ BE =. …… 14分 17．（本小题满分13分）解：（Ⅰ）甲组10名学生阅读量的平均值为12681011121217211010+++++++++=，乙组10名学生阅读量的平均值为124412131616(10)20981010a a+++++++++++=. ……………… 2分 由题意，得981010a+>，即2a <. ……………… 3分 故图中a 的取值为0或1. ……………… 4分 （Ⅱ）由图可知，甲组“阅读达人”有2人，乙组“阅读达人”有3人.由题意，随机变量X 的所有可能取值为：1，2，3. ……………… 5分且212335C C 3(1)C 10P X ⋅===，122335C C 3(2)C 5P X ⋅===， 3335C 1(3)C 10P X ===. …… 8分 所以随机变量的分布列为：……………… 9分 所以3319()123105105E X =⨯+⨯+⨯=. ………………10分 （Ⅲ）222102s s s <<. ……………… 13分18．（本小题满分13分）解：（Ⅰ）由函数()f x 是偶函数，得()()f x f x -=， 即22e()3e 3xx m x m x ---+=-+对于任意实数x 都成立，所以0m =. ……………… 2分此时3()()3h x xf x x x ==-+，则2()33h x x '=-+.由()0h x '=，解得1x =±. ……………… 3分X当x 变化时，()h x '与()h x 的变化情况如下表所示：所以()h x 在(,1)-∞-，(1,)+∞上单调递减，在(1,1)-上单调递增. …………… 5分 所以()h x 有极小值(1)2h -=-，()h x 有极大值(1)2h =. ……………… 6分 （Ⅱ）由2()e 30xf x m x =-+=，得23ex x m -=.所以“()f x 在区间[2,4]-上有两个零点”等价于“直线y m =与曲线23()ex x g x -=，[2,4]x ∈-有且只有两个公共点”. ……………… 8分对函数()g x 求导，得223()e xx x g x -++'=. ……………… 9分由()0g x '=，解得11x =-，23x =. ……………… 10分 当x 变化时，()g x '与()gx 的变化情况如下表所示： 所以()g x 在(2,1)--，(3,4)上单调递减，在(1,3)-上单调递增. …………… 11分 又因为2(2)e g -=，(1)2e g -=-，36(3)(2)e g g =<-，413(4)(1)eg g =>-， 所以当4132e e m -<<或36e m =时，直线y m =与曲线23()ex x g x -=，[2,4]x ∈-有且只有两个公共点. 即当4132e e m -<<或36e m =时，函数()f x 在区间[2,4]-上有两个零点. ……… 13分 19．（本小题满分14分）解：（Ⅰ）由题意，得244a m ==， 解得1m =. ……………… 2分所以椭圆W 方程为2214x y +=. ……………… 3分当0n =，及直线CD ⊥x 轴时，易得(0,1)C ,(0,1)D -. 且(2,0)A -,(2,0)B . 所以||4AB =，||2CD =，显然此时四边形ACBD 为菱形，所以四边形ACBD 的面积为14242⨯⨯=. …… 5分（Ⅱ）当直线CD 的斜率k 不存在时，由题意，得CD 的方程为1x =， 代入椭圆W的方程，得C，(1,D ， 易得CB的方程为2)y x =-.则(4,M,(6,AM =,(3,AD =, 所以2AM AD =，即,,A D M 三点共线. ……………… 7分 当直线CD 的斜率k 存在时，设CD 的方程为(1)(0)y k x k =-≠，11(,)C x y ，22(,)D x y ，联立方程22(1), 1,4y k x x y =-⎧⎪⎨+=⎪⎩ 消去y ，得2222(41)8440k x k x k +-+-=. ……… 9分 由题意，得0∆>恒成立，故2122841k x x k +=+，21224441k x x k -=+. …………… 10分 直线CB 的方程为11(2)2y y x x =--. 令4x =，得112(4,)2y M x -. ……………… 11分 又因为(2,0)A -，22(,)D x y ，则直线AD ，AM 的斜率分别为222AD y k x =+，113(2)AM y k x =-， …………… 12分所以21211221123(2)(2)23(2)3(2)(2)AD AM y y y x y x k k x x x x --+-=-=+--+. 上式中的分子 211221123(2)(2)3(1)(2)(1)(2)y x y x k x x k x x --+=----+121225()8kx x k x x k =-++22224482584141k k k k k k k -=⨯-⨯+++0=，所以0AD AM k k -=.所以,,A D M 三点共线. ……………… 14分 20．（本小题满分13分） 解：（Ⅰ）答案不唯一. 如：……………… 3分（Ⅱ）假设存在10行10列的完美数表A . 根据完美数表的定义，可以得到以下两个结论：（1）把完美数表的任何一列的数变为其相反数（即1+均变为1-，而1-均变为1+），得到的新数表是完美数表；（2）交换完美数表的任意两列，得到的新数表也是完美数表. ……………… 5分 完美数表A 反复经过上述两个结论的变换，前三行可以为如下形式：在这个新数表中，设前三行中的数均为1的有x 列，前三行中“第1, 2行中的数为1，且第3行中的数为-1”的有y 列，前三行中“第1, 3行中的数为1，且第2行中的数为-1”的有z 列，前三行中“第1行中的数为1，且第2, 3行中的数为-1”的有w 列（如上表所示）， 则10x y z w +++=①由120p =，得x y z w +=+； ② 由130p =，得x z y w +=+； ③ 由230p =，得x w y z +=+. ④ 解方程组○1，○2，○3，○4，得52x y z w ====. 这与,,,x y z w ∈N 矛盾，所以不存在10行10列的完美数表. ……………… 8分 （Ⅲ）记第1列前l 行中的数的和112111l a a a X +++=，第2列前l 行中的数的和122222l a a a X +++= ，……，第n 列前l 行中的数的和12n n ln n a a a X +++=，因为对于任意的1,2,,i l =和1,2,,j k =，都有1ij a =，所以12k X X X l ====. ……………… 9分又因为对于任意,s t （st ），都有0st p =，所以22212n X X X ln +++=. ……………… 11分又因为22222221212n k X X X X X X l k ++++++=≥，所以2ln l k ≥，即kl n ≤. ……………… 13分。

北京市西城区 2018 — 2019 学年度第一学期期末试卷高三数学（文科）2019.1第Ⅰ卷（选择题共 40 分）一、选择题：本大题共 8 小题，每小题 5 分，共 40 分．在每小题列出的四个选项中，选出符合题目要求的一项．1. 设集合 A = {x | x > a }，集合 B ={-1,1, 2}，若A B = B ，则实数a 的取值范围是（ ）（A ） (1, +∞) （B ） (-∞,1)（C ）(-1, +∞)（D ）(-∞, -1)2. 下列函数中，值域为[0, +∞) 的偶函数是（）（A ） y = x 2 +1（B ） y = lg x（C ） y =| x |（D ） y = x cos x3. 设 M 是∆ABC 所在平面内一点，且 BM = MC ，则 AM =（）（A ） AB - AC（B ） AB + AC（C ） 1( AB - AC )2 （D ） 1( A B + AC )24．设命题 p ：“若e x > 1，则 x > 0 ”，命题 q ：“若a > b ，则 1 < 1”，则（）a b（A ）“ p ∧ q ”为真命题 （B ）“ p ∨ q ”为真命题 （C ）“ ⌝p ”为真命题（D ）以上都不对5. 一个几何体的三视图如图所示，那么这个几何体的表面积是（ ）（A ）16 + 2（B ）16 + 2正(主)视图侧(左)视图（C ） 20 + 2（D ） 20 + 2俯视图2 235351 1⎨ ⎩2 不超过 4 千米的里程收费 12 元;超过 4 千米的里程按每千米 2 元收费（对于其中不足千米的部分，若其小于0.5 千米则不收费，若其大于或等于 0.5 千米则按 1 千米收费）；当车程超过 4 千米时，另收燃油附加费 1 元.26. “mn < 0 ”是“曲线 x+y= 1是焦点在 x 轴上的双曲线”的（ ）mn（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件⎧ y - x ≤1,7. 设 x ，y 满足约束条件⎪x + y ≤3, ⎪ y ≥m ,若 z = x + 3y 的最大值与最小值的差为 7，则实数m =（ ）（A ） 3 2 （B ） - 32 （C ） 1 4 （D ） - 1 48. 某市乘坐出租车的收费办法如下：相应系统收费的程序框图如图所示，其中 x （单位：千米）为行驶里程， y （单位：元）为所 收费用，用[x ]表示不大于 x 的最大整数，则图中○1处应填（）（A ）y = 2[x - 1] + 4 2 （B ）y = 2[x - 1] + 5 2 （C ）y = 2[x + 1] + 4 2 （D ）y = 2[x + 1] + 5 2第Ⅱ卷（非选择题共 110 分）二、填空题：本大题共 6 小题，每小题 5 分，共 30 分．9. 已知复数 z 满足 z (1+ i) = 2 - 4i ，那么 z = .10.若抛物线C ：y 2 = 2 px 的焦点在直线x + y - 3 = 0 上，则实数 p = ；抛物线 C 的准线方程为.11. 某校某年级有 100 名学生，已知这些学生完成家庭作业的时间均在区间[0.5, 3.5) 内（单位：小时），现将这 100 人完成家 庭作业的时间分为 3 组：[0.5, 1.5) ，[1.5, 2.5) ，[2.5, 3.5) 加以统计，得到如图所示的频率分布直方图.在这 100 人中，采用分层抽样的方法抽取 10 名学生研究其视 力状况与完成作业时间的相关性，则在抽取样本中，完成作业的时间小于 2.5 个小时的有 人.12. 已知函数 f (x ) 的部分图象如图所示，若不等式-2 < f (x + t ) <4的解集为(-1, 2) ，则实数t 的值为.a 0.4 0.1O0.5 1.5 2.5 3.5时间(小时)13. 在∆ ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若sin A = cos( π- B ) ，a = 3，c = 2 ，则cos C = ；2∆ ABC 的面积为 .⎧64,x ≤0,14. 某食品的保鲜时间（t 单位：小时）与储藏温度 x （恒温，单位： C ）满足函数关系t = ⎨ ⎩2 kx +6 ,x > 0.且该食品在4 C 的保鲜时间是 16 小时.○1 该食品在8 C 的保鲜时间是小时；○2 已知甲在某日上午10 时购买了该食品，并将其遗 放在室外，且此日的室外温度随时间变化如图所示，那么到了此日 13 时，甲所购买的食品是否过了保鲜时间 .（填“是”或“否”）y 43O -2x频率 组距MAF三、解答题：本大题共 6 小题，共 80 分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分 13 分）已知数列{a n }是等比数列，并且 a 1,a 2 +1,a 3 是公差为-3 的等差数列.（Ⅰ）求数列{a n }的通项公式；（Ⅱ）设b = a ，记S 为数列{b }的前 n 项和，证明： S <16 . n2nn nn316．（本小题满分 13 分）已知函数 f (x ) = cos x (sin x +3 cos x ) -3 ， x ∈ R .2（Ⅰ）求函数 f (x ) 的最小正周期；（Ⅱ）若 x ∈(0, π) ，求函数 f (x ) 的单调增区间.17．（本小题满分 14 分）如图，在四棱锥P - ABCD 中，底面 ABCD 是平行四边形，∠BCD = 135 ，侧面PAB ⊥ 底面 ABCD ，∠BAP = 90 , AB = AC = PA = 6, E , F 分别为BC , AD 的中点，点M 在线段 PD 上.（Ⅰ）求证： EF ⊥平面PAC ；P（Ⅱ）若M 为 PD 的中点，求证：ME // 平面PAB ；PM = 1（Ⅲ）当 MD 时，求四棱锥M - ECDF 的体积.2 DBEC318．（本小题满分 13 分）甲、乙两人进行射击比赛，各射击 4 局，每局射击 10 次，射击命中目标得 1 分，未命中目标得0 分. 两人 4 局的得分情况如下：甲 6 6 9 9乙79xy（Ⅰ）已知在乙的 4 局比赛中随机选取 1 局时，此局得分小于 6 分的概率不为零，且在 4 局比赛中，乙的平均得分高于甲的平均得分，求 x + y 的值；（Ⅱ）如果 x = 6 ，y = 10 ，从甲、乙两人的 4 局比赛中随机各选取 1 局，并将其得分分别记为a ，b ，求a ≥b 的概率；（Ⅲ）在 4 局比赛中，若甲、乙两人的平均得分相同，且乙的发挥更稳定，写出 x 的所有可能取值.（结论不要求证明）19．（本小题满分 14 分）已知椭圆C : x a2+ y 2 b 2 = 1(a > b > 0) 的离心率为 2 ，点 A (1, ) 在椭圆 C 上，O 为坐标原点. 2（Ⅰ）求椭圆C 的方程；（Ⅱ）设动直线l 与椭圆C 有且仅有一个公共点，且l 与圆 x 2 + y 2 = 5 的相交于不在坐标轴上的两点 P 1 ， P 2 ，记直线OP 1 ， OP 2 的斜率分别为k 1 ， k 2 ，求证： k 1 ⋅ k 2 为定值.20．（本小题满分 13 分）已知函数 f (x ) = 2x + 1 x 2，直线l ：y = kx -1.（Ⅰ）求函数 f (x ) 的极值；（Ⅱ）求证：对于任意k ∈ R ，直线l 都不是曲线 y = f (x ) 的切线； （Ⅲ）试确定曲线 y = f (x ) 与直线l 的交点个数，并说明理由.3 2⎩ 1 1 北京市西城区 2018 — 2019 学年度第一学期期末高三数学（文科）参考答案及评分标准一、选择题：本大题共 8 小题，每小题 5 分，共 40 分. 1．D2．C 3．D 4．B5．B6．B7．C8．D二、填空题：本大题共 6 小题，每小题 5 分，共 30 分. 2019.19． -1- 3i10． 6 x = -311. 9 12．113． 7914．4是注：第 10，13，14 题第一问 2 分，第二问 3 分.三、解答题：本大题共 6 小题，共 80 分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分 13 分）（Ⅰ）解：设等比数列{a n }的公比为q ，因为 a 1, a 2 +1, a 3 是公差为-3 的等差数列，⎧a 2 +1 = a 1 - 3,所以⎨a = (a +1) - 3,……………… 2 分⎩ 3 2⎧a 1q - a 1 = -4, 即⎨a q 2- a q = -2,……………… 3 分解得a 1 = 8,q = 1 . ……………… 5 分2所以a = a qn -1= 8⨯(1)n -1 = 24-n ． ........................................7 分 n12（Ⅱ）证明：因为b n +1 = a 2n +2 = 1， b n a 2n 4所以数列{b }是以b = a = 41.……………… 8 分n124[1- 1 n为首项， 为公比的等比数列4( ) ] 所以S n = 4 1- 1 4……………… 11 分22n =16[1- 1 ( ) ] < 16 ............................................................................................... 13 分 3 4 316．（本小题满分 13 分）（Ⅰ）解： f (x ) = cos x (sin x +3 cos x ) - 32= sin x cos x += 1 sin 2x + 3(2cos 2 x -1)23cos 2x……………… 4 分 2 2= sin(2x + π) ， ............................................... 6 分 3所以函数f (x ) 的最小正周期T = 2π=π ............................................................................... 8 分 2（Ⅱ）解：由2k π - π≤2x + π≤2k π+ π， k ∈ Z ， ................................ 9 分2 3 2得k π - 5π≤x ≤k π+ π，1212所以函数f (x ) 的单调递增区间为[k π - 5π ,k π+ π] ， k ∈ Z ....................................... 11 分 12 12 所以当x ∈(0, π) 时， f (x ) 的增区间为(0, π ] ，[7π, π) .................................................... 13 分 12 12（注：或者写成增区间为(0, π ) ， (7π, π) . ）12 1217．（本小题满分 14 分） （Ⅰ）证明：在平行四边形 ABCD 中，因为 AB = AC ， ∠BCD = 135 所以 AB ⊥ AC .由E , F 分别为BC , AD 的中点，得 EF //AB ，，所以 EF ⊥ AC .因为侧面PAB ⊥底面 ABCD ，且∠BAP = 90 ，………………1 分所以PA ⊥底面 ABCD . ………………2 分又因为EF ⊂底面 ABCD ， 所以 PA ⊥ EF .又因为PA AC = A ， PA ⊂ 平面 PAC ， AC ⊂ 平面 PAC ，………………3 分所以 EF ⊥ 平面 PAC .………………5 分MAF（Ⅱ）证明：因为M 为PD 的中点， F 分别为 AD 的中点，所以MF //PA ，又因为MF ⊄ 平面PAB ， PA ⊂ 平面PAB ， 所以MF // 平面PAB . ………………7 分P同理，得 EF // 平面PAB .又因为MF EF =F ， MF ⊂ 平面MEF ， EF ⊂平面MEF ， 所以平面MEF // 平面PAB . ………………9 分D又因为ME ⊂平面MEF ，B EC 所以ME // 平面PAB .................................................................................................................. 10 分 （Ⅲ）解：在∆PAD 中，过M 作MN //PA 交 AD 于点 N （图略），由 PM = 1 ，得 MN = 2 ， MD 2 PA 3 又因为 PA = 6 ，所以MN = 4 ，........................................................ 12 分 因为PA ⊥底面 ABCD ， 所以MN ⊥ 底面 ABCD ，所以四棱锥M - ECDF 的体积V M -ECDF= 1 ⨯ S 3ECDF⨯ MN = 1 ⨯ 6⨯ 6 ⨯ 4 = 24 . …… 14 分 3 218．（本小题满分 13 分）（Ⅰ）解：由题意，得 7 + 9 + x + y >6 + 6 + 9 + 9 ，即 x + y > 14 ............................................... 2 分 4 4因为在乙的 4 局比赛中，随机选取 1 局，则此局得分小于 6 分的概率不为零，所以x , y 中至少有一个小于 6， .......................................... 4 分又因为 x ≤10, y ≤10 ，且 x , y ∈ N ，所以 x + y ≤15 ，所以 x + y = 15 ....................................................................................................................................... 5 分 （Ⅱ）解：设 “从甲、乙的 4 局比赛中随机各选取 1 局，且得分满足a ≥b ”为事件 M ，……………… 6 分记甲的 4 局比赛为 A 1 ， A 2 ， A 3 ， A 4 ，各局的得分分别是 6，6，9，9；乙的 4 局比赛3 ⎨ x ⎩为 B 1 ， B 2 ， B 3 ， B 4 ，各局的得分分别是 7，9，6，10.则从甲、乙的 4 局比赛中随机各选取 1 局，所有可能的结果有 16 种， 它们是：( A 1, B 1 ) ，( A 1, B 2 ) ，( A 1, B 3 ) ，( A 1, B 4 ) ，( A 2 , B 1 ) ，( A 2 , B 2 ) ，( A 2 , B 3 ) ，( A 2 , B 4 ) ，( A 3 , B 1 ) ，( A 3 , B 2 ) ，( A 3 , B 3 ) ，( A 3 , B 4 ) ，( A 4 , B 1 ) ， ( A 4 , B 2 ) ， ( A 4 , B 3 ) ， ( A 4 , B 4 ) ................................................................... 7 分而事件M 的结果有 8 种，它们是：( A 1, B 3 ) ，( A 2 , B 3 ) ，( A 3 , B 1 ) ，( A 3 , B 2 ) ，( A 3 , B 3 ) ，( A 4 , B 1 ) ，( A 4 , B 2 ) ， ( A 4 , B 3 ) ，................................................ 8 分因此事件 M 的概率 P (M ) = 8 =1 ................................................................................. 10 分 162 （Ⅲ）解： x 的可能取值为6 ， 7 ， 8 ........................................................................................... 13 分19．（本小题满分 14 分） （Ⅰ）解：由题意，得 c=a3， a 2 = b 2 + c 2 ， ................................ 2 分2又因为点 A (1, 3) 在椭圆C 上，2所以 1 + a 2 3 4b 2= 1， ................................................... 3 分解得a = 2 ， b = 1 ， c = ，所以椭圆 C 的方程为 x 4 + y 2 = 1 ...................................................................................... 5 分（Ⅱ）证明：当直线l 的斜率不存在时，由题意知l 的方程为 x = ±2 ，易得直线OP ，OP 的斜率之积k ⋅ k = - 1 ....................................................................... 6 分12124当直线l 的斜率存在时，设l 的方程为 y = kx + m ...................................................... 7 分⎧ y = kx + m , 由方程组⎪2 + y 2 = 1,得(4k 2 +1)x 2 + 8kmx + 4m 2 - 4 = 0 ， ................. 8 分⎪⎩ 4因为直线l 与椭圆 C 有且只有一个公共点，所以∆ = (8km )2 - 4(4k 2 +1)(4m 2 - 4) = 0 ，即 m 2 = 4k 2 +1 ..................................... 9 分⎧ y = kx + m , 由方程组⎨x 2 + y 2 = 5,得(k 2 +1)x 2 + 2kmx + m 2 - 5 = 0 ， ................... 10 分2x x 2 3 2 -2km m 2 - 5设 P 1 (x 1 , y 1 ) ，P 2 (x 2 , y 2 ) ，则 x 1 + x 2 = k 2 + 1 ， x 1 ⋅ x 2 = k 2 + 1 ， ................................ 11 分y y (kx + m )(kx + m ) k 2 x x + km (x + x ) + m 2所以k 1 ⋅ k 2 = 1 2 = 1 2 = 1 21 2x 1 x 2 x 1 x 2 x 1 x 22m 2 - 5-2km2=k ⋅ k 2 + 1 + km ⋅ k 2 + 1 + m m 2 - 5k 2+ 1= m 2 - 5k 2 m 2- 5 ， ....................... 13 分 将 m 2 = 4k 2 +1 代入上式，-k 2 + 1 1得k 1 ⋅ k 2 = 4k 2 - 4 = - 4.综上， k 1 ⋅ k 2为定值- 1 .................................................................................................. 14 分 420．（本小题满分 13 分）（Ⅰ）解：函数 f (x ) 定义域为{x | x ≠ 0}， .......................................1 分 求导，得 f '(x ) =2 -2 ， .................................................2 分 x3令 f '(x ) = 0 ，解得 x = 1．当 x 变化时， f '(x ) 与 f (x ) 的变化情况如下表所示：所以函数 y = f (x ) 的单调增区间为(-∞, 0)，(1, +∞) ，单调减区间为(0,1) ，……………… 3 分所以函数y = f (x ) 有极小值 f (1) = 3 ，无极大值． .......................... 4 分 （Ⅱ）证明：假设存在某个k ∈ R ，使得直线l 与曲线 y = f (x ) 相切， ................ 5 分设切点为 A (x 0 , 2x 0 + 1 ) ，又因为 f '(x ) = 2 - 2， 0所以切线满足斜率k = 2 - 23 ，且过点 A ，所以2x + 1 = (2 - 2)x-1， ........................................ 7 分x 2 x 3即 3= -1 ，此方程显然无解， 0x x所以假设不成立．所以对于任意k ∈R ，直线l 都不是曲线y =f (x) 的切线...................... 8 分（Ⅲ）解：“曲线y =f (x)与直线l 的交点个数”等价于“方程2x +1x2=kx -1的根的个数”.由方程2x +1=kx -1，得k =1+1+ 2 ........................................................................... 9 分x2x3x令t =1，则k =t3+t + 2 ，其中t ∈R ，且t ≠ 0 . x考察函数h(t) =t3 +t+2 ，其中t ∈R，因为h'(t) = 3t2+1 > 0 时，所以函数h(t) 在R 单调递增，且h(t) ∈R ...........................................................................11 分而方程k =t3+t + 2 中，t ∈R ，且t ≠ 0 .所以当k =h(0) = 2 时，方程k =t3 +t +2 无根；当k ≠ 2 时，方程k =t3 +t+2 有且仅有一根，故当k = 2 时，曲线y =f (x) 与直线l 没有交点，而当k ≠ 2 时，曲线y =f (x) 与直线l 有且仅有一个交点.......................................................... 13 分。

北京市西城区高三统一测试数学（文科） 2019.4第Ⅰ卷（选择题 共40分）一、 选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设全集U =R ，集合{|02}A x x =<<，{3,1,1,3}B =--，则集合()U A B =I ð （A ）{3,1}-- （B ）{3,1,3}-- （C ）{1,3} （D ）{1,1}-2．若复数1i2iz -=-，则在复平面内z 对应的点位于 （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限3．下列函数中，值域为R 且在区间(0,)+∞上单调递增的是 （A ）22y x x =+ （B ）12x y += （C ）31y x =+ （D ）(1)||y x x =-4. 执行如图所示的程序框图，则输出的值为 （A ）4 （B ）5 （C ）7 （D ）9k5. 在△ABC 中，已知2a =，1sin()3A B +=，1sin 4A =，则 （A ） （B ）（C ）（D ）6. 设 均为正数，则“”是“”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件 （D ）既不充分也不必要条件7．如图，阴影表示的平面区域W 是由曲线0x y -=，222x y +=所围成的. 若点(,)P x y 在W 内（含边界），则43z x y =+的最大值和最小值分别为 （A）7-（B）-（C ）7，-（D ）7，7-8. 如果把一个平面区域内两点间的距离的最大值称为此区域的直径，那么曲线2||2y x =-围成的平面区域的直径为 （A ）2 （B ）4 （C） （D）c =438343,,a b m b a >a m ab m b+>+第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．设向量a ，b 满足||2=a ，||3=b ，,60>=o <a b ，则()⋅+=a a b ____．10．设1F ，2F 为双曲线2222 1(0,0)x y C a b a b-=>>：的两个焦点，若双曲线C 的两个顶点恰好将线段12F F 三等分，则双曲线C 的离心率为____．11．能说明“在△ABC 中，若sin2sin2A B =，则A B =”为假命题的一组A ，B 的值是____．12．某四棱锥的三视图如图所示，那么该四棱锥的体积为____．13．设函数ln(2), ()1,24, 1.x x f x x x +⎧=⎨⎩---<-≥当()1f a =-时，a =____；如果对于任意的x ∈R 都有()f x b ≥，那么实数b 的取值范围是____．14．团体购买公园门票，票价如下表：现某单位要组织其市场部和生产部的员工游览该公园，这两个部门人数分别为a 和b ()a b ≥，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为990元，那么这两个部门的人数a =____；b =____.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13分）已知函数()sin (cos )f x x x x =-.（Ⅰ）求函数()f x 的最小正周期； （Ⅱ）求函数()f x 在区间π5π[,]312-上的最小值和最大值.16．（本小题满分13分）已知数列{}n a 的前n 项和(1)2n S n n =++，其中*n ∈N .（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若2232,,k k a a a ++（k *∈N ）为等比数列{}n b 的前三项，求数列{}n b 的通项公式.17．（本小题满分13分）为培养学生的阅读习惯，某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动. 活动后，为了解阅读情况，学校统计了甲、乙两组各10名学生的阅读量（单位：本），统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以a 表示.（Ⅰ）若甲组阅读量的平均值大于乙组阅读量的平均值， 求图中a 的所有可能取值；（Ⅱ）将甲、乙两组中阅读量超过．．15本的学生称为“阅读达人”. 设3a =，现从所有的“阅读达人”里任取2人，求至少有1人来自甲组的概率；（Ⅲ）记甲组阅读量的方差为20s . 若在甲组中增加一个阅读量为10的学生，并记新得到的甲组阅读量的方差为21s ，试比较20s ，21s 的大小.（结论不要求证明）（注：2222121[()()()]n s x x x x x x n=-+-++-L ，其中x 为数据12,,,n x x x L 的平均数）18．（本小题满分14分）如图，在多面体ABCDEF 中，底面ABCD 为矩形，侧面ADEF 为梯形，//AF DE ，DE AD ⊥，DC DE =.（Ⅰ）求证：AD CE ⊥； （Ⅱ）求证：//BF 平面CDE ；（Ⅲ）判断线段BE 上是否存在点Q ，使得平面ADQ ⊥平面BCE ？并说明理由．19．（本小题满分13分）设函数2()e 3x f x m x =-+，其中∈m R ．（Ⅰ）当()f x 为偶函数时，求函数()()h x xf x =的极值；（Ⅱ）若函数()f x 在区间[2,4]-上有两个零点，求m 的取值范围．20．（本小题满分14分）已知椭圆W:2214x ym m+=的长轴长为4，左、右顶点分别为,A B，经过点(1,0)P的动直线与椭圆W相交于不同的两点,C D（不与点,A B重合）.（Ⅰ）求椭圆W的方程及离心率；（Ⅱ）求四边形ACBD面积的最大值；（Ⅲ）若直线CB与直线AD相交于点M，判断点M是否位于一条定直线上？若是，写出该直线的方程.（结论不要求证明）北京市西城区高三统一测试数学（文科）参考答案及评分标准 2019.4一、选择题：本大题共8小题，每小题5分，共40分.1．B 2．D 3．C 4．D 5．C 6．C 7．A 8．B 二、填空题：本大题共6小题，每小题5分，共30分. 9．710．311．答案不唯一，如60A =o ，30B =o12．4313．32-；(,2]-∞-14．70；40注：第13题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）解：（Ⅰ）2()sin cos f x x x x =1sin 2cos2)2x x =- ……………… 4分πsin(2)3x =+， ……………… 6分 所以函数()f x 的最小正周期πT =. ……………… 8分（Ⅱ）因为π5π312x -≤≤，所以ππ7π2336x -+≤≤． ……………… 9分所以当ππ232x +=，即π12x =时，()f x 取得最大值1.当ππ233x +=-，即π3x =-时，()f x 取得最小值 ……………… 13分 16．（本小题满分13分）解：（Ⅰ）当1n =时，114S a ==， ……………… 2分 当2n ≥时，由题意，得(1)2n S n n =++，○11(1)2n S n n -=-+，○2由○1-○2，得2n a n =，其中2n ≥. ……………… 5分所以数列{}n a 的通项公式4, 1,2, 2.n n a n n =⎧=⎨⎩≥……………… 7分（Ⅱ）由题意，得22232k k a a a ++=⋅. ……………… 9分即2[2(2)]42(32)k k +=⨯+.解得0k =（舍）或2k =. ……………… 10分所以公比222k a q a +==. ……………… 11分 所以111122n n n n b b q a q --+===. ……………… 13分17．（本小题满分13分）解：（Ⅰ）甲组10名学生阅读量的平均值为12681011121217211010+++++++++=，乙组10名学生阅读量的平均值为124412131616(10)20981010a a+++++++++++=. ……………… 2分由题意，得981010a+>，即2a <. ……………… 3分 故图中a 的取值为0或1. ……………… 4分 （Ⅱ）记事件“从所有的“阅读达人”里任取2人，至少有1人来自甲组”为M . … 5分由图可知，甲组“阅读达人”有2人，在此分别记为1A ，2A ；乙组“阅读达人”有3人，在此分别记为1B ，2B ，3B .则从所有的 “阅读达人” 里任取2人，所有可能结果有10种， 即12(,)A A ，11(,)A B ，12(,)A B ，13(,)A B ，21(,)A B ，22(,)A B ，23(,)A B ，12(,)B B ，13(,)B B ，23(,)B B . …… 7分而事件M 的结果有7种，它们是12(,)A A ，11(,)A B ，12(,)A B ，13(,)A B ，21(,)A B ，22(,)A B ，23(,)A B ，…………… 8分所以7()10P M =. 即从所有的‘阅读达人’里任取2人，至少有1人来自甲组的概率为710. …10分 （Ⅲ）2201s s >. ……………… 13分 18．（本小题满分14分）解：（Ⅰ）由底面ABCD 为矩形，知AD CD ⊥. ……………… 1分又因为DE AD ⊥，DE CD D =I ， ……………… 2分 所以AD ⊥平面CDE . ……………… 3分 又因为CE ⊂平面CDE ，所以AD CE ⊥. ……………… 4分 （Ⅱ）由底面ABCD 为矩形，知//AB CD ，又因为AB ⊄平面CDE ，CD ⊂平面CDE ， 所以//AB 平面CDE .……………… 6分 同理//AF 平面CDE ， 又因为AB AF A =I ，所以平面//ABF 平面CDE . ……………… 8分 又因为BF ⊂平面ABF ，所以//BF 平面CDE . ……………… 9分（Ⅲ）结论：线段BE 上存在点Q （即BE 的中点），使得平面ADQ ⊥平面BCE .… 10分证明如下：取CE 的中点P ，BE 的中点Q ，连接,,AQ DP PQ ，则//PQ BC . 由//AD BC ，得//PQ AD .所以,,,A D P Q 四点共面. ……………… 11分 由（Ⅰ），知AD ⊥平面CDE ， 所以AD DP ⊥，故BC DP ⊥.在△CDE 中，由DC DE =，可得DP CE ⊥. 又因为BC CE C =I ，所以DP ⊥平面BCE . ……………… 13分 又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE （即平面ADQ ⊥平面BCE ）.即线段BE 上存在点Q （即BE 中点），使得平面ADQ ⊥平面BCE . ……… 14分 19．（本小题满分13分）解：（Ⅰ）由函数()f x 是偶函数，得()()f x f x -=，即22e()3e 3xx m x m x ---+=-+对于任意实数x 都成立，所以0m =. ……………… 2分此时3()()3h x xf x x x ==-+，则2()33h x x '=-+.由()0h x '=，解得1x =±. ……………… 3分 当x 变化时，()h x '与()h x 的变化情况如下表所示：所以()h x 在(,1)-∞-，(1,)+∞上单调递减，在(1,1)-上单调递增. …………… 5分 所以()h x 有极小值(1)2h -=-，()h x 有极大值(1)2h =. ……………… 6分（Ⅱ）由2()e 30xf x m x =-+=，得23ex x m -=.所以“()f x 在区间[2,4]-上有两个零点”等价于“直线y m =与曲线23()ex x g x -=，[2,4]x ∈-有且只有两个公共点”. ……………… 8分 对函数()g x 求导，得223()e xx x g x -++'=. ……………… 9分 由()0g x '=，解得11x =-，23x =. ……………… 10分 当x 变化时，()g x '与()g x 的变化情况如下表所示：所以()g x 在(2,1)--，(3,4)上单调递减，在(1,3)-上单调递增. …………… 11分 又因为2(2)e g -=，(1)2e g -=-，36(3)(2)e g g =<-，413(4)(1)e g g =>-， 所以当4132e e m -<<或36e m =时，直线y m =与曲线23()ex x g x -=，[2,4]x ∈-有且只有两个公共点.即当4132e em -<<或36e m =时，函数()f x 在区间[2,4]-上有两个零点. …… 13分20．（本小题满分14分）解：（Ⅰ）由题意，得244a m == , 解得1m =.……………… 1分所以椭圆W 方程为2214x y +=. ……………… 2分故2a =，1b =，c =所以椭圆W的离心率2c e a ==.……………… 4分 （Ⅱ）当直线CD 的斜率k 不存在时，由题意，得CD 的方程为1x =， 代入椭圆W 的方程，得)2C，(1,2D -， 又因为||24AB a ==，AB CD ⊥， 所以四边形ACBD的面积1||||2S AB CD =⨯=. ……………… 6分 当直线CD 的斜率k 存在时，设CD 的方程为(1)(0)y k x k =-≠，11(,)C x y ，22(,)D x y ，联立方程22(1), 1,4y k x x y =-⎧⎪⎨+=⎪⎩消去y ，得2222(41)8440k x k x k +-+-=.…… 7分 由题意，可知0∆>恒成立，则2122841k x x k +=+，21224441k x x k -=+.………… 8分 四边形ACBD 的面积ABC ABD S S S ∆∆=+1211||||||||22AB y AB y =⨯+⨯……… 9分121||||2AB y y =⨯-122|()|k x x =-== 设241k t +=，则四边形ACBD的面积S =1(0,1)t∈，所以S =< 综上，四边形ACBD面积的最大值为………………11分（Ⅲ）结论：点M 在一条定直线上，且该直线的方程为4x =.………………14分。

课题1 金属材料 教学目标： 过日常生活中广泛使用金属材料等具体事例，认识金属材料与人类生活和社会发展的密切联系。

2、了解常见金属的物理性质，知道物质的性质很大程度上决定物质的用途，但还需考虑价格等因素。

3、认识合金，知道生铁和钢等重要合金，以及合金比纯金属具有更广泛的用途。

重点：1、知道物质的性质很大程度上决定物质的用途，但还需考虑价格等因素。

2、认识合金。

难点：采用活动与探究的方式来研究金属及合金的物理性质上的差异 教学过程： 教师先展示一些物品，然后设问：这些物品是由什么材料制成？教师引导学生，如何根据金属的一些用途，推断金属的物理性质。

使学生明白：物质的性质、资源、价格、美观等决定其用途Ag Cu Au Al Zn Fe Pb 导电性逐渐减弱密度Au Pb Ag Cu Fe Zn Al 密度逐渐减少熔点W Fe Cu Au Ag Al Sn 熔点由高到低硬度 Cr Fe Ag Cu Au Al Pb 硬度由大到小 合金：合金是由一种金属跟其它一种或几种金属（或金属跟非金属）一起熔合而成的具有金属特性的物质。

【讲述】合金的简单命名。

【引入】我们在日常生活中接触到的钢铁都是铁碳合金。

根据含碳量的不同，铁碳合金又分为生铁和钢。

一些合金和组成它们的纯金属性质比较 性质比较 现象黄铜铜焊锡锡光泽和颜色硬度结论实验8-2比较焊锡、锡和铅的熔化温度 现象结论最近一些学者研究发现，古罗马人的遗骸中含有大量铅，古罗马帝国的灭亡竟与铅中毒有关。

原来古罗马贵族惯用铅制器皿（瓶、杯、壶等）和含铅化合物的化妆品，甚至输送饮水的水管也是用铅做的，从而导致慢性铅中毒死亡。

根据上述材料回答下列问题： （1）人们日常接触的哪些物质中含铅？ （2）铅对人体有哪些危害？ （3）为防止铅中毒，请你提出几条合理建议。

（4）以小组的形式组织一项调查活动：到附近的加油站，调查汽油的种类，是否还在使用含铅汽油？是什么时候停止使用含铅汽油的？并进行环保宣传。

北京市西城区高三下学期 4 月统一测试（一模）数学（文）试题Word 版含答案数学（文科）第I卷（选择题共40分）选择题：本大题共8小题，每小题5分，共40分．在每小题列出的选出符合题目要求的一项．1．若集合2018. 4四个选项中，[KS5UKS5U] )(2．若复数的实部与虚部相等，则实数A ）（B ）（C ）（D ）3执行如图所示的程序框图值为(A)B)C) D)是奇函数，则■I ■宙・柵5 •正三棱柱的三视图如图所示，该正三棱柱的表面积是B) C)D)6．已知二次函数恒成立 ”的B )必要而不充分条件 (D )既不充分也不必要条件是正方形(A )充分而不必要条件 (C )充分必要条件已知的中心^ 若D)8.如图，在长方体中,占八、、在侧面上. 满足到直线的距离相等的点（ A ）不存在、填空题：本大题共（B）恰有1个（C）恰有2个第n卷（非选择题共no分）D ）有无数个6小题，每小题5分，共30 分．9．函数的定义域是10满足条件的最小值为11 ．已知抛物线的焦点与双曲线个焦点重合___，双曲线的渐近线方程是 _____．12则13 ．能够说明“ 存在不相等的正数使得是真命题的的值为14．某班共有学生40 名，在乒乓球、篮球、排球三项运动中每人至少会其中的一项，有些人会其中的两项，没有人三项均会．若该班18 人不会打乒乓球，24 人不会打篮球，16 人不会打排球，则该班会其中两项运动的学生人数是 _______ ．三、解答题：本大题共 6 小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13 分）设等差数列且成等比数列.(I)求的通项公式;(n ) 设数列16．（本小题满分13 分）的部分图象如图所示．的最小值．函数17.（本小题满分13分）某企业2017年招聘员工，其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用（I）从表中所有应聘人员中随机选择1人，试估计此人被录用的概率；（H）从应聘E岗位的6人中随机选择1名男性和1名女性，求这2人均被录用的概率; （川）表中A、B、C、D、E各岗位的男性、女性录用比例都接近（二者之差的绝对值不大于5%）,但男性的总录用比例却明显高于女性的总录用比例•研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位.（只需写出结论）18.（本小题满分14分）分另为使得平面平面的中点，如图2．(n ) 求证：平面平面（川）线上是否存在点19.（本小题满分14分）已知椭圆的任意三个顶点为顶点的三角形的面积是(I)求椭圆的方程;的右顶点，点轴上. 若椭圆20．（本小题满分13 分）已知函数横坐标的取值范围．其中( I ) 若曲线处的切线与直线的值;的导函数为占八、、且西城区高三统一测试数学（文科）参考答案及评分标准2018.4一、选择题：本大题共8 小题，每小题5 分，共40 分.1．D2．B3．C4．A 5．D6．B7．A8．D二、填空题：本大题共6 小题，每小题 5 分，共30 分.910111213．（答案不唯一）14．22注：第11题第一空 3 分，第二空2 分.三、解答题：本大题共6小题，共80 分. 其他正确解答过程，请参照评分标准给分15．（本小题满分13 分）的公差为解：（I ）设等差数列成等比数列。

北京市西城区抽样测试高三数学试卷（文科）本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.第Ⅰ卷(选择题 共40分)一、本大题共 8 小题，每小题 5 分，共 40 分. 在每小题列出的四个选项中，选出符合题目要求的一项.1. 已知集合{|13},{|||2}A x x B x x =<<=?，那么集合AB 等于（ ）A. {|12}x x <<B. {|23}x x <<C. {|1<2}x x ≤D. {|23}x x ≤< 2. 函数()sin cos f x x x =?的最小正周期为（ ） A.2pB. pC. 2pD. 4p 3. 若数列{}n a 是公差为2的等差数列，则数列{2}n a是（ ）A . 公比为4的等比数列 B. 公比为2的等比数列 C. 公比为12的等比数列 D. 公比为14的等比数列 4. 由1、2、3、4、5组成的无重复数字的五位数中奇数有（ ）A. 48 个B. 72 个C. 96 个D. 120 个5.设实数x , y 满足5003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩，则3z x y =+的最小值为（ ）A . 6-B . 3- C. 5 D. 276. 在平面直角坐标系中， A 为平面内一个动点，(2,0)B . 若||OA BA OB ?u u r u u r u u u r（O 为坐标原点），则动点A 的轨迹是（ ）A. 椭圆B.双曲线C.抛物线D. 圆 7．已知直线a 和平面a ，那么//a a 的一个充分条件是（ ）A. 存在一条直线b ，//,a b b a ÌB. 存在一条直线b ，,a b b a ^^C. 存在一个平面,,//a ββαβ⊂ D. 存在一个平面,,a ββαβ⊥⊥8. 函数f (x )的定义域为D ，若对于任意12,x x D Î，当12x x <时，都有12()()f x f x £，则称函数()f x 在D 上为非减函数 .设函数f (x )在[0，1]上为非减函数，且满足以下三个条件： ○1(0)0f =； ○21()()32x f f x =； ○3(1)1()f x f x -=-.则11()()38f f +等于（ ）A.34 B. 12C. 1D. 23北京市西城区 2009年抽样测试高三数学试卷（文科） 2009.4第Ⅱ卷( 共110分)二、填空题：本大题共 6 小题，每小题 5 分，共 30 分. 把答案填在题中横线上 .9. 某单位有27名老年人，54名中年人，81名青年人. 为了调查他们的身体情况，用分层抽样的方法从他们中抽取了n 个人进行体检，其中有6名老年人，那么n =_________. 10. 522()x x+的展开式中2x 的系数是___________.(用数字作答) 11. 设a 为常数，2()43f x x x =-+.若函数()f x a +为偶函数，则a =__________；(())f f a =_______.12. 设O 为坐标原点，向量 (1,2)OA =.将OA 绕着点 O 按逆时针方向旋转 90得到向量 OB , 则2OA OB +的坐标为____________.13. 已知一个正方体的八个顶点都在同一个球面上. 设此正方体的表面积为1S ，球的表面积2S ，则12S S =_____________. 14．如图，从双曲线221925x y -=的左焦点F 1引圆229x y +=的切线，切点为T ，延长F 1T 交双曲线右支于P 点. 设M 为线段F 1P 的中点，O 为坐标原点，则1||FT =_____________；||||MO MT -=__________.三、解答题：本大题共 6 小题，共 80 分. 解答应写出文字说明，证明过程或演算步骤. 15.（本小题满分12分）设ABC V 的内角A 、B 、C 的对边分别是a 、b 、c，且3,5,a b c ===（Ⅰ）求cos C 的值；（Ⅱ）求6sin()3cos2C Cπ+的值.16.（本小题满分12分）某个高中研究性学习小组共有9名学生，其中有3名男生和6名女生. 在研究学习过程中，要进行两次汇报活动（即开题汇报和结题汇报），每次汇报都从这9名学生中随机选1人作为代表发言. 设每人每次被选中与否均互不影响.（Ⅰ）求两次汇报活动都是由小组成员甲发言的概率； （Ⅱ）求男生发言次数不少于女生发言次数的概率.17.（本小题满分14分）如图，在四棱锥P-ABCD 中，底面ABCD 是直角梯形，90,//,BCDAB CD ?o 又1,2,AB BC PC PB CD AB PC =====^.(Ⅰ) 求证：PC ^平面ABCD ；(Ⅱ) 求PA 与平面ABCD 所成角的大小； (Ⅲ) 求二面角B-PD-C 的大小.18.（本小题满分14分）BD CP设等差数列{}n a 的前n 项和为n S ，且12n n n S na a c =+-（c 是常数，n ÎN *），26a =. （Ⅰ）求c 的值及{}n a 的通项公式； （Ⅱ）证明：1223111118n n a a a a a a ++++<L .19.（本小题满分14分）已知椭圆C 22:14y x +=，过点M (0, 1)的直线l 与椭圆C 相交于两点A 、B . （Ⅰ）若l 与x 轴相交于点P ，且P 为AM 的中点，求直线l 的方程； （Ⅱ）设点1(0,)2N ，求||NA NB +的最大值.20.（本小题满分14分）已知函数32()(,f x x ax b a b =-++∈R ).（Ⅰ）若a =1，函数()f x 的图象能否总在直线y b =的下方？说明理由； （Ⅱ）若函数()f x 在（0，2）上是增函数，求a 的取值范围；（Ⅲ）设123,,x x x 为方程()0f x =的三个根，且1(1,0)x ∈-，2(0,1)x ∈，3(,1)(1,)x ∈-∞-+∞,求证：||1a >.北京市西城区2009年抽样测试参考答案高三数学试卷（文科）2009.4 一、选择题：本大题共8 小题，每小题5 分，共40 分.二、填空题：本大题共6 小题，每小题5 分，共30 分.9. 36 10. 10 11. 2, 8 12. (0,5)13. 2p14. 5, 2注：两空的题目，第一个空3分，第二个空2分.三、解答题：本大题共6 小题，共80 分.15.（本小题满分12分）（Ⅰ）解：由余弦定理222cos2a b cCab+-=，----------------------------3分得925142cos2353C+-==创. ---------------------------5分（Ⅱ）解：由（Ⅰ）知 cos 0C >,所以角C为锐角，所以sin C =， ----------------------------7分则26sin()6(sin cos cos sin )333cos22cos 1C C C C C πππ+⨯+⨯=- --------------------------10分1232324219+=⨯-=所以6sin()3cos2C Cπ+=. ---------------------------12分 16.（本小题满分12分）（Ⅰ）解：记 “2次汇报活动都是由小组成员甲发言” 为事件A . -----------------------------1分由题意，得事件A 的概率111()9981P A =?， 即2次汇报活动都是由小组成员甲发言的概率为181. ---------------------------5分 （Ⅱ）解：由题意，每次汇报时，男生被选为代表的概率为3193=，女生被选为代表的概率为12133-=. ----------------------------6分 记“男生发言次数不少于女生发言次数”为事件B ，由题意，事件B 包括以下两个互斥事件：○1事件B 1：男生发言2次女生发言0次，其概率为 02012111()C ()(1)339P B =-=， ----------------------------8分 ○2事件B 2：男生发言1次女生发言1次，其概率为 11122114()C ()(1)339P B =-=， ----------------------------10分所以，男生发言次数不少于女生发言次数的概率为125()()()9P B P B P B =+=. ---------------------------12分17.（本小题满分14分）方法一：（Ⅰ）证明：在PBC V中，1,BC PC PB ===222BC PC PB \+=， 90PCB\?o ，即PC BC ^， ---------------------------1分,AB PC AB BC B ^=Q I ，PC \^平面ABCD . ---------------------------4分 （Ⅱ）如图，连接AC ，由（Ⅰ）知PC ^平面ABCD ， \AC 为PA 在平面ABCD 内的射影，PAC \?为PA 与平面ABCD 所成的角. --------------6分 在ABC V 中，90ABC ?o ，1AB BC ==，AC \=在PAC V 中，90PCA ?o ，1,PC AC ==tan 2PC PACAC \?=， \PA 与平面ABCD 所成角的大小为arctan 2. ---------------------------8分 （Ⅲ）由（Ⅰ）知PC BC ^，又,BC CD PC CD C ^=I ，BC \^平面PCD . ---------------------------9分如图，过C 作CM PD ^于M ，连接BM ， CM \是BM 在平面PCD 内的射影， BM PD \^，CMB \?为二面角B -PD -C 的平面角. ---------------------------11分在PCD V 中, 90PCD ?o , PC=1, 2CD =，A BD CPMPD \=又CM PD ^，PD CM PC CD \??，PC CD CM PD ×\==， 在CMB V 中, 90BCM?o , BC=1, CM =tan BC CMBCM \?=\二面角B -PD -C的大小为 --------------------------14分 方法二：（Ⅰ）同方法一. ---------------------------4分 （Ⅱ）解：连接AC ，由（Ⅰ）知PC ^平面ABCD ，\AC 为PA 在平面ABCD 内的射影，PAC \?为PA 与平面ABCD 所成的角. ---------------------------6分 如图，在平面ABCD 内，以C 为原点， CD 、CB 、CP 分别为x 、y 、z 轴，建立空间直角坐标系C -xyz ，则(0,0,0),(0,1,0),(2,0,0),(0,0,1),(1,1,0)C B D P A , (1,1,0),(1,1,1)AC AP =--=--uuu r uu u r，---------------------------7分cos ||||AC AP PACAC AP ×\?=×uuu r uu u r uuu r uu u r \PA 与平面ABCD所成角的大小为 ---------------------------9分 （Ⅲ）过C 作CM DP ^于M ，连接BM ，设(,,)M x y z ， 则(,,),(2,,),(MC x y z DM x y z DP =---=-=-uuu r uuu u r uu u rMC DP ^u u u r u u u r Q ， 20MC DPx z \?-=u u u r u u u r ； ○1 ,DM DP u u u u r u u u rQ 共线， 20,2x y z -\==-， ○2由○1○2，解得24,0,55x y z ===， M \点的坐标为24(,0,)55，24(,1,)55MB =--uuu r ，24(,0,)55MC =--uuu r ，440055MB DP?+-=uuu r uu u rQ , MB DP \^，又CM DP ^，CMB \?为二面角B -PD -C 的平面角. ---------------------------12分24(,0,)55MC =--uuu r Q ，24(,1,)55MB =--uuu r ，2cos 3||||MB MC CMB MB MC ×\?=×uuu r uuu r uuu r uuu r ， \二面角B -PD -C 的大小为2arccos 3. --------------------------14分18.（本小题满分14分） （Ⅰ）解：因为12n n n S na a c =+-， 所以当1n =时，11112S a a c =+-，解得12a c =， ---------------------------2分 当2n =时，222S a a c =+-，即1222a a a c +=-，解得23a c =，所以36c =，解得2c =； ---------------------------5分则14a =，数列{}n a 的公差212d a a =-=，所以1(1)22n a a n d n =+-=+. ---------------------------8分 （Ⅱ）因为12231111n n a a a a a a ++++L 1114668(22)(24)n n =+++创++L ---------------------------9分 111111111()()()24626822224n n =-+-++-++L ---------------------------12分 1111111[()()()]246682224n n =-+-++-++L111()2424n =-+1184(2)n =-+. 因为*N n Î， 所以1223111118n n a a a a a a ++++<L . -------------------------14分 注：为降低难度，此题故意给出多余条件，有多种解法，请相应评分. 19.（本小题满分14分） （Ⅰ）解：设A (x 1, y 1)，因为P 为AM 的中点，且P 的纵坐标为0，M 的纵坐标为1，所以1102y +=，解得11y =-， -------------------------1分 又因为点A (x 1, y 1)在椭圆C 上，所以221114y x +=，即21114x +=，解得12x =±，则点A的坐标为(1)2-或(1)2--， -------------------------3分所以直线l的方程为330y -+=，或330y +-=. -------------------------5分（Ⅱ）设A (x 1, y 1)，B (x 2, y 2)，则112211(,),(,),22NA x y NB x y =-=-所以1212(,1)NA NB x x y y +=++-，则||(NA NB x += -------------------------7分 当直线AB 的斜率不存在时，其方程为0x =，(0,2),(0,2)A B -，此时||1NA NB +=；-------------------------8分当直线AB 的斜率存在时，设其方程为1y kx =+，由题设可得A 、B 的坐标是方程组22114y kx y x =+⎧⎪⎨+=⎪⎩的解，消去y 得22(4)230k x kx ++-=，所以221222(2)12(4)0,4k k k x x k -∆=++>+=+， -------------------------10分则121228(1)(1)4y y kx kx k+=+++=+， 所以222222222812||()(1)1144(4)k k NA NB k k k --+=+-=+≤+++，当0k =时，等号成立, 即此时||NA NB +取得最大值1. -------------------------13分综上，当直线AB 的方程为0x =或1y =时，||NA NB +有最大值1. -------------------14分20.（本小题满分14分）（Ⅰ）解：当1a =时，32()f x x x b =-++，因为(1)2f b b -=+>，所以，函数()f x 的图象不能总在直线y b =的下方. ---------------------------3分 （Ⅱ）解：由题意，得2()32f x x ax ¢=-+，令()0f x ¢=，解得0x =或23x a =， --------------------------4分 当0a <时，由()0f x ¢>，解得203a x <<， 所以()f x 在2(,0)3a 上是增函数，与题意不符，舍去；当0a =时，由2()30f x x ¢=-?，与题意不符，舍去； --------------------------6分 当0a >时，由()0f x ¢>，解得203x a <<， 所以()f x 在2(0,)3a 上是增函数， 又()f x 在(0，2)上是增函数，所以223a ³，解得3a ³， 综上，a 的取值范围为[3,)+?. ---------------------------9分 （Ⅲ）解：因为方程32()0f x x ax b =-++=最多只有3个根， 由题意，得在区间(1,0)-内仅有一根， 所以(1)(0)(1)0f f b a b -?++<， ○1同理(0)(1)(1)0f f b a b ?-++<， ○2 --------------------------11分当0b >时，由○1得 10a b ++<，即1a b <--， 由○2得10a b -++<，即1a b <-+，因为11b b --<-+，所以11a b <--<-，即1a <-； 当0b <时，由○1得 10a b ++>，即1a b >--， 由○2得10a b -++>，即1a b >-+，因为11b b --<-+，所以11a b >-+>，即1a >； 当0b =时，因为(0)0f =，所以()0f x =有一根0，这与题意不符.综上，||1a >. ---------------------------14分 注：在第（Ⅲ）问中，得到○1○2后，可以在坐标平面aOb 内，用线性规划方法解. 请相应评分.。

西城区高三统一测试数学（理科）2018.4第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1（A（B（C（D2（A（B（C（D3．以原点为极点，的极坐标方程为（A（B（C（D4．正三棱柱的三视图如图所示，该正三棱柱的表面积是（A（B（C（D5（A（B（C（D6的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件7（A）0对（B）1对（C）2对（D）3对8．某计算机系统在同一时间只能执行一项任务，且该任务完成后才能执行下一项任务．现有三项任务U，V，W，计算机系统执行这三项任务的时间（单位：s一项任务的“相对等待时间”定义为从开始执行第一项任务到完成该任务的时间与计算机系统执行该任务的时间之比．下列四种执行顺序中，使三项任务“相对等待时间”之和最小的是（A）（B）（C）（D）第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．10．11；双曲线的渐近线方程是____．12．13．安排甲、乙、丙、丁4人参加3个运动项目，每人只参加一个项目，每个项目都有人参加．若甲、乙2人不能参加同一个项目，则不同的安排方案的种数为____．（用数字作答）14____．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13分）16．（本小题满分13分）某企业2017年招聘员工，其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用比例（精确到1%）如下：（Ⅰ）从表中所有应聘人员中随机选择1人，试估计此人被录用的概率；（Ⅱ）从应聘E岗位的6人中随机选择22和数学期望；（Ⅲ）表中A、B、C、D、E各岗位的男性、女性录用比例都接近（二者之差的绝对值不大于5%），但男性的总录用比例却明显高于女性的总录用比例．研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位．（只需写出结论）17．（本小题满分14分）如图1，中，，，的中点，的中点，2．图1 图218．（本小题满分13分）19．（本小题满分14分）并证明你的结论．20．（本小题满分13分）（Ⅱ），证明：西城区高三统一测试数学（理科）参考答案及评分标准2018.4一、选择题：本大题共8小题，每小题5分，共40分.1．D 2．C 3．B 4．D5．B 6．C 7．C 8．A二、填空题：本大题共6小题，每小题5分，共30分.91011121314注：第10，11题第一空3分，第二空2分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）解：（Ⅰ）因为所以 [ 1分][ 3分]所以 [ 4分]因为 [ 5分]所以 [ 6分]所以 [ 8分]整理得 [ 9分]解得[11分][12分][13分]16．（本小题满分13分）解：（Ⅰ）因为表中所有应聘人员总数为被该企业录用的人数为所以从表中所有应聘人员中随机选择1[ 3分]（Ⅱ）X[ 4分]因为应聘E岗位的6人中，被录用的有4人，未被录用的有2人，[ 5分]所以[ 8分]所以X的分布列为：[10分]（Ⅲ）这四种岗位是：B、C、D、E． [13分]17．（本小题满分14分）解：（Ⅰ）因为所以所以所以[ 1分]因为所以 [3分]所以[4分]由（Ⅰ）得[5分]所以则即[ 7分]所成的角为则所以[ 9分]设[10分]设所以所以所以[12分]令整理得[13分]解得所以[14分]18．（本小题满分13分）解：[2分]依题意，有[4分]解得 [5分]令[6分]则[ 8分]所以[ 9分]因为故存在，使得[11分]上单调递减，在区间所以[13分]19．（本小题满分14分）解：[ 1分]所以因此[ 3分][ 4分][ 5分][ 6分][ 7分]整理为[9分][11分]因为[13分]所以即所以[14分]20．（本小题满分13分）解：（Ⅰ）因为[ 2分]所以[ 3分]k，所以[ 5分]又因为所以[6分]所以[ 8分]设集合则由（Ⅱ）可知同理所以因为[11分]则且[13分]。

北京市西城区高三统一测试数学（理科）2019.4一、 选择题：本大题共8小题，每小题5分，共40分．1．设全集U =R ，集合{|02}A x x =<<，{3,1,1,3}B =--，则集合()U A B =ð（A ）{3,1}-- （B ）{3,1,3}-- （C ）{1,3}（D ）{1,1}-2．若复数1i 2iz -=-，则在复平面内z 对应的点位于（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限3. 执行如图所示的程序框图，则输出的k 值为（A ）4 （B ）5 （C ）7 （D ）9 4．下列直线中，与曲线C ：12,()24x t t y t =+⎧⎨=-+⎩为参数没有公共点的是（A ）20x y += （B ）240x y +-= （C ）20x y -= （D ）240x y --= 5. 设 ,,a b m 均为正数，则“b a >”是“a m ab m b+>+”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件（D ）既不充分也不必要条件6．如图，阴影表示的平面区域W 是由曲线0x y -=，222x y +=所围成的. 若点(,)P x y 在W 内（含边界），则43z x y =+的最大值和最小值分别为 （A）7- （B）-（C ）7，-（D ）7，7-7. 团体购买公园门票，票价如下表：现某单位要组织其市场部和生产部的员工游览该公园，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为990元，那么这两个部门的人数之差为 （A ）20（B ）30 （C ）35（D ）408. 如果把一个平面区域内两点间的距离的最大值称为此区域的直径，那么曲线422xy +=围成的平面区域的直径为 （A （B ）3 （C ） （D ）4 二、填空题：本大题共6小题，每小题5分，共30分．9. 在等比数列{}n a 中，21a =，58a =，则数列{}n a 的前n 项和n S =____．10．设1F ，2F 为双曲线2222 1(0,0)x y C a b a b-=>>：的两个焦点，若双曲线C 的两个顶点恰好将线段12F F 三等分，则双曲线C 的离心率为____． 11．函数()sin2cos2f x x x =+的最小正周期T=____；如果对于任意的x ∈R 都有()f x a ≤，那么实数a 的取值范围是____．12．某四棱锥的三视图如图所示，那么此四棱锥的体积为____．13. 能说明“若sin cos αβ=，则36090k αβ+=⋅+，其中k ∈Z ”为假命题的一组α，β的值是___． 14．如图所示，玩具计数算盘的三档上各有7个算珠，现将每档算珠分为左右两部分，左侧的每个算珠表示数2，右侧的每个算珠表示数1（允许一侧无珠），记上、中、下三档的数字和分别为a ，b ，c . 例如，图中上档的数字和9a =. 若a ，b ，c 成等差数列，则不同的分珠计数法有____种.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）在△ABC 中，已知222a c b mac +-=，其中m ∈R . （Ⅰ）判断m 能否等于3，并说明理由； （Ⅱ）若1m =-，b =4c =，求sin A ．侧(左)视图正(主)视图俯视图如图，在多面体ABCDEF 中，梯形ADEF 与平行四边形ABCD 所在平面互相垂直， //AF DE ，DE AD ⊥，AD BE ⊥，112AF AD DE ===，AB =（Ⅰ）求证：//BF 平面CDE ； （Ⅱ）求二面角B EF D --的余弦值；（Ⅲ）判断线段BE 上是否存在点Q ，使得平面CDQ ⊥平面BEF ？若存在，求出BQBE的值，若不存在，说明理由．17．（本小题满分13分）为培养学生的阅读习惯，某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动. 活动后，为了解阅读情况，学校统计了甲、乙两组各10名学生的阅读量（单位：本），统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以a 表示.（Ⅰ）若甲组阅读量的平均值大于乙组阅读量的平均值， 求图中a 的所有可能取值；（Ⅱ）将甲、乙两组中阅读量超过．．15本的学生称为“阅读达人”. 设3a =，现从所有“阅读达人”里任取3人，求其中乙组的人数X 的分布列和数学期望.（Ⅲ）记甲组阅读量的方差为20s . 在甲组中增加一名学生A 得到新的甲组，若A 的阅读量为10，则记新甲组阅读量的方差为21s ；若A 的阅读量为20，则记新甲组阅读量的方差为22s ，试比较20s ，21s ，22s 的大小.（结论不要求证明）DABCEF设函数2()e 3x f x m x =-+，其中∈m R ．（Ⅰ）当()f x 为偶函数时，求函数()()h x xf x =的极值；（Ⅱ）若函数()f x 在区间[2,4]-上有两个零点，求m 的取值范围．19．（本小题满分14分）已知椭圆W :2214x y m m +=的长轴长为4，左、右顶点分别为,A B ，经过点(,0)P n 的直线与椭圆W 相交于不同的两点,C D （不与点,A B 重合）.（Ⅰ）当0n =，且直线CD ⊥x 轴时， 求四边形ACBD 的面积；（Ⅱ）设1n =，直线CB 与直线4x =相交于点M ，求证：,,A D M 三点共线.20．（本小题满分13分）如图，设A 是由n n ⨯(2)n ≥个实数组成的n 行n 列的数表，其中ij a (,1,2,,)i j n =表示位于第i 行第j 列的实数，且{1,1}ij a ∈-.定义1122st s t s t sn tn p a a a a a a =+++s 行与第t 行的积. 若对于任意,s t （s t ¹），都有0st p =，则称数表A 为完美数表.（Ⅰ）当2n =时，试写出一个符合条件的完美数表； （Ⅱ）证明：不存在10行10列的完美数表； （Ⅲ）设A 为n 行n 列的完美数表，且对于任意的1,2,,i l =L 和1,2,,j k =L ，都有1ij a =，证明：kl n ≤.北京市西城区高三统一测试 数学（理科）参考答案及评分标准2019.4一、选择题：本大题共8小题，每小题5分，共40分.1．B 2．D 3．D 4．C 5．C 6．A 7．B 8．B 二、填空题：本大题共6小题，每小题5分，共30分.9．1122n --10．3 11． π；a12．43 13．答案不唯一，如110α=，20β= 14．32注：第11题第一问3分，第二问2分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）解：（Ⅰ）当3m =时，由题可知 2223a c b ac +-=，由余弦定理2222cos b a c ac B =+-， 3分得2223cos 22a cb B ac +-==． ……………… 4分 这与cos [1,1]B ∈-矛盾，所以m 不可能等于3 . ………… 6分（Ⅱ）由（Ⅰ），得 1cos 22m B ==-，所以2π3B =. ……………… 7分因为b =4c =，222a c b ac +-=-， 所以216284a a +-=-，解得6a =-（舍）或2a =. ……………… 9分在△ABC 中，由正弦定理sin sin a bA B=， ……………… 11分得sin sina B Ab ==. ……………… 13分 16．（本小题满分14分）解：（Ⅰ）由底面ABCD 为平行四边形，知//AB CD ，又因为AB ⊄平面CDE ，CD ⊂平面CDE ，所以//AB 平面CDE . ……………… 2分 同理//AF 平面CDE ， 又因为ABAF A =，所以平面//ABF 平面CDE . ……………… 3分 又因为BF ⊂平面ABF ，所以//BF 平面CDE . …………… 4分（Ⅱ）连接BD ,因为平面ADEF ⊥平面ABCD ，平面ADEF 平面ABCD AD =，DE AD ⊥，所以DE ⊥平面ABCD . 则DE DB ⊥. 又因为DE AD ⊥，AD BE ⊥，DEBE E =，所以AD ⊥平面BDE ，则AD BD ⊥.故,,DA DB DE 两两垂直，所以以,,DA DB DE 所在的直线分别为x 轴、y 轴和z 轴，如图建立空间直角坐标系， ……………… 6分 则(0,0,0)D ，(1,0,0)A ，(0,1,0)B ，(1,1,0)C -，(0,0,2)E ，(1,0,1)F ， 所以(0,1,2)BE =-,(1,0,1)EF =-，(0,1,0)=n 为平面DEF 的一个法向量. 设平面BEF 的一个法向量为(,,)x y z =m ，由0BE ⋅=m ，0EF ⋅=m ，得20,0,y z x z -+=⎧⎨-=⎩令1z =，得(1,2,1)=m . ………………8分所以cos ,||||3⋅<>==m n m n m n .如图可得二面角B EF D --为锐角， 所以二面角B EF D --的余弦值为………………10分 （Ⅲ）结论：线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF . ………………11分证明如下：设(0,,2)([0,1])BQ BE λλλλ==-∈，所以(0,1,2)DQ DB BQ λλ=+=-.设平面CDQ 的法向量为(,,)a b c =u ，又因为(1,1,0)DC =-， 所以0DQ ⋅=u ，0DC ⋅=u ，即(1)20,0,b c a b λλ-+=⎧⎨-+=⎩……………… 12分若平面CDQ ⊥平面BEF ，则0⋅=m u ，即20a b c ++=， ……………… 13分解得1[0,1]7λ=∈.所以线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF ，且此时17BQ BE =. …… 14分 17．（本小题满分13分）解：（Ⅰ）甲组10名学生阅读量的平均值为12681011121217211010+++++++++=，乙组10名学生阅读量的平均值为124412131616(10)20981010a a+++++++++++=. ……………… 2分由题意，得981010a+>，即2a <. ……………… 3分 故图中a 的取值为0或1. ……………… 4分 （Ⅱ）由图可知，甲组“阅读达人”有2人，乙组“阅读达人”有3人.由题意，随机变量X 的所有可能取值为：1，2，3. ……………… 5分且212335C C 3(1)C 10P X ⋅===，122335C C 3(2)C 5P X ⋅===， 3335C 1(3)C 10P X ===. …… 8分 所以随机变量的分布列为：……………… 9分所以3319()123105105E X =⨯+⨯+⨯=. ………………10分 （Ⅲ）222102s s s <<. ……………… 13分 18．（本小题满分13分）解：（Ⅰ）由函数()f x 是偶函数，得()()f x f x -=，即22e ()3e 3x x m x m x ---+=-+对于任意实数x 都成立，所以0m =. ……… 2分 此时3()()3h x xf x x x ==-+，则2()33h x x '=-+.由()0h x '=，解得1x =±. … 3分 当x 变化时，()h x '与()h x 的变化情况如下表所示：所以()h x 在(,1)-∞-，(1,)+∞上单调递减，在(1,1)-上单调递增. …………… 5分 所以()h x 有极小值(1)2h -=-，()h x 有极大值(1)2h =. ……………… 6分（Ⅱ）由2()e 30xf x m x =-+=，得23e xx m -=.所以“()f x 在区间[2,4]-上有两个零点”等价于“直线y m =与曲线23()ex x g x -=，[2,4]x ∈-X有且只有两个公共点”. ……………… 8分对函数()g x 求导，得223()exx x g x -++'=. ……………… 9分 由()0g x '=，解得11x =-，23x =. ……………… 10分 当x 变化时，()g x '与()g x 的变化情况如下表所示：所以()g x 在(2,1)--，(3,4)上单调递减，在(1,3)-上单调递增. …………… 11分 又因为2(2)e g -=，(1)2e g -=-，36(3)(2)e g g =<-，413(4)(1)e g g =>-， 所以当4132e e m -<<或36em =时，直线y m =与曲线23()e x x g x -=，[2,4]x ∈-有且只有两个公共点.即当4132e e m -<<或36em =时，函数()f x 在区间[2,4]-上有两个零点. ……… 13分19．（本小题满分14分）解：（Ⅰ）由题意，得244a m ==， 解得1m =. ……………… 2分所以椭圆W 方程为2214x y +=.……………… 3分当0n =，及直线CD ⊥x轴时，易得(0,1)C ,(0,1)D -. 且(2,0)A -,(2,0)B . 所以||4AB =，||2CD =，显然此时四边形ACBD 为菱形，所以四边形ACBD 的面积为14242⨯⨯=. …… 5分 （Ⅱ）当直线CD 的斜率k 不存在时，由题意，得CD 的方程为1x =， 代入椭圆W 的方程，得C ，(1,D ，易得CB 的方程为2)y x =-. 则(4,M ,(6,AM =,(3,AD =, 所以2AM AD =，即,,A D M 三点共线. ……………… 7分 当直线CD 的斜率k 存在时，设CD 的方程为(1)(0)y k x k =-≠，11(,)C x y ，22(,)D x y ，联立方程22(1), 1,4y k x x y =-⎧⎪⎨+=⎪⎩ 消去y ，得2222(41)8440k x k x k +-+-=. ……… 9分 由题意，得0∆>恒成立，故2122841k x x k +=+，21224441k x x k -=+. …………… 10分直线CB 的方程为11(2)2y y x x =--. 令4x =，得112(4,)2y M x -. ………… 11分 又因为(2,0)A -，22(,)D x y ， 则直线AD ，AM 的斜率分别为222AD y k x =+，113(2)AM y k x =-， …………… 12分 所以21211221123(2)(2)23(2)3(2)(2)AD AM y y y x y x k k x x x x --+-=-=+--+. 上式中的分子 211221123(2)(2)3(1)(2)(1)(2)y x y x k x x k x x --+=----+121225()8kx x k x x k =-++22224482584141k k k k k k k -=⨯-⨯+++0=， 所以0AD AM k k -=. 所以,,A D M 三点共线. …… 14分20．（本小题满分13分） 解：（Ⅰ）答案不唯一. 如：……………… 3分（Ⅱ）假设存在10行10列的完美数表A .根据完美数表的定义，可以得到以下两个结论：（1）把完美数表的任何一列的数变为其相反数（即1+均变为1-，而1-均变为1+），得到的新数表是完美数表；（2）交换完美数表的任意两列，得到的新数表也是完美数表. ……………… 5分 完美数表A 反复经过上述两个结论的变换，前三行可以为如下形式：x 共列y 共列z 共列w 共列在这个新数表中，设前三行中的数均为1的有x 列，前三行中“第1, 2行中的数为1，且第3行中的数为-1”的有y 列，前三行中“第1, 3行中的数为1，且第2行中的数为-1”的有z 列，前三行中“第1行中的数为1，且第2, 3行中的数为-1”的有w 列（如上表所示），则10x y z w +++= ○1由120p =，得x y z w +=+； ○2 由130p =，得x z y w +=+； ○3 由230p =，得x w y z +=+. ○4 解方程组○1，○2，○3，○4，得52x y z w ====. 这与,,,x y z w ∈N 矛盾， 所以不存在10行10列的完美数表. ……………… 8分 （Ⅲ）记第1列前l 行中的数的和112111l a a a X +++=，第2列前l 行中的数的和12222la a a X +++= ，……，第n 列前l 行中的数的和12n n ln n a a a X +++=，因为对于任意的1,2,,i l =L 和1,2,,j k =L ，都有1ij a =，所以12k X X X l ====. ……………… 9分又因为对于任意,s t （s t ¹），都有0st p =，所以22212n X X X ln +++=. ……………… 11分 又因为22222221212n k X X X X X X l k ++++++=≥，所以2ln l k ≥，即kl n ≤. ……………… 13分。