四边形的定义性质判定

平行四边形的定义,性质及判定方法平行四边形是我们在数学学习中经常会遇到的一个重要几何图形。

它在实际生活和数学理论中都有着广泛的应用。

首先，咱们来聊聊平行四边形的定义。

简单来说，两组对边分别平行的四边形就叫做平行四边形。

这就好比两条平行线，它们永远不会相交，而平行四边形的两组对边就具有这样的特性。

接下来，咱们看看平行四边形都有哪些性质。

平行四边形的对边是相等的。

比如说，如果一个平行四边形的一条边是 5 厘米，那么与它相对的那条边的长度也一定是 5 厘米。

这是因为平行四边形的两组对边分别平行且相等，所以相对的两条边长度是一样的。

平行四边形的对角也是相等的。

假设其中一个角是 60 度，那么与它相对的那个角也必然是 60 度。

平行四边形的邻角是互补的。

什么叫互补呢？就是两个角加起来等于 180 度。

比如说，如果一个角是 70 度，那么与它相邻的角就是 110 度。

平行四边形的两条对角线还互相平分。

也就是说，如果有一条对角线把平行四边形分成了两个三角形，那么这条对角线被另一条对角线分成的两段长度是相等的。

再来说说平行四边形的面积。

平行四边形的面积可以用底边长度乘以这条底边对应的高来计算。

比如说，底边是 8 厘米，对应的高是 4 厘米，那么面积就是 8×4 ＝ 32 平方厘米。

下面咱们讲讲平行四边形的判定方法。

如果一个四边形的两组对边分别相等，那么它就是平行四边形。

比如说，一组对边都是 6 厘米，另一组对边都是 8 厘米，那这个四边形就是平行四边形。

要是一个四边形的一组对边平行且相等，那它也是平行四边形。

比如一条边是 5 厘米，并且与它相对的边和它平行，长度也为 5 厘米，那就可以判定这个四边形是平行四边形。

当一个四边形的两组对边分别平行时，它肯定是平行四边形。

这个就很好理解了，这正好符合平行四边形的定义嘛。

还有，如果四边形的两条对角线互相平分，那它也是平行四边形。

平行四边形在我们的生活中随处可见。

第一章 四边形性质探索一、四边形的相关概念1、四边形在同一平面内，由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形。

2、四边形具有不稳定性3、四边形的内角和定理及外角和定理四边形的内角和定理：四边形的内角和等于360°。

四边形的外角和定理：四边形的外角和等于360°。

推论：多边形的内角和定理：n 边形的内角和等于•-)2(n 180°；多边形的外角和定理：任意多边形的外角和等于360°。

6、设多边形的边数为n ，则多边形的对角线共有2)3(-n n 条。

从n 边形的一个顶点出发能引（n-3）条对角线，将n 边形分成（n-2）个三角形。

二、平行四边形1、平行四边形的定义两组对边分别平行的四边形叫做平行四边形。

2、平行四边形的性质（1）平行四边形的对边平行且相等。

（2）平行四边形相邻的角互补，对角相等（3）平行四边形的对角线互相平分。

（4）平行四边形是中心对称图形，对称中心是对角线的交点。

常用点：（1）若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段的中点是对角线的交点，并且这条直线二等分此平行四边形的面积。

（2）推论：夹在两条平行线间的平行线段相等。

3、平行四边形的判定（1）定义：两组对边分别平行的四边形是平行四边形（2）定理1：两组对角分别相等的四边形是平行四边形（3）定理2：两组对边分别相等的四边形是平行四边形（4）定理3：对角线互相平分的四边形是平行四边形（5）定理4：一组对边平行且相等的四边形是平行四边形4、两条平行线的距离两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线的距离。

平行线间的距离处处相等。

5、平行四边形的面积S平行四边形=底边长×高=ah三、矩形1、矩形的定义有一个角是直角的平行四边形叫做矩形。

2、矩形的性质（1）矩形的对边平行且相等（2）矩形的四个角都是直角（3）矩形的对角线相等且互相平分（4）矩形既是中心对称图形又是轴对称图形；对称中心是对角线的交点（对称中心到矩形四个顶点的距离相等）；对称轴有两条，是对边中点连线所在的直线。

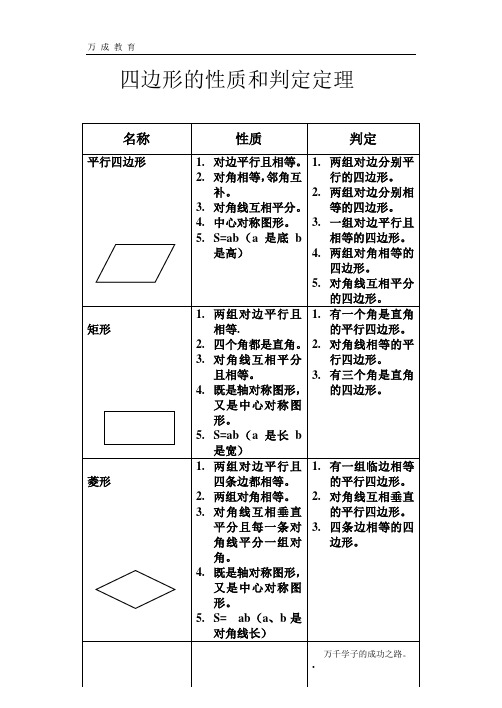
特殊的四边形及三角形的定义、性质、判定、相关计算公式平行四边形1.平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．2.平行四边形的性质：1平行四边形是中心对称图形,对称中心是两条对角线的交点,不是轴对称图形;关于对称性的2平行四边形的对角相等；关于角的3平行四边形的邻角互补；关于角的4平行四边形的对边相等；推论：夹在两条平行线间的平行线段;关于边的5平行四边形的对边平行；关于边的6平行四边形的对角线互相平分;关于对角线的7连接平行四边形各边的中点所得图形是平行四边形;关于中点四边形的3.平行四边形的判定方法：1两组对边分别平行的四边形是平行四边形；定义判定法2两组对边分别相等的四边形是平行四边形；3一组对边平行且相等的四边形是平行四边形；4两组对角相等的四边形是平行四边形；5对角线互相平分的四边形是平行四边形;4. 相关计算公式：平行四边形的面积公式：底×高；如用“h”表示高,“a”表示底,“s”表示平行四边形面积,则S=ah平行四边形周长：2×底1+底2；如用“a"表示底1,“b”表示底2,“c“表示平行四边形周长,则C=2a+b5.平行四边形中常用辅助线的添法：1连结对角线或平移对角线；2过顶点作对边的垂线构成直角三角形；3连结对角线交点与一边中点,或过对角线交点作一边的平行线,构成线段平行或中位线；4连结顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形；5过顶点作对角线的垂线,构成线段平行或三角形全等;矩形1.矩形的定义：有一个角是直角的平行四边形是矩形;2.矩形的性质：1矩形是中心对称图形,也是轴对称图形,对称轴是通过对边中点的直线,对称轴共有两条；关于对称性的2矩形的对角相等；关于角的3矩形的邻角互补；关于角的4矩形的对边相等；关于边的5矩形的对边平行；关于边的6矩形的对角线互相平分；关于对角线的7矩形的四个角都是直角；关于角的8矩形的对角线相等;关于对角线的9矩形所在平面内任一点到其两对角线端点的距离的平方和相等3.矩形的判定方法：1有一个角是直角的平行四边形是矩形；定义判定法2对角线相等的平行四边形是矩形；3关于任何一组对边中点的连线成轴对称图形的平行四边形是矩形4对于平行四边形,若存在一点到两双对顶点的距离的平方和相等,则此平行四边形为矩形5有三个角是直角的四边形是矩形；6四个内角都相等的四边形为矩形；7对角线互相平分且相等的四边形是矩形；8对角线互相平分且有一个内角是直角的四边形是矩形;4.相关计算公式矩形面积：S=ah注:a为边长,h为该边上的高S=ab注:a为长,b为宽矩形周长：C=2a+b注:a为长,b为宽顺次连接矩形各边中点得到的四边形是菱形;菱形1.菱形的定义：有一组邻边相等的平行四边形是菱形;2.菱形的性质：1菱形既是,是两条对角线所在直线,也是中心对称图形；2在60°的菱形中,短对角线等于边长,长对角线是短对角线的√3倍;3菱形的对角相等；关于角的4菱形的邻角互补；关于角的5菱形的对边相等；关于边的6菱形的对边平行；关于边的7菱形的对角线互相平分；关于对角线的8菱形的四边都相等；关于边的9菱形的对角线互相垂直,且平分各内角；关于对角线的10顺次连接菱形各边中点得到的四边形是矩形;关于中点四边形的3.菱形的判定方法：1一组邻边相等的平行四边形是菱形；定义判定法2对角线相互垂直的平行四边形是菱形；3关于两条对角线都成轴对称的四边形是菱形；4四条边都相等的四边形是菱形;4. 相关计算公式：菱形的面积：菱形的面积等于两对角线乘积的一半;只要是对角线互相垂直的四边形都可用正方形1.正方形的定义：1四条边都相等且四个角都是直角的四边形叫做正方形;2有一组邻边相等的矩形是正方形;3有一组邻边相等且一个角是直角的平行四边形是正方形;4有一个角为直角的菱形是正方形;5对角线平分,垂直且相等,并且交角为直角的四边形为正方形;2.正方形的性质：1既是中心对称图形,又是有四条对称轴；关于对称性的2正方形的对角相等；关于角的3正方形的邻角互补；关于角的4正方形的对边相等；关于边的5正方形的相邻边互相垂直；关于边的6正方形的对边平行；关于边的7正方形的对角线互相平分；关于对角线的8正方形的四个角都是直角；关于角的9正方形的对角线相等;关于对角线的10正方形的四边都相等；关于边的（11）正方形的对角线互相垂直,且平分各内角;关于对角线的3.正方形的判定方法：1有一组邻边相等的矩形是正方形；2对角线互相垂直的矩形是正方形；3有一个角为直角的菱形是正方形；4对角线相等的菱形是正方形；5一组邻边相等且有一个角是直角的平行四边形是正方形；6四边均相等,对角线互相垂直平分且相等的平行四边形是正方形；7四边相等,有三个角是直角的四边形是正方形；8对角线相互垂直平分且相等的四边形为正方形;4.相关计算公式：面积计算公式：S=边长×边长或：S=对角线×对角线÷2周长计算公式: C=4×边长顺次连接正方形各边中点得到的四边形是正方形;等腰三角形1.等腰三角形的定义：有两边相等的三角形是等腰三角形;2. 等腰三角形的性质：1等腰三角形的两个底角相等；简写成“等边对等角”2等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合；简写成“三线合一”3等腰三角形的两底角的平分线相等；两条腰上的中线相等,两条腰上的高相等4等腰三角形底边上的垂直平分线到两条腰的距离相等；5等腰三角形的一腰上的高与底边的夹角等于顶角的一半；6等腰三角形底边上任意一点到两腰距离之和等于一腰上的高；需用等面积法证明7等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴;3. 等腰三角形的判定方法：1有两条边相等的三角形是等腰三角形2有两个角相等的三角形是等腰三角形简称：等角对等边等边三角形1.等边三角形的定义：三边都相等的三角形是等边三角形;等边三角形是特殊的等腰三角形;注意：若三角形三边都相等则说这个三角形为等边三角形,而一般不称这个三角形为等腰三角形2.等边三角形的性质：1等边三角形的内角都相等,且为60度；2等边三角形底角边上的中线、底角边上高线和所对顶角的角的平分线互相重合；三线合一3等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或所对角的平分线所在直线;3.等边三角形的判定方法：首先考虑判断三角形是等腰三角形1三边相等的三角形是等边三角形；定义2三个内角都相等的三角形是等边三角形；3有一个角是60度的等腰三角形是等边三角形；4等边三角形是锐角三角形；5有两个角等于60度的等腰三角形是等边三角形;等腰梯形1.等腰梯形的定义:一组对边平行不相等,另一组对边不平行但相等的四边形是等腰梯形;2.等腰梯形的性质：1等腰梯形只有一条对称轴,上底和下底的中垂线就是它的对称轴；2等腰梯形在同一底上的两个角相等；3等腰梯形的两腰相等；4等腰梯形的两底平行；5等腰梯形的两个底角相等；6等腰梯形的对角线相等；7等腰梯形内接于圆;3. 等腰梯形的判定方法：1一组对边不平行边相等的梯形是等腰梯形；2同一底上的两个角相等的梯形是等腰梯形；3对角线相等的梯形是等腰梯形；4一组对边平行不相等,另一组对边相等不平行的四边形是等腰梯形；5对角线相等,形成两个等腰三角形;4.相关计算公式等腰梯形的中位线长是上下底边长度和的一半；等腰梯形的面积公式等于上底加下底和一半乘高,也等于中位线乘高;直角三角形1.直角三角形的定义：有一个角为90°的三角形,叫做直角三角形;2.直角三角形的性质直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质：1直角三角形两直角边的平方和等于斜边的平方;2在直角三角形中,两个锐角互余;3在直角三角形中,斜边上的中线等于斜边的一半即直角三角形的外心位于斜边的中点,外接圆半径R＝C/2;4直角三角形的两直角边的乘积等于斜边与斜边上高的乘积;5在直角三角形中,30°角所对直角边等于斜边的一半;3.直角三角形的判定方法：1有一个角为90°的三角形是直角三角形；2一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形；3若a的平方＋b的平方=c的平方,则以a、b、c为边的三角形是以c为斜边的直角三角形；勾股定理的逆定理;4若一个三角形30°内角所对的边是某一边的一半,那么这个三角形是以这条长边为斜边的直角三角形；5两个锐角互余的三角形是直角三角形;。

平行四边形的定义,性质及判定方法平行四边形的定义、性质及判定方法在我们的数学世界中，平行四边形是一个非常重要的几何图形。

它在日常生活和数学研究中都有着广泛的应用。

接下来，让我们一起深入了解平行四边形的定义、性质以及判定方法。

首先，咱们来说说平行四边形的定义。

简单来说，两组对边分别平行的四边形就叫做平行四边形。

这个定义很关键，它是我们识别和判断一个四边形是否为平行四边形的首要依据。

那平行四边形都有哪些性质呢？其一，平行四边形的两组对边分别相等。

比如说，一个平行四边形ABCD，AB 和 CD 这一组对边是相等的，AD 和 BC 这一组对边也是相等的。

其二，平行四边形的两组对角分别相等。

还是以平行四边形 ABCD 为例，∠A 和∠C 是相等的，∠B 和∠D 也是相等的。

其三，平行四边形的对角线互相平分。

假设 AC 和 BD 是平行四边形 ABCD 的两条对角线，那么 AO ＝ CO，BO ＝ DO，其中 O 是两条对角线的交点。

其四，平行四边形相邻的两个角互补。

也就是∠A 和∠B 的和是180 度，∠C 和∠D 的和也是 180 度。

了解了平行四边形的性质，接下来咱们再看看怎么判定一个四边形是不是平行四边形。

第一种判定方法，如果一个四边形的两组对边分别平行，那么它就是平行四边形。

这其实就是根据平行四边形的定义来判定的。

第二种判定方法，如果一个四边形的两组对边分别相等，那么它也是平行四边形。

比如说，一个四边形 ABCD，AB ＝ CD ，AD ＝ BC，那它就是平行四边形。

第三种判定方法，如果一个四边形的一组对边平行且相等，那这个四边形就是平行四边形。

第四种判定方法，如果一个四边形的两组对角分别相等，那么它就是平行四边形。

第五种判定方法，如果一个四边形的对角线互相平分，那么它就是平行四边形。

在实际应用中，我们经常会遇到需要判断一个四边形是不是平行四边形的情况。

比如说，在建筑设计中，设计师需要根据平行四边形的性质和判定方法来设计房屋的结构；在数学解题中，我们需要根据已知条件，运用平行四边形的相关知识来求解问题。

平行四边形平行四边形的定义：在同一平面内有两组对边分别平行的四边形叫做平行四边形。

平行四边形的定义、性质：（1）平行四边形对边平行且相等。

（2）平行四边形两条对角线互相平分。

（菱形和正方形）（3）平行四边形的对角相等，两邻角互补（4）连接任意四边形各边的中点所得图形是平行四边形。

(推论）（5）平行四边形的面积等于底和高的积。

（可视为矩形）（6）平行四边形是旋转对称图形，旋转中心是两条对角线的交点。

（7）过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形。

（8）平行四边形是中心对称图形，对称中心是两对角线的交点。

（9）一般的平行四边形不是轴对称图形，菱形是轴对称图形。

（10）平行四边形ABCD中，AC、BD是平行四边形ABCD的对角线，则各四边的平方和等于对角线的平方和（可用余弦定理证明）。

（11）平行四边形对角线把平行四边形面积分成四等分。

判定：（1）两组对边分别相等的四边形是平行四边形；（2）对角线互相平分的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对边分别平行的四边形是平行四边形；（5）两组对角分别相等的四边形是平行四边形；（6）一组对边平行一组对角线互相平分的四边形是平行四边形；（7）一组对边平行一组对角相等的四边形是平行四边形；矩形定义有一个角是直角的平行四边形叫做矩形性质1．矩形的四个角都是直角,对边相等2．矩形的对角线相等3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线）。

5．对边平行且相等6．对角线互相平分7.矩形具有平行四边形的所有性质判定1．有一个角是直角的平行四边形是矩形2．对角线相等的平行四边形是矩形3．有三个角是直角的四边形是矩形4．四个内角都相等的四边形为矩形5．关于任何一组对边中点的连线成轴对称图形的平行四边形是矩形6．对于平行四边形，若存在一点到两双对顶点的距离的平方和相等，则此平行四边形为矩形7．对角线互相平分且相等的四边形是矩形8．对角线互相平分且有一个内角是直角的四边形是矩形四边形由四条线段围成的平面图形叫四边形。

特殊四边形知识点总结一．正确理解定义（1）定义：两组对边分别平行的四边形是平行四边形．平行四边形的定义揭示了图形的最本质的属性，它既是平行四边形的一条性质，又是一个判定方法．（2）表示方法：用“□”表示平行四边形，例如：平行四边形ABCD 记作“□ABCD ”，读作“平行四边形ABCD ”． 2．熟练掌握性质：平行四边形的有关性质和判定都是从 边、角、对角线 三个方面的特征进行简述的． （1）角：对角相等，邻角互补； （2）边：对边分别平行且相等； （3）对角线：对角线互相平分；（4）面积：①S ==⨯底高ah ；②平行四边形的对角线将四边形分成4个面积相等的三角形．（5）平行四边形不是轴对称图形。

3．平行四边形的判别方法①定义判定：两组对边分别平行的四边形是平行四边形。

②方法2：两组对角分别相等的四边形是平行四边形。

③方法3：两组对边分别相等的四边形是平行四边形。

④方法4：对角线互相平分的四边形是平行四边形。

⑤方法5：一组平行且相等的四边形是平行四边形。

二、几种特殊平行四边形的有关概念（1）矩形：有一个角是直角的平行四边形是矩形，它是研究矩形的基础，它既可以看作是矩形的性质，也可以看作是矩形的判定方法，对于这个定义，要注意把握：① 平行四边形； ② 一个角是直角，两者缺一不可．（2）菱形：有一组邻边相等的平行四边形是菱形，它是研究菱形的基础，它既可以看作是菱形的性质，也可以看作是菱形的判定方法，对于这个定义，要注意把握：① 平行四边形；② 一组邻边相等，两者缺一不可．（3）正方形：有一组邻边相等且有一个直角的平行四边形叫做正方形，它是最特殊的平行四边形，它既是平行四边形，还是菱形，也是矩形，它兼有这三者的特征，是一种非常完美的图形．三、几种特殊四边形的有关性质（1）矩形： ①边：对边平行且相等；②角：四个角都是直角； ③对角线：对角线互相平分且相等；④对称性：轴对称图形（对边中点连线所在直线，2条）． ⑤面积S =长×宽；A BD OC AD B CO【注意：矩形具有平行四边形的一切性质】（2）菱形：①边：四条边都相等；②角：对角相等、邻角互补；③对角线：对角线互相垂直平分且每条对角线平分每组对角； ④对称性：轴对称图形（对角线所在直线，2条）． ⑤面积S =底×高=对角线乘积的一半；【注意：菱形具有平行四边形的一切性质】（3）正方形：①边：四条边都相等；②角：四角相是直角；③对角线：对角线互相垂直平分且相等，对角线与边的夹角为450； ④对称性：轴对称图形（4条）．⑤面积S =边长×边长=对角线乘积的一半；【注意：正方形具有平行四边形、矩形、菱形的一切性质】四、几种特殊四边形的判定方法（1）矩形的判定： ①有一个角是直角的平行四边形；②对角线相等的平行四边形； ③有三个角是直角的四边形。

四边形的定义和性质和判定
四边形（Quadrangle）是由四条恰好相互垂直的折线组成的闭合面。

它的性质有：一，四边形的边都是相互垂直的；二，任意一条边
上的两个相邻角的和为180°；三，任意一条边上的两个相邻内角的和等于外角；四，任意一个顶点处两个边形成的内角总和等于360°；五，任意三边形成两个外角的和等于180°。

四边形可以根据具体情况相应分类，比如正方形、矩形、平行四
边形、菱形等。

要判定一个四边形是不是某种特定四边形，通常是要
看它是否满足该形状特定的角度和边长关系。

平行四边形的定义及特殊四边形的性质及判定在我们的数学世界中，四边形是一个非常重要的几何图形家族。

其中，平行四边形是一种常见且具有独特性质和判定方法的四边形。

此外，还有一些特殊的四边形，如矩形、菱形和正方形，它们在实际生活和数学问题中都有着广泛的应用。

接下来，让我们一起深入了解平行四边形以及这些特殊四边形的性质和判定。

首先，我们来明确平行四边形的定义。

平行四边形是指两组对边分别平行的四边形。

这是平行四边形最基本的特征。

想象一下，有两组对边就像两条平行的轨道，永远不会相交，这就是平行四边形的样子。

平行四边形具有许多有趣的性质。

它的对边是相等的。

也就是说，如果一个四边形是平行四边形，那么它的两组对边长度分别相等。

例如，AB 边和 CD 边长度相等，AD 边和 BC 边长度也相等。

它的对角也是相等的。

∠A 和∠C 相等，∠B 和∠D 相等。

就好像是两个双胞胎角，长得一模一样。

平行四边形的两条对角线还相互平分。

假设 AC 和 BD 是平行四边形的两条对角线，那么交点 O 会把两条对角线分成相等的两段，AO＝ CO，BO ＝ DO。

了解了平行四边形的性质，我们再来看看它的判定方法。

如果一个四边形的两组对边分别相等，那么它就是平行四边形。

比如，AB ＝CD，AD ＝ BC，那么这个四边形一定是平行四边形。

如果两组对边分别平行，那它也是平行四边形。

这其实就是平行四边形定义的逆运用。

当一组对边平行且相等时，这个四边形同样是平行四边形。

还有，如果两条对角线互相平分，这个四边形也是平行四边形。

接下来，我们再看看那些特殊的四边形。

矩形是一种特殊的平行四边形，它不仅具有平行四边形的所有性质，还有自己独特的特点。

矩形的四个角都是直角。

想象一下，房间的四个角都是方方正正的90 度，这就是矩形的样子。

矩形的对角线相等。

这意味着，如果一个平行四边形的四个角都是直角或者两条对角线相等，那么它就是矩形。

菱形也是一种特殊的平行四边形。