抛物线与相似三角形ppt课件

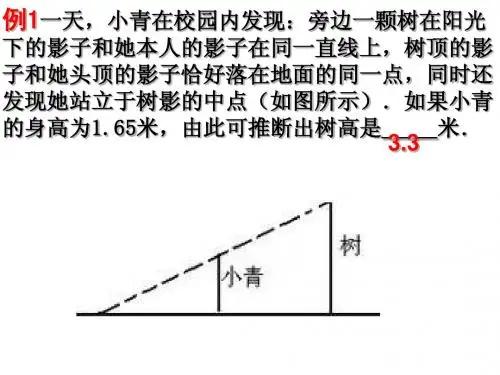
抛物线与相似三角形哎呀，说起抛物线和相似三角形，这可真是让不少同学头疼的知识点呢！但别担心，咱们一起来好好琢磨琢磨。

先来说说抛物线，你想象一下，就像一个调皮的孩子在玩扔球的游戏，球飞出去的轨迹，那就是抛物线。

它的形状弯弯的，有时候高，有时候低，可有意思啦！比如说，咱们去游乐场玩那种打水球的游戏，把水球用力一扔，它在空中划过的那道弧线，就是抛物线。

相似三角形呢，就像是一对对长得很像的“双胞胎”三角形。

它们的角是一样大的，边呢，成比例地放大或者缩小。

这就好比你有两个玩具积木搭成的三角形，一个大一点，一个小一点，但形状特别像，这就是相似三角形啦。

咱们来举个例子啊，有一天我在公园里散步，看到一个小朋友在放风筝。

那风筝线和地面形成的夹角，还有风筝的高度以及小朋友和风筝的距离，这不就构成了一个抛物线和相似三角形的问题嘛！小朋友想知道风筝到底飞多高，咱们就可以用抛物线的知识来算算。

假设风筝线和地面的夹角是 60 度，小朋友离风筝的水平距离是 10 米，而风筝线的长度是 15 米。

那咱们就能通过三角函数算出风筝的高度。

这时候，再想想相似三角形，假如在旁边还有另一个小朋友，他离风筝的距离和第一个小朋友不一样，但是角度相同，咱们就能通过相似三角形的比例关系，算出第二个小朋友看到的风筝高度和第一个小朋友看到的高度之间的关系。

在数学的世界里，抛物线和相似三角形经常会结伴出现。

比如说，一道数学题中，给了你一个抛物线的方程，然后在这个抛物线里面又藏着几个相似三角形。

这时候，咱们就得先把抛物线的图像在脑子里画出来，搞清楚它的对称轴、顶点这些关键的点。

然后再去找那些相似三角形，看看它们的边和角有什么关系。

做题的时候，咱们可以先从简单的入手。

比如说，先找出那些明显的相等的角，或者成比例的边。

就像拼图一样，一块一块地把这些线索拼凑起来，最后就能解开谜题啦！有时候，遇到难题别着急，多画画图，多想想咱们生活中的例子。

比如说，篮球场上投篮的轨迹，是不是也像抛物线？还有建筑工地上的塔吊，它的结构中是不是也能找到相似三角形？总之啊，抛物线和相似三角形虽然有点复杂，但只要咱们多观察，多练习，就一定能把它们拿下！相信自己，加油！。

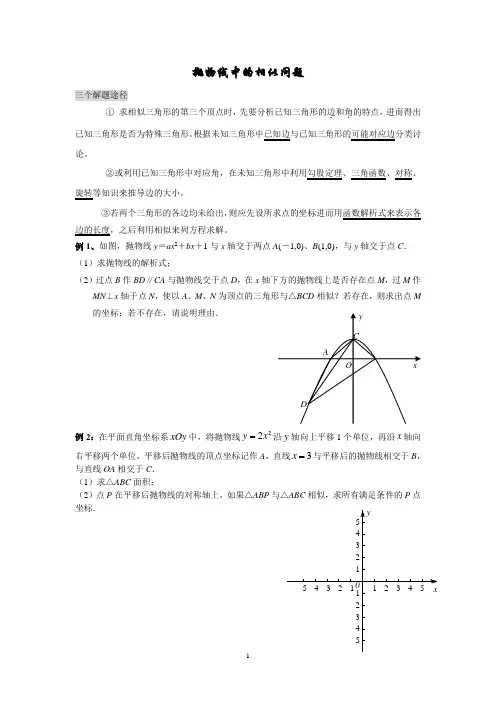
抛物线中的相似问题三个解题途径① 求相似三角形的第三个顶点时，先要分析已知三角形的边．和角．的特点，进而得出已知三角形是否为特殊三角形。

根据未知三角形中已知边与已知三角形的可能对应边分类讨论。

②或利用已知三角形中对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。

③若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式来表示各边的长度，之后利用相似来列方程求解。

例1、如图，抛物线y ＝ax 2＋bx ＋1与x 轴交于两点A (－1,0)、B (1,0)，与y 轴交于点C ． （1）求抛物线的解析式；（2）过点B 作BD ∥CA 与抛物线交于点D ，在x 轴下方的抛物线上是否存在点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，则求出点M 的坐标；若不存在，请说明理由．例2：在平面直角坐标系xOy 中，将抛物线22y x =沿y 轴向上平移1个单位，再沿x 轴向右平移两个单位，平移后抛物线的顶点坐标记作A ，直线3x =与平移后的抛物线相交于B ，与直线OA 相交于C ． （1）求△ABC 面积；（2）点P 在平移后抛物线的对称轴上，如果△ABP 与△ABC 相似，求所有满足条件的P 点坐标．例3、如图，平面直角坐标系中，点A 、B 、C 在x 轴上，点D 、E 在y 轴上，OA =OD =2，OC =OE =4，DB ⊥DC ，直线AD 与经过B 、E 、C 三点的抛物线交于F 、G 两点，与其对称轴交于M .点P 为线段FG 上一个动点(与F 、G 不重合)，PQ ∥y 轴与抛物线交于点Q . (1)求经过B 、E 、C 三点的抛物线的解析式；(2)是否存在点P ，使得以P 、Q 、M 为顶点的三角形与△AOD 相似？若存在，求出满足条件的点P 的坐标；若不存在，请说明理由；练习题： 练1、（09青海）矩形OABC 在平面直角坐标系中位置如图所示，A C 、两点的坐标分别为(60)A ，，(03)C -，，直线34y x =-与BC 边相交于D 点． （1）求点D 的坐标； （2）若抛物线294y ax x =-经过点A ，试确定此抛物线的表达式； （3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P 为对称轴上一动点，以P O M 、、为顶点的三角形与OCD △相似，求符合条件的点P 的坐标．练2、、已知抛物线2y ax bx c =++经过0P E ⎫⎪⎪⎝⎭及原点(00)O ，．（1）求抛物线的解析式．（2）过P 点作平行于x 轴的直线PC 交y 轴于C 点，在抛物线对称轴右侧且位于直线PC 下方的抛物线上，任取一点Q ，过点Q 作直线QA 平行于y 轴交x 轴于A 点，交直线PC 于B 点，直线QA 与直线PC 及两坐标轴围成矩形OABC ．是否存在点Q ，使得OPC△与PQB △相似？若存在，求出Q 点的坐标；若不存在，说明理由．（3）如果符合（2）中的Q 点在x 轴的上方，连结OQ ，矩形OABC 内的四个三角形OPC PQB OQP OQA ，，，△△△△之间存在怎样的关系？为什么？练3：如图1，已知抛物线的顶点为A （0，1），矩形CDEF 的顶点C 、F 在抛物线上，D 、E 在x 轴上，CF 交y 轴于点B （2，0），且其面积为8。

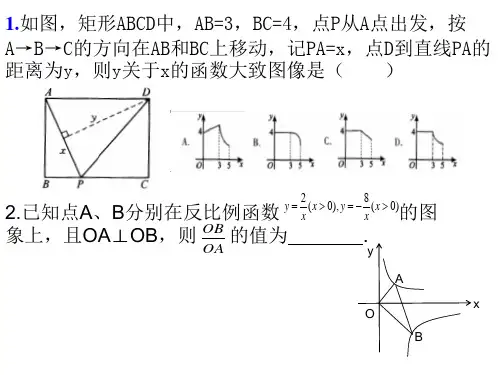
动点问题之相似三角形1．（2022•桂林）如图，抛物线y=-x2+3x+4与x轴交于A，B两点（点A位于点B的左侧），与y轴交于C点，抛物线的对称轴l与x轴交于点N，长为1的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）直接写出A，B，C三点的坐标；（2）求CP+PQ+QB的最小值；（3）过点P作PM⊥y轴于点M，当△CPM和△QBN相似时，求点Q的坐标．2．（2022•辽宁）抛物线y=ax2-2x+c经过点A（3，0），点C（0，-3），直线y=-x+b经过点A，交抛物线于点E．抛物线的对称轴交AE于点B，交x轴于点D，交直线AC于点F．（1）求抛物线的解析式；（2）如图①，点P为直线AC下方抛物线上的点，连接PA，PC，△BAF的面积记为S1，△PAC的面积记为S2，当S2=38 S1时．求点P的横坐标；（3）如图②，连接CD，点Q为平面内直线AE下方的点，以点Q，A，E为顶点的三角形与△CDF相似时（AE与CD不是对应边），请直接写出符合条件的点Q的坐标．3．（2022•山西）综合与实践问题情境：在Rt△ABC中，∠BAC=90°，AB=6，AC=8．直角三角板EDF中∠EDF=90°，将三角板的直角顶点D 放在Rt△ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N．猜想证明：（1）如图①，在三角板旋转过程中，当点M为边AB的中点时，试判断四边形AMDN的形状，并说明理由；问题解决：（2）如图②，在三角板旋转过程中，当∠B=∠MDB时，求线段CN的长；（3）如图③，在三角板旋转过程中，当AM=AN时，直接写出线段AN的长．4．（2022•衡阳）如图，已知抛物线y=x2-x-2交x轴于A、B两点，将该抛物线位于x轴下方的部分沿x轴翻折，其余部分不变，得到的新图象记为“图象W”，图象W交y轴于点C．（1）写出图象W位于线段AB上方部分对应的函数关系式；（2）若直线y=-x+b与图象W有三个交点，请结合图象，直接写出b的值；（3）P为x轴正半轴上一动点，过点P作PM∥y轴交直线BC于点M，交图象W于点N，是否存在这样的点P，使△NCM 与△OBC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．5．（2022•恩施州）在平面直角坐标系中，O 为坐标原点，抛物线y =-x 2+c 与y 轴交于点P （0，4）．（1）直接写出抛物线的解析式．（2）如图，将抛物线y =-x 2+c 向左平移1个单位长度，记平移后的抛物线顶点为Q ，平移后的抛物线与x 轴交于A 、B 两点（点A 在点B 的右侧），与y 轴交于点C ．判断以B 、C 、Q 三点为顶点的三角形是否为直角三角形，并说明理由．（3）直线BC 与抛物线y =-x 2+c 交于M 、N 两点（点N 在点M 的右侧），请探究在x 轴上是否存在点T ，使得以B 、N 、T 三点为顶点的三角形与△ABC 相似，若存在，请求出点T 的坐标；若不存在，请说明理由．（4）若将抛物线y =-x 2+c 进行适当的平移，当平移后的抛物线与直线BC 最多只有一个公共点时，请直接写出抛物线y =-x 2+c 平移的最短距离并求出此时抛物线的顶点坐标．6．（2022•贵港）如图，已知抛物线y =-x 2+bx +c 经过A （0，3）和B （72，-94）两点，直线AB 与x 轴相交于点C ，P 是直线AB 上方的抛物线上的一个动点，PD ⊥x 轴交AB 于点D ．（1）求该抛物线的表达式；（2）若PE ∥x 轴交AB 于点E ，求PD +PE 的最大值；（3）若以A ，P ，D 为顶点的三角形与△AOC 相似，请直接写出所有满足条件的点P ，点D 的坐标．7．（2022•金华）如图，在菱形ABCD 中，AB =10，sinB =35，点E 从点B 出发沿折线B -C -D 向终点D 运动．过点E 作点E 所在的边（BC 或CD ）的垂线，交菱形其它的边于点F ，在EF 的右侧作矩形EFGH ．（1）如图1，点G 在AC 上．求证：FA =FG ．（2）若EF =FG ，当EF 过AC 中点时，求AG 的长．（3）已知FG =8，设点E 的运动路程为s .当s 满足什么条件时，以G ，C ，H 为顶点的三角形与△BEF 相似（包括全等）？8．（2022•玉林）如图，已知抛物线：y =-2x 2+bx +c 与x 轴交于点A ，B （2，0）（A 在B 的左侧），与y 轴交于点C ，对称轴是直线x =12，P 是第一象限内抛物线上的任一点．（1）求抛物线的解析式；（2）若点D 为线段OC 的中点，则△POD 能否是等边三角形？请说明理由；（3）过点P 作x 轴的垂线与线段BC 交于点M ，垂足为点H ，若以P ，M ，C 为顶点的三角形与△BMH 相似，求点P 的坐标．9．（2022•张家界）如图，已知抛物线y=ax2+bx+3（a≠0）与x轴交于A （1，0），B（4，0）两点，与y轴交于点C，点D为抛物线的顶点．（1）求抛物线的函数表达式及点D的坐标；（2）若四边形BCEF为矩形，CE=3．点M以每秒1个单位的速度从点C沿C E向点E运动，同时点N以每秒2个单位的速度从点E沿EF向点F运动，一点到达终点，另一点随之停止．当以M、E、N为顶点的三角形与△BOC相似时，求运动时间t的值；（3）抛物线的对称轴与x轴交于点P，点G是点P关于点D的对称点，点Q是x 轴下方抛物线上的动点．若过点Q的直线l：y=kx+m（|k|<9）与抛物线4只有一个公共点，且分别与线段GA、GB相交于点H、K，求证：GH+GK为定值．。

相似三角形与抛物线的面积比例相似三角形与抛物线是几何学中常见的两个概念。

在本文中，我们将探讨相似三角形与抛物线之间的面积比例关系。

一、什么是相似三角形？相似三角形指的是具有相同形状但不同大小的三角形。

换句话说，它们的内角相等，对应边的比例相等。

根据相似三角形的性质，我们可以得出两个重要结论：1.对应边长的比例：如果两个三角形ABC和DEF相似，则它们对应边的长度比例为AB/DE = AC/DF = BC/EF。

2.面积的比例：如果两个三角形ABC和DEF相似，则它们的面积比例为(△ABC的面积)/(△DEF的面积) = (AB²/DE²) = (AC²/DF²) = (BC²/EF²)。

二、什么是抛物线？抛物线是平面上的一条特殊曲线，它可以由一个或多个焦点和直线（称为准线）上的点的位置关系定义。

抛物线具有以下重要特征：1.焦点和准线：每个抛物线都有一个焦点和一条准线。

焦点是离抛物线最近的点，而准线则是与抛物线关联的一条直线。

2.对称性：抛物线具有对称性。

也就是说，抛物线上任意一点关于焦点的投影到准线上的距离相等。

3.焦准定理：焦距的长度等于焦点到抛物线上任意一点的距离的垂直平方。

三、相似三角形与抛物线的面积比例关系现在我们来探讨相似三角形与抛物线之间的面积比例关系。

假设有一个抛物线和在其上的一个三角形。

我们可以利用相似三角形的性质推导出它们的面积比例。

1.建立坐标系：我们可以在平面上建立一个坐标系，使准线成为x 轴，焦点为原点。

2.确定抛物线方程：假设抛物线的方程为y = ax^2。

3.确定三角形的顶点坐标：假设三角形顶点为(0, a)，(x1, y1)，(x2, y2)，其中x1和x2分别为抛物线上两点的横坐标，y1和y2为抛物线上对应点的纵坐标。

4.计算三角形的面积：通过计算三角形的底边和高，我们可以得到抛物线和三角形的面积。

∆ABC的底边长为x2 - x1，高为a - y，所以∆ABC的面积为(1/2) * (x2 - x1) * (a - y)。

抛物线与相似三角形结合的动点问题一、概述在数学中，抛物线与相似三角形是两个重要的概念。

抛物线具有很多有趣的性质，而相似三角形则是几何学中的重要概念之一。

本文将探讨抛物线与相似三角形结合的动点问题，通过具体的案例分析和推导，探讨这两个概念之间的通联，从而深入理解这一数学问题。

二、抛物线的基本性质1. 抛物线的定义抛物线是平面上所有到定点的距离等于其到定直线的距离的点的轨迹。

在直角坐标系中，抛物线的标准方程为 y=ax^2+bx+c，其中 a、b、c为常数，且a≠0。

2. 抛物线的焦点和准线抛物线的焦点是定点 F，准线是定直线 l。

对于标准方程 y=ax^2 的抛物线来说，焦点的横坐标为 0，纵坐标为 1/(4a)，准线的方程为 y=-1/(4a)。

3. 抛物线的对称性抛物线具有关于焦点的对称性。

即便不考虑直角坐标系下的图像，只需考虑焦点和抛物线上另一点的连线和准线的位置关系即可。

三、相似三角形的基本概念1. 相似三角形的定义相似三角形是指它们的对应角相等，并且对应边成比例。

两个三角形相似的简化表述是它们的形状相似，但尺寸不同。

2. 相似三角形的性质相似三角形的边长之比等于它们的对应边上的线段之比。

并且，对于两个相似三角形来说，它们的面积之比等于它们的相似边长之比的平方。

3. 相似三角形的判定方法判定两个三角形相似的方法有AAA判定法、AA判定法、SAS判定法、SSS判定法等。

通过这些判定方法，可以判断两个三角形是否相似。

四、抛物线与相似三角形结合的动点问题1. 问题描述考虑一个抛物线 y=ax^2 上的动点 P(x,y)，将 P 连接到抛物线的焦点F，将 P 到抛物线的准线的垂直距离记作 h，P 到抛物线的焦点的距离记作 d。

如何根据 P 的位置来求出 h 和 d 之间的关系呢？2. 问题分析我们可以通过抛物线 y=ax^2 的标准方程求解出焦点 F 的坐标，以及准线的方程。

我们可以通过 P 的坐标求出 h 和 d 之间的关系。