(完整版)飞机动力学模型建立

飞行器动力学的数学模型和分析方法飞行器是人类一项重要的创造，其对于人类的交通和工作起到了不可或缺的作用。

要想让飞行器在空中顺利地运作，需要对其动力学进行分析和建模。

本文将介绍飞行器动力学的数学模型和分析方法。

一、飞行器动力学的数学模型飞行器动力学的数学模型是建立在牛顿第二定律的基础之上的，它描述了飞行器在空气中的运动轨迹和受到的力的作用。

在飞行器动力学模型中，需要考虑以下因素：1.飞行器的质量和重心位置：飞行器质量和重心位置是影响其运动的重要因素。

质量越大，飞行器所受到的阻力也越大，需消耗更多的能量才能继续前进。

重心位置影响了飞行器的稳定性和姿态调整能力。

2.气流对飞行器的影响：飞行器在空气中会受到阻力、升力和重力等相互作用的力。

阻力是由于空气的粘滞力和飞行器的速度造成的，如果飞行器速度过快，阻力将随之增大。

升力是由于飞行器的机翼形状和速度产生的，它是支撑飞行器飞行的主要力量。

重力是由于地球的引力引起的，它影响了飞行器的下降速度。

3.飞行器的驱动力：飞行器的驱动力是通过动力系统来提供的。

不同的飞行器有不同的动力系统，如螺旋桨、喷气、火箭等。

动力系统的强弱将直接影响飞行器的速度和高度。

基于以上因素，可以建立飞行器动力学的数学模型。

根据牛顿第二定律，飞行器所受到的合力等于质量乘以加速度，即F=ma。

其中，F为合力，m为质量，a为加速度。

合力可以分解为横向力和纵向力。

横向力由于风向对飞行器横向飞行的影响而产生，其大小与飞行器的侧滑角和速度等因素有关。

纵向力由于飞行器前进时所受到的空气阻力和升力而产生，其大小与飞行器的速度、密度、机翼面积等因素有关。

二、飞行器动力学的分析方法1.离线仿真离线仿真是指在计算机上使用飞行器动力学的数学模型进行模拟。

这种方法的优势在于可以模拟不同场景下的飞行情况，如恶劣天气、机械故障等，从而推测出实际情况下飞行器的运动轨迹和各种指标。

离线仿真还可以对飞行器的设计进行优化和评估。

M
,
N T
。于是式（6.13）可简化为
Ix
dp dt
Ix Iy
qr
I
zx
pq
dr dt
L
Iy
dq dt
Ix Iy
rp Izx
p2 r2
M
Iz
dr dt
Iy Ix
pqIzxqrdp dt
N
对于轴对称飞行器，通常Izx 也为零，从而得到转动动力学 方程的最简形式为
Vz g
w
w
这里进行和航迹坐标轴相关变换：
dxg dt
u cos
cos
v sin sin cos
cos sin
wsin cos cos sin sin
dyg dt
u cos
sin
v sin sin sin
cos cos
wsin cos sin sin cos
dzg u cos v sin cos wcos sin dt
线（指机翼面积和翼展之比），指向前；z轴也在对称平面内，垂直 于y轴，指向下；y轴垂直于对称平面内，指向右。 采用机体坐标系建立动力学方程的优点： （1）可利用飞机的对称面，有 Ixy Izy 0 ，从而使方程简化
（2）在重量不变时，各转动惯量和惯性积是常数
（3）机体轴的姿态角和角速度就是飞机的姿态角和角速度，可用安装在 机上的位置陀螺和角速度陀螺直接测得而不必转换。
Vxz
Vzx
Fy
m
dVz dt
Vyx
Vx y
Fz
将上述的投影表达式代入式（1.35），最终得出的机体轴系中质心动 力学方程组的标量形式为
m
du dt
qw

直升机飞行控制系统动态建模与仿真一、引言直升机是一种垂直起降的飞行器，在现代社会中扮演着重要的角色，广泛应用于军事、民用、医疗、物流等领域。

其飞行控制系统的设计和开发具有十分重要的意义。

直升机的飞行控制系统包括机械设计部分和电子控制部分。

机械设计部分主要包括主旋翼叶片、尾旋翼、机身结构等，而电子控制部分则主要包括传感器、执行器、控制器等。

其中，飞行控制系统的设计不仅需要考虑直升机的稳定性、可靠性和飞行性能等问题，还需要考虑到其复杂的结构和多变的工作环境。

本文旨在通过动态建模和仿真的方法，分析直升机飞行控制系统的工作原理和控制机理，进而提高其稳定性和可靠性，为直升机的应用提供技术支撑。

二、直升机的基本结构直升机是一种可以垂直起降的旋翼飞行器，它具有以下基本结构：（1）旋翼系统旋翼系统是直升机的主要部分，包括主旋翼和尾旋翼。

主旋翼通过旋转产生升力和推力，使直升机获得升力和前进动力。

尾旋翼主要用于平衡机身的姿态和控制机身的方向。

（2）机身结构机身结构是直升机的框架，承担着旋翼系统和发动机的重量。

机身结构的主要材料是铝合金、钛合金、复合材料等。

（3）发动机发动机是直升机的动力系统，一般采用燃气轮机或柴油机。

发动机的功率主要决定着直升机的飞行性能和载荷能力。

（4）电子控制装置电子控制装置是直升机的核心部件，主要负责控制旋翼系统的运动和控制机身的姿态。

电子控制装置包括传感器、执行器和控制器等。

三、直升机控制系统的组成直升机的控制系统由传感器、执行器和控制器三部分组成。

（1）传感器传感器是直升机控制系统的输入部分，可以测量飞机的姿态、速度、位置和加速度等参数。

传感器的主要类型包括角速度陀螺仪、加速度计、地磁传感器、气压计等。

（2）执行器执行器是直升机控制系统的输出部分，根据控制器的指令对飞机进行姿态控制和位置控制。

执行器的主要类型包括电动舵机、平衡阀、电动水平面和液压阀等。

（3）控制器控制器是直升机控制系统的核心部件，它接收传感器的信号，计算控制指令，并将其发送给执行器进行控制。

2023-11-07CATALOGUE目录•飞机大迎角非线性动力学概述•飞机大迎角非线性动力学模型建立•飞机大迎角非线性动力学特性分析•飞机大迎角非线性控制方法研究•飞机大迎角非线性动力学实验验证•结论与展望01飞机大迎角非线性动力学概述大迎角飞行状态是指飞机在飞行过程中，机翼与相对气流夹角较大的情况。

在这种状态下，飞机会受到较大的气动阻力，同时也会产生一些特殊的动力学行为。

大迎角飞行状态通常发生在飞机进行机动飞行或着陆等情况下，对于飞行安全和性能有着重要的影响。

飞机大迎角飞行状态非线性动力学的基本概念非线性动力学是一门研究非线性系统行为和演化的学科。

非线性系统是指其输出与输入之间不是线性关系的系统。

在非线性系统中，微小的输入变化可能会引起系统行为的显著改变。

非线性动力学研究的内容包括系统的稳定性、分岔、混沌等行为，以及这些行为之间的相互作用和演化。

飞机大迎角非线性动力学研究对于提高飞机的性能和安全性具有重要的意义。

通过研究大迎角飞行状态下飞机的动力学行为，可以更好地了解飞机的气动性能和飞行稳定性，为飞机设计和控制算法优化提供理论支持。

大迎角非线性动力学研究还可以为飞行控制系统的设计和优化提供重要的理论基础和技术支持，提高飞机的机动性和安全性。

飞机大迎角非线性动力学研究意义02飞机大迎角非线性动力学模型建立飞机在非线性大迎角下，气动参数会发生变化，包括升力系数、阻力系数和俯仰力矩系数等。

气动参数气动数据库风洞实验利用已有的气动数据库，对飞机在大迎角下的气动特性进行评估和预测。

通过风洞实验获取飞机在不同迎角下的气动系数，以验证和改进气动模型。

03飞机大迎角气动模型建立0201飞机大迎角运动模型建立六自由度模型考虑飞机的六个自由度，包括纵向、横向、垂直方向上的位移和速度，以及滚转、俯仰和偏航方向上的角度和角速度。

非线性模型描述飞机的运动时，需要考虑非线性效应，如重力、推力和空气阻力等。

稳定性分析通过稳定性分析，确定飞机在各种条件下的稳定性和控制性能。

率和姿态角以及起落架的几何关系计算得到。
2.3 合力及合力矩的解算
综合考虑起落架三个机轮处的力和力矩即可求得飞机 跑道上滑跑时通过起落架对飞机的作用力和力矩：
·1435·
第 18 卷第 6 期 2006 年 6 月
系统仿真学报
Fxg = Fxgn + Fxgr + Fxgl Fyg = Fgn + Fgr + Fgl Fzg = Fzgn + Fzgr + Fzgl Mxg = Fzgn × Snj + Fzgr × S rj −Fgr ×
Fxgn
Fxgr Fxgl
图1 起落架的受力分析
2 起落架的动力学模型
建立飞机起落架动力学模型，首先是求出起落架三个轮
收稿日期：2005-04-20
修回日期：2005-11-15
作者简介：朱剑毅(1966-), 男, 陕西人, 高级工程师, 硕士, 研究方向为
飞控系统仿真; 李麟(1974-), 女, 陕西人, 工程师, 硕士, 研究方向为飞
图 3 中，ALF 为飞机的迎角，Wz 为 俯仰角速度，Ny 为法向过载，THETA 为 俯仰角，V 为飞机的速度，H 为飞行高度。 图 4 中，xg、yg、zg 分别为三轮的支撑力， xmg、ymg、zmg 分别为三轮相对于飞机 重心的力矩。横坐标均为时间。从图 3 可 以看出，在起飞阶段，飞机抬头起飞时， 高度从 0 米开始上升，迎角和俯仰角开始 增大，俯仰角速度和法向过载也开始增 大，此时，图 4 中起落架对飞机的作用力 及力矩也变为 0，即在空中起落架对飞机 不影响，而在之前的起飞滑跑阶段，仿真 结果表明，起落架对飞机的作用真实的反 映了实际过程。
ω 2 = ω y × sin ϑ − ωx × cosϑ × cos γ

Re:模型飞机的空气动力学第三节机翼机翼飞行时所受的升力因为是平均分布载重，所以盖板受的力并不大，所以一般盖板用2mm 的巴沙木绰绰有余，有些飞机根本没有盖板只有薄膜也可以，翼肋片只要把翼型撑出形状就好，不可能压力破坏，所以很多人把它挖洞以减轻重量，我曾经把一架25级特技机Joker 的翼肋每片都挖了三个大洞，你猜我省了几公克重量，答案只有3公克，机翼我们比较关心的是弯矩及扭矩应力，飞机飞行时所受的升力图解如﹝图10-5a﹞，剪应力如﹝图10-5b﹞，弯矩应力如﹝图10-5c﹞，可以看出破坏都发生在两边机翼接合处，所以机翼中间应力大的地方都要特别加强，要抵抗弯矩应力应设法使大梁的断面积加大，并使上下大梁距离增加，就像铁轨的断面一样，所以﹝图10-6a﹞配置就比﹝图10-6b﹞好，滑翔机低阻力很薄的翼型就很难处理了，必要时上下梁改用一根实心梁，尾翼因面积小，应力不大，靠后面那跟实心梁支撑也够了，但那根梁的材质要选硬质一点的。

双翼机机翼的结构与单翼机不同，单翼机的机翼是悬臂式结构，双翼机单独一片上翼或下翼都是软趴趴的，加上中间的支撑及钢线成一箱形结构，箱形结构在承受弯矩时上下翼分别承拉力与压力，不像单翼机由同一机翼的上下梁分别承受拉力与压力，因上下翼离的很开所以在结构上很有效，但中间支撑及钢线增加的阻力及上下翼之间的干扰，所以双翼机都不快。

要抵抗扭矩变形应设法使机翼结构成一桶状，使外缘有最多的材料，所以全覆盖的机翼除翼型比较准确外，抗扭性也比较好，小飞机机翼没有全覆盖，也要使前部形成一D桶﹝如图10-7﹞，以便抵抗扭力。

保丽龙是机翼另一种常见的材料，与巴沙木相比，保丽龙可以承受压力虽然没木头强，但完全无法承受拉力，所以使用保丽龙作机翼要加上抗拉力材料，常见的作法有在上下缘埋入木头梁，或是只埋下缘梁以承受拉力，另外就是整个以FRP布包覆，成一桶形结构，这种方式在滑翔机上很常见。

机翼的破坏有一大部分是弯矩破坏，为了防止弯矩破坏有些飞机机翼装有斜撑如塞斯纳152等，斜撑对减低弯矩及剪力很有效，如﹝图10-8﹞可以看出最大弯矩及剪力都降低许多，代价当然是斜撑多出来的重量与阻力。

4.三种模态的简化处理(续)
2.荷兰滚模态的简化处理 初步近似认为滚转运动对荷兰滚模态没有影响，即认为偏航
和侧移运动不受滚转速率和滚转角的影响，得到：
全自由度方程解： 偏差较小：
3）螺旋模态的简化处理
螺旋模态在各运动参数中只占据很小的份额，而且运动参数 的变化慢，因此初步近似时，惯性项可以忽略，令方程中：
二、横侧向扰动运动与三种模态
纵向运动时的同一飞机，以M=0.9.高度h=11000m作定常平飞， 各参数及气动导数如下(对稳定轴系）:
由表中表 达式计算：
拉氏变换后得代数方程:
扰动运动 控制输入为0：a=r=0
特征多项式：
特征根：
扰动运动的解
一对共挽复根代表振荡运动模态 大负根代表滚转快速阻尼模态 小根(可正可负)代表缓慢螺旋运动的模态 飞机横侧扰动运动由此三种典型模态线性叠加而成
飞机：倾斜转弯(bank-to-turn)
2、导弹的控制
利用升力、侧力控制导弹飞行轨迹-产生加速度（过载） 水平舵面—，升力，法向过载，上下飞行 垂直舵面—，侧力，侧向过载，左右飞行 滚转:无a，同一平面舵面的差动偏转—滚转力矩
鸭式导弹 鸭翼，不受气流下洗的影响，改变气动特性
推力矢量控制 导弹舵面气动力小，靠推力改变方向控制
三种模态中，振荡模态的系数最大，说明这一模态在横侧 运动各参数中均有明显的表现。
与纵向短周期相同，航向静稳定性导数Cn起恢复作用， 消除侧滑角；侧力导数CY和航向阻尼力矩导数Cnr起阻尼
作用；
CY和Cnr在数值上很小，因此横侧向振荡模态的衰减很慢。
与纵向短周期模态不同的是:由于横滚静稳定性导数的存 在，伴随着侧滑角的正负振荡，飞机还产生了左右滚转的 运动。航向和滚转运动的耦合。

航空航天领域中的飞行器动力学模型建立与性能评估在航空航天领域，飞行器动力学模型的建立和性能评估是实现飞行器稳定性和控制的关键步骤。

通过建立有效的动力学模型，我们可以更好地理解飞行器的运动特性，并为设计和优化飞行器的控制系统提供依据。

同时，通过性能评估，我们可以验证模型的准确性和飞行器的操控能力。

动力学模型的建立是理解和控制飞行器运动的基础。

在飞行器动力学中，我们关注飞行器的六个自由度，即飞行器的三个平动自由度（俯仰、滚转、偏航）和三个旋转自由度（横滚、俯仰、偏航）。

为了建立准确的动力学模型，我们需要考虑飞行器的质量、惯性矩阵、气动力和推力等因素。

针对不同类型的飞行器，建立动力学模型的方法也各不相同。

例如，对于固定翼飞行器，我们可以利用牛顿力学和运动方程来推导出飞行器的动力学方程。

而对于旋翼飞行器，由于其特殊的气动特性，我们需要考虑旋翼的动力学方程和飞行器的旋转动力学。

在建立动力学模型的过程中，我们还需要考虑飞行器的操纵系统和控制器。

操纵系统包括飞行器的操纵面（如副翼、方向舵、升降舵等）和操纵机构，而控制器则负责计算并输出操纵指令，以实现飞行器的期望运动。

建立准确的操纵系统和控制器模型对于飞行器的稳定性和控制性能至关重要。

飞行器的性能评估是验证动力学模型准确性和操控能力的重要手段。

通过性能评估，我们可以对飞行器的操纵性、稳定性和控制性能进行全面的评估。

常用的性能评估指标包括飞行器的追踪误差、响应时间、稳定性裕度和控制系统的抗干扰能力等。

为了进行性能评估，我们可以利用仿真和实验两种方法。

在仿真中，我们可以通过建立飞行器的动力学模型，模拟飞行器在不同工况下的运动特性，并通过比较仿真结果与期望值来评估性能。

而在实验中，我们可以利用飞行器的实际飞行数据，利用传感器和数据采集设备来获取飞行器的实时状态和控制指令，并进行性能评估。

对于飞行器动力学模型的建立和性能评估，我们还需要考虑建模误差和不确定性的影响。

由于飞行器动力学模型的建立涉及到多个物理参数和气动特性的估计，模型的准确性往往受到这些误差和不确定性的影响。

飞机动力学模型公式飞机动力学模型是研究飞机运动和飞行性能的重要工具。

它基于物理原理和数学模型，描述了飞机在不同飞行阶段的运动规律和动力特性。

本文将从人类视角出发，以生动的语言描述飞机动力学模型，使读者能够感受到仿佛亲身体验飞行的情感。

我们来了解飞机的基本构造。

飞机通常由机翼、机身、机尾和发动机组成。

机翼是飞机最重要的部件之一，它提供了升力，使飞机能够离开地面并在空中飞行。

机身是飞机的主要结构部分，承载着乘客和货物以及各种系统和设备。

机尾包括水平尾翼和垂直尾翼，用于保持飞机的稳定性和操纵性。

接下来，让我们来了解飞机的基本飞行原理。

飞机的升力是通过机翼产生的。

当飞机在空中飞行时，机翼上方的气压较低，下方的气压较高，由此产生了升力。

升力的大小取决于机翼的形状、面积以及飞机的速度和飞行姿态。

除了升力，飞机还需要产生推力才能前进。

推力主要由发动机提供，它通过喷射高速气流或推进螺旋桨来推动飞机向前运动。

推力的大小取决于发动机的性能和工作状态。

在飞行过程中，飞机还需要克服阻力。

阻力是飞机运动过程中受到的空气阻碍力，它包括气动阻力、重力和滑行阻力等。

飞机需要消耗能量来克服阻力，保持飞行的速度和高度。

为了控制飞机的运动，飞行员需要操纵飞机的姿态和舵面。

飞机的姿态包括俯仰、滚转和偏航，分别控制飞机的上下、左右和旋转运动。

舵面则是飞机上的可移动部件，通过改变其位置来改变飞机的姿态和方向。

飞机动力学模型以上述原理为基础，通过建立数学方程和模拟算法，描述了飞机的运动和性能。

它可以预测飞机在不同环境条件下的飞行特性，如起飞距离、爬升率、巡航速度和降落过程等。

飞机动力学模型在飞机设计、飞行控制和飞行仿真等领域具有重要应用价值。

飞机动力学模型是研究飞机运动和飞行性能的重要工具，它基于物理原理和数学模型，描述了飞机在不同飞行阶段的运动规律和动力特性。

通过模拟和预测飞机的运动和性能，飞机动力学模型在飞机设计和飞行控制中发挥着重要作用。

设方向余弦表为矩阵Mbg，用欧拉角描述：
体轴坐标与地轴坐标可以互相转换
Mbg是复共轭矩阵：
x
y
M bg
xg
yg
z
zg
M 1 bg
MbTg
姿态角变化率与角速度分量间的几何关系
地轴系 Oxgyg平面
飞机三个姿态角变化率的方位
—沿ozg轴的向量，向下为正
—在水平面内与ox轴在水平面上的
u vw
F 按各轴分解，表示为： F iX jY kZ
各轴分量：
X m u wq vr
Y
m v ur
wp
Z
m
w
vp
uq
飞机的力方程
2.力矩方程
M
dH dt
dH dH dt 1H dt H
先考虑第一项
H 是动量矩，单元质量dm因角速度引起的动量矩为
dH r ( r )dm
式中：r 为质心至单元质量dm 的向径。
对飞行器的全部质量积分，可得总的动量矩 H r ( r )dm
式中： r ix jy kz, ip jq kr
依据：
i jk r p q r i(qz r y) j(r x pz) k( p y xq)
xyz
i r ( r ) x
xydm Ixy
表示惯性积
依据假设 Ixy=Izy=0 ，H 的各分量
H
x
H y
pI x qI y
rI xz
代入
dH dt
1H
dH dt
H
H
z
rI z
pI xz
可得
dH x dt
pI x rI xz
dH y dt
qI y

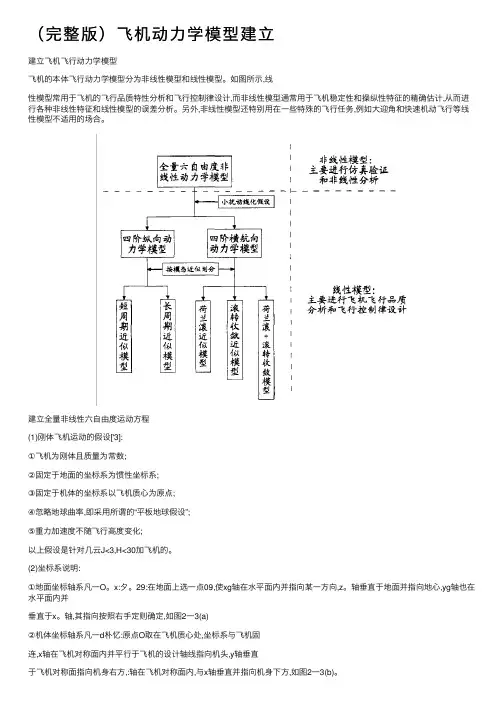
（完整版）飞机动⼒学模型建⽴建⽴飞机飞⾏动⼒学模型飞机的本体飞⾏动⼒学模型分为⾮线性模型和线性模型。

如图所⽰,线性模型常⽤于飞机的飞⾏品质特性分析和飞⾏控制律设计,⽽⾮线性模型通常⽤于飞机稳定性和操纵性特征的精确估计,从⽽进⾏各种⾮线性特征和线性模型的误差分析。

另外,⾮线性模型还特别⽤在⼀些特殊的飞⾏任务,例如⼤迎⾓和快速机动飞⾏等线性模型不适⽤的场合。

建⽴全量⾮线性六⾃由度运动⽅程(1)刚体飞机运动的假设['3]:①飞机为刚体且质量为常数;②固定于地⾯的坐标系为惯性坐标系;③固定于机体的坐标系以飞机质⼼为原点;④忽略地球曲率,即采⽤所谓的“平板地球假设”;⑤重⼒加速度不随飞⾏⾼度变化;以上假设是针对⼏云J<3,H<30加飞机的。

(2)坐标系说明:①地⾯坐标轴系凡⼀O。

x:⼣。

29:在地⾯上选⼀点09,使xg轴在⽔平⾯内并指向某⼀⽅向,z。

轴垂直于地⾯并指向地⼼,yg轴也在⽔平⾯内并垂直于x。

轴,其指向按照右⼿定则确定,如图2⼀3(a)②机体坐标轴系凡⼀d朴忆:原点O取在飞机质⼼处,坐标系与飞机固连,x轴在飞机对称⾯内并平⾏于飞机的设计轴线指向机头,y轴垂直于飞机对称⾯指向机⾝右⽅,:轴在飞机对称⾯内,与x轴垂直并指向机⾝下⽅,如图2⼀3(b)。

(3)刚体飞机的全量六⾃由度⾮线性运动⽅程为:⼒⽅程组:⼒矩⽅程组：运动⽅程组：导航⽅程组：符号说明:建⽴飞机⼩扰动线化⽅程(l)基本假设:①⼩扰动假设:我们把运动状态与飞机基准运动状态差别很⼩的扰动运动称为⼩扰动运动。

采⽤⼩扰动假设线化后的⽅程,在⼤多数情况下均能给出⾜够满意的结果。

这是因为:a、在⼤多数飞⾏情况下,各主要⽓动参数的变化与扰动量成线性关系;b、飞⾏中即使遇到相当强烈的扰动,在有限的时间内飞机的线速度和⾓速度也往往只有很⼩的变化量。

②飞机具有对称⾯(⽓动外形和质量分布均对称)则且略去机体内转动部件的陀螺⼒矩效应。

③在基准运动中,对称平⾯处于铅垂位置(即θ=0),且运动所在平⾯与飞机对称平⾯相重合(即β=O)。

飞机飞行模型的建立飞机的参数重力：W 推力：T 气动力：A 俯仰力矩：M 偏航力矩：N 滚转力矩：L常用气动力由升力L ，阻力D 和侧力C 组成，由空气动力学可知，空气动力的一般计算公式表示如下：L SC V 221L ρ=D SC V 221D ρ=C SC V 221C ρ=式中L C D C C C 分别为升力系数，阻力系数，侧力系数。

1.刚体飞行器运动的假设1)认为飞行器不仅是刚体,而且质量是常数；2)假设地面为惯性参考系，即假设地面坐标为惯性坐标； 3）忽略地面曲率，视地面为平面； 4）假设重力加速度不随飞行高度而变化；5）假设机体坐标系的z o x --平面为飞行器对称平面，且飞行器不仅几何外形对称，而且内部质量分布亦对称，惯性积0==zy xy I I2.旋转坐标系中向量的导数设活动坐标系b b b z y Ox 具有角速度ω （见图 3.1-1）。

向量ω在此坐标系中的分量为r q p ,,，即k r j q i p++=ω （3.1-1） 其中i 、j、k 是b x 、b y 、b z 轴的单位向量。

图3.1-1设有一个可变的向量)(t a，它在此坐标系中的分量为z y x a a a ,,，即k a j a i a a z y x++= （3.1-2）由上式求向量)(t a对时间t 的导数：dtk d a dt j d a dt i d a k dt da j dt da i dt da dt a d zy x z yx +++++= （3.1-3） 从理论力学知，当一个刚体绕定点以角速度ω旋转时，刚体上任何一点P的速度为r dtr d⨯=ω （3.1-4） 其中r是从O 点到P 点的向径。

现在，把单位向量i看作是活动坐标系中一点P 的向径，于是可得：i dtid⨯=ω （3.1-5） b xωb yb zOijk同理可得： j dtj d⨯=ω （3.1-6） k dtk d⨯=ω （3.1-7） 将式（3.1-5）、（3.1-6）及（3.1-7）代入式（3.1-3）中，可得：)(k a j a i a k dtda j dt da i dt da dt a d z y x z y x++⨯+++=ω （3.1-8） 或写为： a t a dt a d⨯+=ωδδ （3.1-9） 其中k dt da j dt da i dt da t a z y x++=δδ taδδ 称为在活动坐标系中的“相对导数”，相当于站在此活动坐标系中的观察者所看到的向量a 的变化率。

飞行动力学仿真报告姓名：学号：单位：航天学院代培班2015/8/15一、飞行动力学模型建立 1．质心动力学方程组在惯性系中，根据牛顿第二定律有mFdt V d i = （1.1）将上式投影到机体坐标系中V dtV d dt V d i⨯+=ω （1.2）其中T r q p ][=ω，T w v u V ][=，第二项k uq vp j wp ur i vr wq wv u r q p kj i V)()()(-+-+-==⨯ω（1.3）将合力投影到机体坐标系中T z y x F F F F ][=，所以质心动力学方程可表示为⎪⎩⎪⎨⎧-+=-+=-+=uq vp wF wp ur v F vr wq u F z y x （1.4）2．绕质心转动动力学方程 根据动量矩定理b bi H dtH d dt H d M⨯+==ω（1.5）其中[]TN ML M =，T r q p ][=ω，T z yxh h h H ][=，飞机关于Oxz面对称，0==yz xy J J ，zx xz J J =，有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------==r J p J q J r J p J r q p J J J J J J J J J J H z zx y xz x z zyzx yz y yxxz xy xω （1.6）式（1.5）中右边第二项就可以写成⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-+-+-==⨯x y z x y z x y z x y z zyxqh ph ph rh rh qh k qh ph j ph rh i rh qh h h h r q pkj iH )()()(ω（1.7）综上pq J J qr p J r J qrJ qpJ pqJ r J pJ N rp J J p r J q J prJ J p J r rpJ qJ M qr J J qp r J p J rqJ qrJ qpJ r J pJ L x y xz z xz x y z xz z x xz y z xz xz x y y z xz x y z xz xz x )()()()()()(2222-+--=+-++-=-+--=-+-+=-++-=-+--= （1.8）3. 角度运动学方程建立⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡ψθφθφφ 00)()(00)(00y x x L L L r q p（1.9）其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=θθθθθcos 0sin 010sin 0cos )(y L ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=φφφφφcos sin 0sin cos 0001)(x L ，所以有 φθψφθφθψφθθψφcos cos sin sin cos cos sin +-=+=-=r q p （1.10）写成欧拉角的微分方程形式有)cos sin (cos 1tan cos tan sin sin cos φφθψθφθφφφφθr q r q p r q +=++=-= （1.11）4. 位置运动方程建立地面坐标系与机体坐标系之间的转换为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+++--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==θφψθφψφψθφψφθφψθφψφψθφψφθψθψθψψψψθθθθφφφφψθφcos cos sin sin cos cos sin cos sin cos sin sin cos sin sin sin sin cos cos cos sin sin sin cos sin sin cos cos cos cos 0sin 010sin 0cos 1000cos sin 0sin cos cos sin 0sin cos 0001)()()(321L L L A gb （1.12）所以，地面坐标系上表示位置的微分方程有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡w v u A z y x T gb g g g （1.13）5. 飞机的动力学模型综上，飞机的动力学方程组为质心动力学方程：⎪⎩⎪⎨⎧-+==-+==-+==uq vp wa m F wp ur va m F vr wq ua m F z z y y x x /// （1.14）绕质心转动动力学方程：⎪⎩⎪⎨⎧----=----=--+-=pq I I qr p I I rN rp I I p r I I q M qr I I pq r I I p L y x xz z x z xz y z y xz x )()()()()()(22 （1.15）飞机的运动学方程组为质心位置方程⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡w v u A z y x T gb g g g （1.16）欧拉角方程)cos sin (cos 1tan cos tan sin sin cos φφθψθφθφφφφθr q r q p r q +=++=-= （1.17）附加方程有22222222211222)()()(tan )(tan aa p a a a a a a a a aa a a a a a a aaa w u v w w uu v w u v w u u w wu w u v u ww v u V +--+=+-=+==++=-- βαβα （1.18）6. 飞机受力计算重力在机体坐标系上的投影为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==θφθφθcos cos cos sin sin 00mg mg mg mg A G Tgb b （1.19）气流坐标系与机体坐标系之间的转换⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=αβαβαββαβαβαββββααααcos sin sin cos sin 0cos sin sin sin cos cos cos 100cos sin 0sin cos cos 0sin 010sin 0cos wb A （1.20）所以空气动力在机体坐标系上的投影为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=αβαβαββαβαβαcos sin sin cos sin cos sin sin sin cos cos cos Z Y X Y X Z Y X Z Y X A C B A R wb （1.21）综上有飞机所受合力在体轴系上的投影为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++-=C mg mg B A mg P F b θφθφθcos cos cos sin sin （1.22）二、飞行动力学模型的求解 1. 飞行动力学模型求解流程动力学方程求解流程图2.1动力学求解流程详解注：上图来自课件，其中欧拉角的微分方程有误图2.2 动力学求解流程简图2. 编程实现动力学模型求解采用C++语言对该问题进行求解，程序见附件。

精选课件
10
基础知识要求
牛顿力学基础； 高等数学初步； 数值计算方法； 自动控制原理； 现代控制理论部分知识； Matlab与C语言；
精选课件
11
涉及到的主要知识点
关于受力分析的基本直觉和一些基本概念(得到的 设计结果都从最直观的地方思考下是否合理)；
泰勒展开(抓住主要矛盾的最基本手段)； 数值求解微分方程组(描述一个对象)； 根轨迹、稳定裕度(工程师的吃饭家伙)与描述函
精选课件
29
制导、导航与控制(GNC)
制导(Guidance)：规划出一条航行轨迹； 导航(Navigation)：测量飞行器的实际姿态
与位置； 控制(Control)：操纵飞行器沿着规划好的
航行轨迹运动。
对应于标准的反馈控制框图，GNC分别对应于哪些元素？
精选课件
30
历史发展
1936年，德国开始进行“制导火箭”研究工程。 著名的V1和V2导弹，是现代制导武器的鼻祖，地地导弹。
在我国以飞行器为研制主体的航空航天在我国以飞行器为研制主体的航空航天领域是目前国内少有的独立进行完全控制领域是目前国内少有的独立进行完全控制系统设计的单位经过多年的不断完善系统设计的单位经过多年的不断完善这一条流水线上培养的控制工程师经过了这一条流水线上培养的控制工程师经过了系统而严格的训练不仅在控制领域具有系统而严格的训练不仅在控制领域具有丰富的经验而且控制工程师也是培养总丰富的经验而且控制工程师也是培养总设计师最多的分系统专业因为这个专业设计师最多的分系统专业因为这个专业需要全面系统的分析和理解问题
数等频域知识；
*状态观测器的设计； *数值逼近与非线性规划的思想； Matlab中主要基本控制分析函数的使用； 熟练使用C或者C++语言；

建立飞机飞行动力学模型飞机的本体飞行动力学模型分为非线性模型和线性模型。

如图所示，线 性模型常用于飞机的飞行品质特性分析和飞行控制律设计，而非线性模型通常 用于飞机稳定性和操纵性特征的精确估计，从而进行各种非线性特征和线性模 型的误差分析。

另外，非线性模型还特别用在一些特殊的飞行任务，例如大迎 角和快速机动飞行等线性模型不适用的场合。

线性模型：主要进行飞机飞行品质 分析歩飞行控制律设计建立全量非线性六自由度运动方程 (1) 刚体飞机运动的假设['3]: ① 飞机为刚体且质量为常数；② 固定于地面的坐标系为惯性坐标系；③ 固定于机体的坐标系以飞机质心为原点；④ 忽略地球曲率，即采用所谓的“平板地球假设”； ⑤ 重力加速度不随飞行高度变化；以上假设是针对几云Jv3,H<30加飞机的。

(2) 坐标系说明：① 地面坐标轴系凡一 Q x:夕。

29:在地面上选一点09,使xg 轴在水平面内 并指向某一方向,z 。

轴垂直于地面并指向地心，yg 轴也在水平面内并 垂直于X 。

轴，其指向按照右手定则确定，如图2 一 3(a)② 机体坐标轴系凡一 d 朴忆:原点O 取在飞机质心处，坐标系与飞机固 连,x 轴在飞机对称面内并平行于飞机的设计轴线指向机头 ,y 轴垂直全董六自由度非蝇性动力学模型非陸模型:主要进行恃奏验证 和非线性分析四阶纵向动 力学模型四外横航向 动力学模型短周期近似模型于飞机对称面指向机身右方 机身下方,如图2 一 3(b)。

oy，:轴在飞机对称面内，与x 轴垂直并指向乩地面坐标轴系氐机体坐标轴系 图2胡常用塑标系说明⑶刚体飞机的全量六自由度非线性运动方程为 力方程组： 力矩方程组： - /)-匚(/十阳)一你3-小)二丄人=A0 二 p + q sin 0 tan 0 十 r cos 0 tan 0W一 心因-几 3 -qJ-钮+v )-4(p —")二览=v 运动方程组: & - i/COS^ 一厂血00 二 ------ (q sin 0 + r cos 0)COS0v - pw一 皿+輕歸讪+ ：(F —圖) w — qu —严+心肌0讣(益+导航方程组：ccs^ + 训一sin 妙LOH0 丰cos sin 9 sin 0 + w (sin 肖sin / + cos sin cos y, = sin y/cos0 + r(co$4y cosc* + siny/sin6?sin 0) + ^-cos^sin + sin^ sin Otosd) h --nsin 0 - vcos^sin^ - wcostf cos^符号说明：心飞机质量，重力加速度：2b E机机翼禹税、平均T动茁长和展検：u,v,w速度矢命在分别在体轴条厂八二上的投影；p.q”体轴宗相对于地轴系旋转角速度矢览分别在体轴^x.y.z上的投影；%动力在体耙系各轴上的投勲貝丹押的,丫皿沖.推力在休轴系各细上的投影*飞机的俯仰角、滚转角和偏航角；飞机迎角*侧滑角和绕速度轴矢戟的滚转角；总机速區矢量.飞机航迹倾斜角.荻迹偏转角；飞机体轴系下各轴的转动惯电：匕机体轴系下谷轴的惯性积；飞机所爱升力、胆力、侧力和发动机抵力：合力矩分别在体轴系「丫2上的投影；E机位垃欠_&在炮轴系上的投影柯飞机岛度：飞机升降蛇偏角、亂罠倔角、方向舵偏角和油门位置：建立飞机小扰动线化方程(I)基本假设：①小扰动假设：我们把运动状态与飞机基准运动状态差别很小的扰动运动称为小扰动运动。

回忆牛顿力学

平动的方程； 转动的方程；
作为刚体的飞行器
质心的移动：力的影响：包括空气动力，发动机的推力和
重力。
绕质心的转动：相对于质心的力矩,，包括空气动力矩， 推力矩。
两个重要坐标系


研究气动力时，以速度坐标系为基准(O取在飞行 器的质心上，Ox3轴与速度矢量重合，Oy3轴位于 机体纵向对称平面内Ox3轴垂直，指向上为正)； 研究气动力矩时，以机体坐标系为基准(Ox1轴与 机体纵轴重合，Oy1轴位于机体纵向对称平面内 Ox1轴垂直，指向上为正) ；
俯仰力矩Mz 偏航力矩My 滚动力矩Mx
注意观察几个控制舵的位置
力的作用点，压心(主要受Ma数 影响)，十分重要
俯仰力矩工程简易计算公式
小攻角和舵偏角情况下:
最关键的主要3项(第2到4项)：恢复力矩、操纵力矩、阻尼力矩
上述三项是控制设计中的主要考虑因素，而恢复与操纵力矩量值又远比阻尼力矩大。 恢复力矩总是自然的去平衡操纵力矩，使得二者之和基本为0，顾名思义。改变操纵 力矩，就必然改变了攻角，从而影响了升力大小(这点在未来设计中可以通过输出曲 线对比的形式深化理解)。
V1导弹倾斜发射，飞行完预设的距离后，转动升降舵，掉头俯冲攻击目标。 大约飞行370km，使用自动驾驶仪，核心是陀螺。 V2导弹投入实用，造成了很大心理威慑。精度：16km/322km 系统组成：方向陀螺进行航向稳定+时间驱动的俯仰指令机构；轴向积分加速度 计，当速度达到要求时，关闭发动机。使用了最早的陀螺与加速度计
课程介绍
结束
第二部分
飞行力学中的基本概念
基本概念

飞行器的受力； 升力如何产生； 制导、导航与控制的关系；

四翼飞行器动力学分析与建模1.引言四轴飞行器，又称四旋翼飞行器、四旋翼直升机，简称四轴、四旋翼。

这四轴飞行器(Quadrotor)是一种多旋翼飞行器。

四轴飞行器的四个螺旋桨都是电机直连的简单机构，十字形的布局允许飞行器通过改变电机转速获得旋转机身的力，从而调整自身姿态。

因为它固有的复杂性，历史上从未有大型的商用四轴飞行器。

近年来得益于微机电控制技术的发展，稳定的四轴飞行器得到了广泛的关注，应用前景十分可观。

本章通过分析四旋翼直升机的动力学机制，运用已知的物理定律和方程来建立表征系统动态过程的数学模型。

2.四旋翼飞行器简介2.1四旋翼飞行器结构四旋翼直升机主体构成有：产生升力的四个旋翼、飞行控制设备及其支撑旋翼的机身。

有时为了保护飞行器，避免旋翼的损坏，特别装设了保护架。

其中，每个旋翼包括直流电机、翼翅及连接件等部分。

如下图所示：2.2四旋翼飞行器飞行原理四旋翼直升机与传统的直升机相比，有着自己独特的地方。

它的四个呈十字平均分布的旋翼取代了传统的单独的旋翼，对机身产生单独的力和力矩。

四旋翼直升机通过改变旋翼转速来控制飞行器的姿态，且四个旋翼的动态特性高度耦合。

3.四旋翼飞行器动力学方程3.1坐标描述及其转换关系飞机的姿态角、飞行速度的大小和方向等参数总是和坐标系联系在一起的，要确切地描述飞机的运动状态，就要先建立适当的坐标系。

下面定义几种坐标系，并分析各坐标之间的相互转换关系：(1)地面坐标系E （OXYZ ）地面坐标系用语研究飞机相对于地面的运动，确定飞机在空间的位置坐标X 、Y 、Z ，从而方便研究飞机的姿态、航向以及飞机相对起飞点的空间位置。

该坐标系原点固定于地面上飞机的起飞点，OX 轴指向飞机制定的飞行方向，OZ 轴垂直水平面向上，OY 轴垂直OXZ 平面。

(2)机体坐标系B （Oxyz ）机体坐标系固定在机体上，原点设在飞机重心，纵轴Ox 平行于前后旋翼的连线，指向前方为正方向，竖轴Oz 平行于左右旋翼的连线，指向右方为正方向；轴Oy 与轴Ox 、Oz 所在平面垂直，并与轴Ox 、轴Oz 组成右手坐标系。