机器人动力学模型和运动学模型的建立

计算力学在机器人运动规划中的应用随着科技的不断进步，机器人在日常生活中的应用越来越广泛。

机器人的运动规划是机器人技术中的重要一环，它涉及到机器人在各种环境中的移动和操作。

而计算力学作为一门研究物体运动和相互作用的学科，为机器人运动规划提供了重要的理论基础和工具。

计算力学是一门基于数学和物理学的学科，它研究物体在力的作用下的运动和变形。

在机器人运动规划中，计算力学可以用于建立机器人的运动模型，并通过数值计算方法来预测机器人在不同情况下的运动轨迹和力学行为。

首先，计算力学可以帮助建立机器人的运动模型。

机器人的运动模型是描述机器人运动的数学模型，它可以用来预测机器人在不同环境下的运动轨迹和力学行为。

计算力学通过建立机器人的运动学和动力学模型，可以准确地描述机器人的运动规律和受力情况。

例如，对于一个由关节连接的机器人，计算力学可以通过运动学方程来描述机器人的位置、速度和加速度之间的关系；而通过动力学方程，可以计算机器人在不同关节力矩作用下的运动轨迹和力学行为。

其次，计算力学可以用于机器人的路径规划。

路径规划是机器人运动规划中的重要一环，它决定了机器人在空间中的运动轨迹和路径。

计算力学可以通过数值计算方法，如最优化算法和搜索算法，来寻找机器人的最佳运动路径。

例如，对于一个需要避开障碍物的机器人，计算力学可以通过数值计算方法来寻找机器人绕过障碍物的最佳路径，从而实现安全和高效的运动。

此外，计算力学还可以用于机器人的动力学分析和控制。

动力学分析是研究机器人在力的作用下的运动和力学行为的过程，它可以帮助理解机器人的运动特性和力学行为。

计算力学可以通过建立机器人的动力学模型，来分析机器人在不同力矩作用下的运动和力学行为。

而动力学控制则是利用计算力学的方法来设计和实现机器人的控制策略，以实现精确和稳定的运动控制。

例如，对于一个需要精确定位的机器人，计算力学可以通过动力学分析和控制方法来实现机器人的精确运动和定位。

综上所述，计算力学在机器人运动规划中的应用是不可忽视的。

非完整系统介绍
轮 式第 机七 器章 人
轮式移动机构 轮式机器人的运动学和动力学
轮式机器人的运动规划及控制
第七章 轮式机器人
第一节 非完整系统简介
第
第七章
一
轮式机器人
节
非
完
“非完整”一词起源于近代分析力学，最早出现于德
整
国学者Hertz.H的著作“力学原理”中，1894年
系
Hertz第一次把约束和系统分成完整和非完整两大类，
0
0 1
第
第七章
三
轮式机器人
节
运
动
机器人的运动学模型
学 和
最后就可以得到差动驱动机器人的前向运动学模型：
动
力
学
x cos
I
y
s in
0
sin cos
0
0 0 1
ห้องสมุดไป่ตู้
r
2
rr
r
XR
学
x
I
y
y P
O
x
XI
第
第七章
三
轮式机器人
节
运
动
机器人的坐标系
学
和 动
YI
正交旋转矩阵
力
YR
XR
学
cos sin 0
R sin cos 0
y
P
0
0 1
O
x
XI
第
第七章
三
轮式机器人
节
运
动
机器人的坐标系
学
和
动
局部参考坐标系
YI
力
YR
XR
学
cos sin 0 x

直角坐标机械臂是一种常见的工业机器人，它由直角坐标系的三个直线轴组成，分别沿着X、Y和Z轴移动。

在工业自动化生产线上，直角坐标机械臂通常用于搬运、装配、喷涂等操作。

在设计直角坐标机械臂时，动力学数学模型是非常重要的。

动力学数学模型可以描述机械臂系统随时间变化的运动规律，是控制机械臂运动的基础。

接下来，将分为以下几个方面来讨论直角坐标机械臂动力学数学模型。

1. 直角坐标机械臂的运动学模型直角坐标机械臂的运动学模型描述了机械臂末端执行器的位置和姿态随时间的变化规律。

通常可以用欧拉角、四元数或变换矩阵来描述机械臂的姿态，而位置可以用直角坐标系的三个坐标来描述。

2. 直角坐标机械臂的动力学模型直角坐标机械臂的动力学模型描述了机械臂系统在受到外界力和力矩作用下，随时间变化的运动规律。

动力学模型可以通过牛顿-欧拉方程或拉格朗日方程来建立。

3. 直角坐标机械臂的质量分布直角坐标机械臂的质量分布对其动力学模型有着重要的影响。

质量分布不均匀会导致机械臂在运动过程中产生惯性力和惯性矩，从而影响机械臂系统的动力学性能。

4. 直角坐标机械臂的关节驱动器模型直角坐标机械臂的关节驱动器模型描述了机械臂关节的驱动器特性，如关节驱动器的转矩-角度关系、转速-角速度关系等。

这对于控制机械臂的运动过程具有重要的指导意义。

5. 直角坐标机械臂的控制策略基于动力学数学模型建立合理的控制策略是保证直角坐标机械臂高效稳定运行的关键。

常见的控制策略包括PID控制、自适应控制、模糊控制等，这些控制策略可以根据机械臂的动力学数学模型来优化设计。

直角坐标机械臂的动力学数学模型是机械臂设计与控制的基础和关键。

建立准确的动力学数学模型可以为机械臂的优化设计、控制策略的制定提供可靠的依据，从而有效提高机械臂系统的运动性能和工作效率。

希望未来能够有更多的研究者投入到直角坐标机械臂动力学数学模型的研究中，促进机械臂技术的不断发展与进步。

直角坐标机械臂是一种工业机器人，广泛应用于工业自动化生产线，能够完成搬运、装配、喷涂等操作。

四足机器人动力学建模：拉格朗日动力学引言在机器人领域中，四足机器人是一种常见的机器人类型。

它们具有四条腿和能够模拟和模仿动物行走的能力。

为了实现自主步行和平稳运动，我们需要对四足机器人的动力学进行建模和分析。

本文将介绍使用拉格朗日动力学方法对四足机器人进行建模的过程和步骤。

拉格朗日动力学简介拉格朗日动力学是一种描述系统动力学行为的方法。

它基于拉格朗日原理，通过最小化系统的运动方程，求解系统中的广义坐标和约束力。

在机器人动力学中，拉格朗日动力学方法被广泛应用于建模和控制。

四足机器人动力学建模步态与坐标系在进行四足机器人动力学建模之前，首先需要确定机器人的步态和坐标系。

通常，四足机器人的步态可以分为步行和跑步两种模式。

对于步行模式，机器人的步态可以简化为前后左右四个联系稳定的点。

在这种情况下，机器人的坐标系可以选择为正前方为x轴正方向，右侧为y轴正方向，地面为z轴正方向。

运动学分析在进行动力学建模之前，需要进行机器人的运动学分析。

运动学分析可以得到机器人各个关节的位置、速度和加速度信息。

这些信息对于后续的动力学建模非常重要。

动力学建模操作要素在进行动力学建模之前，需要确定机器人系统的操作要素。

这些要素包括机器人的质量、惯性、关节约束等。

通过对这些要素的分析和建模，可以得到机器人的整体动力学方程。

拉格朗日方程拉格朗日动力学方法使用拉格朗日方程来描述系统的运动方程。

拉格朗日方程可以通过系统的动能和势能表达式得到。

对于四足机器人，为了简化模型，通常可以假设机器人为刚体，并且忽略其柔软特性。

拉格朗日方程的形式如下：L = T - V其中，L为拉格朗日函数，T为系统的动能，V为系统的势能。

动力学模拟通过对拉格朗日方程进行求解，可以得到系统的运动方程。

为了模拟机器人的动力学行为，可以使用数值方法进行迭代求解。

常见的数值方法有欧拉法和中点法等。

结论通过拉格朗日动力学方法进行建模，可以得到四足机器人的运动方程和动力学模拟。

3、最优时间轨迹规划优化
目前的最优时间轨迹规划方法主要基于数学规划和人工智能算法，如遗传算法、 模拟退火算法等。然而，这些方法可能存在计算量大、优化时间长等缺点。为 改进现有方法，可从以下几个方面着手：
（1）利用机器学习技术：通过训练机器人大量的实际生产数据，学习并优化 机器人的运动模式，提高规划速度和准确性。
2、综合优化时间和能量轨迹规 划的方法
为了实现时间和能量的综合优化，可以采用以下方法：
（1）基于多目标优化算法：采用多目标优化算法（如遗传算法、粒子群算法 等），同时优化时间轨迹和能量轨迹。通过调整各目标函数的权重系数，可以 权衡时间和能源消耗的矛盾关系，得到综合最优解。
谢谢观看
（1）运动学和动力学建模：首先需要建立工业机器人的运动学和动力学模型， 以便准确模拟机器人的运动过程并预测其性能。
（2）路径规划：通过计算机辅助设计（CAD）技术，规划出机器人完成作业所 需的最佳路径，同时确保路径的安全性和可行性。
（3）速度规划：根据任务需求和机器人的运动性能，制定机器人沿最佳路径 移动的速度计划，以保证生产效率和产品质量。
（3）优化算法：采用适当的优化算法，如梯度下降法、遗传算法等，对规划 好的路径进行优化，以实现最小化能源消耗的目标。
3、最优能量轨迹规划优化
目前的最优能量轨迹规划方法主要基于实验研究和经验总结。为了进一步优化 现有方法，可从以下几个方面着手：
（1）建立全面的能量模型：除了电机功耗和负载功耗，还应考虑其他影响因 素，如摩擦力、风阻等，以更精确，实现自我优化和改 进。
（3）考虑动态环境：在规划过程中考虑生产环境的动态变化，如物料供应、 设备故障等因素，以提高规划的适应性。
最优能量轨迹规划
1、最优能量轨迹规划定义

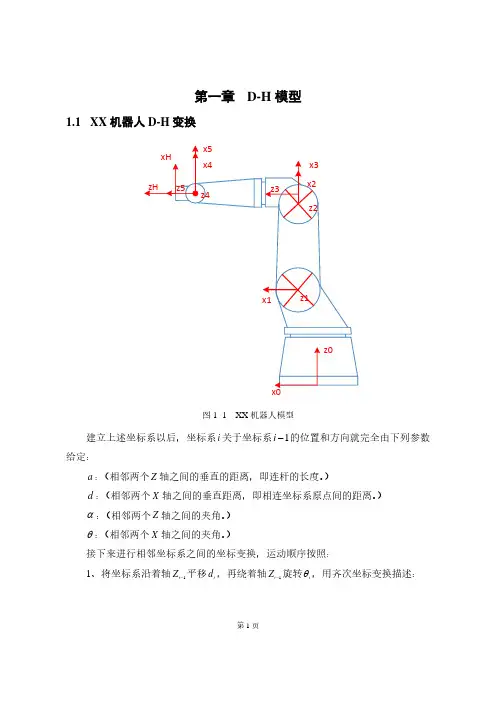
第1页第一章 D-H 模型1.1 XX 机器人D-H 变换z4图1- 1 XX 机器人模型建立上述坐标系以后，坐标系i 关于坐标系1i -的位置和方向就完全由下列参数给定：a ：（相邻两个Z 轴之间的垂直的距离，即连杆的长度。

）d ：（相邻两个X 轴之间的垂直距离，即相连坐标系原点间的距离。

） α：（相邻两个Z 轴之间的夹角。

）θ：（相邻两个X 轴之间的夹角。

） 接下来进行相邻坐标系之间的坐标变换，运动顺序按照：1、将坐标系沿着轴1i Z -平移i d ，再绕着轴1i Z -旋转i θ，用齐次坐标变换描述：1'cos sin 00sin cos 00001001i i i i i i i A d θθθθ--⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2、通过中间坐标系沿着轴'i X 平移i a ，并且绕着轴'i X 旋转i α，用齐次坐标变换描述为：1'1000cos sin 00sin cos 001i i i i i i i a A αααα-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦3、坐标变换通过右乘得到：1cos cos sin sin sin cos sin cos cos cos sin sin 0sin cos 01i i i i i i i i i i i i i i i i i i ia a A d θαθθαθθθαθαθαα--⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦表1- 1 巨轮机器人的DH 参数表θ daα0-1 1θ1d 1a 1α 1-2 2θ 2d2a2α2-3 3θ3d 3a 3α 3-4 4θ 4d 4a 4α 4-5 5θ5d5a5α5-66θ 6d 6a 6α第3页1.2 旋转变换1、参考坐标系绕Z 轴旋转θ角的旋转矩阵为：cos sin 0sin cos 001Z R θθθθθ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦2、参考坐标系绕X 轴旋转α角的旋转矩阵为：1000cos sin 0sin cos x R ααααα⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦ 得到关于两轴的旋转变换：R = [ cos(theta), -cos(alpha)*sin(theta), sin(alpha)*sin(theta)] [ sin(theta), cos(alpha)*cos(theta), -sin(alpha)*cos(theta)] [ 0, sin(alpha), cos(alpha)]1.3 正运动学变换0012345123456n T A A A A A A =1.4 逆运动学变换逆运动学是已知末端连杆的位置和方向，求机器人各个关节变量。

教案首页课程名称农业机器人任课教师李玉柱第3章机器人运动学和动力学计划学时 3教学目的和要求：1.概述，齐次坐标与动系位姿矩阵，了解平移和旋转的齐次变换；2.机器人的运动学方程的建立与求解*；3.机器人的动力学*重点：1.机器人操作机运动学方程的建立及求解；2.工业机器人运动学方程3.机器人动力学难点：1. 机器人动力学方程及雅可比矩阵基本原理思考题：1.简述齐次坐标与动系位姿矩阵基本原理。

2.连杆参数及连杆坐标系如何建立？3.机器人动力学方程及雅可比矩阵基本原理是什么？第3章机器人运动学和动力学教学主要内容：3.2 齐次坐标与动系位姿矩阵3.3 齐次变换3.4 机器操作机运动学方程的建立与求解3.5 机器人运动学方程3.6 机器人动力学本章将主要讨论机器人运动学和动力学基本问题。

先后引入了齐次坐标与动系位姿矩阵、齐次变换，通过对机器人的位姿分析，介绍了机器人运动学方程；在此基础上有对机器人运动学方程进行了较为深入的探讨。

3.1 概述机器人，尤其是关节型机器人最有代表性。

关节型机器人实质上是由一系列关节连接而成的空间连杆开式链机构，要研究关节型机器人，必须对运动学和动力学知识有一个基本的了解。

分析机器人连杆的位置和姿态与关节角之间的关系，理论称为运动学，而研究机器人运动和受力之间的关系的理论则是动力学。

3.2 齐次坐标与动系位姿矩阵3.2.1 点的位置描述在关节型机器人的位姿控制中，首先要精确描述各连杆的位置。

为此，先定义一个固定的坐标系，其原点为机器人处于初始状态的正下方地面上的那个点，如图3-1（a）所示。

记该坐标系为世界坐标系。

在选定的直角坐标系{A}中，空间任一点P的位置可以用3×1的位置向量A P表示，其左上标表示选定的坐标系{A}，此时有A P=XYZ P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦式中：P X、P Y、P Z—点P在坐标系{A}中的三个位置坐标分量，如图3-1（b）。

3.2.2 齐次坐标将一个n维空间的点用n+1维坐标表示，则该n+1维坐标即为n维坐标的齐次坐标．．．．。

机器人运动学机器人运动学是研究机器人运动和姿态变化的一门学科。

它通过分析机器人的构造和动力学参数，研究机器人在特定环境下的运动规律和遵循的动力学约束，以实现机器人的准确控制和运动规划。

本文将从机器人运动学的基本概念、运动学模型、运动学正解和逆解等方面进行介绍。

1. 机器人运动学的基本概念机器人运动学是机器人学中的一个重要分支，主要研究机器人在空间中的运动状态、末端执行器的位置和姿态等基本概念。

其中，运动状态包括位置、方向和速度等；末端执行器的位置和姿态是描述机器人末端执行器在空间中的位置和朝向。

通过研究和分析这些基本概念，可以实现对机器人运动的控制和规划。

2. 运动学模型运动学模型是机器人运动学研究的重要工具，通过建立机器人的运动学模型，可以描述机器人在运动过程中的运动状态和姿态变化。

常见的运动学模型包括平面机器人模型、空间机器人模型、连续关节机器人模型等。

每种模型都有其独特的参数和运动学关系，可以根据实际情况选择合适的模型进行分析和研究。

3. 运动学正解运动学正解是指根据机器人的构造和动力学参数，求解机器人末端执行器的位置和姿态。

具体而言，根据机器人的关节角度、关节长度和连杆长度等参数，可以通过连乘法求解机器人末端执行器的位姿。

运动学正解是机器人运动学中的常见问题，解决这个问题可以帮助我们了解机器人在空间中的运动规律和运动范围。

4. 运动学逆解运动学逆解是指根据机器人末端执行器的位置和姿态，求解机器人的关节角度。

反过来，控制机器人的运动状态就需要求解逆运动学问题。

运动学逆解是机器人运动学研究的重要内容之一，它的解决可以帮助我们实现对机器人的准确定位和控制。

总结：机器人运动学是研究机器人运动和姿态变化的学科，通过运动学模型、运动学正解和运动学逆解等方法，可以描述机器人的运动状态、末端执行器的位置和姿态。

深入研究机器人运动学，可以实现对机器人的准确控制和运动规划。

随着机器人技术的不断发展，机器人运动学的研究也得到了越来越广泛的应用和重视。

基于ADAMS的机器⼈动⼒学分析及轨迹规划2.1 串联机器⼈在ADAMS中⽤连杆模拟机械臂，对两⾃由度的机械臂分别进⾏运动学分析、动⼒学分析及机械臂的轨迹规划。

2.1.1 运动学分析下⾯是建⽴模型并对模型进⾏设置分析的详细过程。

（1） 启动ADAMS/View，在欢迎对话框中选择新建模型，模型取名为Robot_arm，并将单位设置为MMKS，然后单击OK。

（2） 打开坐标系窗⼝。

按下F4键，或者单击菜单【View】→【Coordinate Window】后，打开坐标系窗⼝。

当⿏标在图形区移动时，在坐标窗⼝中显⽰了当前⿏标所在位置的坐标值。

（3） 创建机械臂关节1（连杆）。

单击连杆按钮，勾选连杆的长、宽、深选项，分别将其设置为300mm、40mm、10mm，如图2.1所⽰。

在图形区单击⿏标左键，然后将连杆拖⾄⽔平位置时，在单击⿏标左键。

（4） 在连杆的右端打孔。

在⼏何建模⼯具栏单击打孔按钮，将半径Radius设置为10mm，深度设置为10mm，如图2.2所⽰。

然后在图形区模型附近单击⿏标左键，在与XY平⾯垂直的表⾯上单击⿏标左键。

然后修改孔的位置，在孔附近单击⿏标右键，选择【HOLE_1】→【Modify】，在弹出的对话框中，将Center的坐标值设置成（300，0.0，5.0），如图2.3所⽰。

（5） ⽤（3）的⽅法在关节1右端孔中⼼处创建关节2，如图2.4所⽰。

然后再将关节2向内侧平移10mm。

2.1 创建连杆设置（6）添加约束。

在关节1的左端与⼤地之间添加转动副，在关节1与关节2结合处添加转动副。

单击⼯具栏中的旋转副按钮，并将创建旋转副的选项设置为2Bod-1Loc和Normal Grid，然后在图形区单击关节1和⼤地，之后需要选择⼀个作⽤点，将⿏标移动到关节1的Marker1处出现center信息时，按下⿏标左键后就可以创建旋转副，旋转副的轴垂直于⼯作栅格。

然后⽤同样的⽅法创建关节1与关节2之间的旋转副。

考虑电机惯量的机器人动力学参数辨识机器人动力学参数辨识是机器人控制中不可缺少的步骤之一，能够确定机器人的关节惯性和质量参数等，是机器人运动学和动力学模型建立的基础，对柔性关节机器人、高速机器人等运动性能更高、关节惯性更大的机器人尤为重要。

本文将着重探讨电机惯量的机器人动力学参数辨识。

首先，什么是电机惯量？电机惯量是指电机转动时，由于转子的惯性作用而阻碍加速度变化所需的能量。

在机器人控制中，电机惯量是机器人动力学模型中不可缺少的参数之一，能够影响机器人的控制精度、响应速度等性能指标。

然而，在进行机器人控制时，电机惯量是难以直接测量得到的，需要通过辨识等方法来确定。

下面介绍一些电机惯量辨识常用的方法：1.模型辨识法模型辨识法是目前电机惯量辨识中应用较广的一种方法。

该方法的基本思想是通过测量电机的输入电流、转速和负载扭矩等变量，建立电机的数学模型，进而求解电机动力学参数。

目前，常用的电机模型有传递函数模型、状态空间模型、核函数模型等。

通过将不同的电机模型参数化，可以较为准确地估计电机的惯量参数。

2.自适应控制法自适应控制法是一种实时估计电机惯量参数的方法，具有较高的准确性和适应性。

该方法基于电机控制理论，通过实时调整控制器参数，调节电机的输出，进而估计电机的动力学参数。

自适应控制法可以较好地适应环境变化和负载波动，是一种非常有效的电机惯量辨识方法。

3.信号处理法信号处理法是一种基于信号处理技术实现电机惯量辨识的方法。

该方法适用于需要在机器人运行过程中对电机惯量进行实时辨识的场景，如强交互作业等。

信号处理法常用的技术有功率谱分析、小波变换等，通过对电机输出信号的频谱和时域特征的分析，可以估计电机惯量参数。

综上所述，电机惯量是机器人动力学模型中的重要参数，对机器人运动性能有着重要影响。

电机惯量的辨识方法有多种，常用的有模型辨识法、自适应控制法和信号处理法等。

对于不同类型的机器人，选择不同的辨识方法有助于提高电机惯量辨识的准确性和实用性。

机器人的运动控制技术随着科技的不断发展，机器人已经逐渐走进我们的生活中。

它们可以帮助人们完成一些重复性、易出错的任务，比如生产线上的装配、焊接等。

那么，机器人是如何完成这些任务的呢？这就需要涉及到机器人的运动控制技术。

机器人的运动控制技术主要包括传动装置、运动学模型和控制算法三个方面。

在传动装置方面，机器人通常使用电动机来驱动各个关节，并用连杆或者齿轮传动来实现动力输出。

运动学模型则涉及到机器人的几何结构和关节位置、速度等物理量的描述，通常使用旋转矩阵等数学工具进行建模。

最后，机器人的运动控制算法主要是针对运动学模型进行研究的，目的是通过控制机器人的关节运动来实现所需的运动轨迹和位置控制等。

机器人的运动学模型建立需要考虑到机器人的结构以及各个关节的位置和运动学参数，具体包括关节角度、关节速度、角加速度等。

针对不同机器人的结构，需要考虑到其运动学特性的模型化。

比如一些普通的6自由度机械臂，可以使用DH标准建立其运动学模型，而一些并联机器人则需要进行更复杂的运动学建模。

运动控制算法则需要根据具体应用场景来选择，包括开环控制、闭环控制、自适应控制等不同类型的算法。

比如，在工业自动化领域中，一般使用PID控制算法，通过对误差的反馈来控制机器人的运动轨迹。

而在机器人越野、救援和探险等领域中，通常需要更加智能、自适应的控制算法。

对于机器人的运动控制技术来说，需要在实际应用中考虑到一些实际问题，比如动态响应、控制精度、常见的干扰力和误差来源等。

这些问题可能导致机器人无法完全按照设计要求运动，从而影响其实际性能和使用效果。

因此，需要开发更加高效、精确、智能的控制技术，以提高机器人的稳定性和可靠性。

总之，机器人的运动控制技术是机器人技术发展中的关键组成部分。

只有能够安全、稳定、自适应地控制机器人，才能充分发挥机器人的潜力，让机器人更好地为人类服务。

SolidWorks机器人运动学和动力学仿真技术研究在现代工业中，机器人技术的发展引领着生产制造的进步。

为了提高机器人的操作效率和准确性，研究人员一直致力于开发先进的仿真技术以模拟机器人的运动学和动力学。

其中，SolidWorks作为一款流行的三维设计软件，提供了强大的机器人运动学和动力学仿真工具，成为了研究人员的首选。

机器人的运动学和动力学是机器人技术中的两个重要概念。

运动学研究机器人的位置、速度、加速度和轨迹，而动力学则研究机器人受力状况以及对环境的相互作用。

运动学和动力学的仿真技术可通过SolidWorks的计算机辅助设计（CAD）环境进行实现。

首先，SolidWorks提供了完善的运动学仿真功能，可以准确地模拟机器人的运动轨迹和工作空间。

研究人员可以根据机器人的几何结构、连接关系和约束条件，使用SolidWorks进行运动学建模和仿真。

通过设置关节的运动范围、限制条件以及工作空间的约束，可以模拟机器人在不同任务下的运动情况。

运动学仿真结果可以帮助研究人员评估机器人的动作是否符合设计要求，并对机器人的性能进行分析和改进。

其次，SolidWorks还提供了强大的动力学仿真功能，可以模拟机器人受力情况和对环境的相互作用。

在机器人执行任务时，会受到来自外界的力和力矩，这些外界力会影响机器人的稳定性和动作效果。

通过建立机器人的物理模型，并加入机器人和环境之间的力学力和接触力，可以准确地模拟机器人在各种工作负载和环境条件下的动力学行为。

动力学仿真结果可以帮助研究人员评估机器人的可靠性和稳定性，为设计优化提供指导。

除此之外，SolidWorks还具有其他与机器人运动学和动力学仿真相关的功能。

例如，通过SolidWorks的可视化工具，研究人员可以实时观察机器人的运动过程，并生成动画以及运动轨迹图。

同时，SolidWorks还允许用户对机器人的设计进行参数化建模和优化，在仿真分析的基础上进行机械结构的改进、工作效率的提高等。

机器人静力学,动力学,运动学的关系
机器人的静力学、动力学和运动学是机器人技术研究中三个重要领域，它们之间存在
着相互关联，协同工作，构成了机器人技术的核心。

首先，机器人静力学是指机器人操作过程中机械结构在不变的平衡状态下运动学位置
及实时运动状态估计分析，被誉为机器人外部力分析和内力传递分析的基础学科。

它主要
通过建立机器人机械结构模型，利用关节形变、外力以及内力等物理变量，计算求解机器
人的内外力特性、机构的端部间的平衡、受力特性、稳定性及物体约束特性等。

其次，机器人动力学是指机器人的运动发生时，所做动力学建模、分析及控制的研究，因此它探讨的是关节力学、碰撞识别等方面的有关问题，它主要是要求在运动过程中求解
系统运动参数或者特征值，实现机器人动态分析与控制，研究动力学模型对机器人系统动
态性能的影响。

最后，机器人运动学是指动作规划及机器人运动控制之间相关问题的研究，通过研究
机器人通过方向轮，电机和关节的作用实现有用运动的方法，涉及关节角度、运动轨迹、
几何关系、姿态成份的工程化方法。

它是对机器人机械结构分析和动力学建模的补充，探
讨机器人各关节及机构动作之间相互关系，以及机器人运动要求下，机器人运动解的计算
及实现方法，使得机器人拥有大量的姿态组合，增加机器人的全局适应性。

由此可以看出，机器人的静力学、动力学和运动学形成了一个完整的研究体系，它们
相互交织，共同工作，它们提供了对机器人运动的有效把握，从而实现机器人的运动目标。

因此，机器人的静力学、动力学和运动学十分重要，它们是实现机器人运动控制的基础，
也将在机器人研究中发挥重要作用。

目录摘要............................................................................................................错误!未定义书签。

Abstract ........................................................................................................错误!未定义书签。

1绪论 (4)1.1 引言 (4)1.2机器人研究现状及发展趋势 (5)1.3本课题的主要研究内容和工作安排 (10)1.3.1课题研究的背景及意义 (10)1.3.2课题研究的内容及安排 (12)2四自由度串联机器人本体结构设计 (13)2.1机器人的总体方案设计 (13)2.1.1抓取机器人功能需求分析及其特点 (13)2.1.2机器人驱动方案的确定 (14)2.1.3机械传动方案的确定 (15)2.1.3机器人基本技术参数设计 (15)2.1.4机器人本体的总体结构 (17)2.2机器人本体基本结构设计 (18)2.2.1大臂和小臂机械结构设计 (18)2.2.2腕部机械结构设计 (20)2.2.3直线组件的设计选择 (20)2.2.4支架结构设计 (21)2.2.5步进电机与减速器的计算和选择 (22)2.2.6机器人传动轴的校核 (25)2.2.7机器人本体的三维模型 (26)2.3本章小结 (27)3四自由度抓取机器人运动学分析及仿真 (28)3.1机器人运动学分析 (28)3.1.1奇次坐标变换 (29)3.1.2 Denavt-Hartenberg(D-H)表示法 (30)3.1.3抓取机器人运动学模型的建立 (32)3.2机器人运动学方程的建立 (33)3.2.1抓取机器人的正运动学分析 (33)3.2.2工业机器人工作空间分析 (35)3.2.3机器人雅可比（Jacobian）关系求解 (38)3.2.4 抓取机器人的逆运动学分析 (41)3.3四自由度串联机器人运动学仿真 (45)3.3.1虚拟样机技术概述 (45)3.3.2本文用到的ADAMS软件模块 (46)3.3.3建立机器人仿真模型 (47)3.3.4机器人位移仿真分析 (49)3.3.5机器人速度仿真分析 (50)3.4 本章小结 (51)4. 轨迹规划及仿真分析............................................................................. 错误!未定义书签。

总动能为： 总动能为：
1 1 2 2 &2 2 Ek = (m1l1 + I yy1 + I yy 2 + m2 d 2 )θ1 + m2 d 2 2 2
(3)系统势能 (3)系统势能 因为： 因为：
g = [0 g 0]
则：
T
T
pc1 = [l1c1 l1s1
0]T
E p1 = m1 g pc1 = m1 gl1s1
i
q 和关节速
& q
的函数，因此，从上式可知， 的函数，因此，从上式可知，机器人
的动能是关节变量和关节速度的标量函数，记 的动能是关节变量和关节速度的标量函数， 为 Ek ( q, q ) ，可表示成： & 可表示成：
1 T & & & Ek ( q , q ) = q D ( q ) q 2
式中， nxn阶的机器人惯性矩阵 式中， D ( q ) 是nxn阶的机器人惯性矩阵
Байду номын сангаас
1 1 i Ti i T Eki = miν ciν ci + ω i I i ω i 2 2
系统的动能为n个连杆的动能之和，即： 系统的动能为n个连杆的动能之和，
Ek = ∑ Eki
i =1
n
1 T & & & Ek ( q , q ) = q D ( q ) q 2
由于 ν 度
ci
和 iω 是关节变量
5.1 机器人静力学
机器人静力学研究机器人静止或者缓慢运动时作用在手臂 上的力和力矩问题，特别是当手端与外界环境有接触力时， 上的力和力矩问题，特别是当手端与外界环境有接触力时，各 关节力矩与接触力的关系。 关节力矩与接触力的关系。 下图表示作用在机器人手臂杆件i上的力和力矩。 下图表示作用在机器人手臂杆件i上的力和力矩。其i-1fi 为杆件i 对杆i的作用力， ifi+1为杆i+1对杆 的作用力， 为杆i+1对杆i 为杆件i-1对杆i的作用力，-ifi+1为杆i+1对杆i的作用力，i1Ni为杆件 为杆件i 对杆i的作用力矩， iNi+1为杆i+1对杆 为杆i+1对杆i 1Ni为杆件i-1对杆i的作用力矩，-iNi+1为杆i+1对杆i的作用力 ci为杆 质心。 为杆i 矩，ci为杆i质心。

工业机器人动力学建模与控制一、引言工业机器人在现代工业中扮演着重要角色，而机器人的动力学建模和控制则是实现机器人高效运动的关键技术之一。

本文将对工业机器人动力学建模和控制进行介绍和探讨。

二、工业机器人动力学建模动力学建模能够对机器人进行多种动作规划，从而实现不同的工作功能，这对于机器人在工业中的应用非常重要。

因此，工业机器人的动力学建模一直是研究的热点之一。

1.机器人多链体建模机器人多链体建模是机器人动力学建模的基础，它将机器人抽象成由多个链体组成的系统，每个链体通过关节连接在一起，看作是刚体，通过建立运动学和动力学方程描述其运动规律。

这种建模方式便于求解机器人各关节的位移和速度，并进一步计算机器人在各工作状态下的动力学特性。

2.机器人动力学参数估计机器人运动学和动力学参数的估计是建模的重要步骤。

动力学参数估计的主要目的是根据机器人的外部力矩和电机输入电流估计出机器人的惯性矩阵、电动机阻尼矩阵和电机耦合矩阵，以建立完整的动力学模型。

这些模型可用于机器人的运动规划和控制。

三、工业机器人控制机器人的控制主要是指将机器人动力学模型应用到运动控制中，形成开环和闭环控制系统。

工业机器人常用的控制方式包括位置控制、速度控制和力控制。

1.位置控制位置控制是将运动学模型中的关节角度控制到目标值的操作，主要用于简单重复任务，如加工、装配等。

该控制模式的优点是实现简单、可靠性高，缺点是不能处理运动过程中的不确定性和干扰。

2.速度控制速度控制是将运动学模型中的关节速度控制到目标值的操作，主要用于包含连续运动和协调动作（例如，机器人插针）的应用。

该控制模式是在位置控制基础上的进一步发展，优点是更加灵活，缺点是对铰链振动和干扰等仍然很敏感。

3.力控制力控制是将运动学模型中的终端执行器的施加力控制到目标值的操作，主要用于与环境交互的任务，例如力覺、碰撞监测等。

力控制模式的优点是能够从力学角度对机器人的操作进行精确控制和可视化，缺点是实现成本高，系统较为复杂。

n
1
v Ci

v Ci

1 2

i Ii i )

T

1
[m 2
i 1 n
i
(J L q ) J L q (J A q ) IiJ A q ]
(i) (i) T (i) T T

1
(m 2
i 1
i
q
JL
(i)T
JL q q
(i)
二、机器人静力学关系式推导
以2自由度机械手为例，要产生图a所示的虚位移 , ， r ， 则图b所示各力 , 和 F 之间的关系：
1 2
1
2
由 虚 功 原 理 知 ： 1 1 2 2 F r 0 即： 1
2
1 F 2
当刚体绕过质心的轴线旋转时，角速度ω，角加速度
，惯
性张量
与作用力矩N之间满足欧拉方程：
IC (IC ) N

——欧拉运动方程
Ic R
3 3
是绕重心 c 的惯性矩（转动惯量） N 回转力矩
， I c的各元素表示对应的力
矩元素和加速度元素间
的惯性矩；
回转角速度；
对于对于zz轴轴于是于是12联立可得联立可得对于一般形状连杆对于一般形状连杆除第33分量以外其它分量皆不为分量以外其它分量皆不为00的第1122分量成为改变轴方向的力矩但在固定分量成为改变轴方向的力矩但在固定轴场合与这个力矩平衡的约束力生成轴场合与这个力矩平衡的约束力生成22式中的式中的1122分分量不产生运动
由虚功原理得：
F A x A FB x B 0 即 ： F A L A F B L B 0 ( F A L A F B L B ) 0 F A L A FB L B 0 FB LA LB FA