钢筋屈强比和超强比计算公式

现行规范《混凝土结构工程施工质量验收规范》GB50204-2002中规定：对有抗震设防要求的框架结构，其纵向受力钢筋应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检测所得的强度实测值应符合下列规定：①钢筋抗拉强度实测值与屈服强度实测值的比值应≥1.25；②钢筋的屈服强度实测值与强度标准值的比值应≤1.30.以上规范规定的依据是考虑在地震作用下，框架结构具有较好的延性和整体性，结构局部出现塑性变形，而不允许出现脆性破坏。

规范中规定的这两个比值，前者是要求钢筋具有一定的屈服后承载能力，保证整个结构具有较强的吸收地震能量的能力。

后者是控制超强比，防止改变结构设计变形状态。

不知楼上的回答是否已经使你晕菜了！其实你所提到的这两个比值，就是我们常谈到的“强屈比”和“超强比”。

一、强屈比：钢筋的抗拉强度实际上也就是所谓的“强度极限”，这个值在设计中是不能利用的，常用的指标是钢筋的屈服强度（即屈服极限）。

但是抗拉强度与屈服强度的比值（强屈比），却是评价钢材使用可靠性的一个重要参数。

强屈比愈大，钢材受力超过屈服点工作的时的可靠性就越大，采用这个比值的建筑结构那自然安全性就越高，反之则安全性就越低，这就是对建筑结构最直接的影响。

但是强屈比太大，钢材强度利用率则偏低，会造成材料性能的浪费。

二、超强比：“钢筋的屈服强度实测值与强度标准值的比（超强比）不应大于1.3”,这个数值是《建筑抗震设计规范》上的要求。

设置这个限定的目的是为了避免钢筋超强过多而造成延性不足，使结构从屈服开始到其达到强度极限的过程太快，易产生毫无征兆的快速破坏，这对建筑结构安全性而言，并不是一件好事。

三、另外请楼主注意，抗震规范和混凝土规范同为国标，但是对钢筋材料要求却不一致。

抗震规范仅针对一、二级抗震的框架结构，而混凝土规范指的是一、二级抗震的各类框架。

显然，混凝土规范规定的范围要大于抗震规范。

这一点请在设计时多加留意。

钢板超屈比计算公式钢板超屈比是指在一定条件下，钢板在受到外部力作用时发生屈曲的能力。

这个概念在工程设计中非常重要，因为它可以帮助工程师确定钢板的最大承载能力，从而确保结构的安全性和稳定性。

在本文中，我们将介绍钢板超屈比的计算公式，并探讨其在工程设计中的应用。

钢板超屈比的计算公式可以通过以下步骤得到：1. 首先，确定钢板的几何参数，包括长度（L）、宽度（b）和厚度（t）。

这些参数可以通过实际测量或设计图纸获得。

2. 然后，计算钢板的截面面积（A）和惯性矩（I）。

截面面积可以通过长度和宽度相乘得到，即A = L b。

惯性矩可以通过以下公式计算得到，I = (1/12) b t^3。

3. 接下来，确定钢板的材料参数，包括弹性模量（E）和屈服强度（σy）。

这些参数可以通过材料测试或材料手册获得。

4. 最后，使用以下公式计算钢板的超屈比（λ），λ = (K L) / (r t)。

其中，K是一个与边界条件有关的修正系数，通常为1.0；r是钢板的根号惯性矩，即r =sqrt(I/A)。

通过这个公式，我们可以得到钢板的超屈比，从而评估其抗弯能力。

钢板超屈比的计算公式可以帮助工程师在设计过程中评估钢板的抗弯性能，从而确定其在实际应用中的承载能力。

通过对钢板超屈比的计算和分析，工程师可以选择合适的钢板材料和尺寸，确保结构的安全性和稳定性。

此外，钢板超屈比的计算公式也可以用于优化设计，减少材料使用量，降低成本，提高效率。

除了在工程设计中的应用，钢板超屈比的计算公式还可以用于材料研究和开发。

通过对不同材料和结构参数的超屈比进行计算和比较，可以帮助研究人员了解不同材料的力学性能，并指导新材料的设计和开发。

这对于提高材料的强度和韧性，推动材料科学和工程的发展具有重要意义。

总之，钢板超屈比的计算公式是工程设计和材料研究中的重要工具。

通过对钢板超屈比的计算和分析，可以评估钢板的抗弯性能，指导工程设计和材料研究，确保结构的安全性和稳定性。

抗震钢筋强屈比钢筋是结构工程中最常见的材料之一，其力学性能对混凝土结构工程的整体强度和稳定性至关重要。

抗震钢筋的强屈比是衡量结构的抗震性能的重要指标，它表征了钢筋的抗震强度。

抗震钢筋的强屈比定义为：指在已知条件下，抗震钢筋受拉力或压力时到达限制极限所需的最大变形量与钢筋原有长度的比值；或抗震钢筋受力所发生的最大变形量与钢筋原有长度的比值，即每米钢筋的变形量与米数的比值。

现行国家规范中，抗震钢筋强屈比的规定：钢筋抗弯构件的强屈比为0.8，钢筋抗拉构件的强屈比在抗弯构件的基础上，增加0.1至0.3之间。

当地震作用中，发挥钢筋滞回效应时，应采用较大的强屈比。

抗震钢筋强屈比的优势一方面，大屈比说明钢筋受到外部力施加时，可以保证正常的变形而不受损失；另一方面，钢筋的长度增加，则强屈比也会随之提高。

当受到一定程度的外力时，就可以发挥钢筋的抗震效果。

在抗震设计中，钢筋的强屈比是抗震技术的一个重要环节，不同的强屈比会给结构的整体稳定性、强度和抗震性带来影响。

因此，在设计抗震构造物时，应根据结构的性能要求选择合适的抗震钢筋强屈比，以保证结构的性能和抗震性。

传统的计算中，抗震钢筋强屈比是由结构抗震性能要求所决定的，而不是从建筑材料本身出发来计算。

鉴于抗震强度要求的变化和结构设计要求的影响，一般结构抗震性能要求较高的情况下，要求抗震钢筋的强屈比较大，一般可达 0.8~0.95。

钢筋的抗震性能取决于细节设计中抗震钢筋强屈比的选择，因此，确定抗震钢筋强屈比是抗震设计过程中重要的一环，应根据工程实际情况，严格控制钢筋的强屈比，以保证结构性能和抗震性能。

此外，有些结构需要抗火钢筋，这种钢筋的强屈比规定在0.85以上，且应具备一定的抗火温度，以确保结构在高温条件下的稳定性。

总之，抗震钢筋的强屈比是衡量抗震性能的重要指标，在抗震设计中，钢筋的强屈比是抗震技术中的重要环节，应根据工程实际情况准确选择合适的强屈比，以保证结构的性能和抗震性能。

强屈比和超屈比计算公式一、引言强屈比和超屈比是在力学领域中常用的两个计算公式，用于描述材料的力学性能。

本文将详细介绍强屈比和超屈比的概念、计算公式及其应用。

二、强屈比1. 强屈比概念强屈比即材料的极限抗拉强度与屈服强度之比。

极限抗拉强度是指材料在拉伸过程中，能承受的最大拉力，而屈服强度是指材料开始出现塑性变形的拉力。

强屈比可以用来评估材料的韧性和延展性。

2. 强屈比计算公式强屈比的计算公式为：强屈比 = 极限抗拉强度 / 屈服强度3. 强屈比的应用强屈比可以用来比较不同材料的力学性能。

一般来说，强屈比越大，表示材料的韧性和延展性越好，能够承受更大的拉力而不断变形。

三、超屈比1. 超屈比概念超屈比即材料的极限抗拉强度与屈服强度之差。

超屈比可以用来评估材料的韧性和脆性。

2. 超屈比计算公式超屈比的计算公式为：超屈比 = 极限抗拉强度 - 屈服强度3. 超屈比的应用超屈比可以用来评估材料的抗断裂能力。

一般来说，超屈比越大，表示材料的抗断裂能力越强，能够承受更大的拉力而不发生断裂。

四、强屈比和超屈比的比较1. 计算方法强屈比是通过除法计算得出的，而超屈比是通过减法计算得出的。

2. 含义强屈比主要用来评估材料的韧性和延展性，而超屈比主要用来评估材料的抗断裂能力。

3. 应用范围强屈比适用于评估塑性材料的力学性能，而超屈比适用于评估脆性材料的力学性能。

五、结论强屈比和超屈比是力学领域中常用的两个计算公式，用于评估材料的力学性能。

强屈比主要用来评估材料的韧性和延展性，超屈比主要用来评估材料的抗断裂能力。

根据具体的应用需求，可以选择使用强屈比或超屈比来评估材料的性能。

《建筑工程管理与实务》第一时间详解2014年真题及答案一、单项选择题（共20题，每题1分。

每题只有1个最符合题意）1、某受压细长杆件，两端铰支，其临界力为50kN，若将杆件支座形式改为两端固定，其临界力为（）kN。

A.50B.100C.150D.200答案：D P3解析：本题考查的是临界力的计算。

两端固定时l0=0.5l;两端铰支时，l0=l，然后依据公式计算得出答案，参见教材P32、预应力混凝土构件的混凝土最低强度等级不应低于（）。

A.C30B.C35C.C40D.C45答案：C P6解析：本题考查的是预应力混凝土构件的混凝土最低强度等级不应低于C40，参见教材P6。

3、某受均布线荷载作用的简支梁，受力简图示意如下，其剪力图形状为（）。

A. B. C. D.答案：D P10解析：本题是课本上的原题，考查简支梁的剪力图。

参见教材P10。

4、关于钢筋混凝土框架结构震害严重程度的说法，错误的是（）。

A.柱的震害重于梁B.角柱的震害重于内柱C.短柱的震害重于一般柱D.柱底的震害重于顶柱答案：D P33解析：柱顶的震害重于柱底。

参见教材P33。

5、下列水泥品种中，其水化热最大的是（）。

A.普通水泥B.硅酸盐水泥C.矿渣水泥D.粉煤灰水泥答案：B解析：常用水泥中硅酸盐水泥的水化热最大。

参见教材P44。

6、在混凝土配合比设计时，影响混凝土拌合物和易性最主要的因素是（）。

A.砂率B.单位体积用水量C.拌和方式D.温度答案：B P53解析：单位体积用水量决定水泥浆的数量和稠度，它是影响混凝土和易性的最主要因素。

参见教材P53。

13、钢结构普通螺栓作为永久性连接螺栓使用时，其施工做法错误的是（）。

A.在螺栓一端垫两个垫圈来调节螺栓紧固度B.螺母应和结构件表面的垫圈密贴C.因承受动荷载而设计要求放置的弹簧垫圈必须设置在螺母一侧D.螺栓紧固度可采用锤击法检查答案：A解析：每个螺栓一端不得垫两个及以上的垫圈，并不得采用大螺母代替垫圈。

钢筋计算公式大全钢筋是建筑工程中常用的一种材料，它具有高强度、耐腐蚀、易加工成型等优点，因此在建筑结构中得到了广泛的应用。

在进行钢筋设计时，需要根据具体的工程要求和使用环境，进行合理的计算和选择。

下面将介绍钢筋计算中常用的公式，希望对大家有所帮助。

1. 钢筋拉力计算公式。

钢筋在受拉力作用下，需要满足一定的强度要求。

根据材料力学原理，钢筋的拉力计算公式为：\[ N = A \times f_y \]其中，N为钢筋的拉力，A为钢筋的截面积，f_y为钢筋的屈服强度。

2. 钢筋抗弯计算公式。

在梁、板等结构中，钢筋需要承受弯矩的作用，因此需要进行抗弯计算。

钢筋的抗弯计算公式为：\[ M = W \times f_y \times z \]其中，M为钢筋的抗弯强度，W为截面模量，f_y为钢筋的屈服强度，z为钢筋的有效材料高度。

3. 钢筋截面尺寸计算公式。

在进行钢筋设计时，需要根据结构的受力情况和要求，确定钢筋的截面尺寸。

钢筋截面尺寸计算公式为：\[ A_s = \frac{M}{f_y \times z} \]其中，A_s为钢筋的截面积，M为受弯弯矩，f_y为钢筋的屈服强度，z为钢筋的有效材料高度。

4. 钢筋箍筋计算公式。

在柱、梁等结构中，为了保证钢筋的受压性能，需要设置箍筋。

钢筋箍筋的计算公式为：\[ n = \frac{N}{A_g \times f_y} \]其中，n为箍筋的数量，N为受拉钢筋的拉力，A_g为箍筋的截面积，f_y为箍筋的屈服强度。

5. 钢筋连接长度计算公式。

在钢筋连接的设计中，需要考虑钢筋的受力传递和连接强度。

钢筋连接长度的计算公式为：\[ L_s = \frac{T}{A_s \times f_y} \]其中，L_s为钢筋的连接长度，T为连接的拉力，A_s为钢筋的截面积，f_y为钢筋的屈服强度。

以上就是钢筋计算中常用的公式，希望对大家有所帮助。

在实际应用中，需要根据具体的工程情况和要求，结合相关规范和标准，进行合理的计算和设计，确保结构的安全性和稳定性。

钢筋的计算公式钢筋是在混凝土结构中起到加固和增强的作用，其计算公式是根据结构设计和承载力要求来确定的。

钢筋的计算公式可以分为两种：强度设计与变形设计。

1. 强度设计公式：在强度设计中，主要是根据混凝土结构受力情况，计算钢筋的拉力、压力以及抗弯强度等。

以下是几个常用的强度设计公式。

a. 钢筋的拉力设计公式：钢筋的拉力设计公式可以表示为：T = A * f * γs其中，T表示钢筋的拉力；A表示钢筋的截面面积；f表示钢筋的抗拉强度；γs表示钢筋的安全系数。

b. 钢筋的压力设计公式：钢筋的压力设计公式可以表示为：C = A * f * γs其中，C表示钢筋的压力；A表示钢筋的截面面积；f表示钢筋的抗压强度；γs表示钢筋的安全系数。

c. 抗弯强度设计公式：抗弯强度设计公式可以表示为：M = W * f * γs其中，M表示结构的抗弯强度；W表示截面的抵抗力矩；f表示钢筋的抗拉强度；γs表示钢筋的安全系数。

2. 变形设计公式：在变形设计中，主要是考虑结构的变形和位移等因素，以使结构在荷载作用下不产生大幅度的变形。

以下是几个常用的变形设计公式。

a. 钢筋的弹性变形公式：钢筋的弹性变形公式可以表示为：δ = (P * L) / (A * E)其中，δ表示钢筋的弹性变形；P表示受力；L表示长度；A 表示钢筋的截面面积；E表示钢筋的弹性模量。

b. 钢筋的塑性变形公式：钢筋的塑性变形公式可以表示为：δ = (M * L) / (f * A * γs)其中，δ表示钢筋的塑性变形；M表示结构的弯矩；L表示长度；f表示钢筋的抗拉强度；A表示钢筋的截面面积；γs表示钢筋的安全系数。

这些公式是根据结构设计和钢筋材料性能等因素进行推导和实验验证的，并且在实际工程中得到了广泛应用。

在进行钢筋计算时，需要结合具体的设计要求、结构形式和荷载情况，选取合适的公式进行计算。

同时，还需要根据国家和地区的相关标准进行计算，并参考专业技术书籍和相关工程实例进行验证，以确保计算结果的准确性和安全性。

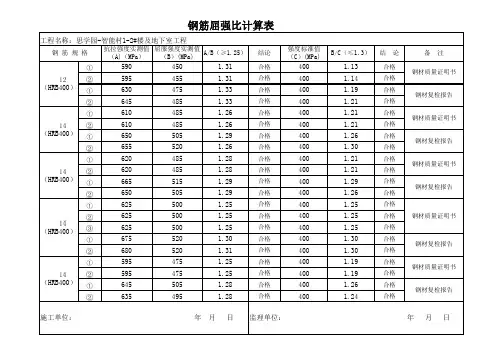
钢筋强屈比和屈强比计算公式
钢筋强屈比和屈强比是结构工程中常用的两个计算公式，用于评估钢筋在混凝
土结构中的性能。

下面将分别介绍钢筋强屈比和屈强比的计算公式。

1. 钢筋强屈比计算公式：
钢筋强屈比是指钢筋的屈服强度与抗拉强度之比。

该计算公式可以用于评估钢
筋的承载能力。

钢筋强屈比的计算公式如下：
钢筋强屈比 = 屈服强度（抗拉强度） / 屈服强度
其中，屈服强度是指材料的屈服点或抗拉强度，个别情况下两者可能是一样的。

钢筋强屈比的数值越大，表示钢筋的承载能力越高。

2. 屈强比计算公式：
屈强比是指结构物在设计负载下的屈服行为与破坏行为之间的比值。

它用于判
断结构的安全性和可靠性。

屈强比的计算公式如下：
屈强比 = 屈服强度（抗拉强度） / 极限承载能力
极限承载能力是指结构承受设计负载而发生破坏时的最大承载能力。

屈强比的
数值越小，表示结构的安全性和可靠性越高。

这两个计算公式在结构工程中具有重要的作用，可用于评估钢筋和结构的性能
和稳定性。

然而，请注意在具体应用中，还需考虑其他因素和实际情况，以得出更准确、可靠的结论。

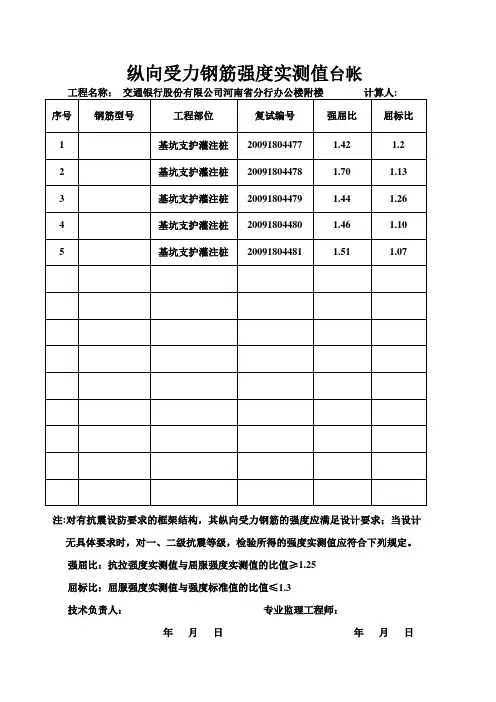
纵向受力钢筋强度实测值台帐注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。

强屈比：抗拉强度实测值与屈服强度实测值的比值≥1.25屈标比：屈服强度实测值与强度标准值的比值≤1.3技术负责人：专业监理工程师：年月日年月日注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。

强屈比：抗拉强度实测值与屈服强度实测值的比值≥1.25屈标比：屈服强度实测值与强度标准值的比值≤1.3技术负责人：专业监理工程师：2009年11月13日年月日注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。

强屈比：抗拉强度实测值与屈服强度实测值的比值≥1.25屈标比：屈服强度实测值与强度标准值的比值≤1.3技术负责人：专业监理工程师：2009年11月28日年月日注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。

强屈比：抗拉强度实测值与屈服强度实测值的比值≥1.25屈标比：屈服强度实测值与强度标准值的比值≤1.3技术负责人：专业监理工程师：2009年12月11日年月日注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。

强屈比：抗拉强度实测值与屈服强度实测值的比值≥1.25屈标比：屈服强度实测值与强度标准值的比值≤1.3技术负责人：专业监理工程师：2009年12月22日年月日注:对有抗震设防要求的框架结构，其纵向受力钢筋的强度应满足设计要求；当设计无具体要求时，对一、二级抗震等级，检验所得的强度实测值应符合下列规定。