2014_结构力学动力计算习题
- 格式:ppt
- 大小:196.50 KB
- 文档页数:12


结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学,以下是一篇结构力学计算题及练习题,包括答案的示例。
结构力学计算题题目:一简支梁AB,跨度为4米,受到均布荷载q=2 kN/m,梁的截面惯性矩I=1.2×10^6 mm^4,弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤:1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式:\[ M_{max} = \frac{ql^2}{8} \]代入已知数据:\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式:\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据:\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案:梁的最大弯矩Mmax为4 kN·m,最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD,长度为3米,受到集中力F=5 kN作用在自由端,梁的截面惯性矩I=1.5×10^6 mm^4,弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax为5 kN·m,最大挠度y_max为0.013 mm。
2. 一连续梁EF,跨度为6米,分为两段,每段长度为3米,中间有一支点G。
梁上受到均布荷载q=1.5kN/m,梁的截面惯性矩I=2×10^6 mm^4,弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案:支点G的反力为4.5 kN,中间梁段的最大弯矩为2.25 kN·m。

2014级《结构力学》复习题及答案2014级《结构力学》复习题及答案一、填空题:1.图示结构的超静定次数为 7 。
2.图示结构,各杆的EIil都相同,用力矩分配法计算时,分配系数µAB等于 0.5 。
3.图示桁架中A支座的竖向反力(设向上为正)为 0 。
4.图示刚架,P=1在AB段移动,E处剪力F SE的影响线在E点处的竖标为 -1 。
5.图示结构支座位移Δ引起的A点水平位移方向为向右。
6.图示对称桁架中,a杆的轴力为 0 。
7.图示桁架中,零杆的根数为 5 根(不含支座链杆)。
8.图示刚架,各杆线刚度相同,用力矩分配法计算时,分配系数μ21= 4/5 ,μ23= 0 ,μ24= 1/5 。
9.位移法典型方程中的系数有r ij = r ji 的关系,它是由 反力互等 定理得到的结果。
10.图示桁架零杆根数为 7 根。
11.若三铰拱上所有截面的弯矩都等于零而且只有轴力,则这时的拱轴线称为 合理拱轴线 。
12.图示结构的动力自由度为 3 (不计杆件质量)。
二、单项选择题:1.图示刚架中,支座B的位移Δ引起B截面的角位移(顺时针为正)为( C )A. Δ/hB. -Δ/hC. Δ/LD. -Δ/L2.图示体系是 ( B )A. 常变体系B. 瞬变体系C. 无多余联系的几何不变体系D. 有多余联系的几何不变体系3.图示体系是( D )A. 瞬变体系B. 常变体系C. 有多余联系的几何不变体系D. 无多余联系的几何不变体系为 ( A )4.图示连续梁,力矩分配系数µBCA. 2/3B. 1/2C. 1/3D. 1/45.图示结构的超静定次数为( C )A. 4B. 3C. 2D. 16.图示桁架中A支座的竖向反力(设向上为正)为( A )A. 0B. 0.5PC. 0PD. 2P7.图示三铰刚架支座A的水平约束反力为( B )A. PB. P/4C. P/2D. 3P/48.图示三铰拱,链杆AB的轴力为(以拉为正)( B )A. -P/2B. P/2C. .P/4D. -P/49.在一个无多余联系的几何不变体系上加上一个二元体,得到的体系为 ( B )A. 有多余联系的几何不变体系B. 无多余联系的几何不变体系C. 常变体系D. 瞬变体系10.位移法典型方程实质是( B ) A. 位移条件 B. 平衡条件C. 物理条件D. 平衡条件和位移条件11.在一个几何瞬变体系上加上一个二元体,得到的体系为 ( C ) A. 无多余联系的几何不变体系 B. 有多余联系的几何不变体系 C. 瞬变体系 D. 常变体系12.求解位移法典型方程中的自由项R 2P 时,要用到 ( D ) A. 1M 图 B. 2M 图 C. 3M 图 D. M P 图13、图 示 体 系 的 几 何 组 成 为 : ( A ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬变 ; D. 常 变 。

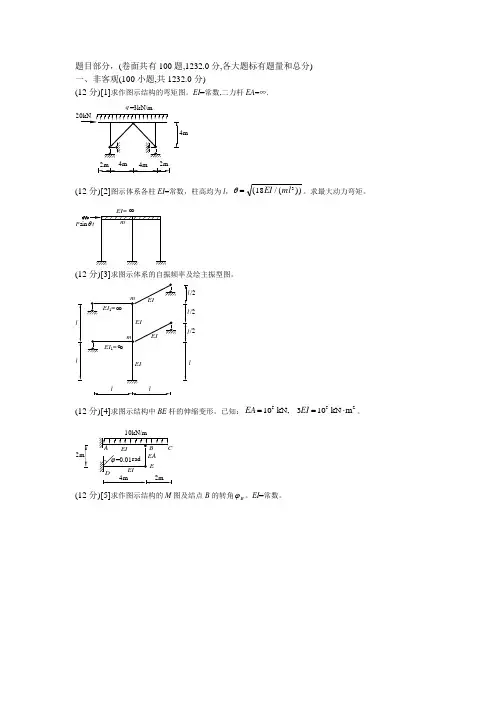
题目部分,(卷面共有100题,1232.0分,各大题标有题量和总分)一、非客观(100小题,共1232.0分)(12分)[1]求作图示结构的弯矩图。
EI =常数,二力杆EA =∞.q =3kN/m(12分)[2]图示体系各柱EI =常数,柱高均为l ,θ=(/())183EI ml 。
求最大动力弯矩。
(12分)[3]求图示体系的自振频率及绘主振型图。
l l /2/2/2(12分)[4]求图示结构中BE 杆的伸缩变形。
已知:EA EI ==⋅10310552kN kN m ,。
4m 2m(12分)[5]求作图示结构的M 图及结点B 的转角ϕB 。
EI =常数。
10kN/m3m(12分)[6]求图示结构D 截面的转角ϕD 。
EI =常数。
l/l ll/2l/2(12分)[7]作图示结构的M 图。
除注明者外,其余各杆EI =常数。
l(12分)[8]求图示梁结构刚度矩阵的各元素K K K K 11122122,,,。
C (12分)[9]图示结构,已知EI 及B支座的弹簧系数k EI l =33/,试用位移法计算,并作M 图。
(10分)[10]求作图示刚架的M 图。
EI =常数。
l /2l l /3l /3(12分)[11]求图示结构杆C 轴力及B 支座反力。
a /2a /2a /2(12分)[12]图示梁端支承抗转弹簧刚度k 12700=⋅kN m /rad ,梁的弹性模量E =⨯200106kN /m ,2 m 4I =⨯-160106。
求作梁的弯矩图。
B k 1q(12分)[13]图示刚架,EI =常数,P =1在AB 间移动。
求反力矩M C 的影响线。
l(12分)[14]求作图示结构的弯矩图。
各杆相对线刚度如图所示。
(12分)[15]利用结构的对称性,选择恰当的方法计算,并作出图示结构的M 图。
EA =∞。
EA EA(11分)[16]绘图示梁的M C 、Q C 的影响线。
(12分)[17]用力法计算图示结构,并绘出M 图。
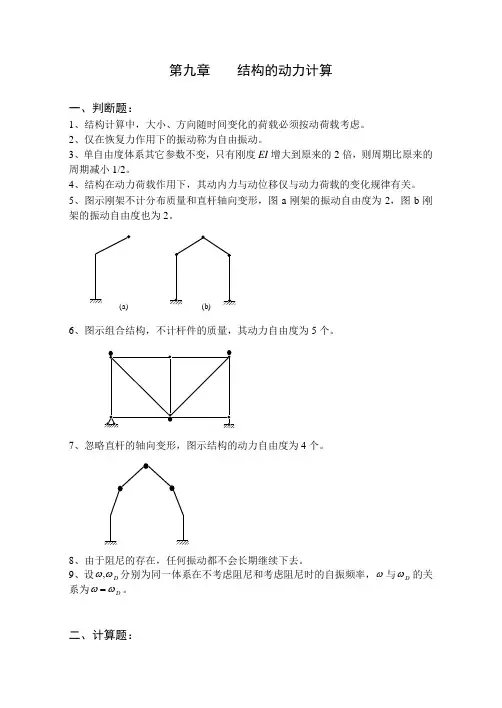
第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
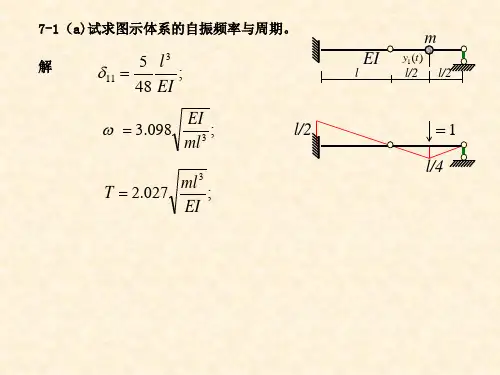
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。

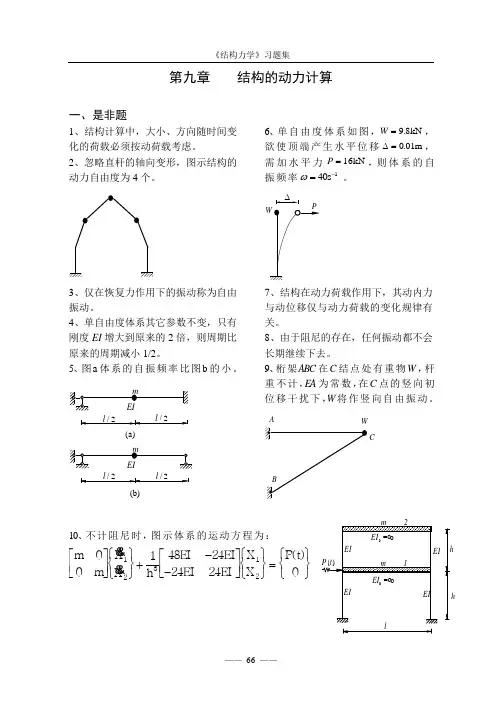
第九章 结构的动力计算一、是非题1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形,图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ,W =98.kN ,欲 使 顶 端 产 生 水 平位 移 ∆=001.m ,需 加 水 平 力 P =16kN ,则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ,杆 重 不 计 ,EA 为 常 数 ,在 C 点 的 竖 向 初 位 移 干 扰 下 ,W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ,图 示 体 系 的 运 动 方 程 为 :m m XX h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ,质 点 的 运 动 方 程 为 : A .()()()y l Ps i n m y EI =-77683θ t /; B .()()m y EIy l Ps i n /+=19273θ t ; C .()()m y EIy l Ps i n /+=38473θ t ; D .()()()y l Ps i n m yEI =-7963θ t / 。
ll0.50.5 2、在 图 示 结 构 中 ,若 要 使 其 自 振 频 率 ω增 大 ,可 以A .增 大 P ;B .增 大 m ;C .增 大 E I ; D .增 大 l 。

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。