导数的应用习题课

(5) (1 + x )α = 1 + αx +
α (α − 1)
2!
x2 + L+
α (α − 1)L (α − n + 1)
n!
x n + o( x n )
Ⅲ 导数的应用
一、函数的极值与单调性
1．函数极值的定义 ． x ∈ U ( x0 , δ ), f ( x ) ≤ f ( x0 ), f ( x0 )为极大值. 为极大值.
0 ∞ 其它型： 其它型： ⋅ ∞ , ∞ − ∞ , 0 , 1 , ∞ , 转化为 “ ”型或“ ” 型 0 型或“ 型或 0 ∞
0 ∞ 0
二、泰勒公式
1．泰勒公式 ．
如果函数在含有一点的开区间内具有直到(n+1)阶导数 阶导数 如果函数在含有一点的开区间内具有直到 f ′′( x0 ) f ( n) ( x0 ) 2 f ( x) = f ( x0 ) + f ′( x0 )( x − x0 ) + ( x − x0 ) + L+ ( x − x0 )n + Rn ( x) 2! n! ( n +1) f (ξ ) Rn ( x ) = ( x − x0 ) n+1 拉格朗日型余项 ( n + 1)!
x ∈ U ( x 0 , δ ), f ( x ) ≥ f ( x0 ), f ( x0 )为极小值 .
o
。
2．函数的驻点 ．
f ′( x 0 ) = 0 则 x 0为 f ( x ) 的驻点。 的驻点。
3．函数的单调区间的判别 ．
函数在[a,b]上连续 在(a,b)内可导 上连续,在 内可导. 函数在 上连续 内可导

an
数列
的前n项和为S n _________.
n 1
解答
1. ′ = 3 2 − 2
= ′
=1
=3−2=1
= 450
题型七 切线问题
解答
2. ′ = −1 1 − −
= −1 1 − − = − + 1 −1
习题
1.若函数 y f ( x) 在区间 ( a, b) 内可导，且 x0 ( a, b) 则 lim
h 0
（
f ( x0 h) f ( x0 h)
的值为
h
）
'
B． 2 f ( x0 )
'
A． f ( x0 )
'
2.若 f ( x0 ) 3 ，则 lim
h 0
A. 3
x
x
x ln 2


















f
x

sin
x
,
f
x

f
x
,
f
x

f
x
,


，
f
x

f
2. 若 0
， 则
1
0
2
1
n 1
n x , n N
f 2005 x
题型四 基本函数的求导公式
解答
1.
C

3
′
+
1 ′

=1−
1
2
错误
= 3 ln 3 错误

习题课——导数的综合应用
课标阐释
1.利用导数研究函数的单调
性、极值,以及连续函数在区
间[a,b]上的最大(小)值.
2.利用导数研究不等式恒成
立问题及含有参数的最值问
题的解法
思维脉络
知识梳理
1.求可导函数y=f(x)的单调区间
求可导函数y=f(x)单调区间的步骤是:
(1)求f'(x);
(2)解不等式f'(x)>0(或f'(x)<0);
∪(0,1].
探究一
探究二
探究三
探究二 含参数的最值问题
【例2】 已知函数f(x)=(4x2+4ax+a2) ,其中a<0.
(1)当a=-4时,求f(x)的递增区间;
(2)若f(x)在区间[1,4]上的最小值为8,求a的值.
分析(1)将a=-4代入,令f'(x)>0得递增区间;(2)先求导,求出单调区间,

③当-2>4,即 a<-8 时,f(x)在[1,4]上的最小值可能在 x=1 或 x=4 处取
得,而 f(1)=8 时没有符合题意的 a 值,由 f(4)=2(64+16a+a2)=8 得
a=-10 或 a=-6(舍去),当 a=-10 时,f(x)在(1,4)上是减少的,f(x)在[1,4]
上的最小值为 8.故 a=-10.
范围是(
)
1
A.a≤-8
C.a≤0
1
B.-8≤a<0
1
D.a≤- 或 a=0
8
解析:由题意知函数 f(x)的定义域为
1
-22 ++1
(0,+∞),f'(x)=-2ax+1=

高等数学习题课
（3）
中值定理与导数的应用
第二课 中值定理与导数应用
I. 目的要求 ⒈ 理解罗尔定理、拉格朗日定理，了解柯西定理； 会用中值定理解决诸如方程根的存在性、不等 式证明等问题； ⒉ 了解泰勒定理的条件、结论及余项，掌握函数 ex , sinx, cosx, ln(1+x), (1+x)α的麦克劳 林公式； ⒊ 熟练掌握用洛必达法则求不定型极限的方法； ⒋ 熟练掌握求函数单调区间、极值、凹凸区间、 拐点的方法，并会用其证明一些相关问题。
证：由条件易知F (x)在 [1,2]上满足罗尔定理条件， 则 (1,2)，使 F(1) 0 又 F(x) 2(x 1) f (x) (x 1)2 f (x) 在 [1,1]上连续，在(1,1)内可导，且 F(1) F(1) 0 由罗尔定理， (1, 1) (1, 2) 使 F() 0 #
(a 0)有极值，试证：曲线y f (x) 在点(a, f (a))处的
切线经过坐标原点。 证：曲线 y f (x) 在 (a, f (a)) 处的切线方程为
y f (a) f (a)(x a)
即 y f (a)x [ f (a) a f (a)]
由条件 (x) 在 x a 点有极值，且易知(x)在 x a 点可导
x
2
分析：只需证明 sin x x 0 3 cos x
证：令
f
(x)
sin x 3 cos x
x
sin
1
x cos 3
x
x
，显见
f
(0)
0；
f
(x)
cos
2 3
x
1 sin
2
x
4
cos 3
x

【例3】设 f ( x)在[0, a]上连续, 在 (0, a)内可导, 且 f (a) 0 . 证明存在一点 (0, a), 使 f ( ) f ( ) 0. 分析 从结论 f ( ) f ( ) 0 看等价于方程 x f ( x) f ( x) 0 有实根，但若利用零点定理，无法验证 f (0) f (a) 0，所以
证明: 设 F ( x) a0 x n a1 x n1 an1 x, 易知多项式函数F ( x)在[0, x0 ] 上连续且可导，由题设
F ( x0 ) 0 F (0).
由罗尔定理，存在 (0, x0 ), 使 F ( ) 0, 即 a0n n1 a1 (n 1) n2 an1 0, 这说明 就是方程 a0nx n1 a1 (n 1) x n2 an1 0 的一个小于 x 0的正根.
2
x 1)
分析 证明函数恒等式，主要是利用拉格朗日定理的推论：
如果函数 f ( x)在区间 I上的导数恒为零，那么 f ( x)在区间 I上是一个常数.
证明：设 f ( x) arcsin x arccos x,(1 x 1)
因 f ( x) 1 1 0,(1 x 1) 1 x2 1 x2
试证在(a,
b)内至少存在一点 ,
使 f (b)
f (a)
f ( ) ln b
a
成立.
分析
将所证等式变形为
f (b)
f (a)
f ( ) 或
ln b ln a 1
f (b) f (a) ln b ln a
f ( x)
ln x
,
x
可见，应对 f ( x)与 ln
x 在[a,
b]上应用
ln b ln a 1

为:S(x)=|AB||BC|=2x3-12x2+16x(0<x<2).
S( x) 6x2 24x 16.
令
S(
x)
0
,得x1
2
2
3 3
,
x2
2
2
3 3
.
x1 (0,2), 所以当 因此当点B为(2 2
x
3
2
,0)
23 3
时,S( x)max
32 9
3
.
时,矩形的最大面积是
32
3.
2
9
谢谢观看
演 练
在 x 2 x 1 都取得极值
3
a, 求 b的值及函数 f (x)
的单调区间
a 1 ,b 2 2
(, 2), (1, ) 3
( 2 ,1) 3
题 05福建
型 已知函数 f (x) x3 bx2 cx d
二 的图像过点 P(0, 2) 且在点 M (1, f (1))
2 ( x 1)3( x 3
0).
则
f
( x)
1 x
1 x2
(x
1)
2( x 1)2
( x 1)3
2x 1 x2 ,
令f (x) 0 ,结合x>0得x=1.
而0<x<1时, f (x) 0;x>1时,f (x) 0 ,所以x=1是f(x)的 极小值点.
所以当x=1时,f(x)取最小值f(1)=1.
导数的应用习题课
导数应用的知识网络结构图：
高考典型题
题型一
（06天津）已知函数 f (x) ax3 bx2 3x
在 x 1 处取得极值
求：(1) f (x) 的解析式 a 1,b 0

例10. 求
解法1 利用中值定理求极限
a a 原式 lim n ( ) 2 n n 1 n 1
2
1
a a ( 在 与 之间） n n 1
n2 a lim n n( n 1) 1 2
a
机动
目录
上页
下页
返回
结束
解法2 利用罗必塔法则
原式 lim
arctan a arctan b x x
机动 目录
x
f ( x)
下页 返回 结束
上页
arctan x ( x 0) . 例8. 证明 ln(1 x) 1 x 证: 设 ( x) (1 x) ln(1 x) arctan x , 则 (0) 0 1 ( x) 1 ln(1 x) 0 ( x 0) 2 1 x 故 x 0 时, (x) 单调增加 , 从而 ( x) (0) 0 arctan x 即 ln(1 x) ( x 0) 1 x 1 x ln(1 x) (0 x 1) 时, 如何设辅助 思考: 证明 1 x arcsin x 函数更好 ? 2 提示: ( x) (1 x) ln(1 x) 1 x arcsin x
二 课堂练习
1. 判断是非（共7个） 3. 计算题（共5个）
1. 掌握四个微分中值定理
罗尔中值定理：
[ 若 f ( x ) : (1)在闭区间a , b]上连续； (2)在开区间 a , b)内可导； (
(3) f (a)= f (b) ;
则至少存在一点 (a , b)，使得
f ( ) 0 .
1 2
1 cos x 1 o 1 . 及时求出已定式的极限. 原式 lim 2 x 0 3 x 2 1 sin x lim 2 x 0 6 x 1 1 1 2 6 12

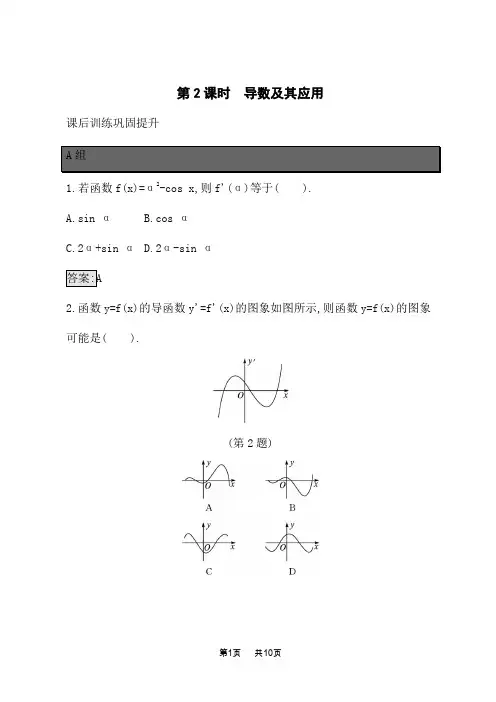
第2课时导数及其应用课后训练巩固提升1.若函数f(x)=α2-cos x,则f'(α)等于( ).A.sin αB.cos αC.2α+sin αD.2α-sin α2.函数y=f(x)的导函数y'=f'(x)的图象如图所示,则函数y=f(x)的图象可能是( ).(第2题)y'=f'(x)的图象与x轴交点的横坐标从左往右依次为x1,x2,x3(其中x1<0<x2<x3),由导函数y'=f'(x)的图象易得当x∈(-∞,x1)∪(x2,x3)时,f'(x)<0;当x∈(x1,x2)∪(x3,+∞)时,f'(x)>0,所以函数f(x)在(-∞,x1),(x2,x3)上单调递减,在(x1,x2),(x3,+∞)上单调递增,观察各选项,只有D选项符合.3.已知y=f(x)是定义在R上的函数,且f(1)=1,f'(x)>1,则f(x)>x的解集是( ).A.(0,1)B.(-1,0)∪(0,1)C.(1,+∞)D.(-∞,-1)∪(1,+∞)f(x)>x可化为f(x)-x>0.设g(x)=f(x)-x,则g'(x)=f'(x)-1,由题意知g'(x)=f'(x)-1>0,∴函数g(x)在R上单调递增.又g(1)=f(1)-1=0,∴g(x)>g(1),即f(x)-x>0的解集为(1,+∞).故选C.4.经过点(2,0)且与曲线y=1x相切的直线方程为 .解析:设切点坐标为x 0,1x 0,x 0≠0,则1x 0x 0-2=-1x 02,解得x 0=1,所以切点为(1,1),斜率为-1.故直线方程为x+y-2=0.5.若函数f(x)=ax 2-1x在区间(0,+∞)上单调递增,则实数a 的取值范围是 . 解析:f'(x)=ax-1x'=a+1x2,由题意得,a+1x2≥0对x ∈(0,+∞)恒成立,即a≥-1x2对x ∈(0,+∞)恒成立,所以a≥0.6.某罐头生产厂计划制造一种圆柱形的密封铁皮罐头盒,其表面积为定值S.若罐头盒的底面半径为r,则罐头盒的体积V 与r 的函数关系式为 ;当r= 时,罐头盒的体积最大.解析:由题意得,罐头盒的高h=S -2πr 22πr,则V=πr 2·S -2πr 22πr=12Sr-πr 30<r<√2πS 2π.V'=12S-3πr 2. 令V'=0,得r=√6πS6π,令V'>0,得0<r<√6πS6π,令V'<0,得√6πS 6π<r<√2πS2π,所以函数V=12Sr-πr 3在区间0,√6πS 6π上单调递增,在区间√6πS 6π,√2πS2π上单调递减. 故当r=√6πS6π时,V 最大.答案:V=12Sr-πr 30<r<√2πS 2π√6πS6π7.求下列函数的导数: (1)y=sin x-x+1; (2)y=-2e x ·x 3; (3)y=lnx x+1-2x .(2)y'=(-2e x ·x 3)'=(-2e x )'·x 3+(-2e x )·(x 3)'=-2e x x 3-6x 2e x . (3)y'=lnx x+1-2x '=lnx x+1'-(2x )'= 1x(x+1)-lnx (x+1)2-2xln2=1x−1x+1−lnx (x+1)2-2x ln2.8.设函数f(x)=aln x+12x+32x+1,其中a ∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y 轴. (1)求a 的值;(2)求函数f(x)的极值.因为f(x)=alnx+12x+32x+1,所以函数f(x)的定义域为(0,+∞),f'(x)=ax −12x2+32.由于曲线y=f(x)在点(1,f(1))处的切线垂直于y轴,故该切线的斜率为0,则f'(1)=a-12+32=0,解得a=-1.(2)由(1)知f(x)=-lnx+12x +32x+1(x>0),f'(x)=-1x−12x2+32=3x2-2x-12x2=(3x+1)(x-1)2x2.令f'(x)=0,解得x1=1,x2=-13(舍去).当x∈(0,1)时,f'(x)<0,函数f(x)在区间(0,1)上单调递减;当x∈(1,+∞)时,f'(x)>0,函数f(x)在区间(1,+∞)上单调递增.故函数f(x)在x=1处取得极小值f(1)=3,无极大值.1.已知函数f(x)=xln x,若f(x)在x0处的函数值与导数值之和等于1,则x0的值等于( ).A.1B.2C.±1D.ef(x)=xlnx,所以函数f(x)的定义域为(0,+∞),f'(x)=lnx+1,于是有x0lnx0+lnx0+1=1,解得x0=1或x0=-1(舍去),故选A.2.设函数f(x)=12x2-9ln x在区间[a-1,a+1]上单调递减,则实数a的取值范围是( ).A.(1,2]B.[4,+∞)C.(-∞,2]D.(0,3]f(x)的定义域为(0,+∞),且f'(x)=x-9x.又x>0,由f'(x)=x-9x≤0,得0<x≤3.因为函数f(x)在区间[a-1,a+1]上单调递减,所以{a-1>0,a+1≤3,解得1<a≤2.3.函数f(x)=xe x的图象为( ).f(x)=xe x ,所以f'(x)=1-xe x.当x<1时,f'(x)>0,函数f(x)=xe x在区间(-∞,1)上单调递增;当x>1时,f'(x)<0,函数f(x)=xe x在区间(1,+∞)上单调递减,只有选项A 中图象符合,故选A.4.若函数f(x)在区间(0,+∞)上可导,且满足f(x)>-xf'(x),则一定有( ). A.函数F(x)=f (x )x 在区间(0,+∞)上单调递增 B.函数F(x)=f (x )x 在区间(0,+∞)上单调递减C.函数G(x)=xf(x)在区间(0,+∞)上单调递增D.函数G(x)=xf(x)在区间(0,+∞)上单调递减则x>0时,G'(x)=xf'(x)+f(x)>0,故G(x)=xf(x)在区间(0,+∞)上单调递增,故选C.5.已知a ∈R,设函数f(x)={x 2-2ax +2a ,x ≤1,x -alnx ,x >1.若关于x 的不等式f(x)≥0在R 上恒成立,则a 的取值范围为( ). A.[0,1] B.[0,2] C.[0,e]D.[1,e]时,f(x)=x 2-2ax+2a≥0恒成立,且f(in =f(a)=2a-a 2≥0,解得0≤a<1. 综上,a≥0.当x>1时,由f(x)=x-alnx≥0恒成立,即a≤xlnx恒成立.设g(x)=xlnx,则g'(x)=lnx -1(lnx )2.令g'(x)=0,得x=e,且当1<x<e时,g'(x)<0,当x>e时,g'(in=g(e)=e,故a≤e.综上,a的取值范围是[0,e].6.已知函数y=f(x)在区间[0,3]上的图象如图所示,记k1=f'(1),k2=f'(2),k3=f(2)-f(1),则k1,k2,k3之间的大小关系为.(请用“>”连接)(第6题)k1=f'(1)与k2=f'(2)分别表示曲线在点A与点B处的切线的斜率,而k3=f(2)-f(1)=f(2)-f(1)表示直线AB的斜率,结合2-1图象知k1>k3>k2.>k21>k37.设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c的图象的一个公共点,两函数的图象在点P处有相同的切线.试用t表示实数a,b,c.f(x),g(x)的图象都过点(t,0),所以f(t)=0,即t3+at=0.因为t≠0,所以a=-t2.由g(t)=0,得bt2+c=0,即c=ab.又因为函数f(x),g(x)的图象在点(t,0)处有相同的切线,所以f'(t)=g'(t).而f'(x)=3x2+a,g'(x)=2bx,所以3t2+a=2bt.将a=-t2代入上式得b=t,从而c=ab=-t3.故a=-t2,b=t,c=-t3.8.设函数f(x)=ln x-a(x-1)e x,其中a∈R.(1)若a≤0,讨论f(x)的单调性;(2)若0<a<1e,求证:f(x)恰有两个零点.f(x)的定义域为(0,+∞),且f'(x)=1x -[ae x+a(x-1)e x]=1-ax2e xx.因为当a≤0时,1-ax2e x>0,从而f'(x)>0,所以函数f(x)在区间(0,+∞)上单调递增.(1)知,f'(x)=1-ax 2e xx. 设g(x)=1-ax2e x(x>0).因为g'(x)=-axe x(2+x),且0<a<1e,所以g'(x)<0,从而函数g(x)在区间(0,+∞)上单调递减.又g(1)=1-ae>0,且ln1a >1,g ln1a=1-a ln1a21a=1-ln1a2<0,所以方程g(x)=0在区间(0,+∞)上有唯一解,从而f'(x)=0在区间(0,+∞)上有唯一解,不妨设为x0,则1<x0<ln1a.当x∈(0,x0)时,f'(x)=g(x)x >g(x0)x=0,所以f(x)在区间(0,x0)上单调递增;当x∈(x0,+∞)时,f'(x)=g(x)x <g(x0)x=0,所以f(x)在区间(x0,+∞)上单调递减,因此x0是函数f(x)的极大值点,也是唯一的极值点.设h(x)=lnx-x+1(x>0),当x>1时,h'(x)=1x-1<0,则h(x)在区间(1,+∞)上单调递减,从而当x>1时,h(x)<h(1)=0,所以当x>1时,lnx<x-1.所以f ln1a =ln ln1a-a ln1a-1e ln1a=ln ln1a-ln1a+1=h ln1a<0,又因为f(x0)>f(1)=0,所以f(x)在区间(x0,+∞)上有唯一零点.又因为f(x)在区间(0,x0)上有唯一零点1,所以函数f(x)在区间(0,+∞)上恰有两个零点.。

第一章 1.2
导数及其应用 导数的计算 习题课
回顾与总结
1.常见函数的导数公式 常见函数的导数公式. 常见函数的导数公式
为常数) (C )′ = 0 (C 为常数) 为有理数) ( x n )′ = nx n−1 ( n 为有理数) (sin x )′ = cos x (cos x )′ = －sin x (a x )′ = a x ln a (a > 0，a ≠ 1) 特殊地 (e x )′ = e x 1 1 (log a x )′ = log a e = (a > 0, a ≠ 1) 且 x x ln a 1 特殊地 (ln x )′ = x
2 ∴k2 = y′ |x=3 = − . 3 因为k 所以两条切线互相垂直.从而命题成立 因为 1k2=-1,所以两条切线互相垂直 从而命题成立 所以两条切线互相垂直 从而命题成立.
9 8 − x2 9
利用上述方法可得圆锥曲线的切线方程如下: 利用上述方法可得圆锥曲线的切线方程如下 圆锥曲线的切线方程如下 (1)过圆 过圆(x-a)2+(y-b)2=r2上一点 0(x0,y0)的切线方程是 上一点P 的切线方程是: 过圆 的切线方程是 (x0-a)(x-a)+(y0-b)(y-b)=r2.
2 3 2 3
说明:在对法则的运用熟练后 就不必再写中间步骤 说明 在对法则的运用熟练后,就不必再写中间步骤 在对法则的运用熟练后 就不必再写中间步骤.
y′ = 4(1 + sin x) （1+ sin x） ⋅ x
2 3 2 ’
= 4(1 + sin2 x)3 ⋅ 2sin x ⋅ cos x = 4sin 2x ⋅ (1 + sin2 x)3 .

例4: 如图,在二次函数f(x)=
4x-x2的图象与x轴所
y
围成的图形中有一个
内接矩形ABCD,求这
个矩形的最大面积.
解:设B(x,0)(0<x<2), 则
x
A(x, 4x-x2).
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0<x<2).
2
3
f ( )
3
33 8
,又f(0)=f(π)=0,[
f ( )]max
33 8
.
故当 x 3 , y
2
3 4
时,
( xy)max
33 8
.
例6:证明不等式: ln x 1 1 ( x 1)2 1 2 (1 x)3( x 0).
x2
3
证:设
f
(x)
ln
x
1 x
1 2
(x
1)2
解:函数的定义域为(,0) (0,1) (1,).
当x<0或x>1时, f (x) x x 1 2x2 2x 1 .
x 1 x x(x 1)
f ( x)
2x 1 x2( x 1)2
.
故当x<0时,
f (x) 0;当x>1时, f (x) 0.
当0<x<1时,
f (x)
2x2 2x 1 ,
设 x 1 cos , y 1 sin ,由x,y为正实数得: 0 .
xy
1
(1
2
cosBiblioteka ) s in.2
设 f ( ) 1 (1 cos )sin .

所以 f′(1)＝ln 1＋a＋1＝a＋1＝2，a＝1.
[方法技巧]
一般已知曲线上一点P(x0，y0)的切线与已知直线的关系(平行或垂直)，确定 该切线的斜率k，再求出函数的导函数，然后利用导数的几何意义得到k＝f′(x0) ＝tan α，其中倾斜角α∈[0，π)，根据范围进一步求得角α或有关参数的值．
数 f(x)的图象在点(0,1)处的切线斜率为－1，∴函数 f(x)的图象在点(0，f(0))处的
切线方程为 y＝－x＋1，即 x＋y－1＝0.故选 B.
答案：B
2．(2022·新课标Ⅱ卷)曲线 y＝ln|x|过坐标原点的两条切线的方程为________， ________.
解析：先求当 x>0 时，曲线 y＝ln x 过原点的切线方程，设切点为(x0，y0)， 则由 y′＝1x，得切线斜率为x10，又切线的斜率为xy00，所以x10＝xy00，解得 y0＝1， 代入 y＝ln x，得 x0＝e，所以切线斜率为1e，切线方程为 y＝1ex.同理可求得当 x<0 时的切线方程为 y＝－1ex.综上可知，两条切线方程为 y＝1ex，y＝－1ex.
答案：y＝1ex y＝－1ex
高频考点二|求切点坐标
[例2] 已知函数f(x)＝xln x在点P(x0，f(x0))处的切线与直线x＋y＝0垂直， 则切点P(x0，f(x0))的坐标为________．
[解析] ∵f(x)＝xln x，∴f′(x)＝ln x＋1，由题意得f′(x0)·(－1)＝－1，即 f′(x0)＝1，∴ln x0＋1＝1，ln x0＝0，∴x0＝1，∴f(x0)＝0，即P(1,0)．
2．若函数f(x)＝ln x＋ax存在与直线2x－y＝0平行的切线，则实数a的取值范围是
()

[集训冲关]
1．函数f(x)＝1＋3x－x3
()
A．有极小值，无极大值
B．无极小值，有极大值
C．无极小值，无极大值
D．有极小值，有极大值
解析：f′(x)＝－3x2＋3，由f′(x)＝0，得x＝±1.当x∈(－1,1)时，f′(x)>0， ∴f(x)的单调递增区间为(－1,1)；同理，f(x)的单调递减区间为(－∞，－1)和 (1，＋∞)，∴当x＝－1时，函数有极小值－1，当x＝1时，函数有极大值3， 故选D.
递减．
(2)证明：f(x)－g(x)＝x2ex－1－x3＝x2(ex－1－x)． 设h(x)＝ex－1－x，h′(x)＝ex－1－1， 由h′(x)＝0得x＝1， 则当x<1时，h′(x)<0，即函数h(x)在(－∞，1)上单调递减； 当x>1时，h′(x)>0，即函数h(x)在(1，＋∞)上单调递增． 因此，当x＝1时，h(x)取最小值h(1)＝0. 即对任意实数x都有h(x)≥0，又x2≥0， 所以f(x)－g(x)≥0， 故对任意实数x，恒有f(x)≥g(x)．
[集训冲关]
1．函数 f(x)＝2x2－ln x 的单调递增区间是
A.0，12
B．－12，0和12，＋∞
C.12，＋∞
D．－∞，－12和0，12
()
解析：由题意得 f′(x)＝4x－1x＝4x2x－1，且 x>0，由 f′(x)>0，即 4x2－1>0， 解得 x>12.故选 C.
答案：C
2．已知函数 f(x)＝－12x2＋2x－aex. (1)若 a＝1，求 f(x)在 x＝1 处的切线方程；
令 g′(x)＝0，解得 x＝3，列表如下：
故函数 g(x)在 x＝3 处取得极小值，亦即最小值， 即 g(x)min＝－e13，∴a≤－e13， 故实数 a 的取值范围是－∞，－e13.

详细描述
复合函数的导数是通过对中间变量求导，然后将结果代入到外层函数中求导得 到的。掌握复合函数的导数可以帮助我们解决一些复杂的函数问题，如求极值 、判断单调性等。
隐函数的导数
总结词
掌握隐函数的导数是解决隐函数问题 的关键。
详细描述
隐函数的导数是通过对等式两边同时 求导，然后解出对x的导数得到的。掌 握隐函数的导数可以帮助我们解决一 些涉及多个变量的问题，如求最值、 判断曲线的形状等。
THANKS
感谢观看
总结词
导数具有连续性、可加性、可乘性和链式法则等性质 。
详细描述
导数具有一系列重要的性质，包括连续性、可加性、可 乘性和链式法则等。连续性是指函数在某一点的导数等 于该点附近的极限值；可加性是指函数在两点之间的导 数等于两端点导数的和；可乘性是指函数与常数的乘积 的导数等于该常数与函数导数的乘积；链式法则是指复 合函数的导数等于复合函数内部函数的导数与外部函数 的导数的乘积。这些性质在研究函数的单调性、极值和 曲线的拐点等方面具有广泛应用。
导数与函数的最值的综合题
总结词
这类题目通常涉及到利用导 数研究函数的极值和最值，
解决最优化问题。
详细描述
这类题目要求熟练掌握导数 的计算方法和函数的极值判 定，能够利用导数研究函数 的极值和最值，解决最优化
问题。
示例
设函数$f(x) = x^{3} ax^{2} + bx$，若$f(x)$在$( - infty,0)$和$(2, + infty)$上 单调递增，在$(0,2)$上单调 递减，且$f(x)$在$x = 2$处 取得极小值，求$a,b$的值及 $f(x)$的最小值。
导数与函数的零点的综合题
总结词

在时,利用F(x)的单调性求最小值,证明F(x)min>0.
2.证明不等式:ex≥1+x.
证明:设函数f(x)=ex-1-x,则f'(x)=ex-1.
令f'(x)=0,得x=0.
当x>0时,f'(x)>0,函数f(x)在区间(0,+∞)内单调递增;
当x<0时,f'(x)<0,函数f(x)在区间(-∞,0)内单调递减.
+18x.
2
令V'=0,得x=0(舍去)或x=1.
根据V=-6x3+9x2的单调性,可知V=-6x3+9x2在x=1处取得极大值也是最大
值.
故当该长方体的长、宽、高分别为2 m,1 m,1.5 m时,体积最大,最大体积
为3 m3.
答案:(1)A (2)3 m3
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“ ”,错误的画“×”.
证明:先证ln x<x(x>0).
设 f(x)=x-ln x(x>0),则
1
f'(x)=1
=
-1
.

令f'(x)=0,解得x=1.
当0<x<1时,f'(x)<0,函数f(x)在区间(0,1)内单调递减;
当x>1时,f'(x)>0,函数f(x)在区间(1,+∞)内单调递增.
所以当x=1时,函数f(x)有极小值,也是最小值,最小值为f(1)=1>0.
得m>1,
∴m的取值范围为(1,+∞).
探究三
导数在实际问题中的应用
【例3】 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:

(3)令 u＝lnx，则 y＝lnu， ∴y′x＝y′u·u′x ＝1u·1x＝xl1nx. (4)令 u＝2x2＋1，则 y＝eu， ∴y′x＝y′u·u′x＝eu·4x ＝4x·e2x2＋1.
例2 求下列函数的导数． (1)y＝(x2－4)2； (2)y＝log2(2x2＋3x＋1)； (3)y＝esin(ax＋b) 分析 先将复合函数分解，找出中间变量，然后按复合 函数求导公式y′＝y′u·u′x进行求导．
gf((xx))f(x)g(xg)(x)f2(x)g(x)(g(x)0)
解 根据推论 1 可得 (3x4) = 3(x4) ， (5cos x) = 5(cos x) ，又(x4) = 4x3，
(cos x) = - sin x，(ex) = ex，(1) = 0，
故f (x) = (3x4 - ex + 5cos x - 1) = (3x4) -(ex ) + (5cos x) - (1) = 12x3 - ex - 5sin x . f (0) = (12x3 - ex - 5sin x)|x=0 = - 1
公 式 6 : (e x ) ' e x ;
公 式 7 : (lo g a x ) '
1
(a 0 , 且 a 1);
x ln a
公 式 8 : (ln x ) ' 1 ; x
需要使用导数的运算法则求导:
f(x)g(x)f(x)g(x)
f(x)•g(x)f(x)g(x)f(x)g(x)
推论 1 (cu(x)) = cu (x) (c 为常数).
20XX
感谢观赏 求简单复合函数f(ax＋b)的导数
求简单复合函数的导数，实质是运用整体思想，先把简单复

1 由于直线 x 2 y 3 0 的斜率为 ，且过点 (1,1) ， 2
f (1) 1, 故 1 即 f '(1) 2 , b 1, a 1 2 b 2 ,
解得 a 1 ， b 1 .
例题讲解
ln x 1 , 所以 （Ⅱ）由（Ⅰ）知 f(x)= x 1 x
当 a 2 时， x1 a，x2 a ，从而 f ( x ) 在 f ( x ) 的定义域内没有零点， 故 f ( x ) 无极值． 当a
2 时， x1 a ， x2 a ， f ( x ) 在 f ( x) 的定义域内有两个不同的零点，
由极值判别方法知 f ( x ) 在 x x1，x x2 取得极值． 综上， f ( x ) 存在极值时， a 的取值范围为 ( 2， ) ．
在该区间上的最大值.
【思路点拨】 （1）要使 f ( x ) 在 ( 2 , ) 上存在单调递增区间，需 f ' (x) 在 ( 2 , )
3
3
上恒大于零，即得 a 的取值范围.（2）首先求出 f ( x ) 在 [1, 4] 上的最小值为 f(4), 从而求出 a 的值，进一步易求 f ( x ) 在该区间上的最大值为 f(2).
2 x 2 2ax 1 （Ⅱ） f ( x ) 的定义域为 (a， ) ， f ( x) ． xa
方程 2 x 2ax 1 0 的判别式 4a 8 ．
2 2
（ⅰ）若 0 ，即 2 a （ⅱ）若 0 ，则 a
2 ，在 f ( x) 的定义域内 f ( x) 0 ，故 f ( x) 无极值．
a b 2 1 . (2)由f(α)=-1和f(β)=1可得: 2 a b 1

习题课(二) 导数的几何意义及其应用一、选择题 1．曲线y ＝1－2x ＋2在点(－1，－1)处的切线方程为( ) A ．y ＝2x ＋1 B ．y ＝2x －1 C ．y ＝－2x －3 D ．y ＝－2x －2解析：选A 因为y ＝1－2x ＋2＝x x ＋2， 所以y ′＝x ＋2－x x ＋22＝2x ＋22，y ′| x ＝－1＝2，所以曲线在点(－1，－1)处的切线的斜率为2，所以所求切线方程为y ＋1＝2(x ＋1)，即y ＝2x ＋1.2．已知曲线y ＝x 24－3ln x 的一条切线的斜率为12，则切点的横坐标为( )A ．3B ．2C ．1D ．12解析：选A 因为y ′＝x 2－3x ，所以令y ′＝12，解得x ＝3，即切点的横坐标为3.3．已知函数f (x )＝x ln x ＋a 的图象在点(1，f (1))处的切线经过原点，则实数a 的值为( )A ．1B ．0 C.1eD ．－1解析：选A ∵f (x )＝x ln x ＋a ，∴f ′(x )＝ln x ＋1， ∴f ′(1)＝1，f (1)＝a ，∴切线方程为y ＝x －1＋a ， ∴0＝0－1＋a ，解得a ＝1，故选A.4．若点P 是函数y ＝e x －e －x－3x ⎝ ⎛⎭⎪⎫－12≤x ≤12图象上任意一点，且在点P 处切线的倾斜角为α，则α的最小值是( )A.5π6 B ．3π4C.π4D ．π6解析：选B 由导数的几何意义，k ＝y ′＝e x＋e －x－3≥2e x ·e －x－3＝－1，当且仅当x ＝0时等号成立．即tan α≥－1，α∈[0，π)．又－12≤x ≤12，tan α＝k <0，所以α的最小值是3π4，故选B.5．若曲线y ＝f (x )＝ln x ＋ax 2(a 为常数)不存在斜率为负数的切线，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－12，＋∞ B ．⎣⎢⎡⎭⎪⎫－12，＋∞C ．(0，＋∞)D ．[0，＋∞)解析：选D f ′(x )＝1x ＋2ax ＝2ax 2＋1x(x >0)．根据题意有f ′(x )≥0(x >0)恒成立，所以2ax 2＋1≥0(x >0)恒成立，即2a ≥－1x2(x >0)恒成立，所以a ≥0，故实数a 的取值范围为[0，＋∞)．6.意大利画家列奥纳多·达·芬奇(1452.4—1519.5)的画作《抱银貂的女人》中，女士脖颈上黑色珍珠项链与主人相互映衬，呈现出不一样的美与光泽，达·芬奇提出：固定项链的两端，使其在重力的作用下自然下垂，项链所形成的曲线是什么？这就是著名的“悬链线问题”，后人给出了悬链线的函数解析式：f (x )＝a cosh x a，其中a 为悬链线系数，cosh x 称为双曲余弦函数，其函数表达式为cosh x ＝e x ＋e －x 2，相应地双曲正弦函数的表达式为sinh x ＝e x －e－x2.若直线x ＝m 与双曲余弦函数C 1、双曲正弦函数C 2的图象分别相交于点A ，B ，曲线C 1在点A 处的切线l 1与曲线C 2在点B 处的切线l 2相交于点P ，则下列结论正确的为( )A ．cosh(x －y )＝cosh x cosh y －sinh x sinh yB ．y ＝sinh x cosh x 是偶函数C ．(cosh x )′＝sinh xD ．若△PAB 是以A 为直角顶点的直角三角形，则实数m ＝0解析：选ACD cosh x cosh y －sinh x sinh y ＝e x＋e －x2·e y ＋e －y 2－e x －e －x 2·e y －e －y2＝ex －y＋e －x ＋y2＝cosh(x －y )，A 正确；y ＝sinh x cosh x ＝e 2x －e－2x4，记h (x )＝e 2x －e－2x4，则h (－x )＝e －2x－e 2x4＝－h (x )，h (x )为奇函数，即y ＝sinh x cosh x 是奇函数，B 错误；⎝ ⎛⎭⎪⎫e x＋e －x2′＝e x－e－x2，即(cosh x )′＝sinh x ，C 正确；对于D ，因为AB ⊥x 轴，因此若△PAB 是以A为直角顶点的直角三角形，则k PA ＝0，由k PA ＝e m －e－m2＝0，解得m ＝0，D 正确．二、填空题7．若曲线f (x )＝a cos x 与曲线g (x )＝x 2＋bx ＋1在交点(0，m )处有公切线，则a ＋b ＝________.解析：依题意得，f ′(x )＝－a sin x ，g ′(x )＝2x ＋b ，f ′(0)＝g ′(0)，即－a sin 0＝2×0＋b ，得b ＝0.又m ＝f (0)＝g (0)，即m ＝a ＝1，因此a ＋b ＝1.答案：18．若曲线y ＝ln(x ＋a )的一条切线为y ＝e x ＋b ，其中a ，b 为正实数，则a ＋eb ＋2的取值范围为________．解析：由y ＝ln(x ＋a )，得y ′＝1x ＋a. 设切点为(x 0，y 0)，则有⎩⎪⎨⎪⎧1x 0＋a＝e ，ln x 0＋a ＝e x 0＋b ⇒b ＝a e －2.∵b >0，∴a >2e ，∴a ＋e b ＋2＝a ＋1a≥2，当且仅当a ＝1时等号成立． 答案：[2，＋∞)9．设曲线y ＝e x在点(0,1)处的切线与曲线y ＝1x(x >0)上点P 处的切线垂直，则点P 的坐标为________．解析：y ′＝e x ，则曲线y ＝e x在点(0,1)处的切线的斜率为1，又曲线y ＝1x(x >0)上点P处的切线与曲线y ＝e x在点(0,1)处的切线垂直，所以曲线y ＝1x(x >0)在点P 处的切线的斜率为－1.设P (a ，b )，则曲线y ＝1x(x >0)上点P 处的切线的斜率为y ′|x ＝a ＝－a －2＝－1，可得a ＝1，又P (a ，b )在y ＝1x上，所以b ＝1，故P (1,1)．答案：(1,1) 三、解答题 10．已知函数f (x )＝a ln x x ＋1＋bx，曲线y ＝f (x )在点(1，f (1))处的切线方程为x ＋2y －3＝0，求a ，b 的值．解：f ′(x )＝a ⎝⎛⎭⎪⎫x ＋1x －ln x x ＋12－bx2.因为直线x ＋2y －3＝0的斜率为－12，且过点(1,1)，所以f (1)＝1，f ′(1)＝－12，即b ＝1，a 2－b ＝－12，解得a ＝1，b ＝1.11．已知函数f (x )＝x ，g (x )＝a ln x ，a ∈R.若曲线y ＝f (x )与曲线y ＝g (x )相交且在交点处有相同的切线，求a 的值及该切线的方程．解：f ′(x )＝12x ，g ′(x )＝ax (x >0)，设两曲线的交点为P (x 0，y 0)，则⎩⎪⎨⎪⎧x 0＝a ln x 0，12x 0＝ax 0，解得a ＝e 2，x 0＝e 2，所以两条曲线交点的坐标为(e 2，e)． 切线的斜率为k ＝f ′(e 2)＝12e， 所以切线的方程为y －e ＝12e (x －e 2)，即x －2e y ＋e 2＝0.12．设f (x )＝x 3＋ax 2＋bx ＋1的导数f ′(x )满足f ′(1)＝2a ，f ′(2)＝－b ，其中常数a ，b ∈R ，求曲线y ＝f (x )在点(1，f (1))处的切线方程．解：因为f (x )＝x 3＋ax 2＋bx ＋1， 所以f ′(x )＝3x 2＋2ax ＋b . 令x ＝1，得f ′(1)＝3＋2a ＋b ， 又f ′(1)＝2a ，则3＋2a ＋b ＝2a ， 解得b ＝－3.令x ＝2得f ′(2)＝12＋4a ＋b ， 又f ′(2)＝－b ， 所以12＋4a ＋b ＝－b ， 解得a ＝－32.则f (x )＝x 3－32x 2－3x ＋1，从而f (1)＝－52.又f ′(1)＝2×⎝ ⎛⎭⎪⎫－32＝－3， 所以曲线y ＝f (x )在点(1，f (1))处的切线方程为y －⎝ ⎛⎭⎪⎫－52＝－3(x －1)，即6x ＋2y －1＝0.。