第三章《勾股定理》单元测试

第三章勾股定理数学八年级上册-单元测试卷-苏科版(含答案)一、单选题(共15题，共计45分)1、如图，等边△ABC在平面直角坐标系中的位置如图所示，其中顶点，，则顶点C的坐标为（）A. B. C. D.2、如图，在中，以点为圆心，任意长为半径作弧，交射线于点，交射线于点，再分别以、为圆心，的长为半径，两弧在的内部交于点，作射线，若，则两点之间距离为（）A.10B.12C.13D.3、如图是一张直角三角形的纸片，两直角边AC＝6cm、BC＝8cm，现将△ABC折叠，使点B 与点A重合，折痕为DE，则BE的长为( )A.4cmB.5cmC.6cmD.10cm4、如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH.连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则的值是（）A. B. C. D.5、如图，直线AB、CD、BC分别与⊙O相切于E、F、G，且AB∥CD，若OB=6cm，OC=8cm，则BE+CG的长等于（）A.13B.12C.11D.106、如图以数轴的单位长线段为边作一个正方形，以数轴的原点为旋转中心，将过原点的对角线顺时针旋转，使对角线的另一端点落在数轴正半轴的点处，则点表示的数是（）A. B. C. D.7、绍兴是著名的桥乡，如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（）A.4mB.5mC.6mD.8m8、如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（）A.y=  B.y=C.y=D.y=9、以下列线段a、b、c的长为边，能构成直角三角形的是（）A.a=3，b=4，c=6B.a=1，b= ，c=C.a=5，b=6，c=8 D.a= ，b=2，c=10、若为△ABC的三边，且，则△ABC的形状不可能是（）．A.锐角三角形B.钝角三角形C.等腰三角形D.直角三角形11、如图，在正方形ABCD中，AD=5，点E、F是正方形ABCD内的两点，且AE=FC=3，BE=DF=4，则EF的长为（）A. B. C. D.12、三角形的三边长ａ,ｂ,ｃ满足2ａｂ=(ａ+ｂ)2－ｃ2,则此三角形是（）A.钝角三角形B.锐角三角形C.直角三角形D.等边三角形13、如图，在矩形ABCD中，AB=6，BC=8，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，则DF的长为（）A.1B.2C.3D.414、将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（）A.3cmB.6cmC.3 cmD.6 cm15、底面周长为12cm，高为8cm的圆柱体上有一只小蚂蚁要从A点爬到B点，则蚂蚁爬行的最短距离是（）cm．A.10B.8C.5D.4二、填空题(共10题，共计30分)16、如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为________．17、如图，为直角三角形，其中，则的长为________。

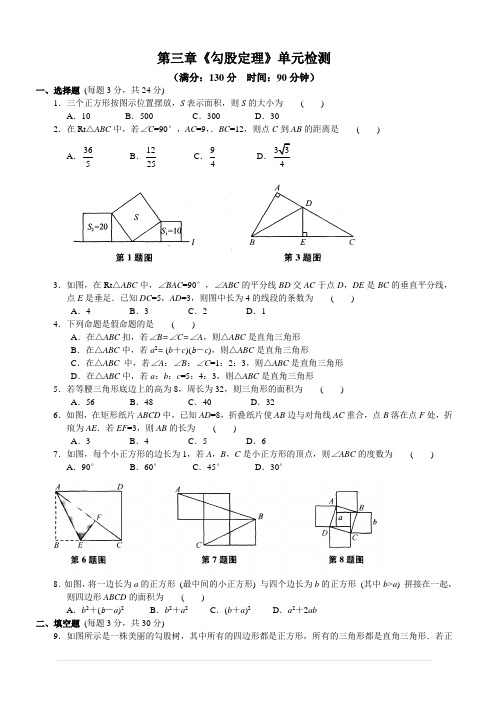
第三章《勾股定理》单元检测（满分：130 分 时间：90 分钟）一、选择题 (每题 3 分，共 24 分) 1．三个正方形按图示位置摆放，S 表示面积，则 S 的大小为 ( ) A．10 B．500 C．300 D．30 2．在 Rt△ABC 中，若∠C=90°，AC=9， ．BC=12，则点 C 到 AB 的距离是 A．()36 5B．12 25C．9 4D．3 3 43．如图，在 Rt△ABC 中，∠BAC=90°，∠ABC 的平分线 BD 交 AC 于点 D，DE 是 BC 的垂直平分线， 点 E 是垂足．已知 DC=5，AD=3，则图中长为 4 的线段的条数为 ( ) A．4 B ．3 C．2 D．1 4．下列命题是假命题的是 ( ) A．在△ABC 扣，若∠B=∠C=∠A，则△ABC 是直角三角形 B．在△ABC 中，若 a2= (b＋c)(b－c)，则△ABC 是直角三角形 C．在△ABC 中，若∠A：∠B：∠C=1：2：3，则△ABC 是直角三角形 D．在△ABC 中，若 a：b：c=5：4：3，则△ABC 是直角三角形 5．若等腰三角形底边上的高为 8，周长为 32，则三角形的面积为 ( ) A．56 B．48 C．40 D．32 6．如图，在矩形纸片 ABCD 中，已知 AD=8，折叠纸片使 AB 边与对角线 AC 重合，点 B 落在点 F 处，折 痕为 AE．若 EF=3，则 AB 的长为 ( ) A．3 B ．4 C．5 D．6 7．如图，每个小正方形的边长为 1，若 A，B，C 是小正方形的顶点，则∠ABC 的度数为 ( ) A．90° B．60° C．45° D．30°8． 如图， 将一边长为 a 的正方形 (最中间的小正方形) 与四个边长为 b 的正方形 (其中 b>a) 拼接在一起， 则四边形 ABCD 的面积为 ( ) 2 2 2 2 A．b ＋(b－a) B．b ＋a C．(b＋a)2 D．a2＋2ab 二、填空题 (每题 3 分，共 30 分) 9．如图所示是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形 A，B，C，D 的边长分别是 3，4，2，3，则最大正方形 E 的面积是 10．若一个直角三角形的三边长的平方和为 200，则斜边长为 ．．11．在△ABC 中，AB=5 cm，BC=6 cm，若 BC 边上的中线 AD=4 cm，则∠ADC= ． 12．如图，在四边形 ABCD 中，AB：BC：CD：DA=2：2：3：1．若∠ABC=90°，则∠DAB= 13．若一个三角形的三边之比为 5：12：13，且周长为 60cm，则它的面积为 cm2． 14．已知 a，b，c 为三个正整数，如果 a＋b＋c=12，那么以 a，b，c 为边能组成的三角形是：①等腰三 角形；②等边三角形；③直角三角形；④钝角三角形．以上符合条件的正确结论是 ．(填序 号) 15．一座垂直于两岸的桥长 12 米，一艘小船自桥北头出发，向正南方向驶去，因水流原因，到达南岸后， 发现已偏离桥南头 9 米，则小船实际行驶了 米． 16． 如图， 在△ABC 中， CD⊥AB， 垂足为点 D， E 是 AC 的中点． 若 AD=6， DE=5， 则 CD 的长等于 .17．在锐角三角形 ABC 中．BC= 32 ，∠ABC=45°，BD 平分∠ABC．若 M，N 分别是边 BD，BC 上的 动点，则 CM＋MN 的最小值是 ． 18．如图，△ABC 是边长为 6 cm 的等边三角形，动点 P，Q 同时从 A，B 两点出发，分别在 AB，BC 边 上匀速移动，它们的速度分别为 2 cm／s 和 1cm／s，当点 P 到达点 B 时，P，Q 两点停止运动，设点 P 的运动时间为 ts，则当 t= s 时，△PBQ 为直角三角形． 三、解答题 (共 76 分) 19．(本题 6 分) 如图，每个小方格的边长都为 1，求图中格点四边形 ABCD 的面积．20．(本题 6 分) 如图，在△ABC 中，已知∠A=90°，D 是 BC 的中点，且 DE⊥BC，垂足为点 D，交 AB于点 E．求证：BE －EA2=AC2．221．(本题 6 分) 一块地如图所示∠ADC=90°，AD=12m，CD=9 m，AB=39m，BC=36 m，求这块地的面 积．22．(本题 8 分) 如图，在△ABC 中，AB=AC=13，点 D 在边 BC 上，AD=12，BD=5，试问 AD 平分∠BAC 吗? 为什么?23．(本题 8 分) 如图，已知 AB=12，AB⊥BC，垂足为点 B，AB⊥AD，垂足为点 A，AD=5，BC=10，点 E 是 CD 的中点，求 AE 的长．24．(本题 8 分) 如图，在等腰直角三角形 ABC 中，∠ABC=90°，D 为边 AC 的中点，过点 D 作 DE⊥DF， 交 AB 于点 E，交 BC 于点 F．若 AE=4，FC=3，求 EF 的长．25．(本题 10 分) 小东拿着一根长竹竿进一个宽为 3 米的城门，他先横着拿，进不去，又竖起来拿，结果 竿比城门高 1 米，当他把竿斜着时，两端刚好顶着城门的对角，问：竿长多少米?26．(本题 12 分) 如图，将 Rt△ABC 绕其锐角顶点 A 旋转 90°得到 Rt△ADE，连接 BE，延长 DE，BC 相交于点 F，则有∠BFE=90°，且四边形 ACFD 是一个正方形． (1) 判断△ABE 的形状，并证明你的结论； (2) 用含 b 的代数式表示四边形 ABFE 的面积； (3) 求证：a2＋b2=c2．27．(本题 12 分) 如图，△ABC 中，∠ABC= 45°，CD⊥AB，BE⊥AC，垂足分别为点 D，E，F 为 BC 的 中点，BE 与 DF，DC 分别交于点 G，H，∠ABE=∠CBE． (1) 线段 BH 与 AC 相等吗? 若相等，请给予证明；若不相等，请说明理由． 2 (2) 求证：BG －GE2=EA2．参考答案一、选择题 1．D 2．A 3．B 4．A 5．B 6．D 7．C 8．A [提示：中间最小正方形四周的直角 1 1 2 三角形的面积均为 b (b－a)，故所求四边形的面积为 4× b (b－a)＋a2=b ＋(b－ a)2] 2 2 二、填空题 9．38 10．10 11．90° 12．135° 13．120 14．①②③ 15．15 16．8 17．4 (提示： 3 12 过点 C 作 CE⊥AB，垂足为点 E，线段 CE 的长即等于 CM+MN 的最小值) 18． 或 [提示：AP=2tcm， 2 5 3 12 BP = (6－2t)cm，BQ =tcn. 当∠BQP=90°时，t = ；当 ∠BPQ = 90°时，t = ] 2 5 三、解答题19．连接 AC. S 四边形 ABCD = S△ADC+S△ABC = 5×2×= 12．5 2 2 20． 连接 CE． ∵ D 是 BC 的中点， DE⊥BC ， ∴ BE=CE． ∵∠A=90°， ∴ CE2－EA2=AC2， ∴ BE2－EA2=AC2 21． 连接 AC． ∵ ∠ADC=90°， AD=12 m， CD=9 m， ∴ AC=15 m． 又∵AB=39 m， BC=36m， ∴ AC2+BC2=AB2， 1 1 1 ∴ ∠ACB=90°，∴ S△ABC= ×15×36=270 (m2)，又 S△ADC= ×AD×DC= ×12×9=54 (m2)，∴ 这块 2 2 2 地的面积为 S△ABC—S△ADC=270－54=216 (m2) 22．AD 平分∠BAC．∵ AB=AC=13，AD=12，BD=5，∴ BD2+AD2=AB2，∴ △ABD 是直角三角形，且∠ADB= ∠ADC=90°，即 AD⊥BC．又 AB=AC，∴ AD 平分∠BAC，即结论成立 23．延长 AE 交 BC 于点 F．∵ AB⊥BC，AB⊥AD，∴ AD∥BC，∴ ∠D=∠C，∠DAE=∠CFE．又∵ 点 E 是 CD 的中点，∴ DE=CE．∵在△AED 与△FEC 中，∠D=∠C， ∠DAE=∠CFE，DE=CE， ∴ △AED≌△FEC， ∴ AE=FE， AD=FC． ∵ AD=5， BC=10， ∴ BF=5． 在 Rt△ABF 中， AF2=AB2+BF2=169， ∴ AF=13，∴ AE=6．5 24．连接 BD．∵ △ABC 是等腰直角三角形，D 为边 AC 的中点，∴ BD=DC，∠ABD=∠C=45°，BD⊥AC， ∴ ∠BDF+∠FDC=90°．又∵ DE⊥DF，∴ ∠BDF+∠BDE= 90°，∴ ∠FDC=∠BDE，∴ △BED≌△CFD，∴ BE=FC=3，BF=BC－FC=AB－BE=AE=4．∴ EF=5 2 25．设竿长 x 米，则城门高(x－1)米，根据题意得 x2=(x－1) ＋32，解得 x=5．即竿长 5 米 26． (1) △ABE 是等腰直角三角形． 证明： ∵ △ABC≌△AED， ∴ AB=AE， ∠BAC=∠EAD， ∴ ∠BAE=90°， 即△ABE 是等腰直角三角形 (2) S 四边形 ABFE=S 四边形 ACFE+S△ABC= 1 2 1 S 四边形 ACFE+S△AED=S 四边形 ACFD=b2 (3) S 四边形 ABFE=S△ABE+S△BEF= c ＋ (b－a)(b＋a)，由(2)知 S 四边形 2 2 1 2 1 2 2 c ＋ (b－a)(b＋a)=b2，∴ a ＋b2－c2 ABFE=b ，即 2 2 27 ． (1) 相等 ∵ ∠ BDC= ∠ BEC= ∠ CDA=90 °， ∠ ABC=45 °，∴ ∠ BCD=45 ° = ∠ ABC ， ∠ A+ ∠ DCA=90°，∠A+∠ABE=90°，∴ DB=DC，∠ABE=∠DCA．在△DBH 和△DCA 中，∵ ∠DBH=∠ DCA，∠BDH=∠CDA，BD=CD，∴ △DBH≌△DCA，∴ BH=AC (2)连接 CG．∵ F 为 BC 的中点， DB=DC，∴ DF 垂直平分 BC，∴ BG=GG．∵ ∠ABE=∠CBE，BE⊥AC，∴ ∠AEB=∠CEB．在△ ABE 和△CBE 中，∵ ∠AEB=∠CEB，BE=BE，∠CBE=∠ABE，∴ △ABE≌△CBE，∴ EC=EA．在 Rt△CGE 中，由勾股定理得 CG2－GE2=CE2，∴ BG2－GE2=EA21＋5×3×1。

第三章勾股定理数学八年级上册-单元测试卷-苏科版(含答案)一、单选题(共15题，共计45分)1、在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的，∠BAC=90°，AB=6，AC=8，点D，E，F，G，H， I都在长方形KLMJ的边上，则长方形KLMJ的面积为（）A.360B.400C.440D.4842、下列各组线段中的三个长度：①9，12，15；②7，24，25；③32， 42， 52；④3a，4a，5a（a＞0）；⑤m2-n2， 2mn，m2+n2（m，n为正整数，且m＞n）其中可以构成直角三角形的有（）组。

A.2B.3C.4D.53、若三边长满足，则是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4、如图所示，正方体的顶点P处放了一点糖，四只蚂蚁从同一顶点A处分别沿表面不同的路线爬向P处，则所爬行的路程最短的是（）A.甲B.乙C.丙D.丁5、小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高是( )．A.8米B.10米C.12米D.14米6、下列命题中，是假命题的是( )A.在△ABC中，若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形B.在△ABC中，若a 2＝(b＋c) (b－c)，则△ABC是直角三角形C.在△ABC 中，若∠B＝∠C＝∠A，则△ABC是直角三角形D.在△ABC中，若a：b：c＝5：4：3，则△ABC是直角三角形7、如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC＝1，则AB的长度为（）A. B. C. D.8、如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM的取值范围是（）A.3≤OM≤5B.3≤OM＜5C.4≤OM≤5D.4≤OM＜59、如图，将一块等腰直角三角板放置在平面直角坐标系中，其直角顶点落在轴上，点落在轴上，点落在第一象限内，已知点，点，连接，则线段的长度为（）A.4B.C.6D.10、在Rt△ABC中，∠C=90°，AC=5，AB=13，则tan B的值是（）A. B. C. D.11、如图,O是正方形ABCD的对角线BD上一点,☉O与边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF折叠,折痕EF与☉O相切,此时点D恰好落在圆心O处.若DE=2,则正方形ABCD的边长是( )A.3B.4C.2+D.212、如图表示的是一个十字路口，O是两条公路的交点，点A、B、C、D表示的是公路上的四辆车，若OC=8cm，AC=17cm，AB=5cm，BD=10m，则C，D两辆车之间的距离为（）A.5mB.4mC.3mD.2m13、如图，在中，，，，则（）A. B. C. D.14、已知：在等腰梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，则梯形的面积是（）A.25B.50C.D.15、放学以后，小明和小强从学校分手，分别沿东南方向和西南方向回家，若小明和小强行走的速度都是40米/分，小明用15分钟到家，小强用20分钟到家，小明家和小强家的距离为（）A.600米B.800米C.1000米D.不能确定二、填空题(共10题，共计30分)16、如图，在平面直角坐标系中，长方形ABCO的边COOA分别在x轴，y轴上，点E在边BC上，将该长方形沿AE折叠，点B恰好落在边OC上的点F处，若OA=8，CF=4，则AE所在直线的表达式为________。

八年级上册数学单元测试卷-第三章勾股定理-苏科版(含答案)一、单选题(共15题，共计45分)1、如图是“赵爽弦图”，由个全等的直角三角形拼成，若大正方形的面积是13，小正方形的面积是1，设直角三角形较长直角边为a，较短直角边为．则a+b的值是（）A. B. C. D.2、如图，一根长5米的竹竿斜靠在竖直的墙上，这时为4米，若竹竿的顶端沿墙下滑2米至处，则竹竿底端外移的距离（）A.小于2米B.等于2米C.大于2米D.以上都不对3、如图，一棵高5米的树被强台风吹斜，与地面形成夹角，之后又被超强台风在点处吹断，点恰好落在边上的点处，若，则的长是（）A.2B.3C.D.4、如图，▱ABCD的对角线交于点，且AC：：3，那么AC的长为（）A. B. C.3 D.45、下列四组数据中，不能作为直角三角形三边长的是（）A.5，12，13B.1，2，3C.9，40，41D.3，4，56、如图，架在消防车上的云梯AB长为10m，∠ADB=90°,AD=2BD，云梯底部离地面的距离BC为2m，则云梯的顶端离地面的距离AE为( )A.(2 +2)mB.(4 +2)mC.(5 +2)mD.7m7、如图，直线，表示一条河的两岸，且∥现要在这条河上建一座桥（桥与河的两岸相互垂直），使得从村庄A经桥过河到村庄B的路程最短，应该选择路线（）A. B. C.D.8、如图，在中，，分别以点A和点B为圆心，大于的长为半径画弧，两弧相交于两点，作直线交于点D，连接，则的长为（）A. B. C. D.9、以下列各组线段为边，能构成直角三角形的是（）.A.1cm，2cm，3cmB. cm，cm，cmC.1cm，2cm，cmD.2cm，3cm，4cm10、如图，长方体的透明玻璃鱼缸，假设其长AD=80cm，高AB=60 cm，水深为AE=40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG=60 cm；一小虫想从鱼缸外的A 点沿壁爬进鱼缸内G处吃鱼饵，则小动物爬行的最短路线长为（）A.40 cmB.60 cmC.80 cmD.100 cm11、如图，点C是⊙O上一点，⊙O的半径为，D、E分别是弦AC、BC上一动点，且OD=OE= ，则AB的最大值为（）A. B. C. D.12、一透明的敞口正方体容器装有一些液体，棱始终在水平桌面上，容器底部的倾斜角为（，如图1所示）．如图1，液面刚好过棱，并与棱交于点，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．则此时的长为（）A. B. C. D.13、如图，⊙O的弦AB=6，M是AB上任意一点，且OM最小值为4，则⊙O的半径为（）A.5B.4C.3D.214、如图，已知菱形，，，E为中点，P为对角线上一点，则的最小值等于( )A. B. C. D.815、等边三角形的一边长为6cm，则以这边上高线为边长的正方形的面积为（）A.36cm 2B.27cm 2C.18cm 2D.12cm 2二、填空题(共10题，共计30分)16、一个三角形三边满足（a+b）2﹣c2=2ab，则这个三角形是________ 三角形．17、如图，在正方形ABCD中，E为AB边的中点，G，F分别为AD、BC边上的点．若AG=1，BF=2，∠GEF=90°，则GF的长为________．18、如图，和都是等腰直角三角形，若，，，则________.19、如图，正方形ABCD的边长为16，M在DC上，且DM=4，N是AC上的一动点，则DN+MN 的最小值是________．20、已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD=BE=6，则AC的长等于________ .21、观察下列勾股数第一组：3=2×1+1，4=2×1×（1+1），5=2×1×（1+1）+1第二组：5=2×2+1，12=2×2×（2+1），13=2×2×（2+1）+1第三组：7=2×3+1，24=2×3×（3+1），25=2×3×（3+1）+1第四组：9=2×4+1，40=2×4×（4+1），41=2×4×（4+1）+1…观察以上各组勾股数组成特点，第7组勾股数是________（只填数，不填等式）22、若直线向下平移个单位长度后与x轴的交点为点A，点B的坐标为，则线段的长为________．23、在平面直角坐标系中，已知点P的坐标是（3，4），则线段OP的长为________。

2020-2021学年八年级数学上册单元测试卷（苏科版）第三章《勾股定理》一．选择题（每题2分，共16分）1．如图，阴影部分是一个长方形，它的面积是（）A．3cm2B．4cm2C．5cm2D．6cm2【答案】C（cm），∴S阴影=5×1=5（cm2），故选C．2．在∴ABC中，∴A，∴B，∴C的对应边分别是a，b，c，若∴B＝90°，则下列等式中成立的是( ) A．a2＋b2＝c2B．b2＋c2＝a2C．a2＋c2＝b2D．c2－a2＝b2【答案】C【解析】∴在∴ABC中，∴A+∴C=90°，∴∴B=90°，∴∴ABC为直角三角形，则根据勾股定理得：a²+c²=b².故选C∆的周长为24，，且，则BC等于（）3.Rt ABCA．6B．8C．10D．12【答案】B【解析】设AB=5x，BC=3x，在Rt△ACB中，由勾股定理得：AC2=AB2-BC2，4x==直角三角形ABC的周长为：5x+4x+3x=24，x=2，所以，AC=2×4=8，故选B．4.如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点'C处，点B落在点'B处，其中，FC的长为（）则'A ．3B ．4C ．4．5D ．5【答案】D【解析】设'FC x =，则9FD x =-．∴6BC =，四边形ABCD 为矩形，点'C 为AD 的中点． ∴，在'Rt PC D 中，由勾股定理得222''FC FD C D =+，即()22293x x =-+，解得5x =．故选D ．5.以a ，b ，c 为边长，不能组成直角三角形的是( ) A ．a ＝6，b ＝8，c ＝10 B ．a ＝0.3，b ＝0.4，c ＝0.5 C ．a ＝8，b ＝15，c ＝17 D ．a ＝13，b ＝14，c ＝15【答案】D【解析】A 选项a ＝6,b ＝8,c ＝10,因为,所以A 选项中能组成直角三角形,B 选项a ＝0.3,b ＝0.4,c ＝0.5, 因为2220.30.40.5+=,所以B 选项中能组成直角三角形,C 选项 a ＝8,b ＝15,c ＝17, 因为,所以C 选项中能组成直角三角形,D 选项, a ＝13,b ＝14,c ＝15, 因为,所以D 选项中不能组成直角三角形,故选D. 6.如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD 的面积比是（ ） A ．3:4 B ．5:8 C ．9: 16 D ．1:2【答案】B 【解析】解：阴影部分面积为214413=166=102-⨯⨯⨯-，正方形ABCD 面积为16， ∴阴影部分面积与正方形ABCD 的面积比是10∴16=5∴8. 故选B7.将一根长24cm 的筷子，置于底面直径为5cm 、高为12cm 的圆柱形水杯中，设筷子露在杯子外面的长为cm h ，则h 的取值范围是（ ） A ．B ．C ．1112h ≤≤D ．【答案】C【解析】首先根据圆柱的高，知筷子在杯内的最小长度是12cm ，则在杯外的最大长度是24-12=12；再根据勾股定理求得筷子在杯内的最大长度是（如图）==13，则在杯外的最小长度是24-13=11cm ． 所以h 的取值范围是11≤h≤12．故选C8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边（x y >），下列四个说法：∴2249x y +=，∴2x y -=，∴2449xy +=，∴9x y +=. 其中说法正确的是( ) A ．∴∴ B ．∴∴∴C ．∴∴∴D ．∴∴∴∴【答案】B【解析】可设大正方形边长为a,小正方形边长为b ，所以据题意可得a 2=49,b 2=4; 根据直角三角形勾股定理得a 2=x 2+y 2,所以x 2+y 2=49，式∴正确； 因为是四个全等三角形，所以有x=y+2,所以x -y=2，式∴正确；根据三角形面积公式可得S ∴=xy/2,而大正方形的面积也等于四个三角形面积加上小正方形的面积，所以44492xy⨯+=，化简得2xy+4=49，式∴正确； 而据式∴和式∴得2x=11,x=5.5,y=3.5,将x,y 代入式∴或∴都不正确，因而式∴不正确． 综上所述，这一题的正确答案为B ． 二．填空题（每题2分，共20分）9．若一个直角三角形两边长为12和5，第三边为x ，则x 2=________． 【答案】169或119【解析】解：（1）若12是直角边，则第三边x 是斜边，由勾股定理，得122+52=x 2，所以x 2=169； （2）若12是斜边，则第三边x 为直角边，由勾股定理，得x 2=122-52，所以x 2=119； 故答案为:169或119．10.一直角三角形的斜边长比直角边长大2，另一直角边长为6，则斜边长为_____【解析】设一条直角边为a ，则斜边为a+2， ∴另一直角边长为6，∴222(2)6a a +=+，解得a=8， ∴a+2=8+2=10． 故答案为10．11.如图中阴影部分是一个正方形，如果正方形的面积为64厘米2，则x 的长为________厘米．【答案】17 【解析】解:正方形的面积为64,正方形的边长为:8,则x 的长为17=12.如图所示，∴ABC 为等边三角形，AD 为BC 边上的高，且AB ＝2，则正方形ADEF 的面积为________．【答案】3【解析】∴AD∴BC,∴AD 2+BD 2=AB 2,即=∴正方形ADEF 的面积为S=AD 2=3, 故答案为: 3．13.一根旗杆在离地面4.5 m 的地方折断，旗杆顶端落在离旗杆底部6 m 外，则旗杆折断前的高度是________． 【答案】12米【解析】解：如图所示，AC=6米，BC=4.5米，由勾股定理得，AB==7.5（米）． 故旗杆折断前高为：4.5+7.5=12（米）． 故答案为：12米．14.在∴ABC 中，∴C ＝90°，AB ＝5，则AB 2＋AC 2＋BC 2＝______．【解析】在Rt∴ABC 中，BC 2+AC 2=AB 2，∴AB=5，∴BC 2+AC 2=25，∴AB 2+AC 2+BC 2=2AB 2=2×52=2×25=50． 故答案为50．15.如图，在长方形纸片ABCD 中，12AB =，5BC =，点E 在AB 上，将DAE ∆沿DE 折叠，使点落在对角线BD 上的点处，则AE 的长为_______. 【答案】【解析】∴AB=12，BC=5，∴AD=5，，根据折叠可得：AD=A′D=5，∴A′B=13-5=8， 设AE=x ，则A′E=x ，BE=12-x ，在Rt∴A′EB 中：（12-x ）2=x 2+82，解得：x=， 故答案为：．16.如图,一圆柱高8cm ,底面圆半径为6πcm,一只蚂蚁从点爬到点B 处吃食，要爬行的最短路程是________cm ．【答案】10【解析】如下图所示：将圆柱的侧面展开，连接AB 即可得到爬行的最短路程.底面圆周长为62212C r cm πππ==⨯⨯=，底面半圆弧长为162C cm =，根据题意，展开得，根据勾股定理得， 故答案为：10．17.如图①，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图②，其中四边形ABCD 和四边形EFGH 都是正方形，△ABF 、△BCG 、△CDH 、△DAE 是四个全等的直角三角形．若EF =2，DE =8，则AB 的长为______．【答案】10．【解析】解：依题意知，BG=AF=DE=8∴EF=FG=2∴∴BF=BG∴BF=6∴∴直角∴ABF 中，利用勾股定理得：．故答案为10∴18.在直线上依次摆着七个正方形(如图)，已知斜放置的三个正方形的面积分别为1，2，3，正放置的四个正方形的面积是S1，S2，S3，S4，则S1＋S2-S3-S4＝_________．【答案】-2【解析】【分析】观察图形根据勾股定理的几何意义，边的平方的几何意义就是以该边为边的正方形的面积．【详解】解：由勾股定理的几何意义可知：S1+S2=1，S3+S4=3，故S1＋S2-S3-S4＝（S1＋S2）-（S3+S4）＝1-3=-2，故答案为-2三．解答题(共64分)19.（8分）如图，已知CD＝3，AD=4，BC＝12，AB=13，∴ADC=90°，试求阴影部分的面积.【答案】24【解析】解：由勾股定理可知，又∴AC2+BC2=52+122=132=AB2，∴∴ABC是直角三角形故所求面积=S∴ABC-S∴ACD=12×5×12-12×3×4=30-6=24.20.(本题8分）如图，在∴ABC中，AB＝AC＝5，BC＝6，M为BC的中点，MN∴AC于点N，求MN的长．【答案】MN＝2.4.【解析】解:连接AM,∴AB＝AC,M为BC的中点,∴AM∴BC,CM＝BC＝3.由勾股定理得AM 2＝AC 2－CM 2＝52－32＝16, ∴AM ＝4. ∴MN∴AC,∴S ∴ACM ＝CM·AM ＝AC·MN, 即3×4＝5MN, ∴MN ＝2.4.21.(本题8分）如图，长7.5m 的梯子靠在墙上，梯子的底部离墙的底端4.5m. （1）求梯子的顶端到地面的距离；（2）由于地面有水，梯子底部向右滑动1.5m ，则梯子顶端向下滑多少米？【答案】（1）6m ；（2）1.5m. 【解析】 （1）如图，在Rt ABC ∆中，,∴7.5, 4.5,AB m BC m ==∴6AC m ==.答：梯子的顶端到地面的距离为6m .（2）如图，，6CF m ∴=，∴ 4.5EC m =，∴ 1.5AE m =.答：梯子顶端向下滑1.5米.22.(本题10分）如图，方格纸中的每个小正方形的边长均为1，点，B 在小正方形的顶点上，在图中画ABC ∆（点C 在小正方形的顶点上），使ABC ∆为直角三角形，并说明理由.（要求画出两个，且两个三角形不全等）【答案】ABC ∆为直角三角形，理由详见解析. 【解析】 解：如图所示.图1 图2 如图1，在ABC ∆中，5AC =，3BC=，2223534AB =+=因为， 所以，即ABC ∆为直角三角形. 如图2，在Rt ACD ∆中， .在Rt BCE ∆中，.在Rt ABF ∆中，222223534AB AF BF =+=+=. 所以，所以，即ABC ∆为直角三角形.23.(本题10分）课间，小明拿着老师的等腰三角板玩，不小心掉到两墙之间，如图． （1）求证：∴ADC∴∴CEB ；（2）从三角板的刻度可知AC=25cm ，请你帮小明求出砌墙砖块的厚度a 的大小（每块砖的厚度相等）．【答案】（1）证明见解析；（2）5cm ．【解析】（1）根据题意得：AC=BC ，∴ACB=90°，AD∴DE ，BE∴DE ， ∴∴ADC=∴CEB=90°，∴∴ACD+∴BCE=90°，∴ACD+∴DAC=90°，∴∴BCE=∴DAC，在∴ADC和∴CEB中，，∴∴ADC∴∴CEB（AAS）；（2）由题意得：AD=4a，BE=3a，由（1）得：∴ADC∴∴CEB，∴DC=BE=3a，在Rt∴ACD中：AD2+CD2=AC2，∴（4a）2+（3a）2=252，∴a＞0，解得a=5，答：砌墙砖块的厚度a为5cm．24.(本题10分）已知∴ABC中，AB=20，AC=15，BC边上的高为12，求∴ABC的面积．【答案】150或42．【解析】作AD∴BC于D，则AD为BC边上的高，AD=12．分两种情况：∴高AD在三角形内，如图1所示：在Rt∴ADC中，由勾股定理得：AC2=AD2+DC2，∴DC=9．在Rt∴ADB中，由勾股定理得：AB2=AD2+BD2，∴BD=16，∴BC=BD+DC=16+9=25，∴S∴ABC=12×25×12=150；∴高AD在三角形外，如图2所示：在Rt∴ADC中，由勾股定理得：AC2=AD2+DC2∴DC=9．在Rt∴ADB中，由勾股定理得：AB2=AD2+BD2，∴BD=16，∴BC=BD﹣DC=16﹣9=7，∴S∴ABC=12×7×12=42．故答案为150或42．25.(本题10分）勾股定理神秘而美妙，探索方法多样、巧妙，各有不同，其中的面积法给了小聪灵感，他惊喜地发现，当两个全等的直角三角形如图1或如图2摆放时，都可以用面积法来说明.下面是小聪利用图1说明勾股定理的过程：如图1，其中90DAB ∠=︒，试说明222+=a b c .解：连接CD ，DB ，过点D 作BC 边上的高DF ，则. 因为21122ACD ABC ADCB S S S b ab ∆∆=+=+四边形， 又因为()21122ADB DCB ADCB S S S c a b a ∆∆=+=+-四边形， 所以.所以222+=a b c .请参照上述方法，利用图2说明勾股定理.【答案】详见解析【解析】证明：连结BD ，BE,过点B 作DE 边上的高BF ，可得BF=b−a ，∴S ACBED 五边形=SACB+SABE+SADE=2111222ab b ab ++， 又∴S ACBED 五边形=S ACB +S ABD +S BDE =12ab+12c+12a(b−a)，∴12ab+12b+12ab=12ab+12c+12a(b−a)， ∴a+b=c。

《第3章勾股定理》一、填空题1．如图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是米．2．直角三角形一条直角边与斜边分别为4cm和5cm，则斜边上的高等于cm．3．如图，在直角三角形ABC中，∠C=90°，AC=12，BC=5，则以AB为直径的半圆的面积为．4．如图，在四边形ABCD中，∠A=90°，AB=4，AD=3，CD=12，BC=13，则四边形ABCD的面积为．5．木工师傅要做一个长方形桌面，做好后量得长为80cm，宽为60cm，对角线为100cm，则这个桌面（填“合格”或“不合格”）．6．甲、乙两人同时从同一地点出发，甲往东走了8km，乙往南走了6km，这时两人相距km．7．如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．8．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=a，则图中阴影部分的面积为．9．如图，在Rt△ABC中，∠BCA=90°，点D是BC上一点，AD=BD，若AB=8，BD=5，则CD= ．10．动手操作：在矩形纸片ABCD中，AB=3，AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为．二、选择题11．下列长度的线段中，可以构成直角三角形的是（）A．13，16，19 B．17，21，21 C．18，24，26 D．12，35，3712．下列命题中是假命题的是（）A．△ABC中，若∠B=∠C﹣∠A，则△ABC是直角三角形B．△ABC中，若a2=（b+c）（b﹣c），则△ABC是直角三角形C．△ABC中，若∠A：∠B：∠C=3：4：5，则△ABC是直角三角形D．△ABC中，若a：b：c=5：4：3，则△ABC是直角三角形13．一直角三角形的三边分别为2、3、x，那么以x为边长的正方形的面积为（）A．13 B．5 C．13或5 D．414．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（）A．13 B．26 C．47 D．9415．在Rt△ABC中，∠C=90°，AC=3，BC=4，则AB边上的高是（）A．2 B．2.4 C．3 D．3.416．已知一直角三角形的木版，三边的平方和为1800cm2，则斜边长为（）A．80cm B．30cm C．90cm D．120cm17．底面周长为12，高为8的圆柱体上有一只小蚂蚁要从A点爬到B点，则蚂蚁爬行的最短距离是（）A．10 B．8 C．5 D．418．如图，已知矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=8，AB=4，则DE的长为（）A．3 B．4 C．5 D．619．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．∠ADC=30°，AD=3，BD=5，则CD的长为（）A． B．4 C． D．4.520．如图，设正方体ABCD﹣A1B1C1D1的棱长为1，黑、白两个甲壳虫同时从A点出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA1→A1D1→…，白甲壳虫爬行的路线是AB→BB1→…，并且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（）A．0 B．1 C．D．三、解答题21．如图，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9．（1）求DC的长．（2）求AB的长．22．观察下列各式，你有什么发现？32=4+5，52=12+13，72=24+25，92=40+41，…这到底是巧合，还是有什么规律蕴涵其中呢？请你结合有关知识进行研究．若132=a+b，则a，b的值可能是多少？23．如图，一轮船以16n mi1e/h的速度从港口A出发向东北方向航行，另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行，那么离开港口A2h后，两船相距多远？24．如图是用硬纸板做成的四个全等的直角三角形，两直角边长分别是a，b，斜边长为c和一个边长为c的正方形，请你将它们拼成一个能证明勾股定理的图形．（1）画出拼成的这个图形的示意图．（2）证明勾股定理．25．如图所示，A、B两村在河岸CD的同侧，A、B两村到河岸的距离分别为AC=1km，BD=3km，又CD=3km，现要在河岸CD上建一水厂向A、B两村输送自来水，铺设水管的工程费用为每千米20000元，请你在CD上选择水厂的位置O，使铺设水管的费用最省，并求出铺设水管的总费用．26．如图，公路MN与公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否受到噪音影响？说明理由；如果受影响，且知拖拉机的速度为18km/h，那么学校受影响的时间是多少秒？《第3章勾股定理》（江苏省南京市高淳县）参考答案与试题解析一、填空题1．如图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是8 米．【考点】勾股定理的应用．【专题】压轴题．【分析】由题意得，在直角三角形中，知道了两直角边，运用勾股定理直接解答即可求出斜边．【解答】解：∵AC=4米，BC=3米，∠ACB=90°，∴折断的部分长为=5，∴折断前高度为5+3=8（米）．【点评】此题主要考查学生对勾股定理在实际生活中的运用能力．2．直角三角形一条直角边与斜边分别为4cm和5cm，则斜边上的高等于cm．【考点】勾股定理．【分析】首先利用勾股定理得出AC的长，再利用三角形面积公式求出即可．【解答】解：设CD是直角三角形斜边上的高，∵直角三角形一条直角边与斜边分别为4cm和5cm，设BC=4cm，AB=5cm，∴AC=3cm，∴CD×AB=AC×BC，∴DC==（cm）．故答案为：．【点评】此题主要考查了勾股定理以及三角形面积公式应用，熟练应用三角形面积公式是解题关键．3．如图，在直角三角形ABC中，∠C=90°，AC=12，BC=5，则以AB为直径的半圆的面积为π．【考点】勾股定理．【分析】利用勾股定理列式求出AB，再根据圆的面积公式列式计算即可得解．【解答】解：∵∠C=90°，AC=12，BC=5，∴AB===13，∴以AB为直径的半圆的面积=π（）2=π（）2=π．故答案为：π．【点评】本题考查了勾股定理，圆的面积公式，熟记定理与公式是解题的关键，要注意AB是半圆的直径，而非半径．4．如图，在四边形ABCD中，∠A=90°，AB=4，AD=3，CD=12，BC=13，则四边形ABCD的面积为36 ．【考点】勾股定理的逆定理；勾股定理．【分析】连接BD，知四边形的面积是△ADB和△BCD的面积和，由已知得其符合勾股定理的逆定理从而得到△BCD是一个直角三角形．则四边形面积可求．【解答】解：连接BD，则有BD===5，∵52+122=132，即BD 2+CD 2=BC 2，∴△BCD 为直角三角形，∴四边形的面积=S △ADB +S △BCD =AD •AB+BD •CD=×3×4+×5×12=36．【点评】本题利用了勾股定理和它的逆定理及直角三角形的面积公式求解．隐含了整体的数学思想和正确运算的能力．5．木工师傅要做一个长方形桌面，做好后量得长为80cm ，宽为60cm ，对角线为100cm ，则这个桌面 合格 （填“合格”或“不合格”）．【考点】矩形的判定；勾股定理的应用．【分析】只要算出桌面的长与宽的平方和是否等于对角线的平方，如果相等可得长、宽、对角线构成的是直角三角形，由此可得到每个角都是直角，根据矩形的判定：有三个角是直角的四边形是矩形，可得此桌面合格．【解答】解：∵802+602=10000=1002，即：AD 2+DC 2=AC 2，∴∠D=90°，同理：∠B=∠BCD=90°，∴四边形ABCD是矩形，∴这个桌面合格．故答案为：合格．【点评】本题考查的是勾股定理逆定理在实际中的应用，以及矩形的判定，关键是熟练掌握勾股定理逆定理与矩形的判定方法；勾股定理逆定理：在一个三角形中，两条边的平方和等于另一条边的平方，那么这个三角形就是直角三角形；矩形的判定方法：①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形．6．甲、乙两人同时从同一地点出发，甲往东走了8km，乙往南走了6km，这时两人相距10 km．【考点】勾股定理的应用．【分析】因为甲向东走，乙向南走，刚好构成一个直角．两人走的距离分别是两直角边，则根据勾股定理可求得斜边即两人的距离．【解答】解：如图，∵∠AOB=90°，OA=6km，OB=8km，∴AB==10（km）．故答案为：10．【点评】本题考查了勾股定理的基本运用，把方向运动构建成一个沿三角形两边的运动，再由勾股定理进行计算求解．7．如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了 4 步路（假设2步为1米），却踩伤了花草．【考点】勾股定理的应用．【专题】应用题．【分析】本题关键是求出路长，即三角形的斜边长．求两直角边的和与斜边的差．【解答】解：根据勾股定理可得斜边长是=5m．则少走的距离是3+4﹣5=2m，∵2步为1米，∴少走了4步，故答案为：4．【点评】本题就是一个简单的勾股定理的应用问题．8．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=a，则图中阴影部分的面积为a2．【考点】勾股定理．，再利用等腰直角三角【分析】根据勾股定理可得AC2+BC2=AB2，然后判断出阴影部分的面积=2S△ABE形的面积等于直角边的平方的一半计算即可得解．【解答】解：∵△ABC是直角三角形，∴AC2+BC2=AB2，∵三个阴影部分三角形都是等腰直角三角形，=2וa•（a）=a2．∴阴影部分的面积=2S△ABE故答案为： a2．【点评】本题考查了勾股定理，等腰直角三角形的性质，熟记定理与等腰直角三角形的面积的求法是解题的关键．9．如图，在Rt△ABC中，∠BCA=90°，点D是BC上一点，AD=BD，若AB=8，BD=5，则CD= 1.4 ．【考点】勾股定理．【分析】设CD=x，在Rt△ACD和Rt△ABC中，利用勾股定理列式表示出AC2，然后解方程即可．【解答】解：设CD=x，则BC=5+x，在Rt△ACD中，AC2=AD2﹣CD2=25﹣x2，在Rt△ABC中，AC2=AB2﹣BC2=64﹣（5+x）2，所以，25﹣x2=64﹣（5+x）2，解得x=1.4，即CD=1.4．故答案为：1.4．【点评】本题考查了勾股定理，熟记定理并在两个三角形列出等式表示出AC2，然后列出方程是解题的关键．10．动手操作：在矩形纸片ABCD中，AB=3，AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 2 ．【考点】翻折变换（折叠问题）．【分析】本题关键在于找到两个极端，即BA′取最大或最小值时，点P或Q的位置．经实验不难发现，分别求出点P与B重合时，BA′取最大值3和当点Q与D重合时，BA′的最小值1．所以可求点A′在BC边上移动的最大距离为2．【解答】解：当点P与B重合时，BA′取最大值是3，当点Q与D重合时（如图），由勾股定理得A′C=4，此时BA′取最小值为1．则点A′在BC边上移动的最大距离为3﹣1=2．故答案为：2【点评】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．二、选择题11．下列长度的线段中，可以构成直角三角形的是（）A．13，16，19 B．17，21，21 C．18，24，26 D．12，35，37【考点】勾股定理的逆定理．【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果有这种关系，这个就是直角三角形．【解答】解：A、∵132+162≠192，∴该三角形不符合勾股定理的逆定理，故不是直角三角形，故错误；B、∵172+212≠212，∴该三角形不符合勾股定理的逆定理，故不是直角三角形，故错误；C、∵182+242≠262，∴该三角形不符合勾股定理的逆定理，故不是直角三角形，故错误；D、∵122+352=372，∴该三角形符合勾股定理的逆定理，故是直角三角形，故正确；故选D．【点评】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．12．下列命题中是假命题的是（）A．△ABC中，若∠B=∠C﹣∠A，则△ABC是直角三角形B．△ABC中，若a2=（b+c）（b﹣c），则△ABC是直角三角形C．△ABC中，若∠A：∠B：∠C=3：4：5，则△ABC是直角三角形D．△ABC中，若a：b：c=5：4：3，则△ABC是直角三角形【考点】勾股定理的逆定理；三角形内角和定理；命题与定理．【分析】有一个角是直角的三角形是直角三角形，两边的平方和等于第三边的平方的三角形是直角三角形．【解答】解：A、∠B+∠A=∠C，所以∠C=90°，所以△ABC是直角三角形，故本选项不符合题意．B、若a2=（b+c）（b﹣c），所以a2+c2=b2，所以△ABC是直角三角形，故本选项不符合题意．C、若∠A：∠B：∠C=3：4：5，最大角为75°，故本选项符合题意．D、若a：b：c=5：4：3，则△ABC是直角三角形，故本选不项符合题意．故选C．【点评】本题考查直角三角形的概念，和勾股定理的应用．13．一直角三角形的三边分别为2、3、x，那么以x为边长的正方形的面积为（）A．13 B．5 C．13或5 D．4【考点】勾股定理．【分析】以x为边长的正方形的面积即为x2．此题应考虑两种情况：2和3都是直角边或3是斜边，熟练运用勾股定理进行计算．【解答】解：当2和3都是直角边时，则x2=4+9=13；当3是斜边时，则x 2=9﹣4=5．故选C ．【点评】此类题在没有明确直角边或斜边的时候，一定要注意分情况考虑，熟练运用勾股定理进行计算．14．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A ，B ，C ，D 的边长分别是3，5，2，3，则最大正方形E 的面积是（ ）A ．13B ．26C ．47D ．94【考点】勾股定理．【专题】数形结合．【分析】根据正方形的面积公式，结合勾股定理，能够导出正方形A ，B ，C ，D 的面积和即为最大正方形的面积．【解答】解：根据勾股定理的几何意义，可得A 、B 的面积和为S 1，C 、D 的面积和为S 2，S 1+S 2=S 3，于是S 3=S 1+S 2，即S 3=9+25+4+9=47．故选：C．【点评】能够发现正方形A，B，C，D的边长正好是两个直角三角形的四条直角边，根据勾股定理最终能够证明正方形A，B，C，D的面积和即是最大正方形的面积．15．在Rt△ABC中，∠C=90°，AC=3，BC=4，则AB边上的高是（）A．2 B．2.4 C．3 D．3.4【考点】勾股定理；三角形的角平分线、中线和高；三角形的面积．【专题】计算题．【分析】先根据勾股定理可求得AB，再根据面积公式可得出AB边上的高．【解答】解：∵∠C=90°，AC=3，BC=4，∴AB===5，∵AC•BC=AB•AB边上的高，∴AB边上的高===2.4．故选B．【点评】本题考查了勾股定理，三角形的面积，是基础知识要熟练掌握．16．已知一直角三角形的木版，三边的平方和为1800cm2，则斜边长为（）A．80cm B．30cm C．90cm D．120cm【考点】勾股定理．【分析】设此直角三角形的斜边是c，根据勾股定理及已知不难求得斜边的长．【解答】解：设此直角三角形的斜边是c，根据勾股定理知，两条直角边的平方和等于斜边的平方．所以三边的平方和即2c2=1800，c=±30（负值舍去），取c=30．故选B．【点评】熟练运用勾股定理进行计算，从而求出斜边的长．17．底面周长为12，高为8的圆柱体上有一只小蚂蚁要从A点爬到B点，则蚂蚁爬行的最短距离是（）A．10 B．8 C．5 D．4【考点】平面展开-最短路径问题．【分析】将圆柱的侧面展开，得到一个长方体，再然后利用两点之间线段最短解答．【解答】解：如图所示：由于圆柱体的底面周长为12cm，则BC=12×=6cm．又因为AC=8cm，所以AB==10cm．故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是10cm．故选A．【点评】此题趣味性强，有利于培养同学们的学习兴趣，将圆柱的侧面展开，构造出直角三角形是解题的关键．18．如图，已知矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=8，AB=4，则DE的长为（）A．3 B．4 C．5 D．6【考点】翻折变换（折叠问题）；勾股定理；矩形的性质．【分析】根据折叠前后角相等可知△ABE≌△C′ED，利用勾股定理可求出．【解答】解：设DE=x，则AE=8﹣x，AB=4，在直角三角形ABE中，x2=（8﹣x）2+16，解之得，x=5．故选C．【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．19．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．∠ADC=30°，AD=3，BD=5，则CD的长为（）A． B．4 C． D．4.5【考点】等边三角形的判定与性质；全等三角形的判定与性质；勾股定理．【分析】首先以CD为边作等边△CDE，连接AE，利用全等三角形的判定得出△BCD≌△ACE，进而求出DE的长即可．【解答】解：如图，以CD为边作等边△CDE，连接AE．∵∠BCD=∠BCA+∠ACD=∠DCE+∠ACD=∠ACE，∴在△BCD和△ACE中，，∴△BCD≌△ACE（SAS），∴BD=AE．又∵∠ADC=30°，∴∠ADE=90°．在Rt△ADE中，AE=5，AD=3，于是DE=，∴CD=DE=4．故选：B．【点评】此题主要考查了等边三角形的性质以及全等三角形的判定与性质，根据已知得出∠ADE=90°是解题关键．20．如图，设正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，黑、白两个甲壳虫同时从A 点出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA 1→A 1D 1→…，白甲壳虫爬行的路线是AB →BB 1→…，并且都遵循如下规则：所爬行的第n+2与第n 条棱所在的直线必须是既不平行也不相交（其中n 是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（ ）A ．0B ．1C ．D ．【考点】勾股定理的应用．【分析】先确定黑、白两个甲壳虫各爬行完第2013条棱分别停止的点，再根据停止点确定它们之间的距离．【解答】解：根据题意可知黑甲壳虫爬行一圈的路线是AA 1→A 1D 1→D 1C 1→C 1C →CB →BA ，回到起点． 乙甲壳虫爬行一圈的路线是AB →BB 1→B 1C 1→C 1D 1→D 1A 1→A 1A ．因此可以判断两个甲壳虫爬行一圈都是6条棱，因为2013÷6=335…3，所以黑、白两个甲壳虫各爬行完第2013条棱分别停止的点都是C，所以它1们之间的距离是0．故选A．【点评】此题是一道趣味性题目，不仅考查了阅读理解能力，还考查了勾股定理在空间的应用，综合性较强．三、解答题21．如图，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9．（1）求DC的长．（2）求AB的长．【考点】勾股定理．【分析】（1）由题意可知三角形CDB是直角三角形，利用已知数据和勾股定理直接可求出DC的长；（2）有（1）的数据和勾股定理求出AD的长，进而求出AB的长．【解答】解：（1）∵CD⊥AB于D，且BC=15，BD=9，AC=20∴∠CDA=∠CDB=90°在Rt△CDB中，CD2+BD2=CB2，∴CD2+92=152∴CD=12；（2）在Rt△CDA中，CD2+AD2=AC2∴122+AD2=202∴AD=16，∴AB=AD+BD=16+9=25．【点评】本题考查了勾股定理，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．22．观察下列各式，你有什么发现？32=4+5，52=12+13，72=24+25，92=40+41，…这到底是巧合，还是有什么规律蕴涵其中呢？请你结合有关知识进行研究．若132=a+b，则a，b的值可能是多少？【考点】规律型：数字的变化类；勾股数．【分析】观察三个数之间的关系可得出规律：第n组数为（2n+1）2，（），（）由此规律解决问题．【解答】解：题目蕴含的规律为：（2n+1）2=+；∵13=2×6+1，∴132=+=84+85，∴a=84，b=85．【点评】本题考查了数字的规律变化，解答本题的关键是仔细观察所给式子，得出规律，解决问题．23．如图，一轮船以16n mi1e/h的速度从港口A出发向东北方向航行，另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行，那么离开港口A2h后，两船相距多远？【考点】勾股定理的应用．【分析】首先根据方向角得出∠BAC=90°，再利用勾股定理得出BC的长．【解答】解：∵一轮船以16n mi1e/h的速度从港口A出发向东北方向航行，另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行，∴∠BAC=90°，离开港口A2h后，AB=32n mi1e，AC=24n mi1e，∴BC==40（n mi1e）．答：离开港口A2h后，两船相距40n mi1e．【点评】此题主要考查了勾股定理的应用以及方向角问题，得出AB，AC的长是解题关键．24．如图是用硬纸板做成的四个全等的直角三角形，两直角边长分别是a，b，斜边长为c和一个边长为c的正方形，请你将它们拼成一个能证明勾股定理的图形．（1）画出拼成的这个图形的示意图．（2）证明勾股定理．【考点】勾股定理的证明．【专题】作图题；证明题．【分析】勾股定理的证明可以通过图形的面积之间的关系来完成．【解答】解法一：（1）如图；（2）证明：∵大正方形的面积表示为（a+b）2大正方形的面积也可表示为c2+4×ab ∴（a+b）2=c2+4×ab，a2+b2+2ab=c2+2ab∴a2+b2=c2即直角三角形两直角边的平方和等于斜边的平方．解法二：（1）如图（2）证明：∵大正方形的面积表示为：c2又可以表示为： ab×4+（b﹣a）2∴c2=ab×4+（b﹣a）2，c2=2ab+b2﹣2ab+a2，∴c2=a2+b2即直角三角形两直角边的平方和等于斜边的平方．【点评】利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．25．如图所示，A、B两村在河岸CD的同侧，A、B两村到河岸的距离分别为AC=1km，BD=3km，又CD=3km，现要在河岸CD上建一水厂向A、B两村输送自来水，铺设水管的工程费用为每千米20000元，请你在CD上选择水厂的位置O，使铺设水管的费用最省，并求出铺设水管的总费用．【考点】作图—应用与设计作图；轴对称-最短路线问题．【专题】作图题．【分析】作出点B关于CD的对称点B′，连接AB′交CD于点O，连接BO，根据对称性可知，在点O处建水厂，铺设水管最短，所需费用最低．【解答】解：如图所示，点O就是建水厂的位置，∵AC=1km，BD=3km，CD=3km，∴AE=AC+CE=AC+DB′=AC+BD=1+3=4km，B′E=CD=3km，AB′===5km，铺设水管长度为：AO+OB=AO+OB′=AB′=5km，∵铺设水管的工程费用为每千米20 000元，∴铺设水管的总费用为：5×20 000=100 000元．故答案为：100 000元．【点评】本题考查了应用与设计作图，主要利用轴对称的性质，找出点B关于CD的对称点是确定建水厂位置O的关键．26．如图，公路MN与公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否受到噪音影响？说明理由；如果受影响，且知拖拉机的速度为18km/h，那么学校受影响的时间是多少秒？【考点】直线与圆的位置关系．【专题】计算题．【分析】作AH⊥MN于H，根据含30度的直角三角形三边的关系得到AH=PA=80m，由于这个距离小于100m，所以可判断拖拉机在公路MN上沿PN方向行驶时，学校受到噪音影响；然后以点A为圆心，100m为半径作⊙A交MN于B、C，根据垂径定理得到BH=CH，再根据勾股定理计算出BH=60m，则BC=2BH=120m，然后根据速度公式计算出拖拉机在线段BC上行驶所需要的时间．【解答】解：学校受到噪音影响．理由如下：作AH⊥MN于H，如图，∵PA=160m，∠QPN=30°，∴AH=PA=80m，而80m＜100m，∴拖拉机在公路MN上沿PN方向行驶时，学校受到噪音影响，以点A为圆心，100m为半径作⊙A交MN于B、C，如图，∵AH⊥BC，∴BH=CH，在Rt△ABH中，AB=100m，AH=80m，BH==60m，∴BC=2BH=120m，∵拖拉机的速度=18km/h=5m/s，∴拖拉机在线段BC上行驶所需要的时间==24（秒），∴学校受影响的时间为24秒．【点评】本题考查了直线与圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d，直线l 和⊙O相交⇔d＜r；直线l和⊙O相切⇔d=r；当直线l和⊙O相离⇔d＞r．也考查了垂径定理、勾股定理以及含30度的直角三角形三边的关系．。

第3章《勾股定理》单元测试（含答案）第3章《勾股定理》单元测试（满分100分时间90分钟）⼀、单选题（共8题；共24分）1.要登上某建筑物，靠墙有⼀架梯⼦，底端离建筑物3m，顶端离地⾯4m，则梯⼦的长度为（）A.2mB.3mC.4mD.5m2.若直⾓三⾓形的两边长分别为a，b，且满⾜a2-6a+9+|b﹣4|=0，则该直⾓三⾓形的第三边长为（）A.5B.7C.4D.5或73.在△ABC中，AB=15，AC=13，⾼AD=12，则△ABC的周长为（）A．42 B．32 C．42或32D．37或334.⼀直⾓三⾓形两边分别为3和5，则第三边为（）A、4B、C、4或D、25.两只⼩鼹⿏在地下从同⼀处开始打洞，⼀只朝北⾯挖，每分钟挖8cm，另⼀只朝东⾯挖，每分钟挖6cm，10分钟之后两只⼩鼹⿏相距（）A.100cmB.50cmC.140cmD.80cm6.如图，阴影部分是⼀个长⽅形，它的⾯积是（）A、3cm2B、4cm2C、5cm2D、6cm27. 已知，如图长⽅形ABCD中，AB=3cm，AD=9cm，将此长⽅形折叠，使点B 与点D重合，折痕为EF，则△ABE的⾯积为（）A．3cm2B．4cm2C．6cm2D．12cm28.如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC、BC为直径作半圆，⾯积分别记为S1、S2，则S1+S2等于________．A.3πB.2πC.6πD.4π⼆、填空题(每题3分，共30分)9. 如果三⾓形三边长分别为3，4，5，那么最长边上的中线长为.10.若⼀个三⾓形的三边长之⽐为5：12：13，且周长为60 cm，则它的⾯积为cm2.11.⼀根旗杆在离底部4.5⽶的地⽅折断，旗杆顶端落在离旗杆底部6⽶处，则旗杆折断前⾼为______12.如图中阴影部分是⼀个正⽅形，如果正⽅形的⾯积为64厘⽶2，则x的长为___厘⽶．13.⼀个直⾓三⾓形，两直⾓边长分别为3和2，则三⾓形的周长为________．14.在RT△ABC中，∠ACB=90°，且c+a=9,c-a=4，则b=。

勾股定理单元测试卷一、选择题（每题2分，共10分）1. 勾股定理适用于哪种三角形？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 任意三角形2. 勾股定理中的两个直角边的平方和等于斜边的平方，斜边被称为：A. 勾B. 股C. 斜边D. 高3. 在直角三角形中，若直角边的长度分别为3和4，则斜边的长度是：A. 5B. 6C. 7D. 84. 勾股定理的发现者是谁？A. 毕达哥拉斯B. 欧几里得C. 阿基米德D. 哥白尼A. a² + b² = c²B. c² = a² + b²C. a² b² = c²D. c² a² = b²二、填空题（每题2分，共10分）6. 勾股定理的公式是：__________。

7. 在直角三角形中，若直角边的长度分别为5和12，则斜边的长度是__________。

8. 勾股定理在中国被称为__________。

9. 勾股定理的发现时间大约在公元前__________年。

10. 勾股定理的发现者毕达哥拉斯是__________国人。

三、解答题（每题5分，共20分）11. 已知直角三角形的两个直角边长度分别为8和15，求斜边的长度。

12. 在直角三角形中，若斜边的长度为17，且一个直角边的长度为8，求另一个直角边的长度。

13. 勾股定理的证明方法有很多种，请简述其中一种证明方法。

14. 请举例说明勾股定理在实际生活中的应用。

答案部分一、选择题答案1. B2. C3. A4. A5. C二、填空题答案6. a² + b² = c²7. 138. 勾三股四弦五9. 50010. 希腊三、解答题答案11. 斜边长度为17。

12. 另一个直角边的长度为15。

13. 勾股定理的证明方法有很多种，其中一种是通过面积证明。

将直角三角形分为两个小直角三角形和一个矩形，分别计算它们的面积，然后通过面积关系推导出勾股定理。

第三章《勾股定理》复习卷（满分：100分时间：90分钟）一、选择题(每题2分，共20分)1．有六根细木棒，它们的长度分别是2，4，6，8，10，12 (单位：cm)．若从中取出三根，首尾顺次连接搭成一个直角三角形，则这三根木棒的长度分别为( )A．2，4，8 B．4，8，10 C．6，8，10 D．8，10，12 2．将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形( ) A．可能是锐角三角形B．不可能是直角三角形C．仍然是直角三角形D．可能是钝角三角形3．在△ABC中，已知AB=17，AC=10．若BC边上的高AD=8，则边BC的长为( ) A．21 B．15 C．6或9 D．9或21 4．一个直角三角形的斜边长比其中一条直角边的长大2，若另一条直角边的长为6，则斜边长为( )A．4 B．8 C．10 D．12 5．如图，一架云梯长25 m，斜靠在一面墙上，梯子底端离墙7 m．如果梯子的顶端下滑4 m，那么梯子的底部在水平方向上滑动了( )A．4 m B．6 m C．8 m D．10 m 6．如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D，E为BC边上的两点，且∠DAE=45°，连接EF，BF，下列结论不正确的是( )A．△AED≌△AEF B．B E＋DC=DEC．B E＋DC>DE D．BE2+DC2=DE27．如图，用4个全等的直角三角形与1个小正方形镶嵌成正方形图案，已知大正方形的面积为49，小正方形的面积为4．若分别用x，y表示直角三角形的两条直角边(x>y)，给出下列四个结论：①x2＋y2=49；②x－y=2；③2x y＋4=49；④x＋y=9．其中正确的结论是( )A．①②B．①②③C．①②④D．①②③④8．如图，在矩形ABCD中，AB=5，BC=7，点E为BC上一动点，把△ABE沿AE折叠．当点B的对应点B'落在∠ADC的角平分线上时，则点B'到BC的距离为( )A．1或2 B．2或3 C．3或4 D．4或5 9．如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）A ．B ．C ．D ．10．如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S 1、S 2、S 3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S 4、S 5、S 6．其中S 1=16，S 2=45，S 5=11，S 6=14，则S 3+S 4=（ ）A ．86B ．64C ．54D ．48二、填空题 (每题2分，共20分)11．一个三角形的两边长分别是3和5，若要使这个三角形成为直角三角形，则第三边边长的平方是 ．12．若等腰三角形的腰长为5，一腰上的高为3，则这个等腰三角形底边长的平方为 ．13．如果△ABC 的三边长a ，b ，c 满足关系式 (a ＋2b －60)2＋18b -＋30c -=0，那么△ABC 的形状是 ．14．所谓的勾股数就是使等式a 2＋b 2=c 2成立的任何三个正整数．我国清代数学家罗士林钻研出一种求勾股数的方法，对于任意正整数m ，n (m >n )，取a =m 2－n 2，b =2mn ，c =m 2＋n 2，则a ，b ，c 就是一组勾股数．请你结合这种方法，写出85 (三个数中最大)，84和 组成一组勾股数．15．如图，在四边形ABCD 中，AB=20，BC=15，CD=7，AD=24，∠B =90°，则∠A ＋∠C= °．16．如图，在Rt △ABC 中，∠C=90°，AC=6 cm ．，BC=8 cm ，如果按图中所示的方法将△ACD 沿AD 折叠，使点C 落在AB 边上的C'点，那么△BDC'的面积是 ．17．如图，每个小方格都是边长为1的正方形，点A ，B 是方格纸的两个格点 (即正方形的顶点)．在这个6×6的方格纸中，找出格点C ，使△ABC 的面积为1个平方单位的直角三角形的个数是 .18．如图，已知AB=12，AB ⊥BC ，AB ⊥AD ，垂足分别为点B ，A ，AD =5，BC =10．若点E是CD的中点，则AE的长是．19．如图，有一个三级台阶，它的每一级的长、宽和高分别为20，3，2，A和B是这个台阶的两个相对的端点．若A点有一只蚂蚁想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是．20．如图，长为12 cm的弹性皮筋拉直放置在一轴上，固定两端A和B，然后把中点C 向上拉升8 cm至D点，则弹性皮筋被拉长了cm．三、解答题(共60分)21．(本题6分) 如图，已知在△ABC中，CD⊥AB，垂足为点D，AC=20，BC=15，DB=9．(1) 求CD的长；(2) 求AB的长．22．(本题6分) 如图，每个小正方形的边长都为1，△ABC的顶点都在格点上．(1) 判断△ABC是什么形状，并说明理由．(2) 求△ABC的面积．23．(本题6分) 印度数学家什迦逻(1141年—1225年) 曾提出过“荷花问题”：“平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边，渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅?”请用学过的数学知识回答这个问题．24．(本题8分) 如图，∠AOB=90°，OA=9 cm，OB=3 cm，一机器人在点B处看见一个小球从点A 出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿BC方向匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?25．(本题6分) 如图，在直角三角形纸片ABC中，∠C=90°，AC=6，BC=8，折叠△ABC的一角，使点B与点A重合，展开得折痕DE，求BD的长．26．(本题8分) 如图，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AB=21，AD=9，求AC的长．27．(本题10分) 如图，P是等边三角形ABC内的一点，连接P A，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连接CQ．(1) 观察并猜想AP与CQ之间的大小关系，并证明你的结论；(2) 若P A：PB：PC=3：4：5，连接PQ，试判断△PQC的形状，并说明理由．28．(本题10分) 在△ABC中，BC=a，AC=b，AB=c，设c为最长的边．当a2＋b2=c2时，△ABC是直角三角形；当a2＋b2≠c2时，利用代数式a2＋b2和c2的大小关系，探究△ABC的形状(按角分类)．(1) 当△ABC的三边长分别为6，8，9时，△ABC为三角形；当△ABC的三边长分别为6，8，11时，△ABC为三角形．(2) 猜想：当a2＋b2c2时，△ABC为锐角三角形；当a2＋b2c2时，△ABC为钝角三角形．(3) 当a=2，b=4时，判断△ABC的形状，并求出对应的c2的取值范围．参考答案一、选择题1．C 2．C 3．D 4．C 5．C 6．B 7．B 8．A [提示：过点B'作B'M ⊥AD ，垂足为点M ，∵ 点B'在∠ADC 的角平分线上，∴ ∠ADB'=45°，∴ B'M=DM ．设B'M=DM=x ，∵ B'M 2+AM 2=AB' 2，∴ x 2+(7－x )2=25，解得x = 3或x = 4，即B'M = 3或4 ，∴ 点B'到BC 的距离为1或2]9．D 10．A二、填空题11．16或34 12．10或90 13．直角三角形 14．13 15．180 16．6 cm 2 17．6 18．132 19．25 20．8 (提示：∵AC=CB = 6cm ，DC = 8cm ，D C ⊥AB ，∴DB = DA = 10 cm ，∴拉长的长度为D A ＋DB －AB = 10c m ＋10cm －12cm = 8cm)三、解答题21．(1) ∵ CD ⊥AB ，∴ CD 2＋BD 2=BC 2，∴ CD 2=BC 2－BD 2=152－92=122，∴ CD =12(2) ∵ CD ⊥AB ，∴ CD 2＋AD 2=AC 2，∴ AD 2=AC 2－CD 2=202－122=l62，∴ AD =16，∴ AB=AD ＋DB =16＋9=2522．(1) △ABC 是直角三角形．理由如下：∵ AC 2=12＋82=65，AB 2=22＋32=13，BC 2=42＋62=52，∴ AC 2=AB 2＋BC 2．∴ △ABC 是直角三角形，且∠ABC=90° (2) S=12×AB ×BC=12=13 23．设湖水的深为x 尺，则红莲总长为 (x ＋0．5) 尺，根据勾股定理得x 2＋22=(x ＋0．5)2，解得x=3．75，即湖水深3．75尺24．∵ 小球滚动的速度与机器人行走的速度相等，运动时间相等，∴ BC=CA ．设AC为x ，则OC =9－x ，由勾股定理得OB 2＋OC 2=BC 2．又∵ OA=9，OB=3，∴ 32＋(9－x )2=x 2，解得x =5，∴ 机器人行走的路程BC 是5 cm25．由题意知AD=BD ，设BD =x ，则AD =x ，CD =8－x ，在Rt △ACD 中，由AC 2＋CD 2－AD 2，得62＋(8－x )2=x 2，解得x =254．即BD 的长为25426．在AB 上截取AE=AD ，连接EC ．∵ AC 平分∠BAD ，∴ ∠DAC=∠BAC ，∴ △ADC≌△AEC ，∴ AE=AD =9，CE=CD=10=BC ．作CF ⊥AB ，垂足为点F ，∴ EF=FB=12BE =12(AB －AE )=6．在Rt △BFC (或Rt △EFC ) 中，由勾股定理得CF =8，在Rt △AFC 中，由勾股定理得AC =17，∴ AC 的长为1727．(1) 猜想：AP=CQ ．证明：∵ ∠ABP ＋∠PBC =60°，∠QBC ＋∠PBC=60°，∴ ∠ABP =∠QBC ．又∵ AB=BC ，BP=BQ ，∴ △ABP ≌△CBQ ，∴ AP=CQ (2) 由P A ：PB ：PC =3：4：5，可设P A =3a ，PB =4a ，PC =5a ．连接PQ ，在△PBQ 中，PB=BQ =4a ，且∠PBQ =60°，∴ △PBQ 为正三角形，∴ PQ =4a ．在△PQC 中，∵ PQ 2＋QC 2=16a 2＋9a 2=25a 2=PC 2，∴ △PQC 是直角三角形28．(1) 锐角 钝角 (2) ＞ ＜ (3) ∵ c 为最长的边，2＋4=6，∴ 4≤c ＜6，a 2＋b 2=22＋42=20．①a 2＋b 2＞c 2，即c 2＜20，∴ 当l6≤c 2＜20时，这个三角形是锐角三角形；②a 2＋b 2=c 2，即c 2=20，∴ 当c 2=20时，这个三角形是直角三角形；③a 2+ b 2＜c 2，即c 2 ＞20，∴ 当20＜c 2＜36时，这个三角形是钝角三角形。

第三章勾股定理数学八年级上册-单元测试卷-苏科版(含答案)一、单选题(共15题，共计45分)1、若直角三角形两条直角边的边长分别为6和8，则斜边上的高是（）A.5B.10C.D.2、如图点A，B，C在正方形网格中的格点上，每个小正方形的边长为1，则下列关于△ABC边长的说法，正确的是( )A.AB，BC长均为有理数，AC长为无理数B.AC长是有理数，AB，BC长均为无理数C.AB长是有理数，4C，BC长均为无理数D.三边长均为无理数3、在△ABC中，AC=6，AB=8，BC=10，则（）A.∠A=90°B.∠B=90°C.∠C=90°D.△ABC不是直角三角形4、如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（）A.5B.10C.10D.155、下列各组线段中，不能够组成直角三角形的是（）A.6，8，10B.3，4，5C.4，5，6D.5，12，136、如图，菱形ABCD的周长为8m，高AE的长为cm，则对角线BD的长为（）A.2cmB.3cmC. cmD.2 cm7、以下列各组数为边长能组成直角三角形的是( )A.4，5，6B.2，3，4C.11，12，13D.8，15，178、已知如图，中，，，D为线段上一点，将线段绕点A逆时针旋转得到线段，F为中点，直线交射线于点G.下列说法：①若连接，则；②；③；④若，则.其中正确的有（）A.1个B.2个C.3个D.4个9、△ABC中，∠BAC=60°，AD⊥BC于D，且AD= ，E、F、G分别为边BC、CA、AB上的点，则△EFG周长的最小值为（）A. B.2 C.3 D.310、以长度分别为下列各组数的线段为边，其中能构成直角三角形的是（）A. B. C. D.11、如图，在平行四边形ABCD中，AD＝BD＝5，AB＝6，E为AB的中点，F为CD上一点，连接EF交BD于点G，若S△FDG：S△EDG＝2：3，则EF的长是（）A. B.2 C.2 D.512、如图，在□ABCD中，对角线AC，BD交于点O，∠BAC=90°，E为AB的中点，若AE=3，AO=4，则AD的长为（）A.10B.12C.D.13、一个矩形按如图1的方式分割成三个直角三角形，最小三角形的面积为S1，把较大两个三角形纸片按图2方式放置，图2中的阴影部分面积为S2，若S2＝2S1，则矩形的长宽之比（）A.2B.C.D.14、小红同学经常要测量学校旗杆的高度，她发现旗杆的绳子刚好垂到地面上，当她把绳子下端拉开5m后，发现这时绳子的下端正好距地面1m，学校旗杆的高度是（）A.21mB.13mC.10mD.8m15、如图，在Rt△ABC中，∠BAC=90°，D，E分别是AB，BC的中点，F在CA延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（）A.16B.20C.18D.22二、填空题(共10题，共计30分)16、已知中，是边上一点，DE∥BC交于点E，将沿翻折得到，若是直角三角形，则长为________.17、如图，将一块等腰直角三角尺的锐角顶点放在以为直径的半圆上，的两边分别交半圆于，两点，若，则的长是________.18、点P（-3，-4）到原点的距离为________ .19、如图所示，中，，，，E为斜边上一点，连接，若，则线段的长为________．20、如图，四边形ABCD中，∠B＝∠D＝90°，∠C＝50°，在BC、CD边上分别找到点M、N，当△AMN周长最小时，∠AMN＋∠ANM的度数为________.21、如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是________22、如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；②若点M（﹣2，y1）、点N（，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为.其中正确判断的序号是________.23、在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为，此时正方形EFGH的面积为5．问：当格点弦图中的正方形ABCD的边长为时，正方形EFGH的面积的所有可能值是________（不包括5）．24、如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N．若AD=2，则MN=________．25、在直线l上依次摆放着七个正方形（如图）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1， S2， S3， S4，则S1+S4=________．三、解答题(共5题，共计25分)26、如图，方格纸上每个小正方形的面积为1．⑴在方格纸上，以线段AB为边画正方形ABCD，并计算所画正方形ABCD的面积．⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A2B2C2D2，正方形的各个顶点都在方格纸的格点上．27、在Rt△ABC中，∠C=90°，AD平分∠CAB，CD=6，AB=10．求△ABD的面积．28、如图，修公路遇到一座山，于是要修一条隧道，为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过点C作直线AB的垂线l，过点B作一直线（在山的旁边经过），与l相交于D点，经测量∠ABD=135°，BD=800m，求直线l上距离D点多远的C处开挖？（≈1.414，精确到1米）29、如图，从高8米的电杆AC的顶部A处，向地面的固定点B处拉一根铁丝，若B点距电杆底部的距离为6米.现在准备一根长为9.9米长的铁丝，够用吗？请你说明理由.30、如图，草原上，一牧童在A处放马，牧童家在B处，A、B处距河岸的距离AC，BD的长分别为500m和700m，且CD=500m，天黑前牧童从A点将马牵到河边去饮水后，再赶回家，牧童将马牵到河边什么地方饮水，才能使走过的路程最短？牧童最少要走多少m？参考答案一、单选题(共15题，共计45分)1、D2、B3、A4、B5、C6、D7、D8、C10、D11、B12、A13、A14、B15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、28、29、。