天津市宝坻区林亭口高级中学2017届高三9月月考数学(理)试题

天津林亭口高级中学高三数学文月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1.参考答案：C2. 在正方体ABCD-A1B1C1D1中，E为棱AB上一点，且，以E为球心，线段EC的长为半径的球与棱A1D1，DD1分别交于F，G两点，则△AFG的面积为（）A．B． C. D．4参考答案：D3. 已知向量，，，则k（A）-12 （B）-6 （C）6 （D）12参考答案：D本题考查了向量数量积的坐标运算，属于基础知识的考查，难度较小。

，，故，选D。

4. 某城市收集并整理了该市2017年1月份至10月份各月最低气温与最髙气温(单元：)的数据，绘制了如图的折线图. 已知该市的各月最低气温与最高气温具有较好的线性关系，则根据该折线图,下列结论错误的是（）A.最低气温与最高气温为正相关B.10月的最高气温不低于5月的最高气温C.月温差(最高气温减最低气温)的最大值出现在1月D.最低气温低于的月份有4个参考答案：D5. 设是等差数列的前项和，若，则＝( )A.1B.－1C. 2D.参考答案：A6. 函数的定义域为（）A． B． C． D．参考答案：D试题分析：函数有意义等价于，所以定义域为，故选D.考点：函数的定义域.7. 已知函数的零点分别为，则的大小关系是A． B． C． D．不能确定参考答案：A8. 化简三角式（）A .B .1C .2D .参考答案：B9. 某校为了解本校高三学生学习心里状态，采用系统抽样方法从800人中抽取40人参加某种测试，为此将题目随机编号，分组后再第一组采用简单随机抽样的方法抽到号码为18，抽到的40人中，编号落入区间的人做试卷，编号落入区间的人做试卷,其余的人做试卷，则做试卷的人数为A.10B.12C.18D.28参考答案：B【知识点】抽样方法. I1解析：设抽到的学生的编号构成数列，则，由得，，19到40有12个整数，故选 B.【思路点拨】根据系统抽样的定义求解.10. 若等边△ABC的边长为3，平面内一点M满足，则的值为（）A．2 B．C．D．﹣2参考答案：A 【考点】平面向量数量积的运算．【分析】利用向量的坐标运算和数乘运算、数量积运算即可得出．【解答】解：如图所示，A（，0），B（0，），C（﹣，0），∴=（，），=（3，0），∴=（，）+（3，0）=（2，），∴=+=（，），∴=﹣=（﹣1，），=﹣=（﹣，），∴=﹣1×（﹣）+×=2，故选：A．二、填空题:本大题共7小题,每小题4分,共28分11. 如果实数x，y满足条件，若z=的最小值小于0，则实数a的取值范围是．参考答案：a＞【考点】简单线性规划．【专题】数形结合；转化法；不等式．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，建立条件关系进行求解即可．【解答】解：作出不等式组对应的平面区域如图：则a大于C点的横坐标，则z=的几何意义是区域内的点到定点（0，﹣1）的斜率，则OA的斜率最小，由得，即A（a，2﹣2a），∵z=的最小值小于0，∴此时=＜0，得a＞或a＜0（舍），故答案为：a＞．【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合是解决本题的关键．12. 定义某种运算,运算原理如右框图所示,则式子的值为_________.参考答案：13 13. 执行右面的程序框图，若输入的的值为1，则输出的的值为.参考答案：314. 若实数x，y满足条件，则的最大值为参考答案：115. 将高三（1）班参加体检的36名学生，编号为：1，2，3，…，36，若采用系统抽样的方法抽取一个容量为4的样本，已知样本中含有编号为6号、24号、33号的学生，则样本中剩余一名学生的编号是．参考答案：15【考点】系统抽样方法．【专题】计算题；整体思想；定义法；概率与统计．【分析】根据系统抽样的定义，求出样本间隔即可．【解答】解：样本间距为36÷4=9，则另外一个编号为6+9=15，故答案为：15．【点评】本题主要考查系统抽样的应用，求出样本间隔是解决本题的关键．16. 已知实数x，y满足，则的最大值是__________．参考答案：8【分析】画出约束条件的可行域，求出三角形的顶点坐标，根据的几何意义，求出最值取得的点，代入目标函数求解即可．【详解】由约束条件可知可行域为图中阴影部分所示：其中，，又，可知的几何意义为可行域中的点到直线距离的倍可行域中点到直线距离最大的点为本题正确结果：【点睛】本题考查利用线性规划求解最值的问题，关键是能够明确目标函数所表示的几何意义，利用数形结合来进行求解．17. 球为棱长为的正方体的内切球，为球的球面上动点，为中点，,则点的轨迹周长为．参考答案：三、解答题：本大题共5小题，共72分。

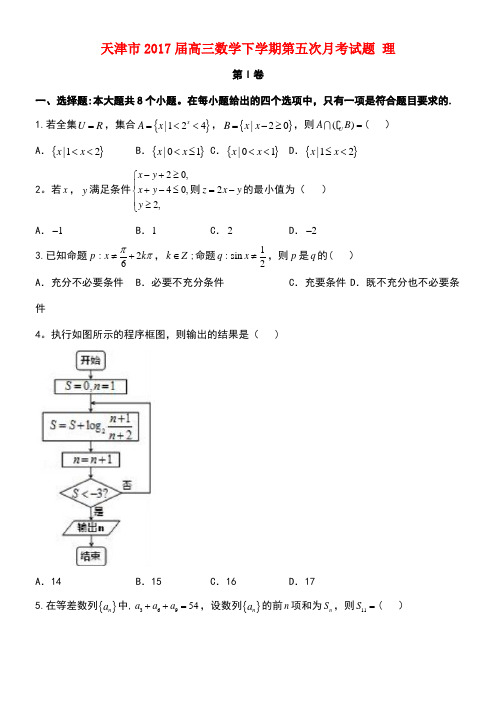
天津市2017届高三数学下学期第五次月考试题 理第Ⅰ卷一、选择题:本大题共8个小题。

在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若全集U R =，集合{}|124x A x =<<，{}|20B x x =-≥，则()U A B =( ） A ．{}|12x x <<B ．{}|01x x <≤C ．{}|01x x <<D ．{}|12x x ≤<2。

若x ，y 满足条件20,40,2,x y x y y -+≥⎧⎪+-≤⎨⎪≥⎩则2z x y =-的最小值为（ ）A ．1-B ．1C ．2D ．2-3.已知命题p :26xk ππ≠+，k Z ∈;命题q :1sin 2x ≠，则p 是q 的( ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件4。

执行如图所示的程序框图，则输出的结果是（ )A ．14B ．15C ．16D ．175.在等差数列{}n a 中,36954a a a ++=，设数列{}n a 的前n 项和为n S ，则11S =( ）A ．18B ．99C ．198D ．2976。

已知双曲线22221x y a b -=（0a >,0b >）的左右焦点分别为1(,0)F c -，2(,0)F c ,以线段12F F 为直径的圆与双曲线在第二象限的交点为P ,若直线2PF 与圆E ：222()216c b x y -+=相切，则双曲线的渐近线方程是( )A ．y x =±B ．y =C ．y =D ．2y x =±7.设函数321()33f x x x x =+-，若方程2|()||()|10f x t f x ++=有12个不同的根，则实数t 的取值范围为（ ） A ．10(,2)3-- B ．(,2)-∞- C ．34215t -<<- D ．(1,2)- 8。

天津市宝坻区林亭口镇2017届高三数学下学期第一次月考试题文本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分.考试时间120分钟．祝各位考生考试顺利！第I卷（选择题，共40分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上。

一、选择题(本题共8个小题，每小题5分，共40分）1.已知复数z满足11zi=+(i为虚数单位)，则z=（）A．12i-B．12i+C．1i-D．1i+2。

已知直线l：y kx b=+，曲线C：22(1)1x y+-=,则“1b=”是“直线l与曲线C有公共点"的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件3。

若ππ23sinlog,3log,552.0===cba，则( ）A．b c a>> B。

b a c>> C.a b c>> D．c a b>>4.执行如图所示的程序框图，输出的S值为8,则判断条件是（ )A．2k< B．4<k C．3<k D．3≤k5。

点P为ABC∆边AB上任一点，则使ABCPBCSS∆∆≤31的概率是( ）A。

31B.32C。

95D.946. 函数()sin(2)3f x x π=+的图象向左平移ϕ（0ϕ>）个单位后关于原点对称,则ϕ的最小值为（ ) A ．56π B ．3π C ．4π D ．6π 7。

已知12,F F 分别为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,过1F 的直线l 与双曲线C 的左右两支分别交于,A B 两点,若22::4:3:5AB BF AF =，则双曲线的离心率为( ）A ．13B ．15C ．2D ．58.在等腰梯形ABCD 中，已知AB ∥DC ，AC 与BD 交于点M ，AB=2CD=4．若AC •BD=–1,则cos ∠BMC（ )1811713121.D C B A 二。

天津市高三上学期数学9月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题；共8分)1. （2分）甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，，分别表示甲、乙两名运动员这项测试成绩的平均数，，分别表示甲、乙两名运动员这项测试成绩的标准差，则有（）A .B .C .D .2. （2分）函数，则f（x）－g（x）是（）A . 奇函数B . 偶函数C . 既不是奇函数又不是偶函数D . 既是奇函数又是偶函数3. （2分） (2016高二上·重庆期中) 已知F1 ， F2是椭圆和双曲线的公共焦点，P是它们的一个公共点．且∠F1PF2= ，则椭圆和双曲线的离心率的倒数之和的最大值为（）A .B .C . 3D . 24. （2分） (2019高一上·长春期中) 函数与函数的图象关于（）A . 直线对称B . 点对称C . 原点对称D . 轴对称二、填空题 (共11题；共11分)5. （1分） (2019高一上·温州期中) 已知集合，，若，则________.6. （1分）(2019·丽水月考) 已知为虚数单位，复数，且复数满足，则________； ________.7. （1分） (2017高二下·济南期末) 不等式x2﹣3x+2≤0成立的充要条件是________．8. （1分） (2017高二下·溧水期末) 若tan（α﹣）= ．则tanα=________．9. （1分） (2017高二下·姚安期中) 已知变量x，y满足约束条件则z=2x+y的最大值为________．10. （1分） 2004年元月9日，第十届全国运动会筹备委员会正式成立，由二名主任和6名副主任组成主席团成员．若章程规定：表决一项决议必须在二名主任都同意，且副主任同意的人数超过半数才能通过．一次主席团全体成员表决一项决议，结果有6人同意，则决议通过的概率是________ （结果用分数表示）．11. （1分）如图所示，在三棱锥S﹣ABC中，SA⊥SB，SB⊥SC，SC⊥SA，且SA，SB，SC和底面ABC所成的角分别为α1 ，α2 ，α3 ，△SBC，△SAC，△SAB的面积分别为S1 ， S2 ， S3 ，类比三角形中的正弦定理，给出空间图形的一个猜想是________．12. （1分）椭圆x2+4y2=16被直线y= x+1截得的弦长为________．13. （1分）(2020·晋城模拟) 对于等差数列和等比数列，我国古代很早就有研究成果，北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”，就是关于高阶等差级数求和的问题.现有一货物堆，从上向下查，第一层有2个货物，第二层比第一层多3个，第三层比第二层多4个，以此类推，记第层货物的个数为，则数列的通项公式 ________，数列的前项和 ________.14. （1分）(2020·普陀模拟) 设是边长为的正六边形的边上的任意一点，长度为的线段是该正六边形外接圆的一条动弦，则的取值范围为________.15. （1分） (2019高一上·仁寿期中) 已知函数为R上的奇函数，当时，，则的解集为________.三、解答题 (共6题；共61分)16. （1分） (2017高二下·河北期中) 在（x﹣）6的展开式中，x2的系数为________．17. （10分）如图，三棱柱ABC﹣A1B1C1是直棱柱，AB⊥AC，AB=AC=AA1=2，点M，N分别是A1B和A1C的中点．（1）求证：直线MN∥面ABC（2）求三棱锥B﹣ACM的体积．18. （10分） (2017高一上·大庆月考) 已知函数，设上的最大值为（1）求的表达式；（2）是否存在实数，使得的定义域为，值域为？若存在，求出的值；若不存在，说明理由.19. （15分） (2019高一上·杭州期中) 已知函数．（1）已知f（x）的图象关于原点对称，求实数的值；（2）若，已知常数满足：对任意恒成立，求实数的取值范围．20. （10分） (2018高三上·三明期末) 已知是椭圆（）的左顶点，左焦点是线段的中点，抛物线的准线恰好过点．（1）求椭圆的方程；（2）如图所示，过点作斜率为的直线交椭圆于点，交轴于点，若为线段的中点，过作与直线垂直的直线，证明对于任意的（），直线过定点，并求出此定点坐标．21. （15分） (2019高二上·辽宁月考) 已知数列的前项和为，且（1）求数列的通项公式；（2）若数列满足，求数列的通项公式；（3）在（）的条件下，设，问是否存在实数使得数列是单调递增数列？若存在，求出的取值范围；若不存在，请说明理由.参考答案一、单选题 (共4题；共8分)1-1、2-1、3-1、4-1、二、填空题 (共11题；共11分)5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共6题；共61分) 16-1、17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、21-3、。

天津市宝坻区林亭口高级中学2017届高三数学上学期第二次质量检测试题理注意事项： 1．答题前填写好自己的姓名、班级、考号等信息；2．试卷共20小题，将选择题答案填涂在小答题卡上、主观题写在答题纸上；3. 本试卷共2页,考试结束后试卷保存好，只交答题卡和答题纸.祝同学们考试顺利！一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中， 只有一项是最符合题目要求的.）1、已知全集{}8,7,6,5,4,3,2,1=U ，集合{}6,5,3,2=A ,集合{}7,6,4,3,1=B ， 则集合=B C A U ( )A.{}5,2B.{}6,3C.{}6,5,2D.{}8,6,5,3,22、命题2,1:≥≥y x p ，命题3:≥+y x q ，则命题p 是命题q 的（ ）A.充分不必要条件B.必要不充分条件C.充分必要条件D.即不充分也不必要条件3、设2log ,2,3.03.03.02===c b a ，则（ ）A.a ＜b ＜cB.b ＜c ＜aC.a ＜c ＜bD.c ＜a ＜b4、函数x x x f 2)2ln()(--=的零点所在的一个大致区间是（ ）A.)2,1(B.)3,2(C.)4,3(D.)5,4(5、在ABC ∆中，内角C B A ,,的对边分别是c b a ,,，若C A ac c b sin 32sin ,322==-, 则角B 等于（ ）A.060B.030C.0150D.0120 6、函数)65(log )(22+-=x x x f 的单调递减区间是（ ）A.),25(+∞B.),3(+∞C.)25,(-∞D.)2,(-∞7、设函数()sin()(0,0)2f x x πωϕωϕ=+><<的部分图象，如图所示，直线6x π=是它的一条对称轴，则函数()f x 的解析式为( )A ．()sin()3f x x π=+B ．()sin(2)6f x x π=- C ．()sin(4)3f x x π=+D ．()sin(2)6f x x π=+ 8、已知()f x 是定义在R 上的奇函数，且0x >时，2()23f x x x =--，若方程()f x a =有两个根，则实数a 的取值范围是( )A.[-4,4]B.[)(]{}3,00,34,4-- C.[]{}3,34,4-- D.()4,4-二、填空题（本大题共6个小题，每题5分，共30分，将答案的最简形式填写在横线上）9、已知R b a ∈,,i 是虚数单位.若bi i i a =++)1)((，则=+bi a10、若31tan =α，21)tan(=+βα，则=βtan 11、曲线2x y =与直线x y =所围城的封闭图形的面积为12、函数2)(1+=-x a x f （a ＞0且1≠a ）的图像恒过定点A ，呢么曲线423+-=x x y 在点A 处的切线的倾斜角为13、在平行四边形ABCD 中，2=AD ，060=∠BAD ，E 为CD 的中点，若1=⋅BE AC ,则边长AB 为14、设)(x f 是定义在R 上的偶函数，且)2()2(x f x f -=+，当[]0,2-∈x 时， 122)(-⎪⎪⎭⎫ ⎝⎛=xx f ，若在区间)6,2(-内，函数a x x f y a (),2(log )(+-=＞0，且1≠a )恰有1个零点，则实属a 的取值范围是三、解答题（本大题共6个小题，共80分，写出必要的文字说明或解题步骤）15、（本小题满分13分）已知向量)21,2(cos -=x ，)cos ,2sin 3(x x=，R x ∈,设函数x f ⋅=)(.（1）求函数)(x f 的单调递减区间；（2）求)(x f 在区间⎥⎦⎤⎢⎣⎡2,0π上的最大值及取得最大值时x 的值.16、（本小题满分13分）已知函数x x x f ln )(⋅=.（1）求函数)(x f 的单调性.（2）对于任意的正实数x ，不等式)(x f >21-kx 恒成立，求实数k 的取值范围.17、（本小题满分13分）已知函数.,1)4(cos 22cos 3)(2R x x x x f ∈--+=π（1）求)(x f 的最小正周期；（2）求)(x f 在区间⎥⎦⎤⎢⎣⎡-2,3ππ上的最大值和最小值.18、（本小题满分13分）等差数列{}n a 的前n 项和为n S ，公差d ＞0，且满足22,1175243=+=⋅a a a a .（1）求数列的通向n a ；（2）若数列{}n b 满足c n Sb n n +=，是否存在非零实数c ，使得{}n b 为等差数列？若存在，求出c 的值；若不存在，请说明理由.19、（本小题满分14分） 已知函数2()2ln(1)()f x x a x a R =+-∈，试求：（1）当2-=a 时,求函数)(x f 的单调区间和极值；（2）若()f x 在[)1,1-上是单调函数,求实数a 的取值范围；20、（本小题满分14分）已知函数x x f ln )(=，bx ax x f x g ++=2)()(,函数)(x g 的图像在点))1(,1(g 处的切 线平行于x 轴.（1）确定a 与b 的关系式；（2）当a ≠0时，讨论函数)(x g 的单调性.林亭口高中2016-2017学年第二次质量调查高三数学（理） 参考答案 （2016年10月）注意事项： 1．答题前填写好自己的姓名、班级、考号等信息；2．试卷共20小题，将选择题答案填涂在小答题卡上、主观题写在答题纸上；3. 本试卷共2页,考试结束后试卷保存好，只交答题卡和答题纸. 一、1--4： A A D C 5--8： B D D B二、9、 i 21+10、 7111、 6112、 4π13、 314、 ()()4,11,0三、15、（1）)6sin()(π-=x x f递减区间：.,235,232Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ（2）最大值为23，此时.2π=x16、（1）单调递增区间：⎪⎭⎫ ⎝⎛+∞,1e ；单调递减区间：⎪⎭⎫⎝⎛e 1,0.（2）2ln 1- k .17、（1）)32sin(2)(π+=x x f ， 最小正周期π=T .（2）最大值：2； 最小值：3-.18、（1）34-=n a n ；（2）存在；21-=c .19、（1）单调递增区间：()1,-∞-； 单调递减区间：()1,1-； 极小值是：2ln 41-；无极大值.（2）若单增：2-≤a ； 若单减：41≥a .20、（1）12-=+b a ；（2）0 a 时，单增：()1,0；单减：()+∞,1； 210 a 时，单增：()⎪⎭⎫ ⎝⎛+∞,21,1,0a ； 单减：⎪⎭⎫⎝⎛a 21,1；21=a 时，单增：()+∞,0，无减区间； 21 a 时，单增：()+∞⎪⎭⎫ ⎝⎛,1,21,0a ； 单减：⎪⎭⎫⎝⎛1,21a .。

2016-2017学年天津市宝坻区林亭口高中高三（下）第一次月考数学试卷（理科）一、选择题：（每小题5分，共40分）1．（5分）已知集合M＝{x∈R||x|＞2}，N＝{x∈R|x2﹣4x+3＜0}，则集合（∁R M）∩N等于（）A．{x|x＜2}B．{x|﹣2≤x≤2}C．{x|﹣2≤x＜1}D．{x|1＜x≤2} 2．（5分）下列四个命题中正确命题的个数是①“函数y＝sin2x的最小正周期为”为真命题；②∃x∈R，e x≤0；③“若，则tan a＝1”的逆否命题是“若tan a≠l，则”；④“∃x∈R，x＞1”的否定是“∀x∈R，x＞1”．（）A．0B．1C．2D．33．（5分）运行如图所示的程序框图，则输出的结果是（）A．B．C．D．04．（5分）在△ABC中，AB＝3，AC＝5，BC＝2，则△ABC的面积为（）A．B．C．6D．125．（5分）如图是一个几何体的三视图，根据图中数据，可得该几何体的体积是（）A．9πB．C．D．6．（5分）已知实数x，y满足则z＝2x+4y的最大值是（）A．﹣4B．2C．6D．87．（5分）如图，椭圆的左、右焦点为F1，F2，上顶点为A，点P为第一象限内椭圆上的一点，若点A到PF1的距离是点F2到PF1距离的2倍，则直线PF1的斜率为（）A．B．C．D．8．（5分）已知f（x）是定义在R上的奇函数，且x＞0时，f（x）＝x2﹣2x﹣3，若方程f （x）＝a有两个根，则实数a的取值范围是（）A．[﹣4，4]B．[﹣3，0）∪（0，3]∪{﹣4，4}C．[﹣3，3]∪{﹣4，4}D．（﹣4，4）二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上，9．（5分）已知i是虚数单位，若复数，则m＝．10．（5分）在的二项展开式中，x2的系数为．11．（5分）如图所示，在边长为1的正方形f（x）中任取一点f（x），则点[﹣1，1）恰好取自阴影部分的概率为．12．（5分）已知双曲线﹣＝1的右焦点与抛物线y2＝12x的焦点重合，求该双曲线的焦点到其渐近线的距离．13．（5分）若直线x﹣y+t＝0被曲线（θ为参数）截得的弦长为，则实数t的值为．14．（5分）在△ABC中，已知AB＝AC＝3，BC＝4，P为BC边上的动点，则的值为．三、解答题：（本大题共6小题，共80分）15．（13分）已知函数f（x）＝cos x sin（x+）﹣cos2x+，x∈R（1）求f（x）的最小正周期及单调减区间；（2）求f（x）在闭区间，上的最大值和最小值．16．（13分）某市A、B两所中学的学生组队参加辩论赛，A中学推荐了3名男生、2名女生，B中学推荐了3名男生、4名女生，两校所推荐的学生一起参加集训．由于集训后队员水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队．（Ⅰ）求A中学至少有1名学生入选代表队的概率；（Ⅱ）某场比赛前，从代表队的6名队员中随机抽取4人参赛，设X表示参赛的男生人数，求X的分布列和数学期望．17．（13分）如图，底面为直角梯形的四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面ABCD，E为A1B1的中点，且△ABE为等腰直角三角形，AB∥CD，AB⊥BC，AB＝2CD＝2BC．（Ⅰ）求证：AB⊥DE；（Ⅱ）求直线EC与平面ABE所成角的正弦值；（Ⅲ）线段EA上是否存在点F，使EC∥平面FBD？若存在，求出；若不存在，说明理由．18．（13分）已知数列{a n}的前n项和为S n满足：（a为常数，且a≠0，a≠1）（1）若a＝2，求数列{a n}的通项公式（2）设，若数列{b n}为等比数列，求a的值．（3）在满足条件（2）的情形下，设，数列{c n}前n项和为T n，求证．19．（14分）设椭圆的中心在坐标原点，对称轴是坐标轴，一个顶点为A（0，2），右焦点F 到点的距离为2．（I）求椭圆的方程；（Ⅱ）设经过点（0，﹣3）的直线l与椭圆相交于不同两点M，N满足，试求直线l的方程．20．（14分）已知函数f（x）＝x2+2aln（1﹣x）（a∈R），试求：（1）当a＝﹣2时，求函数f（x）的单调区间和极值；（2）若f（x）在[﹣1，1）上是单调函数，求实数a的取值范围．2016-2017学年天津市宝坻区林亭口高中高三（下）第一次月考数学试卷（理科）参考答案与试题解析一、选择题：（每小题5分，共40分）1．（5分）已知集合M＝{x∈R||x|＞2}，N＝{x∈R|x2﹣4x+3＜0}，则集合（∁R M）∩N等于（）A．{x|x＜2}B．{x|﹣2≤x≤2}C．{x|﹣2≤x＜1}D．{x|1＜x≤2}【解答】解：由M中的不等式解得：x＞2或x＜﹣2，即M＝{x|x＞2或x＜﹣2}，∴∁R M＝{x|﹣2≤x≤2}，由N中的不等式变形得：（x﹣1）（x﹣3）＜0，解得：1＜x＜3，即N＝{x|1＜x＜3}，则（∁R M）∩N＝{x|1＜x≤2}．故选：D．2．（5分）下列四个命题中正确命题的个数是①“函数y＝sin2x的最小正周期为”为真命题；②∃x∈R，e x≤0；③“若，则tan a＝1”的逆否命题是“若tan a≠l，则”；④“∃x∈R，x＞1”的否定是“∀x∈R，x＞1”．（）A．0B．1C．2D．3【解答】解：对于①，函数y＝sin2x的最小正周期是T＝π，∴命题①错误；对于②，∀x∈R，e x＞0是真命题，∴该命题的否定是假命题，∴命题②错误；对于③，根据“若p，则q”的逆否命题是“若￢q，则￢p”判定命题③正确；对于④，“∃x∈R，x＞1”的否定是“∀x∈R，x≤1”，∴命题④错误．∴正确的命题的序号是③；故选：B．3．（5分）运行如图所示的程序框图，则输出的结果是（）A．B．C．D．0【解答】解：由程序框图知：本程序是计算S＝sin+sin+sinπ+…+sin+sin的值，∵y＝sin x的周期是2π，∴sin+sin+sinπ+sin+sin+sin2π＝+0﹣+0＝0，即一个周期内的6个数值之和为0，则S＝sin+sin+sinπ+…+sin+sin＝sin+sin+sinπ+sin +335×0＝+0＝，故选：B．4．（5分）在△ABC中，AB＝3，AC＝5，BC＝2，则△ABC的面积为（）A．B．C．6D．12【解答】解：∵AB＝3，AC＝5，BC＝2，∴由余弦定理cos A＝＝＝∴sin A＝，∴△ABC的面积为，故选：C．5．（5分）如图是一个几何体的三视图，根据图中数据，可得该几何体的体积是（）A．9πB．C．D．【解答】解：由三视图知几何体的上部为一球体，且球的直径为2；下部是圆柱挖去一个同底等高的圆锥，且圆柱的底面圆的直径为2，高为3，∴几何体的体积V＝V球+V圆柱﹣V圆锥＝π+π×12×3﹣×π×3＝π．故选：C．6．（5分）已知实数x，y满足则z＝2x+4y的最大值是（）A．﹣4B．2C．6D．8【解答】解：由已知不等式组得到平面区域如图：z＝2x+4y变形为y＝，此直线经过图中D（0，2）时，在y轴截距最大即z最大，所以z的最大值为2×0+4×2＝8；故选：D．7．（5分）如图，椭圆的左、右焦点为F1，F2，上顶点为A，点P为第一象限内椭圆上的一点，若点A到PF1的距离是点F2到PF1距离的2倍，则直线PF1的斜率为（）A．B．C．D．【解答】解：设直线PF1的斜率为k，则直线PF1的方程为y＝k（x+1），即kx﹣y+k＝0，∵A（0，），F2（1，0），点A到PF1的距离是点F2到PF1距离的2倍，∴，∵点P为第一象限内椭圆上的一点，∴k＝．故选：C．8．（5分）已知f（x）是定义在R上的奇函数，且x＞0时，f（x）＝x2﹣2x﹣3，若方程f （x）＝a有两个根，则实数a的取值范围是（）A．[﹣4，4]B．[﹣3，0）∪（0，3]∪{﹣4，4}C．[﹣3，3]∪{﹣4，4}D．（﹣4，4）【解答】解：∵f（x）是定义在R上的奇函数，∴f（0）＝0，若x＜0，则﹣x＞0，∵x＞0时，f（x）＝x2﹣2x﹣3，∴f（﹣x）＝x2+2x﹣3＝﹣f（x），∴x＜0时，f（x）＝﹣x2﹣2x+3，则f（x）＝，作出函数f（x）的图象如图：要使f（x）＝a有两个根，则a＝4或a＝﹣4，0＜a≤3或﹣3≤a＜0，即实数a的取值范围是[﹣3，0）∪（0，3]∪{﹣4，4}，故选：B．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上，9．（5分）已知i是虚数单位，若复数，则m＝1．【解答】解：由，得＝1+i，∴m＝1．故答案为：1．10．（5分）在的二项展开式中，x2的系数为1120．【解答】解：根据二项式定理，的通项为T r+1＝C8r•2r•（﹣1）8﹣r•，当＝2时，即r＝4时，可得T5＝1120x2．即x2项的系数为1120，故答案为：1120．11．（5分）如图所示，在边长为1的正方形f（x）中任取一点f（x），则点[﹣1，1）恰好取自阴影部分的概率为．【解答】解：根据题意，该题是几何概型的应用问题，正方形OABC的面积为1×1＝1，而阴影部分由函数y＝x与y＝围成，其面积为（﹣x）dx＝（﹣x2）＝；则所求的概率为P＝．故答案为：．12．（5分）已知双曲线﹣＝1的右焦点与抛物线y2＝12x的焦点重合，求该双曲线的焦点到其渐近线的距离．【解答】解：∵抛物线y2＝12x的p＝6，开口方向向右，∴焦点是（3，0），∵双曲线﹣＝1的右焦点与抛物线y2＝12x的焦点重合，∴4+b2＝9，∴b2＝5∴双曲线的渐近线方程为y＝，即∴双曲线的焦点到其渐近线的距离为＝．13．（5分）若直线x﹣y+t＝0被曲线（θ为参数）截得的弦长为，则实数t的值为﹣2或6．【解答】解：由，得，①2+②2得，（x﹣1）2+（y﹣3）2＝16．所以曲线表示以（1，3）为圆心，以4为半径的圆．因为直线x﹣y+t＝0被曲线（θ为参数）截得的弦长为，则半弦长为．所以圆心（1，3）到直线x﹣y+t＝0的距离d＝．解得t＝﹣2或t＝6．故答案为﹣2或6．14．（5分）在△ABC中，已知AB＝AC＝3，BC＝4，P为BC边上的动点，则的值为10．【解答】解：如图所示，△ABC中，AB＝AC＝3，BC＝4，P为BC边上的动点，∴＝+＝+λ＝+λ（﹣）＝（1﹣λ）+λ，∴＝（1﹣λ）+λ+•＝（1﹣λ）×32+λ×32+3×3×＝10．故答案为：10．三、解答题：（本大题共6小题，共80分）15．（13分）已知函数f（x）＝cos x sin（x+）﹣cos2x+，x∈R（1）求f（x）的最小正周期及单调减区间；（2）求f（x）在闭区间，上的最大值和最小值．【解答】解：（1）函数f（x）＝cos x sin（x+）﹣cos2x+＝sin x cos x+cos2x﹣cos2x+＝sin2x﹣cos2x＝sin（2x﹣），∴f（x）的最小正周期T＝＝π；令2kπ+≤2x﹣≤2kπ+，求得kπ+≤x≤kπ+，可得f（x）的减区间为，．（2）在闭区间，上，2x﹣∈[﹣，]，故当2x﹣＝时，函数f（x）取得最大值为，当2x﹣＝﹣时，函数f（x）取得最小值为﹣．16．（13分）某市A、B两所中学的学生组队参加辩论赛，A中学推荐了3名男生、2名女生，B中学推荐了3名男生、4名女生，两校所推荐的学生一起参加集训．由于集训后队员水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队．（Ⅰ）求A中学至少有1名学生入选代表队的概率；（Ⅱ）某场比赛前，从代表队的6名队员中随机抽取4人参赛，设X表示参赛的男生人数，求X的分布列和数学期望．【解答】解：（Ⅰ）由题意，参加集训的男、女学生共有6人，参赛学生全从B中抽出（等价于A中没有学生入选代表队）的概率为：＝，因此A中学至少有1名学生入选代表队的概率为：1﹣＝；（Ⅱ）某场比赛前，从代表队的6名队员中随机抽取4人参赛，X表示参赛的男生人数，则X的可能取值为：1，2，3，P（X＝1）＝＝，P（X＝2）＝＝，P（X＝3）＝＝．X的分布列：和数学期望EX＝1×＝2．17．（13分）如图，底面为直角梯形的四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面ABCD，E为A1B1的中点，且△ABE为等腰直角三角形，AB∥CD，AB⊥BC，AB＝2CD＝2BC．（Ⅰ）求证：AB⊥DE；（Ⅱ）求直线EC与平面ABE所成角的正弦值；（Ⅲ）线段EA上是否存在点F，使EC∥平面FBD？若存在，求出；若不存在，说明理由．【解答】证明：（Ⅰ）取AB的中点O，连结EO，DO，∵EB＝EA，∴EO⊥AB，∵四边形ABCD是直角梯形，AB＝2CD＝2BC，AB⊥BC，∴四边形OBCD为正方形，∴AB⊥OD，又EO，OD为平面EOD内的两条相交直线，∴AB⊥平面EOD，由ED⊂平面EOD，∴AB⊥DE（Ⅱ）∵平面ABE⊥平面ABCD，且EO⊥AB，∴EO⊥平面ABCD，∴EO⊥OD，由OD，OA，OE两两垂直，建立如图所示的空间直角坐标系O﹣xyz，∵△EAB为等腰直角三角形，∴OA＝0B＝0D＝0E，设OB＝1，则O（0，0，0），A（0，1，0），B（0，﹣1，0），C（1，﹣1，0），D（1，0，0），E（0，0，1），∴，平面ABE的一个法向量为，设直线EC与平面ABE所成角为θ，则sin＝，即直线EC与平面ABE所成角的正弦值是．（Ⅲ）存在F，且＝时，有EC∥平面FBD，证明如下：由，F（0，），∴，，设平面FBD的法向量为，则，即，令a＝1，则，∵，即，∵EC⊄平面FBD，∴EC∥平面FBD．即当F满足＝时，有EC∥平面FBD．18．（13分）已知数列{a n}的前n项和为S n满足：（a为常数，且a≠0，a≠1）（1）若a＝2，求数列{a n}的通项公式（2）设，若数列{b n}为等比数列，求a的值．（3）在满足条件（2）的情形下，设，数列{c n}前n项和为T n，求证．【解答】解：（1）当a＝2时，S n＝2a n﹣2当n＝1时，S1＝2a1﹣2⇒a1＝2…（1分）当n≥2时，S n＝2a n﹣2S n﹣1＝2a n﹣1′﹣2…（2分）两式相减得到a n＝2a n﹣2a n﹣1，（a n﹣1≠0）得到…（3分）…（4分）（2）由（1）知，，若{b n}为等比数列，则有，而，故，解得，再将代入得成立，所以．…（9分）（3）证明：由（2）知，所以＝＝， (11)由得，所以， (13)从而＝＝．即． (14)19．（14分）设椭圆的中心在坐标原点，对称轴是坐标轴，一个顶点为A（0，2），右焦点F 到点的距离为2．（I）求椭圆的方程；（Ⅱ）设经过点（0，﹣3）的直线l与椭圆相交于不同两点M，N满足，试求直线l的方程．【解答】解：（Ⅰ）依题意，设椭圆方程为，则其右焦点坐标为，由|FB|＝2，得，即，故．又∵b＝2，∴a2＝＝12，∴所求椭圆方程为．（Ⅱ）由题意可设直线l的方程为y＝kx﹣3（k≠0），由，知点A在线段MN的垂直平分线上，由得x2+3（kx﹣3）2＝12即（1+3k2）x2﹣18kx+15＝0①△＝（﹣18k）2﹣4（1+3k2）×15＝144k2﹣60＞0即时方程①有两个不相等的实数根设M（x1，y1），N（x2，y2），线段MN的中点P（x0，y0）则x1，x2是方程①的两个不等的实根，故有从而有，于是，可得线段MN的中点P的坐标为又由于k≠0，因此直线AP的斜率为由AP⊥MN，得即5+6k2＝9，解得，∴，∴所求直线l的方程为：．20．（14分）已知函数f（x）＝x2+2aln（1﹣x）（a∈R），试求：（1）当a＝﹣2时，求函数f（x）的单调区间和极值；（2）若f（x）在[﹣1，1）上是单调函数，求实数a的取值范围．【解答】解：（1）f（x）＝﹣4ln（1﹣x）+x2，定义域为（﹣∞，1），f′（x）＝2x+＝，令f'（x）＞0，解得：得x＞﹣1，令f′（x）＜0，解得：x＜﹣1，故f（x）在（﹣1，1）递增，在（﹣∞，﹣1）递减，f（x）极小值＝f（﹣1）＝1﹣4ln2．（2）f′（x）＝2x﹣，若f'（x）≥0，即2x﹣≥0⇒a≤[x（1﹣x）]min⇒a≤﹣2，若f'（x）≤0，即2x﹣≤0⇒a≥[x（1﹣x）]max⇒a≥，所以a≤﹣2或a≥．。

天津市宝坻区2017届高三数学理科训练4一、选择题： 1. 已知集合},2|{2R x x x x A ∈-==，},1{m B =，若B A ⊆，则m 的值为( )A . 2B . 1-C . 1-或2D . 2或22.执行如题(1)图所示的程序框图，则输出的结果为（ ） A ．189 B ．381 C ．93 D ．453.某几何体的三视图如题(2)图所示，则该几何体的体积为（ ） A ．1333π+ B ．52π+ C ．53π+ D ．1332π+4. 将函数sin 2y x =的图象向右平移4π个单位，再向上平移1个单位，所得函数图象对应的解析式为( ) A ．sin(2)14y x π=-+ B ．22cos y x = C ．22sin y x = D ．cos 2y x =-5.设20(12)a x dx =-⎰,则二项式62a x x ⎛⎫+ ⎪⎝⎭的常数项是( )A. 240-B. 240C. 160-D. 1606. 已知等差数列{}n a 的前n 项和为n S ，满足23142,4,4,a a a a ≤≤+≥当4a 取得最大值时，数列{}n a 的公差为( )A ．1B ．4C ．2D ．37.已知函数()f x 是定义在R 上的奇函数,它的图象关于1x =对称,且() (01)f x x x =<≤.若函数1()y f x a x =--在区间[10,10]-上有10个不同零点，则实a 数的取值范围是（ ） A. 44[,]55- B. 44(,)55- C. 11[,]1010- D. 11(,)1010-8. 如图，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线,AC BD ，设内层椭圆方程为22221(0)x y a b a b+=>>，若直线AC 与图（1）图（2）AOCD B y xBD 的斜率之积为14-，则椭圆的离心率为（ ）A ． 12 B．． 34二、填空题： 9. 已知复数32iz -=+（i 为虚数单位），则||z 的值为 ． 10.已知曲线C的参数方程为x ty t⎧=⎪⎨=⎪⎩ (t 为参数), C 在点(1,1)处的切线为l ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,则l 的极坐标方程为 ．11. 如图，AB 是半圆O 的直径，延长AB 到C ，使BC =，CD 切半圆O 于点D ，DE ⊥AB ，垂足为E ．若AE ∶EB =3∶1，求DE 的长 ．12. O 是平面上一点，,,A B C 是平面上不共线三点，动点P 满足：(),[1,2],OP OA AB AC λλ=++∈- 已知1λ=时，||2AP =，则PA PB PA PC ⋅+⋅ 的最大值为 .13.抛物线24(0)y mx m =>的焦点为F ，点P 为该抛物线上的动点，又点A(,0)m -，则PF PA的最小值为 .14. 函数)(x f 的导函数为)(x f '，对x ∀∈R ，都有2()()f x f x '>成立，若2)4ln (=f ，则不等式2()x f x e >的解集是 ． 三、解答题：15.设角A ，B ，C 是△ABC 的三个内角，已知向量m＝(sin A ＋sin C ，sin B －sin A )， n ＝(sin A －sin C ，sin B )，且m ⊥n.(1)求角C 的大小；(2)若向量s ＝(0，－1)，t ＝(cos A,2cos 2B 2)，求|s ＋t |的取值范围．16.生产A ，B 两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于 82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：（1）试分别估计元件A 、元件B 为正品的概率；（2）生产一件元件A ，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B ，若是正品可盈利100元，若是次品则亏损20元，在（1）的前提下；（i ）求生产5件元件B 所获得的利润不少于300元的概率；（ii ）记X 为生产1件元件A 和1件元件B 所得的总利润，求随机变量X 的分布列和数学期望．17．如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD （1）若点M 是棱PC 的中点，求证：PA // 平面BMQ ； （2）求证：平面PQB ⊥平面PAD ；（3）若二面角M-BQ-C 为30°，设PM =tMC ，试确定t 的值 ．PABCDQM天津市宝坻区2017届高三数学理科训练4参考答案一、 选择题：AADCB BCC二、填空题：9.10. sin()4πρθ+=11. 3212. 2413.214. (ln 4,)+∞三、解答题：15. (1)由题意得m·n ＝(sin 2A －sin 2C )＋(sin 2B －sin A sin B )＝0，即sin 2C ＝sin 2A ＋sin 2B －sin A sin B ，设a ，b ，c 为内角A ，B ，C 所对的边长，由正弦定理得c 2＝a 2＋b 2－ab ，再由余弦定理得cos C ＝a 2＋b 2－c 22ab ＝12，∵0<C <π，∴C ＝π3.(2)∵s ＋t ＝(cos A,2cos 2B2－1)＝(cos A ，cos B )， ∴|s ＋t |2＝cos 2A ＋cos 2B＝cos 2A ＋cos 2(2π3－A )＝1＋cos2A2＋1＋cos(4π3－2A )2＝14cos2A －34sin2A ＋1 ＝－12sin(2A －π6)＋1，∵0<A <2π3，∴－π6<2A －π6<7π6，∴－12<sin(2A －π6)≤1，∴12≤|s ＋t |2<54，∴22≤|s ＋t |<52. 16. （Ⅰ）由题可知 元件A 为正品的概率为45，元件B 为正品的概率为34。

2016-2017学年天津市宝坻区林亭口高中高三（下）第一次月考数学试卷（文科）一、选择题（本题共8个小题，每小题5分，共40分）1．（5分）已知复数z满足z＝（i为虚数单位），则z＝（）A．B．C．1﹣i D．1+i2．（5分）已知直线l：y＝kx+b，曲线C：x2+（y﹣1）2＝1，则“b＝1”是“直线l与曲线C有公共点”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．（5分）若a＝50.2，b＝logπ3，c＝log5sinπ，则（）A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞a＞b4．（5分）执行如图所示的程序框图，输出的S值为8，则判断条件是（）A．k＜2B．k＜4C．k＜3D．k≤35．（5分）点P为△ABC边AB上任一点，则使S△PBC≤S△ABC的概率是（）A．B．C．D．6．（5分）函数f（x）＝sin（2x+）的图象向左平移φ（φ＞0）个单位后关于原点对称，则φ的最小值为（）A．B．C．D．7．（5分）已知F1，F2分别为双曲线C：﹣＝1（a＞0，b＞0）的左右焦点，过F1的直线l与双曲线C的左右两支分别交于A，B两点，若|AB|：|BF2|：|AF2|＝4：3：5，则双曲线的离心率为（）A．B．C．2D．8．（5分）在等腰梯形ABCD中，已知AB∥DC，AC与BD交于点M，AB＝2CD＝4．若•＝﹣1，则cos∠BMC（）A．B．C．D．二.填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卷中相应的横线上. 9．（5分）某学校小学部有270人，初中部有360人，高中部有300人，为了调查学生身体发育状况的某项指标，若从初中部抽取了12人，则从该校应一共抽取人进行该项调查．10．（5分）甲几何体（上）与乙几何体（下）的组合体的三视图如图所示，甲、乙几何体的体积分别为V1、V2，则V1：V2等于．11．（5分）一个棱长为的正方体被一个平面截去一部分后，剩余部分的三视图如图所示，则此剩余部分的体积为．12．（5分）函数的单调递增区间是．13．（5分）已知数列{a n}，a1＝1，a2＝3，a n+2＝a n+1﹣a n，则a2016＝．14．（5分）若函数f（x）＝x2+2a|x|+a2﹣6的图象与x轴有三个不同的交点，函数g（x）＝f（x）﹣b有4个零点，则实数b的取值范围是．三.解答题：本大题6小题，共80分．解答应写出文字说明，证明过程或演算步骤．15．（13分）已知函数f（x）＝cos x（cos x +sin x）．（Ⅰ）求f（x）的最小值；（Ⅱ）在△ABC中，角A、B、C的对边分别是a、b、c，若f（C）＝1且c ＝，a+b＝4，求S△ABC．16．（13分）某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载新产品A、B若干件，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：并且B产品的数量不超过A产品数量的2倍．如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？17．（13分）如图，斜三棱柱ABC﹣A1B1C1中，平面ACC1A1⊥平面BCC1B1，E为棱CC1的中点，A1B与AB1交于点O．若AC＝CC1＝2BC＝2，∠ACC1＝∠CBB1＝60°．（Ⅰ）证明：直线OE∥平面ABC；（Ⅱ）证明：平面ABE⊥平面AB1E；（Ⅲ）求直线A1B与平面ABE所成角的正弦值．18．（13分）已知椭圆E：+＝1（a＞b＞0）的长轴长为短轴长的倍．（1）求椭圆E的离心率；（2）设椭圆E的焦距为2，直线l与椭圆E交于P，Q两点，且OP⊥OQ，求证：直线l恒与圆x2+y2＝相切．19．（14分）已知数列{a n}的前n项和为S n，S n＝2a n﹣2．（1）求数列{a n}的通项公式；（2）设b n＝，T n为{b n}的前n项和，求T2n．20．（14分）已知函数f（x）＝ax﹣1﹣lnx．（a∈R）（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）若函数f（x）在x＝2处的切线斜率为，不等式f（x）≥bx﹣2对任意x∈（0，+∞）恒成立，求实数b的取值范围；（Ⅲ）证明对于任意n∈N，n≥2有：+++…+＜．2016-2017学年天津市宝坻区林亭口高中高三（下）第一次月考数学试卷（文科）参考答案与试题解析一、选择题（本题共8个小题，每小题5分，共40分）1．（5分）已知复数z满足z＝（i为虚数单位），则z＝（）A．B．C．1﹣i D．1+i【解答】解：z＝＝，故选：A．2．（5分）已知直线l：y＝kx+b，曲线C：x2+（y﹣1）2＝1，则“b＝1”是“直线l与曲线C有公共点”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：直线l与曲线C有公共点⇔≤1，化为|b﹣1|≤．可知：b＝1时，满足上式；反之不成立，取b＝也可以．∴“b＝1”是“直线l与曲线C有公共点”的充分不必要条件．故选：A．3．（5分）若a＝50.2，b＝logπ3，c＝log5sinπ，则（）A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞a＞b【解答】解：∵a＝50.2＞50＝1，0＜b＝logπ3＜logππ＝1，c＝log5sinπ≤0，∴a＞b＞c．故选：C．4．（5分）执行如图所示的程序框图，输出的S值为8，则判断条件是（）A．k＜2B．k＜4C．k＜3D．k≤3【解答】解：模拟执行程序框图，可得k＝0，s＝1应满足条件，执行循环体，s＝1，k＝1应满足条件，执行循环体，s＝2，k＝2应满足条件，执行循环体，s＝8，k＝3此时，由题意，应该不满足条件，退出循环，输出s的值为8．则判断框内应为：k＜3？故选：C．5．（5分）点P为△ABC边AB上任一点，则使S△PBC≤S△ABC的概率是（）A．B．C．D．【解答】解：设P到BC的距离为h，∵三角形ABC的面积为S，设BC边上的高为d，因为两个三角形有共同的边BC，所以满足S△PBC≤S△ABC时，h≤d，所以使S△PBC≤S△ABC的概率为＝；故选：A．6．（5分）函数f（x）＝sin（2x+）的图象向左平移φ（φ＞0）个单位后关于原点对称，则φ的最小值为（）A．B．C．D．【解答】解：∵f（x）＝sin（2x+），∴图象向左平移φ（φ＞0）个单位长度得到y＝sin[2（x+φ）+]＝sin（2x+2φ+），∵所得的图象关于原点对称，∴2φ+＝kπ（k∈Z），φ＞0，则φ的最小正值为．故选：B．7．（5分）已知F1，F2分别为双曲线C：﹣＝1（a＞0，b＞0）的左右焦点，过F1的直线l与双曲线C的左右两支分别交于A，B两点，若|AB|：|BF2|：|AF2|＝4：3：5，则双曲线的离心率为（）A．B．C．2D．【解答】解：设|AF1|＝t，|AB|＝4x，则|BF2|＝3x，|AF2|＝5x，根据双曲线的定义，得|AF2|﹣|AF1|＝|BF1|﹣|BF2|＝2a，即5x﹣t＝（4x+t）﹣3x＝2a，解得t＝2x，x＝a，即|AF1|＝，|AF2|＝，∵|AB|：|BF2|：|AF2|＝4：3：5，得△ABF2是以B为直角的Rt△，∴cos∠BAF2＝＝，可得cos∠F2AF1＝﹣，△F2AF1中，|F1F2|2＝|AF1|2+|AF2|2﹣2|AF1|•|AF2|cos∠F2AF1＝a2+a2﹣2×a×a×（﹣）＝20a2，可得|F1F2|＝2a，即c＝a，因此，该双曲线的离心率e＝＝．故选：D．8．（5分）在等腰梯形ABCD中，已知AB∥DC，AC与BD交于点M，AB＝2CD＝4．若•＝﹣1，则cos∠BMC（）A．B．C．D．【解答】解：如图，由题意可知，△MCD∽△MAB∵AB＝2CD＝4，∴AM＝2MC，BM＝2MD，设MD＝MC＝m，则AC＝BD＝3m，由•＝﹣1，得9m2cos∠CMD＝﹣1，∴cos∠CMD＝﹣在△CMD中，有22＝m2+m2﹣2m2cos∠CMD，即4＝2m2+m2+2m2•，解得：m2＝．∴cos∠CMD＝﹣．则cos∠BMC＝cos（π﹣∠BMD）＝﹣cos∠CMD＝．故选：C．二.填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卷中相应的横线上. 9．（5分）某学校小学部有270人，初中部有360人，高中部有300人，为了调查学生身体发育状况的某项指标，若从初中部抽取了12人，则从该校应一共抽取31人进行该项调查．【解答】解：解：由分层抽样的定义得该校共抽取：（270+360+300）＝31，故答案为：31；10．（5分）甲几何体（上）与乙几何体（下）的组合体的三视图如图所示，甲、乙几何体的体积分别为V1、V2，则V1：V2等于1：3．【解答】解：由三视图可知：该几何体是由上下两部分组成的，上面是一个球，下面是一个圆锥．∴V1＝＝，V2＝＝4π．∴V1：V2＝1：3．故答案为：1：3．11．（5分）一个棱长为的正方体被一个平面截去一部分后，剩余部分的三视图如图所示，则此剩余部分的体积为5．【解答】解：由三视图可知几何体是正方体在一个角上截去一个三棱锥，∵正方体的棱长是，∴三棱锥的体积V1＝××××＝1，∴剩余部分体积V＝××﹣V1＝6﹣1＝5，故答案为：5．12．（5分）函数的单调递增区间是（2，3）．【解答】解：∵函数，∴﹣x2+4x﹣3＞0，解得1＜x＜3，∵t＝﹣x2+4x﹣3是开口向下，对称轴为x＝2的抛物线，∴由复合函数的单调性的性质知函数的单调递增区间是（2，3）．故答案为：（2，3）．13．（5分）已知数列{a n}，a1＝1，a2＝3，a n+2＝a n+1﹣a n，则a2016＝﹣2．【解答】解：∵数列{a n}，a1＝1，a2＝3，a n+2＝a n+1﹣a n，∴a3＝a2﹣a1＝2，同理可得：a4＝﹣1，a5＝﹣3，a6＝﹣2，a7＝1，a8＝3，…，∴a n+6＝a n．则a2016＝a335×6+6＝a6＝﹣2，故答案为：﹣2．14．（5分）若函数f（x）＝x2+2a|x|+a2﹣6的图象与x轴有三个不同的交点，函数g（x）＝f（x）﹣b有4个零点，则实数b的取值范围是（﹣6，0）．【解答】解：∵函数f（x）是偶函数，∴f（x）＝x2+2a|x|+a2﹣6的图象与x轴有三个不同的交点，则必有f（0）＝0，即a2﹣6＝0，即a2＝6，即a＝±，当a＝时，f（x）＝x2+2|x|，此时函数f（x）只有1个零点，不满足条件．当a＝﹣时，f（x）＝x2﹣2|x|，此时函数f（x）有3个零点，满足条件，此时f（x）＝x2﹣2|x|＝（|x|﹣）2﹣6，∴f（x）≥﹣6，由g（x）＝f（x）﹣b＝0得b＝f（x），作出函数f（x）的图象如图：要使函数g（x）＝f（x）﹣b有4个零点，则﹣6＜b＜0，故答案为：（﹣6，0）三.解答题：本大题6小题，共80分．解答应写出文字说明，证明过程或演算步骤．15．（13分）已知函数f（x）＝cos x（cos x+sin x）．（Ⅰ）求f（x）的最小值；（Ⅱ）在△ABC中，角A、B、C的对边分别是a、b、c，若f（C）＝1且c＝，a+b＝4，求S△ABC．【解答】解：（Ⅰ）＝＝．当时，f（x）取最小值为．（Ⅱ），∴．在△ABC中，∵C∈（0，π），，∴，又c2＝a2+b2﹣2ab cos C，（a+b）2﹣3ab＝7．∴ab＝3．∴．16．（13分）某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载新产品A、B若干件，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：并且B产品的数量不超过A产品数量的2倍．如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？【解答】解：设搭载A产品x件，B产品y件，则预计收益z＝1000x+1200y．则有．作出可行域如图：作直线l：1000x+1200y＝0，即直线x+1.2y＝0．把直线l向右上方平移到l1的位置，直线l1经过可行域上的点B，此时z＝1000x+1200y取得最大值．由，解得点M的坐标为（3，6）．∴当x＝3，y＝6时，z max＝3×1000+6×1200＝10200（百元）．答：搭载A产品3件，B产品6件，才能使总预计收益达到最大，最大预计收益为10200百元．故答案为：10200百元．17．（13分）如图，斜三棱柱ABC﹣A1B1C1中，平面ACC1A1⊥平面BCC1B1，E为棱CC1的中点，A1B与AB1交于点O．若AC＝CC1＝2BC＝2，∠ACC1＝∠CBB1＝60°．（Ⅰ）证明：直线OE∥平面ABC；（Ⅱ）证明：平面ABE⊥平面AB1E；（Ⅲ）求直线A1B与平面ABE所成角的正弦值．【解答】解：（Ⅰ）取BB1的中点F，连结OF，EF∵E，O分别为CC1，BA1的中点，∴OF∥AB，EF∥BC，∵OF⊄平面ABC，EF⊄平面ABC，AB⊂平面ABC，BC⊂平面ABC，∴OF∥平面ABC，EF∥平面ABC，又OF⊂平面OEF，EF⊂平面OEF，OF∩EF＝F，∴平面OEF∥平面ABC，∵OE⊂平面OEF，∴直线OE∥平面ABC．（Ⅱ）∵AC＝2CE＝2，∠ACC1＝60°，∴AE⊥CC1，∵平面ACC1A1⊥平面BCC1B1，平面ACC1A1∩平面BCC1B1＝CC1，AE⊂平面ACC1A1，∴AE⊥平面BCC1B1，∴AE⊥BE．∵BC＝CE＝EC1＝C1B1＝1，∠CBB1＝60°，∴∠CEB＝30°，∠C1EB1＝60°，∴∠BEB1＝90°，即BE⊥EB1．又AE⊂平面AB1E，B1E⊂平面AB1E，AE∩B1E＝E，∴BE⊥平面AB1E，∵BE⊂平面ABE，∴平面ABE⊥平面AB1E．（Ⅲ）作OM⊥AE，M为垂足，连结BM．由（Ⅱ）知OM⊥平面ABE，∴∠OBM即为直线A1B与平面ABE所成角．∵OM⊥AE，EB1⊥AE，∴OM∥EB1，又O为AB1的中点，∴OM＝EB1＝，EM＝AE＝，∴BM＝，从而BO＝2，∴sin∠OBM＝，即直线A1B与平面ABE所成角的正弦值为．18．（13分）已知椭圆E：+＝1（a＞b＞0）的长轴长为短轴长的倍．（1）求椭圆E的离心率；（2）设椭圆E的焦距为2，直线l与椭圆E交于P，Q两点，且OP⊥OQ，求证：直线l恒与圆x2+y2＝相切．【解答】解：（1）由题意可得2a＝2b，即a＝b，c＝＝＝a，可得e＝＝；（2）证明：由题意可得c＝，由（1）可得a＝，b＝1，椭圆的方程为+y2＝1，当直线l的斜率不存在时，设直线l的方程为x＝m，代入椭圆方程，可得y＝±，由OP⊥OQ，可得m2﹣（1﹣）＝0，解得m＝±，由圆心（0，0）到直线x＝m的距离为，即有直线l与圆x2+y2＝相切；当直线的斜率存在时，设l：y＝kx+t，代入椭圆方程x2+3y2＝3，可得（1+3k2）x2+6ktx+3t2﹣3＝0，设P（x1，y1），Q（x2，y2），可得x1+x2＝﹣，x1x2＝，y1y2＝（kx1+t）（kx2+t）＝k2x1x2+kt（x1+x2）+t2，由题意OP⊥OQ，可得x1x2+y1y2＝0，即为（1+k2）x1x2+kt（x1+x2）+t2＝0，即（1+k2）•+kt（﹣）+t2＝0，化简可得4t2＝3+3k2，由圆心（0，0）到直线y＝kx+t的距离为d＝＝＝，即为半径．则直线l恒与圆x2+y2＝相切．19．（14分）已知数列{a n}的前n项和为S n，S n＝2a n﹣2．（1）求数列{a n}的通项公式；（2）设b n＝，T n为{b n}的前n项和，求T2n．【解答】解：（1）∵S n＝2a n﹣2，∴n＝1时，a1＝2a1﹣2，解得a1＝2．当n≥2时，a n＝S n﹣S n﹣1＝2a n﹣2﹣（2a n﹣1﹣2），化为a n＝2a n﹣1．∴数列{a n}是等比数列，公比为2．∴a n＝2n，b n＝（2）当n为奇数时，b n＝＝；当n为偶数时，b n＝＝．设数列{}的前k项和为A k，则A k＝+…+＝＝．设数列{}的前k项和为B k，则B k＝，＝，∴＝2＝2，∴B k＝（﹣）＝﹣．∴T2n＝+﹣．20．（14分）已知函数f（x）＝ax﹣1﹣lnx．（a∈R）（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）若函数f（x）在x＝2处的切线斜率为，不等式f（x）≥bx﹣2对任意x∈（0，+∞）恒成立，求实数b的取值范围；（Ⅲ）证明对于任意n∈N，n≥2有：+++…+＜．【解答】解：（Ⅰ）∵函数f（x）的定义域为（0，+∞），…（1分）当a≤0时，ax﹣1＜0，从而f'（x）＜0，故函数f（x）在（0，+∞）上单调递减…（2分）当a＞0时，若，则ax﹣1＜0，从而f'（x）＜0，…（3分）若，则ax﹣1＞0，从而f'（x）＞0，…（4分）故函数f（x）在上单调递减，在上单调递增；…（5分）（Ⅱ）求导数：，∴，解得a＝1．…（6分）所以f（x）≥bx﹣2，即x﹣1﹣lnx≥bx﹣2，由于x＞0，即．…（7分）令，则，当0＜x＜e2时，g'（x）＜0；当x＞e2时，g'（x）＞0∴g（x）在（0，e2）上单调递减，在（e2，+∞）上单调递增；…（9分）故，所以实数b的取值范围为…（10分）（3）证明：由当a＝1，x＞1时，，f（x）为增函数，∵f（1）＝0∴f（x）＝x﹣1﹣lnx＞0即lnx＜x﹣1…（11分）∴当n≥2时，lnn2＜n2﹣1，…（12分）∴…（13分）＝∴（n∈N*，n≥2）．…（14分）。

2016-2017学年度林亭口高中9月月考卷高三地理四第I卷（选择题）一、选择题（题型注释）（本题4分）一架飞机从甲地（45°N,100°W）起飞，沿最近航线匀速飞行10小时抵达乙地（45°N,80°E）。

据此回答下列各题。

1．飞机飞行航线A．一直不变 B．先向东北后向东南C．先向西北后向西南 D．先向北后向南2．这架飞机若以同样的速度，沿45°N纬线飞行，抵达乙地大约需要A．8小时 B．10小时 C．14小时 D．20小时3．（本题2分）图中，符合甲在乙地西北、丙在丁地东南的是（本题4分）读下图，完成下列小题。

4．图中①②③区域面积相比（）A．①>② B．②>③ C．①＝③ D．无法比较5．下列相关说法，正确的是（）A．③区域海面距地心距离比①稍长B．③区域位于①区域的西北方向C．③区域位于北半球、东半球D．东北航向是②区域向③区域飞行的最近航线（本题4分）读我国东部沿海某地等高线图（单位：m），完成下列各题。

6．关于图中所反映信息表述正确的是A．图中河流的流向为从南流向北后再向东北 B．陡崖的相对高度H：100m＜H＜200m C．①地位于山地的迎风坡，降水比②地多 D．甲丙两地一年四季都能看到海上日出7．当地为发展旅游业，打算修建一条直达山顶（492 m处）的观光索道，最合适的选线是A．从甲处到山顶 B．从乙处到山顶 C．从丙处到山顶 D．从丁处到山顶（本题6分）读某地等髙线图，据此完成下列问题。

8．图中陡崖的相对高度可能是①18m ②21m ③36m ④43mA．①② B．②③ C．③④ D．①④9．图中陡崖顶部的海拔范围是A．（40M,50M） B．（45M,60M） C．（50M，60M） D．（50M,55M）10．有关P、Q两处地形的正确叙述是①P为山坡上的洼地②Q为山坡上的洼地③P为山坡上的小丘④Q为山坡上的小丘A．①② B．②③ C．③④ D．①④（本题6分）下图为世界某区域示意图，图中两条等值线为全球变暖条件下两个年份的相同月份的月均温为2℃的等温线。

林亭口高中2017届第一次质量调查英语试卷第Ⅰ卷第一部分：听力（共两节，满分20分）第一节：（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What is Betty doing?A. Having a meal.B. Doing some cooking.C. Washing the dishes.2. Where does the conversation most probably take place?A. In Xi’an.B. In a train.C. In a plane.3. What is probably the man?A. A doctor.B. A repairman.C. A telephone operator.4. Who are the two speakers talking about?A. Families.B. Managers.C. Children.5. What is Jack best at?A. Drawing.B. Singing.C. Skating.第二节：（共10小题；每小题1.5分，满分15分）听下面3段对材料。

每段材料后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段材料前，你将有时间阅读每个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段材料读两遍听下面一段对话，回答第6至第8小题。

6. Where does the conversation most likely take place?A. At a science conference.B. In a science laboratory.C. In a professor’s office.7. What does the woman say about her recent life?A. She’s been busy with her classes.B. She’s been busy with her final exams.C. She’s been working on the final paper.8. Why has the woman come here?A. To work on a project.B. To prepare for her speech.C. To talk with Professor Johnston.听下面一段对话，回答第9至第11小题。