中考数学选择填空压轴题训练整理

根据考试大纲，填空压轴题仍将以探究规律类型题为主要考察方向。

题型一：数字规律【例1】一组按一定规律排列的式子：－，，－，，…，（0a ≠）,则第n 个式子是 （n为正整数）．【答案】【例2】按一定规律排列的一列数依次为：,916,79,54,31 ……，按此规律排列下去，这列数中的第5个数是 ，第n 个数是 ．【答案】1125,122+n n【例3】一组按规律排列的整数5，7，11，19，…，第6个整数为____ _，根据上述规律，第n 个整数为____ （n 为正整数）.【答案】67；32+n （n 为正整数）【例4】将除去零以外的自然数按以下规律排列，根据第一列的奇数行的数的规律，写出第一列第9行的数为 ，再结合第一行的偶数列的数的规律，判断2011所在的位置是第 行第 列.【答案】81;第45行第15列2a 52a 83a 114a 31(1)n na n --例题精讲填空题压轴题【例5】某些植物发芽有这样一种规律：当年所发新芽第二年不发芽，老芽在以后每年都发芽.发芽规律见下表（设第一年前的新芽数为a ）第n 年 1 2 3 4 5 … 老芽率 a a 2a 3a 5a … 新芽率 0 a a 2a 3a … 总芽率a2 a3a5a8a…照这样下去，第8年老芽数与总芽数的比值为 .【解析】由规律可以看出，从第3年开始，老芽率、新芽率，总芽率都分别是前两年之和，因此，第8年的老芽为21，总芽为34，因此答案为2134． 【解析】2134题型二：多边形上存在的点数【例6】如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是 ．【解析】此类型题首先要找到边数的特点，然后找每条边上点的数目，第n 个图形是2n +边形，而且每个边上有n 个点。

【答案】(2)n n +或22n n +或2(1)1n +-【例7】用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第n 个“口”字需用棋子___________【答案】4n【例8】用“O”摆出如图所示的图案，若按照同样的方式构造图案，则第10个图案需要 个“O”．① ② ③ ④ 【答案】181第2个“口”第1个“口” 第3个“口”第n 个“口”………………第1个图形第2个图形第3个图形第4个图形题型三：藏头露尾型【例9】如下图是一组有规律的图案，第1个 图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n (n 是正整数)个图案中由 个基础图形组成．【解析】此类问题重点要找到“头是谁”“尾是谁”，①13+；②132+⨯；③133+⨯，……第n 个31n + 【答案】31n +【例10】搭建如图①的单顶帐篷需要17根钢管，这样的帐篷按图②，图③的方式串起来搭建，则串7顶这样的帐篷需要 根钢管．图1 图2 图3【答案】83．题型四：成倍数变化型【例11】如图，ABC ∆中，90ACB ∠=︒，1AC BC ==，取斜边的中点，向斜边做垂线，画出一个新的等腰直角三角形，如此继续下去，直到所画直角三角形的斜边与ABC ∆的BC 边重叠为止，此时这个三角形的斜边长为_____．【解析】注意每一次变化所变化的倍数 【答案】81；11(2)2n n - 【例12】如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，．．．．．．依次作下去，图中所作的第三个四边形的周长为________； 所作的第n 个四边形的周长为_________________．【答案】2,24()2n【例13】如图，在ABC ∆中，A α∠=，ABC ∠的平分线与ACD ∠的平分线交于点1A ，得1A ∠，则1______A ∠=．1A BC ∠的平分线与1ACD ∠的平分线交于点2A ，得2A ∠，……，2009A BC ∠的平分线与2009A CD ∠的平分线交于点2010A ，得2010A ∠，则2010A ∠= ．【答案】2α,20102α(1)(2)(3)……A 2A 1DC A【例14】如图，小正方形ABCD 的面积为1，把它的各边延长一倍得到新正方形1111A B C D ，正方形1111A B C D 的面积为 ； 再把正方形1111A B C D 的各边延长一倍得到正方形2222A B C D ， 如此进行下去，正方形n n n n D C B A 的面积为 ． （用含有n 的式子表示，n 为正整数）【答案】5，n5【例15】把一个正三角形分成四个全等的三角形，第一次挖去中间的一个小三角形，对剩下的三个小正三角形再重复以上做法……一直到第n 次挖去后剩下的三角形有 个．第一次 第二次 第三次 第四次【答案】3n题型五：相似与探究规律【例16】已知ABC AB AC m ∆==中，，72ABC ∠=︒，1BB 平分ABC ∠交AC 于1B ，过1B 作12B B //BC交AB 于2B ，作23B B 平分21AB B ∠，交AC 于3B ，过3B 作34//B B BC ，交AB 于4B ……依次进行下去，则910B B 线段的长度用含有m 的代数式可以表示为 .【答案】m 6215⎪⎪⎭⎫⎝⎛-【例17】如图，矩形纸片ABCD 中，6,10AB BC ==.第一次将纸片折叠，使点B 与点D 重合，折痕与BD交于点1O ；设1O D 的中点为1D ，第二次将纸片折叠使 点B 与点1D 重合，折痕与BD 交于点2O ；设21O D 的中点 为2D ，第三次将纸片折叠使点B 与点2D 重合，折痕与BD 交于点3O ，… .按上述方法折叠，第n 次折叠后的折痕与BD 交于点n O ，则1BO = ，n BO = ．第一次折叠 第二次折叠 第三次折叠【答案】2；12332n n -- B AD C 1O 1O 2O 1D 1D 2D 1O 2O 3O B AD C B ADCBA DC【例18】如图，直线x y 33=，点1A 坐标为（1，0），过点1A 作x 轴的垂线交直线于点1B ，以原点O 为圆心，1OB 长为半径画弧交x 轴于点2A ；再过点2A 作x 轴的垂线 交直线于点2B ，以原点O 为圆心，2OB 长为半径画弧交x 轴于 点3A ，…，按此做法进行下去，点4A 的坐标为（ ， ）； 点n A （ ， ）．【答案】（938，0）（1)332(-n ，0） 【例19】如图，以等腰三角形AOB 的斜边为直角边向外作第2个等腰直角三角形1ABA ，再以等腰直角三角形1ABA 的斜边为直角边向外作第3个等腰直角三角形11A BB ，……，如此作下去，若1OA OB ==，则第n 个等腰直角三角形的面积n S = ________（n 为正整数）.【解析】由题干可知：123124 (222)S S S ===，，可知22n n S -=【答案】22n -【例20】如图，n +1个边长为2的等边三角形有一条边在同一直线上，设211B D C ∆的面积为1S ，322B D C ∆的面积为2S ，…，1n n n B D C +∆的面积为n S ，则2S = ；n S =____ （用含n 的式子表示）．【答案】233,31nn + 【例21】如图，P 为ABC ∆的边BC 上的任意一点，设BC a =，当1B 、1C 分别为AB 、AC 的中点时，1112B C a =，当2B 、2C 分别为1BB 、1CC 的中点时，2234B C a =，当3B 、3C 分别为2BB 、2CC 的中点时，3378B C a =，当4B 、4C 分别为3BB 、3CC 的中点时，441516B C a =当5B 、5C 分别为4BB 、4CC 的中点时，55_____B C =当n B 、n C 分别为1n BB -、1n CC -的中点时，则n n B C = ；设ABC ∆中BC 边上的高为h ，则n n PB C ∆的面积为______(用含a 、h 的式子表示)．【答案】a 3231,a n n 212-, ah n n 12212+-D 4D 3D 2D 1C 5C 4C 3C 2C 1B 5B 4B 3B 2B 1A……B 2B 1A 1BOAC 3B 3B 2C 2C 1B 1CBA【例22】如图，在梯形ABCD 中，AB CD ∥，AB a =，CD b =，E 为边AD 上的任意一点，EF AB ∥，且EF 交BC 于点F ．若E 为边AD 上的中点，则______EF =（用含有a ，b 的式子表示）；若E 为边AD 上距点A 最近的n 等分点（2n ≥，且n 为整数），则______EF =（用含有n ，a ，b 的式子表示）．【答案】2a b +；(1)b n an+-【例23】已知在ABC ∆中，BC a =.如图1，点1B 、1C 分别是AB 、AC 的中点，则线段11B C 的长是_______； 如图2，点1B 、2B ,1C 、2C 分别是AB 、AC 的三等分点，则线段1122B C B C +的值是__________；如图3, 点12......、、、n B B B ，12......、、、n C C C 分别是AB 、AC 的(1)n +等分点，则线段1122n n B C B C B C ++⋅⋅⋅+的值是 ______.【答案】1,2a a ,12na 【例24】已知：如图，在Rt ABC ∆中，点1D 是斜边AB 的中点，过点1D 作11D E AC ⊥于点1E ，连接1BE 交1CD 于点2D ；过点2D 作22D E AC ⊥于点2E ，连接2BE ，交1CD 于点3D ；过点3D 作33D E AC ⊥于点3E ，如此继续，可以依次得到点4D 、5D 、…n D ， 分别记11BD E ∆、22BD E ∆、33BD E ∆、…n n BD E ∆的面积 为1S 、2S 、3S …n S ．设ABC ∆的面积是1,则1______S =， ______n S =（用含n 的代数式表示）.【答案】14，21(1)n +题型六：折叠与探究规律【例25】如图，将正方形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C ，D 重合），压平后得到折痕MN ．设2AB =，当12CE CD =时，则________AMBN=． 若1CE CD n =（n 为整数），则_______AM BN=．（用含n 的式子表示） 【答案】15；1)1(22+-n n【例26】如图，正方形ABCD ，E 为AB 上的动点，（E 不与A 、B 重合）连接DE ，作DE 的中垂线，交图3图2图12n-1B 2C 2A BCB 1C 1C 1B 1CBA FE D CBANMFEDCBAB321AD 于点F ．⑴若E 为AB 中点，则______DFAE= ⑵若E 为AB 的n 等分点(靠近点A )，则________DFAE= 【答案】251,42n n+题型七：其他类型【例27】图1是一个八角星形纸板，图中有八个直角，八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割，无缝隙无重叠的拼成图3所示的大正方形,其面积为8+3中线段AB 的长为 .图1 图2 图31+【例28】如图，1P 是一块半径为1的半圆形纸板，在1P 的左下端剪去一个半径为12的半圆后得到图形2P ，然后依次剪去一个更小的半圆（其直径为前一个被剪掉半圆的半径）得图形34,,,,n P P P ，记纸板n P 的面积为n S ，试计算求出=-23S S ；并猜想得到1n n S S --=()2n ≥【答案】1)41(2,32---n ππ【例29】如图，图①是一块边长为1，周长记为1P 的正三角形纸板，沿图①的底边剪去一块边长为12的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的21）后，得图③，④，…，记第)3(≥n n 块纸板的周长为n P ，则=-34P P ；1--n n P P = ．P 3P 2P 1【答案】81,121-⎪⎭⎫⎝⎛n【例30】已知一个面积为S 的等边三角形，现将其各边n （n 为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．当8n =时，共向外作出了 个小等边三角形；当n k =时，共向外作出了 个小等边三角形，这些小等边三角形的面积和是 （用含k 的式子表示）．【答案】18； 【例31】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为(10)，，点D 的坐标为(02)，．延长CB 交x 轴于点1A ，作正方形111A B C C ；延长11C B 交x 轴于点2A ，作正方形2221A B C C …按这样 的规律进行下去，第3个正方形的面积为________；第n 个正方形的面积为___________（用含n 的代数式表示）．【答案】4235）（,22235-⎪⎭⎫ ⎝⎛n【例32】如图所示，111()P x y ，、222()P x y ，，……()n n n P x y ，在函数4y x=(0x >)的图象上，11OP A ∆，212P A A ∆，323P A A ∆…1n n n P A A -∆都是等腰三角形，斜边1OA 、12A A …1n n A A -，都在x 轴上， 则1_____y =，12______n y y y ++⋅⋅⋅+=【答案】2 , 2n【例33】如图所示，直线1+=x y 与y 轴交于点1A ，以1OA 为边作正方形111OA B C ，然后延长11C B 与直线1+=x y 交于点2A ，得到第一个梯形112AOC A ；再以12C A 为边作正方形1222C A B C ，同样延长22C B 与直线1+=x y 交于点3A 得到第二个梯形2123A C C A ；，再以23C A 为边作正方形2333C A B C ，延长33C B ，得到第三个梯形；……则第2个梯形2123A C C A 的面积是 ；第n （n 是正整数）个梯形的面积是 （用含n 的式子表示）．3(-2)k 23(2)k s k-n =3n =5……n =4① ② ③ ④C 2B 2A 2C 1B 1A 1DC B AO yx【答案】6；2n 2223-⨯或1n 423-⨯【例34】在平面直角坐标系中，我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点 正方形，如图，菱形ABCD 的四个顶点坐标分别是(80)-，，(04)，，(80)，，(04)-，，则菱形ABCD 能覆盖的单位格点正方形的个数是_______个；若菱形n n n n A B C D 的四个顶点坐标分别为(20)-，n ， (0)，n ，(20)，n ，(0)-，n （n 为正整数）， 则菱形n n n n A B C D 能覆盖的单位格点正方形的 个数为_________（用含有n 的式子表示）．【答案】单位格点个数为48，单位格点个数为n n 442-【例35】在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形1111A B C D 、2222A B C D 、3333A B C D 每个正方形四条边上的整点的个数．按此规律推算出正方形10101010A B C D 四条边上的整点共有 个．【答案】80【例36】对于每个正整数n ，抛物线2211(1)(1)n n n n n y x x +++=-+与x 轴交于n A ，n B 两点，若n n A B 表示这两点间的距离，则n n A B = （用含n 的代数式表示）；112220112011A B A B A B +++的值为 ．【答案】()20122011,11+n nyxOD 1D 2D 3C 1C 2C 3B 1B 2B 3A 3A 2A 1123-1-2-3-3-2-1321-8-448ODC BAyx。

2020年中考数学选择填空压轴题汇编：规律探索1.（2020某某某某）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200，若2100＝S，用含S的式子表示这组数据的和是（）A．2S2﹣S B．2S2+S C．2S2﹣2S D．2S2﹣2S﹣2【解答】解：∵2100＝S，∴2100+2101+2102+…+2199+2200＝S+2S+22S+…+299S+2100S＝S（1+2+22+…+299+2100）＝S（1+2100﹣2+2100）＝S（2S﹣1）＝2S2﹣S．故选：A．2．（2020某某某某）观察下列等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；2+22+23+24+25＝26﹣2；…已知按一定规律排列的一组数：220，221，222，223，224，…，238，239，240，若220＝m，则220+221+222+223+224+…+238+239+240＝m（2m﹣1）（结果用含m的代数式表示）．【解答】解：∵220＝m，∴220+221+222+223+224+…+238+239+240＝220（1+2+22+…+219+220）＝220（1+221﹣2）＝m（2m﹣1）．故答案为：m（2m﹣1）．3．（2020某某鹤岗）如图，直线AM的解析式为y＝x+1与x轴交于点M，与y轴交于点A，以OA为边作正方形ABCO，点B坐标为（1，1）．过点B作EO1⊥MA交MA于点E，交x轴于点O1，过点O1作x轴的垂线交MA于点A1，以O1A1为边作正方形O1A1B1C1，点B1的坐标为（5，3）．过点B1作E1O2⊥MA交MA于E1，交x轴于点O2，过点O2作x轴的垂线交MA于点A2．以O2A2为边作正方形O2A2B2C2．…．则点B2020的坐标2×32020﹣1，32020．【解答】解：∵点B坐标为（1，1），∴OA＝AB＝BC＝CO＝CO1＝1，∵A1（2，3），∴A1O1＝A1B1＝B1C1＝C1O2＝3，∴B1（5，3），∴A2（8，9），∴A2O2＝A2B2＝B2C2＝C2O3＝9，∴B2（17，9），同理可得B4（53，27），B5（161，81），…由上可知，Bn（2×3n﹣1，3n），∴当n＝2020时，Bn（2×32020﹣1，32020）．故答案为：（2×32020﹣1，32020）．4.（2020某某某某）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，4√2），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+12√2，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是22020．【解答】解：∵点A1（0，2），×2×2=2，∴第1个等腰直角三角形的面积=12∵A2（6，0），=2√2，∴第2个等腰直角三角形的边长为√2×2√2×2√2=4＝22，∴第2个等腰直角三角形的面积=12∵A4（10，4√2），∴第3个等腰直角三角形的边长为10﹣6＝4，×4×4=8＝23，∴第3个等腰直角三角形的面积=12…则第2020个等腰直角三角形的面积是22020；故答案为：22020（形式可以不同，正确即得分）．5．（2020某某某某）如图各图形是由大小相同的黑点组成，图1中有2个点，图2中有7个点，图3中有14个点，…，按此规律，第10个图中黑点的个数是119 ．【解答】解：∵图1中黑点的个数2×1×（1+1）÷2+（1﹣1）＝2，图2中黑点的个数2×2×（1+2）÷2+（2﹣1）＝7，图3中黑点的个数2×3×（1+3）÷2+（3﹣1）＝14，……∴第n个图形中黑点的个数为2n（n+1）÷2+（n﹣1）＝n2+2n﹣1，∴第10个图形中黑点的个数为102+2×10﹣1＝119．故答案为：119．（x＞0）的图象上，点B1，B2，B3，…B n在y 6.（2020•某某某某）如图，点A1，A2，A3…在反比例函数y=1x轴上，且∠B1OA1＝∠B2B1A2＝∠B3B2A3＝…，直线y＝x与双曲线y=1交于点A1，B1A1⊥OA1，B2A2⊥B1A2，B3A3x⊥B2A3…，则B n（n为正整数）的坐标是（）A．（2√x，0）B．（0，√2x+1）C．（0，√2x(x−1)）D．（0，2√x）【解答】解：由题意，△OA1B1，△B1A2B2，△B2A3B3，…，都是等腰直角三角形，∵A1（1，1），∴OB1＝2，设A2（m，2+m），则有m（2+m）＝1，解得m=√2−1，∴OB2＝2√2，设A3（a，2√2+n），则有n＝a（2√2+a）＝1，解得a=√3−√2，∴OB3＝2√3，同法可得，OB4＝2√4，∴OB n＝2√x，∴B n（0，2√x）．故选：D．7．（2020某某某某州）如图，在平面直角坐标系中，△ABC的顶点坐标分别为：A（﹣2，0），B（1，2），C （1，﹣2）．已知N（﹣1，0），作点N关于点A的对称点N1，点N1关于点B的对称点N2，点N2关于点C 的对称点N3，点N3关于点A的对称点N4，点N4关于点B的对称点N5，…，依此类推，则点N2020的坐标为（﹣1，8）．【解答】解：由题意得，作出如下图形：N点坐标为（﹣1，0），N点关于A点对称的N1点的坐标为（﹣3，0），N1点关于B点对称的N2点的坐标为（5，4），N2点关于C点对称的N3点的坐标为（﹣3，8），N3点关于A点对称的N4点的坐标为（﹣1，8），N4点关于B点对称的N5点的坐标为（3，﹣4），N5点关于C点对称的N6点的坐标为（﹣1，0），此时刚好回到最开始的点N处，∴其每6个点循环一次，∴2020÷6＝336……4，即循环了336次后余下4，故N2020的坐标与N4点的坐标相同，其坐标为（﹣1，8）．故答案为：（﹣1，8）．8．（2020某某仙桃）如图，已知直线a：y＝x，直线b：y=−12x和点P（1，0），过点P作y轴的平行线交直线a于点P1，过点P1作x轴的平行线交直线b于点P2，过点P2作y轴的平行线交直线a于点P3，过点P3作x轴的平行线交直线b于点P4，…，按此作法进行下去，则点P2020的横坐标为21010．【解答】解：∵点P（1，0），P1在直线y＝x上，∴P1（1，1），∵P1P2∥x轴，∴P2的纵坐标＝P1的纵坐标＝1，∵P2在直线y=−12x上，∴1=−12x，∴x＝﹣2，∴P2（﹣2，1），即P2的横坐标为﹣2＝﹣21，同理，P3的横坐标为﹣2＝﹣21，P4的横坐标为4＝22，P5＝22，P6＝﹣23，P7＝﹣23，P8＝24…，∴P4n＝212x，∴P2020的横坐标为212×2020=21010，故答案为：21010．9.（2020某某某某）如图，将一枚跳棋放在七边形ABCDEFG 的顶点A 处，按顺时针方向移动这枚跳棋2020次．移动规则是：第k 次移动k 个顶点（如第一次移动1个顶点，跳棋停留在B 处，第二次移动2个顶点，跳棋停留在D 处），按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是（ ）A ．C 、EB ．E 、FC ．G 、C 、ED ．E 、C 、F【解答】解：经实验或按下方法可求得顶点C ，E 和F 棋子不可能停到． 设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格，因棋子移动了k 次后走过的总格数是1+2+3+…+k =12k （k +1），应停在第12k （k +1）﹣7p 格， 这时P 是整数，且使0≤12k （k +1）﹣7p ≤6，分别取k ＝1，2，3，4，5，6，7时，12k （k +1）﹣7p ＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋，若7＜k ≤2020，设k ＝7+t （t ＝1，2，3）代入可得，12k （k +1）﹣7p ＝7m +12t （t +1），由此可知，停棋的情形与k ＝t 时相同，故第2，4，5格没有停棋，即顶点C ，E 和F 棋子不可能停到． 故选：D ．10.（2020某某某某）如图，在平面直角坐标系中，点P 1的坐标为（√22，√22），将线段OP 1绕点O 按顺时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；又将线段OP 2绕点O 按顺时针方向旋转45°，长度伸长为OP 2的2倍，得到线段OP 3；如此下去，得到线段OP 4，OP 5，…，OP n （n 为正整数），则点P 2020的坐标是 （0，﹣22019） ．【解答】解：∵点P 1的坐标为（√22，√22），将线段OP 1绕点O 按逆时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；∴OP 1＝1，OP 2＝2，∴OP 3＝4，如此下去，得到线段OP 4＝23，OP 5＝24…， ∴OP n ＝2n ﹣1，由题意可得出线段每旋转8次旋转一周， ∵2020÷8＝252…4，∴点P 2020的坐标与点P 4的坐标在同一直线上，正好在y 轴的负半轴上， ∴点P 2020的坐标是（0，﹣22019）．故答案为：（0，﹣22019）．11.（2020某某某某）如图，△OB 1A 1，△A 1B 2A 2，△A 2B 3A 3，…，△A n ﹣1B n A n ，都是一边在x 轴上的等边三角形，点B 1，B 2，B 3，…，B n 都在反比例函数y =√3x（x ＞0）的图象上，点A 1，A 2，A 3，…，A n ，都在x 轴上，则A n 的坐标为 （2√x ，0） ．【解答】解：如图，过点B 1作B 1C ⊥x 轴于点C ，过点B 2作B 2D ⊥x 轴于点D ，过点B 3作B 3E ⊥x 轴于点E ，∵△OA1B1为等边三角形，∴∠B1OC＝60°，OC＝A1C，∴B1C=√3OC，设OC的长度为t，则B1的坐标为（t，√3t），得t•√3t=√3，解得t＝1或t＝﹣1（舍去），把B1（t，√3t）代入y=√3x∴OA1＝2OC＝2，∴A1（2，0），设A1D的长度为m，同理得到B2D=√3m，则B2的坐标表示为（2+m，√3m），得（2+m）×√3m=√3，解得m=√2−1或m=−√2−1（舍去），把B2（2+m，√3m）代入y=√3x∴A1D=√2−1，A1A2=2√2−2，OA2=2+2√2−2=2√2，∴A2（2√2，0）设A2E的长度为n，同理，B3E为√3n，B3的坐标表示为（2√2+n，√3n），得（2√2+n）•√3n=√3，把B3（2√2+n，√3n）代入y=√3x∴A2E=√3−√2，A2A3=2√3−2√2，OA3=2√2+2√3−2√2=2√3，∴A3（2√3，0），综上可得：A n（2√x，0），故答案为：(2√x，0)．12.（2020某某湘西州）观察下列结论：（1）如图①，在正三角形ABC中，点M，N是AB，BC上的点，且AM＝BN，则AN＝CM，∠NOC＝60°；（2）如图2，在正方形ABCD中，点M，N是AB，BC上的点，且AM＝BN，则AN＝DM，∠NOD＝90°；（3）如图③，在正五边形ABCDE中点M，N是AB，BC上的点，且AM＝BN，则AN＝EM，∠NOE＝108°；…根据以上规律，在正n边形A1A2A3A4…A n中，对相邻的三边实施同样的操作过程，即点M，N是A1A2，A2A3．上的点，且A1M＝A2N，A1N与A n M相交于O．也会有类似的结论，你的结论是A1N＝A n M，∠NOA n=(x−2)×180°x【解答】解：∵（1）如图①，在正三角形ABC中，点M，N是AB，BC上的点，且AM＝BN，则AN＝CM，=60°；∠NOC=(3−2)×180°3=90°；（2）如图2，在正方形ABCD中，点M，N是AB，BC上的点，且AM＝BN，则AN＝DM，∠NOD=(4−2)×180°4=108°；（3）如图③，在正五边形ABCDE中点M，N是AB，BC上的点，且AM＝BN，则AN＝EM，∠NOE=(5−2)×180°5…根据以上规律，在正n边形A1A2A3A4…A n中，对相邻的三边实施同样的操作过程，即点M，N是A1A2，A2A3上的点，且A1M＝A2N，A1N与A n M相交于O．．也有类似的结论是A1N＝A n M，∠NOA n=(x−2)×180°x故答案为：A1N＝A n M，∠NOA n=(x−2)×180°．x13．（2020某某某某）如图是用黑色棋子摆成的美丽图案，按照这样的规律摆下去，第10个这样的图案需要黑色棋子的个数为（）A．148B．152C．174D．202【解答】解：根据图形，第1个图案有12枚棋子，第2个图案有22枚棋子，第3个图案有34枚棋子，…第n个图案有2（1+2+…+n+2）+2（n﹣1）＝n2+7n+4枚棋子，故第10个这样的图案需要黑色棋子的个数为102+7×10+4＝100+70+4＝174（枚）．故选：C．14．（2020某某某某）小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体，…按照此规律，从第（100）个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是（ ）A ．1100B ．120C ．1101D ．2101【解答】解：由题意知，第100个图形中，正方体一共有1+2+3+……+99+100＝5050（个），其中写有“心”字的正方体有100个，∴抽到带“心”字正方体的概率是1005050=2101， 故选：D ．15．（2020某某威海）如图①，某广场地面是用A ，B ，C 三种类型地砖平铺而成的．三种类型地砖上表面图案如图②所示．现用有序数对表示每一块地砖的位置：第一行的第一块（A 型）地砖记作（1，1），第二块（B 型）地砖记作（2，1）…若（m ，n ）位置恰好为A 型地砖，则正整数m ，n 须满足的条件是m 、n 同为奇数或m 、n 同为偶数 ．【解答】解：观察图形，A 型地砖在列数为奇数，行数也为奇数的位置上或列数为偶数，行数也为偶数的位置上，若用（m ，n ）位置恰好为A 型地砖，正整数m ，n 须满足的条件为m 、n 同为奇数或m 、n 同为偶数． 故答案为m 、n 同为奇数或m 、n 同为偶数．16．（2020某某潍坊）如图，四边形ABCD 是正方形，曲线DA 1B 1C 1D 1A 2…是由一段段90度的弧组成的．其中：xx 1̂的圆心为点A ，半径为AD ；x 1x 1̂的圆心为点B ，半径为BA 1；x 1x 1̂的圆心为点C ，半径为CB 1；x 1x 1̂的圆心为点D ，半径为DC 1；⋯xx 1̂，x 1x 1̂，x 1x 1̂，x 1x 1̂，…的圆心依次按点A ，B ，C ，D 循环．若正方形ABCD 的边长为1，则x 2020x 2020̂的长是 4039π．【解答】解：由图可知，曲线DA 1B 1C 1D 1A 2…是由一段段90度的弧组成的，半径每次比前一段弧半径+1，AD ＝AA 1＝1，BA 1＝BB 1＝2，……，AD n ﹣1＝AA n ＝4（n ﹣1）+1，BA n ＝BB n ＝4（n ﹣1）+2，故x 2020x 2020̂的半径为BA 2020＝BB 2020＝4（2020﹣1）+2＝8078，x 2020x 2020̂的弧长=90180×8078x =4039x ．故答案为：4039π．17．（2020某某达州）已知k 为正整数，无论k 取何值，直线11：y ＝kx +k +1与直线12：y ＝（k +1）x +k +2都交于一个固定的点，这个点的坐标是 （﹣1，1） ；记直线11和12与x 轴围成的三角形面积为S k ，则S 1＝14，S 1+S 2+S 3+…+S 100的值为50101．【解答】解：∵直线11：y ＝kx +k +1＝k （x +1）+1， ∴直线12：y ＝（k +1）x +k +2经过点（﹣1，1）；∵直线12：y ＝（k +1）x +k +2＝k （x +1）+（x +1）+1＝（k +1）（x +1）+1， ∴直线12：y ＝（k +1）x +k +2经过点（﹣1，1）．∴无论k 取何值，直线l 1与l 2的交点均为定点（﹣1，1）．∵直线11：y ＝kx +k +1与x 轴的交点为（−x +1x，0）， 直线12：y ＝（k +1）x +k +2与x 轴的交点为（−x +2x +1，0）， ∴S K =12×|−x +1x +x +2x +1|×1=12x (x +1)， ∴S 1=12×11×2=14；∴S 1+S 2+S 3+…+S 100=12[11×2+12×3+⋯1100×101] =12[（1−12）+（12−13）+…+（1100−1101）] =12×（1−1101）=12×100101=50101．故答案为（﹣1，1）；14；50101．18．（2020某某某某）如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中“▱”的个数为a 1，第2幅图中“▱”的个数为a 2，第3幅图中“▱”的个数为a 3，…，以此类推，若2x 1+2x 2+2x 3+⋯+2x x=x2020．（n 为正整数），则n 的值为 4039 ．【解答】解：由图形知a 1＝1×2，a 2＝2×3，a 3＝3×4， ∴a n ＝n （n +1），∵2x 1+2x 2+2x 3+⋯+2x x=x2020，∴21×2+22×3+23×4+⋯+2x (x +1)=x2020， ∴2×（1−12+12−13+13−14+⋯⋯+1x −1x +1）=x 2020， ∴2×（1−1x +1）=x2020， 1−1x +1=x4040， 解得n ＝4039，经检验：n ＝4039是分式方程的解， 故答案为：4039．19．（2020某某某某）如图，直线y =−√3x +b 与y 轴交于点A ，与双曲线y =xx 在第三象限交于B 、C 两点，且AB •AC ＝16．下列等边三角形△OD 1E 1，△E 1D 2E 2，△E 2D 3E 3，…的边OE 1，E 1E 2，E 2E 3，…在x 轴上，顶点D 1，D 2，D 3，…在该双曲线第一象限的分支上，则k ＝ 4√3，前25个等边三角形的周长之和为 60 ．【解答】解：设直线y =−√3x +b 与x 轴交于点D ，作BE ⊥y 轴于E ，CF ⊥y 轴于F ． ∵y =−√3x +b ，∴当y ＝0时，x =√33b ，即点D 的坐标为（√33b ，0）， 当x ＝0时，y ＝b ，即A 点坐标为（0，b ），∴OA ＝﹣b ，OD =−√33b ．∵在Rt △AOD 中，tan ∠ADO =xxxx=√3，∴∠ADO ＝60°．∵直线y =−√3x +b 与双曲线y =x x在第三象限交于B 、C 两点，∴−√3x +b =xx ，整理得，−√3x 2+bx ﹣k ＝0，由韦达定理得：x 1x 2=√33k ，即EB •FC =√33k ，∵xxxx =cos60°=12， ∴AB ＝2EB ，同理可得：AC＝2FC，k＝16，∴AB•AC＝（2EB）（2FC）＝4EB•FC=4√33解得：k＝4√3．由题意可以假设D1（m，m√3），∴m2•√3=4√3，∴m＝2∴OE1＝4，即第一个三角形的周长为12，设D2（4+n，√3n），∵（4+n）•√3n＝4√3，解得n＝2√2−2，∴E1E2＝4√2−4，即第二个三角形的周长为12√2−12，设D3（4√2+a，√3a），由题意（4√2+a）•√3a＝4√3，解得a＝2√3−2√2，即第三个三角形的周长为12√3−12√2，…，∴第四个三角形的周长为12√4−12√3，∴前25个等边三角形的周长之和12+12√2−12+12√3−12√2+12√4−12√3+⋯+12√25−12√24=12√25=60，故答案为4√3，60．。

中考数学选择填空压轴题一、动点问题1．如图，C为⊙O直径AB上一动点，过点C的直线交⊙O于D、E两点，且∠ACD=45°，DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时，设AF=x，DE=y，以下中图象中，能表示y与x的函数关系式的图象大体是（）2．如图，A，B，C，D为圆O的四均分点，动点P从圆心O出发，沿O—C—D—O路线作匀速运动，设运动时间为x（s）．∠APB=y（°），右图函数图象表示y与x之间函数关系，则点M的横坐标应为．3．如图，AB是⊙O的直径，且AB=10，弦MN的长为8，若弦MN的两端在圆上滑动时，一直与AB订交，记点A、B到MN的距离分别为h1，h2，则|h1－h2|等于（）A、5B、6C、7D、84．如图，已知Rt△ABC的直角边AC=24，斜边AB=25，一个以点P为圆心、半径为1的圆在△ABC内部沿顺时针方向转动，且运动过程中⊙P向来保持与△ABC的边相切，当点P第一次回到它的初始地点时所经过路径的长度是（）A .56B.25C.112D.56 335．在△ABC中，ABAC12cm，BC6cm，D为BC的中点，动点P从B点出发，以每秒1cm的速度沿B A C的方向运动．设运动时间为t，那么当t秒时，过D、P两点的直线将△ABC的周长分成两个部分，使此中一部分是另一部分的2倍．6．如图,正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动．假如Q点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从B点出发，沿图中所示方向按B→C→D→A→B 滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为（）A．2B．4πC．πD．π1A DA DQM中，AB F EEFGB7．如图，矩形ABCD3cm，AD 6cm，点E为AB边上的任意一点，四边形也是矩形，EF2BE，△（）2．S cm且则B C AFC G B CRA．8B．9C．83D．938．△ABC是⊙O的内接三角形，∠BAC＝60°，D是的中点，AD＝ａ，则四边形ABDC的面积为．9．如图，ADA B在梯形中，PBMCAD ∥BC ，ABC90°，AD AB 6，BC14，点M 是线段 BC 上必定点，且MC =8．动点P 从C 点出发沿CDA B 的路线运动，运动到点 B 停止．在点P 的运动过程中，使△PMC 为等腰三角形的点P 有个10．如图在边长为2的正方形ABCD 中，E ，F ，O 分别是AB ，CD ，AD 的中点，以O 为圆心，以OE 为半径画弧EF.P 是 上的一个动点，连接 OP ，并延长OP 交线段BC 于点K ，过点P作⊙O 的切线，分别交射线AB 于点M ，交直线BC 于点G.若BG3，则BK ﹦.BM二、面积与长度问题AOD1．如图，△ABC 是直角边长为a 的等腰直角三半圆O 1的直径，半圆EFMO 2过C 点且与半圆 O 1相切，则图中暗影部A ．7a 2B ．5a 2BK CG3636D ．5a 236角形，直角边AB 是分的面积是（）72C ．a2．如图，在x 轴上有五个点，它们的横坐标挨次为l ，2，3，4，5．分别过这些点作 x 轴的垂线与三条直线y=ax ，y=(a+1)x ，y=(a+2)x订交，此中a>0．则图中暗影部分的面积是( )A ．12．5B ．25C ．12．5aD ．25a3．如图，在反比率函数y2 0）的图象上，有点P 1，P 2，P 3，P 41，（x，它们的横坐标挨次为x2 ，，．分别过这些点作 x 轴与y 轴的垂线，图中所构成的暗影部分的面积从左到右挨次为3 4S 1，S 2，S 3，则S 1S 2S 3．yP 1P 2P 3P 4O1234x4．已知,A 、B 、C 、D 、E 是反比率函数y16（x>0）图象上五个整数点（横、纵坐标均为整数），x分别以这些点向横轴或纵轴作垂线段， 由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，构成如图 5所示的五个橄榄形（暗影部分） ，则这五个橄榄形的面积总和是（用含π的代数式表示）5．如图，在x 轴的正半轴上挨次截取OA 1 A 1A 2yA 2A 3A 3A 4A 4A 5，P 1P 2P 3P 4P 5OA 1A 2A 3A 4A 5x过点A 1、A 2、A 3、A 4、A 5分别作x 轴的垂线与反比率函数y 2xx的图象订交于点 P 1、P 2、P 3、P 4、P 5，得直角三角形(暗影部分)并设其面积分别为S 、S 、S 、S 、S ，．1234 5则S 5的值为6．如图，把一个棱长为 3的正方体的每个面均分成 9个小正方形，而后沿每个面正中心的一个正方形向里挖空（相当于挖去了7个小正方体），所获得的几何体的表面积是（）A ．78B ．72C ．54D ．487．如图，平行于y 轴的直线l 被抛物线y ＝1x21、y ＝1x 21 所截．当直22线l 向右平移 3个单位时，直线l 被两条抛物线所截得的线段扫过的图形面 积为平方单位．8．如图，在 Rt △ABC中，∠C90°，AC4，BC2，AC、 BC为直径画半圆，则图分别以中暗影部分的面积为．（结果保留 ）9．如图，Rt △ABC 中，ACB 90，CAB30，BC 2，O ，H 分别为边AB ，AC 的中点，将△ABC 绕点B 顺时针旋转120到△的地点，则整个旋转过程中线段 OH 所扫A 1BC 1 HC过部分的面积（即暗影部分面积）为（）AOBA ．7π73B ．4π73C ．πD ．4π33 838310．如图，正方形ABCD 的面积为 12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD PE 的和最小，则这个最小值为（）A ．23B ．26C ．3D ．611．如AD 图△ABCC，在锐角中 ，PAB4 2，BAC45°，BAC 的均分线交EDMBC于点D ，M 、N 分别是AD和AB 上的动点，则BCBMMN 的最小值是AN___________．B12．如图，在矩形ABCD 中，AB=3，AD=4，点P 在AD 上，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE+PF等于（ ）Ａ．7Ｂ．12Ｃ．13Ｄ．14555513．正方AP D形ABCD中，E 是BC 边上一点， E以E 为F 圆心、EC为半径的半圆与以A 为圆BC心，AB 为半径的圆弧外切，则sin EAB 的值为（）43C ．4 D ．3A ．B ．553414．在Rt △ABC 内有边长分别为 a,b,c 的三个正方形，则a,b,c 满足关系式．15．一张等腰三角形纸片，底边长l5cm ，底边上的高长22．5cm ．现 沿底边挨次从下往上裁剪宽度均为 3cm的矩形纸条，以以下图．已知剪得的纸条中有一张是正方形，则这 张正方形纸条是( )A ．第4张B．第5张C.第6张D．第7张16．如图，等腰△ABC 中，底边BCa ，A 36，ABC 的均分线交AC 于D ，BCD 的均分线交BD 于E ，设k51，则DE（）2A ．k 2aB ．k 3aC ．aD ．aAk 2k 3C ，大部分圆M 的弦AB 与小半圆N 相切于点F ，17．如图，直径分别为CD 、CE 的两个半圆相切于点 且AB ∥CD ，AB=4，设弧CD 、弧CE 的长分别为x 、y ，线段ED 的长为z ，则z （x+y ）=.三、多结论问题DAC ，D 、E 是斜边BC 上两点，且∠DAE=45°，将△ADC1．如图，在Rt △ABC 中，AB E绕点A 顺时针旋转90后，获得△AFB ，连接EF ，以下结论：BC①△AED ≌△AEF ；②△ABE ∽△ACD ；③BEDC DE ；④BE 2 DC 2DE 2此中必定正确的选项是（）A ．②④B ．①③C ．②③D ．①④2．如图，在等腰Rt △ABC 中，∠C=90o ，AC=8，F 是AB 边上的中点，点 D 、E 分别在AC 、BC边上运动，且保持AD=CE ，连接DE 、DF 、EF 。

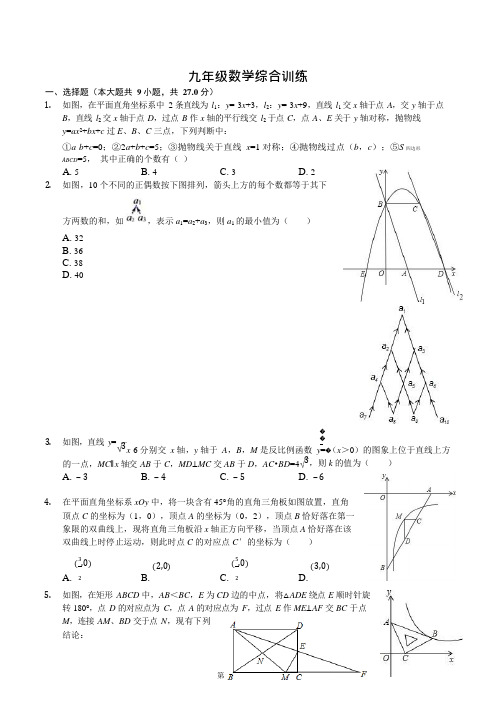
九年级数学综合训练一、选择题（本大题共9 小题，共27.0 分）1.如图，在平面直角坐标系中2 条直线为l1：y=-3x+3，l2：y=-3x+9，直线l1交x 轴于点A，交y 轴于点B，直线l2交x 轴于点D，过点B 作x 轴的平行线交l2于点C，点A、E 关于y 轴对称，抛物线y=ax2+bx+c 过E、B、C 三点，下列判断中：①a-b+c=0；②2a+b+c=5；③抛物线关于直线x=1 对称；④抛物线过点（b，c）；⑤S 四边形ABCD=5，其中正确的个数有（）A. 5B. 4C. 3D. 22.如图，10 个不同的正偶数按下图排列，箭头上方的每个数都等于其下方两数的和，如，表示a1=a2+a3，则a1的最小值为（）A.32B.36C.38D.403.如图，直线y= ��x -6 分别交x 轴，y 轴于A，B，M 是反比例函数y=�（x＞0）的图象上位于直线上方的一点，MC∥x 轴交AB 于C，MD⊥MC 交AB 于D，AC•BD=43，则k 的值为（）A. ‒ 3B. ‒ 4C. ‒ 5D. ‒ 64.在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐标为（1，0），顶点A 的坐标为（0，2），顶点B 恰好落在第一象限的双曲线上，现将直角三角板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点C′的坐标为（）(3,0) (2,0) (5,0) (3,0)A. 2B.C. 2D.5.如图，在矩形ABCD 中，AB＜BC，E 为CD 边的中点，将△ADE 绕点E 顺时针旋转180°，点D 的对应点为C，点A 的对应点为F，过点E 作ME⊥AF 交BC 于点M，连接AM、BD 交于点N，现有下列结论：35 ①AM =AD +MC ；②AM =DE +BM ；③DE 2=AD •CM ；④点 N 为△ABM 的外心． 其中正确的个数为（）A. 1 个B. 2 个C. 3 个D. 4 个6. 规定：如果关于 x 的一元二次方程 ax 2+bx +c =0（a ≠0）有两个实数根，且其中一个根是另一个根的 2倍，则称这样的方程为“倍根方程”．现有下列结论：①方程 x 2+2x -8=0 是倍根方程；②若关于 x 的方程 x 2+ax +2=0 是倍根方程，则 a =±3；③若关于 x 的方程 ax 2-6ax +c =0（a ≠0）是倍根方程，则抛物线 y =ax 2-6ax +c 与 x 轴的公共点的坐标是 （2，0）和（4，0）； 4 ④若点（m ，n ）在反比例函数 y =x 的图象上，则关于 x 的方程 mx 2+5x +n =0 是倍根方程． 上述结论中正确的有（ ）A. ①②B. ③④C. ②③D. ②④7. 如图，六边形 ABCDEF 的内角都相等，∠DAB =60°，AB =DE ，则下列结论成立的个数是（） ①AB ∥DE ；②EF ∥AD ∥BC ；③AF =CD ；④四边形 ACDF 是平行四边形；⑤六边形 ABCDEF 既是中心对称图形，又是轴对称图形．A. 2B. 3C. 4D. 58. 如图，在 Rt △ABC 中，∠C =90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）A. 4B. 5C. 6D. 79. 如图，矩形 ABCD 中，AE ⊥BD 于点 E ，CF 平分∠BCD ，交 EA 的延长线于点 F ，且 BC =4，CD =2，给出下列结论：①∠BAE =∠CAD ；4②∠DBC =30°；③AE =5 5；④AF =2 ，其中正确结论的个数有（ ）A. 1 个B. 2 个C. 3 个D. 4 个二、填空题（本大题共 10 小题，共 30.0 分）10.如图，在Rt△ABC 中，∠BAC=30°，以直角边AB 为直径作半圆交AC 于点D，以AD 为边作等边△ADE，延长ED 交BC 于点F，BC=2 3，则图中阴影部分的面积为．（结果不取近似值）11.如图，在6×6 的网格内填入1 至6 的数字后，使每行、每列、每个小粗线宫中的数字不重复，则a×c=．12.如图，正方形ABCD 中，BE=EF=FC，CG=2GD，BG 分别交AE，AF 于M，N．下列结论：4 �M 3 1①AF⊥BG；②BN=3NF；③M G=8；④S 四边形CGNF=2S 四边形ANGD．其中正确的结论的序号是．13.已知：如图，在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm．将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB 的交点D 恰好为AB 的中点，则线段B1D= cm．14.如图，边长为4 的正六边形ABCDEF 的中心与坐标原点O 重合，AF∥x 轴，将正六边形ABCDEF 绕原点O 顺时针旋转n 次，每次旋转60°．当n=2017 时，顶点A 的坐标为．15.如图，在Rt△ABC 中，BC=2，∠BAC=30°，斜边AB 的两个端点分别在相互垂直的射线OM、ON 上滑动，下列结论：①若C、O 两点关于AB 对称，则OA=2 3；②C、O 两点距离的最大值为4；③若AB 平分CO，则AB⊥CO；�④斜边AB 的中点D 运动路径的长为2；其中正确的是（把你认为正确结论的序号都填上）．16.如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N（3，0）是OB 上的一定点，点M 是ON 的中点，∠AOB=30°，要使PM+PN 最小，则点P 的坐标为．17.在一条笔直的公路上有A、B、C 三地，C 地位于A、B 两地之间，甲车从A地沿这条公路匀速驶向C 地，乙车从B 地沿这条公路匀速驶向A 地，在甲车出发至甲车到达C 地的过程中，甲、乙两车各自与C 地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h 时，两车相遇；②乙车出发1.5h 时，两车相距170km；③乙车出5发27h 时，两车相遇；④甲车到达C 地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．�18.如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y=x（x＞0）的图象经过A，B 两点．若点A 的坐标为（n，1），则k 的值为．19.如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A（-1，1），B（0，-2），C（1，0），点P（0，2）绕点A 旋转180°得到点P1，点P1绕点B 旋转180°得到点P2，点P2绕点C 旋转180°得到点P3，点P3绕点A 旋转180°得到点P4，…，按此作法进行下去，则点P2017的坐标为．答案和解析1.【答案】C【解析】解：∵直线l1：y=-3x+3 交x 轴于点A，交y 轴于点B，∴A（1，0），B（0，3），∵点A、E 关于y 轴对称，∴E（-1，0）．∵直线l2：y=-3x+9 交x 轴于点D，过点B 作x 轴的平行线交l2 于点C，∴D（3，0），C 点纵坐标与B 点纵坐标相同都是3，把y=3 代入y=-3x+9，得3=-3x+9，解得x=2，∴C（2，3）．∵抛物线y=ax2+bx+c 过E、B、C 三点，∴，解得，∴y=-x2+2x+3．①∵抛物线y=ax2+bx+c 过E（-1，0），∴a-b+c=0，故①正确；②∵a=-1，b=2，c=3，∴2a+b+c=-2+2+3=3≠5，故②错误；③∵抛物线过B（0，3），C（2，3）两点，∴对称轴是直线x=1，∴抛物线关于直线x=1 对称，故③正确；④∵b=2，c=3，抛物线过C（2，3）点，∴抛物线过点（b，c），故④正确；⑤∵直线l1∥l2，即AB∥CD，又BC∥AD，∴四边形ABCD 是平行四边形，∴S 四边形ABCD=BC•OB=2×3=6≠5，故⑤错误．综上可知，正确的结论有3个．故选：C．根据直线l1的解析式求出A（1，0），B（0，3），根据关于y 轴对称的两点坐标特征求出E（- 1，0）．根据平行于x 轴的直线上任意两点纵坐标相同得出C 点纵坐标与B 点纵坐标相同都是3，再根据二次函数图象上点的坐标特征求出C（2，3）．利用待定系数法求出抛物线的解析式为y=-x2+2x+3，进而判断各选项即可．本题考查了抛物线与x 轴的交点，一次函数、二次函数图象上点的坐标特征，关于y 轴对称的两点坐标特征，平行于x 轴的直线上任意两点坐标特征，待定系数法求抛物线的解析式，平行四边形的判定及面积公式，综合性较强，求出抛物线的解析式是解题的关键．2.【答案】D【解析】解：∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3（a8+a9）+a10，∴要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，∵a5=a8+a9=6，则a7、a10 中不能有6，若a7=8、a10=10，则a4=10=a10，不符合题意，舍去；若a7=10、a10=8，则a4=12、a6=4+8=12，不符合题意，舍去；若a7=10、a10=12，则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40，符合题意；综上，a1的最小值为40，故选：D．由a1=a7+3（a8+a9）+a10 知要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，根据a5=a8+a9=6，则a7、a10 中不能有6，据此对于a7、a8，分别取8、10、12 检验可得，从而得出答案．本题主要考查数字的变化类，根据题目要求得出a1取得最小值的切入点是解题的关键．3.【答案】A【解析】解：过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，令x=0 代入y= x-6，∴y=-6，∴B（0，-6），∴OB=6，令y=0 代入y= x-6，∴x=2 ，∴（2 ，0），∴OA=2 ，∴勾股定理可知：AB=4 ，∴sin∠OAB= = ，cos∠OAB= =设M（x，y），∴CF=-y，ED=x，∴sin∠OAB= ，∴AC=- y，∵cos∠OAB=cos∠EDB= ，∴BD=2x，∵AC•BD=4，∴- y×2x=4 ，∴xy=-3，∵M 在反比例函数的图象上，∴k=xy=-3，故选（A）过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，然后求出OA 与OB 的长度，即可求出∠OAB 的正弦值与余弦值，再设M（x，y），从而可表示出BD 与AC 的长度，根据AC•BD=4列出即可求出k 的值．本题考查反比例函数与一次函数的综合问题，解题的关键是根据∠OAB 的锐角三角函数值求出BD、AC，本题属于中等题型．4.【答案】C【解析】解：过点B 作BD⊥x 轴于点D，∵∠ACO+∠BCD=90°，∠OAC+∠ACO=90°，∴∠OAC=∠BCD，在△ACO 与△BCD 中，∴△ACO➴△BCD（AAS）∴OC=BD，OA=CD，∵A（0，2），C（1，0）∴OD=3，BD=1，∴B（3，1），∴设反比例函数的解析式为y= ，将B（3，1）代入y= ，∴k=3，∴y= ，∴把y=2 代入y= ，∴x= ，当顶点A 恰好落在该双曲线上时，此时点A 移动了个单位长度，∴C 也移动了个单位长度，此时点C 的对应点C′的坐标为（，0）故选：C．过点B 作BD⊥x 轴于点D，易证△ACO➴△BCD（AAS），从而可求出B 的坐标，进而可求出反比例函数的解析式，根据解析式与 A 的坐标即可得知平移的单位长度，从而求出 C 的对应点．本题考查反比例函数的综合问题，涉及全等三角形的性质与判定，反比例函数的解析式，平移的性质等知识，综合程度较高，属于中等题型．5.【答案】B【解析】解：∵E 为CD 边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE➴△FCE，∴AD=CF，AE=FE，又∵ME⊥AF，∴ME 垂直平分AF，∴AM=MF=MC+CF，∴AM=MC+AD，故①正确；如图，延长CB 至G，使得∠BAG=∠DAE，由AM=MF，AD∥BF，可得∠DAE=∠F=∠EAM，可设∠BAG=∠DAE=∠EAM=α，∠BAM=β，则∠AED=∠EAB=∠GAM=α+β，由∠BAG=∠DAE，∠ABG=∠ADE=90°，可得△ABG∽△ADE，∴∠G=∠AED=α+β，∴∠G=∠GAM，∴AM=GM=BG+BM，由△ABG∽△ADE，可得= ，而AB＜BC=AD，∴BG＜DE，∴BG+BM＜DE+BM，即AM＜DE+BM，∴AM=DE+BM 不成立，故②错误；∵ME⊥FF，EC⊥MF，∴EC2=CM×CF，又∵EC=DE，AD=CF，∴DE2=AD•CM，故③正确；∵∠ABM=90°，∴AM 是△ABM 的❧➓圆的直径，∵BM＜AD，∴当BM∥AD 时，= ＜1，∴N 不是AM 的中点，∴点N 不是△ABM 的❧心，故④错误．综上所述，正确的结论有2 个，故选：B．根据全等三角形的性质以及线段垂直平分线的性质，即可得出AM=MC+AD；根据△ABG∽△ ADE，且AB＜BC，即可得出BG＜DE，再根据AM=GM=BG+BM，即可得出AM=DE+BM 不成立；根据ME⊥FF，EC⊥MF，运用射影定理即可得出EC2=CM×CF，据此可得DE2=AD•CM 成立；根据N 不是AM 的中点，可得点N 不是△ABM 的❧心．本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质以及旋转的性质的综合应用，解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导，解题时注意：三角形❧➓圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的❧心，故❧心到三角形三个顶点的距离相等．6.【答案】C【解析】解：①由x2-2x-8=0，得（x-4）（x+2）=0，解得x1=4，x2=-2，∵x1≠2x2，或x2≠2x1，1 1 ∴方程 x 2-2x-8=0 不是倍根方程． 故①错误；②关于 x 的方程 x 2+ax+2=0 是倍根方程，∴设 x 2=2x 1，∴x 1•x 2=2x 2=2，∴x 1=±1，当 x 1=1 时 ，x 2=2，当 x 1=-1 时 ，x 2=-2，∴x 1+x 2=-a=±3，∴a=±3，故②正确；③关于 x 的方程 ax 2-6ax+c=0（a≠0）是倍根方程，∴x 2=2x 1，∵抛物线 y=ax 2-6ax+c 的对称轴是直线 x=3，∴抛物线 y=ax 2-6ax+c 与 x 轴的交点的坐标是（2，0）和（4，0），故③正确；④∵点（m ，n ）在反比例函数 y= 的图象上，∴mn=4，解 mx 2+5x+n=0 得 x 1=- ，x 2=- ，∴x 2=4x 1，∴关于 x 的方程 mx 2+5x+n=0 不是倍根方程；故选：C ．①通过解方程得到该方程的根，结合“倍根方程”的定义进行判断；②设 x 2=2x 1，得到 x 1•x 2=2x 2=2，得到当 x 1=1 时，x 2=2，当 x 1=-1 时，x 2=-2，于是得到结论；③根据“倍根方程”的定义即可得到结论；④若点（m，n）在反比例函数y= 的图象上，得到mn=4，然后解方程mx2+5x+n=0 即可得到正确的结论；本题考查了反比例函数图象上点的坐标特征，根与系数的关系，正确的理解倍根方程的定义是解题的关键．7.【答案】D【解析】解：∵六边形ABCDEF 的内角都相等，∴∠EFA=∠FED=∠FAB=∠ABC=120°，∵∠DAB=60°，∴∠DAF=60°，∴∠EFA+∠DAF=180°，∠DAB+∠ABC=180°，∴AD∥EF∥CB，故②正确，∴∠FED+∠EDA=180°，∴∠EDA=∠ADC=60°，∴∠EDA=∠DAB，∴AB∥DE，故①正确，∵∠FAD=∠EDA，∠CDA=∠BAD，EF∥AD∥BC，∴四边形EFAD，四边形BCDA 是等腰梯形，∴AF=DE，AB=CD，∵AB=DE，∴AF=CD，故③正确，连➓CF 与AD 交于点O，连➓DF、AC、AE、DB、BE．∵∠CDA=∠DAF，∴AF∥CD，AF=CD，∴四边形AFDC 是平行四边形，故④正确，同法可证四边形AEDB 是平行四边形，∴AD 与CF，AD 与BE 互相平分，∴OF=OC，OE=OB，OA=OD，∴六边形ABCDEF 既是中心对称图形，故⑤正确，故选D．根据六边形ABCDEF 的内角都相等，∠DAB=60°，平行线的判定，平行四边形的判定，中心对称图形的定义一一判断即可．本题考查平行四边形的判定和性质、平行线的判定和性质、轴对称图形、中心对称图形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．8.【答案】D【解析】解：如图：故选：D．①以B 为圆心，BC 长为半径画弧，交AB 于点D，△BCD 就是等腰三角形；②以A 为圆心，AC 长为半径画弧，交AB 于点E，△ACE 就是等腰三角形；③以C 为圆心，BC 长为半径画弧，交AC 于点F，△BCF 就是等腰三角形；④以C 为圆心，BC 长为半径画弧，交AB 于点K，△BCK 就是等腰三角形；⑤作AB 的垂直平分线交AC 于G，则△AGB 是等腰三角形；➅作BC 的垂直平分线交AB 于I，则△BCI 和△ACI 是等腰三角形．本题考查了等腰三角形的判定的应用，主要考查学生的理解能力和动手操作能力．9.【答案】C【解析】解：在矩形ABCD 中，∵∠BAD=90°，∵AE⊥BD，∴∠AED=90°，∴∠ADE+∠DAE=∠DAE+∠BAE=90°，∴∠BAE=∠ADB，∵∠CAD=∠ADB，∴∠BAE=∠CAD，故①正确；∵BC=4，CD=2，∴tan∠DBC= = ，∴∠DBC≠30°，故②错误；∵BD= =2 ，∵AB=CD=2，AD=BC=4，∵△ABE∽△DBA，∴，即，∴AE= ；故③正确；∵CF 平分∠BCD，∴∠BCF=45°，∴∠ACF=45°-∠ACB，∵AD∥BC，∴∠DAC=∠BAE=∠ACB，∴∠EAC=90°-2∠ACB，∴∠EAC=2∠ACF，∵∠EAC=∠ACF+∠F，∴∠ACF=∠F，∴AF=AC，∵AC=BD=2 ，∴AF=2 ，故④正确；故选C．根据余角的性质得到∠BAE=∠ADB，等量代换得到∠BAE=∠CAD，故①正确；根据三角函数的定义得到tan∠DBC= = ，于是得到∠DBC≠30°，故②错误；由勾股定理得到BD==2 ，根据相似三角形的性质得到AE= ；故③正确；根据角平分线的定义得到∠BCF=45°，求得∠ACF=45°-∠ACB，推出∠EAC=2∠ACF，根据❧角的性质得到∠EAC=∠ACF+∠F，得到∠ACF=∠F，根据等腰三角形的判定得到AF=AC，于是得到AF=2 ，故④正确．本题考查了矩形的性质，相似三角形的判定和性质，三角形的❧角的性质，角平分线的定义，熟练掌握相似三角形的判定和性质是解题的关键．10.【答案】3【解析】3 3-2π解：如图所示：设半圆的圆心为O，连➓DO，过D 作DG⊥AB 于点G，过D 作DN⊥CB 于点N，∵在Rt△ABC 中，∠BAC=30°，∴∠ACB=60°，∠ABC=90°，∵以AD 为边作等边△ADE，∴∠EAD=60°，∴∠EAB=60°+30°=90°，可得：AE∥BC，则△ADE∽△CDF，∴△CDF 是等边三角形，∵在Rt△ABC 中，∠BAC=30°，BC=2 ，∴AC=4 ，AB=6，∠DOG=60°，则AO=BO=3，故DG=DO•sin60°=，则AD=3 ，DC=AC-AD= ，故DN=DC•sin60°=×= ，则S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF= ×2 ×6- ×3×- - × ×=3 - π．故答案为：3 - π．根据题意结合等边三角形的性质分别得出AB，AC，AD，DC 的长，进而利用S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF 求出答案．此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识，正确分割图形是解题关键．11.【答案】2【解析】解：对各个小宫格编号如下：先看己：已经有了数字3、5、6，缺少1、2、4；观察发现：4 不能在第四列，2 不能在第五列，而2 不能在第六列；所以2 只能在第六行第四列，即a=2；则b 和c 有一个是1，有一个是4，不确定，如下：观察上图发现：第四列已经有数字2、3、4、6，缺少1 和5，由于5 不能在第二行，所以5 在第四行，那么1 在第二行；如下：再看乙部分：已经有了数字1、2、3，缺少数字4、5、6，观察上图发现：5 不能在第六列，所以5在第五列的第一行；4 和6 在第六列的第一行和第二行，不确定，分两种情况：①当4 在第一行时，6 在第二行；那么第二行第二列就是4，如下：再看甲部分：已经有了数字1、3、4、5，缺少数字2、6，观察上图发现：2 不能在第三列，所以2 在第二列，则6 在第三列的第一行，如下：观察上图可知：第三列少1 和4，4 不能在第三行，所以4 在第五行，则1 在第三行，如下：观察上图可知：第五行缺少1 和2，1 不能在第1 列，所以1 在第五列，则2 在第一列，即c=1，所以b=4，如下：观察上图可知：第六列缺少1 和2，1 不能在第三行，则在第四行，所以2 在第三行，如下：再看戊部分：已经有了数字2、3、4、5，缺少数字1、6，观察上图发现：1 不能在第一列，所以1 在第二列，则6 在第一列，如下：观察上图可知：第一列缺少3 和4，4 不能在第三行，所以4 在第四行，则3 在第三行，如下：观察上图可知：第二列缺少5 和6，5 不能在第四行，所以5 在第三行，则6 在第四行，如下：观察上图可知：第三行第五列少6，第四行第五列少3，如下：所以，a=2，c=1，ac=2；②当6 在第一行，4 在第二行时，那么第二行第二列就是6，如下：再看甲部分：已经有了数字1、3、5、6，缺少数字2、4，观察上图发现：2 不能在第三列，所以2 在第2 列，4 在第三列，如下：观察上图可知：第三列缺少数字1 和6，6 不能在第五行，所以6 在第三行，则1 在第五行，所以c=4，b=1，如下：观察上图可知：第五列缺少数字3 和6，6 不能在第三行，所以6 在第四行，则3 在第三行，如下：观察上图可知：第六列缺少数字1 和2，2 不能在第四行，所以2 在第三行，则1 在第四行，如下：观察上图可知：第三行缺少数字1 和5，1 和5 都不能在第一列，所以此种情况不成立；综上所述：a=2，c=1，a×c=2；故答案为：2．粗线把这个数独分成了6 块，为了便于解答，对各部分进行编号：甲、乙、丙、丁、戊、己，先从各部分中数字最多的己出发，找出其各个小方格里面的数，再根据每行、每列、每小宫格都不出现重复的数字进行推算．本题是六阶数独，比较复杂，关键是找出突破口，先推算出一个区域或者一行、一列，再逐步的进行推算．12.【答案】①③【解析】解：①∵四边形ABCD 为正方形，∴AB=BC=CD，∵BE=EF=FC，CG=2GD，∴BF=CG，∵在△ABF 和△BCG 中，，∴△ABF➴△BCG，∴∠BAF=∠CBG，∵∠BAF+∠BFA=90°，∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；②∵在△BNF 和△BCG 中，，∴△BNF∽△BCG，∴ = = ，∴BN= NF；②错误；③作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，AF= = ，∵S△ABF= AF•BN=AB•BF，∴BN= ，NF= BN= ，∴AN=AF-NF= ，∵E 是BF 中点，∴EH 是△BFN 的中位线，∴EH= ，NH= ，BN∥EH，∴AH= ， = ，解得：MN= ，∴BM=BN-MN= ，MG=BG-BM= ，∴ = ；③正确；④连➓AG，FG，根据③中结论，则NG=BG-BN= ，∵S 四边形CGNF=S△CFG+S△GNF= CG•CF+NF•NG=1+= ，S 四边形ANGD=S△ANG+S△ADG= AN•GN+AD•DG= + = ，∴S 四边形CGNF≠S 四边形ANGD，④错误；故答案为①③．①易证△ABF➴△BCG，即可解题；②易证△BNF∽△BCG，即可求得的值，即可解题；③作EH⊥AF，令AB=3，即可求得MN，BM 的值，即可解题；④连➓AG，FG，根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD，即可解题．本题考查了全等三角形的判定和性质，考查了相似三角形的判定和对应边成比例的性质，本题中令AB=3 求得AN，BN，NG，NF 的值是解题的关键．13.【答案】1.5【解析】解：∵在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm，∴AB= =5cm，∵点D 为AB 的中点，∴OD= AB=2.5cm．∵将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1 处，∴OB1=OB=4cm，∴B1D=OB1-OD=1.5cm．故答案为1.5．先在直角△AOB 中利用勾股定理求出AB= =5cm，再利用直角三角形斜边上的中线等于斜边的一半得出OD= AB=2.5cm．然后根据旋转的性质得到OB1=OB=4cm，那么B1D=OB1-OD=1.5cm．本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理．14.【答案】（2，2 3）【解析】解：2017×60°÷360°=336…1，即与正六边形ABCDEF 绕原点O 顺时针旋转1 次时点A 的坐标是一样的．当点A 按顺时针旋转60°时，与原F 点重合．连➓OF，过点F 作FH⊥x 轴，垂足为H；由已知EF=4，∠FOE=60°（正六边形的性质），∴△OEF 是等边三角形，∴OF=EF=4，∴F（2，2 ），即旋转2017 后点A 的坐标是（2，2 ），故答案是：（2，2 ）．将正六边形ABCDEF 绕原点O 顺时针旋转2017 次时，点A 所在的位置就是原F 点所在的位置．此题主要考查了正六边形的性质，坐标与图形的性质-旋转．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．15.【答案】①②③【解析】解：在Rt△ABC 中，∵BC=2，∠BAC=30°，∴AB=4，AC= =2 ，①若C、O 两点关于AB 对称，如图1，∴AB 是OC 的垂直平分线，则OA=AC=2 ；所以①正确；②如图1，取AB 的中点为E，连➓OE、CE，∵∠AOB=∠ACB=90°，∴OE=CE= AB=2，当OC 经过点E 时，OC 最大，则C、O 两点距离的最大值为4；所以②正确；③如图2，同理取AB 的中点E，则OE=CE，∵AB 平分CO，∴OF=CF，∴AB⊥OC，所以③正确；④如图3，斜边AB 的中点D 运动路径是：以O 为圆心，以2 为半径的圆周的，则：=π．所以④不正确；综上所述，本题正确的有：①②③；故答案为：①②③．①先根据直角三角形30°的性质和勾股定理分别求AC 和AB，由对称的性质可知：AB 是OC 的垂直平分线，所以OA=AC；②当OC 经过AB 的中点E 时，OC 最大，则C、O 两点距离的最大值为4；③如图2，根据等腰三角形三线合一可知：AB⊥OC；④如图3，半径为2，圆心角为90°，根据弧长公式进行计算即可．本题是三角形的综合题，考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式，熟练掌握直角三角形斜边中线等于斜边一半是本题的关键，难度适中．3 316.【答案】（2， 2 ）【解析】解：作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，∵OA 垂直平分NN′，∴ON=ON′，∠N′ON=2∠AON=60°，∴△NON′是等边三角形，∵点M 是ON 的中点，∴N′M⊥ON，∵点N（3，0），∴ON=3，∵点M 是ON 的中点，∴OM=1.5，∴PM= ，∴P（，）．故答案为：（，）．作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，由作图得到ON=ON′，∠N′ON=2∠AON=60°，求得△NON′是等边三角形，根据等边三角形的性质得到N′M⊥ON，解直角三角形即可得到结论．本题考查了轴对称-最短路线问题，等边三角形的判定和性质，解直角三角形，关键是确定P 的位置．17.【答案】②③④【解析】解：①观察函数图象可知，当t=2 时，两函数图象相交，∵C 地位于A、B 两地之间，∴交点代表了两车离C 地的距离相等，并不是两车相遇，结论①错误；②甲车的速度为240÷4=60（km/h），乙车的速度为200÷（3.5-1）=80（km/h），∵（240+200-60-170）÷（60+80）=1.5（h），∴乙车出发1.5h 时，两车相距170km，结论②正确；③∵（240+200-60）÷（60+80）=2 （h），∴乙车出发2 h 时，两车相遇，结论③正确；④∵80×（4-3.5）=40（km），∴甲车到达C 地时，两车相距40km，结论④正确．综上所述，正确的结论有：②③④．故答案为：②③④．①观察函数图象可知，当t=2 时，两函数图象相交，结合交点代表的意义，即可得出结论①错误；②根据速度=路程÷时间分别求出甲、乙两车的速度，再根据时间=路程÷速度和可求出乙车出发1.5h 时，两车相距170km，结论②正确；③根据时间=路程÷速度和可求出乙车出发2 h 时，两车相遇，结论③正确；④结合函数图象可知当甲到C 地时，乙车离开C 地0.5 小时，根据路程=速度×时间，即可得出结论④正确．综上即可得出结论．本题考查了一次函数的应用，根据函数图象逐一分析四条结论的正误是解题的关键．18.【答案】【解析】5 ‒ 1 2解：作AE⊥x 轴于E，BF⊥x 轴于F，过B 点作BC⊥y 轴于C，交AE 于G，如图所示：则AG⊥BC，∵∠OAB=90°，∴∠OAE+∠BAG=90°，∵∠OAE+∠AOE=90°，∴∠AOE=∠GAB ，在△AOE 和△BAG 中，，∴△AOE ➴△BAG （AAS ），∴OE=AG ，AE=BG ，∵点 A （n ，1），∴AG=OE=n ，BG=AE=1，∴B （n+1，1-n ），∴k=n×1=（n+1）（1-n ），整理得：n 2+n-1=0，解得：n= ∴n=，（负值舍去）， ∴k=故答案为： ；．作 AE ⊥x 轴于 E ，BF ⊥x 轴于 F ，过 B 点作 BC ⊥y 轴于 C ，交 AE 于 G ，则 AG ⊥BC ，先求得△ AOE ➴△BAG ，得出 AG=OE=n ，BG=AE=1，从而求得 B （n+1，1-n ），根据 k=n×1=（n+1）（1-n ）得出方程，解方程即可．本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识；熟练掌握反比例函数图象上点的坐标特征，证明三角形全等是解决问题的关键．19.【答案】（-2，0）【解析】解：如图所示，P 1（-2，0），P 2（2，-4），P 3（0，4），P 4（-2，-2），P 5（2，-2），P 6（0，2），发现 6 次一个循环，∵2017÷6=336…1，∴点 P 2017 的坐标与 P 1 的坐标相同，即 P 2017（-2，0），故答案为（-2，0）．画出P1～P6，寻找规律后即可解决问题．本题考查坐标与图形的性质、点的坐标等知识，解题的关键是循环探究问题的方法，属于中考常考题型．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

安徽省中考数学试题分类解析汇编————押轴题汇总（1）一、选择题1. （2001安徽省4分）⊙O 1、⊙O 2和⊙O 3是三个半径为1的等圆，的等圆，且圆心在同一条直线上．若⊙O 2分别与⊙O 1，⊙O 3相交，⊙O 1与⊙O 3不相交，则⊙O 1与⊙O 3的圆心距d 的取值范围是的取值范围是。

2-1. （2002安徽省4分）如图，在△ABC 中，中，BC BC BC＝＝a ，B 1，B 2，B 3，B 4是AB边的五等分点；边的五等分点；C C 1，C 2．C 3．C 4是AC 边的五等分点，则B 1C 1＋B 2C 2＋B 3C 3＋B 4C 4＝．2-2.（2002安徽省4分）（华东版教材实验区试题）如图是2002年6月份的日历，现有一矩形在日历任意．．框出4个数a b c d，请用一个等式表示，请用一个等式表示a 、b 、c 、d 之间的关系：之间的关系：。

3. 如图，在平行四边形ABCD 中，中，AC=4AC=4AC=4，，BD=6BD=6，，P 是BD 上的任一点，过P 作EF∥AC，与平行四边形的两条边分别交于点E ，F 。

设BP=x BP=x，，EF=y EF=y，则能反映，则能反映y 与x 之间关系的图象为【之间关系的图象为【】A ：B ：C ：D ：4. （2004安徽省4分）“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点．用S 1、S 2分别表示乌龟和兔子所行的路程，分别表示乌龟和兔子所行的路程，t t 为时间，则下列图象中与故事情节相吻合的是【为时间，则下列图象中与故事情节相吻合的是【 】．】．(A)(B) (C) (D)5. （2005安徽省大纲4分）下图是某地区用水量与人口数情况统计图．日平均用水量为400万吨的那一年，人口数大约是【年，人口数大约是【】A 、180万B 、200万C 、300万D 、400万6. （2005安徽省课标4分）如图所示，圆O 的半径OA=6OA=6，以，以A 为圆心，为圆心，OA OA 为半径的弧交圆O 于B 、C 点，则BC 为【为【】 A. 63 B.62 C. 33 D. 32 7. （2006安徽省大纲4分）生产季节性产品的企业，当它的产品无利润时就会及时停产．现有一生产季节性产品的企业，其一年中获得的利润y 和月份n 之间函数关系式为2y n 14n 24=-+-，则该企业一年中应停产的月份是【应停产的月份是【】 A ．1月、月、22月、月、33月 B ．2月、月、33月、月、44月 C ．1月、月、22月、月、1212月 D ．1月、月、1111月、月、1212月8. （2006安徽省课标4分）如图是由10把相同的折扇组成的“蝶恋花”把相同的折扇组成的“蝶恋花”（图（图1）和梅花图案和梅花图案（图（图2）（图中的折扇无重叠），则梅花图案中的五角星的五个锐角均为【中的折扇无重叠），则梅花图案中的五角星的五个锐角均为【】A ．36° B．42° C．45° D．48°9. （2007安徽省4分）如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC∥QR，则∠AOQ=【接正方形，BC∥QR，则∠AOQ=【】 A ．60° B．65° C．72° D．75°10. （2008安徽省4分）如图，在△ABC 中，中，AB=AC=5AB=AC=5AB=AC=5，，BC=6BC=6，点，点M 为BC 中点，MN⊥AC于点N ，则MN 等于【等于【】 A.65 B. 95 C. 125 D. 16511. （2009安徽省4分）△ABC 中，中，AB AB AB＝＝AC AC，∠A ，∠A 为锐角，为锐角，CD CD 为AB 边上的高，边上的高，I I 为△ACD 的内切圆圆心，则∠AIB 的度数是【的度数是【】 A ．120° B．125° C．135° D．150°12. （2009安徽省4分）甲、乙两个准备在一段长为1200米的笔直公路上进行跑步，甲、乙跑步的速度分别为4m/s 和6m/s 6m/s，起跑前乙在起点，甲在乙前面，起跑前乙在起点，甲在乙前面100米处，若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲、乙两之间的距离y （m ）与时间t （s ）的函数图象是【）的函数图象是【】 A ． B ． C ． D ．13. （2011安徽省4分）如图，点P 是菱形ABCD 的对角线AC 上的一个动点，过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点．设AC AC＝＝2，BD BD＝＝1，AP AP＝＝x ，△AMN 的面积为y ，则y 关于x 的函数图象大致形状是【状是【】 14. （2012安徽省4分）在一张直角三角形纸片的两直角边上各取一点，在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是【的斜边长是【】 A.10 B.54 C. 10或54 D.10或172 二、填空题1. （2001安徽省4分）如图，如图，AB AB 是⊙O 的直径，的直径，l l 1，l 2是⊙O 的两条切线，且l 1∥AB∥l 2，若P 是PA PA、、PB 上一点，直线PA PA、、PB 交l 2于点C 、D ，设⊙O 的面积为S 1，△PCD 的面积为S 2，则12S S =【 】 A ．π B ．2p C ．4p D ．8p 2. （2002安徽省4分）如图，在矩形ABCD 中，中，AB AB AB＝＝3，AD AD＝＝4．P 是AD 上的动点，PE⊥AC 于E ，PE⊥BD 于F ．则PE PE＋＋PF 的值为【的值为【】 A ．512 B ．2 C ．25 D ．5133. （2003安徽省4分）如图，如图，l l 是四形形ABCD 的对称轴，如果AD∥BC，有下列结论：①AB∥CD ②AB=BC ③AB⊥BC ④AO=OC 其中正确的结论是其中正确的结论是。

中考数学---几何选择填空压轴题精选1一．选择题：1．如下图1，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连接DF交BE的延长线于点H，连接OH交DC于点G，连接HC．则以下四个结论中正确结论的个数为（）①OH=BF；②∠CHF=45°；③GH=BC；④DH2=HE•HB．A. 1个B. 2个C. 3个D. 4个2、如上图2，梯形ABCD中，AD∥BC，，∠ABC=45°，AE⊥BC于点E，BF⊥AC于点F，交AE于点G，AD=BE，连接DG、CG．以下结论：①△BEG≌△AEC；②∠GAC=∠GCA；③DG=DC；④G为AE中点时，△AGC的面积有最大值．其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个3．如上图3，正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G下列结论：①EC=2DG；②∠GDH=∠GHD；③S△CDG=S▭DHGE；④图中有8个等腰三角形．其中正确的是（）A.①③ B.②④ C.①④ D.②③4．如下图1，矩形ABCD的面积为5，它的两条对角线交于点O1，以AB，AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交BD于点02，同样以AB，AO2为两邻边作平行四边形ABC2O2．…，依此类推，则平行四边形ABC2009O2009的面积为（）A.B. C. D.5、如上图2，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（）A.1个 B.2个 C.3个 D.4个6．Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下图1，下列结论：①（BE+CF）=BC；②S△AEF ≤S△ABC；③S四边形AEDF=AD•EF；④AD≥EF；⑤AD与EF可能互相平分，其中正确结论的个数是（）A.1个B.2个C.3个D.4个7．如上图2，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连接GF．下列结论①∠ADG=22.5°；②tan∠AED=2；③S△AGD =S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确的结论有（）A.①④⑤B.①②④C.③④⑤D.②③④8．如上图3，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE，连接并延长AE 交CD于F，连接BD分别交CE、AF于G、H，下列结论：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④BG=DG；⑤．其中正确的结论是（）A.①②③B.①②④C.①②⑤D.②④⑤9．如下图1，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△CEH的周长为定值，其中正确的结论有（）A.①②③B.①②④C.①③④D.①②③④10．正方形ABCD、正方形BEFG和正方形RKPF的位置如上图2所示，点G在线段DK上，正方形BEFG 的边长为4，则△DEK的面积为（）A. 10B. 12C. 14D. 16二．填空题1．如下图1，观察图中菱形的个数：图1中有1个菱形，图2中有5个菱形，图3中有14个菱形， 图4中有30个菱形…，则第6个图中菱形的个数是 个．2.如下图2，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1； ∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012= ．3．如下图1，已知Rt △ABC 中，AC=3，BC=4，过直角顶点C 作CA 1⊥AB ，垂足为A 1，再过A 1作A 1C 1⊥BC ，垂足为C 1，过C 1作C 1A 2⊥AB ，垂足为A 2，再过A 2作A 2C 2⊥BC ，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1= ，= ．4、如上图2，点A 1，A 2，A 3，A 4，…，A n 在射线OA 上，点B 1，B 2，B 3，…，B n ﹣1在射线OB 上， 且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ﹣1B n ﹣1，A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n ﹣1，△A 1A 2B 1，△A 2A 3B 2，…，△A n ﹣1A n B n ﹣1为阴影三角形，若△A 2B 1B 2，△A 3B 2B 3的面积分别为1、4，则△A 1A 2B 1的面为 ； 面积小于2011的阴影三角形共有 个． 5、如下图1，已知点A 1（a ，1）在直线l ：上，以点A 1为圆心，以为半径画弧，交x 轴于点B 1、B 2，过点B 2作A 1B 1的平行线交直线l 于点A 2，在x 轴上取一点B 3，使得A 2B 3=A 2B 2，再过点B 3作A 2B 2的平行线交直线l 于点A 3，在x 轴上取一点B 4，使得A 3B 4=A 3B 3，按此规律继续作下去， 则①a= ；②△A 4B 4B 5的面积是 ．6、如下图，在梯形ABCD中，AD∥BC，EA⊥AD，M是AE上一点，F、G分别是AB、CM的中点，且∠BAE=∠MCE，∠MBE=45°，则给出以下五个结论：①AB=CM；②A E⊥BC；③∠BMC=90°；④EF=EG；⑤△BMC是等腰直角三角形．上述结论中始终正确的序号有．7、如图，边长为1的菱形ABCD中，∠DAB=60度．连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第n个菱形的边长为．8、如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，若EH=3，EF=4，那么线段AD与AB的比等于．9．如图，E、F分别是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD =15cm2，S△BQC=25cm2，则阴影部分的面积为cm2．中考数学---几何选择填空压轴题精选1答案一．选择题：1、解：作EJ⊥BD于J，连接EF①∵BE平分∠DBC ∴EC=EJ，∴△DJE≌△ECF ∴DE=FE∴∠HEF=45°+22.5°=67.5°∴∠HFE==22.5°∴∠EHF=180°﹣67.5°﹣22.5°=90°∵DH=HF，OH是△DBF的中位线∴OH∥BF ∴OH=BF②∵四边形ABCD是正方形，BE是∠DBC的平分线，∴BC=CD，∠BCD=∠DCF，∠EBC=22.5°，∵CE=CF，∴Rt△BCE≌Rt△DCF，∴∠EBC=∠CDF=22.5°，∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°，∵OH是△DBF的中位线，CD⊥AF，∴OH是CD的垂直平分线，∴DH=CH，∴∠CDF=∠DCH=22.5°，∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°，∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°，故②正确；③∵OH是△BFD的中位线，∴DG=CG=BC，GH=CF，∵CE=CF，∴GH=CF=CE∵CE＜CG=BC，∴GH＜BC，故此结论不成立；④∵∠DBE=45°，BE是∠DBF的平分线，∴∠DBH=22.5°，由②知∠HBC=∠CDF=22.5°，∴∠DBH=∠CDF，∵∠BHD=∠BHD，∴△DHE∽△BHD，∴=∴DH=HE•HB，故④成立；所以①②④正确．故选C．（第5题图）2、解：根据BE=AE，∠GBE=∠CAE，∠BEG=∠CEA可判定①△BEG≌△AEC；用反证法证明②∠GAC≠∠GCA，假设∠GAC=∠GCA，则有△AGC为等腰三角形，F为AC的中点，又BF⊥AC，可证得AB=BC，与题设不符；由①知△BEG≌△AEC 所以GE=CE 连接ED、四边形ABED为平行四边形，∵∠ABC=45°，AE⊥BC于点E，∴∠GED=∠CED=45°，∴△GED≌△CED，∴DG=DC；④设AG为X，则易求出GE=EC=2﹣X 因此，S△AGC =SAEC﹣SGEC=﹣+x=﹣（x2﹣2x）=﹣（x2﹣2x+1﹣1）=﹣（x﹣1）2+，当X取1时，面积最大，所以AG等于1，所以G是AE中点，故G为AE中点时，GF最长，故此时△AGC的面积有最大值．故正确的个数有3个．故选C．3、解：∵DF=BD，∴∠DFB=∠DBF，∵AD∥BC，DE=BC，∴∠DEC=∠DBC=45°，∴∠DEC=2∠EFB，∴∠EFB=22.5°，∠CGB=∠CBG=22.5°，∴CG=BC=DE，∵DE=DC，∴∠DEG=∠DCE，∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°，∠DGE=180°﹣（∠BGD+∠EGF）=180°﹣（∠BGD+∠BGC），=180°﹣（180°﹣∠DCG）÷2=180°﹣（180°﹣45°）÷2=112.5°，∴∠GHC=∠DGE，∴△CHG≌△EGD，∴∠EDG=∠CGB=∠CBF，∴∠GDH=∠GHD，∴S△CDG =S▭DHGE．故选D．4、解：∵矩形ABCD的对角线互相平分，面积为5，∴平行四边形ABC1O1的面积为，∵平行四边形ABC1O1的对角线互相平分，∴平行四边形ABC2O2的面积为×=，…，依此类推，平行四边形ABC2009O2009的面积为．故选B．5、解：①∵BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，∴PM=BC，PN=BC，∴PM=PN，正确；②在△ABM与△ACN中，∵∠A=∠A，∠AMB=∠ANC=90°，∴△ABM∽△ACN，∴，正确；③∵∠A=60°，BM⊥AC于点M，CN⊥AB于点N，∴∠ABM=∠ACN=30°，在△ABC中，∠BCN+∠CBM═180°﹣60°﹣30°×2=60°，∵点P是BC的中点，BM⊥AC，CN⊥AB，∴PM=PN=PB=PC，∴∠BPN=2∠BCN，∠CPM=2∠CBM，∴∠BPN+∠CPM=2（∠BCN+∠CBM）=2×60°=120°，∴∠MPN=60°，∴△PMN是等边三角形，正确；（见上图）④当∠ABC=45°时，∵CN⊥AB于点N，∴∠BNC=90°，∠BCN=45°，∴BN=CN，∵P为BC边的中点，∴PN⊥BC，△BPN为等腰直角三角形；∴BN=PB=PC，正确．故选D．6、解：∵Rt△ABC中，AB=AC，点D为BC中点，∴∠C=∠BAD=45°，AD=BD=CD，∵∠MDN=90°，∴∠ADE+∠ADF=∠ADF+∠CDF=90°，∴∠ADE=∠CDF．在△AED与△CFD中，∵，∴△AED≌△CFD（ASA），∴AE=CF，在Rt△ABD中，BE+CF=BE+AE=AB==BD=BC．故①正确；设AB=AC=a，AE=CF=x，则AF=a﹣x．∵S△AEF =AE•AF=x（a﹣x）=﹣（x﹣a）2+a2，∴当x=a时，S△AEF有最大值a2，又∵S△ABC =×a2=a2，∴S△AEF≤S△ABC．故②正确；EF2=AE2+AF2=x2+（a﹣x）2=2（x﹣a）2+a2，∴当x=a时，EF2取得最小值a2，∴EF≥a（等号当且仅当x=a时成立），而AD=a，∴EF≥AD．故④错误；由①的证明知△AED≌△CFD，∴S四边形AEDF =S△AED+S△ADF=S△CFD+S△ADF=S△ADC=AD2，∵EF≥AD，∴AD•EF≥AD2，∴AD•EF＞S四边形AEDF故③错误；当E、F分别为AB、AC的中点时，四边形AEDF为正方形，此时AD与EF互相平分．故⑤正确．综上所述，正确的有：①②⑤，共3个．故选C．7、解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG=∠ADO=22.5°，故①正确．∵tan∠AED=，由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴tan∠AED=＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD ＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF=OG，∴BE=EF=×OG=2OG．故⑤正确．∴其中正确结论的序号是：①④⑤．故选：A．8、解：①由∠ABC=90°，△BEC为等边三角形，△ABE为等腰三角形，∠AEB+∠BEC+∠CEH=180°，可求得∠CEH=45°，此结论正确；②由△EGD≌△DFE，EF=GD，再由△HDE为等腰三角形，∠DEH=30°，得出△HGF为等腰三角形，∠HFG=30°，可求得GF∥DE，此结论正确；③由图可知2（OH+HD）=2OD=BD，所以2OH+DH=BD此结论不正确；④如图，过点G作GM⊥CD垂足为M，GN⊥BC垂足为N，设GM=x，则GN=x，进一步利用勾股定理求得GD=x，BG=x，得出BG=GD，此结论不正确；⑤由图可知△BCE和△BCG同底不等高，它们的面积比即是两个三角形的高之比，由④可知△BCE的高为（x+x）和△BCG的高为x，因此S△BCE ：S△BCG=（x+x）：x=，此结论正确；故正确的结论有①②⑤．故选C．9、解：（1）连接FC，延长HF交AD于点L，∵BD为正方形ABCD的对角线，∴∠ADB=∠CDF=45°．∵AD=CD，DF=DF，∴△ADF≌△CDF．∴FC=AF，∠ECF=∠DAF．∵∠ALH+∠LAF=90°，∴∠LHC+∠DAF=90°．∵∠ECF=∠DAF，∴∠FHC=∠FCH，∴FH=FC．∴FH=AF．（上图2）（2）∵FH⊥AE，FH=AF，∴∠HAE=45°．（3）连接AC交BD于点O，可知：BD=2OA，（上图3）∵∠AFO+∠GFH=∠GHF+∠GFH，∴∠AFO=∠GHF．∵AF=HF，∠AOF=∠FGH=90°，∴△AOF≌△FGH．∴OA=GF．∵BD=2OA，∴BD=2FG．（4）延长AD至点M，使AD=DM，过点C作CI∥HL，则：LI=HC，根据△MEC≌△CIM，（见下图2）可得：CE=IM，同理，可得：AL=HE，∴HE+HC+EC=AL+LI+IM=AM=8．∴△CEH的周长为8，为定值．故（1）（2）（3）（4）结论都正确．故选D．10、解：如下图1，连DB，GE，FK，则DB∥GE∥FK，在梯形GDBE中，S△DGE =S△GEB（同底等高的两三角形面积相等），同理S△GKE=S△GFE．∴S阴影=S△DGE+S△GKE=S△GEB+S△GEF=S正方形GBEF=4×4=16 故选D．二．填空题：1、解：观察图形，发现规律：图1中有1个菱形，图2中有1+22=5个菱形，图3中有5+32=14个菱形，图4中有14+42=30个菱形，则第5个图中菱形的个数是30+52=55，第6个图中菱形的个数是55+62=91个．故答案为91．2、解：∵∠ABC与∠ACD的平分线交于点A1，∴∠A1BC=∠ABC，∠A1CD=∠ACD，根据三角形的外角性质，∠A+∠ABC=∠ACD，∠A1+∠A1BC=∠A1CD，∴∠A1+∠A1BC=∠A1+∠ABC=（∠A+∠ABC），整理得，∠A1=∠A=，同理可得，∠A2=∠A1=×=，…，∠A2012=．故答案为：．3、解：在Rt△ABC中，AC=3，BC=4，∴AB=，又因为CA1⊥AB，∴AB•CA1=AC•BC，即CA1===．∵C4A5⊥AB，∴△BA5C4∽△BCA，∴，∴==．所以应填和．4、解：由题意得，△A2B1B2∽△A3B2B3，∴==，==，又∵A1B1∥A2B2∥A3B3，∴===，==，∴OA1=A1A2，B1B2=B2B3继而可得出规律：A1A2=A2A3=A3A4…；B1B2=B2B3=B3B4…又△A2B1B2，△A3B2B3的面积分别为1、4，∴S△A1B1A2=，S△A2B2A3=2，继而可推出S△A3B3A4=8，S△A4B4A5=32，S△A5B5A6=128，S△A6B6A7=512，S△A7B7A8=2048，故可得小于2011的阴影三角形的有：△A1B1A2，△A2B2A3，△A3B3A4，△A4B4A5，△A5B5A6，△A6B6A7，共6个．故答案是：；6．5、解：如图所示：①将点A1（a，1）代入直线1中，可得，所以a=．②△A1B1B2的面积为：S==；因为△OA1B1∽△OA2B2，所以2A1B1=A2B2，又因为两线段平行，可知△A1B1B2∽△A2B2B3，所以△A2B2B3的面积为S1=4S；以此类推，△A4B4B5的面积等于64S=．6、解：∵梯形ABCD中，AD∥BC，EA⊥AD，∴AE⊥BC，即②正确．∵∠MBE=45°，∴BE=ME．在△ABE与△CME中，∵∠BAE=∠MCE，∠AEB=∠CEM=90°，BE=ME，∴△ABE≌△CME，∴AB=CM，即①正确．∵∠MCE=∠BAE=90°﹣∠ABE＜90°﹣∠MBE=45°，∴∠MCE+∠MBC＜90°，∴∠BMC＞90°，即③⑤错误．∵∠AEB=∠CEM=90°，F、G分别是AB、CM的中点，∴EF=AB，EG=CM．又∵AB=CM，∴EF=EG，即④正确．故正确的是①②④．7、解：连接DB，∵四边形ABCD是菱形，∴AD=AB．AC⊥DB，∵∠DAB=60°，∴△ADB是等边三角形，∴DB=AD=1，∴BM=，∴AM==，∴AC=，同理可得AC1=AC=（）2，AC2=AC1=3=（）3，按此规律所作的第n个菱形的边长为（）n﹣1故答案为（）n﹣1．8、解：∵∠1=∠2，∠3=∠4，∴∠2+∠3=90°，∴∠HEF=90°，（见上图3）同理四边形EFGH的其它内角都是90°，∴四边形EFGH是矩形．∴EH=FG（矩形的对边相等）；又∵∠1+∠4=90°，∠4+∠5=90°，∴∠1=∠5（等量代换），同理∠5=∠7=∠8，∴∠1=∠8，∴Rt△AHE≌Rt△CFG，∴AH=CF=FN，又∵HD=HN，∴AD=HF，在Rt△HEF中，EH=3，EF=4，根据勾股定理得HF=，∴HF=5，又∵HE•EF=HF•EM，∴EM=，又∵AE=EM=EB（折叠后A、B都落在M点上），∴AB=2EM=，∴AD：AB=5：=．故答案为：．9、解：如图，连接EF；∵△ADF与△DEF同底等高，∴S△ADF =S△DEF即S△ADF﹣S△DPF=S△DEF﹣S△DPF，即S△APD =S△EPF=15cm2，同理可得S△BQC=S△EFQ=25cm2，∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2．故答案为40．。

中考数学选择填空压轴题 Modified by JEEP on December 26th, 2020.
中考数学：选择、填空压轴题
百题冲刺
编辑：XXXX（不告诉你）
花了很长时间整理的
肯定要卖贵点
嘿嘿嘿
目录：
专题一数与式
专题二方程、不等式与函数
专题三图形的性质与变换
专题四圆
专题五点的运动路径
专题六几何最值问题
专题七探究型几何问题
专题一数与式
【定义新运算】
【定义新运算：与高中知识有关】
【定义新概念】
【流程图】
【等差数列】【等差数列求和】【等比数列】【等比数列求和】
【二阶等差数列】
【循环型规律】
【递进型规律】
专题二方程、不等式与函数专题三图形的性质与变换
专题四圆
专题五点的运动路径
专题六几何最值问题
专题七探究型几何问题。

第1讲选择压轴题专练--代数证明巩固训练1．有依次排列的3个正整数：x ，y ，z ，且y z x >>，现规定：对任相邻的两个数，都用右边的数减去左边的数，所得的差写在这两个数之间，可产生一个新数串：x ，()y x -，y ，()z y -，z ，这称为第一次操作；做第二次同样的操作后可产生又一个新数串，……，继续依次操作下去．下列说法：①第一次操作后，所有数之和为：2z y +．②第二次同样操作后的数串是：x ，()2y x -，()y x -，x ，y ，()2z y -，()z y -，y ，z ．③第n 次同样操作后，所有数之和为：()x y z n z x +++-．其中正确的个数是（）A ．0B ．1C ．2D ．32．有依次排列的3个整式：,6,3x x x +-，对任意相邻的两个整式，都用右边的整式减去左边的整式，所得之差写在这两个整式之间，可以产生一个新整式串．例如：,6,6,9,3x x x +--，我们称它为整式串1；将整式串1按上述方式再做一次操作，可以得到整式串2；以此类推．通过实际操作，得出以下结论：①整式串2为：,6,6,,6,15,9,6,3x x x x x x x -+---+-；②整式串3的所有整式的和比整式串2的所有整式的和大3；③整式串5共67个整式；④整式串2022的所有整式的和为36063x -；上述四个结论正确的有（）个．A ．1B ．2C ．3D ．4第2讲填空压轴题专练--材料阅读（新定义）知识储备：有理数的混合运算，绝对值的意义、列代数式、整式的加减、二元一次方程组的应用、不等式组的整数解、实数的运算、不定方程的应用、乘法公式、因式分解的运用、数的整除、分类讨论思想等——代数综合题型，考察代数综合能力！类型一：整除1、如果一个三位数m 满足各个数位上的数字互不相同，且都不为零，那么称这个三位数为“互异数”．将“互异数”m 的个位数字去掉，得到一个两位数m '，将其与m 的个位数字的差记为()F m ，将m 的十位数字与个位数字的差记为()G m ．已知一个三位正整数()20512m x y =++（其中x 、y 都是整数，且19,19x y ≤≤≤≤）是“互异数”，()()F m G m 为整数且能被13整除，则满足条件的“互异数”m 的最大值___________．2、把一个四位数N 的各个数位上的数字(均不为零)之和记为()G N ，把N 的千位数字与百位数字的乘积记为()P N ，十位数字与个位数字的乘积记为()Q N ，称()()()G N P N Q N -为N 的“乐育天下值”．(1)8253的“乐育天下值”为______；(2)若N 的千位与个位数字之和能被8整除，且()15G N =，N 的“乐育天下值”为3，则满足条件的N 的最大值是______．3．材料一：对于一个三位正整数，若百位数字与个位数字之和减去十位数字的差为3，则称这个三位数为“尚美数”，例如：234，因为2433+-=，所以234是“尚美数”；材料二：若t abc =(19a ≤≤，09b ≤≤，09c ≤≤，且a ，b ，c 均为整数)，记()2F t a c =-．已知12t yz =，2t myn =是两个不同的“尚美数(18y ≤≤，19z ≤≤，19m n ≤<≤且y ，z ，m ，n 均为整数)，且()()1224F t F t n ++能被13整除，则1t 的值为______．类型二：特殊数型1、如果一个四位自然数t 的各个数位上的数字均不为0，且满足千位数字与十位数字的和为9，百位数字与个位数字的差为1，那么称t 为“九一数”．把t 的千位数字的2倍与个位数字的和记为()P t ，百位数字的2倍与十位数字的和记为()Q t ，令()()()2P t G t Q t =，当()G t 为整数时，则称t 为“整九一数”．若2000100010010M a b c d =++++（其中14a ≤≤，19b ≤≤，19c ≤≤，19d ≤≤且a 、b 、c 、d 均为整数）是“整九一数”，则满足条件的M 的最大值为______．2．对于一个各数位数字均不为零的四位自然数m ，若千位与百位数字之和等于十位与个数位数字之和，则称m 为“一致数”．设一个“一致数”m abcd =满足8a ≤且1d =，将m 的千位与十位数字对调，百位与个位数字对调得到新数m '，并记()101m m F m '+=；一个两位数102N a b =+，将N 的各个数位数字之和记为()G N ；当2()()43F m G N a k --=+（k 为整数）时，则所有满足条件的“一致数”m 中，满足()G N 为偶数时，k 的值为______，m 的值为______．3、一个各位数字都不为0的四位正整数m ，若千位与个位数字相同，百位与十位数字相同，则称这个数m 为“双胞蛋数”，将千位与百位数字交换，十位与个位数字交换，得到一个新的“双胞蛋数”m '，并规定()11m m F m '-=．若已知数m 为“双胞蛋数”，设m 的千位数字为a ，百位数字为b ，且a b ¹，若()54F m 是一个完全平方数，则a b -=__________，满足条件的m 的最小值为__________．4、若一个四位正整数abcd 满足：a c b d +=+，我们就称该数是“交替数”，则最小的“交替数”是______；若一个“交替数”m 满足千位数字与百位数字的平方差是15，且十位数字与个位数的和能被5整除．则满足条件的“交替数”m 的最大值为______．类型三：给定等量关系（方程）1、对任意一个四位数m ，如果m 各个数位上的数字都不为零且互不相同，满足个位与千位的和等于十位与百位的和，那么称这个数为“镜面数”，将一个“镜面数”个位与千位两个数位对调后得到一个新的四位数1m ，将它的十位与百位两个数位对调后得到另一个新四位数2m ，记F （m ）＝121111m m +．例如1234m =，对调个位与千位上的数字得到14321=m ，对调十位与百位上的数字得到21324m =，这两个四位数的和为12432113245555+=+=m m ，所以()1255551234511111111+===m m F ，若s ，t 都是“镜面数”，其中100010032,150010s x y t e f=++=++（19,19,1919,,,,x y e ，f x y e f ≤≤≤≤≤≤≤≤都是正整数），规定：()=（）F S K F t ，当()()19F s F t +=时，k 的最大值为k =________．.2、对于任意一个四位数m ，若它的千位数字与百位数字的和等于十位数字与个位数字的和，则称这个四位数m 为“天平数”，记()F m 为m 的各个数位上的数字之和．例如：1432m =，1432+=+ ，1432∴是“天平数”，()1432143210F =+++=；6397m =，6397+≠+ ，6397∴不是“天平数”．求出()5234F ______；已知M ，N 均为“天平数”，其中1000100320M x b y =+++，（19x ≤≤，06b ≤≤，09y ≤≤，x ，b ，y 是整数），200010010N a b c d =+++，（14a ≤≤，06b ≤≤，09c ≤≤，09d ≤≤，a ，b ，c ，d 是整数），若()()264F M F N ⋅=，求出满足条件的M 的最大值______．类型四：构造（转化思想）1、若一个两位数N 满足N ab a b =++，其中a 、b 均为正整数，则称N 为好数，那么最大的好数是________；若a 、b 同时还满足3ab a b=+或4，则称N 为绝对好数，那么绝对好数的个数为________．第3讲解答压轴题专练--几何证明【高频考点一】中点证明【高频考点二】线段关系猜想与证明及系数构造1、（BZ ）在Rt ABC ∆中，90CAB ∠=︒，点D 是边AB 的中点，连接CD ，点E 在边BC 上，且AE CD ⊥交CD 于点F ．（1）如图1，当60ACB ∠=︒时，若CD =AF 的长；（2）如图2，当45ACB ∠=︒时，连接BF ，求证：CD DF AF +=；（3）如图3，当75ACB ∠=︒时，直接写出FA CF 的值．2、（YZ ）在ABC 和ADE V 中，90BAC ADE ∠=∠=︒，AB AC =，DE DA =，且AB AD >．（1）如图1，当点D 在线段AB 上时，连接EC ，若AC =，3AE =，求线段EC 的长；（2）如图2，将图1中ADE V 绕着点A 逆时针旋转，使点D 在ABC 的内部，连接BD ，CD ．线段AE ，BD 相交于点F ，当DCB DAC ∠=∠时，求证：BF DF =；线段关系猜想与证明3、（BSBS）在平行四边形ABCD中，AC＝BC，BE⊥AC分别交直线AC、AD于点E、F．点G是BC上一点，连接EG，过点G作GQ⊥AB分别交BF、AB于点P、Q．（1）如图1，若AB＝AC，BE＝3，求AF的长度．（2）如图2，若PG＝2BQ，请探究EG、BG、CG的数量关系，并说明理由．【实战演练】1．（NK ）如图，在平行四边形ABCD 中，AE 平分BAD ∠，交BC 于点E ，点F 是线段BE 上一点，连接AF ，点G 是线段AB 上一点，连接EG ，交AF 于点N ．（1）如图1，若45B ∠=︒，AB =，求ABE 的面积；（2）如图2，点H 是线段AF 的中点，连接EH ，若B BEH AEG ∠=∠=∠，求证：CD BF BG =+；2.（BS ）ABC 中，AB AC =，D 为BC 上一点．（1）如图1，若30C ∠=︒，2AB AD CD ⊥=，，求BC ．（2）如图2，点E 为ABC 外一点，且满足BD CE =，连接AE ，点F 为AC 上一点，连接BF 交AD 于点M ，若180CBF AEC ACE ACB ∠=∠∠+∠=︒，，求证：AM DM =．3.（BZ ）如图，在ABC 中，90BAC ∠=︒，AB AC =，D ，E 分别为BC 上两动点，BD CE =．（1）如图1，若EH AD ⊥于H 交AB 于K ，求证：AE EK =；（2）如图2，若EF AD ∥交AC 于F ，GF AG ⊥，AG GF =，求证：AD EF +=；第4讲解答压轴题专练--几何最值瓜豆原理（主从联动）最值问题【模型总结】运动轨迹为直线问题1：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？问题2：如图，点C为定点，点P、Q为动点，CP=CQ，且∠PCQ为定值，当点P在直线AB上运动，Q的运动轨迹是？模型总结条件：主动点、从动点与定点连线的夹角是定量；主动点、从动点到定点的距离之比是定量．结论：①主动点、从动点的运动轨迹是同样的图形；②主动点路径做在直线与从动点路径所在直线的夹角等于定角③当主动点、从动点到定点的距离相等时，从动点的运动路径长等于主动点的运动路径长；【例题精讲】【例1】.如图，在平面直角坐标系中，A（－3，0），点B是y轴正半轴上一动点，点C、D在x正半轴上，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．变式训练【变式1-1】．如图，△APQ是等腰直角三角形，∠PAQ＝90°，当点P在线段BC上运动时，画出点Q的运动轨迹．【变式1-2】．如图，等边△ABC中，AB＝BC＝AC＝6，点M是BC边上的高AD所在直线上的点，以BM为边作等边△BMN，连接DN，则DN的最小值为．【变式1-3】．如图，已知点A（﹣3，0），B（0，3），C（﹣1，4），动点P在线段AB 上，点P、C、M按逆时针顺序排列，且∠CPM＝90°，CP＝MP，当点P从点A运动到点B时，则点M运动的路径长为．【例2】．如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（）A．B．1C．2D．变式训练【变式2-1】．如图，等边△ABC的边长为4，点D是边AC上的一动点，连接BD，以BD为斜边向上作等腰Rt△BDE，连接AE，则AE的最小值为（）A．1B．C．2D．2【变式2-2】．如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB 边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为（）A．0.5B．2.5C．D．1【变式2-3】．如图，等腰Rt△ABC中，斜边AB的长为4，O为AB的中点，P为AC 边上的动点，OQ⊥OP交BC于点Q，M为PQ的中点，当点P从点A运动到点C 时，点M所经过的路线长为．【实战演练】1．（BZ ）如图，在ABC 中，90BAC ∠=︒，AB AC =，D ，E 分别为BC 上两动点，BD CE =．（1）如图1，若EH AD ⊥于H 交AB 于K ，求证：AE EK =；（2）如图2，若EF AD ∥交AC 于F ，GF AG ⊥，AG GF =，求证：AD EF +=；（3）如图3，若4AB =，将AE 绕点E 顺时针旋转90︒得EM ，N 为BM 中点，当1AN+AM 2取得最小值时，请直接写出ACD 的面积．2.（BS ）ABC 中，AB AC =，D 为BC 上一点．（1）如图1，若30C ∠=︒，2AB AD CD ⊥=，，求BC ．（2）如图2，点E 为ABC 外一点，且满足BD CE =，连接AE ，点F 为AC 上一点，连接BF 交AD 于点M ，若180CBF AEC ACE ACB ∠=∠∠+∠=︒，，求证：AM DM =．（3）如图3，当AB =+，60BAC ∠=︒且D 为BC 中点时，E 为射线AD 上一动点，连接CE ，以CE 为边作等边CEF △，连接BF ．EF 交BC 于点M ，当满足BF BM =时，N 为FM 上一点，且1FN 2=，作NH CM ∥交CF 于点H ，将CFM △绕点C 顺时针旋转()0360αα︒≤<得CF M '' ，N 、H 的对应点分别为N H ''、，直接写出整个旋转过程中ABH ' 面积的最小值．3.（NK ）如图，在平行四边形ABCD 中，AE 平分BAD ∠，交BC 于点E ，点F 是线段BE 上一点，连接AF ，点G 是线段AB 上一点，连接EG ，交AF 于点N ．（1）如图1，若45B ∠=︒，AB =，求ABE 的面积；（2）如图2，点H 是线段AF 的中点，连接EH ，若B BEH AEG ∠=∠=∠，求证：CD BF BG =+；（3）如图3，若=60B ∠︒，AG BF =，24BE EC ==，4ANG EAF ∠=∠，将ANG绕着点A 旋转，得到''AN G ．连接'N D ．点O 是线段'N D 的中点，连接CO ．请直接写出线段CO 长度的最小值.。

专题01代数式的求值问题例1．观察下列等式：1＝2＝3＝4＝5＝6＝64,…,根据这个规律，则1)＋2\S\UP6(2)＋2\S\UP6(3)＋2\S\UP6(4)＋…＋2\S\UP6(2017的末位数字是（）A．0 B．2 C．4 D．6同类题型1.1计算：1＝2＝3＝4＝5＝31,…归纳各计算结果中的个位数字规律，猜测2016的个位数字是（）A．1 B．3 C．7 D．5同类题型1.2观察下列算式1＝2＝3＝4＝5＝6＝7＝2187…根据上述算式中的规律，你认为2018的末位数字是（）A．3 B．9 C．7 D．1例2．下列定义一种关于n的运算：①当n是奇数时，结果为3n＋5②n为偶数时结果是n2\S\UP6(k)(其中k是使n2\S\UP6(k)是奇数的正整数），并且运算重复进行．例如：取n＝26，则…，若n＝449,则第449次运算结果是（）A．1 B．2 C．7 D．8同类题型2.1定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5;②当n为偶数时，结果为n2\S\UP6(k) (其中k是使n2\S\UP6(k)为奇数的正整数），并且运算重复进行．例如，取n＝26，那么当n＝26时，第2016次“F运算”的结果是________．同类题型2.2对于任意正整数n，定义"n!!"如下：当n是偶数时,n!!＝n﹒(n－2)﹒(n－4)…6﹒4﹒2,当n是奇数时,n!!＝n﹒(n－2)﹒(n－4)…5﹒3﹒1,且有n!＝n﹒(n－1)﹒(n－2)…3﹒2﹒1则有四个命题：①(2015!!)﹒(2016!!)＝2016!②2016!!＝2018③2015!!的个位数是5④2014!!的个位数是0其中正确的命题有（）A．1个B．2个C．3个D．4个例3．一列数123满足条件：1＝12n＝1n－1且n为整数），则2017等于（）A．－1 B．12C．1 D．2同类题型 3.1一列数123满足条件：1＝12n＝1n－1且n为整数），则1)＋a\S\DO(2)＋a\S\DO(3)＋…＋a\S\DO(2017＝________．同类题型3.2 1、2、3、20是20个由1,0,－1组成的数，且满足下列两个等式：①1)＋x\S\DO(2)＋x\S\DO(3)＋…＋x\S\DO(20＝4，②(\l(x\S\DO(1)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(2)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(3)－1))\S\UP6(2)＋…＋\b\bc\((\l(x\S\DO(20)－1))\S\UP6(2＝32，则这列数中1的个数为（）A．8 B．10 C．12 D．14例4．设△ABC的面积为1．如图1，分别将AC,BC边2等分1),E\S\DO(1是其分点，连接1)BD\S\DO(1交于点1得到四边形1)F\S\DO(1)E\S\DO(1其面积1＝13．如图2，分别将AC,BC边3等分1),D\S\DO(2),E\S\DO(1),E\S\DO(2是其分点，连接2)BD\S\DO(2交于点2得到四边形2)F\S\DO(2)E\S\DO(2其面积2＝16如图3，分别将AC,BC边4等分1),D\S\DO(2),D\S\DO(3),E\S\DO(1),E\S\DO(2),E\S\DO(3是其分点，连接3)BD\S\DO(3交于点3得到四边形3)F\S\DO(3)E\S\DO(3其面积3＝110…按照这个规律进行下去，若分别将AC,BC边(n＋1)等分，…，得到四边形n)F\S\DO(n)E\S\DO(n其面积n ＝________．同类题型4.1庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1＝112)3)n．4.2图图2也是一种无限分割：在△ABC中，∠C＝90°,∠B＝30°,过点C作1于点1再过点1作1)C\S\DO(2于点2又过点2作2)C\S\DO(3于点3如此无限继续下去，则可将利△ABC分割成1、1)C\S\DO(2、1)C\S\DO(2)C\S\DO(3、2)C\S\DO(3)C\S\DO(4、…、n－2)C\S\DO(n－1)C\S\DO(n、…．假设AC＝2，这些三角形的面积和可以得到一个等式是________________________________．同类题型4.2 如图，顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形，再顺次连接所得的小三角形各边中点得到第2个小三角形，如此操作下去，则第n个小三角形的面积为________．例5．如图，一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水，将瓶盖盖好后倒置，墨水水面高为h厘米，则瓶内的墨水的体积约占玻璃瓶容积的（）A．aa＋b B．ba＋b C．ha＋b D．ha＋h例5图 5.1图同类题型5.1如图，一个啤酒瓶的高度为30cm，瓶中装有高度12cm的水，将瓶盖盖好后倒置，这时瓶中水面高度20cm，则瓶中水的体积和瓶子的容积之比为________．（瓶底的厚度不计）同类题型5.2一艘轮船往返甲、乙两港之间，第一次往返航行时，水流速度为a千米/时，第二次往返航行时，正遇上发大水，水流速度为b千米/时（b＞a），已知该船在两次航行中的静水速度相同，则该船这两次往返航行所用时间的关系是（）A．第一次往返航行用的时间少B．第二次往返航行用的时间少C．两种情况所用时间相等D．以上均有可能例6．若1x＝3，求2)x\S\UP6(4)＋x\S\UP6(2)＋1的值是（）A．18 B．110 C．12 D．14同类题型6.1 已知a，b，c满足|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2＝2＋2ac，则a－b＋c的值为（）A．2 B．4 C．6 D．8同类题型6.2已知a，b，c满足ab－ca＋c5，则a＋c2a＋b的值为（）A．12 B．34 C．1 D．2参考答案例1．观察下列等式：1＝2＝3＝4＝5＝6＝64,…,根据这个规律，则1)＋2\S\UP6(2)＋2\S\UP6(3)＋2\S\UP6(4)＋…＋2\S\UP6(2017的末位数字是（）A．0 B．2 C．4 D．6解：∵1＝2＝3＝4＝5＝6＝64,…,∴2017÷4＝504…1,∵(2＋4＋8＋6)×504的末尾数字是0,∴1)＋2\S\UP6(2)＋2\S\UP6(3)＋2\S\UP6(4)＋…＋2\S\UP6(2017的末位数字是2，选B．同类题型1.1计算：1＝2＝3＝4＝5＝31,…归纳各计算结果中的个位数字规律，猜测2016的个位数字是（）A．1 B．3 C．7 D．5解：∵1＝2＝3＝4＝15，5＝6＝7＝8＝255…∴由此可以猜测个位数字以4为周期按照1,3,7,5的顺序进行循环，知道2016除以4为504,而第4个数字为5，所以可以猜测2016的个位数字是5．选D．同类题型1.2观察下列算式1＝2＝3＝4＝5＝6＝7＝2187…根据上述算式中的规律，你认为2018的末位数字是（）A．3 B．9 C．7 D．1解：以3为底的幂的末位数字是3,9,7,1依次循环的，2018÷4＝504…2,所以2018的个位数字是9，选B．例2．下列定义一种关于n的运算：①当n是奇数时，结果为3n＋5②n为偶数时结果是n2\S\UP6(k)(其中k是使n2\S\UP6(k)是奇数的正整数），并且运算重复进行．例如：取n＝26，则…，若n＝449,则第449次运算结果是（）A．1 B．2 C．7 D．8解：第一次：3×449＋5＝1352,第二次：1352k根据题意k＝3时结果为169;第三次：3×169＋5＝512,第四次：因为512是2的9次方，所以k＝9，计算结果是1；第五次：1×3＋5＝8；第六次：8k因为8是2的3次方，所以k＝3，计算结果是1，此后计算结果8和1循环．因为449是奇数，所以第449次运算结果是8．选D．同类题型2.1定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5;②当n为偶数时，结果为n2\S\UP6(k) (其中k是使n2\S\UP6(k)为奇数的正整数），并且运算重复进行．例如，取n＝26，那么当n＝26时，第2016次“F运算”的结果是________．解：根据题意，得当n＝26时，第1次的计算结果是262＝13，第2次的计算结果是13×3＋5＝44，第3次的计算结果是442\S\UP6(2)＝11，第4次的计算结果是11×3＋5＝38，第5次的计算结果是382＝19，第6次的计算结果是19×3＋5＝62，第7次的计算结果是622＝31，第8次的计算结果是31×3＋5＝98，第9次的计算结果是982＝49，第10次的计算结果是49×3＋5＝152,第11次的计算结果是1522\S\UP6(3)＝19，以下每6次运算一循环，∵(2016－4)÷6＝335…2,∴第2016次“F运算”的结果与第6次的计算结果相同，为62，故答案为：62．同类题型2.2对于任意正整数n，定义"n!!"如下：当n是偶数时,n!!＝n﹒(n－2)﹒(n－4)…6﹒4﹒2,当n是奇数时,n!!＝n﹒(n－2)﹒(n－4)…5﹒3﹒1,且有n!＝n﹒(n－1)﹒(n－2)…3﹒2﹒1则有四个命题：①(2015!!)﹒(2016!!)＝2016!②2016!!＝2018③2015!!的个位数是5④2014!!的个位数是0其中正确的命题有（）A．1个B．2个C．3个D．4个解：根据题意，依次分析四个命题可得：对于①,(2015!!)﹒(2016!!)＝(2﹒4﹒6﹒8…2008﹒2010﹒2012﹒2014﹒2016)﹒(1﹒3﹒5﹒7…2009﹒2011﹒2013﹒2015)＝1﹒2﹒3﹒4﹒5…﹒2012﹒2013﹒2014﹒2015﹒2016＝2016!,故①正确；对于②,2016!!＝2﹒4﹒6﹒8﹒10…2008﹒2010﹒2012﹒2014﹒2016＝1008)(1﹒2﹒3﹒4…1008＝1008故②正确；对于③,2015!＝2015×2011×2009×…×3×1,其个位数字与1×3×5×7×9的个位数字相同，故其个位数字为5，故正确；对于④,2014!!＝2﹒4﹒6﹒8…2008﹒2010﹒2012﹒2014,其中含有10，故个位数字为0，故正确；选D．例3．一列数123满足条件：1＝12n＝1n－1且n为整数），则2017等于（）A．－1 B．12C．1 D．2解：∵1＝12n＝1n－1∴2＝11－a\S\DO(1)＝112＝2，3＝11－a\S\DO(2)＝11－2＝－1，4＝11－a\S\DO(3)＝11－(－1)＝12…∴这列数每3个数为一循环周期，∵2017÷3＝672…1,∴2017＝1＝12选B．同类题型 3.1一列数123满足条件：1＝12n＝1n－1且n为整数），则1)＋a\S\DO(2)＋a\S\DO(3)＋…＋a\S\DO(2017＝________．解：∵1＝12n＝1n－1∴2＝11－a\S\DO(1)＝112＝2，3＝11－a\S\DO(2)＝11－2＝－1，4＝11－a\S\DO(3)＝11－(－1)＝12…∴这列数每3个数为一循环周期，∵2017÷3＝672…1,∴2017＝1＝12又∵1)＋a\S\DO(2)＋a\S\DO(3＝12＝32∴1)＋a\S\DO(2)＋a\S\DO(3)＋…＋a\S\DO(2017＝312＝12．答案为12．同类题型3.2 1、2、3、20是20个由1,0,－1组成的数，且满足下列两个等式：①1)＋x\S\DO(2)＋x\S\DO(3)＋…＋x\S\DO(20＝4，②(\l(x\S\DO(1)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(2)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(3)－1))\S\UP6(2)＋…＋\b\bc\((\l(x\S\DO(20)－1))\S\UP6(2＝32，则这列数中1的个数为（）A．8 B．10 C．12 D．14解：∵1、2、3、20是20个由1,0,－1组成的数，且满足下列两个等式：①1)＋x\S\DO(2)＋x\S\DO(3)＋…＋x\S\DO(20＝4，②(\l(x\S\DO(1)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(2)－1))\S\UP6(2)＋\b\bc\((\l(x\S\DO(3)－1))\S\UP6(2)＋…＋\b\bc\((\l(x\S\DO(20)－1))\S\UP6(2＝32，∴－1的个数有8个，则1的个数有12个．故选C．例4．设△ABC的面积为1．如图1，分别将AC,BC边2等分1),E\S\DO(1是其分点，连接1)BD\S\DO(1交于点1得到四边形1)F\S\DO(1)E\S\DO(1其面积1＝13．如图2，分别将AC,BC边3等分1),D\S\DO(2),E\S\DO(1),E\S\DO(2是其分点，连接2)BD\S\DO(2交于点2得到四边形2)F\S\DO(2)E\S\DO(2其面积2＝16如图3，分别将AC,BC边4等分1),D\S\DO(2),D\S\DO(3),E\S\DO(1),E\S\DO(2),E\S\DO(3是其分点，连接3)BD\S\DO(3交于点3得到四边形3)F\S\DO(3)E\S\DO(3其面积3＝110…按照这个规律进行下去，若分别将AC,BC边(n＋1)等分，…，得到四边形n)F\S\DO(n)E\S\DO(n其面积n ＝________．解：如图所示，连接12)E\S\DO(23∵图1中1),E\S\DO(1是△ABC两边的中点，∴1)∥ABD\S\DO(1)E\S\DO(1＝12∴1)E\S\DO(1且1)E\S\DO(1)BF\S\DO(1)＝1)E\S\DO(1)AB＝12∴△CD1E1＝14)S\S\DO(△ABC＝14∵1是BC的中点，∴△BD1E1＝△CD1E1＝14∴△D1E1F1＝13)S\S\DO(△BD1E1＝114＝112∴1＝△CD1E1)＋S\S\DO(△D1E1F1＝1112＝13同理可得：图2中2＝△CD2E2)＋S\S\DO(△D2E2F2＝1118＝16图3中3＝△CD3E3)＋S\S\DO(△D3E3F3＝1380＝110以此类推，将AC,BC边(n＋1)等分，得到四边形n)E\S\DO(n)F\S\DO(n其面积n＝1n＋1)\S\UP6(2)n＋1)\S\UP6(2)1＋n＋1＝2n＋1)(n＋2答案为2(n+1)(n+2)．同类题型4.1庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1＝112)3)n．图2也是一种无限分割：在△ABC中，∠C＝90°,∠B＝30°,过点C作1于点1再过点1作1)C\S\DO(2于点2又过点2作2)C\S\DO(3于点3如此无限继续下去，则可将利△ABC分割成1、1)C\S\DO(2、1)C\S\DO(2)C\S\DO(3、2)C\S\DO(3)C\S\DO(4、…、n－2)C\S\DO(n－1)C\S\DO(n、…．假设AC＝2，这些三角形的面积和可以得到一个等式是________．解：如图2，∵AC＝2,∠B＝1∴1中1＝30°,且BC＝3∴1＝12＝1＝3)AC\S\DO(1＝3∴△ACC1＝12)﹒AC\S\DO(1)﹒CC\S\DO(1＝13＝32∵1)C\S\DO(2∴1)C\S\DO(2＝1＝30°,∴2＝12)CC\S\DO(1＝321＝3)CC\S\DO(2＝32∴△CC)\S\DO(1)C\S\DO(2＝12)﹒CC\S\DO(2)﹒C\S\DO(1)C\S\DO(2＝1\R(332＝334同理可得，△C)\S\DO(1)C\S\DO(2)C\S\DO(3＝3(\l(\F(32△C)\S\DO(2)C\S\DO(3)C\S\DO(4＝3(\l(\F(33…∴△C)\S\DO(n－2)C\S\DO(n－1)C\S\DO(n＝3(\l(\F(3n－1又∵△ABC＝12＝13＝3∴3＝3\R(33\R(3(\l(\F(323(\l(\F(333(\l(\F(3n－1∴3＝3\l(1＋\F(3(\l(\F(323n－1n)＋…．答案为3＝3\l(1+\F(3(\l(\F(323n-1n)+…．同类题型4.2 如图，顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形，再顺次连接所得的小三角形各边中点得到第2个小三角形，如此操作下去，则第n个小三角形的面积为________．解：记原来三角形的面积为s，第一个小三角形的面积为1第二个小三角形的面积为2∵1＝14＝122＝114＝143＝16∴n＝12\S\UP6(2n)＝12n)2＝12n－1答案为12\S\UP6(2n－1)．例5．如图，一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水，将瓶盖盖好后倒置，墨水水面高为h厘米，则瓶内的墨水的体积约占玻璃瓶容积的（）A．aa＋b B．ba＋b C．ha＋b D．ha＋h解：设规则瓶体部分的底面积为S平方厘米．倒立放置时，空余部分的体积为bS立方厘米，正立放置时，有墨水部分的体积是aS立方厘米，因此墨水的体积约占玻璃瓶容积的asas＋bs＝aa＋b．选A．同类题型5.1如图，一个啤酒瓶的高度为30cm，瓶中装有高度12cm的水，将瓶盖盖好后倒置，这时瓶中水面高度20cm，则瓶中水的体积和瓶子的容积之比为________．（瓶底的厚度不计）解：设瓶的底面积为2，则左图V水＝12S cm3，右图V空＝10S cm3，∵V瓶＝V水＋V空＝22S cm3，∴V水：V瓶＝6：11．故答案为611．同类题型5.2一艘轮船往返甲、乙两港之间，第一次往返航行时，水流速度为a千米/时，第二次往返航行时，正遇上发大水，水流速度为b千米/时（b＞a），已知该船在两次航行中的静水速度相同，则该船这两次往返航行所用时间的关系是（）A．第一次往返航行用的时间少B．第二次往返航行用的时间少C．两种情况所用时间相等D．以上均有可能解：设两次航行的路程都为S，静水速度设为v，第一次所用时间为：SS2vS2)－a\S\UP6(2第二次所用时间为：SS2vS2)－b\S\UP6(2∵b＞a，∴2)＞a\S\UP6(2，∴2)－b\S\UP6(2)＜v\S\UP6(2)－a\S\UP6(2∴2vS2)－b\S\UP6(2)2)－a\S\UP6(2∴第一次的时间要短些．选A．例6．若1x＝3，求2)x\S\UP6(4)＋x\S\UP6(2)＋1的值是（）A．18 B．110 C．12 D．14解：∵1x＝3，∴1x)）\S\UP6(2＝9，即1x\S\UP6(2)＝9－2＝7，∴4)＋x\S\UP6(22))＝x\S\UP6(22＝7＋1＝8，∴24)＋x\S\UP6(2)＋18．选A．同类题型6.1 已知a，b，c满足|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2＝2＋2ac，则a－b＋c的值为（）A．2 B．4 C．6 D．8解：∵已知a，b，c满足|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2＝2＋2ac，∴|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2－2ac＝2，…①且(a－3)b\S\UP6(2)必有意义，又∵2≥0，∴a－3≥0①当a－3＞0时，|2a－4|＞2，有|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2－2ac＞2，则这与①式相矛盾，即a－3＞0不成立；②当a－3＝0时，a＝3，则|2a－4|＋|b＋2|(a－3)b\S\UP6(2))＋a\S\UP6(2)＋c\S\UP6(2－2ac＝2＋|b＋2|2＝2，|b＋2|2＝0，又∵|b＋2|≥0，2≥0，∴必有b＋2＝0，c－3＝0即：b＝－2，c＝3∴a－b＋c＝3－（－2）＋3＝8选D．同类题型6.2已知a，b，c满足ab－ca＋c5，则a＋c2a＋b的值为（）A．12 B．34 C．1 D．2解：设ab－ca＋c5＝k，则a＝2k①，b－c＝3k②，a＋c＝5k③．①＋②＋③得：2a＋b＝10k．∴a＋c5k12．选A．专题02方程、不等式中的含参问题例1．已知三个非负实数a，b，c满足：3a＋2b＋c＝5和2a＋b－3c＝1，若m＝3a＋b－7c，则m的最小值为__________．同类题型1.1 已知x＋2y－3z＝0，2x＋3y＋5z＝0，则x＋y＋zx－y＋z＝________．同类题型1.2 方程组4x＋3m＝28x－3y＝m)的解x，y满足x＞y，则m的取值范围是（）A．910 B．109 C．1910 D．1019例2．关于x的方程2＋mx－9＝0和2)－3x＋m\S\UP6(2＋6m＝0有公共根，则m的值为________．同类题型2.1 已知a是一元二次方程2－2018x＋1＝0的一个根，则代数式2018a\S\UP6(2)＋1的值是___．同类题型2.2 已知关于x的方程2)－1）x\S\UP6(2＋（2k－1）x＋1＝0有两个不相等的实数根，那么实数k的取值范围为_____________．同类题型2.3 已知α、β是方程2－2x－4＝0的两个实数根，则3＋8β＋6的值为（）A．－1B．2C．22D．30例3．已知方程11a的两根分别为a，1a，则方程11a－1的根是（）A．a，1a－1 B．1a－1，a－1C．1a，a－1D．a，aa－1同类题型3.1 若关于x的方程2x－bx－1＝3的解是非负数，则b的取值范围是________．同类题型3.2 观察分析下列方程：①2x＝3；②6x＝5；③12x＝7．请利用它们所蕴含的规律，求关于x的方程2)＋nx－4＝2n＋5（n为正整数）的根，你的答案是_________________．同类题型3.3 已知关于x的方程2a＋13a x－1)(x＋2只有整数解，则整数a的值为_____________．例4．[x]表示不超过x的最大整数．如，[π]＝3，[2]＝2，[－2.1]＝－3．则下列结论：①[－x]＝－[x]；②若[x]＝n，则x的取值范围是n≤x＜n＋1；③当－1＜x＜1时，[1＋x]＋[1－x]的值为1或2；④x＝－2.75是方程4x－2[x]＋5＝0的唯一一个解．其中正确的结论有_________（写出所有正确结论的序号）．同类题型4.1 设[x]表示不大于x的最大整数，{x}表示不小于x的最小整数，（x）表示最接近x的整数（x ≠n＋0.5，n为整数）．例如[3.4]＝3，{3.4}＝4，（3.4）＝3．则不等式8≤2x＋[x]＋3{x}＋4（x）≤14的解为（）A．0.5≤x≤2 B．0.5＜x＜1.5或1.5＜x＜2C．0.5＜x＜1.5D．1.5＜x＜2同类题型4.2规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n＋0.5，n为整数），例如：[2.3]＝2，（2.3）＝3，[2.3）＝2．则下列说法正确的是___________．（写出所有正确说法的序号）①当x＝1.7时，[x]＋（x）＋[x）＝6；②当x＝－2.1时，[x]＋（x）＋[x）＝－7；③方程4[x]＋3（x）＋[x）＝11的解为1＜x＜1.5；④当－1＜x＜1时，函数y＝[x]＋（x）＋x的图象与正比例函数y＝4x的图象有两个交点．同类题型4.3 如果关于x的不等式（a＋b）x＋2a－b＞0的解集是52，那么关于x的不等式（b－a）x＋a ＋2b≤0的解集是____________．同类题型4.4 若关于x的不等式组\F(x＋4x2x－a＜0解集为x＜2，则a的取值范围是___________．同类题型4.5 按如图的程序计算，若开始输入的值x为正数，最后输出的结果为656，则满足条件的x的不同值最多有___________．参考答案例1．已知三个非负实数a，b，c满足：3a＋2b＋c＝5和2a＋b－3c＝1，若m＝3a＋b－7c，则m的最小值为__________．解：由题意可得3a＋2b＋c＝52a＋b－3c＝1m＝3a＋b－7c，解得7﹒(m＋2)3－3，11﹒(m＋2)3，m＋23，由于a，b，c是三个非负实数，∴a≥0，b≥0，c≥0，∴157．所以m_(最小值)＝57．故本题答案为：－57．同类题型1.1 已知x＋2y－3z＝0，2x＋3y＋5z＝0，则x＋y＋zx－y＋z＝________．解：由题意得：x＋2y－3z＝0①2x＋3y＋5z＝0②)，①×2－②得y＝11z，代入①得x＝－19z，原式x＋y＋z－19z＋11z＋z729．同类题型1.2 方程组4x＋3m＝28x－3y＝m)的解x，y满足x＞y，则m的取值范围是（）A．910 B．109 C．1910 D．1019解：4x＋3m＝2①8x－3y＝m②)由①得2－3m4，代入②得，2－3m4－3y＝m，4－7m3．∵x＞y，即2－3m4－7m3，解得1019．选D．例2．关于x的方程2＋mx－9＝0和2)－3x＋m\S\UP6(2＋6m＝0有公共根，则m的值为________．解：设这个公共根为α．则方程2＋mx－9＝0的两根为α、－m－α；方程2)－3x＋m\S\UP6(2＋6m＝0的两根为α、3－α，由根与系数的关系有：α（－m－α）＝－9，2＋6m，整理得，2＋mα＝9①，2)－3α＋m\S\UP6(2＋6m＝0②，②－①得，2＋6m－3α－mα＝－9，即2－α（m＋3）＝0，（m＋3）（m＋3－α）＝0，所以m＋3＝0或m＋3－α＝0，解得m＝－3或α＝m＋3，把α＝m＋3代入①得，2＋m（m＋3）＝9，2)＋6m＋9＋m\S\UP6(2＋3m＝9，m（2m＋9）＝0，所以m＝0或2m＋9＝0，解得m＝0或m＝－4.5，综上所述，m的值为－3，0，－4.5．同类题型2.1 已知a是一元二次方程2－2018x＋1＝0的一个根，则代数式2018a\S\UP6(2)＋1的值是___．解：由题意，把根a代入2－2018x＋1＝0，可得：2－2018a＋1＝0，∴2－2017a－a＋1＝0，2＋1＝2018a；∴2－2017a＝a－1，∴20182)＋11a－122018a a－1＝2018－1，＝2017．同类题型2.2 已知关于x的方程2)－1）x\S\UP6(2＋（2k－1）x＋1＝0有两个不相等的实数根，那么实数k的取值范围为_____________．解：由题意知，k≠±1，2)－4（k\S\UP6(2－1）＝5－4k＞0∴54且k≠±1．同类题型2.3 已知α、β是方程2－2x－4＝0的两个实数根，则3＋8β＋6的值为（）A．－1 B．2 C．22 D．30解：∵α、β是方程2－2x－4＝0的两个实数根，∴α＋β＝2，2－2α－4＝0，∴2＝2α＋4∴3)＋8β＋6＝α﹒α\S\UP6(2＋8β＋6＝α﹒（2α＋4）＋8β＋62＋4α＋8β＋6＝2（2α＋4）＋4α＋8β＋6＝8α＋8β＋14＝8（α＋β）＋14＝30，故选D．例3．已知方程11a的两根分别为a，1a，则方程11a－1的根是（）A．a，1a－1 B．1a－1，a－1 C．1a，a－1 D．a，aa－1解：方程11a－1可以写成11a－1的形式，∵方程11a的两根分别为a，1a，∴方程11a－1的两根的关系式为x－1＝a－1，1a－1，即方程的根为x＝a或aa－1，∴方程11a－1的根是a，aa－1．选D．同类题型3.1 若关于x的方程2x－bx－1＝3的解是非负数，则b的取值范围是________．解：去分母得，2x－b＝3x－3∴x＝3－b∵x≥0∴3－b≥0解得，b≤3又∵x－1≠0∴x≠1即3－b≠1，b≠2则b的取值范围是b≤3且b≠2．同类题型3.2 观察分析下列方程：①2x＝3；②6x＝5；③12x＝7．请利用它们所蕴含的规律，求关于x的方程2)＋nx－4＝2n＋5（n为正整数）的根，你的答案是_________________．解：1×2x＝3，解得：x＝2或x＝1；2×3x＝5，解得：x＝2或x＝3；3×4x＝7，解得：x＝3或x＝4，得到规律mnx＝m＋n的解为：x＝m或x＝n，所求方程整理得：n(n＋1)x－4＝2n＋1，根据规律得：x－4＝n或x－4＝n＋1，解得：x＝n＋4或x＝n＋5．同类题型3.3 已知关于x的方程2a＋13a x－1)(x＋2只有整数解，则整数a的值为_____________．解：方程两边同乘以（x－1）（x＋2），得：2（x＋2）－（a＋1）（x－1）＝3a，解得：2a－531－a，∵方程只有整数解，∴1－a＝3或1或－3或－1，当1－a＝3，即a＝－2时，x＝－2－1＝－3，检验，将x＝－3代入（x－1）（x＋2）＝4≠0，故x＝－3是原分式方程的解；当1－a＝1，即a＝0时，x＝－2－3＝－5，检验，将x＝－5代入（x－1）（x＋2）＝18≠0，故x＝－7是原分式方程的解；当1－a＝－3，即a＝4时，x＝－2＋1＝－1，检验，将x＝－1代入（x－1）（x＋2）＝－2≠0，故x＝－1是原分式方程的解；当1－a＝－1，即a＝2时，x＝1，检验，将x＝1代入（x－1）（x＋2）＝0，故x＝1不是原分式方程的解；∴整数a的值为：－2，0或4．例4．[x]表示不超过x的最大整数．如，[π]＝3，[2]＝2，[－2.1]＝－3．则下列结论：①[－x]＝－[x]；②若[x]＝n，则x的取值范围是n≤x＜n＋1；③当－1＜x＜1时，[1＋x]＋[1－x]的值为1或2；④x＝－2.75是方程4x－2[x]＋5＝0的唯一一个解．其中正确的结论有_________（写出所有正确结论的序号）．解：①当x＝－3.5时，[－3.5]＝－4，－[x]＝－3，不相等，故原来的说法错误；②若[x]＝n，则x的取值范围是n≤x＜n＋1是正确的；③当－1＜x＜0时，[1＋x]＋[1－x]＝0＋1＝1；当x＝0时，[1＋x]＋[1－x]＝1＋1＝2；当0＜x＜1时，[1＋x]＋[1－x]＝1＋0＝1；故当－1＜x＜1时，[1＋x]＋[1－x]的值为1或2是正确的；④x－[x]的范围为0～1，4x－2[x]＋5＝0，－5≤2x＜－7，即－2.5≤x＜－3.5，x＝－2.75或x＝－3.25都是方程4x－2[x]＋5＝0，故原来的说法错误．故答案为：②③．同类题型4.1 设[x]表示不大于x的最大整数，{x}表示不小于x的最小整数，（x）表示最接近x的整数（x ≠n＋0.5，n为整数）．例如[3.4]＝3，{3.4}＝4，（3.4）＝3．则不等式8≤2x＋[x]＋3{x}＋4（x）≤14的解为（）A．0.5≤x≤2 B．0.5＜x＜1.5或1.5＜x＜2C．0.5＜x＜1.5 D．1.5＜x＜2解：根据题意得：x＞0，若x≥2，则2x≥4，[x]≥2，3{x}≥6，4（x）≥8，不等式不成立．故只需分析0＜x＜2时的情形即可，①0＜x≤0.5时，不等式可化为：8≤2x＋0＋3＋0≤14，解得：2.5≤x≤5.5，不符合不等式；②当0.5＜x≤1时，不等式可化为：8≤2x＋0＋3＋4≤14，解得：0.5≤x≤3，因此0.5＜x≤1，符合不等式；③当1＜x＜1.5时，不等式可化为：8≤2x＋1＋6＋4≤14，解得：－1.5≤x≤1.5，因此1＜x＜1.5，符合不等式；④当1.5＜x＜2时，不等式可化为：8≤2x＋1＋6＋8≤14，解得：－3.5≤x≤－0.5，不符合不等式．故原不等式的解集为：0.5＜x＜1.5．故选C．同类题型4.2规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n＋0.5，n为整数），例如：[2.3]＝2，（2.3）＝3，[2.3）＝2．则下列说法正确的是___________．（写出所有正确说法的序号）①当x＝1.7时，[x]＋（x）＋[x）＝6；②当x＝－2.1时，[x]＋（x）＋[x）＝－7；③方程4[x]＋3（x）＋[x）＝11的解为1＜x＜1.5；④当－1＜x＜1时，函数y＝[x]＋（x）＋x的图象与正比例函数y＝4x的图象有两个交点．解：①当x＝1.7时，[x]＋（x）＋[x）＝[1.7]＋（1.7）＋[1.7）＝1＋2＋2＝5，故①错误；②当x＝－2.1时，[x]＋（x）＋[x）＝[－2.1]＋（－2.1）＋[－2.1）＝（－3）＋（－2）＋（－2）＝－7，故②正确；③4[x]＋3（x）＋[x）＝11，7[x]＋3＋[x）＝11，7[x]＋[x）＝8，1＜x＜1.5，故③正确；④∵－1＜x＜1时，∴当－1＜x＜－0.5时，y＝[x]＋（x）＋x＝－1＋0＋x＝x－1，当－0.5＜x＜0时，y＝[x]＋（x）＋x＝－1＋0＋x＝x－1，当x＝0时，y＝[x]＋（x）＋x＝0＋0＋0＝0，当0＜x＜0.5时，y＝[x]＋（x）＋x＝0＋1＋x＝x＋1，当0.5＜x＜1时，y＝[x]＋（x）＋x＝0＋1＋x＝x＋1，∵y＝4x，则x－1＝4x时，得13；x＋1＝4x时，得13；当x＝0时，y＝4x＝0，∴当－1＜x＜1时，函数y＝[x]＋（x）＋x的图象与正比例函数y＝4x的图象有三个交点，故④错误，故答案为：②③．同类题型4.3 如果关于x的不等式（a＋b）x＋2a－b＞0的解集是52，那么关于x的不等式（b－a）x＋a ＋2b≤0的解集是____________．解：∵关于x的不等式（a＋b）x＋2a－b＞0的解集是52，∴b－2aa＋b，∴b－2a52，且a＋b＜0，即b＝－3a，a＋b＜0，∴a－3a＜0，即a＞0，∴b－a＝－4a＜0，∴关于x的不等式（b－a）x＋a＋2b≤0的解集是－a－2bb－a，∵－a－2b－a＋6a54，∴关于x的不等式（b－a）x＋a＋2b≤0的解集是54．同类题型4.4 若关于x的不等式组\F(x＋4x2x－a＜0解集为x＜2，则a的取值范围是___________．解：由x＋4x2＋1，得2x＋8＞3x＋6，解得x＜2，由x－a＜0，得x＜a，又因关于x的不等式组\F(x＋4x2x－a＜0解集为x＜2，所以a≥2．同类题型4.5 按如图的程序计算，若开始输入的值x为正数，最后输出的结果为656，则满足条件的x的不同值最多有___________．解：∵最后输出的数为656，∴5x＋1＝656，得：x＝131＞0，∴5x＋1＝131，得：x＝26＞0，∴5x＋1＝26，得：x＝5＞0，∴5x＋1＝5，得：x＝0.8＞0；∴5x＋1＝0.8，得：x＝－0.04＜0，不符合题意，故x的值可取131，26，5，0.8共4个．专题03函数的几何综合问题例1．如图，在平面直角坐标系中，直线l：3\R(33与x轴交于点1，以1为边长作等边三角形1)OB\S\DO(1，过点1作1)B\S\DO(2平行于x轴，交直线l于点2，以1)B\S\DO(2为边长作等边三角形2)A\S\DO(1)B\S\DO(2，过点2作2)B\S\DO(3平行于x轴，交直线l于点3，以2)B\S\DO(3为边长作等边三角形3)A\S\DO(2)B\S\DO(3，…，则点2017的横坐标是____________．同类题型1.1 如图，直线l：y＝x＋1交y轴于点1，在x轴正方向上取点1，使1)＝OA\S\DO(1；过点1作2)B\S\DO(1⊥x轴，交l于点2，在x轴正方向上取点2，使1)B\S\DO(2)＝B\S\DO(1)A\S\DO(2；过点2作3)B\S\DO(2⊥x轴，交l于点3，在x轴正方向上取点3，使2)B\S\DO(3)＝B\S\DO(2)A\S\DO(3；…记1)B\S\DO(1面积为1，1)A\S\DO(2)B\S\DO(2面积为2，2)A\S\DO(3)B\S\DO(3面积为3，…则2017等于（）A．4030 B．4031 C．4032 D．4033同类题型1.2 如图，已知直线l：33x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点1；过点1作y轴的垂线交直线l于点1，过点1作直线l的垂线交y轴于点2；…；按此作法继续下去，则点4的坐标为（）A．（0，128）B．（0，256）C．（0，512）D．（0，1024）同类题型1.3 如图，在平面直角坐标系中，直线l：33x＋1交x轴于点B，交y轴于点A，过点A作1⊥AB 交x轴于点1，过点1作1)A\S\DO(1⊥x轴交直线l于点2…依次作下去，则点n的横坐标为____________．例2．高速公路上依次有3个标志点A、B、C，甲、乙两车分别从A、C两点同时出发，匀速行驶，甲车从A→B→C，乙车从C→B→A，甲、乙两车离B的距离1、2（千米）与行驶时间x（小时）之间的函数关系图象如图所示．观察图象，给出下列结论：①A、C之间的路程为690千米；②乙车比甲车每小时快30千米；③4.5小时两车相遇；④点E的坐标为（7，180），其中正确的有_________（把所有正确结论的序号都填在横线上）．同类题型2.1 甲、乙两辆汽车沿同一路线从A地前往B地，甲车以a千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B地，比甲车早30分钟到达．到达B地后，乙车按原速度返回A地，甲车以2a千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（小时），s与t之间的函数图象如图所示．下列说法：①a＝40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t的值为5.25；④当t＝3时，两车相距40千米，其中不正确的个数为（）A．0个B．1个C．2个D．3个同类题型2.2 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：（1）a＝40，m＝1；（2）乙的速度是80km/h；（3）甲比乙迟74h到达B地；（4）乙车行驶94小时或194小时，两车恰好相距50km．正确的个数是（）A．1B．2C．3D．4同类题型2.3 甲、乙两人从科技馆出发，沿相同的路线分别以不同的速度匀速跑向极地馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向极地馆．如图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x（秒）的函数图象．则下列四种说法：①甲的速度为1.5米/秒；②a＝750；③乙在途中等候甲100秒；④乙出发后第一次与甲相遇时乙跑了375米．其中正确的个数是（）A．1个B．2个C．3个D．4个例3．如图，已知动点P在函数12x（x＞0）的图象上运动，PM⊥x轴于点M，PN⊥y轴于点N，线段PM、PN分别与直线AB：y＝－x＋1交于点E，F，则AF﹒BE的值为（）A．4B．2C．1D．12同类题型3.1 如图，在反比例函数32x的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第二象限内有一点C，满足AC＝BC，当点A运动时，点C始终在函数kx的图象上运动，若tan∠CAB＝2，则k的值为（）A．－3B．－6C．－9D．－12同类题型3.2 如图，在平面直角坐标系中，点A在x轴的正半轴上，点B在第一象限，点C在线段AB上，点D在AB的右侧，△OAB和△BCD都是等腰直角三角形，∠OAB＝∠BCD＝90°，若函数6x（x＞0）的图象经过点D，则△OAB与△BCD的面积之差为（）A．12 B．6 C．3 D．2同类题型3.3 如图，在平面直角坐标系xOy中，已知直线y＝kx（k＞0）分别交反比例函数1x和9x在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交1x的图象于点C，连结A C．若△ABC是等腰三角形，则k的值是___________．例4．如图，一次函数y＝x＋b的图象与反比例函数kx的图象交于点A（3，6）与点B，且与y轴交于点C，若点P是反比例函数kx图象上的一个动点，作直线AP与x轴、y轴分别交于点M、N，连结BN、CM．若△ACM)＝S\S\DO(△ABN，则APAN的值为__________．同类题型4.1 当12≤x≤2时，函数y＝－2x＋b的图象上至少有一点在函数1x的图象下方，则b的取值范围为（）A．2 B．92 C．b＜3D．92同类题型4.2 方程2＋3x－1＝0的根可视为函数y＝x＋3的图象与函数1x的图象交点的横坐标，那么用此方法可推断出方程2＋2x－1＝0的实数根0所在的范围是（）A．0＜0 B．0＜1 C．0＜2 D．0＜3例5．在平面直角坐标系xOy中，抛物线2)＋2mx－m\S\UP6(2－m＋1交y轴于点为A，顶点为D，对称轴与x轴交于点H．当抛物线顶点D在第二象限时，如果∠ADH＝∠AHO，则m＝__________．同类题型5.1 已知抛物线14)x\S\UP6(2＋1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为3，3），P是抛物线14)x\S\UP6(2＋1上一个动点，则△PMF周长的最小值是（）A．3 B．4 C．5 D．6同类题型5.2 抛物线2＋bx＋3（a≠0）经过点A（－1，0），32，0），且与y轴相交于点C．设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．同类题型5.3小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为__________cm．参考答案例1．如图，在平面直角坐标系中，直线l：3\R(33与x轴交于点1，以1为边长作等边三角形1)OB\S\DO(1，过点1作1)B\S\DO(2平行于x轴，交直线l于点2，以1)B\S\DO(2为边长作等边三角形2)A\S\DO(1)B\S\DO(2，过点2作2)B\S\DO(3平行于x轴，交直线l于点3，以2)B\S\DO(3为边长作等边三角形3)A\S\DO(2)B\S\DO(3，…，则点2017的横坐标是____________．解：由直线l：3\R(33与x轴交于点1，可得1（1，0），D（0，33），∴1＝1，1D＝30°，如图所示，过1作1)A⊥OB\S\DO(1于A，则112，即1的横坐标为12\S\UP6(12，由题可得1)B\S\DO(2)B\S\DO(1)＝∠OB\S\DO(1D＝30°，2)A\S\DO(1)B\S\DO(1)＝∠A\S\DO(1)B\S\DO(1O ＝60°，∴1)B\S\DO(1)B\S\DO(2＝90°，∴1)B\S\DO(2)＝2A\S\DO(1)B\S\DO(1＝2，过2作2)B⊥A\S\DO(1)B\S\DO(2于B，则12)A\S\DO(1)B\S\DO(2＝1，即2的横坐标为132\S\UP6(22，过3作3)C⊥A\S\DO(2)B\S\DO(3于C，同理可得，2)B\S\DO(3)＝2A\S\DO(2)B\S\DO(2＝4，12)A\S\DO(2)B\S\DO(3＝2，即3的横坐标为172\S\UP6(32，同理可得，4的横坐标为1152\S\UP6(42，由此可得，n的横坐标为n)－12，∴点2017的横坐标是2017)－12．同类题型1.1 如图，直线l：y＝x＋1交y轴于点1，在x轴正方向上取点1，使1)＝OA\S\DO(1；过点1作2)B\S\DO(1⊥x轴，交l于点2，在x轴正方向上取点2，使1)B\S\DO(2)＝B\S\DO(1)A\S\DO(2；过点2作3)B\S\DO(2⊥x轴，交l于点3，在x轴正方向上取点3，使2)B\S\DO(3)＝B\S\DO(2)A\S\DO(3；…记1)B\S\DO(1面积为1，1)A\S\DO(2)B\S\DO(2面积为2，2)A\S\DO(3)B\S\DO(3面积为3，…则2017等于（）A．4030 B．4031 C．4032 D．4033解：∵1)＝OA\S\DO(1；过点1作2)B\S\DO(1⊥x轴，1)B\S\DO(2)＝B\S\DO(1)A\S\DO(2)；A\S\DO(3)B\S\DO(2⊥x轴，2)B\S\DO(3)＝B\S\DO(2)A\S\DO(3；…∴1)B\S\DO(1，1)A\S\DO(2)B\S\DO(2，2)A\S\DO(3)B\S\DO(3是等腰直角三角形，∵y＝x＋1交y轴于点1，∴1（0，1），∴1（1，0），∴1)＝OA\S\DO(1＝1，∴112，同理112，112；…∴12)×2\S\UP6(2n－2)＝2\S\UP6(2n－3，∴2017)＝2\S\UP6(2×2017－3)＝2\S\UP6(4031，选B．同类题型1.2 如图，已知直线l：33x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点1；过点1作y轴的垂线交直线l于点1，过点1作直线l的垂线交y轴于点2；…；按此作法继续下去，则点4的坐标为（）A．（0，128）B．（0，256）C．（0，512）D．（0，1024）解：∵直线l的解析式为33x，∴l与x轴的夹角为30°，∵AB∥x轴，∴∠ABO＝30°，∵OA＝1，∴OB＝2，∴3，∵1B⊥l，∴1＝60°，∴1O＝4，∴1（0，4），同理可得2（0，16），…∴4纵坐标为4＝256，∴4（0，256）．选B．同类题型1.3 如图，在平面直角坐标系中，直线l：33x＋1交x轴于点B，交y轴于点A，过点A作1⊥AB 交x轴于点1，过点1作1)A\S\DO(1⊥x轴交直线l于点2…依次作下去，则点n的横坐标为____________．解：由直线l：33x＋1交x轴于点B，交y轴于点A，可得A（0，1），3，0），∴33，即∠ABO＝30°，∴BA＝2AO＝2，又∵1⊥AB交x轴于点1，AO＝1，∴23，∴1中，43；由题可得83，∴23，∴1)B\S\DO(2中，163；由题可得329，∴33，∴2)B\S\DO(3中，643，…以此类推，\F(4n3，又∵3，∴\F(4n3，∴点n的横坐标为4n3．例2．高速公路上依次有3个标志点A、B、C，甲、乙两车分别从A、C两点同时出发，匀速行驶，甲车从A→B→C，乙车从C→B→A，甲、乙两车离B的距离1、2（千米）与行驶时间x（小时）之间的函数关系图象如图所示．观察图象，给出下列结论：①A、C之间的路程为690千米；②乙车比甲车每小时快30千米；③4.5小时两车相遇；④点E的坐标为（7，180），其中正确的有_________（把所有正确结论的序号都填在横线上）．解：①450＋240＝690（千米）．故A、C之间的路程为690千米是正确的；②450÷5－240÷4＝90－60＝30（千米/小时）．故乙车比甲车每小时快30千米是正确的；③690÷（450÷5＋240÷4）＝690÷（90＋60）＝690÷150＝4.6（小时）．故4.6小时两车相遇，原来的说法是错误的；④（450－240）÷（450÷5－240÷4）＝210÷（90－60）＝210÷30＝7（小时），450÷5×7－450＝630－450＝180（千米）．故点E的坐标为（7，180）是正确的，故其中正确的有①②④．同类题型2.1 甲、乙两辆汽车沿同一路线从A地前往B地，甲车以a千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B地，比甲车早30分钟到达．到达B地后，乙车按原速度返回A地，甲车以2a千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（小时），s与t之间的函数图象如图所示．下列说法：①a＝40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t的值为5.25；④当t＝3时，两车相距40千米，其中不正确的个数为（）A．0个B．1个C．2个D．3个解：①由函数图象，得a＝120÷3＝40故①正确，②由题意，得5.5－3－120÷（40×2），＝2.5－1.5，＝1．∴甲车维修的时间为1小时；故②正确，③如图：∵甲车维修的时间是1小时，∴B（4，120）．∵乙在甲出发2小时后匀速前往B地，比甲早30分钟到达．∴E（5，240）．∴乙行驶的速度为：240÷3＝80，∴乙返回的时间为：240÷80＝3，∴F（8，0）．设BC的解析式为1)＝k\S\DO(1)t＋b\S\DO(1，EF的解析式为2)＝k\S\DO(2)t＋b\S\DO(2，由图象，得120＝4k\S\DO(1)＋b\S\DO(1)240＝5.5k\S\DO(1)＋b\S\DO(，))，240＝5k\S\DO(2)＋b\S\DO(2)0＝8k\S\DO(2)＋b\S\DO(2))解得k\S\DO(1)＝80b\S\DO(1)＝－200)，k\S\DO(2)＝－80b\S\DO(2)＝640)，∴1＝80t－200，2＝－80t＋640，当1)＝y\S\DO(2时，80t－200＝－80t＋640，t＝5.25．∴两车在途中第二次相遇时t的值为5.25小时，故弄③正确，④当t＝3时，甲车行的路程为：120km，乙车行的路程为：80×（3－2）＝80km，∴两车相距的路程为：120－80＝40千米，故④正确，选A．同类题型2.2 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：（1）a＝40，m＝1；（2）乙的速度是80km/h；（3）甲比乙迟74h到达B地；（4）乙车行驶94小时或194小时，两车恰好相距50km．。