12与官科大专家讨论全国中学生物理竞赛题正文12
- 格式:pdf
- 大小:497.42 KB
- 文档页数:6

2012年29届全国中学生物理竞赛决赛试题一、(15分)如图,竖直的光滑墙面上有A 和B 两个钉子,二者处于同一水平高度,间距为l ,有一原长为l 、劲度系数为k 的轻橡皮筋,一端由A 钉固定,另一端系有一质量为m =4kl g的小球,其中g 为重力加速度.钉子和小球都可视为质点,小球和任何物体碰撞都是完全非弹性碰撞而且不发生粘连.现将小球水平向右拉伸到与A 钉距离为2l 的C 点,B 钉恰好处于橡皮筋下面并始终与之光滑接触.初始时刻小球获得大小为20gl v、方向竖直向下的速度,试确定此后小球沿竖直方向的速度为零的时刻.如图所示,三个质量均为m的小球固定于由刚性轻质杆构成的丁字形架的三个顶点A、B和C 处.AD⊥BC,且AD=BD=CD=a,小球可视为质点,整个杆球体系置于水平桌面上,三个小球和桌面接触,轻质杆架悬空.桌面和三小球之间的静摩擦和滑动摩擦因数均为μ,在AD杆上距A点a/4和3a/4两处分别施加一垂直于此杆的推力,且两推力大小相等、方向相反.1.试论证在上述推力作用下,杆球体系处于由静止转变为运动的临界状态时,三球所受桌面的摩擦力都达到最大静摩擦力;2.如果在AD杆上有一转轴,随推力由零逐渐增加,整个装置将从静止开始绕该转轴转动.问转轴在AD杆上什么位置时,推动该体系所需的推力最小,并求出该推力的大小.不光滑水平地面上有一质量为m的刚性柱体,两者之间的摩擦因数记为μ.柱体正视图如图所示,正视图下部为一高度为h的矩形,上部为一半径为R的半圆形.柱体上表面静置一质量同为m的均匀柔软的链条,链条两端距地面的高度均为h/2,链条和柱体表面始终光滑接触.初始时,链条受到微小扰动而沿柱体右侧面下滑.试求在链条开始下滑直至其右端接触地面之前的过程中,当题中所给参数满足什么关系时,1.柱体能在地面上滑动;2.柱体能向一侧倾倒;3.在前两条件满足的情形下,柱体滑动先于倾倒发生.如图所示,在一光滑水平圆桌面上有两个质量、电荷都均匀分布的介质球,两球半径均为a,A球质量为m,所带电荷量为Q,B球质量为4m,所带电荷量为-4Q.在初始时刻,两球球心距为4a,各有一定的初速度,以使得两球在以后的运动过程中不发生碰撞,且都不会从圆桌面掉落.现要求在此前提下尽量减小桌面面积,试求1.两球初速度的方向和大小;2.圆桌面的最小半径.假设两球在运动过程中,其所带电荷量始终保持均匀分布:桌面也不发生极化效应.已知两个均匀带电球之间的静电相互作用力,等于电荷集中在球心的两个点电荷之间的相互作用力;静电力常量为k e.如图所示,一半径为R 的轻质绝缘塑料薄圆盘水平放置,可绕过圆盘中心的竖直固定轴无摩擦地自由转动.一半径为a 的轻质小圆线圈(a<<R)固定在盘面上,圆线圈与圆盘共轴.在盘边缘处等间隔地固定4个质量均为m 的带正电的金属小球,每个小球所带电荷量均为q .此装置处在一磁感应强度大小为B 0、方向竖直向上的均匀强磁场中.初始时圆盘静止,圆线圈中通有恒定电流I .方向沿顺时针方向(从上往下看).若切断圆线圈中的电流,则圆盘将发生转动.求薄圆盘稳定转动后,圆盘在水平方向对每个金属球小的作用力的大小.假设金属小球可视为质点,不计小圆线圈的自感和带电金属小球因运动所产生的磁场. 已知固定在圆盘面上的半径为a 、通有电流I 的圆线圈在圆盘面内、距线圈圆心的距离为r 处(r >>a )产生的磁场的磁感应强度的大小为B =322r I a k m ,式中k m 为已知常量,当线圈中的电流沿顺时针方向时,磁场方向垂直于圆盘平面且竖直向上.静电力常量为ke .如图,一水平放置的刚性密闭气缸,缸壁是绝热的,活塞把气缸内空间分为两个体积相同的密闭室A 和B .活塞由一层热容量很小(略去其影响)、导热良好的材料(与气缸壁有摩擦)和一薄层绝热材料(与气缸壁没有摩擦)压制而成,绝热层在A 室一侧.初始时,A 室和B 室充有绝对温度均为T 0的同种多原子分子理想气体,A 室气体压强是B 室气体压强的4倍.现释放活塞,活塞由于其导热部分与汽缸壁之间存在摩擦而运动缓慢,最后停止在平衡位置(此时活塞与缸壁间无静摩擦).已知气缸中的气体具有如下特性:在温度高于某个临界温度T d (>T 0)时,部分多原子气体分子将发生分解,一个多原子分子可以分解为另外两个相同的多原子分子.被分解的气体摩尔数与发生分解前气体总摩尔数之比a 满足关系a =)(d T T -β,其中β=2.00T 0-1.分解过程是可逆的,分解1摩尔分子所需能量φ=CT 0/l0,1摩尔气体的内能与绝对温度T 的关系为u =CT (C 是与气体的种类无关的常量).已知当压强为P 、体积为V 的这种气体绝热缓慢膨胀时,PV γ=常量,其中γ=4/3.1.对于具有上述特性的某种气体,若实验测得在上述过程结束时没有任何分子发生了分解,求这种分子发生分解的临界温度T d 的可能值;2.对于具有上述特性的另一种气体,若实验测得在上述过程结束时有a =l0.0%的分子分解了,求这种分子发生分解的临界温度T d .如图一所示的光学系统是由平行光管、载物台和望远镜组成.已知望远镜物镜L0的焦距为l6.00cm.在L0的焦平面P处,放置带十字叉丝线的分划板和亮十字物,如图二所示.在载物台上放置双面平行的平面镜M,通过望远镜的目镜Le观察时,能同时清楚地看到分划板上的十字叉丝线和十字物经过L0折射、M 反射、再经L0折射后在分划板上所成的十字像,十字像位于A点,与上十字叉丝线的距离为5.2mm.绕载物台转轴(沿竖直方向)转动载物台,使平面镜转l80°,此时十字像位于B点,与上十字叉丝线的距离为18.8mm.根据以上情况和数据可计算出,此时望远镜光轴与水平面的夹角为rad;据此结果,调节望返镜,使其光轴与载物台的转轴垂直.平行光管是由十字缝S和凸透镜L组成.去掉光学系统中的平面镜M,并用钠光灯照亮S.沿水平方向移动S,当S到平行光管中的透镜L距离为8.25cm时,通过望远镜目镜能清楚地看到十字缝的像恰好成在分划板中心十字叉丝线上,由此可以推知,L的焦距等于cm.将载物台平面调至与载物台的转轴垂直,在载物台上放置长、宽、高均为3.00cm、折射率为1.52的分束棱镜abed(分束棱镜是由两块直角三棱镜密接而成,接触面既能透光又能反光)和待测凹球面镜O,O 到L的距离为l5.00cm,并保证分束棱镜的ab面与图三中的XX′轴垂直、凹球面镜的光轴与图三中的XX′轴重合;再将望远镜绕载物台的中心轴转90°,如图三所示。


全国中学生物理竞赛预赛试题参考解答、评分标准一、参考解答(1)在地面附近,沙尘扬起要能悬浮在空中,则空气阻力至少应与重力平衡,即201Av mg αρ= ① 式中m 为沙尘颗粒的质量,而2A r π= ②3s 43m r πρ= ③得 1v =④ 代入数据得 11 4.0m s v =⋅- ⑤(2)用h ρ、h 分别表达19.0m s v =⋅-时扬沙到达的最高处的空气密度和高度,则有0h (1)Ch ρρ=- ⑥此时式①应为2h Av mg αρ= ⑦由②、③、⑥、⑦可解得20s 4113r g h C v ραρ⎛⎫=- ⎪⎝⎭⑧ 代入数据得 36.810m h =⨯ ⑨评分标准:本题15分。
1. 第一小题8分。
其中①式3分,②式1分,③式1分,④式2分,⑤式1分。
2. 第二小题7分。
其中⑥式1分,⑦式1分,⑧式3分,⑨式2分。
二、参考解答(1)212C E ,0 (2)214C E ,212C E评分标准:本题20分。
(1)10分。
其中每个空5分。
(2)10分。
其中每个空5分。
三、参考解答(1)神舟3号(2)设飞船飞行时间为t ,绕地球飞行的圈数为N ,周期为T ,飞船的质量为m ,离地面的平均高度为h ,地球半径为R ,地球质量为M ,则有t T N= ① 222()()mM G m R h T R h π⎛⎫=+ ⎪+⎝⎭② 2Mm Gmg R = ③ 由①、②、③式解得 1/322224gR t h R N π⎛⎫=- ⎪⎝⎭ ④由题给数据可知55.853610s t =⨯,代入t 及其它有关数据得52.910m h =⨯ ⑤评分标准:本题20分(1)4分(2)16分。
其中①、②、③、④式各3分,⑤式4分(答案在52.710m ⨯~53.110m ⨯之间均给这4分)四、参考解答根据题设的条件,可知:开始时A 中氦气的质量3He 4.00310kg m -=⨯,B 中氪气的质量3Kr 83.810kg m -=⨯,C 中氙气的质量3Xe 131.310kg m -=⨯。

第23届全国中学生物理竞赛决赛试题2006年11月深圳★理论试题一、建造一条能通向太空的天梯,是人们长期的梦想.当今在美国宇航局(NASA )支持下,洛斯阿拉莫斯国家实验室的科学家已在进行这方面的研究.一种简单的设计是把天梯看作一条长度达千万层楼高的质量均匀分布的缆绳,它由一种高强度、很轻的纳米碳管制成,由传统的太空飞船运到太空上,然后慢慢垂到地球表面.最后达到这样的状态和位置:天梯本身呈直线状;其上端指向太空,下端刚与地面接触但与地面之间无相互作用;整个天梯相对于地球静止不动.如果只考虑地球对天梯的万有引力,试求此天梯的长度.已知地球半径R 0=6.37×106m ,地球表面处的重力加速度g =9.80m ·s -2.二、如图所示,一内半径为R 的圆筒(图中2R 为其内直径)位于水平地面上.筒内放一矩形物.矩形物中的A 、B 是两根长度相等、质量皆为m 的细圆棍,它们平行地固连在一质量可以不计的,长为l =R 的矩形薄片的两端.初始时矩形物位于水平位置且处于静止状态,A 、B 皆与圆筒内表面接触.已知A 、B 与圆筒内表面间的静摩擦因数μ都等于1.现令圆筒绕其中心轴线非常缓慢地转动,使A 逐渐升高.1.矩形物转过多大角度后,它开始与圆筒之间不再能保持相对静止? 答:___________________________(只要求写出数值,不要求写出推导过程)lA 2R2.如果矩形物与圆筒之间刚不能保持相对静止时,立即令圆筒停止转动.令θ表示A的中点和B的中点的连线与竖直线之间的夹角,求此后θ等于多少度时,B 相对于圆筒开始滑动.(要求在卷面上写出必要的推导过程.最后用计算器对方程式进行数值求解,最终结果要求写出三位数字.)三、由于地球的自转及不同高度处的大气对太阳辐射吸收的差异,静止的大气中不同高度处气体的温度、密度都是不同的.对于干燥的静止空气,在离地面的高度小于20km的大气层内,大气温度T e随高度的增大而降低,已知其变化率=-6.0×10-3K·m-1z为竖直向上的坐标.现考查大气层中的一质量一定的微小空气团(在确定它在空间的位置时可当作质点处理),取其初始位置为坐标原点(z=0),这时气团的温度T、密度ρ、压强p都分别与周围大气的温度T e、密度ρe、压强p e相等.由于某种原因,该微气团发生向上的小位移.因为大气的压强随高度的增加而减小,微气团在向上移动的过程中,其体积要膨胀,温度要变化(温度随高度变化可视为线性的).由于过程进行得不是非常快,微气团内气体的压强已来得及随时调整到与周围大气的压强相等,但尚来不及与周围大气发生热交换,因而可以把过程视为绝热过程.现假定大气可视为理想气体,理想气体在绝热过程中,其压强p与体积V满足绝热过程方程pVγ=C.式中C和γ都是常量,但γ与气体种类有关,对空气,γ=1.40.已知空气的摩尔质量μ=0.029kg?mol-1,普适气体恒量R=8.31J?(K?mol)-1.试在上述条件下定量讨论微气团以后的运动.设重力加速度g=9.8m·s-2,z=0处大气的温度T e0=300K.四、图1中K 为带电粒子发射源,从中可持续不断地射出质量、电荷都相同的带正电的粒子流,它们的速度方向都沿图中虚线O ′O ,速度的大小具有一切可能值但都是有限的.当粒子打在垂直于O ′O 的屏NN ′上时,会在屏上留下永久性的痕迹.屏内有一与虚线垂直的坐标轴Y ,其原点位于屏与虚线的交点O 处,Y 的正方向由O 指向N .虚线上的A 、B 两处,各有一电子阀门a 和b .阀门可以根据指令开启或关闭.开始时两阀门都处于关闭状态,挡住粒子流.M 、M ′是两块较大的平行金属平板,到虚线O ′O 的距离都是d ,板M 接地.在两板间加上如图2所示的周期为2T 的交变电压u ,u 的正向最大值为2U ,负向最大值为U .已知当带电粒子处在两平板间的空间时,若两平板间的电压为U ,则粒子在电场作用下的加速度a 、电压u 的半周期T 和平板到虚线的距离d 满足以下关系aT 2=d已知AB 间的距离、B 到金属板左端的距离、金属板的长度以及金属板右端到屏的距离都是l .不计重力的作用.不计带电粒子间的相互作用.打开阀门上的粒子被阀门吸收,不会影响以后带电粒子的运动.只考虑MM ′之间的电场并把它视为匀强电场.1.假定阀门从开启到关闭经历的时间δ比T 小得多,可忽略不计.现在某时刻突然开启阀门a 又立即关闭;经过时间T ,再次开启阀门a 又立即关闭;再经过时间T ,第3次开启阀门a 同时开启阀门b ,立即同时关闭a 、b .若以开启阀门b 的时刻作为图2中t =0的时刻,则屏上可能出现的粒子痕迹的Y 坐标(只要写出结果,不必写出计算过程)为t /T24681012u2U 图2KOMN NO M B A a bllll__________________________________________________________________________.2.假定阀门从开启到关闭经历的时间δ=,现在某时刻突然开启阀门a ,经过时间δ立即关闭a ;从刚开启a 的时刻起,经过时间T ,突然开启阀门b ,经过时间δ关闭b .若以刚开启阀门b 的时刻作为图2中t =0的时刻,则从B 处射出的具有最大速率的粒子射到屏上所产生的痕迹的Y 坐标(只要写出结果,不必写出计算过程)为_____________________________________________________________________________.具有最小速率的粒子射到屏上所产生的痕迹的Y 坐标(只要写出结果,不必写出计算过程)为_____________________________________________________________________________.五、如图所示,坐标系Oxyz 的x 轴和z轴都位于纸面内,y 轴垂直纸面向里.两无限大金属极板P 和Q 分别位于x =-d 和x =d 处.磁感应强度大小为B 的匀强磁场的方向平行于Oxz 坐标平面,与z 轴的夹角为α.在坐标原点O 处,有一电荷为q (>0)、质量为m的带电粒子,以沿y 轴正方向的初速度v 0开始运动.不计重力作用.1.若两极板间未加电场,欲使该粒子在空间上恰好能到达极板(但与板不接触),则初速度v 0应为多大?所需最短时间t 0是多少?2.若在两极板间沿x 轴正方向加上一场强为E 的匀强电场,使该粒子能在第1问中所求得的时间t 0到达极板,则该粒子的初速度v 0应为多大?若α=,求粒子到达极板时粒子的坐标.六、在高能物理中,实验证明,在实验室参考系中,一个运动的质子与一个静止的质子相碰时,碰后可能再产生一个质子和一个反质子,即总共存在三个质子和一个反质子.试求发生这一情况时,碰前那个运动质子的能量(对实验室参考系)的最小值(即阈值)是多少.已知质子和反质子的静止质量都是m 0=1.67×10-27kg .不考虑粒子间的静电作用.第23届全国中学生物理竞赛决赛参考解答一、要使天梯相对于地球静止不动,由地面伸向太空,与地面之间无相互作用力,这样的天梯的下端只能位于赤道上某处,且天梯与该处地球表面垂直,并与地球同步转动.如图1所示.从坐标原点与地球中心固连、坐标轴指向恒星的惯性参考系来看,天梯和地球一起匀速转动.天梯所受的外力只有地球的万有引力.把天梯看作是由线密度为ρ的许多非常小的小段组成,则每小段到地球中心的距离不同,因而所受地球引力的大小也不同,其中与地心的距离为r i -1到r i 间的长度为△r i 的小段所受地球引力为f i =G )(1)整个天梯所受的地球引力F 就等于每小段所受地球引力之和, 即F =1n i i f =∑=21nii i M r Gr ρ=∑(2)图1符号1ni =∑表示对所有小段求和.因△r i =r i -r i -1是个小量,注意到r i r i -1=r i (r i -△r i )≈r ,因此用R 0表示地球半径,也就是天梯下端到地心的距离,R l 表示天梯上端到地心的距离,则r 0=R 0,r n =R l ,代入(2)式得F =GM ρ(-)(3)整个天梯的质量m =ρ(R l -R 0)(4)天梯的质心位于天梯的中点,它到地心的距离r C =R 0+(5)根据质心运动定理,有F =mr C ()2(6)式中T 为地球自转的周期.由(3)、(4)、(5)、(6)式可得(R l -R 0)(R +R 0R l -)=0R l -R 0=0,表示天梯无长度,不符合题意,符合题意的天梯长度满足的方程为R +R 0R l -=0(7)因为GM =Rg ,所以得R +R 0R l -=0(8)【从跟随地球一起转动的参考系看,也可得到(8)式.这时,天梯在地球引力和惯性离心力的作用下,处于平衡静止状态,地球引力仍为(3)式,天梯所受的惯性离心力可由下面的方法求得:仍把天梯看作由很多长度为△r i 的小段组成,则第i 小段受的惯性离心力为f i ′=ρ△r i ()2r i (4′)对所有小段求和,就得到整个天梯所受的惯性离心力F ′=1ni i f ='∑=1ni ρ=∑()2r i △r i (5′)(5′)式中所示的和可以用图2过原点的直线y =ρ()2r 下的一个带阴影的梯形面积来表示,即F ′=ρ()2(R l -R 0)(6′)因为地球引力与惯性离心力平衡,由(3)式和(6′)式可得GM (-)=()2(R l -R 0)(7′)因为GM =Rg ,化简(7′)式最后也能得到(8)式.】 解(8)式得R l =+2R 0gT 2π2),2)(9)根号前取正号,代入有关数据,注意到T =8.64×104s ,得R l =1.50×108 m (10)所以天梯的长度L =R l -R 0=1.44×108 m (11)二、1.90°.2.当矩形物处于竖直位置即θ=0°时,B 不会滑动,矩形物静止.当圆筒缓慢转动使θ刚超过0°时,A将离开圆筒内表面而开始倾倒,按题意此时圆筒已停止OR 0R lρ()2R lρ()2R 0图2转动.假定B 仍不动,此后,A 在竖直平面内从静止开始绕B 做圆周运动.圆周运动的径向方程(牛顿第二定律)为m =mg cos θ-T (1)这里v 表示A 的速度.T 是刚性薄片对A 的作用力,规定其方向从B 到A 为正.根据能量守恒,有mgl (1-cos θ)=mv 2(2)联立(1)、(2)式,得T =mg (3cos θ-2)(3)如果令T =0,可得θ=arccos()=48.2°显见,θ<48.2°时,作用力是径向正向,对A 是推力;θ>48.2°时,作用力是径向反向,对A 是拉力.现在再来看前面被假定不动的B 是否运动.我们可以在B 处画圆筒内表面的切面,它与水平面成30°夹角.因为假定B 不动,其加速度为零,所以B 在垂直于切面方向的受力方程为f ⊥-mg cos30°-T cos(30°-θ)=0(4)这里f ⊥是圆筒内壁对B 的支持力.由(4)式和(3)式可以论证,如果在θ等于60°(A 将与圆筒相碰)之前B 不动,则f ⊥必将始终不等于零,这就是说,在B 开始滑动以前,B 不会离开筒壁.B 对筒壁的正压力是f ⊥的反作用力,大小和f ⊥相同.式中的T 是刚性薄片对B 的作用力,它和(1)式中的T 大小相等(因薄片质量不计).由于μ=1,所以最大静摩擦力f max 的大小就等于正压力.12030A θf max=μf⊥=mg cos30°+T cos(30°-θ)(5)其方向是沿切面方向.沿切面方向除摩擦力外,B还受到其他力f∥=mg sin30°+T sin(30°-θ)(6)只要f∥不大于最大静摩擦力,B就不滑动.这个条件写出来就是f∥≤f max(7)B滑动与否的临界点就应由f∥=f max求出,即mg cos30°+T cos(30°-θ)=mg sin30°+T sin(30°-θ)(8)将(3)式的T代入(8)式,化简后得方程(3cosθ-2)[cosθ+(2+)sinθ]+1=0(9)这个方程可用数值求解,即取不同的θ值代入逐步逼近,最后可得θ=54.9°(10)θ超过此值,B将开始滑动.三、设微气团中空气的质量为m,当其位移为z时,气团的体积为V,气团内气体的密度为ρ,气团周围大气的密度为ρe.气团受到竖直向下的重力mg=Vρg和竖直向上的浮力Vρe g作用,若气团的加速度为α,则由牛顿第二定律有mα=-Vρg+Vρe g=-V(ρ-ρe)g(1)或有α=-g(2)根据理想气体状态方程pV=RT(3)可知气体的密度ρ==(4)利用(4)式,注意到p=p e,(2)式可化成α=-g(5)周围大气在z处的温度T e等于z=0处的温度T e0加从0到z温度的增量,即T e=T e0+z(6)若气团中气体温度随高度的变化率为,根据题意,有T=T0+z(7)T0为气团位于初始位置时气团中气体的温度.根据题意T e0=T0,把(6)、(7)式代入(5)式得α=-(-)z(8)在(8)式中,若(-)>0,则加速度方向向下,作用于气团的力有使气团回到初始位置的趋势,这样,大气层中的大气就处于稳定状态;反之,气团将远离其初始位置,大气层中的大气处在不稳定状态.因周围大气温度随高度的变化率是已知的,故只要知道气团中气体温度随高度的变化率,便可对气团的运动作出判断.大气的压强随高度的增加而减小,在高度为z和z+△z处的压强差△p e=-ρe g△z(9)式中ρe为z处的空气的密度,与温度、压强有关,由(4)式表示.式中负号表示高度增加时,大气压强是减小的.把(4)式代入(9)式得△p e=-g△z(10)质量为m的气团在上升过程中,其压强将随周围大气的压强的减小而减小,体积要增大,气团对周围空气做功.因为过程是绝热的,气团的内能要减少,因而温度要降低,温度、压强的变化应满足绝热过程的规律.试题给出的绝热过程方程是关于压强与体积间的关系,利用理想气体状态方程,可把绝热过程方程表示为温度与压强间的关系.由(3)式得V=(11)把(11)式代入pVγ=C 得T=1Cγ1pγγ-(12)当气团的压强由p变到p+△p时,气团的温度将由T变到T+△T.由(12)式T+△T=1Cγ(p+△p)1γγ-利用二项式定理,忽略△p的高次方项,并注意到(12)式得T+△T=1Cγ[1pγγ-+11pγγ--(△p)]=T+△p故有△T=△p(13)根据题意,p=p e,△p=△p e,由(7)式、(10)式和(13)式得=-+)z)(14)已知=-6.0×10-3K·m-1,代入有关数据可求得=9.8×10-3K·m-1当z不是很大时,有T e0+(+)z≈T e0故有=-(15)代入题给的有关数据得=-9.8×10-3K·m-1(16)负号表示高度增加时,气团的温度要下降.可见(-)>0,作用于气团的合力的方向与气团位移的方向相反,指向气团的初始位置,气团发生向上位移后,将要回到初始位置.当z不是很大时,(8)式中的T e可以用T e0代替,可知气团将在初始位置附近做简谐振动.振动的圆频率ω=(17)代入数据,得ω=1.1×10-2s-1(18)四、1.Y1=-0.3d,Y2=0.9d.2.Y′=-0.138d,Y′′=-0.138d.附参考解法:1.当阀门a第1次开启时,具有各种速率的粒子(称之为第一批粒子)从A处进入AB之间,在a第2次开启时刻,第一批粒子中速率为v1=(1)的粒子正好射到B处,被阀门b挡住.与此同时,第二批具有各种速率的粒子从A处进入AB之间.在阀门a第3次开启的时刻,第一批进入AB间的粒子中速率为v2==v1(2)的粒子与第二批进入AB间的粒子中速率为v1的粒子同时到达B处.因此时阀门b已开启,这些粒子都从B处沿虚线射向两平行板,而第三批进入AB间的粒子在它们到达B处时,被b挡住.由此可知,能从B处射向两平行板的粒子具有v1和v2两种不同的速率.根据题意,粒子从B处射出的时刻为t=0,故速率为v1的粒子在时刻t1==T进入两平行板之间,由本题图2可知,两板间的电压u=-U粒子在两板间的电场作用下的加速度为-a,粒子通过两板经历的时间为△t1==T在△t1时间内粒子在Y方向获得的分速度和位移分别为v1y=-a△t1=-aT(3)y1=-a(△t1)2=-aT2(4)因aT2=d,故|y1|=d<d,表明速率为v1的粒子能穿出平板,粒子穿出平板后做匀速运动.在从射出平板至射到屏的时间内,粒子在Y方向的位移△y1=v1y=-aT2(5)粒子在屏上产生的痕迹的Y坐标为Y1=y1+△y1=-aT2-aT2=-aT2=-0.3d(6)速率为v2的粒子在时刻t2==2T进入两平行板之间,由本题图2可知,两板间的电压u=2U粒子在电场作用下的加速度为2a,粒子通过两板经历的时间为△t2==2T因为两板间的电压在时间△t2内由2U变为-U,粒子的加速度亦将从2a变成-a,由此可求得在△t2时间内粒子在Y方向获得的分速度和位移分别为v2y=2aT-aT=aT(7)y2=(2a)T2+(2aT)T-aT2=aT2(8)因aT2=d,故y2=d<d,表明速率为v2的粒子亦能穿出平板.粒子穿出平板后做匀速运动.在从射出平板至射到屏的时间内,粒子在Y方向的位移△y2=v2y=2aT2(9)粒子打在屏上产生的痕迹的Y坐标为Y2=y2+△y2=aT2+2aT2=aT2=0.9d(10)即粒子在屏上产生的痕迹是两个点,它们的Y坐标分别为Y1和Y2.2.由于阀门从开启到关闭要经历一段时间,在阀门a开启到关闭经历的δ时间间隔内的不同时刻,都有各种不同速率的粒子从A处进入AB间,有的早进入,有的晚进入.由于阀门b从开启到关闭也要经历一段时间δ,粒子可能在最早的时刻即t=0的时刻从B处射出,也可能在最晚的时刻即t=δ时刻从B处射出.在a刚开启的时刻从A处射入AB间,并在t=δ时刻从B处射出的粒子的速率最小,这最小速率为v min=(11)在阀门a刚要关闭时刻从A处射进AB间,并在t=0的时刻从B处射出的粒子的速率最大,这最大速率为v max=(12)在t=0时刻从B处射出的速率为v max的粒子在时刻t1==T-δ进入两平板之间,在时刻t1′=t1+=2T-2δ离开两平板.由本题图2可知,在T-δ到T时间内,两板间的电压为2U,在T到2T-2δ时间内,两板间的电压为-U,与电压对应的粒子的加速度分别为2a和-a.在粒子通过平板的时间内,粒子在Y方向获得的分速度和位移分别为v1y=2aδ-a(T-2δ)=-aT+4aδ(13)y1=(2a)δ2+(2a)δ(T-2δ)-a(T-2δ)2=-aT2+4aδT-5aδ2(14)粒子穿出平板后做匀速运动.从射出平板至射到屏的时间内,粒子在Y方向的位移△y1=v1y=(-aT+4aδ)(T-δ)=-aT2+5aδT-4aδ2(15)粒子在屏上产生的痕迹的Y坐标为Y1=y1+△y1=-aT2+9aTδ-9aδ2(16)根据题意,代入数据得Y1=-0.138d(17)在t=δ时刻从B处射出的速度为v min的粒子在时刻t2=δ+=T+2δ进入两平板之间,在时刻t2′=t2+=2T+3δ离开两平板.由本题图2可知,在T+2δ到2T时间内,两板间的电压为-U,在2T到2T+3δ时间内,两板间的电压为2U,与电压对应的粒子的加速度分别为-a 和2a.在粒子通过平板的时间内,粒子在Y方向获得的分速度和位移分别为v2y=-a(T-2δ)+(2a)3δ=-aT+8aδ(18)y2=-a(T-2δ)2-a(T-2δ)3δ+(2a)(3δ)2=-aT2-aTδ+13aδ2(19)粒子穿出平板后做匀速运动.在从射出平板至射到屏的时间内,粒子在Y方向的位移△y2=v2y=(-aT+8aδ)(T+δ)=-aT2+7aTδ+8aδ2(20)粒子在屏上产生的痕迹的Y坐标为Y2=y2+△y2=-aT2+6aTδ+21aδ2(21)根据题意,代入数据得Y2=-0.138d(22)由以上分析可知,速率最小和速率最大的粒子打在屏上产生的痕迹是位于Y轴上的同一点.五、解法一1.平行板间仅有磁场,带电粒子初速度v 0的方向垂直于磁场,在洛伦兹力的作用下,粒子将在垂直于磁场方向的平面内做匀速圆周运动,圆周半径R 0=(1)轨道平面与Oxz 坐标平面的交线如图1中NN ′所示.要使粒子刚能到达极板Q (与板刚未接触),圆心C 应是ON ′的中点,有CN ′=R 0=(2)由(1)、(2)式得v 0=(3)粒子由O 经过半个圆周到达N ′,所经历的最短时间为圆周运动的半个周期t 0==(4)2.以y 轴为旋转轴,顺时针转动α角,建立新坐标系Ox ′y ′z ′,如图2所示.在新坐标系中电场强度E 的分量为E x ′=E cos αE y ′=0E z ′=E sin α(5)图1zz By ,xO α图Ev 0α磁感应强度B的分量为B x′=0B y′=0B z′=B(6)带电粒子所受到的电场力的分量为f Ex′=qE x′=qE cosαf Ey′=0f Ez′=qE z′=qE sinα(7)当带电粒子速度为v时,带电粒子所受到磁场力的分量为f Bx′=qv y′Bf By′=-qv x′Bf Bz′=0(8)(i)关于带电粒子在Ox′y′平面内的分运动现设想起始时刻带电粒子沿y′轴正方向的初速度v0用下式表示v0=v0+v1-v1=v2-v1式中v2=v0+v1(9)现把v0看成沿y′轴负方向运动的速度v1和沿y′轴正方向运动的v2的合成.这样,与前者联系的运动使带电粒子受到沿x′轴的负方向的磁场力作用,它与电场力的分量f Ex′的方向相反,当v1取数值v1==cosα(10)时,与-v1相联系的磁场力与f Ex′的合力为零,其效果是带电粒子沿y′轴负方向以速度v1做匀速运动;与后者联系的运动使带电粒子仅受到磁场力作用,此力的方向既垂直于磁场方向(z′轴方向),又垂直于速度v2,即位于Ox′y′平面内,其大小为f x′y′=qv2B(11)粒子在此力作用下在平面内做速度为v2的匀速圆周运动,圆周的半径R=(12)其圆频率ω=B (13)由以上分析可知带电粒子一方面在Ox ′y ′平面内做上述匀速圆周运动,另一方面圆心沿y ′轴负方向以速度v 1=cos α做匀速直线运动.(ii )关于粒子沿z ′轴的分运动由(7)、(8)两式可知,粒子在z ′方向仅受电场力作用,其加速度a z ′==sin α(14)即粒子沿着z ′轴以加速度a z ′做匀加速直线运动. (iii )关于粒子在Ox ′y ′z ′坐标系中的运动方程 在只考虑圆周运动的情况下,粒子的坐标随时间变的关系为x ′=R (1-cos ωt )(15) y ′=R sin ωt (16) z ′=0(17)考虑了圆心运动及粒子沿z ′轴的运动并注意到(9)、(10)、(12)式,在Ox ′y ′z ′坐标系中,粒子的运动方程为x ′=(1-cos ωt )=(+)(1-cos ωt )(18) y ′=R sin ωt -v 1t =(+)sin ωt -t (19) z ′=t 2(20)图(iv)粒子在Oxyz坐标系中的运动方程利用坐标变换x=x′cosα+z′sinαy=y′z=-x′sinα+z′cosα并注意到(5)、(9)、(10)、(13)各式,可将(18)、(19)、(20)式转换至Oxyz坐标系,得到粒子在Oxyz坐标系中的运动方程式为x=(v0cosα+)(1-cos Bt)+t2(21)y=(v0+)sin Bt-t(22)z=-(v0sinα+)(1-cos Bt)+t2(23)根据题意,将x=d和t=t0==代(21)式,解得v0=(24)将α=,t=t0==和(24)式代入(21)、(22)、(23)各式,可得粒子到达极板Q时粒子的坐标为x=d(25)y=-(26)z=-d+(27)解法二1.与解法一相同.2.以y轴为旋转轴,顺时针转动α角,建立新坐标系Ox′y′z′,设粒子速度在坐标系Ox′y′z′中分量分别为v x′、v y′、v z′,牛顿第二定律的三个分量形式为m=qE x′+qv y′B(1)m=-qv x′B(2)m=qE z′(3)将(2)式表示为=-两边积分后得v y′=-()x′+C1C1为待定常量,当t=0时,x′=0,v y′=v0,故求得C1=v0,上式应表为v y′=-Bx′+v0(4)将(4)式代入(1)式,得m=qE x′+q(-x′+v0)B=-()2x′+()2(+)(5)令R=(+)(6)ω=B(7)X′=x′-R(8)(5)式可表为=-ω2X′(9)这是简谐运动方程,其解为X′=A cos(ωt+θ)(10)由(8)式得x′=A cos(ωt+θ)+R(11)=v x′=-ωA sin(ωt+θ)(12)利用初始条件,由(11)与(12)式,得-R=A cosθ0=-ωA sinθ解得θ=0(13)A=-R再由(6)式,得A=-(+)(14)代入(11)式x′=(+)(1-cosωt)(15)将(12)式代入(2)式,整理后得=ω2A sinωt对上式积分,考虑初始条件,得v y′==-ωA cosωt-(16)积分(16)式,考虑初始条件及(14)式,得y′=(+)sinωt-t(17)对(3)式积分可得z′=t2(18)(15)、(17)、(18)式分别与解法一中的(18)、(19)、(20)式相同,接下去的讨论与解法一相同.解法三设粒子速度在Oxyz坐标中分量分别为v x、v y、v z,牛顿第二定律的三个分量方程为m=qE x+qv y B z(1)m=-qv x B z+qv z B x(2)m=-qB x v y(3)令ω=(4)v1=cosα(5)方程变为如下形式=ωv y cosα+(6)=-ωv x cosα+ωv z sinα(7)=-ωv y sinα(8)对(6)、(8)两式积分,利用初始条件t=0时,v x=0,x=0,y=0,得v x=ωy cosα+ω()t(9)v z=-ωy sinα(10)将(9)、(10)两式代入(7)式,得=-ω2y-ω2v1t=-ω2(y+v1t)令Y=y+v1t(11)得=-ω2Y(12)其解为Y=A cos(ωt+θ)由(11)式可得y=A cos(ωt+θ)-v1t(13)由(13)式得v y=-Aωsin(ωt+θ)-v1(14)由初始条件t=0时,v y=v0,y=0,得A cosθ=0v0=-Aωsinθ-v1θ=A=-(15)由(15)式,注意到(4)式、(5)式,得y=(v0+)sin Bt-t(16)v y=(v0+)cos Bt-(17)把(17)式代入(1)式,经积分并利用初始条件,可得x=(v0cosα+)(1-cos Bt)+t2(18)将(17)式代入(8)式,经积分并利用初始条件,得z=-(v0sinα+)(1-cos Bt)+t2(19)(18)、(16)、(19)式分别与解法一中的(21)、(22)、(23)式相同,接下去的讨论与解法一相同.六、在讨论本题之前,先看一下相对论能量和动量的普遍关系式,即(mc2)2=c2p2+m02c4(1)式中c为光在真空中的速度,m为粒子的质量,p为其动量,m0为静止质量.【此关系式可由能量E=mc2和动量p=mv=导出,v为粒子的速度.E2-c2p2=-c2=m02c4=m02c4故E2=c2p2+m02c4】由此关系式可知,对每一个粒子,其能量的平方与p2成线性关系.从实验室参考系来看,碰前系统的总动量等于运动的那个质子的动量,设其方向沿x轴正方向,碰撞前后系统的总动量守恒,总能量守恒.若要碰后能存在三个质子和一个反质子且总能量为最小值,则可论证这四个粒子的动量必定相等.1.先讨论碰后四个粒子的动量都沿x轴正方向的情况.令p1、p2、p3、p4分别表示它们动量的大小,这四个动量中,若有任何两个不相等,如p1≠p2,设p1<p2,则若将p1增加△p(△p<p2-p1)而将p2减少△p(这时总动量不变),则有(p1+△p)2-p12=2p1△p+(△p)2p22-(p2-△p)2=2p2△p-(△p)2这样一来,第一个粒子能量的平方增加了c2[2p1△p+(△p)2],而第二个粒子能量的平方减少了c2[2p2△p-(△p)2],两个粒子能量平方的净增量为c2[2p1△p+(△p)2]-c2[2p2△p-(△p)2]=c2[2△p(p1-p2+△p)]因已设p1<p2,且△p<p2-p1,所以净增量是负的,总能量将减少.这就是说,设p1≠p2时对应的总能量并不是最小值.由此可判断,四个粒子的动量必相等.2.若四个粒子中,有一个粒子其动量p1沿x轴的负方向,因为总动量守恒,则必有沿x轴正方向运动的另一粒子的动量增加了p1,因为能量的平方与p2成线性关系,所以这时的总能量必然大于p1沿x轴正方向运动时的能量.也就是说,只要四个粒子中,有沿x轴负方向运动的,则总能量必不是最小值.3.若四个粒子的动量的方向不在同一直线上,这时将它们沿x轴方向和垂直于x轴方向分解,沿x轴方向总动量守恒;垂直于x轴方向的动量互相抵消,但它们却使粒子的能量增大了,也就是说,这时的能量也不是最小值.总结以上可见,要想碰后四个粒子的总能量最小,根据总动量守恒、能量守恒及相对论能量和动量关系式可知,碰后四个粒子的动量必相等.设碰前运动质子的动量为p,质量为m,碰后四个粒子的动量为p1、p2、p3和p4,四个粒子的质量为m1、m2、m3和m4,根据动量守恒和能量守恒,有p=p1+p2+p3+p4(2)mc2+m0c2=m1c2+m2c2+m3c2+m4c2(3)由上面论述可知p1=p2=p3=p4=(4)再由(1)式可知,碰后四个粒子的能量从而质量必相等.以m′表示碰后四个粒子中每个粒子的质量,由(3)式得mc2+m0c2=4m′c2(5)对碰前那个运动的质子,由相对论能量和动量关系有(mc2)2=c2p2+m02c4(6)对四个粒子中任一个粒子,由相对论能量和动量关系有(m′c2)2=c2()2+m02c4(7)由(5)、(6)、(7)式可得mc2=7m0c2(8)代入数据得mc2=1.05×10-9J(9)。

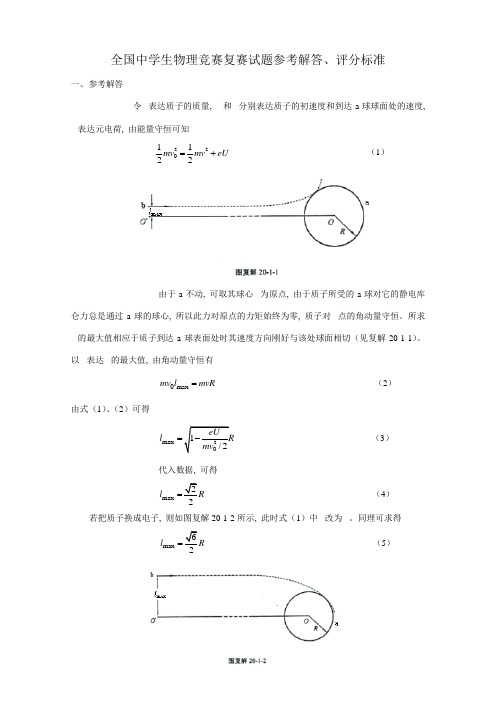
全国中学生物理竞赛复赛试题参考解答、评分标准一、参考解答令 表达质子的质量, 和 分别表达质子的初速度和到达a 球球面处的速度, 表达元电荷, 由能量守恒可知2201122mv mv eU =+ (1)由于a 不动, 可取其球心 为原点, 由于质子所受的a 球对它的静电库仑力总是通过a 球的球心, 所以此力对原点的力矩始终为零, 质子对 点的角动量守恒。
所求 的最大值相应于质子到达a 球表面处时其速度方向刚好与该处球面相切(见复解20-1-1)。
以 表达 的最大值, 由角动量守恒有 max 0mv l mvR = (2)由式(1)、(2)可得20max 1/2eU l R mv =- (3) 代入数据, 可得max 22l R = (4) 若把质子换成电子, 则如图复解20-1-2所示, 此时式(1)中 改为 。
同理可求得 max 62l R =(5)评分标准: 本题15分。
式(1)、(2)各4分, 式(4)2分, 式(5)5分。
二、参考解答在温度为 时, 气柱中的空气的压强和体积分别为, (1)1C V lS = (2)当气柱中空气的温度升高时, 气柱两侧的水银将被缓慢压入A 管和B 管。
设温度升高届时 , 气柱右侧水银刚好所有压到B 管中, 使管中水银高度增大C BbS h S ∆= (3) 由此导致气柱中空气体积的增大量为C V bS '∆= (4)与此同时, 气柱左侧的水银也有一部分进入A 管, 进入A 管的水银使A 管中的水银高度也应增大 , 使两支管的压强平衡, 由此导致气柱空气体积增大量为A V hS ''∆=∆ (5)所以, 当温度为 时空气的体积和压强分别为21V V V V '''=+∆+∆ (6)21p p h =+∆ (7)由状态方程知112212p V p V T T = (8) 由以上各式, 代入数据可得2347.7T =K (9)此值小于题给的最终温度 K, 所以温度将继续升高。
全国中学生物理竞赛决赛试题北京★ 理论部分一、足球比赛,一攻方队员在图中所示旳 A 处沿 Ax 方向传球,球在草地上以速度 v 匀速滚动,守方有一队员在图中 B 处,以 d 表达 A ,B 间旳距离,以 θ 表达 AB 与Ax 之间旳夹角,已知 θ<90° .设在球离开 A 处旳同步,位于 B 处旳守方队员开始沿一直线在匀速运动中去抢球,以 v p 表达他旳速率.在不考虑场地边界线制旳条件下,求解如下问题(规定用题中给出旳有关参量间旳关系式表达所求得旳成果):1.求出守方队员可以抢到球旳必要条件.2.假如攻方有一接球队员处在 Ax 线上等球,以 l r 表达他到 A 点旳距离,求出球不被原在 B 处旳守方队员抢断旳条件.3.假如攻方有一接球队员处在 Ax 线上,以L 表达他离开 A 点旳距离.在球离开 A 处旳同步,他开始匀速跑动去接球,以 v r 表达其速率,求在这种状况下球不被原在 B 处旳守方队员抢断旳条件.二、卫星旳运动可由地面观测来确定;而懂得了卫星旳运动,又可以用它来确定空间飞行体或地面上物体旳运动.这都波及时间和空间坐标旳测定.为简化分析和计算,不考虑地球旳A自转和公转,把它当做惯性系.1.先来考虑卫星运动旳测定.设不考虑相对论效应.在卫星上装有发射电波旳装置和高精度旳原子钟.假设从卫星上每次发出旳电波信号,都包括该信号发出旳时刻这一信息.(I)地面观测系统(包括若干个观测站)可运用从电波中接受到旳这一信息,并根据自己所处旳已知位置和自己旳时钟来确定卫星每一时刻旳位置,从而测定卫星旳运动.这种测量系统至少需要包括几种地面观测站?列出可以确定卫星位置旳方程.(II)设有两个观测站D1,D2,分别位于同一经线上北纬θ和南纬θ(单位:(°))处.若它们同步收届时间τ之前卫星发出旳电波信号.(i)试求出发出电波时刻卫星距地面旳最大高度H;(ii)当D1,D2处观测站位置旳纬度有很小旳误差△θ时,试求H旳误△,试求H 旳误差.差;(iii)假如上述旳时间τ有很小旳误差τ2.在第1(II)小题中,若θ= 45°,τ= 0.10 s .(i)试问卫星发出电波时刻卫星距△= 地面最大高度H 是多少千米?(ii)若△θ= ±1.0′′ ,定出旳H 有多大误差?(iii)若τ±0.010 μs ,定出旳H 有多大误差?假设地球为半径R = 6.38 × 103 km 旳球体,光速c = 2.998 ×108 m / s ,地面处旳重力加速度g = 9.81 m / s2.3.再来考虑根据参照卫星旳运动来测定一种物体旳运动.设不考虑相对论效应.假设从卫星持续发出旳电波信号包括卫星运动状态旳信息,即每个信号发出旳时刻及该时刻卫星所处旳位置.再假设被观测物体上有一台卫星信号接受器(设其上没有时钟),从而可获知这些信息.为了运用这种信息来确定物体旳运动状态,即物体接受到卫星信号时物体当时所处旳位置以及当时旳时刻,一般来说物体至少需要同步接受到几种不一样卫星发来旳信号电波?列出确定当时物体旳位置和该时刻旳方程.4.根据狭义相对论,运动旳钟比静止旳钟慢.根据广义相对论,钟在引力场中变慢.目前来考虑在上述测量中相对论旳这两种效应.已知天上卫星旳钟与地面观测站旳钟零点已经对准.假设卫星在离地面h = 2.00 ×104 km 旳圆形轨道上运行,地球半径R、光速c 和地面重力加速度g 取第2小题中给旳值.(I)根据狭义相对论,试估算地上旳钟通过24h 后它旳示数与卫星上旳钟旳示数差多少?设在处理这一问题时,可以把匀速直线运动中时钟走慢旳公式用于匀速圆周运动.(II)根据广义相对论,钟在引力场中变慢旳因子是(1-2φ/ c2 )1 / 2 ,φ是钟所在位置旳引力势(即引力势能与受引力作用旳物体质量之比;取无限远处引力势为零)旳大小.试问地上旳钟24 h 后,卫星上旳钟旳示数与地上旳钟旳示数差多少?三、致冷机是通过外界对机器做功,把从低温处吸取旳热量连同外界对机器做功所得到旳能量一起送到高温处旳机器;它能使低温处旳温度减少,高温处旳温度升高.已知当致冷机工作在绝对温度为T1 旳高温处和绝对温度为T2 旳低温处之间时,若致冷机从低温处吸取旳热量为Q,外界对致冷机做旳功为W,则有QW≤T2T1-T2,式中“=”对应于理论上旳理想状况.某致冷机在冬天作为热泵使用(即取暖空调机),在室外温度为-5.00℃旳状况下,使某房间内旳温度保持在20.00℃.由于室内温度高于室外,故将有热量从室内传递到室外.本题只考虑传导方式旳传热,它服从如下旳规律:设一块导热层,其厚度为l ,面积为S,两侧温度差旳大小为T,则单位时间内通过导热层由高温处传导到低温处旳热量为H = k △Tl S ,其中k 称为热导率,取决于导热层材料旳性质.1.假设该房间向外散热是由面向室外旳面积S = 5.00 m2、厚度l = 2.00 mm 旳玻璃板引起旳.已知该玻璃旳热导率k = 0.75 W / ( m • K ),电费为每度0.50元.试求在理想状况下该热泵工作12 h 需要多少电费?2.若将上述玻璃板换为“双层玻璃板”,两层玻璃旳厚度均为2.00mm ,玻璃板之间夹有厚度l0= 0.50 mm 旳空气层,假设空气旳热导率k0 = 0.025 W / ( m • K ),电费仍为每度0.50元.若该热泵仍然工作12 h ,问这时旳电费比上一问单层玻璃情形节省多少?四、如图1所示,器件由互相紧密接触旳金属层( M )、薄绝缘层( I )和金属层( M )构成.按照经典物理旳观点,在I层绝缘性能理想旳状况下,电子不也许从一种金属层穿过绝缘层抵达另MIM 图1一种金属层.不过,按照量子物理旳原理,在一定旳条件下,这种渡越是也许旳,习惯上将这一过程称为隧穿,它是电子具有波动性旳成果.隧穿是单个电子旳过程,是分立旳事件,通过绝缘层转移旳电荷量只能是电子电荷量-e ( e = 1.60 ×10-19C )旳整数倍,因此也称为单电子隧穿,MIM 器件亦称为隧穿结或单电子隧穿结.本题波及对单电子隧穿过程控制旳库仑阻塞原理,由于据此可望制成尺寸很小旳单电子器件,这是目前研究得诸多、有应用前景旳领域.1.显示库仑阻塞原理旳最简朴旳做法是将图1旳器件当作一种电容为C 旳电容器,如图2所示.电容器极板上旳电荷来源于金属极板上导电电子云相对于正电荷背景旳很小位移,可以持续变化.如前所述,以隧穿方式通过绝缘层旳只能是分立旳单电子电荷.假如隧穿过程会导致体系静电能量上升,则此过程不能发生,这种现象称为库仑阻塞.试求出发生库仑阻塞旳条件即电容器极板间旳电势差V AB = V A -V B 在什么范围内单电子隧穿过程被严禁.2.假定 V AB = 0.10 mV 是刚能发生隧穿旳电压.试估算电容 C 旳大小.3.将图1旳器件与电压为 V 旳恒压源相接时,一般采用图2所示旳双构造器件来观测单电子隧穿,防止杂散电容旳影响.中间旳金属块层称为单电子岛.作为电极旳左、右金属块层分别记为 S ,D .若已知岛中有净电荷量-ne ,其中净电子数 n 可为正、负整数或零,e 为电子电荷量旳大小,两个 MIM 结旳电容分别为 C S 和 C D .试证明双结构造器件旳静电能中与岛上净电荷量有关旳静电能(简称单电子岛旳静电能)为U n = (-ne )22( C S +C D ).4.在图3给出旳具有源( S )、漏( D )电极双结构造旳基础上,通过和岛连接旳电容 C G添加门电极( G )构成如图4给出旳单电子三极管构造,门电极和岛间没有单电子隧穿事件发图2生.在 V 较小且固定旳状况下,通过门电压 V G 可控制岛中旳净电子数 n .对于 V G 怎样控制 n ,简朴旳模型是将 V G 旳作用视为岛中附加了等效电荷 q 0 =C G V G .这时,单电子岛旳静电能可近似为 U n = (-ne + q 0 )2 / 2C∑,式中C∑= C S +C D +C G .运用方格图(图5),考虑库仑阻塞效应,用粗线画出岛中净电子数从 n = 0开始,C G V G / e 由0增大到3旳过程中,单电子岛旳静电能 U n 随 C G V G 变化旳图线(纵坐标表达 U n ,取 U n 旳单位为 e 2 / 2C∑;横坐标表达 C G V G ,取 C G V G 旳单位为 e ).规定标出要点旳坐标,并把 n = 0 ,1 ,2 ,3时 C G V G / e 旳变化范围填在表格中.(此小题只按作图及所填表格(表1)评分).表1图3图4图5U n( e 2 / 2C∑)C G V Ge五、折射率n = 1.50 、半径为R旳透明半圆柱体放在空气中,其垂直于柱体轴线旳横截面如图所示,图中O 点为横截面与轴线旳交z 点.光仅容许从半圆柱体旳平面AB 进入,一束足够宽旳平行单色光沿垂直于圆柱轴旳方向以入射角i射至AB 整个平面上,其中有一部分入射光束能通过半圆柱体从圆柱面射出.这部分光束在入射到AB 面上时沿y 轴方向旳长度用 d 表达.本题不考虑光线在透明圆柱体内经一次或多次反射后再射出柱体旳复杂情形.1.当平行入射光旳入射角i 在0°~90°变化时,试求 d 旳最小值d min 和最大值d max.2.在如图所示旳平面内,求出射光束与柱面相交旳圆弧对O 点旳张角与入射角i 旳关系.并求在掠入射时上述圆弧旳位置.六、根据广义相对论,光线在星体旳引力场中会发生弯曲,在包括引力中心旳平面内是一条在引力中心附近微弯旳曲线.它距离引力中心近来旳点称为光线旳近星点.通过近星点与引力中心旳直线是光线旳对称轴.若在光线所在平面内选择引力中心为平面极坐标(r ,φ)旳原点,选用光线旳对称轴为坐标极轴,则光线方程(光子旳轨迹方程)为r =GM / c2a cosφ+a2 ( 1 + sin2φ),G 是万有引力恒量,M 是星体质量,c 是光速,a 是绝对值远不不小于1旳参数.目前假设离地球80.0光年处有一星体,在它与地球连线旳中点处有一白矮星.假如通过该白矮星两侧旳星光对地球上旳观测者所张旳视角是1.80×10-7rad ,试问此白矮星旳质量是多少公斤?已知G = 6.673 ×10-11 m3 / ( kg •s2 )七、1.假设对氦原子基态采用玻尔模型,认为每个电子都在以氦核为中心旳圆周上运动,半径相似,角动量均为:= h / 2π,其中h 是普朗克常量.(I)假如忽视电子间旳互相作用,氦原子旳一级电离能是多少电子伏?一级电离能是指把其中一种电子移到无限远所需要旳能量.(II)试验测得旳氦原子一级电离能是24.6 eV .若在上述玻尔模型旳基础上来考虑电子之间旳互相作用,深入假设两个电子总处在通过氦核旳一条直径旳两端.试用此模型和假设,求出电子运动轨道旳半径r0、基态能量E0以及一级电离能E+,并与试验测得旳氦原子一级电离能相比较.已知电子质量m = 0.511 MeV / c2,c是光速,组合常量c =197.3 MeV • fm = 197.3 eV• nm ,ke2 = 1.44 MeV • fm = 1.44 eV • nm ,k是静电力常量,e 是基本电荷量.2.右图是某种粒子穿过云室留下旳径迹旳照片.径迹在纸面内,图旳中间是一块与纸面垂直旳铅板,外加恒定匀强磁场旳方向垂直纸面向里.假设粒子电荷旳大小是一种基本电荷量e:e = 1.60×10-19 C ,铅板下部径迹旳曲率半径r d= 210 mm ,铅板上部径迹旳曲率半径r u= 76.0 mm ,铅板内旳径迹与铅板法线成θ= 15.0°,铅板厚度d = 6.00 mm ,磁感应强度B = 1.00 T ,粒子质量m = 9.11 ×10-31 kg = 0.511 MeV / c2.不考虑云室中气体对粒子旳阻力.(I)写出粒子运动旳方向和电荷旳正负.(II)试问铅板在粒子穿过期间所受旳力平均为多少牛?(III)假设射向铅板旳不是一种粒子,而是从加速器引出旳流量为j = 5.00 ×1018 / s 旳脉冲粒子束,一种脉冲持续时间为 =2.50 ns .试问铅板在此脉冲粒子束穿过期间所受旳力平均为多少牛?铅板在此期间吸取旳热量又是多少焦?第25届全国中学生物理竞赛决赛参照解答一、1 .解法一:设守方队员通过时间t 在Ax 上旳C图1点抢到球,用l 表达A 与C 之间旳距离,l p 表达B 与C 之间旳距离(如图1所示),则有l = vt ,l p = v p t (1)和l2p= d2 + l2-2dl cosθ.(2)解式(1),(2)可得l =d1-( v p / v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }.(3)由式(3)可知,球被抢到旳必要条件是该式有实数解,即v p ≥v sinθ.(4)解法二:设BA 与BC 旳夹角为φ(如图1).按正弦定理有l psinθ=lsinφ.运用式(1)有v pv= sinθsinφ.从sinφ≤1可得必要条件(4).2.用l min 表达守方队员能抢断球旳地方与A 点间旳最小距离.由式(3)知l min =d1-( v p / v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }.(5)若攻方接球队员到 A 点旳距离不不小于l min ,则他将先控制球而不被守方队员抢断.故球不被抢断旳条件是l r <l min .(6)由(5),(6)两式得l r <d1-( v p / v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }(7)由式(7)可知,若位于Ax 轴上等球旳攻方球员到A 点旳距离l r 满足该式,则球不被原位于B 处旳守方球员抢断.3.解法一:假如在位于 B 处旳守方球员抵达Ax 上距离A 点l min 旳C1 点之前,攻方接球队员可以抵达距 A 点不不小于l min 处,球就不会被原位于 B 处旳守方队员抢断(如图2所示).若L≤l min 就相称于第2小题.若L>l min ,设攻方接球员位于Ax 方向上某点 E处,则他跑到C1 点所需时间t rm = ( L-l min ) / v r ;(8)守方队员抵达C1 处所需时间t pm = ( d2+ l2min-2dl min cosθ)1 / 2/v p.球不被守方抢断旳条件是t rm <t pm .(9)即L<v rv p( d2 + l2min-2dl min cosθ)1 / 2 + l min ,(10)式中l min 由式(5)给出.解法二:守方队员抵达C1 点旳时间和球抵达该点旳时间相似,因此有t pm = l min / v .从球不被守方队员抢断旳条件(9)以及式(8)可得到L<( 1 + v r / v ) l min(11)式中l min也由式(5)给出.易证明式(11)与(10)相似.二、1.(I)选择一种坐标系来测定卫星旳运动,就是测定每一时刻卫星旳位置坐标x,y,z.设卫星在t时刻发出旳信号电波抵达第i 个地面站旳时刻为t i.由于卫星信号电波以图2光速c 传播,于是可以写出(x-x i )2 + (y-y i )2 + (z -z i )2 = c2 (t-t i )2( i = 1 ,2 ,3 ),(1)式中x i,y i,z i是第i个地面站旳位置坐标,可以预先测定,是已知旳;t i 也可以由地面站旳时钟来测定;t 由卫星信号电波给出,也是已知旳.因此,方程(1)中有三个未知数x,y,z,要有三个互相独立旳方程,也就是说,至少需要包括三个地面站,三个方程对应于式(1)中i = 1 ,2 ,3 旳状况.(II)(i)如图所示,以地心O和两个观测站D1,D2旳位置为顶点所构成旳三角形是等腰三角形,腰长为R .根据题意,可知卫星发出信号电波时距离两个观测站旳距离相等,都是L = cτ.(2)当卫星P 处在上述三角形所在旳平面内时,距离地面旳高度最大,即H.以θ表达D1,D2 所处旳纬度,由余弦定理可知L2 = R2 + ( H + R )2 -2R ( H + R ) cosθ.(3)由(2),(3)两式得H = (cτ)2 -(R sinθ)2 -R ( 1-cosθ) .(4)式(4)也可据图直接写出.(ii)按题意,假如纬度有很小旳误差△θ,则由式(3)可知,将引起H发生误差△H .这时有L2 = R2 + ( H +△H + R )2 -2R ( H +△H + R ) cos ( θ+△θ).(5)将式(5)展开,因△θ很小,从而△H 也很小,可略去高次项,再与式(3)相减,得△H = -R ( R +H ) sin θ△θH + ( 1-cos θ ) R, (6)其中 H 由(4)式给出.(iii )假如时间τ有τ△旳误差,则 L 有误差△L = c τ△ . (7)由式(3)可知,这将引起 H 产生误差△H .这时有( L +△L )2 = R 2 + ( H +△H + R )2 -2R ( H +△H + R ) cos θ. (8)由式(7),(8)和(3),略去高次项,可得△H = c 2ττ△H + R ( 1-cos θ ), (9)其中 H 由式(4)给出.2.(i )在式(4)中代入数据,算得 H = 2.8 ×104 km .(ii )在式(6)中代入数据,算得△H =25m .(iii )在式(9)中代入数据,算得△H = ±3.0 m .3.选择一种坐标系,设被测物体待定位置旳坐标为 x ,y ,z ,待定期刻为 t ,第 i 个卫星在 t i 时刻旳坐标为 x i ,y i ,z i .卫星信号电波以光速传播,可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ,4 ), (10) 由于方程(1)有四个未知数 t ,x ,y ,z ,需要四个独立方程才有确定旳解,故需同步接受至少四个不一样卫星旳信号.确定当时物体旳位置和该时刻所需要旳是式(10)中 i = 1 ,2 ,3 ,4 所对应旳四个独立方程.4.(I )由于卫星上钟旳变慢因子为[ 1-( v / c )2] 1 / 2 ,地上旳钟旳示数 T 与卫星上旳钟旳示数 t 之差为T -t = T -1-(vc )2 T = [ 1-1-(vc)2 ] T , (11)这里 v 是卫星相对地面旳速度,可由下列方程定出:v 2r = GMr2 , (12) 其中 G 是万有引力常量,M 是地球质量,r 是轨道半径.式(11)给出v =GMr= g rR = gR + hR , 其中 R 是地球半径,h 是卫星离地面旳高度,g = GM / R 2 是地面重力加速度;代入数值有 v = 3.89 km / s .于是 ( v / c )2 ≈1.68 ×10-10,这是很小旳数.因此[ 1- (v c )2 ]1 / 2 ≈1- 12 (vc)2 .最终,可以算出 24 h 旳时差T-t ≈12 (v c )2T = 12 gR 2c 2 ( R + h )T = 7.3 μs . (13)(II )卫星上旳钟旳示数t 与无限远惯性系中旳钟旳示数T 0之差t -T 0 =1-2φc 2 T 0-T 0 = (1-2φc 2-1 )T 0 . (14)卫星上旳钟所处旳重力势能旳大小为φ= GM R + h = R 2R + h g . (15)因此 φc 2 = gR 2c 2 ( R + h ) ;代入数值有φ/ c 2 = 1.68 ×10-10,这是很小旳数.式(14)近似为t-T 0 ≈- φc 2T 0 . (16)类似地,地面上旳钟旳示数 T 与无限远惯性系旳钟旳示数之差T-T 0 =1-2Eφ c 2 T 0-T 0= ( 1-2Eφ c 2-1 )T 0 . (17)地面上旳钟所处旳重力势能旳大小为E φ= GMR =gR . (18)因此Eφ c 2 = gR c 2; 代入数值有E φ/ c 2 = 6.96 ×10-10,这是很小旳数.与上面旳情形类似,式(17)近似为T-T 0 ≈-Eφ c 2T 0 . (19)(16),(19)两式相减,即得卫星上旳钟旳示数与地面上旳钟旳示数之差t-T ≈-Eφφ- c 2T 0 . (20)从式(19)中解出 T 0 ,并代入式(20)得t -T ≈-Eφφ- c 2/ (1-Eφ c 2 )T≈-Eφφ- c 2T =gR c 2 h R + hT . (21) 注意,题目中旳 24 h 是指地面旳钟走过旳时间 T .最终,算出 24 h 卫星上旳钟旳示数与地面上旳钟旳示数之差t -T = 46 μs . (22)三、1.依题意,为使室内温度保持不变,热泵向室内放热旳功率应与房间向室外散热旳功率相等.设热泵在室内放热旳功率为 q ,需要消耗旳电功率为 P ,则它从室外(低温处)吸取热量旳功率为 q -P .根据题意有q -P P ≤ T 2T 1-T 2, (1) 式中 T 1 为室内(高温处)旳绝对温度,T 2 为室外旳绝对温度.由(1)式得P ≥ T 1-T 2T 1q . (2)显然,为使电费至少,P 应取最小值;即式(2)中旳“≥”号应取等号,对应于理想状况下 P 最小.故最小电功率P min =T 1-T 2T 1q . (3)又依题意,房间由玻璃板通过热传导方式向外散热,散热旳功率H =k T1-T2l S .(4)要保持室内温度恒定,应有q = H .(5)由(3)~(5)三式得P min =k S ( T1-T2 )2lT1.(6)设热泵工作时间为t,每度电旳电费为c,则热泵工作需花费旳至少电费C min = P min tc .(7)注意到T1 = 20.00 K + 273.15 K = 293.15 K ,T2 = -5.00 K + 273.15 K = 268.15 K ,1度电= 1 kW • h .由(6),(7)两式,并代入有关数据得C min = ( T1-T2 )2T1l Sktc = 23.99 元.(8)因此,在理想状况下,该热泵工作12 h 需约24元电费.2.设中间空气层内表面旳温度为T i,外表面旳温度为T0 ,则单位时间内通过内层玻璃、中间空气层和外层玻璃传导旳热量分别为H1=k T1-T il S ,(9)H2=k0T i-T0l0S ,(10)H3=k T0-T2l S .(11)在稳定传热旳状况下,有H1= H2= H3 .(12)由(9)~(12)四式得k T1-T il= k0T i-T0l0和T1-T i = T0-T2.(13)解式(13)得T i = l0k + lk0l0k + 2lk0T1 +lk0l0k + 2lk0T2.(14)将(14)式代入(9)式得H1 =kk0l0k + 2lk0( T1-T2 )S .(15)要保持室内温度恒定,应有q =H1.由式(3)知,在双层玻璃状况下热泵消耗旳最小电功率P′min =kk0l0k + 2lk0( T1-T2 )2T1S .(16)在理想状况下,热泵工作时间t需要旳电费C ′min = P′min tc ;(17)代入有关数据得C′min = 2.52 元.(18)因此,改用所选旳双层玻璃板后,该热泵工作12 h 可以节省旳电费△C min = C min -C′min = 21.47 元.(19)四、1.先假设由于隧穿效应,单电子能从电容器旳极板A 隧穿到极板B.以Q 表达单电子隧穿前极板A 所带旳电荷量,V AB 表达两极板间旳电压(如题目中图3所示),则有V AB = Q / C .(1)这时电容器储能U= 12CV2AB.(2)当单电子隧穿到极板B后,极板A所带旳电荷量为Q′ = Q + e ,(3)式中e 为电子电荷量旳大小.这时,电容器两极板间旳电压和电容器分别储能为V′AB = Q + eC,U′ =12CV ′2AB.(4)若发生库仑阻塞,即隧穿过程被严禁,则规定U′-U >0 .(5)由(1)~(5)五式得V AB >-12eC .(6)再假设单电子能从电容器旳极板B隧穿到极板A.仍以Q表达单电子隧穿前极板A 所带旳电荷量,V AB 表达两极板间旳电压.当单电子从极板B隧穿到极板A时,极板A所带旳电荷量为Q′ = Q-e .通过类似旳计算,可得单电子从极板B 到极板A旳隧穿不能发生旳条件是V AB <12eC .(7)由(6),(7)两式知,当电压V AB 在-e / 2C~e / 2C 之间时,单电子隧穿受到库仑阻塞,即库仑阻塞旳条件为-12eC <V AB <12eC .(8)2.依题意和式(8)可知,恰好能发生隧穿时有V AB =12eC = 0.10 mV .(9)由式(9),并代入有关数据得C =8.0 ×10-16 F .(10)3.设题目中图3中左边旳MIM 结旳电容为C S,右边旳MIM 结旳电容为CD .双结构造体系如图a所示,以Q1 ,Q2 分别表达电容C S ,图aC D所带旳电荷量.根据题意,中间单电子岛上旳电荷量为-ne= Q2-Q1 .(11)体系旳静电能为C S 和C D 中静电能旳总和,即U = Q212C S+Q222C D;(12)电压V = Q1C S+Q2C D.(13)由(11)~(13)三式解得U = 12CV2 +(Q2-Q1)22 ( C S + C D ).(14)由于V为恒量,从式(13)可知体系旳静电能中与岛上净电荷有关旳静电能U n= (-ne )2 / 2 (C S + C D ).4.U n 随C G V G 变化旳图线如图b;C G V G / e 旳变化范围如表2.表2U n( e2 / 2C )图b五、1.在图1中,z 轴垂直于 AB 面.考察平行光束中两条光线分别在 AB 面上 C 与 C ′ 点以入射角 i射入透明圆柱时旳状况,r 为折射角,在圆柱体中两折射光线分别射达圆柱面旳 D 和 D ′ ,对圆柱面其入射角分别为 i 2 与 i ′2 .在△OCD 中,O 点与入射点 C 旳距离 y c 由正弦定理得y c sin i 2 = R sin ( 90° + r ) ,即 y c = sin i 2cos rR . (1) 同理在△OC ′D ′ 中,O 点与入射点 C ′ 旳距离有y c ′sin i ′2 = R sin ( 90°-r ),即 y c ′ = sin i ′2cos r R . (2) 当变化入射角 i 时,折射角 r 与柱面上旳入射角 i 2 与 i ′2 亦随之变化.在柱面上旳入射角满足临界角i 20 = arcsin ( 1 / n ) ≈ 41.8° (3)时,发生全反射.将 i 2 = i ′2 = i 20 分别代入式(1),(2)得y o c = y o c ′ = sin i 20cos rR , (4) 即 d = 2y o c = 2sin i 20cos rR . (5) 当 y c > y o c 和 y c ′ > y o c ′ 时,入射光线进入柱体,通过折射后射达柱面时旳入射角不小于临界角 i 20 ,由于发生全反射不能射出柱体.因折射角 r 随入射角 i 增大而增大.由式(4)知,当 r = 0 ,即 i = 0(垂直入射)时,d 取最小值d min = 2R sin i 20 = 1.33 R . (6)图1当i →90°(掠入射)时,r→41.8°.将r =41.8°代入式(4)得d max = 1.79 R.(7)2.由图2可见,φ是Oz 轴与线段OD 旳夹角,φ′是Oz 轴与线段OD′旳夹角.发生全反射时,有φ= i20 + r ,(8)φ′= i20-r ,(9)和θ= φ+φ′=2i20≈83.6°.(10)由此可见,θ与i 无关,即θ独立于i .在掠入射时,i ≈90°,r =41.8°,由式(8),(9)两式得φ= 83.6°,φ′= 0°.(11)六、由于方程r =GM / c2a cosφ + a2 ( 1 + sin2φ)(1)是φ旳偶函数,光线有关极轴对称.光线在坐标原点左侧旳情形对应于a<0 ;光线在坐标原点右侧旳情形对应a>0 .右图是a<0旳情形,图中极轴为Ox,白矮星在原点O处.在式(1)中代入近星点坐标r = r m,φ= π,并注意到a 2| a | ,有a≈-GM / c2r m .(2)通过白矮星两侧旳星光对观测者所张旳视角θS 可以有不一样旳体现方式,对应旳问题有不一样旳解法.解法一:若从白矮星到地球旳距离为d,则可近似地写出ySrxOEr mφ图2θS≈2r m / d.(3)在式(1)中代入观测者旳坐标r = d,φ= -π/ 2,有a2≈GM / 2c2d.(4)由(2)与(4)两式消去a,可以解出r m = 2GMd / c2 .(5)把式(5)代入式(3)得θS≈8GM / c2d;(6)即M≈θ2Sc2d / 8G ,(7)其中d = 3.787 ×1017 m ;代入数值就可算出M≈2.07 ×1030 kg .(8)解法二:光线射向无限远处旳坐标可以写成r→∞,φ= -π2+θ2.(9)近似地取θS≈θ,把式(9)代入式(1),规定式(1)分母为零,并注意到θ1,有aθ / 2 + 2a2= 0 .因此θS≈θ=-4a = 8GM / c2d,(10)其中用到式(4),并注意到a<0 .式(10)与式(6)相似,从而也有式(8).解法三:星光对观测者所张旳视角θS 应等于两条光线在观测者处切线旳夹角,有sin θS2=△( r cosφ)△r= cosφ-r sinφ△φ△r.(11)由光线方程(1)算出△φ/△r ,有sin θS2= cosφ-r sinφGM / c2r2a sinφ= cosφ-GMc2ra;代入观测者旳坐标r = d, = -π/ 2以及a旳体现式(4),并注意到θS很小,就有θS≈2GMc2d2c2dGM =8GMc2d,与式(6)相似.因此,也得到了式(8).解法四:用式(2)把方程(1)改写成-r m = r cosφ-GMc2r m r[ (r cosφ )2 + 2 (r sinφ)2 ] ,即x = -r m + GMc2r m r( x2 +2y2 ) .(12)当y→-∞时,式(12)旳渐近式为x = -r m-2GMc2r m y.这是直线方程,它在x轴上旳截距为-r m ,斜率为1-2GM/ c2r m ≈1-tan ( θS / 2 )≈-1θS / 2 .于是有θS ≈4GM/ c2r m.r m用式(5)代入后,得到式(6),从而也有式(8).七、1.(I)氦原子中有两个电子,一级电离能E+ 是把其中一种电子移到无限远处所需要旳能量满足He + E+ →He+ + e-.为了得到氦原子旳一级电离能E+ ,需规定出一种电子电离后来氦离子体系旳能量E*.这是一种电子围绕氦核运动旳体系,下面给出两种解法.解法一:在力学方程2ke2r2= mv2 r中,r 是轨道半径,v 是电子速度.对基态,用玻尔量子化条件(角动量为)可以解出r0 =2/ 2ke2m .(1)于是氦离子能量E* = p22m-2ke2r0= -2k2e4m2,(2)其中p0 为基态电子动量旳大小;代入数值得E* = -2( ke2 )2mc2(c)2≈-54.4 eV .(3)由于不计电子间旳互相作用,氦原子基态旳能量E0 是该值旳2倍,即E0 =2E* ≈-108.8 eV .(4)氦离子能量E*与氦原子基态能量E0之差就是氦原子旳一级电离能E+ =E*-E0 = -E*≈ 54.4 eV .(5)解法二:氦离子能量E*= p22m-2ke2r.把基态旳角动量关系rp=代入,式(3)可以改写成E* =22mr2-2ke2r=22m(1r-2ke2m2)2-2k2e4m2.因基态旳能量最小,式(4)等号右边旳第一项为零,因此半径和能量r 0 =22ke2m,E*= -2k2e4m2分别与(1),(2)两式相似.(II)下面,同样给出求氦原子基态能量E0和半径r0旳两种解法.解法一:运用力学方程mv2r= 2ke2r2-ke2( 2r )2=7ke24r2和基态量子化条件rmv =,可以解出半径r0 = 42/ 7ke2m,(6)于是氦原子基态能量E 0 = 2 ( p22m-2ke2r0) +ke22r0= -49k2e4m162;(7)代入数值算得E0 = -49( ke2 )2mc216(c)2≈-83.4 eV ,(8)r0 = 4 (c)27ke2mc2≈ 0.0302 nm .因此,氦原子旳一级电离能E+ =E*-E0≈ 29.0 eV .(9)这仍比试验测得旳氦原子一级电离能24.6 eV 高出4.4 eV .解法二:氦原子能量E = 2 (p22m-2ke2r) +ke22r=2mr2-7ke22r可以化成E =2m(1r-7ke2m42)2-49k2e4m162.当上式等号右边第一项为零时,能量最小.由此可知,基态能量与半径E 0 =-49k2e4m162,r0=427ke2m分别与(7),(6)两式相似.2.(I)粒子从下部射向并穿过铅板向上运动,其电荷为正.(II)如题图所示,粒子旳运动速度v 与磁场方向垂直,洛伦兹力在纸面内;磁力不变化荷电粒子动量旳大小,只变化其方向.若不考虑云室中气体对粒子旳阻力,荷电粒子在恒定磁场作用下旳运动轨迹就是曲率半径为一定值旳圆弧;可以写出其运动方程qBv=|△p△t| =p△φ△t=pvr,(1)其中q 是粒子电荷,v 是粒子速度旳大小,p 是粒子动量旳大小,△φ是粒子在△t时间内转过旳角度,r是轨迹曲率半径.于是有p= qBr .(2)按题意,q=e .用p d 和p u 分别表达粒子射入铅板和自铅板射出时动量旳大小,并在式(1)中代入有关数据,可以算得p d =63.0 MeV / c ,p u= 22.8 MeV / c .(3)注意到当pc mc2 时应使用狭义相对论,从p=mv1-(v / c)2.(4)中可以得到v=c1+(mc / p)2.(5)用v d 和v u 分别表达粒子进入和离开铅板时旳速度大小.把式(2)以及m = 0.511 MeV / c2代入式(3),可得v d ≈c,v u≈c.(6)于是,粒子穿过铅板旳平均速度v= ( 1 / 2 ) ( v d + v u )≈c.用△t表达粒子穿过铅板旳时间,则有v cosθ△t = d.(7)再用△p du表达粒子穿过铅板动量变化量旳大小,铅板所受到旳平均力旳大小f = △p du△t=p d-p ud / (v cosθ)≈( p d-p u ) c cosθd;(8)代入有关数值得f ≈1.04 ×10-9 N .(9)(III)一种粒子穿过铅板旳时间△t =dv cosθ≈dc cosθ≈2.07 ×10-11 s = 0.0207 ns,(10)比粒子束流旳脉冲周期 = 2.50 ns 小得多.铅板在此脉冲粒子束穿过期间所受旳力旳平均大小F ≈( p d-p u ) j;(11)。
2012年第二十二届全国初中应用物理竞赛试题一、选择题:1. 早晨,小明骑着自行车沿平直的公路驶向学校,强劲的北风迎面吹来,此时地面对车前轮的摩擦力为f 1,对车后轮的摩擦力为f2.则下列说法中正确的是( A )A .f 1与前进的方向相反,f 1<f 2B .f 2与前进的方向相反,f 1>f 2C .f 1与前进的方向相同,f 1<f 2D .f 2与前进的方向相同,f 1>f 22. 小明发现,有些电线杆上装有如图1所示的“小风车”,这些风车在微风中能不停地旋转,且旋转叶片的一面还装有反光的小镜子。
关于这样的“小风车”的作用,下列说法中正确的是( D )A .为了警示此处有电B .为了测定风向C .为了测量风速大小D .为了驱赶小鸟,避免小鸟在上面做窝而导致电路短路3. 一名军人在一次执行任务时需要从正在正常向前行驶的卡车右侧跳下。
对于跳车的方法,以下四种方案中最安全的是( C )A .脸向车后并相对于车向后跳B .脸向车后并相对于车向前跳C .脸向车前并相对于车向后跳D .脸向车前并相对于车向前跳4. 我国不少地区把阴霾天气现象并入雾一起作为灾害性天气,统称为“雾霾天气”。
关于雾和霾的认识,下列说法中正确的是( B )A .霾是大量的小水滴或冰晶浮游在近地面空气层中形成的B .雾和霾是两种不同的天气现象C .雾是由悬浮在大气中的大量微小尘粒、烟粒或盐粒等颗粒形成的D .雾和霾是同一个概念的两种不同说法5.北京奥运会上的花样游泳运动员,由于在水面上、下都能听到音乐指令,从而以其优美的舞姿、随音乐节拍而精确完成的动作,让观众感受到了体育之美。
关于运动员在水下是如何接收到音乐指令的下列说法中,符合实际情况的是( D )A .仅在水面以上放有音箱,当运动员的头部在水面以下时,声音经由空气、水,最终传到运动员的耳朵B .仅在水面以下放有音箱,当运动员的头部在水面以下时,声音通过水传到运动员的耳朵C .运动员通过无线耳机,接收来自控制室的电磁波信号,再将其转化成声音,被耳朵接收D .在水面以上和以下都放有音箱,使运动员的头部无论是在水面以上还是在水面以下,都 能听到清晰的音乐声6. 小明学习了浮力知识以后,对热气球运动产生了兴趣,他在网上收集了许多关于热气球的知识及类似图2所示的图片。
第32届全国中学生物理竞赛预赛试卷本卷共l6题,满分200分。
一、选择题.本题共5小题,每小题6分.在每小题给出的4个选项中,有的小题只有一项符合题意,有的小题有多项符合题意。
把符合题意的选项前面的英文字母写在每小题后面的方括号内.全部选对的得6分,选对但不全的得3分,有选错或不答的得0分.1. 2014年3月8日凌晨2点40分,马来西亚航空公司一架波音777-200飞机与管制中心失去联系.2014年3月24日晚,初步确定失事地点位于南纬31o52′、东经115 o 52′的澳大利亚西南城市珀斯附近的海域.有一A .B .C .D . 2. 23892U A . 8次αC . 4次α3.如图,),下A . 在左球B .在左球C . 在左球D . 4.如图,0.05 m .取A .BCD . 5将面积为S ,电阻为"的矩形导线框abcd 沿图示方位水平放置于地面上某处,将其从图示位置绕东西轴转180o ,测得通过线框的电荷量为Q 1;将其从图示位置绕东西轴转90 o ,测得通过线框的电荷量为Q 2。
该处地磁场的磁感应强度大小应为A . 22214Q Q S R + B . 2221Q Q S R + C . 2221212Q Q Q Q S R ++ D . 222121Q Q Q Q S R ++ 二、填空题.把答案填在题中的横线上.只要给出结果,不需写出求得结果的过程.6.(10分)水平力F 方向确定,大小随时间的变化如图a 所示;用力F 拉静止在水平桌面上的小物块,在F 从0开始逐渐增大的过程中,物块的加速度a随时间变化的图象如图b所示.重力加速度大小为10m/s2。
由图示可知,物块与水平桌面间的最大静摩擦力为;物块与水平桌面间的动摩擦因数为;在0~4s时间内,合外力做的功为。
7.(10分)如图,物块A、C置于光滑水平桌面上,通过轻质滑轮和细绳悬挂物块B,物块A、B的质量均为2kg,物块C的质量为1 kg,重力加速度大小为10m/s2。
第27届全国中学生物理竞赛决赛试题及答案一、25分填空题1.一个粗细均匀的细圆环形橡皮圈;其质量为M ;劲度系数为k ;无形变时半径为R ..现将它用力抛向空中;忽略重力的影响;设稳定时其形状仍然保持为圆形;且在平动的同时以角速度ω绕通过圆心垂直于圆面的轴线匀速旋转;这时它的半径应为.. 2.鸽哨的频率是f ..如果鸽子飞行的最大速度是u ;由于多普勒效应;观察者可能观测到的频率范围是从到..设声速为V ..3.如图所示;在一个质量为M 、内部横截面积为A 的竖直放置的绝气体..活塞也热气缸中;用活塞封闭了一定量温度度为0T 的理想是绝热的;活塞质量以及活塞和气缸之间的摩擦力都可忽略不缓慢上提;当计..已知大气压强为0p ;重力加速度为g ;现将活塞活塞到达气缸开口处时;气缸刚好离开地面..已知理想气体在缓慢变化的绝热过程中pV γ保持不变;其中p 是气体的压强;V 是气体的体积;γ是一常数..根据以上所述;可求得活塞到达气缸开口处时气体的温度为..4.本题答案保留两位有效数字在电子显微镜中;电子束取代了光束被用来“照射”被观测物..要想分辨101.010m -⨯即原子尺度的结构;则电子的物质波波长不能大于此尺度..据此推测电子的速度至少需被加速到..如果要想进一步分辨121.010m -⨯尺度的结构;则电子的速度至少需被加速到;且为使电子达到这一速度;所需的加速电压为 ..已知电子的静止质量319.110kg e m -=⨯;电子的电量191.610C e -=-⨯;普朗克常量346.710J s h -=⨯⋅;光速813.010m s c -=⨯⋅..二、20分图示为一利用传输带输送货物的装置;物块视为质点自平台经斜面滑到一以恒定速度v 运动的水平长传输带上;再由传输带输送到远处目的地;已知斜面高2.0m h =;水平边长 4.0m L =;传输带宽 2.0m d =;传输带的运动速度3.0m/s v =..物块与斜面间的摩擦系数10.30μ=..物块自斜面顶端下滑的初速度为零..沿斜面下滑的速度方向与传输带运动方向垂直..设斜面与传输带接触处为非常小的一段圆弧;使得物块通过斜面与传输带交界处时其速度的大小不变;重力加速度210m/s g =..1.为使物块滑到传输带上后不会从传输边缘脱离;物块与传输带之间的摩擦系数2μ至少为多少2.假设传输带由一带有稳速装置的直流电机驱动;与电机连接的电源的电动势200V E =;内阻可忽略;电机的内阻10R =Ω;传输带空载无输送货物时工作电流0 2.0A I =;求当货物的平均流量单位时间内输送货物的质量;稳定在640kg/s 9η=时;电机的平均工作电流等于多少 假设除了货物与传输带之间的摩擦损耗和电机的内阻热损耗外;其它部分的能量损耗与传输带上的货物量无关..三、20分如图;刚性细轻杆其质量可视为零可绕通过其中的点O 的光滑水平轴在竖直面内自由转动..两质量分别为2m 和m 的小球1和2可视为质点串在轻杆上;它们与轻杆之间的静摩擦系数为μ..开始时轻杆静止在水平位置;小球1和2分别位于紧靠轻杆两端A 和B 的位置..现让系统自水平位置以零初速下摆;求 1.小球1脱离轻杆时的位置用小球1脱离杆时杆与水平线的夹角表示; 2.小球2脱离轻杆时的位置用小球2脱离杆时杆与水平线的夹角表示..四、如图所示;A 、B 、C 为三个质点;A 的质量远远大于B 、C 的质量;B 和C 的质量相等..已知A 、B 之间;A 、C 之间存在相互吸引力..B 、C 之间存在相互排斥力;三个把质点在相互间引力或斥力的作用下运动;如果作用力合适;可以存在一种如下形式的运动:A 、B 、C 的相对位置固定;它们构成一个平面;三个质点绕着位于这个平面内的某条轴匀速转动;因为质点A 的质量远远大于B 、C 的质量;可认为该轴过质点A 且固定不动;连线AB 与转轴的夹角1ϕ与连线AC 与转轴的夹角2ϕ不相等;且1π02ϕ<<;2π02ϕ<<..若AB 之间吸引力的大小aAB f kAB=;AC 之间吸引力的大小为aa f kAC=;其中AB、AC 分别为A 、B 与A 、C 之间的距离;k 为比例系数;不计重力的影响..试问a 的值在什么范围内;上述运动才能实现五、15分南极冰架崩裂形成一座巨型冰山;随洋流漂近一个城市..有人设计了一个利用这座冰山来发电的方案;具体过程为:()a 先将环境中一定量的空气装入体积可变的容器;在保持压强不变的条件下通过与冰山接触容器内空气温度降至冰山温度;()b 使容器脱离冰山;保持其体积不变;让容器中的冰空气从环境中吸收热量;使其温度升至环境温度;()c 在保持容器体积不变的情况下让空气从容器中喷出;带动发电装置发电..如此重复;直至整座冰山融化..已知环境温度293K a T =;冰山的温度为冰的熔点1273K T =;可利用的冰山的质量111.010kg m =⨯;为了估算可能获得的电能;设计者做出的假设和利用的数据如下:1.空气可视为理想气体..2.冰的熔解热53.3410J/kg L =⨯;冰融化成温度为1T 的水之后即不再利用.. 3.压强为p 、体积为V 的空气内能 2.5U pV =..4.容器与环境之间的热传导良好;可以保证喷气过程中容器中空气温度不变.. 5.喷气过程可分解为一连串小过程;每次喷出的气体的体积都是u ;且u 远小于容器的体积..在每个小过程中;喷管中的气体在内外压强差的作用下加速;从而获得一定动能E ∆;从喷嘴喷出..不考虑喷出气体在加速过程中体积的改变;并认为在喷气过程中容器内的气体压强仍是均匀的;外压强的大气压..6.假设可能获得的电能是E ∆总和的45% 7.当1x时;()ln 1x x +≈..试根据设计者的假设;计算利用这座冰山可以获得的电能..六、15分如图;两块大金属板A 和B 沿竖直方向平行放置;相距为d ;两板间加有恒定电压U ;一表面涂有金属膜的乒乓球垂吊在两板之间;其质量为m ..轻推乒乓球;使之向其中一金属板运动;乒乓球与该板碰撞后返回;并与另一板碰撞;如此不断反复..假设乒乓球与两板的碰撞为非弹性碰撞;其恢复系数为e ;乒乓球与金属板接触的时间极短;并在这段时间内达到静电平衡..达到静电平衡时;乒乓球所带的电荷量q 与两极板间电势差的关系可表示为0qC U=;其中0C 为一常量..同时假设乒乓球半径远小于两金属板间距d;乒乓球上的电荷不影响金属板上的电荷分布;连接乒乓球的绳子足够长;乒乓球的运动可近似为沿水平方向的直线运动;乒乓球第一次与金属板碰撞时的初动能可忽略;空气阻力可忽略..试求:1.乒乓球运动过程中可能获得的最大动能;2.经过足够长时间后;通过外电路的平均电流..七、20分如图()a所示;十二根均匀的导线杆联成一边长为l的刚性正方体;每根导线杆的电阻均为R..该正方体在匀强磁场中绕通过其中心且与abcd面垂直的转动轴作匀速转动;角速度为ω;已知磁感应强度大小为B;方向与转动轴垂直..忽略电路的自感..当正方体转动到如图()b所示位置对角线bd与磁场方向夹角为θ时;求1.通过导线ba、ad、bc和cd的电流强度..2.为维持正方体作匀速转动所需的外力矩..八、10分空心激光束是一种在传播方向上中心光强为零的圆筒形光束..由于这一特征;它可以把某些微小粒子约束在激光束的中心部位;作为激光导管;激光镊子、光学扳手等;实现对纳米粒子、生物细胞等微小粒子的精确操控..空心激光技术目前在生物学、激光加工、原子冷却等方面得到了广泛的应用;正逐渐成为一门新兴的学科分支..产生空心激光束的基本做法是利用光学系统将一束实心的圆柱形激光转换成为一束空心的激光..给定如下光学器件:焦距为f的凸透镜;圆锥角为45︒的锥面反射镜;半径为R的球面镜中间有圆孔;如图:利用上述光学器件设计一光学系统;使得一束很细的实心圆柱入射激光转化成一束空心的出射激光;且空腔为圆柱形;半径为r..请回答如下问题:1.画出该光学系统的光路图..2.求该光学系统中锥面镜顶点到球面镜球心的距离x..一、25分填空题1.2224π4πkRk M ω-6分2.fV V u +;fV V u-4分3.11001Mg T p A γ-⎛⎫- ⎪⎝⎭6分4.617.310m s -⨯⋅;812.810m s -⨯⋅;58.410V ⨯9分 二、20分1.令m 表示物块的质量;物块在斜面上滑动的加速度()11sin cos sin cos mg mg a g mθμθθμθ-==-;1物块滑到斜面底端的速度()01221cot 4.0m/s sin ahv gh μθθ==-= 2以传输带为参照系;物块滑到传输带的初速度大小2200 5.0m/s v v V '=+=..3运动方向与传输带边缘的夹角α满足4tan 3α=.. 4物块在传输带上作减速运动;其加速大小为22mga g mμμ'==..5当物块与传输带相对静止时在传输带上运动的距离2200122v v s a gμ'''==; 6物块不超过传输带的边缘对应的最小摩擦系数2μ应满足202sin sin 2v s dgααμ''== 7因此可得202sin 0.52v gdαμ'==..82.物块对传输带的摩擦力大小202gF v v g ημημ''=⋅=; 9方向与0v '的方向相同..从地面参照系来看;传送带速度为V ;单位时间内物块对传输带所做的功cos W FV α=-;10因此负载所引起的附加功率2640W P W V η∆=-==..11考虑到无负载时电机的输出功率2000360W P I E I R =-=..12有负载时电机的输出功率为01000W P P P =+∆=..13设有负载时的工作电流为I ;则2P IE I R =-;14解之得10A I =..15评分标准:2式2分;3、4式共2分;6式2分;7式3分;8式1分;9式4分;10式2分;13式2分;15式2分.. 三、20分设轻杆的杆长为2l ;当杆与水平线的夹角为θ时;球1和球2的速度分别为1v 和2v ;杆转动的角速度为ω..因机械能守恒;有()2212110sin 2sin 222mgl mgl m v mv θθ=-++..1又因12v v l ω==;2可由1、2解得ω=3轻杆与两小球构成的系统对转轴的角动量 122L mlv mlv =+;4由角动量定律有2cos cos Lmgl mgl tθθ∆-=∆.. 5根据角加速度β的定义tωβ∆=∆; 6由2、4、5、6各式得cos 3g lθβ=.. 7当两球都未脱离轻杆时;两球都绕转轴作圆周运动;球1的切向加速度和法向加速度分别为lt a l β= 8lt a l ω=9以1N 表示沿垂直于轻杆方向球1与杆的相互作用力的大小;以1f 表示沿着轻杆方向球1与杆的相互作用力的大小;根据牛顿第二定律;有12cos 2lt mg N ma θ-=; 1012sin 2ltf mg ma θ-= 11由3、9、10、11各式得14cos 3N mg θ=.. 12 110sin 3f mg θ=.. 13对2球作同样的分析;沿垂直于轻杆方向球2与杆的相互作用力的大小2N 与沿着轻杆方向球2与杆的相互作用力的大小2f 分别为24cos 3N mg θ=; 1421sin 3f mg θ=.. 15由12、14式可知;杆与小球1、杆与小球2的最大静摩擦力相等;而13、14式表明小球1与杆的摩擦力大于小球2与杆的摩擦力;故在转动过程中;小球1与杆之间的摩擦力先达到最大静摩擦力;故小球1先滑动..设1球开始滑动时;细杆与水平线夹角为1θ;则()()1111f N θμθ=;即11103sin cos 34mg mg θμθ=; 16由16式并代入数据得1π6θ=.. 17当1θθ=时;球1开始向外滑动..由于球1的初始位置紧靠轻杆末端;球1从开始滑动到脱离细杆的时间可忽略不计;因此球1脱离细杆与水平线夹角也为1π6θ=..球1一旦脱离轻杆;因轻杆没有质量;球2与轻杆间的相互作用立即消失;此后球2只受重力作用而作斜舞女运动;注意到2、3、7各式;抛出时的初速度0v == 18初速度的方向与水平线的夹角01ππ23θθ=-=..19在球2作抛体运动的过程中;球与轻杆间虽无相互作用;但球仍套在杆上;轻杆将跟着球运动;但不会干扰小球的运动..当球离转轴的距离再次等于l 时;球2便脱离轻杆..建立如图所示的坐标系Oxy ;根据斜抛运动规律可得任意t 时刻取球2开始作抛体运动的时刻为计时起点球2的位置坐标100cos cos x l v t θθ=-+;20 21001sin sin 2y l v t gt θθ=+-;21球2脱离细杆时有222l x y =+..22利用17、18、19各式得222203l l t t t g g ⎛⎫--= ⎪ ⎪⎝⎭; 23从而解得1513l t g ⎛⎫=+ ⎪ ⎪⎝⎭.. 24此时23562156x l y l ⎧-=-⎪⎪⎨+⎪=-⎪⎩.. 25设球2脱离细杆时细杆与水平线夹角也为2θ如图;则2235cos 6x l θ-==; 262235arccos 78.26θ⎛⎫-==︒ ⎪⎪⎝⎭或1.36弧度.. 27评分标准:3式2分;7式3分;12~15式各1分;16式2分;17式1分;18式2分;19式1分;20~22式各1分;26、27式各1分.. 四、15分 解法1:以m 表示质点B 的质点;θ表示连线BC 与竖直方向的夹角;ω表示定律有转动角速度;BC f 表示BC 间排斥力的大小..根据牛顿211sin sin sin AB BC f f m AB ϕθωϕ-=;11cos cos 0AB BC f f ϕθ-=; 2222sin sin sin AC BC f f m AC ϕθωϕ+=;32cos cos 0AC BC f f ϕθ-=.. 4由1、3两式并利用2、4两式可得()()1122sin sin sin sin AB AC AB f f AC ϕϕθϕθϕ-=+.. 5考虑到几何关系()()21sin sin AB ACϕθϕθ+=- 6并利用已知AB f 和BC f 的表示式..可由5得到212sin sin a AB AC ϕϕ-⎛⎫=⎪ ⎪⎝⎭7又;由2、4式可得21cos cos AB AC f f ϕϕ=.. 8带入已知的AB f 和BC f 的表达式可得21cos cos AB ACααϕϕ=.. 9联立7、9从而有221122sin cos sin cos ααααϕϕϕϕ--=..10如果12ϕϕ≠;则意味着方程2sin cos 0C ααϕϕ--=11在π02⎛⎫ ⎪⎝⎭,区间有两个不同的解;其中C 为某一合适的常数..这要求函数2sin cos ααϕϕ-在π02⎛⎫ ⎪⎝⎭,区间不能是单调函数;也就是说sin αϕ和2cos αϕ-不能同时为单调增函数或单调减函数..因此当ϕ增大时;若sin αϕ增大;则2cos αϕ-应减小;反之;若sin αϕ减小;则2cos αϕ-应增大;故α与2α-同号..因此有0α<12 2a >..13对0a <;可知2sin cos ααϕϕ--在0ϕ=及π2时均为零;因此2sin cos ααϕ--在π02⎛⎫⎪⎝⎭,区间一定存在极值点;意味着方程11在C 合适选取的情况下必有两个或两个以上的不同解..对2a >亦然..因此条件12、13是符合题意要求的充分必要条件..评分标准:1~4式各1分;6式1分;10式6分;12、13式及其以下说明共4分.. 解法2:如图;设B 、C 间的排斥力是f ;它们受到A 的吸引力分别是AB f 、AC f ;向心力分别是1C f 、2C f ;距离A 分别是1r 、2r ;根据三角形的相似关系;有11C AB f f fr AB BD ==; 1a 22AC C f f fr AD CD==.. 2a以上两式相比可得1212C AB AC C f f r CDf r f BD==3a依题意有12AB AC f r f r α⎛⎫= ⎪⎝⎭; 4a111222sin sin C C f r EB f FC r ϕϕ==; 5a 2211cos cos r CD AF BD AE r ϕϕ==; 6a将4a~6a 代入3a 得11112222211sin cos sin cos r r r r r r αϕϕϕϕ-⎛⎫==⎪⎝⎭.. 7a由7a 得221122sin cos sin cos ααααϕϕϕϕ--=..8a之后的讨论与“参考解答1”相同.. 评分标准:考虑“参考解答1”.. 五、15分以a p 表示环境中大气的压强;则初始时装入容器的空气的压强为a p ;温度为a T ;以a V 表示其体积..当容器与冰山接触;达到平衡时;容器中空气的温度为1T ;体积减小为0V ;根据题意;空气经历的过程为等压过程;故有01aaV V T T = 1在这一过程中;容器中空气内能的增加量为()02.5a a U p V V ∆=-;2大气所考察空气做功为()0a a W p V v =--3若以Q 表示此过程中冰山传给容器中空气的热量;根据热力第一定律有Q U W=∆-.. 4由以上四式得13.5a a a a T T Q p V T ⎛⎫-= ⎪⎝⎭55式给出的Q 是负的;表示在这一过程中;实际上是容器中的空气把热量传给冰山.. 容器中空气的温度降至冰山温度后;又经一过等容升温过程;即保持体积0V 不变;温度从1T 升至环境温度a T ;并从周围环境吸热..若以1p 表示所考虑空气的压强;则有11aa p p T T = 6设喷管的体积为u ;当喷管中的气体第一次被喷出时;容器中空气的压强由1p 降到2p ;根据题目给出的条件;有()1020p V u p V -=;7即0210V u p p V -= 8喷出气体获得的动能()k11a E p p u ∆=-..9当喷管中的空气第二次喷出后;容器中空气压强由2p 降到3p ;根据题给出的条件可得032V up p V -= 10喷出气体获得的动能()k22a E p p u ∆=-..11当喷管中的空气第N 次被喷出后;容器内空气的压强由N p 降到1N p -;根据题给出的条件可得010N NV u p p V +-= 12喷出气体获得的动能()1k N a E p p u ∆=-..13如果经过N 次喷射后;容器中空气的压强降到周围大气的压强;即1N a p p +=;14这时喷气过程终止;在整过喷气过程中;喷出气体的总动能..k k12k kN E E E E =∆+∆++∆15利用8到13式;15式可化成2100010001N k a V u V u V u E p u Np u V V V -⎡⎤⎛⎫⎛⎫⎛⎫---⎢⎥=++++- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦; 1616式等号右边第1项方括号内是N 项的等比级数;故有00k 10011Na V u V E p u Np u V u V ⎛⎫-- ⎪⎝⎭=---.. 17又;根据8、10、12、14各式可得010Na V u p p V ⎛⎫-= ⎪⎝⎭; 18对18式等式两边取自然对数得01ln 1ln ap u N V p ⎛⎫-= ⎪⎝⎭.. 19因0uV ;可利用近似公式()ln 1x x +≈把19进一步化简;即01ln aV p N u p =20进而由17、18、20三式得()1k 100lna a ap E p p V p V p =-- 21将1、6代入21式;可得111k 1ln a a a a a T T T E p v T T T ⎛⎫=-+ ⎪⎝⎭..22根据题意;这些动能可转化成的电能为1110.451ln a a a a a T T T E p V T T T ⎛⎫=-+ ⎪⎝⎭..23以上讨论表明;要获得电能E ;冰山必须吸收Q -的热量;整座冰山化掉可吸收的总热量1Q mL =..24因此可产生的总电量为1mLE E Q=-.. 25将5和23带入25式;得111111ln 9701a a aaT T T T T T E mL T T -+=-; 26代入数据后有141 1.510J E =⨯27评分标准:5式3分;7式1分;9式2分;17式2分;18式1分;22式3分;25~27式各1分.. 参考解答2:以a p 表示环境中大气的压强..设融化整座冰山可使n 摩尔的空气参与如题所述的过程;且在过程()a 中体积和温度变化分别为V ∆和1a T T T ∆=-;则在此过程中这部分气体放出的热量为52a a Q p V p V =-∆-∆.. 1其中右边第一项表示大气对系统做的功;第二项表示系统内能的变化;考虑到物态方程;有()172a Q nR T T =-; 2这部分热量等于冰山融化吸收的熔解热;故因此联立2、3可得()127a mLn R T T =-..4在气体等容吸热的过程()b 中;设最后达到压强0p ;体积达到0V ;则易得1a a a T p p T =; 5 00anRT V p =6再考虑喷气过程:因为等温;在每个喷气的小过程中过后;容器内的压强增量p ∆满足00V up p p V -+∆=; 7其中0V 为过程()b 中系统的体积;p 为这个喷气过程中容器内的压强;那么喷出的气体的动能()a E p p u ∆=-;8与7联立;消去u ;得()0k a pE p p V p∆∆=--.. 9因此;做变换E dE ∆→;p dp ∆→;总的动能则为()0k 0ap a p dp E p p V p=--⎰ 10最后;据题意所获得的总的电能为k 0.45E E =;11将4、5、6、10带入11式;得11111ln 9701a a aaT T T T T T E mL T T -+=-; 12代入数据后有141.510J E =⨯..13评分标准:参考“参考解答1”的评分标准..1.根据题意;乒乓球与金属板第一次碰撞前其动能和速度分别为10v =2刚碰后;乒乓球带的电荷量 0q C U =3其动能和速度分别为k10E '= 410v '= 5此后在电场力作用下乒乓球向另一金属板加速运动..当它到达另一金属板;与金属板第二次碰撞前其动能为k2k2E E qU '=+ 6注意到3、4式有2k20E C U =7与金属板第二次碰撞前的速度为2v =8第二次碰撞后的速度和动能分别22v ev '= 9 2k2212E mv ''= 10由9、10式得2k2k2E e E '= 11乒乓球与金属板第三次撞前动能为k2k2E E qU '=+ 12由3、711、12式得 ()2k301E e C U 2=+15乒乓球与金属板第三次碰撞前速度1v =16乒乓球与金属板第三次碰撞后的速度和动能分别为33v ev '= 17 3k33k E e E '= 18乒乓球与金属板四次碰撞前的动能k4k3E E qU '=+ 19由3、15、18、19式得 ()242k401E e e C U =++20乒乓球与金属板第四次碰撞前速度为4v =21乒乓球与金属板第四次碰撞后的速度和动能分别为44v ev '= 22 2k4k4E e E '= 23以此类推;可得乒乓球与金属板第n 次碰撞前、后的动能分别为()2222kn 01n E e e C U -⎡⎤=+++⎣⎦ 24 ()222222kn01n E e e eC U -⎡⎤'=++⎣⎦25即()212kn 0211n e E C U e--=- 26 ()2122ln211n e eE C U e -⎡⎤-⎣⎦'=-27对非弹性碰撞;1e <;可由以上两式看出kn E 和knE '均随碰撞次数单调递增..当n →∞时有 2k?0211E C U e=- 2822k 021e E C U e∞'=- 29乒乓球运动过程中达到的最大动能应与金属板碰撞前的极限动能;即2kmax k 0211E E C U e∞==- 302.经过足够长时间后亦即n →∞时;乒乓球在某一次与金属板碰撞后和下一次碰撞前的速度分别为v ∞'=31v ∞ 32此间时间间隔2dT v v ∞∞='+ 33因此可得;通过外电路的平均电流强度q I T= 34由31、32、33、34各式得I =35评分标准:26、27式或28、29式共8分;30式2分;31~33式各1分;35式2分.. 七、 参考答案1:1.a a '和cc'中的感应电动势为21sin a a cc E E εωθ''===1b b '和dd '中的感应电动势为22cos 2b b dd εεεωθ''===2根据电路的对称性可知1ba a b d c cd I I I I I '''''====;2ad d a c b bc I I I I I ''''====3根据基耳霍夫第一定律;有12aa c c I I I I ''==- 4 12b b dd I I I I ''==+5根据基耳霍夫第二定律;有11121aa bb I R I R I R I R εε''+++=- 6 1221dd ad I R I R I R I R εε'++-=+7 ()212cos sin 8bc ad Bl I I I Rωθθ===-8 ()222cos sin 8adbc Bl I I I Rωθθ===+92.当正方体转动到任意位置对角线db 与磁场夹角为任意θ时;通过a a '、cc ';b b '、dd '的电流22sin 4a a ad ba Bl I I I R ωθ'=-=1022sin 44cc bc cd Bl I I I ωθ'=-= 11 22cos 4b b ba bc BI I I I R ωθ'=+= 12 22cos 4dd ad cd Bl I I I Rωθ'=+= 13为维持正方体作匀速转动所需的外力矩等于磁场对电路作用的合力矩;即a a cc a a F F BlI '''==;b b dd b b F F BlI '''==14222sin 2cos 22a ab b M F l F l θθ''=+ 15将11~14代入15;得242B l M Rω=.. 16评分标准:1、2式共2分;4、5式共4分;6、7式共4分;10~13式共2分;14式1分;15式2分;16式1分.. 参考解答2:1.a a '和cc '中的感应电动势为22sin 2a a cc Bl εεωθ''==1bb b '和dd '中的感应电动势为22cos 2b b dd Bl εεωθ''==2b先计算b b ε'和dd ε'单独存在a a ε'和cc ε'短路时流过各支路的电流..若将a a '和cc '断开;则等效电路如图所示;则通过b b '和dd '电流()()2112cos 44b b dd b b dd Bl I I R Rεεωθ''''+=== 3b通过ba 、ad 、bc 和cd 的电流强度()()()()2111112cos 28bd ad cdb b Bl I I I I Rωθ'==== 4b根据电路的对称性;此时a '、a 之间;c 、c '之间的电势差0a a cc U U ''==5b由此连接a a '和cc '后流过a a '和cc '的电流..()()110aa cc I I ''==6b因此连接a a '和cc '不影响ba 和ad 中的电流.. 支路的电流..再计算a a ε'和cc ε'单独存在b b ε'和dd ε'短路时流过各若将b b '和dd '断开;等效短路时如图所示..采用与上述一样的方法;可得a a ε'和cc ε'单独存在时流进a a '和cc '电流()()2222sin 4a a cc Bl I I Rωθ''== 7b通过ba 、ad 、bc 和cd 的电流()()2222sin 8ba cd Bl I I R ωθ==- 8b()()2222sin 8ad bcBl I I Rωθ== 9b此时b '、b 之间和d 、d '之间的电势差0b b dd U U ''==;由此连接b b '和dd '后流过b b '和dd '的电流()()220b b dd I I ''==10b因此连接bb '和dd '不影响各支路中的电流..根据叠加原理;ba 、ad 、bc 和cd 的电流强度;()()()212cos sin 8ba ba baBl I I I R ωθθ=+=- 11b()())12cos sin ad ad ad I I I θθ=+=+ 12b()())12cos sin bc bc bc I I I θθ=+=+ 13b()())12cos sin cd cd cd I I I θθ=+=- 14b 2.与“参考解答1”相同..评分标准:参考“参考解答1”的评分标准..八、参考解答:1.光路图如下;指出被球面镜反射的光线汇累于凸透镜的焦点..2.参照所给光路图;可知CO x =;设CAO a =∠;有如下几何关系: sin x R α=; 1()cot 2r f α=2 两式联立;可求得1sin arctan 2f x R r ⎛⎫= ⎪⎝⎭.. 3评分标准:正确画出光路图5分;3式5分..。