运筹学 (单纯形法原理)
- 格式:ppt
- 大小:479.50 KB
- 文档页数:29
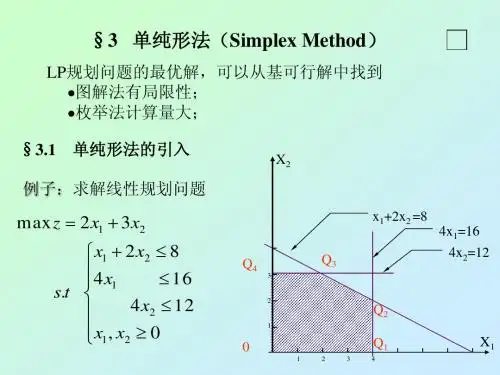

单纯形法的基本原理单纯形法是一种用于求解线性规划问题的数学方法,它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。
在解决实际问题中,我们经常会遇到一些资源有限,而需要在这些资源限制下最大化或最小化某个指标的情况,这时就需要用到线性规划问题。
而单纯形法正是针对这类问题提出的一种高效的求解方法。
单纯形法的基本原理可以用几个关键步骤来概括。
首先,我们需要将线性规划问题转化为标准型,即目标函数为最大化,约束条件为等式的形式。
接着,我们需要找到一个初始可行解,这个可行解需要满足所有的约束条件。
然后,我们通过一系列的基本变量的替换,不断地移动解空间中的顶点,直到找到最优解为止。
在单纯形法中,我们需要利用单纯形表来进行计算。
单纯形表是一个表格,其中包含了目标函数、约束条件、基本变量等信息。
通过对单纯形表的不断变换和计算,我们可以逐步逼近最优解。
在每一步的计算中,我们需要选择一个入基变量和一个出基变量,通过一系列的行变换和列变换来更新单纯形表,直到找到最优解为止。
单纯形法的基本原理虽然看起来比较复杂,但实际上它是建立在一些简单的数学原理之上的。
通过对解空间中的顶点进行移动,我们可以逐步逼近最优解,这是单纯形法能够高效求解线性规划问题的关键所在。
在实际应用中,单纯形法已经被证明是一种非常有效的方法,它可以帮助我们在资源有限的情况下做出最优的决策。
总的来说,单纯形法是一种用于求解线性规划问题的高效方法,它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。
通过对单纯形表的计算和变换,我们可以逐步找到最优解。
在实际应用中,单纯形法已经被广泛地应用于各个领域,它为我们解决资源有限的最优化问题提供了一个强大的工具。
希望本文对单纯形法的基本原理有所帮助,谢谢阅读!。




运筹学单纯形法的迭代原理讲解
单纯形法是一种用于解决线性规划问题的常用方法,其基本思想是通过迭代的方式逐步接近最优解。
下面是单纯形法的迭代原理的讲解:
1. 初始解的选择:首先需要选择一个初始解,通常选择的方法是构造一个基可行解,即使所有的约束条件都满足的解。
2. 判断最优性:在每一次迭代中,需要判断当前解是否为最优解。
首先,计算当前解对应的目标函数值。
然后,检查是否存在非基变量的系数大于等于0(对于最小化问题)或者小于等于0(对于最大化问题),如果存在这样的非基变量,则当前解不是最优解;如果不存在这样的非基变量,则当前解是最优解。
3. 生成新解:如果当前解不是最优解,则需要生成新的解。
首先,选择一个非基变量,使得目标函数的值可以通过增加(对于最小化问题)或减少(对于最大化问题)该变量的值来改善。
然后,需要计算这个非基变量能够增加或减少的最大量,称为变量的进步长度。
最后,通过调整基变量的值来生成新的解。
4. 更新目标函数和约束条件:在生成新解之后,需要更新目标函数和约束条件,以便于下一次迭代。
具体操作包括计算新解对应的目标函数值,计算新解对应的约束条件的值,调整目标函数和约束条件的系数。
5. 重复迭代:根据判断最优性的结果,进行下一次迭代。
如果当前解是最优解,
则算法结束;否则,继续进行下一次迭代。
通过不断重复这一迭代过程,直到找到最优解或者确定问题无解为止。
单纯形法的迭代过程一般会在有限次数内结束,并且能够得到最优解。