多元统计分析之聚类分析

应用多元统计分析聚类分析多元统计分析是一种利用多个变量对数据进行综合分析的方法，通过对各个变量之间的关系进行分析，可以帮助我们了解数据的内在规律，揭示变量之间的相互作用，为问题的解决提供依据和参考。

其中，聚类分析是多元统计分析中的一种方法，它通过将样本数据划分为不同的组别，使得组内的样本之间相似度较高，组间的样本相似度较低，从而实现数据的分类和整理。

聚类分析的过程一般可分为以下几个步骤：1.确定聚类的目标与方法：在进行聚类分析之前，需要明确分析的目标，即希望把样本分成多少个组别，以及采用什么样的分析方法。

2.选择合适的变量和数据：聚类分析需要选择一些具有代表性的变量作为分析对象，并准备好相应的数据。

这些变量可以是数值型、名义型或顺序型的，但需要注意的是，不同类型的变量需要采用不同的距离度量。

3.计算样本间的距离：通过选择合适的距离度量方法，可以度量各个样本之间的相似度或距离，常用的距离度量方法有欧氏距离、曼哈顿距离和相关系数等。

4.执行聚类分析：根据选定的聚类方法，进行聚类分析。

常用的聚类方法有层次聚类和非层次聚类两种，其中层次聚类可以进一步分为凝聚聚类和分裂聚类等。

5.判断聚类结果的合理性：根据实际情况和问题要求，对得到的聚类结果进行合理性检验。

可以通过观察不同聚类组别内的样本特征和组间的差异度，评估聚类结果的合理性。

6.解释和应用聚类结果：根据聚类分析得到的结果，可以对分类的样本进行解释和应用。

例如，可以找到各个类别的典型样本，分析其特征和规律，为问题的解决提供参考和支持。

聚类分析在实际应用中具有很广泛的应用价值。

例如，在市场细分方面，可以利用聚类分析将消费者划分为不同的群体，有针对性地开展精准营销；在医药领域中，可以通过聚类分析将疾病患者划分为不同的病种，帮助医生进行诊断和治疗方案的选择；在社会科学研究中，可以利用聚类分析将受访者划分为不同的人群，通过对不同人群的特征分析，了解社会问题背后的机制和原因。

在多元统计分析中，因子分析和聚类分析是两种常用的数据分析方法。

它们可以帮助我们理解数据中的潜在结构和相似性，从而揭示数据背后的规律和关系。

首先，让我们来了解一下因子分析。

因子分析是一种主成分分析方法，用于研究多个变量之间的相关性。

通过对原始数据进行因子提取，可以将一组相关的变量转换为少数几个无关的维度，这些维度被称为因子。

因子分析的核心思想是将一组相关的变量解释为共同的因素或维度，从而减少数据的复杂性。

因子分析可以帮助我们理解变量之间的内在结构，并找到隐藏在数据背后的影响因素。

聚类分析是一种无监督学习方法，用于将数据集中的对象划分为不同的群组。

聚类分析的目标是找到数据中的相似性并将其归类到同一组中。

聚类分析可以帮助我们识别数据中的模式和群组，并进行数据的分类和分析。

聚类分析可以基于数据的相似性进行聚类，也可以基于数据的距离进行聚类。

通过聚类分析，我们可以发现数据中的群组结构，并推断这些群组之间的关系。

因子分析和聚类分析在多元统计分析中扮演着不同的角色。

因子分析更侧重于变量之间的相关性和潜在结构，可以帮助我们理解变量之间的共同特征和因素。

聚类分析则更侧重于数据的相似性和群组结构，可以帮助我们找到数据中的模式和群组。

由于它们的不同特点和应用场景，因子分析和聚类分析常常被结合使用，以获得更全面的数据分析结果。

在实际应用中，因子分析和聚类分析可以用于许多领域。

在社会科学中，因子分析可以用于分析调查问卷数据，找到共同的问题维度和影响因素。

聚类分析可以用于市场细分和受众分析，帮助企业发现潜在的目标市场并制定相应的营销策略。

在医学研究中，因子分析可以用于分析疾病的症状和因素，聚类分析可以用于发现疾病的亚型和患者的分类。

综上所述，因子分析和聚类分析在多元统计分析中发挥着重要作用。

它们可以帮助我们理解数据中的潜在结构和相似性，并用于数据分类、模式识别和关联分析。

因子分析和聚类分析是数据分析中常用的工具，研究人员可以根据具体问题和数据特点选择合适的方法。

第9章 聚类分析9.1 引言俗话说：“物以聚类，人以群分”，在现实世界中存在着大量的分类问题。

例如，生物可以分成动物和植物，动物又可分为脊椎动物和无脊椎动物等；人按年龄可分为少年、青年、中年、老年，对少年的身体形态、身体素质及生理功能的各项指标进行测试，据此对少年又可进行分类；在环境科学中，我们可以对按大气污染的轻重分成几类区域；在经济学中，根据人均国民收入、人均工农业产值和人均消费水平等多项指标对世界上所有国家的经济发展状况进行分类；在产品质量管理中，要根据各产品的某些重要指标可以将其分为一等品，二等品等。

研究事物分类问题的基本方法有两种：一是判别分析，二是聚类分析。

若已知总体的类别数目及各类的特征，要对类别未知的个体正确地归属其中某一类，这时需要用判别分析法。

若事先对总体到底有几种类型无从知晓，则要想知道观测到的个体的具体的分类情况，这时就需要用聚类分析法。

聚类分析的基本思想：首先定义能度量样品（或变量）间相似程度（亲疏关系）的统计量，在此基础上求出各样品（或变量）间相似程度的度量值；然后按相似程度的大小，把样品（或变量）逐一归类，关系密切的聚集到一个小的分类单位，关系疏远的聚合到一个大的分类单位，直到所有的样品（或变量）都聚合完毕，把不同的类型一一划分出来，形成一个由小到大的分类系统；最后根据整个分类系统画出一副分群图，称之为亲疏关系谱系图。

聚类分析给人们提供了丰富多彩的分类方法，大致可归为：⑴系统聚类法：首先，将n 个样品看成n 类，然后将性质最接近的两类合并成一个新类，得到1 n 类，合并后重新计算新类与其它类的距离与相近性测度。

这一过程一直继续直到所有对象归为一类为止，并且类的过程可用一张谱系聚类图描述。

⑵动态聚类法（调优法）：首先对n 个对象初步分类，然后根据分类的损失函数尽可能小的原则进行调整，直到分类合理为止。

⑶有序样品聚类法（最优分割法）：开始将所有样品看成一类，然后根据某种最优准则将它们分割为二类、三类，一直分割到所需的K类为止。

多元统计分析-聚类分析聚类分析是⼀个迭代的过程对于n个p维数据，我们最开始将他们分为n组每次迭代将距离最近的两组合并成⼀组若给出需要聚成k类，则迭代到k类是，停⽌计算初始情况的距离矩阵⼀般⽤马⽒距离或欧式距离个⼈认为考试只考 1,2⽐较有⽤的⽅法是3,4,5,8最喜欢第8种距离的计算 欧式距离 距离的⼆范数 马⽒距离 对于X1, X2均属于N(u, Σ) X1,X2的距离为 (X1 - X2) / sqrt(Σ)那么不同的聚类⽅法其实也就是不同的计算类间距离的⽅法1.最短距离法 计算两组间距离时，将两组间距离最短的元素作为两组间的距离2.最长距离法 将两组间最长的距离作为两组间的距离3.中间距离法 将G p,G q合并成为G r 计算G r与G k的距离时使⽤如下公式 D2kr = 1/2 * D2kp + 1/2 * D2kq + β * D2pq β是提前给定的超参数-0.25<=β<=04.重⼼法 每⼀组都可以看成⼀组多为空间中点的集合，计算组间距离时，可使⽤这两组点的重⼼之间的距离作为类间距离 若使⽤的是欧⽒距离 那么有如下计算公式 D2kr = n p/n r * D2kp + n q/n r * D2kq - (n p*n q / n r*n r ) * D2pq5.类平均法 两组之间的距离 = 组间每两个样本距离平⽅的平均值开根号 表达式为D2kr = n p/n r * D2kp + n q/n r * D2kq6.可变类平均法 可以反映合并的两类的距离的影响 表达式为D2kr = n p/n r *(1- β) * D2kp + n q/n r *(1- β) * D2kq + β*D2pq 0<=β<17.可变法 D2kr = (1- β)/2 * (D2kp + D2kq) + β*D2pq8.离差平⽅和法 这个⽅法⽐较实⽤ 就是计算两类距离的话，就计算，如果将他们两类合在⼀起之后的离差平⽅和 因为若两类本⾝就是⼀类，和本⾝不是⼀类，他们的离差平⽅和相差较⼤ 离差平⽅和:类中每个元素与这⼀类中的均值距离的平⽅之和 若统⼀成之前的公式就是 D2kr = (n k + n p)/(n r + n k) * D2kp + (n k + n q)/(n r + n k) -(n k)/(n r + n k) * * D2pq⼀些性质 除了中间距离法之外，其他的所有聚类⽅法都具有单调性 单调性就是指每次聚类搞掉的距离递增 空间的浓缩和扩张 D(A)>=D(B) 表⽰A矩阵中的每个元素都不⼩于B D(短) <= D(平) <= D(长) D(短，平) <= 0 D(长，平) >= 0 中间距离法⽆法判断。

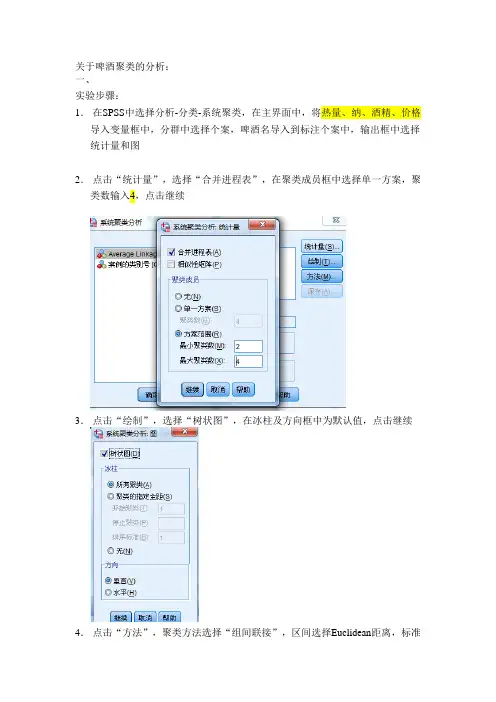
关于啤酒聚类的分析：一、实验步骤：1．在SPSS中选择分析-分类-系统聚类，在主界面中，将热量、纳、酒精、价格导入变量框中，分群中选择个案，啤酒名导入到标注个案中，输出框中选择统计量和图2．点击“统计量”，选择“合并进程表”，在聚类成员框中选择单一方案，聚类数输入4，点击继续3．点击“绘制”，选择“树状图”，在冰柱及方向框中为默认值，点击继续4．点击“方法”，聚类方法选择“组间联接”，区间选择Euclidean距离，标准化中选择Z得分，点击继续45．点击“保存”，选择单一方案，聚类数设置为二、输出结果：聚类表含义：在第一步，将1和17聚成一类，第二步将1和17的总体和11并在一起，在进行分类时，当后面的首次出现阶群集为0时，前面的群集组合为一类，当后面的首次出现不为0时，需按首次出现向前寻找，进行聚类，以此类推。

2. 冰柱图在分成19类时，17和1并在一起；分成18类时，11、17、1并在一起。

当分成四类时，在纵坐标等于4时画一条横线，四类分别为19/16,13/12/10/20/9,14/15/5/4,7/3/2/18/8/6/11/17/1。

.3. 树状图* * * * * * * * * * * * * * * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * * * * * * * * * * * * * * *Dendrogram using Ward MethodRescaled Distance Cluster CombineC A S E 0 5 10 15 20 25 Label Num +---------+---------+---------+---------+---------+Budweiser 1 -+Hamms 17 -+-----+Coors 11 -+ +-+Strchsbohemi 8 -+---+ | |Heilemans 18 -+ +-+ +-------------------------------+Milnaukee 6 -----+ | |Schlitz 2 ---+-+ | |Ionenbrau 3 ---+ +---+ +-------+ Aucsberger 7 -----+ | | Heineken 5 -+ | | Kkirin 15 -+-----+ | | Kronensourc 4 -+ +---------------------------------+ | Secrs 14 -------+ | Miller-lite 9 -+-+ | Schlite 20 -+ +-+ | Sudeiser 10 ---+ +-----------+ | Coorslicht 12 ---+-+ +-------------------------------+ Michelos 13 ---+ |Pabst 16 -----+-----------+Olympia 19 -----+在树状图中，分成四类处画一条竖线，得到结果和冰柱图相同。

多元统计聚类分析方法实例
一、概述
多元统计聚类分析是一种建立数据从不同特征维度上的理解和描述的
方法。

它是通过对多维数据进行聚类分析，将具有共同特征的不同数据项
归纳到一组中，以便进一步分析和解释这些数据项之间的相似性和差异性，从而达到更深入地理解和把握数据特征的目的。

二、基本多元统计聚类分析步骤
1、数据准备
首先，在开始进行多元统计聚类分析之前，需要准备足够的数据，以
便进行模型的建立和应用。

在进行数据准备时，要注意把握数据的准确性，避免数据准备过程中的错误，以保证后续步骤正确的进行。

2、聚类分析
在进行聚类分析时，需要根据实际的数据情况，确定聚类的参数，并
计算不同类簇之间的距离，作为聚类的依据。

在此过程中，要根据聚类的
具体目的，采用相应的聚类分析方法，以便达到更理想的聚类效果。

3、聚类评价
接下来，需要对聚类结果进行评价，以识别聚类的质量和准确性，并
可以根据评价结果，对聚类的方法和参数进行调整，以获得更理想的聚类
结果。

4、聚类结果应用
最后，在聚类分析完成后，可以将聚类结果应用到实际的问题中，以获得有效的决策依据。

多元统计分析——聚类分析多元统计分析中的聚类分析(Cluster Analysis)是一种将相似的个体或对象归为一类的数据分析方法。

聚类分析的目的是通过寻找数据中的相似性来识别或发现存在的模式和结构，可以帮助我们理解和解释数据中的复杂性。

聚类分析在许多领域中都得到了广泛的应用，例如市场细分、社会学、生物学、医学等。

聚类分析的基本原理是将数据样本根据其相似性归为不同的组或类。

相似性可以通过计算数据之间的距离或相似度来度量。

常用的距离度量方法有欧氏距离、曼哈顿距离、闵可夫斯基距离等，相似度度量方法有相关系数、夹角余弦等。

在聚类分析中，我们通常将相似的样本放在同一类别中，不相似的样本放在不同类别中。

聚类分析可以分为两种类型：层次聚类和划分聚类。

层次聚类是一种将数据样本分层次地组织成树状结构的聚类方法。

划分聚类则是将数据样本划分为预先确定的K个不重叠的类的聚类方法。

其中最常用的层次聚类算法有聚合法和分裂法，最常用的划分聚类算法是K均值算法。

聚类分析的基本步骤包括数据准备、相似度度量、类别划分和结果解释。

在数据准备阶段，需要选择合适的变量和样本。

相似度度量是聚类分析的核心，不同的距离或相似性度量方法可能会导致不同的聚类结构。

类别划分可以根据层次聚类算法或划分聚类算法来进行。

结果解释则是对聚类结果进行分析和解释，常用的方法包括聚类矩阵、平均距离图、树状图等。

聚类分析的优势在于能够帮助我们理解数据中的结构和模式，发现数据中的共性和差异性。

聚类分析可以为我们提供有关样本之间的关系和特征的重要信息。

此外，聚类分析还可以帮助我们进行市场细分和目标市场选择、发现新的疾病群和药物靶点等。

然而，聚类分析也存在一些局限性。

首先，聚类结果可能会受到初始聚类中心选择的影响。

其次，聚类结果的解释需要结合领域知识和专家判断，可能存在主观性。

此外，聚类分析对数据的样本大小和变量数目也有一定的要求，数据的维度增加会导致计算量的增加。