当前位置：文档之家 › 最新多元统计分析-因子分析案例

最新多元统计分析-因子分析案例

  • 格式：ppt
  • 大小：542.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

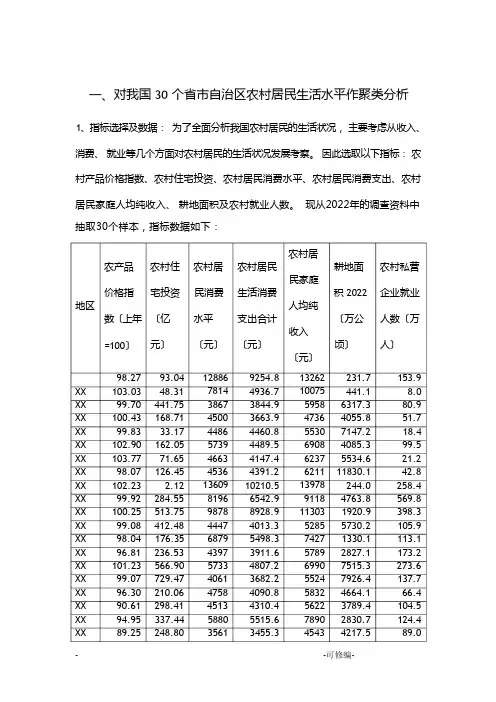
多元统计分析案例分析(2)

多元统计分析案例分析(2)

一、对我国30 个省市自治区农村居民生活水平作聚类分析1、指标选择及数据：为了全面分析我国农村居民的生活状况，主要考虑从收入、消费、就业等几个方面对农村居民的生活状况发展考察。

因此选取以下指标：农村产品价格指数、农村住宅投资、农村居民消费水平、农村居民消费支出、农村居民家庭人均纯收入、耕地面积及农村就业人数。

现从2022年的调查资料中抽取30个样本，指标数据如下：农村居民生活消费支出合计〔元〕9254.84936.73844.93663.94460.84489.54147.44391.2 10210.56542.98928.94013.35498.33911.64807.23682.24090.84310.45515.63455.3农村私营企业就业人数〔万人〕153.98.080.951.718.499.521.242.8258.4569.8398.3105.9113.1173.2273.6137.766.4104.5124.489.0 农村居民家庭人均纯收入〔元〕132621007559584736553069086237621113978911811303528574275789699055245832562278904543农产品价格指数〔上年=100〕98.27 103.0399.70 100.4399.83 102.90 103.7798.07 102.2399.92 100.2599.0898.0496.81 101.2399.0796.3090.6194.9589.25耕地面积2022〔万公顷〕231.7441.16317.34055.87147.24085.35534.611830.1244.04763.81920.95730.21330.12827.17515.37926.44664.13789.42830.74217.5 农村居民消费水平〔元〕1288678143867450044865739466345361360981969878444768794397573340614758451358803561农村住宅投资〔亿元〕93.0448.31441.75168.7133.17162.0571.65126.452.12284.55513.75412.48176.35236.53566.90729.47210.06298.41337.44248.80地区XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX数据来源： ?中国统计年鉴 2022?．2、将数据发展标准化变换：农村居民生活消费支出合计〔元〕2.53 0.15 -0.46 -0.56 -0.12 -0.10 -0.29 -0.153.06 1.04 2.35 -0.36 0.46 -0.42 0.08 -0.55 -0.32 -0.20 农村居民家庭人均纯收入〔元〕2.37 1.30 -0.07 -0.48 -0.21 0.25 0.02 0.01 2.60 0.98 1.71 -0.30 0.42 -0.13 0.27 -0.22 -0.11 -0.18农产品价格指数〔上年=100〕0.09 1.33 0.47 0.65 0.50 1.30 1.52 0.04 1.12 0.52 0.61 0.30 0.04 -0.28 0.86 0.30 -0.42 -1.89农村居民消费水平〔元〕2.82 0.92 -0.56 -0.33 -0.33 0.14 -0.26 -0.313.09 1.06 1.69 -0.35 0.57 -0.36 0.14 -0.49 -0.23 -0.32 农村私营企业就业人数〔万人〕 0.37 -0.78 -0.21 -0.44-0.70 -0.06 -0.68 -0.51 1.20 3.66 2.31 -0.01 0.05 0.52 1.32 0.24 -0.32 -0.02农村住宅投资〔亿元〕-0.67 -0.91 1.24 -0.25 -0.99 -0.29 -0.78 -0.48 -1.16 0.38 1.64 1.08 -0.21 0.12 1.93 2.82 -0.03 0.46耕地面积 2022 〔万公顷〕-1.36 -1.29 0.84 0.02 1.15 0.03 0.56 2.84 -1.36 0.28 -0.75 0.63 -0.97 -0.42 1.28 1.43 0.24 -0.07地区XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XXXX 101.91 26.22 3846 3446.2 5275 727.5 5.3 XX 88.99 80.12 3652 3624.6 5277 2235.9 36.7675 XX 96.94 456.10 4748 3897.5 5087 5947.4 140.3 XX 96.11 137.22 2926 2852.5 3472 4485.3 25.4 XX 96.50 158.97 3603 3398.3 3952 6072.1 41.3XX 95.83 151.79 3683 3793.8 4105 4050.3 1.7 XX 100.22 97.33 2975 2942.0 3425 4658.8 22.0 XX 94.61 63.63 3684 3863 542.7 10.5 11.4 XX 99.39 29.51 3894 4675 1107.1 43.6 16.7 XX 92.87 79.35 3590 3457.9 4643 4124.6 18.73、用K－均值聚类法对样本发展分类如下：聚类成员案例号地区聚类距离12 3 4 5 6 7 8 910111213141516171819 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX12343233121324333421069.193060.35920.651506.42577.122453.891487.955006.412094.382853.423015.141204.491612.461880.402088.551282.272230.152053.351119.98XX -0.77 0.67 0.19 0.47 0.57 -0.42 0.14 XX -2.24 0.19 -0.68 -0.67 -0.54 0.08 -0.14 XX 1.04 -1.03 -0.57 -0.68 -0.30 -1.18 -0.81 XX -2.31 -0.74 -0.64 -0.58 -0.30 -0.64 -0.56 XX -0.25 1.32 -0.23 -0.43 -0.36 0.71 0.26 XX -0.46 -0.42 -0.92 -1.00 -0.90 0.18 -0.65 XX -0.36 -0.31 -0.66 -0.70 -0.74 0.75 -0.52 XX -0.54 -0.34 -0.63 -0.48 -0.69 0.02 -0.83 XX 0.60 -0.64 -0.90 -0.96 -0.92 0.24 -0.67 XX -0.85 -0.83 -0.63 -0.45 -1.88 -1.44 -0.76 XX 0.39 -1.01 -0.55 0.00 -1.69 -1.43 -0.71 XX -1.30 -0.74 -0.67 -0.67 -0.51 0.05 -0.70分四类的情况下，最终分类结果如下：第一类：、XX、XX。

多元统计分析 第8章(因子分析)

多元统计分析 第8章(因子分析)


.
.
.
.. .
X5
0.63 0.49 0.19 0.29 1.00
.
.
.. .
X6
0.40 0.52 0.36 0.46 0.34 1.00
.
.. .
X7
0.28 0.31 0.73 0.27 0.17 0.32 1.00
.. .
X8
0.20 0.36 0.24 0.39 0.23 0.33 0.24 1.00 . .
用这m个不可观测的相互独立的公因 子 F1， F2， ，Fm (也称潜因子)和一
个特殊 i来描述原始可测的相关变量
(科目成绩) x1 , x2 , , x p , 并解释分析学 生的学习能力.
11
教育测量中的项目反应理论模型：
Pj ( ) exp aj ( bj ) 1 exp aj ( bj )
2 1
,
,
2 p
)
(特 殊 因 子 间 不 相 关)
cov(F , ) 0(公 共 因 子 与 特 殊 因 子 间不 相 关)
19
其中：
x x1 x2 x p 是 可 观 测 的 随 机 向 量 ，
F (F1 F2 Fm )(m p)是 不 可 观 测 的 随 机 向 量 ，F1 F2 Fm 一 般 对x 每 一 个 分 量xi 都 有 作 用 ， 所 以 称 为x 的公 共 因 子， 而
24
二、正交因子模型中各个量的统计意义 1. 因子载荷的统计意义 2. 变量共同度的统计意义 3. 公因子Fi的方差贡献的统计意义
25
1. 因子载荷的统计意义
若
var(
x
i
)
1,
则x
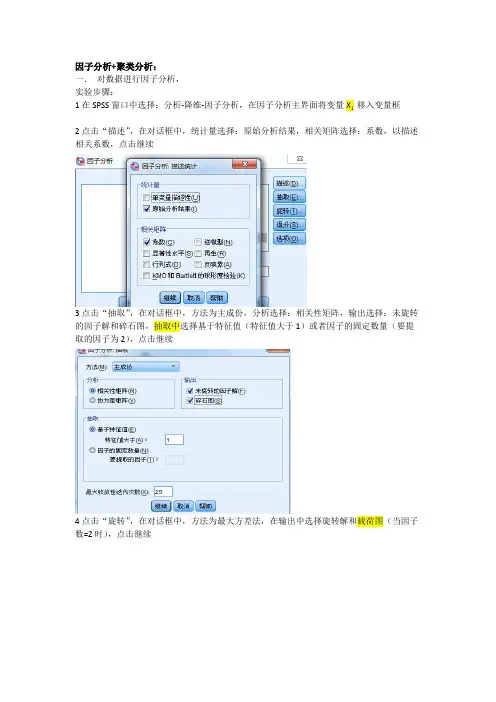
多元统计分析因子分析（方法步骤分析总结）

多元统计分析因子分析（方法步骤分析总结）

因子分析+聚类分析：一．对数据进行因子分析，实验步骤：1在SPSS窗口中选择：分析-降维-因子分析，在因子分析主界面将变量X1 移入变量框2点击“描述”，在对话框中，统计量选择：原始分析结果，相关矩阵选择：系数，以描述相关系数，点击继续3点击“抽取”，在对话框中，方法为主成份，分析选择：相关性矩阵，输出选择：未旋转的因子解和碎石图，抽取中选择基于特征值（特征值大于1）或者因子的固定数量（要提取的因子为2），点击继续4点击“旋转”，在对话框中，方法为最大方差法，在输出中选择旋转解和载荷图（当因子数=2时），点击继续5点击“得分”，在对话框中，选中“保存为变量”和“显示因子得分系数矩阵”，在方法中选择“回归”，点击继续6点击确定实验结果分析：1.特征根和累计贡献率由表中可以看出，因为成份1和2的特征值>1，被提取出来，而且由于第三个特征根相比下降比较快，我们也只选取两个公共因子，对1和2旋转后其累计贡献率为82.488%。

由碎石图，我们也可以看出1和2的特征值大于1，可以被提取出来，其余变量特征值过小，不予提取。

从旋转成份矩阵可以看出，经过旋转的载荷系数产生了明显的区别，横向找到最大的一个数，如上表中黄色部分画出，第一个公因子在v1,v3,v5上占有较大载荷，说明于这三个指标有较大的相关性，命名为；第二个公因子在v2,v4,v6上有较大载荷，有较大相关性，归为一类，可命名为。

该表为成分转换矩阵，给出旋转所需的矩阵可以用成份得分系数矩阵写出各个因子关于中心标准化后的变量的表达式。

F1=0.385x1-0.001x2+…..F2=…..(分析的举例：第一个因子在外貌自信心洞察力推销能力工作魄力志向抱负理解能力潜能等变量上有较大的系数，可以抽象为应聘者主客观工作能力因子第二个因子在简历格式工作经验适应力变量上有较大的系数，可抽象为应聘者对客观环境的适应力因子第三个因子在兴趣爱好诚信度求职渴望度变量上有较大的系数，可抽象为应聘者的兴趣和诚信因子。

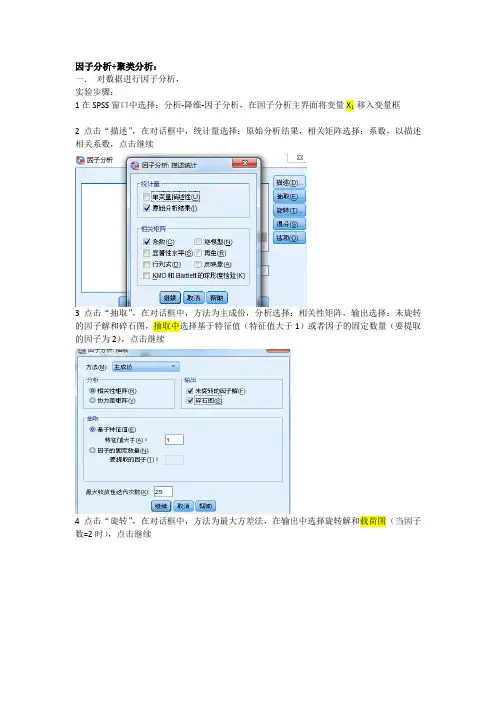
多元统计分析 因子分析(方法+步骤+分析 总结)

多元统计分析 因子分析(方法+步骤+分析 总结)

因子分析+聚类分析：一．对数据进行因子分析，实验步骤：1在SPSS窗口中选择：分析-降维-因子分析，在因子分析主界面将变量X1 移入变量框2点击“描述”，在对话框中，统计量选择：原始分析结果，相关矩阵选择：系数，以描述相关系数，点击继续3点击“抽取”，在对话框中，方法为主成份，分析选择：相关性矩阵，输出选择：未旋转的因子解和碎石图，抽取中选择基于特征值（特征值大于1）或者因子的固定数量（要提取的因子为2），点击继续4点击“旋转”，在对话框中，方法为最大方差法，在输出中选择旋转解和载荷图（当因子数=2时），点击继续5点击“得分”，在对话框中，选中“保存为变量”和“显示因子得分系数矩阵”，在方法中选择“回归”，点击继续6点击确定实验结果分析：1.特征根和累计贡献率解释的总方差成份初始特征值提取平方和载入旋转平方和载入合计方差的 % 累积 % 合计方差的 % 累积 % 合计方差的 % 累积 %1 2.731 45.520 45.520 2.731 45.520 45.520 2.688 44.802 44.8022 2.218 36.969 82.488 2.218 36.969 82.488 2.261 37.687 82.4883 .442 7.360 89.8484 .341 5.688 95.5365 .183 3.044 98.5806 .085 1.420 100.000提取方法：主成份分析。

由表中可以看出，因为成份1和2的特征值>1，被提取出来，而且由于第三个特征根相比下降比较快，我们也只选取两个公共因子，对1和2旋转后其累计贡献率为82.488%。

由碎石图，我们也可以看出1和2的特征值大于1，可以被提取出来，其余变量特征值过小，不予提取。

成份矩阵a成份1 2v1 .928 .253v2 -.301 .795v3 .936 .131v4 -.342 .789v5 -.869 -.351v6 -.177 .871由旋转前的成分矩阵可以写出每个原始变量关于各个成份的表达式。

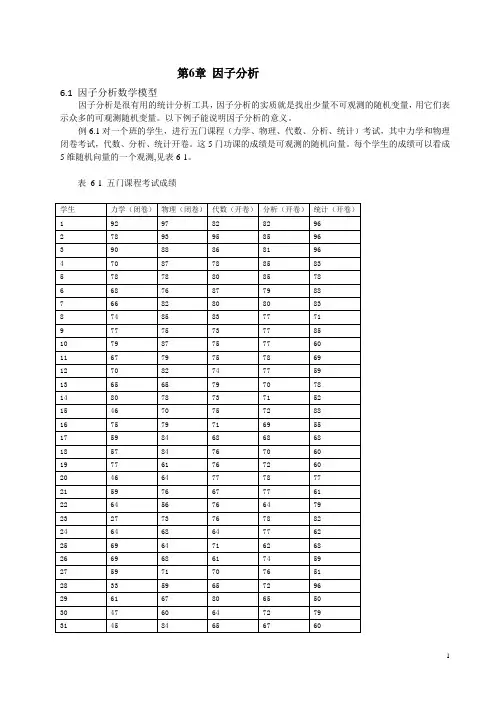
多元统计分析第六章 因子分析

多元统计分析第六章 因子分析

第6章因子分析6.1 因子分析数学模型因子分析是很有用的统计分析工具，因子分析的实质就是找出少量不可观测的随机变量，用它们表示众多的可观测随机变量。

以下例子能说明因子分析的意义。

例6.1对一个班的学生，进行五门课程（力学、物理、代数、分析、统计）考试，其中力学和物理闭卷考试，代数、分析、统计开卷。

这5门功课的成绩是可观测的随机向量。

每个学生的成绩可以看成5维随机向量的一个观测,见表6-1。

表6-1 五门课程考试成绩经过一定计算（因子分析）后发现存在不可观测的随机变量：1f 、2f ，它们和51,...x x 间有关系 521542143213221212116377.1091469.9750.678264.162258.5364.721559.013358.6909.720269.564838.7523.721220.864570.8409.62v f f x v f f x v f f x v f f x v f f x +-+=+-+=+-+=+++=+++= （6.1） 其中1f 、2f 是不可观测的随机变量。

我们认为它们分别表示学生的学习能力和适应开闭卷能力，所以可分别称为学习因子和适应开闭卷因子。

（6.1）揭示了这两个因子如何影响5门功课的成绩，也揭示5门课成绩的实质：每门课的成绩由学习因子和适应开闭卷因子的线性组合，加上常数，再加上随机变量而得。

这是是很有意义的。

象例6.1那样，找出少量不可观测因子（例如1f 、2f ），并给出它们影响可观测随机变量（例如51,...x x ）方式的统计分析，就是因子分析。

因子分析与主成分分析不同：主成分分析是寻求若干个可观测随机变量的少量线性组合，说明其含义；因子分析主要的目的是找出不一定可观测的潜在变量作为公共因子，并解释公共因子的意义，及如何用不可观测随机变量，计算可观测随机变量。

因子分析方法在心理学，经济，医学，生物学，教育学等方面有重要用途。

多元统计分析因子分析（方法步骤分析总结）

多元统计分析因子分析（方法步骤分析总结）

因子分析+聚类分析：一．对数据进行因子分析，实验步骤：1在SPSS窗口中选择：分析-降维-因子分析，在因子分析主界面将变量X1 移入变量框2点击“描述”，在对话框中，统计量选择：原始分析结果，相关矩阵选择：系数，以描述相关系数，点击继续3点击“抽取”，在对话框中，方法为主成份，分析选择：相关性矩阵，输出选择：未旋转的因子解和碎石图，抽取中选择基于特征值（特征值大于1）或者因子的固定数量（要提取的因子为2），点击继续4点击“旋转”，在对话框中，方法为最大方差法，在输出中选择旋转解和载荷图（当因子数=2时），点击继续5点击“得分”，在对话框中，选中“保存为变量”和“显示因子得分系数矩阵”，在方法中选择“回归”，点击继续6点击确定实验结果分析：1.特征根和累计贡献率由表中可以看出，因为成份1和2的特征值>1，被提取出来，而且由于第三个特征根相比下降比较快，我们也只选取两个公共因子，对1和2旋转后其累计贡献率为82.488%。

由碎石图，我们也可以看出1和2的特征值大于1，可以被提取出来，其余变量特征值过小，不予提取。

从旋转成份矩阵可以看出，经过旋转的载荷系数产生了明显的区别，横向找到最大的一个数，如上表中黄色部分画出，第一个公因子在v1,v3,v5上占有较大载荷，说明于这三个指标有较大的相关性，命名为；第二个公因子在v2,v4,v6上有较大载荷，有较大相关性，归为一类，可命名为。

该表为成分转换矩阵，给出旋转所需的矩阵可以用成份得分系数矩阵写出各个因子关于中心标准化后的变量的表达式。

F1=0.385x1-0.001x2+…..F2=…..(分析的举例：第一个因子在外貌自信心洞察力推销能力工作魄力志向抱负理解能力潜能等变量上有较大的系数，可以抽象为应聘者主客观工作能力因子第二个因子在简历格式工作经验适应力变量上有较大的系数，可抽象为应聘者对客观环境的适应力因子第三个因子在兴趣爱好诚信度求职渴望度变量上有较大的系数，可抽象为应聘者的兴趣和诚信因子。

Eviews多元因子分析案例分析

Eviews多元因子分析案例分析

Eviews多元因子分析案例分析
多元因子分析是一种常用的经济数据分析方法，它能够帮助我
们解释变量之间的关系以及其对观察数据的影响程度。

本文将以一
个案例为例，演示如何使用Eviews进行多元因子分析。

案例背景
在这个案例中，我们有一组经济数据，包括GDP增长率、通
货膨胀率、利率、失业率和投资增长率。

我们希望通过多元因子分析，找出这些变量之间的主要关系，并解释它们对经济发展的影响。

数据准备
在进行多元因子分析之前，我们首先需要准备好数据。

将数据
导入Eviews软件，并确保数据格式正确。

模型建立
在Eviews中，我们可以使用多元线性回归模型来进行因子分析。

通过选择适当的解释变量和因变量，我们可以建立一个能够解
释经济数据变动的模型。

数据分析
在模型建立完成后，我们可以进行数据分析。

通过观察回归结果，我们可以得出变量之间的关系以及各自的影响程度。

同时，我
们还可以进行统计检验，以评估模型的拟合程度和变量的显著性。

结论
通过Eviews多元因子分析，我们可以得出经济数据变量之间
的关系和影响程度。

这些结果可以帮助我们更好地理解经济的运行
规律，为决策提供参考。

以上就是Eviews多元因子分析的案例分析。

通过这个案例，
我们可以更好地掌握使用Eviews进行多元因子分析的方法和步骤。

希望本文对您有所帮助！。

应用多元分析第八章 因子分析

应用多元分析第八章 因子分析


1.00 0.32 0.33 0.18 0.00
1.00 0.24 1.00 0.34 0.24 1.00 -0.02 0.17 -0.00 1.00
例8.1.2 为了评价即将进大学的高中生的学习能力， 抽了200名高中生进行问卷调查，共50个问题。素 有这些问题可以归结为阅读理解、数学水平和艺 术素养三个方面。 例8.1.3 公司老板对48名应聘者进行面试，并给出 他们在15个方面的得分，这15个方面是：申请书 的形式(x1)、外貌(x2)、专业能力(x3)、讨人喜欢 (x4)、自信心(x5)、精明(x6)、诚实(x7)、推销能力 (x8)、经验(x9)、积极性(x10)、抱负(x11)、理解能 力(x12)、潜力(x13)、交际能力(x14)、适应性(x15)。 通过因子分析，这15个方面可归结为应聘者的外露 能力、讨人喜欢的程度、经验、专业能 i i 1,,10.
j 1
4
十项全能运动员得分相关矩阵
X1
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 1.00 0.59 0.35 0.34 0.63 0.40 0.28 0.20 0.11 -0.77
X2
X3
X4
X5
X6
X7


i 1
i
i 1
一、主成分法：
1 n 1 n x xi , S ( xi x )( xi x ) ' n i 1 n 1 i 1
ˆ ˆ 1、求出S的特征值1 p 0, 相应的正交单位特征向量
ˆ ti , i 1, , p。
2、估计：




data examp733(type=corr); input x1-x8; cards; 1.000 . . . . . . . 0.923 1.000 . . . . . . 0.841 0.851 1.000 . . . . . 0.756 0.807 0.870 1.000 . . . . 0.700 0.775 0.835 0.918 1.000 . . . 0.619 0.695 0.779 0.864 0.928 1.000 . . 0.633 0.697 0.787 0.869 0.935 0.975 1.000 . 0.520 0.596 0.705 0.806 0.866 0.932 0.943 1.000 ; proc factor data=examp733(type=corr); var x1-x8; proc factor data=examp733(type=corr) n=2; var x1-x8; run;
多元统计实验报告--因子分析

多元统计实验报告--因子分析

多元统计实验报告设计题目：因子分析一、分析数据1995年我国社会发展状况的数据二、基本原理因子分析的基本思想是把每个研究变量分解为几个影响因素变量，将每个原始变量分解成两部分因素，一部分是由所有变量共同具有的少数几个公共因子组成的，另一部分是每个变量独自具有的因素，即特殊因子。

三、实验步骤及其结果分析1、选择Analyze→Data Reduction→Factor，打开Factor Analysis主对话框；2、选择变量X1至X6，点击向右的箭头按钮，将六个变量移到Variable栏中；3、点击Descriptives…按钮，打开Descriptives子对话框。

在此对话框的Statistics下选择Initial solution；Correlation Matrix下选择coefficients，单击Continue按钮，返回Factor Analysis主对话框；4、单击Extraction…按钮，打开Extraction子对话框。

在此对话框的Method 下选择Principal components；Analyze下选择Correlation Matrix；Extract下选择Number of Factor，并在其右端的矩形框键入6；Display下选择Unrotated factor 和Scree plot，单击Continue按钮，返回Factor Analysis主对话框；点击OK按钮，显示结果清单。

（1）相关矩阵从表Correlation Matrix（相关矩阵）可知，各变量间存在较强的相关关系，因此有必要进行因子分析。

表中主对角线上的元素为1，表明变量自身于自身的相关系数为1。

（2）解释总方差从表Total Variance Explained（解释总方差）可知，前三个因子一起解释总方差的93.466%（累计贡献率），这说明前三个因子提供了原始数据的足够信息。

5、根据以上分析提取因子情况，单击Extraction…按钮，打开Extraction子对话框。

金融统计案例分析3： 因子分析

金融统计案例分析3： 因子分析

Bartlett‘s球形检验：用于检验相关阵是否是单位阵，即各 变量是否各自独立。如果结论为不拒绝该假设，则说明这 些变量可能各自独立提供一些信息，相互独立，之间恐怕 没什么联系。
（五）有关概念及分析步骤
重要概念：
（1）因子负荷：即前面因子分析表达式中各因子的系数值，用于反映因 子和各个变量间的密切程度。当各公因子间完全不相关时，因子负荷值 就等于因子与变量的相关系数。它的绝对值越大，说明该因子对当前变 量的影响程度越大。如前面举的食品的例子中，第一公因子主要影响价 格、是否快餐食品和能量，第二公因子则主要影响味道和风味。 （2）公因子方差比(communalities)：指的是提取公因子后，各变量中信 息分别被提取出的比例，或者说原变量的方差中由公因子决定的比例。 公因子方差比在0~1之间，取值越大，说明该变量能被因子说明的程度越 高，如果各因子间完全独立，则公因子方差比和因子负荷实际上是等价。 （3）特征根(eigenvalue)：它可以被看成是主成分影响力度的指标，代 表引入该因子/主成分后可以解释平均原始变量的信息。
数据降维方法②——因子分析方法
因子分析也是一种将多变量化简的技术，它可以被看成是主成分分析的 推广。因子分析的目的是分解原始变量，从中归纳出潜在的“类别”，相 关性较强的指标归为一类，不同类间变量的相关性则较低。每一类变量代 表了一个“共同因子”，即一种内在结构，因子分析就是要寻找该结构。 比如在市场调查中收集了食品的五项指标：味道X1，价格X2，风味X3，是 否快餐食品X4，能量X5。经过因子分析后发现结果如下：
（4）内在结构证实：在有的情况下，研究者根据某些理论或其他知 识已对可能的内在结构进行了假设，此时可利用因子分析来验证该假 设是否成立，这种因子分析也被称为证实性因子分析，在心理学研究 中较为常见。
因子分析

因子分析


Component Plot in Rotated Space
1.0 math cphheyms
.5
Component 2
0.0 ehnigsltiosrhy
literat
-.5
-1.0
-1.0
-.5
0.0
.5
1.0
Component 1
可以直观看出每个因子代表了一类学科
计算因子得分
可以根据输出计算出每个学生的第一个因子和 第二个因子的大小，即算出每个学生的因子得 分f1和f2。
在Method选择一个方法（如果是主成分分析，则选Principal Components），
下面的选项可以随意，比如要画碎石图就选Scree plot，另外在 Extract选项可以按照特征值的大小选主成分（或因子），也可 以选定因子的数目；
之后回到主对话框（用Continue）。然后点击Rotation，再在该 对话框中的Method选择一个旋转方法（如果是主成分分析就选 None），
因子分析 （factor analysis）
一、方法简介
因子分析的形成和早期发展一般认为是 从Charles Spearman在1904年发表的文章 开始．他提出的这种方法当时用来解决 智力测验得分的统计分析。目前因子分 析在心理学、社会学、经济学等学科都 有广泛而成功的应用．
因子分析是主成分分析的推广和发 展，是多元统计分析中降维的一种方法。 因子分析研究相关阵或协差阵的内部依赖 关系，它将多个变量综合为少数几个因子， 科学再现原始变量与因子之间的相关关系。 实际上主成分分析可以说是因子分析的一 个特例或特定方法。
这些问题可以归结为如下几个方面：申
请者外露的能力，讨人喜欢的程度，申
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y3
0.372 -0.017 -0.500 0.575 -0.295 -0.182 0.361 -0.245 0.099 -0.100 -0.256 -0.134 -0.078 0.560 0.103
y4
-0.119 0.289 0.710 0.361 -0.178 -0.070 0.448 -0.230 0.070 -0.165 -0.206 0.092 0.213 -0.234 -0.028
5、主成分的含义解释
6、初始因子载荷矩阵
载荷
X1 X2 X3 X4 X5 X6
Y1
0.459 0.517 0.335 0.858 0.890 0.790
Y2
0. 837 0.780 0.767 -0.420 -0.329 -0.495
7、旋转后的因子载荷阵矩阵
教学水平 教学态度
载荷
X1 X2 X3 X4 X5 X6
F1
0.007 0.080 -0.030 0.949 0.945 0.931
F2
0. 932 0.958 0.469 0.089 0.085 -0.068
8、因子得分
例2：In a job interview , 48 applicants were each judged on 15 variables. The variables were
0.308 -0.014 -0.414 0.476 -0.244 -0.151 0.298 -0.202 0.082 -0.083 -0.212 -0.111 -0.065 0.463 0.085
初始因子载荷矩阵
y1
X1
0.445
X2
0.583
X3
0.109
X4
0.606
X5
0.799
X6
0.865
多元统计分析-因子分析案例
1、 求相关系数矩阵R
1
0.905 1
R
0.683
0.617
1
0.052 0.131 0.067 1
00.0.09387
0.186 0.000
0.085 0.086
0.870 0.824
0.8103
2、 计算R的特征值
主成分
特征根 贡献率（%） 累计贡献率
Y1
f3
f4
-0.872
0.928
-0.863
-0.538
-0.522
第一公共因子 f1 : 申请者外露的能力
第二公共因子 f2 :
经验
第三公共因子 f3 :
讨人喜欢
第四公共因子 f4 :
学术能力
“外貌”和“交际能力”在任何一个因子上都没 有大的载荷值。
将上章例子对全国 31个地区的社会经济发 展的17 项指标作因子分析。 数据见cd.pcrex01
1、 求相关系数矩阵R 2、 计算R的特征值
Y1
特 征 根 7.50 贡献率（%） 50 累 计 贡 献 率 50
Y2
2.06 13.73 63.73
Y3
1.46 9.73 73.46
Y4
1.21 0.74 8.07 81.53
特征向量
y1
y2
y3
y4
申请书
X1
外貌
X2
学术
X3
讨人喜欢 X4
自信
反映地区社会经济发展的指标体系
X1：国内生产总值（GDP） X3：第三产业产值占GDP比重 X5：工业企业劳动生产率 X7：每万人拥有卫生技术人员数 X9：教育经费投入占GDP比重 X11：人均邮电业务总量 X13：人均固定资产投资 X15：地方财政收入占GDP比重 X17：科研经费占GDP比重
X2：人均GDP X4：人均出口额 X6：人均社会消费品零售额 X8：每万人高等学校在校生数 X10：人均货运总量 X12：每万人电话机装机数 X14：人均实际利用外资 X16：每万人科研机构数
X7
0.433
X8
0.881
X9 X10 X11
0.365 0.864
X12பைடு நூலகம்
0.873
X13
0.908
X14
0.912
X15
0.710
0.646
y2
0.618 -0.048 0.340 -0.180 -0.358 -0.188 -0.576 -0.056 0.795 0.066 -0.098 -0.031 0.035 -0.114 0.605
X5
精明
X6
诚实
X7
推销
X8
经验
X9
积极性
X10
抱负
X11
理解
X12
潜力
X13
交际能力 X14
适应性
X15
0.162 0.213 0.040 0.221 0.292 0.316 0.158 0.322 0.133 0.315 0.319 0.332 0.333 0.259 0.236
0.431 -0.033 0.237 -0.125 -0.249 -0.131 -0.400 -0.039 0.553 0.046 -0.068 -0.022 0.024 -0.079 0.421
教学水平 教学态度
4、 由特征向量写出主成分的表达式
y 1 0 . 2 x 1 7 0 . 3 x 6 2 1 0 . 2 x 3 3 0 0 . 5 x 2 4 1 0 . 5 x 8 5 3 0 . 4 x 8 6 7 y 2 0 . 5 x 1 3 0 . 5 x 2 8 0 0 . 4 x 0 3 9 0 . 2 x 2 4 7 0 . 2 x 0 5 1 0 . 3 x 6 2 1
2.741 45.69 45.69
Y2
2.428 40.46 86.15
Y3
0.438 7.30 93.45
3、 求特征根所对应的单位特征向量
特征向量
X1 X2 X3 X4 X5 X6
Y1 0.276 0.313 0.202 0.518 0.538 0.477
Y2 0.538 0.500 0.492 -0.270 -0.212 -0.318
1) Form of letter of application 2) Appearance 3) Academic ability 4) Likeability 5) Self-confidence 6) Lucidity 7) Honesty 8) Salesmanship
9) Experience 10) Drive 11) Ambition 12) Grasp 13) Potential 14) Keenness to join 15) Suitability
旋转后的因子载荷矩阵
申请书
X1
外貌
X2
学术
X3
讨人喜欢 X4
自信
X5
精明
X6
诚实
X7
推销 经验 积极性 抱负 理解 潜力 交际能力
X8 X9 X10 X11 X12 X13
适应性
X14
X15
f1
0.918 0.863 0.917 0.798 0.917 0.806 0.741
f2
0.83
0.852 0.797