当前位置：文档之家 › 传感器基本特性1

传感器基本特性1

  • 格式：ppt
  • 大小：155.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

第1章 传感器的基本知识

第1章 传感器的基本知识

2
几何量：
长度、厚度、角度、直径、间距、形状、粗糙度、 硬度、材料 缺陷等
燕山大学电气工程学院
第1章 传感器的基本知识
物体的性质和成分量 ：
空气的湿度（绝对、相对）、气体的化学成分、浓度、液体 的粘度、浊度、透明度、物体的颜色
状态量：
工作机械的运动状态（启停等）、生产设备的异常状态（超 温、过载、泄漏、变形、磨损、堵塞、断裂等）
x
△Rmax1正行程的最大重复性偏差， △Rmax2反行程的最大重复性偏差。
重复性误差也常用绝对误差表示。检测时也可选取几个测试点， 对应每一点多次从同一方向趋近，获得输出值系列 yi1 ， yi2 ， yi3 ，…，yin ，算出最大值与最小值之差或 3σ作为重复性偏差 ΔRi，在几个ΔRi中取出最大值ΔRmax 作为重复性误差。
燕山大学电气工程学院
传感器依赖其结构参数变化 实现信息转换 传感器依赖其敏感元件物理 特性的变化实现信息转换 传感器直接将被测量的能量 转换为输出量的能量 由外部供给传感器能量，而 由被测量来控制输出的能量 输出为模拟量 输出为数字量
第1章 传感器的基本知识
1.1.3 传感器的物理定律
（ 1 ）守恒定律（能量、动量、电荷量等守恒定律）
燕山大学电气工程学院
第1章 传感器的基本知识
工业检测中涉及的物理量分类 热工量：
温度t（℃ 、K、℉ ） 3 压力（压强）p（Pa）、压差Δ p 、真空度、流量q（t、m ）、 流速v（m/s）、物位、液位h（m）
机械量：
直线位移x（m）、角位移α、速度、加速度a（ m/s ） 、转速n （r/min）、应变 ε （m/m ）、力矩T（Nm）、振动、噪声、质量 （重量）m（kg、t）
1传感器的静态特性主要有那些

1传感器的静态特性主要有那些

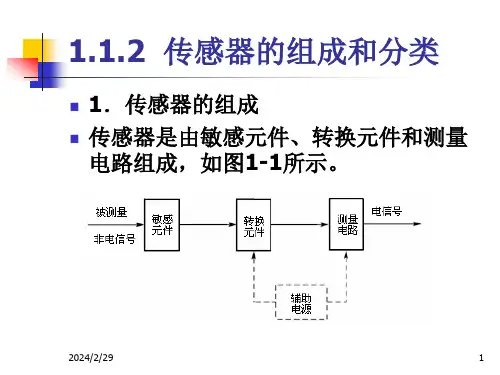
1．传感器的静态特性主要有那些？说明什么是线性度？传感器的特性主要是指传感器的输入（被测量）与输出（电量）的关系。

静态特性表示传感器在被测量各个值处于稳定状态时的输入输出关系。

也即当输入量为常量，或变化极慢时，这一关系就称为静态特性。

传感器的静态特性主要有：线性度、迟滞性、灵敏度、稳定性、重复性、阈值等。

传感器的静特性曲线可实际测试获得，用下列多项式程表示为：n n x a x a x a x a a y +++++= 332210式中y 为输出量、x 为输入量、0a 为零点输出、1a 为理论灵敏度、n a a a ,,32为非线性项系数。

在获得特性趋向之后，可以说问题已经得到解决。

但是为了标定和数据处理的方便，希望得到线性关系。

这时可采用各种方法，其中也包括硬件或软件补偿，进行显性化处理。

一般来说，这些办法都比较复杂。

所以在非线性误差不太大的情况下，总是采用直线拟合的方法来线性化。

在采用直线拟合线性化时，输出输入的校正曲线之间的最大偏差，就称为非线性误差，也就是线性度： max (/)100L L FS y γ=±⨯△%由此可见，非线性偏差的大小是以一定的拟合直线为基准直线而得来的。

拟合直线不同，非线性误差也不同。

所以，选择拟合直线的主要出发点，应是获得最小的非线性误差。

另外，还应考虑使用是否方便，计算是否简便。

2．什么是传感器的静态误差？传感器的静态误差是如何评定的？静态误差是指传感器在其全量程内任一点的输出值与其理论值的偏离程度。

静态误差的求取方法如下：把全部输出数据与拟合直线上对应值的残差，看成是随即分布，求出其标准偏差σ，即 21)y (11∑-==n i i n △σ 式中 i y △— 各测试点的残差；n —测试点数。

取2σ和3σ值即为传感器的静态误差。

静态误差也可用相对误差来表示，即%100)/3(⨯±=FS y σγ （1-15）静态误差也是一向综合指标，他基本上包括了前面叙述的非线性误差、迟滞误差、重复性误差、灵敏度误差等，若者几项误差是随机的、独立的、正态分布的，也可以把这几个单项误差综合而得，即：2222S R H L γγγγγ+++±=3.某测温系统由以下四个环节组成，各自的灵敏度如下：铂电阻温度传感器：0.45Ω/℃电桥： 0.02V/Ω放大器： 100(放大倍数)笔式记录仪： 0.2cm/V求：(1)测温系统的总灵敏度； (2)记录仪笔尖位移4cm 时，所对应的温度变化值。

第一章 传感器的一般特性2zz

第一章 传感器的一般特性2zz


7、漂移

漂移是指传感器的被测量不变，而其输出 量却发生了不希望有的改变。
y 灵敏度漂移
零点漂移 灵敏度漂移 时间漂移(时漂) 温度漂移(温漂)
2 1 零点漂移 O x
8 分辨力和阈值
(1)阈值：当传感器的输入从零开始缓慢增加时， 只有在达到了某一值后，输出才发生可观测的变化，这 个值说明了传感器可测出的最小输入量，称为传感器的 阈值。 (2)分辨力：当传感器的输入从非零的任意值缓慢 增加时，只有在超过某一输入增量后，输出才发生可观 测的变化，这个输入增量称为传感器的分辨力。
取较大者为
RMax
ΔRmax2 ΔRmax1
R ( R Max yFS ) 100%
x
6.稳定性 稳定性表示传感器在较长时间内保持 其性能参数的能力，故又称长期稳定性。 稳定性可用相对误差或绝对误差表示。 表示方式如： 个月不超过 %满量程输 出。有时也采用给出标定的有效期来表示。
第一章 传感器的一般特性
在工程应用中，任何测量装置性能的优劣总要 以一系列的指标参数衡量，通过这些参数可以方便地 知道其性能。这些指标又称之为特性指标。 传感器可看作二端口网络，即有两个输入端和 两个输出端，输出输入特性是其基本特性，可用静态 特性和动态特性来描述。
输入
传感器
输出
1. 1 传感器的静特性
九、抗干扰能力
设计、选用、购买
1、量程和范围
传感器所能测量的最大被测量（输入量）的数值称为测量上
限，最小被测量称为测量下限，上限与下限之间的区间，则 称为测量范围。

量程---测量上限与下限的代数差。
测量范围为-20～+20℃，量程为40℃； 测量范围为-5～+10g，量程为15g； 测量范围为100～1000Pa，量程为900Pa；
1 传感器的基础知识-半导体传感器原理与应用-李新-清华大学出版社

1 传感器的基础知识-半导体传感器原理与应用-李新-清华大学出版社

y=a0+a1x+a2x2+…….+anxn
线性模型： y=a0+a1x或y=ax ➢ 动态模型（输入信号随时间变化）： 微分方程
and n y / dtn a1dy / dt a0 y bmd mx / dtm b1dx / dt b0x c
当传感器的数学模型初值为0时，对其进行拉氏变换，可得
1、传感器的基础知识
取决于传感器本身，可通过传感器本身的改善来加以抑制， 有时也可以对外界条件加以限制。
冲振
外界影响
温度
电磁场
电源
输入
输出
Sensor
线性 迟滞 重复性
温漂 稳定性（零漂） 灵敏度
衡量传感器特性的主要技术指标
传感器的输入-输出关系
1、传感器的基本特性
➢ 传感器的数学模型 指传感器的输入输出关系。 ➢ 传感器的静态模型（输入信号不随时间变化）：
➢最小二乘法线性度
设拟合直线方程： y=kx+b
y
yi
若实际校准测试点有n个，则第i个校准
数据与拟合直线上响应值之间的残差为 0
Δi=yi-(kxi+b)
y=kx+b
xI
x
最小二乘拟合法
最小二乘法拟合直线的原理就是使 2i 为最小值，即
n
n
2
2i yi kxi b min
i 1
i 1
2i 对k和b一阶偏导数等于零，求出b和k的表达式
规定工作条件下，环境温度每变化1℃，零点输出变化（灵敏度变化） 与满量程输出（灵敏度）之比，称为零点温漂（灵敏度温漂）。
➢ 精度 表征测试系统的测量结果与被测量真值的符合程度。
方和根表示法：
传感器原理及应用(第三版)第1章

传感器原理及应用(第三版)第1章

=0.0987/（e-1）=5.75%（非线性误差最小，拟合精度最高）
三、精确度（精度）
精确度由三个指标：精密度、正确度和精确度 （一）精密度
它说明测量结果的分散性。即对某一稳定的对象（被测量）由 同一测量者用同一传感器和测量仪表在相当短的时间内连续反复测 量多次其测量量的分散程度。 愈小则说明测量越精密。
常数；对非线性
传感器而言，灵
敏度随输入量的
变化而变化。
从输出曲线看，
曲线越陡，灵敏
度越高。可以通
xmax
过作该曲线某一 点的切线的方法
x （作图法）求得 曲线上任一点的
灵敏度。
灵敏度太高，检测系统的稳定性将降低。
例1 ：已知某传感器静态特性方程y=ex，试分别用切线 法，端基法和最小二乘法，在0<x<1范围内拟合基准直 线方程，并求出相应的线性度。
电阻R/ 765 826 873 942 1032
电阻R随温度t的变化规律必须用MATLAB进行曲线拟合
1100
1000
900
800
700
20
40
60
80
100
例：一组测量数据的曲线拟合
已知一组（二维）数据，即平面上 n个点（xi,yi) i=1,…n，利用MATLAB，可以寻求到一个函数（曲线） y=f(x), 使 y=f(x)在某种准则下与所有数据点最为接近， 即曲线拟合得最好。
Y a1X a2 X 2 a4 X 4
（4）具有 X奇、偶次阶项的非线性[图1-1(d)]
Y a1X a2 X 2 a3 X 3 a4 X 4
上一页
下一页
返回
奇次项的曲 线在原点附 近较接近直 线
1-1测量的基本概念、测量误差1-2传感器及其基本特性

1-1测量的基本概念、测量误差1-2传感器及其基本特性


作图法求灵敏度过程 切点 y Δy
传感器 特性曲线
x1
y K x
0 Δx
xmax
x
2、分辨力：
指传感器能检出被测信 号的最小变化量，是有量纲 的数。当被测量的变化小于 分辨力时，传感器对输入量 的变化无任何反应。对数字 仪表而言，如果没有其他附 加说明，可以认为该表的最 后一位所表示的数值就是它 的分辨力。一般地说，分辨 力的数值小于等于仪表的最 大绝对误差。
传感器实例
温度传感器
压力传感器
液位传感器
三、传感器基本特性
传感器的特性一般指输入、输出特性。 包括：灵敏度、分辨力、线性度、稳定度、 电磁兼容性、可靠性等。
1、灵敏度 ：
灵敏度是指传感器在稳态下输出变化值与 输入变化值之比，用K 来表示：
dy y K dx x
（1－6）
对线性传感器而言，灵敏度为一常数；对非 线性传感器而言，灵敏度随输入量的变化而变 化。
产生粗大误差的一个例子
2.系统误差：
系统误差也称装置误差，它反映 了测量值偏离真值的程度。凡误差的 数值固定或按一定规律变化者，均属 于系统误差。
系统误差是有规律性的，因此可 以通过实验的方法或引入修正值的方 法计算修正，也可以重新调整测量仪 表的有关部件予以消除。
夏天摆钟变慢的原 因是什么？
3.随机误差
误差产生的因素：
1.粗大误差
明显偏离真值的误差称为粗大误差，也叫 过失误差。粗大误差主要是由于测量人员的粗 心大意及电子测量仪器受到突然而强大的干扰 所引起的。如测错、读错、记错、外界过电压 尖峰干扰等造成的误差。就数值大小而言，粗 大误差明显超过正常条件下的误差。当发现粗 大误差时，应予以剔除。
传感器与检测技术ppt课件第一章

传感器与检测技术ppt课件第一章


2024/2/29
16
1.2检测技术理论基础
1.2.2 测量方法
1) 直接测量、间接测量和组合测量 (又称联立 测量)。经过求解联立方程组，才能得到被测物理量的最后
结果，则称这样的测量为组合测量。
2) 偏差式测量、零位式测量与微差式测量
3) 等精度测量与非等精度测量
4) 静态测量与动态测量
2024/2/29
2024/2/29
23
2024/2/29
3
1.1.3 传感器基本特性
当传感器的输入信号是常量，不随时间变化时，其 输入输出关系特性称为静态特性。
传感器的基本特性是指系统的输入与输出关系特性 ，即传感器系统的输出信号y(t)和输入信号（被测 量）x(t)之间的关系，传感器系统示意图如下图所 示。
2024/2/29
4
1.1.3 传感器基本特性
2．传感器的分类
（1）按照其工作原理，传感器可分为电参数式(如电阻式、 电感式和电容式)传感器、压电式传感器、光电式传感器及 热电式传感器等。
（2）按照其被测量对象，传感器可分为力、位移、速度、 加速度传感器等。常见的被测物理量有机械量、声、磁、温 度和光等。
（3）按照其结构，传感器可分为结构型、物性型和复合型 传感器。物性型传感器是依靠敏感元件材料本身物理性质的 变化来实现信号变换，如：水银温度计。结构型传感器是依 靠传感器结构参数的变化实现信号变换，如：电容式传感器。
敏感元件输出的物理量转换成适于传输或测量电信号 的元件。
测量电路(measuring circuit)： 将转换
元件输出的电信号进行进一步转换和处理的部分，如 放大、滤波、线性化、补偿等，以获得更好的品质特 性，便于后续电路实现显示、记录、处理及控制等功 能。
第1章 传感器的特性

第1章 传感器的特性

29
3.重复性（Repeatability） 传感器在同一工 作条件下输入量 按同一方向(同为 正行程或同为反 行程)作全量程连 续多次变动时所 得特性曲线的不 一致程度。
重复性误差：
Rmax R 100% YFS
△Rmax：正（反）行程中的最大重复偏差
特性曲线一致性好, 重复性就好,误差就小。
3
传感器的特性：传感器所有性质的总称。 传感器的基本特性：输出/输入特性。
概述
静态特性 ： 被测参量基本不随时间变化或变化很缓慢时，传 感器的输出/输入特性。
动态特性 ：
被测参量随时间变化时 ，传感器的输出/输入特 性。
5
传感器的特性
1.1 传感器静态特性方程与特性曲线 1.2 传感器的静态特性 1.3 传感器的动态特性
取2σ或3σ值即为传感器静态误差。静态误差也 可用相对误差表示，即：
3 100% y FS
静态误差是一项综合性指标，基本上包含了前面 叙述的非线性误差、迟滞误差、重复性误差、灵敏度 误差等。所以也可以把这几个单项误差综合而得，即：
L H R S
2 2 2
（3-3）
32
1.2 传感器静态特性的主要指标
• 由于受很多因素的影响，会引起灵敏度变化从而产生灵敏 度误差，习惯上用相对误差表示
s
k k
100%
• 灵敏度的量纲： 输出的量纲/输入的量纲。V/℃、mv/g、A/g、mv/mm
• 能量控制型传感器，灵敏度与供给sensor的电源电压有关。 例如：100(mv/mm.V) 某位移传感器，当电源电压为1V时，每1mm位移的变化量 引起输出电压变化100mv。
|
温度稳定性（温漂）：传感器在外界温度变化情况下输 出量发生的变化，又称为温度漂移。 抗干扰能力稳定性：传感器对各种外界干扰的抵抗能力。
武汉大学传感器技术课件-传感器一般特性

武汉大学传感器技术课件-传感器一般特性

传感器技术
主讲人： 吴琼水
武汉大学电子信息学院
第1章 传感器的一般特性
1.1 传感器静态特性
静态特性指标
（1）线性度 （2）灵敏度 （3）精确度(精度) （4）最小检测量和分辨力 （5）迟滞 （6）重复性 （7）稳定性 （8）漂移
线性度(Linearity)
在规定的条件下，传感器静态校准曲线(实际曲线)与拟合直线间最大偏差 与满量程输出值的百分比称为线性度。
传感器技术
主讲人： 吴琼水
武汉大学电子信息学院
第1章 传感器的一般特性
1.1 传感器静态特性
静态特性指标
（1）线性度 （2）灵敏度 （3）精确度(精度) （4）最小检测量和分辨力 （5）迟滞 （6）重复性 （7）稳定性 （8）漂移
迟滞
传感器在输入量由小到大(正行程)及输入量由大到小(反行程)变化期间其输入 输出特性曲线不重合的现象称迟滞。
例：某电子秤： 增加砝码
电桥输出 减砝码输出
0 g —— 50g —— 100g —— 200g 0.5 mv --- 2.0mv -- 4.0mv --- 8.0mv 0.6 mv --- 2.2mv ---4.5mv --- 8.0mv
H
H max
/Y FS
100%
产生这种现象的主要原因是由于传感器敏感元件材 料的物理性质和机械另部件的缺陷所造成的，例如弹 性敏感元件弹性滞后、运动部件摩擦、传动机构的间 隙、紧固件松动等。
准确度
说明传感器输出值与真值的偏离程度。准确度是系统误差大小的标志。
精确度
是精密度与准确度两者的综合优良程度。
低精密度， 低正确度
高精密度， 低正确度
低精密度， 高正确度
第一章传感器技术基础知识

第一章传感器技术基础知识

频带：传感器增益保持在一定值内的频率范围为传感器频带 或通频带，对应有上、下截止频率。
时间常数：用时间常数τ来表征一阶传感器的动态特性。τ越小， 频带越宽。
固有频率：二阶传感器的固有频率ωn表征了其动态特性。
传感器的选用原则
与测量条件有关的因素 (1)测量的目的 (2)被测试量的选择 (3)测量范围 (4)输入信号的幅值，频带宽度 (5)精度要求 (6)测量所需要的时间
相应的响应曲线 ：
传感器存在惯性，它的输出不能立即复现输入信号，而是从零开 始，按指数规律上升，最终达到稳态值。 理论上传感器的响应只在t趋于无穷大时才达到稳态值，但实际上 当t=4τ时其输出达到稳态值的98.2%，可以认为已达到稳态。 τ越小，响应曲线越接近于输入阶跃曲线， 因此，τ值是一阶传感器重要的性能参数。
测量
测量是指人们用实验的方法，借助于一定的仪器或 设备，将被测量与同性质的单位标准量进行比较，
并确定被测量对标准量的倍数，从而获得关于被测
量的定量信息。
xnu或
x——被测量值；
n x u
u——标准量，即测量单位；
n——比值，含有测量误差。
测量过程
传感器从被测对象获取被测量的信息，建立起 测量信号，经过变换、传输、处理，从而获得 被测量量值的过程。
线性传感器
S y x
灵敏度是它的静态特性的斜率，即S为常数。
非线性传感器
它的灵敏度S为一变量，用下式表示。
S dy dx
传感器的灵敏度如图1-3所示。
Y
Y
S y - y0
Yo
x
X O
a）线形传感器
Байду номын сангаас
Y dy
dx S dy dx X
第1章 传感器的一般特性

第1章 传感器的一般特性


1.2.1 动态特性的一般数学模型

1、零阶传感器的数学模型
a0Y (t ) b0 X (t )
Y (t )
b0 X (t ) KX (t ) a0
例3 图1-8所示线性电位器是一个 图1-8 线性电位器 零阶传感器。设电位器的阻值 沿长度L是线性分布的，则输出电压和电刷位移之间的关系为
0
1
1 2
1 2 2 1 2
1 d 2T1 2 dT1 T1 T0 2 2 0 dt 0 dt
1.2.2 传递函数
传递函数是输出量和输入量之间关系的数学表示。如 果传递函数已知，那么由任一输入量就可求出相应输出量。 传递函数的定义是输出信号与输入信号之比。 (an Dn an1Dn1 a1D a0 )Y (t )
根据一阶线性微分方程，如果已知T0的变化规律，求出微 分方程式的解，就可以得到热电偶对介质温度的时间响应。
1.2.1 动态特性的一般数学模型

3、二阶传感器的数学模型
( D2
d 2Y (t ) d Y (t ) a2 a1 a0Y (t ) b0 X (t ) 2 dt dt a0 b0 a1 / 2 a0 a2 0 K a2 a0
i 1
n
2
n 1
重复性所反映的是测量结果 偶然误差的大小，而不表示与真值 之间的差别。有时重复性虽然很好， 但可能远离真值。
图1-7 传感器的重复性
1.1.2 静态特性指标


7、零点漂移 传感器无输入(或某一输入值不变)时，每隔一段时间进 行读数，其输出偏离零值(或原指示值)，即为零点漂移。 Y0 零漂 100% YFS 8、温漂 温漂表示温度变化时，传感器输出值的偏离程度。一般 以温度变化1 ℃输出最大偏差与满量程的百分比来表示。

第1章-传感器的特性


j=1, 2, …, m;
n ——
yji的含义是,若输入值x=xj,则在相同条件下进行n次 重复试验,获得n个输出值yj1～yjn
i —— y j ——算术平均值。
或
S Wn dn
(1.9)
第1章
式中： Wn——极差,是指某一测量点校准数据的最大
dn——极差系数。 极差系数可根据所用数据的数目n由表1.4查得。理 论与实践证明,n不能太大,如n大于12,则计算精度变差, 这时要修正dn 。
第1章 表1.4
第1章
3.
迟滞表明传感器在正（输入量增大）、反（输入
量减小）行程期间,输出-输入曲线不重合的程度。也就 是说,对应于同一大小的输入信号,传感器正、反行程的 输出信号大小不相等。迟滞是传感器的一个性能指标, 它反映了传感器的机械部分和结构材料方面不可避免
的弱点,如轴承摩擦、灰尘积塞、间隙不适当,元件磨蚀、
Δi=yi-(b+kxi)
第1章
n
按 最 小 二 乘 法 原 理 , 应 使 i2 最 小 。 故
n
n
i 1
由 i2 [ yi (kxi b)]2 min ,分别对k和b求一阶
偏导i数1 并令i其1 等于零，即可求得k和b：
n
k
n
xi yi xi2 (
xi xi )2
n b
设ai≥0, a0≥0。
1) 这种情况见图1.2(a)。此时
a0=a2=a3=…=an=0 于是
y=a1x
(1.2)
因为直线上任何点的斜率都相等,所以传感器的灵
敏度为
a1= y =k=常数（1.3 x
第1章
2) 输出这种情况见图1.2（b）。此时,在原点附近相当范 围内曲线基本成线性,式（1.1）只存在奇次项：

大学物理实验报告23——PN结温度传感器特性1

天津大学物理实验报告姓名： 专业： 班级： 学号： 实验日期： 实验教室： 指导教师：【实验名称】 PN 结物理特性综合实验 【实验目的】1. 在室温时，测量PN 结电流与电压关系，证明此关系符合波耳兹曼分布规律2. 在不同温度条件下，测量玻尔兹曼常数3. 学习用运算放大器组成电流-电压变换器测量弱电流4. 测量PN 结电压与温度关系，求出该PN 结温度传感器的灵敏度5. 计算在0K 温度时，半导体硅材料的近似禁带宽度 【实验仪器】半导体PN 结的物理特性实验仪 资产编号：××××，型号：×××（必须填写） 【实验原理】1．PN 结的伏安特性及玻尔兹曼常数测量 PN 结的正向电流-电压关系满足：]1)/[exp(0-=kT eU I I (1)当()exp /1eU kT >>时,(1)式括号内-1项完全可以忽略，于是有：0exp(/)I I eU kT = (2)也即PN 结正向电流随正向电压按指数规律变化。

若测得PN 结I U -关系值，则利用(1)式可以求出/e kT 。

在测得温度T 后，就可以得到/e k ，把电子电量e 作为已知值代入，即可求得玻尔兹曼常数k 。

实验线路如图1所示。

2、弱电流测量LF356是一个高输入阻抗集成运算放大器，用它组成电流-电压变换器(弱电流放大器),如图2所示。

其中虚线框内电阻r Z 为电流-电压变换器等效输入阻抗。

运算放大器的输入电压0U 为：00i U K U =- (3)式(3)中i U 为输入电压，0K 为运算放大器的开环电压增益，即图2中电阻f R →∞时的电压增益（fR 称反馈电阻）。

因而有：0(1)i i s ffU U U K I R R -+==(4)由（4）式可得电流-电压变换器等效输入阻抗x Z 为1i f f x sU R R Z I K K ==≈+ (5)由(3)式和(4)式可得电流-电压变换器输入电流s I 与输出电压0U 之间的关系式，即：图1 PN 结扩散电源与结电压关系测量线路图1MLF356-+74+15V-15V236ecbV 1V 2100Ω1.5VTIP31TIP31ebc LF35612348765R fI sK o-+U 0U iZ rI s图2 电流－电压变换器i s frU UI Z R ==-(6)只要测得输出电压0U 和已知f R 值，即可求得s I 值。

第1讲传感器的输入输出特性


满量程输出电压
2.2 传感器的主要静态性能指标及其计算
2.2.6 线性度
•
对于非理想直线特性的传感器，需要进行非线 性校正，常采用以下方法。
2.2 传感器的主要静态性能指标及其计算
2.2.6 线性度-端点法
实际特性上分别 对应于测量下限xmin 和测量上限xmax的点A 和B的连线称端点拟 合直线。
2.2 传感器的主要静态性能指标及其计算
2.2.4 零漂及温漂
如温度系数（温漂） a）零点温度系数：在工作温度范围内，环境温度 每变化1℃时，引起的零点输出变化与额定输出的百分 比，称为零点温度系数。
y 0 a 1 0 0 % 0 T y F S
b）灵敏度温度系数：当温度升高时，系统的灵敏 度变化，温度每升高1℃，灵敏度系数变化的百分比， 称为灵敏度温度系数。
2.2 传感器的主要静态性能指标及其计算
2.2.11 可靠性：装置在规定时期内，及在保持其运
行指标不超限的情况下执行其功能的性能。包括： a) 平均无故障时间（Mean Time Between Failure, MTBF）：表示相邻两次故障间隔时间的平均值 b) 可信任概率P：表示在给定时间内误差保持在规 定限度内的概率。概率P越大，系统可靠性越高，但是会 增加成本。P的最佳值为0.8～0.9。 c) 故障率或失效率（1/MTBF）：平均无故障时间的 倒数。 d) 有效度或可用度A：用MTTR代表平均修复时间 (Mean Time to Repair)，若修复时间长，则有效使用时 M T B F 间短，A表示为 A =
m a x nm 1 0 0 % a x y F S
2.2 传感器的主要静态性能指标及其计算
2.2.9．准确度

传感器静态特性的指标及公式

传感器静态特性的指标及公式1. 灵敏度(Sensitivity)灵敏度是指传感器输出量对输入量变化的响应程度，也可以理解为传感器输出信号的变化量与输入量变化的比值，通常用一定范围内最大输出变化与输入量变化的比值表示。

灵敏度的计算公式如下：S=∆Y/∆X其中，S为灵敏度，∆Y为输出量的变化值，∆X为输入量的变化值。

2. 线性度(Linearity)线性度是指传感器输出量与输入量之间的线性关系程度，即输出量的变化是否与输入量的变化成正比。

线性度可以通过传感器的线性度误差来描述，通常用百分比或者绝对值来表示。

线性度的计算公式如下：L=，(Y实测-Y理论)/Y理论，×100%其中，L为线性度，Y实测为实际测量输出量，Y理论为理论预期输出量。

3. 零偏误差(Zero Offset Error)零偏误差是指在无输入量时，传感器的输出量和零点之间的差值。

零偏误差可以通过传感器的测量输出量和零输入量的差值来计算，常表达为绝对值或者百分比。

零偏误差的计算公式如下：E=，Y测-Y零，×100%其中，E为零偏误差，Y测为实际测量输出量，Y零为零输入量。

4. 分辨力(Resolution)分辨力是指传感器能够分辨最小输入量变化的能力，通常是输出量变化的最小有效值。

分辨力可以通过量程与分辨率的比值来计算，分辨率可以是数字量的最小变化值，也可以是模拟量的最小变化量。

分辨力的计算公式如下：R=量程/分辨率其中，R为分辨力，量程为传感器的工作范围，分辨率为传感器输出量的最小变化值。

5. 稳定性(Stability)稳定性是指传感器输出量在一定环境条件下长时间内保持不变的能力，通常用输出量的标准差来衡量。

稳定性可以通过传感器长时间测量得到的输出量数据的标准差来计算，也可以通过计算测量输出量序列的方差来估计。

稳定性的计算公式如下：S=√[Σ(Yi-Ȳ)²/(N-1)]其中，S为稳定性，Yi为第i个测量输出量，Ȳ为所有测量输出量的平均值，N为测量次数。

第1章 传感器的一般特性-2


31
（3） 传感器的时域动态性能指标 ：
①上升时间tr ②峰值时间tp ③调节时间ts ④超调量σ%
32
tr-上升时间,系统输出响应从零开始第一次上升到稳态值时间。 tp-峰值时间，系统输出响应从零开始第一次到达峰值时间。 ts-调节时间，系统输出响应达到并保持在稳态值±5%(±2%)误差 33
yt y20 t
6
静态测量不确定度
又称静态误差，指传感器在其全量程内任 一点的输出值与其理论值的可能偏离程度。 常用标准差σ计算
1 n 2 (yi ) n 1 i 1
(2 ~ 3) 100% YFS
7
例子：
• 测控技术与仪器专业——“量子”科技创 新团队研制了一台称重传感器的样机，对 该传感器进行校准实验后获得下表所列的 数据。 • 试根据表中的数据确定该传感器的线性度 、灵敏度、迟滞等静态特性参数指标。
Lmax L 100% YFS
2
• 线性度计算时拟合直线常用的拟合方法有：
– – – – –
y YF S
理论拟合 过零旋转拟合 端点连线拟合 端点平移拟合 最小二乘拟合
Lm ax
y y
y YF S
Lm ax
L1 ＝ Lm ax
YF S
YF S
L3 ＝ Lm ax
28
(2） 二阶传感器的单位阶跃响应
二阶传感器的微分方程为
d 2 y (t ) dy(t ) 2 2 2 y ( t ) 0 0 0 kx(t ) 2 dt dt
设传感器的静态灵敏度k=1，其二阶传感器的传递函数为
2 0 H ( s) 2 2 s 20 s 0
9
例子：热电偶测温
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二、传感器的动态特性
动态特性指传感器对随时间变化的输入量的响应特性。 被测量随时间变化的形式可能是各种各样的，只 要输入量是时间的函数，则其输出量也将是时间的函 数。通常研究动态特性是根据标准输入特性来考虑传 感器的响应特性。 标准输入有三种：
正弦变化的输入 阶跃变化的输入 线性输入
动态测温的响应特性
Lmax L 100% YFS Lmax静态曲线与拟合直线之 间 的最大偏差的绝对值 YFS 满量程输出值
2．迟滞
传感器在正(输入量增大)反 （输入量减小）行程中输出 输入曲线不重合称为迟滞。 迟滞特性如图所示，它一般 是由实验方法测得。迟滞误 差一般以满量程输出的百分 数表示,即
yFS
x
△Rmax1正行程的最大重复性偏差绝对值， △Rmax2反行程的最大重复性偏差绝对值。
4．灵敏度
灵敏度是传感器对被测量变化的反应能力，是传 感器的基本指标。 传感器输出的变化量 Δy与引起该变化量的输入变 化量 Δ x之比即为其静态灵敏度，其表达式为
K=Δy/Δx
可见，传感器特性曲线的斜率就是其灵敏度。对线性 特性的传感器，其特性曲线的斜率处处相同，灵敏度 k是一常数。一般要求选灵敏度高的传感器。
y ⊿Hmax
0
迟滞特性
x
H max H 100% y FS
式中△ Hmax—正反行程间输出的最大差值绝对值。
3．重复性
重复性是指传感器在输入 按同一方向连续多次变动时 所得特性曲线不一致的程度。 重复性误差可用正反行程的最 大偏差绝对值表示，即
y
⊿Rmax2
⊿Rmax1
0
Rmax R 100% YFS
传感器的基本特性
传感器特性主要是指输出与输入之间的关系。 当输入量为常量，或变化极慢时，这一关系 称为静态特性； 当输入量随时间较快地变化时，这一关系称 为动态特性。 传感器的静态特性只是动态特性的一个特例。
一、静态特性技术指标
1．线性度
在采用直线拟合线性化时，输出-输入的关系曲线 与其拟合直线之间的最大偏差，就称为非线性误差或线 性度。 通常用相对误差 γL 表示：
5．分辨率
分辨率表示传感器能检测到输入量的最小变化能力。 当传感器的输入量缓慢变化, 超过某一增量时，传感器 才能检测到输入量的变化，这个输入量的增量称为传感 器的分辨率。
6．稳定性
稳定性表示在较长时间内传感器对于大小相同的 输入量，其输出量发生漂移变化的程度，一般在室温 条件下，经过规定的时间间隔后传感器输出的差值称 为稳定性误差。
测量显示温度到达稳定的时间与传感器时间常数有关， 时间常数反映了传感器惯性的大小。
作业
• 某学生做电子秤实验，交叉点为测量数据，根据实验数据 画出如图所示特性曲线，要求：（1）根据特性曲线计算 电子秤的灵敏度，（2）根据特性曲