热力学第一定律-广西师范大学化学与药学学院

格式：pdf
大小：154.41 KB
文档页数：3

下载文档原格式

04 热力学第一定律

一、理想气体内能
1、焦耳实验 ┅ ┅ 自由膨胀过程 W= 0，Ｑ = 0
C
A 焦耳实验理想气体宏观特性：满足pV=νRT关系；满足道尔顿分压定律；满足阿伏加德罗定律；满足焦耳定律 U＝U(T)。
22
d U= 0
U1 (T1 ,V 1) ＝U2 (T2 ,V2)＝常量 B 证明：理想气体内能仅是状态(Ｔ)的函数，与体积无关，称为焦耳定律
Q是系统所吸收的能量，W是外界对系统所作的功
dU dQ dW或dQ dU pdV
（1）确定了内能变化的两种量度（功和热量），是说明：能量转换和守恒定律在热力学过程中的应用，功热转换是通过内能变化实现的。
( 2) W系统 W外界 Q U
第一类永动机是不可能制造的┅ ┅热力学第一定律的另一表述系统做功（Ｗ）┅ ┅Ｖ（3）功、内能和热量变化正负号内能（Ｕ）┅ ┅Ｔ的判断热量（Ｑ）┅ ┅定律
p
dQ vC p , m dT Q v C p , m dT
T1 T2
0
V
W

V2
V1
PdV P (V2 V1 ) R(T2 T 1) RT
在相同情况下质量扩大一倍时，强度量不变。
如前面提到的：P，F，σ，E等都是强度量
10
四、热量与热质说
热量：它是从高温物体传递给
低温物体的能量
T1 T2
热量是过程量功与热量的异同
T1 Q T2
热质说 1）过程量：与过程有关； 2）等效性：改变系统热运动状态作用相同； 1卡 = 4.18 J ， 1 J = 0.24 卡 3）功与热量的物理本质不同 . 功宏观运动分子热运动热量分子热运动分子热运动

物理化学：热力学第一定律PPT课件

要的热量为Q，则就定义
1 n
δQ p dT
为该物质在该温度
下的摩尔定压热容，以 C p , m 表示，
Cp,m
1 δQp n dT
对恒压过程
δ Q p d H p n d H m ,p
代入有
C p ,m
1H n Tp
H m Tp
—— C p , m 定义式
单位： Jm o l1K 1
(2) 应用——计算单纯pVT 过程H
第二章热力学第一定律
热力学是自然科学中建立最早的学科之一
1. 第一定律：能量守恒，解决过程的能量衡算问题（功、热、热力学能等）
2. 第二定律：过程进行的方向判据 3. 第三定律：解决物质熵的计算
热力学基本定律是生产经验和科学实验的总结，它们不能用其它理论方法加以证明，但其正确性毋庸置疑。需要指出：（1）经典热力学研究含有大量质点的宏观系统：其原理、结论不能用于描述单个的微观粒子；（2）经典热力学只考虑平衡问题：只考虑系统由始态到末态的净结果，并依此解决诸如过程能量衡算、过程的方向、限度的判断等热力学问题，至于由始态到末态的过程是如何发生与进行的、沿什么途径、变化的快慢等等一些问题，经典热力学往往不予考虑。
W p a m b V 2 V 1p V 2 V 1 p 1 V 1 p 2 V 2 由热力学第一定律可得: Q p UW =U 2 p2V 2 U 1 p1 V 1
定义 : HdefU pV
H为焓，为状态函数，广延量，单位 J Qp H δQp dH
即恒压热与过程的焓能变在量值上相等
注：H 的计算的基本公式： H= U+ (pV) 恒压过程 H = Q
§2.1 基本概念和术语

第二章热力学第一定律

3．0.1kg C6H6(l)在 pӨ，沸点 353.35K 下蒸发，已知 l H m (C6H6) =30.80 kJ mol-1。
___（上升，下降，不变） _，其（
7．在室温常压下，H2（g）经节流膨胀后温度_ 样条件下，空气经节流膨胀后温度___ _。
H ）T_ P
_0，同
8． (1)某反应在恒压 P，绝热，W，=0 的条件下进行，系统温度由 T1 升到 T2，则过程△H ____0。
， (2)上述反应在恒 T，P，W =0 的条件下进行，则△H____0。
6．任何气体经绝热自由膨胀，温度不变 (
7． H2O(l)的标准摩尔生成焓△fHӨm 也是同温度下 H2(g)的标准摩尔燃烧焓 (
四、计算题
1．1mol理想气体由100kPa、10dm3恒压压缩到1dm3，再恒容升压到1000kPa。试
5
广西师范大学精品课程……………《物理化学》
计算整个过程的W、Q、U、H。 2．在 298K 时，有 2molN2(g)，始态体积为 15dm3，保持温度不变，经下列三个过程膨胀到终态体积为 50dm3，计算各过程的 U ， H ，W 和 Q 的值。设气体为理想气体。 (1) 自由膨胀； (2) 反抗恒定外压 100kPa 膨胀； (3) 可逆膨胀。
2．一理想气体在恒定外压为 1.01×102 kPa 下，从 10 dm3 膨胀到 16 dm3，同时吸热 125 J。则此过程的 ΔU 为( (A) -248 J (B) +842 J )焦耳。 (C) -482 J (D) +482 J
3．一理想气体在恒定外压为 1.01×102 kPa 下，从 10 dm3 膨胀到 16 dm3，同时吸热 125 J。则此过程的 ΔH 为( (A) +215 J (B) -125 J ) )焦耳。 (C) -215 J (D) +125 J

什么是热力学第一定律及第二定律

什么是热力学第一定律及第二定律下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!热力学第一定律和第二定律是热力学领域中两个非常重要的基本定律，它们为我们解释了自然界中能量转化和热力学系统的行为提供了基本原理。

热力学第一定律课件

的增加。
(3)若过程的始末状态物体的内能不变,即 ΔU=0,则 W+Q=0 或 W=-Q,
外界对物体做的功等于物体放出的热量。
4.判断是否做功的方法
一般情况下外界对物体做功与否,需看物体的体积是否变化。
(1)若物体体积增大,表明物体对外界做功,W<0;
(2)若物体体积变小,表明外界对物体做功,W>0。
为另一种形式,或者从一个物体转移到别的物体,在转化或转移的过程中,能
量的总量保持不变。
2.意义
(1)能量守恒定律告诉我们,各种形式的能量可以相互转化。
(2)各种互不相关的物理现象——力学的、热学的、电学的、磁学的、
光学的、化学的、生物学的等可以用能量守恒定律联系在一起。
三、永动机不可能制成
1.第一类永动机:人们设想中的不需要任何动力或燃料,却能不断地对
提示前者能制成而后者不能制成。这是因为可以用太阳能、电能等
能源代替石油能源制造出太阳能汽车、电动汽车等,但是不消耗任何能量
的汽车不可能制成,因为它违背能量守恒定律。
2.热力学第一定律与能量守恒定律是什么关系?
提示能量守恒定律是各种形式的能相互转化或转移的过程,总能量保
持不变,它包括各个领域,其范围广泛。热力学第一定律是物体内能与其他
(2)突破了人们关于物质运动的认识范围,从本质上表明了各种运动形
式之间相互转化的可能性。能量守恒定律比机械能守恒定律更普遍,它是物
理学中解决问题的重要思维方法。能量守恒定律与细胞学说、生物进化论
并称 19 世纪自然科学中三大发现,其重要意义由此可见。
(3)具有重大实践意义,即彻底粉碎了永动机的幻想。
外做功的机器。
2.第一类永动机不可制成的原因:违背了能量守恒定律。

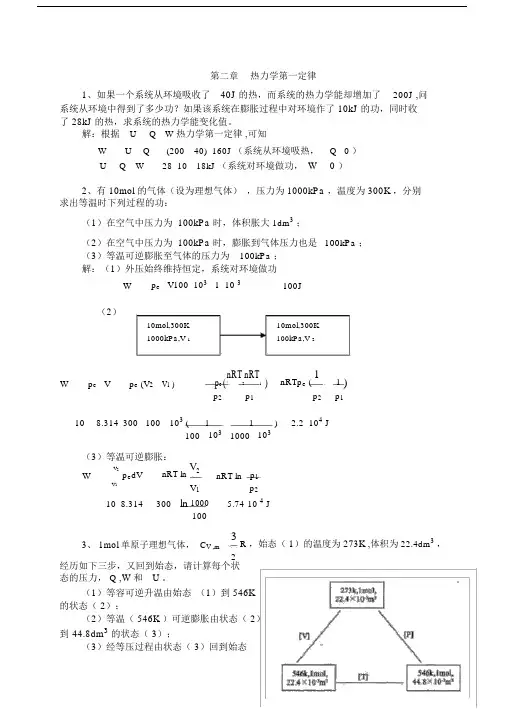
(完整版)第二章热力学第一定律.doc

第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热，而系统的热力学能却增加了200J ,问系统从环境中得到了多少功？如果该系统在膨胀过程中对环境作了 10kJ 的功，同时收了 28kJ 的热，求系统的热力学能变化值。

解：根据U Q W 热力学第一定律,可知W U Q (200 40) 160J （系统从环境吸热，Q 0 ）U Q W 28 10 18kJ （系统对环境做功，W 0 ）2、有 10mol 的气体（设为理想气体），压力为 1000kPa ，温度为 300K ，分别求出等温时下列过程的功：（1）在空气中压力为 100kPa 时，体积胀大1dm3；（2）在空气中压力为 100kPa 时，膨胀到气体压力也是100kPa ；（3）等温可逆膨胀至气体的压力为100kPa ；解：（1）外压始终维持恒定，系统对环境做功W p e V100 103 1 10 3 100J（2）10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000（3）等温可逆膨胀：V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体，C V ,m 3R ，始态（1）的温度为273K ,体积为 22.4dm3，2经历如下三步，又回到始态，请计算每个状态的压力， Q ,W和U 。

（1）等容可逆升温由始态（1）到 546K 的状态（ 2）；（2）等温（ 546K ）可逆膨胀由状态（ 2）到44.8dm3的状态（ 3）；（3）经等压过程由状态（ 3）回到始态（ 1）；解：（1）等容可逆升温过程：W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12（2）等温可逆膨胀过程：U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J（3）等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下， 1molZn (s) 溶于足量稀盐酸中，置换出 1molH 2 ( g) ，并放热 152kJ 。

热力学第一定律课件

1．不同形式的能量之间可以相互转化． (1)各种运动形式都有对应的能，如机械运动对应机械能，分子热运动对应内能等． (2)不同形式的能量之间可以相互转化，如“摩擦生热”机械能转化为内能，“电炉取热”电能转化为内能等．
2．能量守恒定律及意义．各种不同形式的能之间相互转化时保持总量不变．意义：一切物理过程都适用，比机械能守恒定律更普遍，是 19 世纪自然科学的三大发现之一．
2．判断是否做功的方法．一般情况下外界对系统做功与否，需看系统的体积是否变化． (1)若系统体积增大，表明系统对外界做功，W<0； (2)若系统体积变小，表明外界对系统做功，W>0.
【典例 2】一定量的理想气体在某一过程中，从外界吸收热量 2.5×104 J，气体对外界做功 1.0×104 J，则该理想气体的( )
1．对热力学第一定律的理解． (1)对ΔU＝W＋Q 的理解：做功和热传递都可以改变内能，如果系统跟外界同时发生做功和热传递的过程，那么外界对系统所做的功 W 加上物体从外界吸收的热量 Q 等于系统内能的增加ΔU，即ΔU＝Q＋W.
(2)对ΔU、Q、W 符号的规定． ①功 W：外界对系统做功，W>0，即 W 为正值；系统对外界做功，W<0，即 W 为负值． ②热量 Q：系统吸热为正：Q>0；系统放热为负：Q<0. ③内能变化：系统内能增加，ΔU>0，即ΔU 为正值；系统内能减少，ΔU<0，即ΔU 为负值．
解析：根据太阳能的工作原理可知，太阳能热水器把太阳能转化为内能，所以 A 正确；风力发电是通过电磁感应将风能转化为电能，所以 B 正确；电风扇是将电能转化为机械能，所以 C 正确；蜡烛燃烧是将化学能转化为内能，所以 D 错误．本题选择错误的，故选 D.

热力学第一定律精选全文完整版

可编辑修改精选全文完整版热力学第一定律科技名词定义中文名称：热力学第一定律英文名称：first law of thermodynamics其他名称：能量守恒和转换定律定义：热力系内物质的能量可以传递，其形式可以转换，在转换和传递过程中各种形式能源的总量保持不变。

概述热力学第一定律热力学第一定律：△U=Q+W。

系统在过程中能量的变化关系英文翻译：the first law of thermodynamics简单解释在热力学中，系统发生变化时，设与环境之间交换的热为Q（吸热为正，放热为负），与环境交换的功为W（对外做功为负，外界对物体做功为正），可得热力学能（亦称内能）的变化为ΔU = Q+ W或ΔU=Q-W物理中普遍使用第一种，而化学中通常是说系统对外做功，故会用后一种。

定义自然界一切物体都具有能量，能量有各种不同形式，它能从一种形式转化为另一种形式，从一个物体传递给另一个物体，在转化和传递过程中能量的总和不变。

英文翻译：The first explicit statement of the first law of thermodynamics, byRudolf Clausiusin 1850, referred to cyclic thermodynamic processes "In all cases in which work is produced by the agency of heat, a quantity of heat is consumed which is proportional to the work done; and conversely,by the expenditure of an equal quantity of work an equal quantity of heat is produced."基本内容能量是永恒的，不会被制造出来，也不会被消灭。

ppt热力学第一定律

dH d(U pV ) dU pdV Vdp
系统由始态到末态旳焓变
H U ( pV )4. Q来自 U ，Qp H 两关系式旳意义
特定条件下，不同途径旳热已经分别与过程旳热力学能变、焓变相等，故不同途径旳恒容热相等，不同途径旳恒压热相等，而不再与途径有关。
把特殊过程旳过程量和状态量联络起来。
状态函数旳特征可描述为：异途同归，值变相等；周而复始，数值还原。
状态函数在数学上具有全微分旳性质。
（2）广度量和强度量用宏观可测性质来描述系统旳热力学状态，
故这些性质又称为热力学变量。可分为两类：
广度性质（extensive properties）又称为容量性质，它旳数值与系统旳物质旳量成正比，如体积、质量、熵等。这种性质有加和性。
系统始态为a压力为pa；末态为z压力为pz，
pz＝1/5pa 。
可逆过程系统对环境做最大功（相反过程环境对系统作最小功）。
3.理想气体恒温可逆过程
可逆过程,外压和内压相差无穷小
δWr
pdV ,Wr
V2 V1
pdV
理想气体恒温膨胀,则
Wr
nRT
V2 V1
dV V
nRTlnV2 V1
物理化学
第二章热力学第一定律
The First Law of Thermodynamics
学习要求：
了解热力学基本概念、热力学能和焓旳定义；掌握热力学第一定律旳文字表述及数学表述。了解热与功旳概念并掌握其正、负号旳要求；掌握体积功计算，同步了解可逆过程旳意义特点。要点掌握利用热力学数据计算在单纯pVT 变化、相变化、化学变化过程中系统旳热力学能变、焓变以及过程热和体积功。
( H p

热力学第一定律课件

• 在气泡缓慢上升的过程中，气泡外部的压强逐渐减小，气泡膨胀，对外做功，故气泡中空气分子的内能减小，温度降低．但由于外部恒温，且气泡缓慢上升，故可以认为上升过程中气泡内空气的温度始终等于外界温度，内能不变，故须从外界吸收热量，且吸收的热量等于对外界所做的功．答案为B.
• 【答案】 B
【方法总结】
• 【答案】 C
• 【方法总结】 • 应用热力学第一定律解题的一般步骤： • (1)根据符号法则写出各已知量(W、Q、ΔU)的正、负； • (2)根据方程ΔU＝W＋Q求出未知量； • (3)再根据未知量结果的正、负来确定吸热、放热情况或做
功情况或内能增减情况．
•
热力学第一定律与气体的综合应用
•
一个气泡从恒温水槽的底部缓慢向上浮起，(若
在理想气体状态发生变化时，应用热力学第一定律的关
键是：
(1)理想气体的内能完全由温度来决定．
(2)注意应用理想气体状ຫໍສະໝຸດ 方程p1V1 T1＝
p2V2 T2
分析状态参量
的变化．
(3)理想气体状态变化时，体积变大，气体对外做功
W<0；体积变小，外界对气体做功W>0(自由膨胀例外)．且
在p-V图中，p-V图线下方的“面积”表示功的多少．如图
不计气泡内空气分子势能的变化)则( )
• A．气泡对外做功，内能不变，同时放热
• B．气泡对外做功，内能不变，同时吸热
• C．气泡内能减少，同时放热
• D．气泡内能不变，不吸热也不放热
• 【解析】气泡上升过程中，由于压强减小，体积增大，故对外做功，缓慢上升指有时间发生热传递，可认为温度是不变的．
• A．A中水银的内能增量大于B中水银的内能增量 • B．B中水银的内能增量大于A中水银的内能增量 • C．A和B中水银体积保持不变，故内能增量相同 • D．A和B中水银温度始终相同，故内能增量相同

热力学第一定律

• 定义： ξ =
o nB − nB
νB
• B 为参与反应的任何物质；νB参与反应各物的计量系数，对反应物为负，对产物为正，无量纲。 • 对同一化学反应， ξ的值与反应计量方程式的写法有关，而与选取参与反应的哪一种物质无关。 • ξ的值可正，可负，可为0，也可大于1。
• 当反应进度∆ξ = 1 mol时，化学反应进行了1 mol 的反应进度，简称摩尔反应进度。 • 摩尔反应进度时的等压反应热∆rH称为摩尔反应焓(变)，用∆rHm表示。
• ∆rUm：表示等温等容下按给定的反应方程式完成
ξ＝1 mol反应的QV
• 2) 标准态
• 标准态的规定：气体物质为标准压力p°和反应温度下，纯的理想气体。 • 液体或固体物质均为标准压力p°和某反应温度下纯的液体或固体物质。
• 3) 标准摩尔反应焓（变）∆ r H (T )
o m
• 某温度下，反应各物均处于标准状态，进行 ξ ＝ 1mol的反应热。 aA + bB = yY + zZ
• 1）气相反应 • 参与反应各物均为气体，称为气相反应。若反应系统压力不太高，温度不太低，还可视为理想气体反应。则等温下： • ∆(pV) = (∑nB(产物) – ∑ nB(反应物) )RT • • = (∑νB)RT = (∆n)gRT Qp= QV + (∆n)gRT • (∆n)g是指气体物的反应前后的计量系数之差。 • 该式对气相反应适用，或有气体物质同时有固体物或液体物参与的复相反应。
石墨,1p 石墨 CO2 (g,1p0) C (石墨 0) +O2 ∆rHm°(298.15K)= –393.5 kJ.mol-1 (g,1p0) (298.15K, 1p0)

热力学第一定律(物理化学)

特定条件下，不同途径的热已经分别与过程的热力学能变、焓变相等，故不同途径的恒容热相等，不同途径的恒压热相等，而不再与途径有关。把特殊过程的过程量和状态量联系起来。
4. ，两关系式的意义
在100kpa、100oc下，1mol液态水变成水蒸气需吸热40.65KJ，若将H2O(g)看作理想气体，试求系统的
(温度变化很小)
平均热容定义：
单位
1.6 热容（heat capacity）
1.5 热容（heat capacity）
单击此处添加小标题
单击此处添加小标题
单击此处添加小标题
添加标题
规定物质的数量为1 mol的热容。
摩尔热容Cm：
单位为：。
比热
打开率
35%
25%
20%
03
单击此处添加小标题
04
热容与温度的函数关系因物质、物态和温度区间的不同而有不同的形式。例如，气体的等压摩尔热容与T 的关系有如下经验式：
热容与温度的关系：
或
式中a,b,c,c’,... 是经验常数，由各种物质本身的特性决定，可从热力学数据表中查找。
理想气体恒容变温过程
对理想气体，
对理想气体，
2.等外压膨胀（pe保持不变）
因为
dWe,1 = pedV =0
dWe,2 = pe(V2- V1)
1．3 可逆过程和最大功 —理想气体在不同过程中的体积功
功与过程
外压比内压小一个无穷小的值
功与过程
外压比内压小一个无穷小的值
添加标题
外相当于一杯水，水不断蒸发，这样的膨胀过程是无限缓慢的，每一步都接近于平衡态。所作的功为：
DU=Q +W
第一章

大学热学第十讲热力学第一定律课件

烹饪
热力学第一定律可以解释烹饪过程中食物热量的变化，例如烤肉时肉质的熟
度和香味的形成。
取Hale Waihona Puke 与制冷在家居环境中，利用热力学第一定律可以优化供暖和制冷系统的效率，降低
能源消耗。
热水供应
在日常生活中，利用热力学第一定律可以更有效地加热和利用热水，例如在
太阳能热水器中。
在工程领域的应用
能源转换
02
平衡态是热力学系统的一种稳定状态，系统在平衡态时，宏观
物理量如温度、压力、体积等均到达稳定值。
平衡态是热力学过程进行的前提和基础，是研究热力学过程的
03
重要概念。
热力学的过程与状态
01
热力学过程是指系统状态随时间的变化过程，包括等温过程、等压过程、绝热过程等。
02
状态是指系统在某一时刻的宏观物理量，如温度、压力、体积等。
适用范围
• 热力学第一定律适用于宏观、可逆、封闭或开放的热力学系统。它不仅适用于理想气体，也适用于其他物质形态，如液体、固体和等离子体等。
02
热力学第一定律的历史与发展
早期发展
热力学的起源
热力学作为一门科学，起源于18世纪的工业革命时期，当时人们开始探索热能的转换和利用。
早期科学家对热力学的贡献
01
1. 设定实验初始条件，如初始温度、压力等。
03
02
实验操作
04
2. 点燃燃料，记录实验过程中温度、压力的变化。
3. 测量燃料燃烧释放的热量。
05
06
4. 分析实验数据，计算热力学第一定律的各项参数。
实验结果分析
数据整理
将实验过程中测得的数据整理成表格或图表情势。

热力学第一定律课件

(1)汽缸内部气体内能的增量ΔU；解析密封气体的压强 p＝p0－GS 密封气体对外做功W＝pS×0.1L 由热力学第一定律ΔU＝Q－W 得ΔU＝Q－0.1pபைடு நூலகம்SL＋0.1LG 答案 Q－0.1p0SL＋0.1LG
(2)最终的环境温度T. 解析该过程是等压变化，由盖—吕萨克定律有 LTS0 ＝L＋0T.1LS 解得T＝1.1T0 答案 1.1T0
2.能量守恒定律及意义各种不同形式的能之间相互转化或转移时能量的总量保持不变. 意义：一切物理过程都适用，比机械能守恒定律更普遍，是19世纪自然科学的三大发现之一.
3.第一类永动机是不可能制成的 (1)不消耗能量而能源源不断地对外做功的机器，叫第一类永动机.因为第一类永动机违背了能量守恒定律，所以无一例外地归于失败. (2)永动机给我们的启示人类利用和改造自然时，必须遵循自然规律.
三、气体实验定律和热力学第一定律的综合应用气体实验定律和热力学第一定律的结合点是温度和体积. 注意三种特殊过程的特点： 1.等温过程：内能不变，ΔU＝0 2.等容过程：体积不变，W＝0 3.绝热过程：Q＝0
例3 如图2所示，倒悬的导热汽缸中封闭着一定质量的理想气体，轻质活塞可无摩擦地上下移动，活塞的横截面积为S，活塞的下面吊着一个重为G的物体，大气压强恒为p0，起初环境的热力学温度为T0 图2 时，活塞到汽缸底面的距离为L.当环境温度逐渐升高，导致活塞缓慢下降，该过程中活塞下降了0.1L，汽缸中的气体吸收的热量为Q.求：
1.第一类永动机：人们把设想的不消耗能量的机器称为第一类永动机. 2.第一类永动机由于违背了能量守恒定律，所以不可能制成.
例1 空气压缩机在一次压缩中，活塞对空气做了2×105 J 的功，同时空气的内能增加了1.5×105 J，这一过程中空气向外界传递的热量是多少？解析选择被压缩的空气为研究对象，根据热力学第一定律有ΔU＝W＋Q. 由题意可知W＝2×105 J，ΔU＝1.5×105 J，代入上式得 Q＝ΔU－W＝1.5×105 J－2×105 J＝－5×104 J.

什么是热力学第一定律及第二定律

什么是热力学第一定律及第二定律热力学定律，听起来是不是有点高深莫测？别担心，咱们来点简单直白的。

想象一下，你口袋里有一堆金币，突然有一天，你发现这堆金币不见了。

没错，就是不见了！这就是“热力学第一定律”，也叫能量守恒定律。

它告诉我们，不管发生了什么，能量都是守恒的，不会凭空消失或增加。

所以啊，如果你口袋里的钱不见了，那肯定是因为有人拿走了，而不是因为宇宙的能量突然多出来或者少少了。

再来说说“热力学第二定律”，也叫做熵增原理。

这个原理有点拗口，但说白了，就是一切物体都在向无序状态发展。

就像是你手里有个球，如果它开始滚动，最后总是会停下来，而且越滚越乱。

这就是熵增的过程，也就是能量从有序状态向无序状态转化的过程。

就像你刚买的手机，用了一段时间后，可能就会卡顿、发热，甚至出现故障，这就是能量在从有序状态向无序状态转化。

这两个定律有什么用呢？简单来说，它们就像是我们生活中的指南针，告诉我们能量是怎么流动的，以及物质是如何变化的。

比如，你知道夏天为什么热吗？那是因为太阳把热量传给了地球。

而冬天冷是因为地球把热量传给了太空。

这就是能量的传递和转化。

这些定律并不是一成不变的。

科学家们通过实验和观察，不断深化对热力学定律的理解。

比如，科学家们发现了一些有趣的现象，比如气体的扩散、液体的凝固等等，这些都与热力学定律有关。

热力学定律就像是我们生活中的指南针，帮助我们理解能量的流动和物质的变化。

虽然听起来有点复杂，但只要我们用心去理解，就会发现它们其实很有趣也很有用。

下次当你看到太阳、火焰或者冰箱工作时，不妨想想这些定律，说不定你会发现更多的乐趣呢！。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章热力学第一定律
一、选择题
1．（A）2．（C）3．（D）4．（D）
5．（B）6．（D）7．（D）8．（B）
9．（B）10．（A）11．（B）12．（D）
13．（B）14．（A）15．( D ) 16．( C )
17．（D）18．（B）19．( B ) 20．( D )
21．（C）22．（B）23．( A ) 24．( C )
25．（A, C）26．（B, C, E）27．( A ) 28．( B )
二．填空题
1．上升，上升2．任一，恒容
3．封闭系统，理想气体，可逆绝热过程，W’=0，单纯PVT变化，C p,m/C v,m为常数。

4．减小，零。

5．△C HӨm(CO(g))
6．△H=0，下降7．上升，>，下降。

8．(1)△H=0，(2)△H<0
9．<，<，<，<
10．恒温，节流，恒压绝热
三．判断题
1．×，2．√，3．×，4．√，5．×，6．×，7．√
四．计算题
1．1mol理想气体由100kPa、10dm3恒压压缩到1dm3，再恒容升压到1000kPa。

试计算整个过程的W、Q、∆U、∆H。

解：变化过程如下：
根据理想气体状态方程，
p1V1/T1 = p3V3/T3
可得： T 3=T 1（ p 3V 3/ p 1V 1）= T 1（1000kPa×1dm 3）/(100kPa×10dm 3) =T 1 即终态与始态的温度相同，根据理想气体的内能U 和焓H 仅与温度有关，因此 ∆U = ∆H =0
过程的功
W =W (恒压)+W （恒容）= - p 1 (V 2 - V 1) + 0 = -100 000Pa×(1-10) ×0.001m 3 = 900J Q=∆U - W = 0 - 900J = - 900 J
2．在298K 时，有2molN 2(g)，始态体积为15dm 3，保持温度不变，经下列三个过程膨胀到终态体积为50dm 3，计算各过程的U ∆，H ∆，W 和Q 的值。

设气体为理想气体。

(1) 自由膨胀；
(2) 反抗恒定外压100kPa 膨胀；
(3) 可逆膨胀。

解：始态：，，mol n 2=3115dm V =K T 2981=
终态：
3250dm V =(1) 自由膨胀：0=∆-=V p W 外，0)(==∆=∆T f H U ，0=-∆=W U Q
(2) 反抗恒定外压100kPa 膨胀：
J m Pa V p W 350010)1550(10100333-=⨯-⨯⨯-=∆-=-外
0)(==∆=∆T f H U ，J W U Q 3500=-∆=
(3) 可逆膨胀：
J
dm
dm K V V nRT W 86.5965 1550ln 298K mol 8.314J -2mol ln 33
1-1-1
2
-=⨯⨯⋅⋅⨯=-= 0)(==∆=∆T f H U ，J W U Q 86.5965=-∆=
3．0.1kg C 6H 6(l)在p Ө，沸点353.35K 下蒸发，已知(C 6H 6) =30.80 kJ mol -1。

试计算此过程Q ，W ，ΔU 和ΔH 值。

m g
l H ∆解：等温等压相变。

n (C 6H 6) =100/78 mol , ΔH = Q = n = 39.5 kJ , m g l H ∆ W = - nRT = -3.77 kJ , ΔU =Q +W=35.7 kJ
4．设一礼堂的体积是1000m 3，室温是290K ，气压为O
p ，今欲将温度升至300K ，
需吸收热量多少?(若将空气视为理想气体，并已知其C p ,m 为29.29 J K -1 ·mol -1。

)
解：理想气体等压升温（n 变）。

T nC Q p d m ,=δ,
⎰=300290m ,d RT T pV C Q p =1.2×107 J 5．1mol 单原子分子理想气体,从298K,2p Ө经(1)等温可逆; (2)绝热可逆; (3)沿p=10132.5V+b 的路径可逆膨胀至体积加倍, 求各过程的Q,W,∆U 和∆H? 解: (1)理想气体等温过程 ∆U=0; ∆H=0
Q=-W=nRTln(V 2/V 1)=1717.3 J
(2) 绝热过程: Q
=0 γ=5/3 有绝热过程方程式: p 1V 1γ=p 2V 2γ p 1=2p 0 V 1=12.226 dm 3 V 2=24.452 dm 3
p 2=p 1V 1γ/V 2γ=0.63p 0 T 2=p 2V 2/nR=187.7 K
∆U=Cv (T 2-T 1)=3/2R(187.7-298)=-1375 J
W=∆U=-1375 J ∆H=C p (T 2-T 1)=-2292 J
(3) 求b: b=p 1-10132.5V 1=78770
p 2=10132.5×V 2+78770=326530Pa=3.223p Ө
T 2=p 2V 2/R=960.3K ∆U=C v ∆T=8260 J
∆H=C p ∆T=13767 J W=-∫pdV=-∫(10132.5V+78770)dV=-3240 J
Q=∆U-W=11500 J
6．2 mol 单原子理想气体，由600K ，1.0MPa 对抗恒外压p Ө绝热膨胀到p Ө。

计算该过程的Q 、W 、ΔU 和ΔH 。

(C p ,m =2.5 R)
解：理想气体绝热不可逆膨胀Q ＝0 。

ΔU ＝W ，即 nC V ,m (T 2-T 1)= - p 2 (V 2-V 1), 因V 2= nRT 2/ p 2 , V 1= nRT 1/ p 1 ，求出T 2=384K 。

ΔU ＝W ＝nC V ,m (T 2-T 1)＝-5.39kJ ，ΔH ＝nC p ,m (T 2-T 1)＝-8.98 kJ
7．2mol,101.33 kPa,373K 的液态水放入一小球中,小球放入373K 恒温真空箱中。

打破小球,刚好使H 2O(l)蒸发为101.33kPa,373K 的H 2O(g)(视H 2O(g)为理想气体)求此过程的Q ，W ，ΔU ，ΔH ;　若此蒸发过程在常压下进行,则Q ，W ，ΔU ，ΔH 的值各为多少? 已知水的蒸发热在373K, 101.33kPa 时为40.66kJ·mol －1。

. 解：101.33kPa , 373K H 2O(l)→H 2O(g)
(1)等温等压可逆相变, ΔH =Q =n H m = 81.3 kJ ,
g l ∆W = -nR T =-6.2 kJ, ,ΔU =Q +W =75.1 kJ
(2)向真空蒸发W =0, 初、终态相同ΔH =81.3 kJ，ΔU =75.1 kJ，Q =ΔU ＝75.1 kJ。

热力学第一定律和应用(C)

页数:1
第二章-热力学第一定律--题加答案

页数:11
第一章热力学第一定律及应用练习题.

页数:3
热力学第一定律与能量守恒定律

页数:2
物化试卷理想气体与热力学第一定律

页数:6
热力学第一定律的理解

页数:14
热力学基础第1讲——热力学第一定律及其在理想气体等值过程中的应用

页数:23
内能与热力学第一定律(答案)

页数:3
物化试卷理想气体与热力学第一定律

页数:9
第二章热力学第一定律练习题与解答

页数:8

热力学第一定律-广西师范大学化学与药学学院

合集下载

04 热力学第一定律

物理化学：热力学第一定律PPT课件

第二章热力学第一定律

什么是热力学第一定律及第二定律

热力学第一定律课件

(完整版)第二章热力学第一定律.doc

热力学第一定律课件

热力学第一定律精选全文完整版

ppt热力学第一定律

热力学第一定律课件

热力学第一定律

热力学第一定律(物理化学)

最新第一章热力学第一定律(药学专业)-药学医学精品资料

大学热学第十讲热力学第一定律课件

热力学第一定律课件

什么是热力学第一定律及第二定律

文档推荐

最新文档

热力学第一定律-广西师范大学化学与药学学院

合集下载

04 热力学第一定律

物理化学：热力学第一定律PPT课件

第二章 热力学第一定律

什么是热力学第一定律及第二定律

热力学第一定律 课件

(完整版)第二章热力学第一定律.doc

热力学第一定律 课件

热力学第一定律精选全文完整版

ppt热力学第一定律

热力学第一定律 课件

热力学第一定律

热力学第一定律(物理化学)

最新第一章 热力学第一定律(药学专业)-药学医学精品资料

大学热学第十讲热力学第一定律课件

热力学第一定律 课件

什么是热力学第一定律及第二定律

文档推荐

最新文档

第二章热力学第一定律

热力学第一定律课件

热力学第一定律课件

热力学第一定律课件

最新第一章热力学第一定律(药学专业)-药学医学精品资料

热力学第一定律课件