磁力矩公式在非均匀磁场中的应用
- 格式:pdf
- 大小:264.44 KB
- 文档页数:3

高中物理《磁场中的磁力和力矩》教案
标题:磁场中的磁力和力矩
引言:
在磁场中,磁力和力矩起着重要的作用。
磁场中的物体受到磁力的作用,而力矩则描述了物体在磁场中受到的力的引起的旋转。
主体:
1. 磁力的定义和计算方法:
- 磁力是磁场对磁性物质施加的力。
它遵循洛伦兹力的规律,即磁力等于电荷的速度与磁场强度和两者之间的夹角的乘积。
- 可以使用以下公式计算磁力:磁力(F)= 电荷(q)×速
度(v)×磁场强度(B)× sin(夹角)
2. 磁场中的力矩:
- 力矩是力绕轴线引起物体旋转的倾向。
在磁场中,力矩可
由磁场中的磁力引起。
- 磁场中的力矩可以通过以下公式计算:力矩(τ)= 磁力(F)×轴线到力的垂直距离(r)
3. 磁场中的磁力和力矩实例:
- 可以通过实例,如电动机和电磁铁,来展示磁场中的磁力和力矩的应用。
- 探索这些实例并讨论它们在现实世界中的应用。
结论:
通过学习磁场中的磁力和力矩,学生可以深入理解磁场对物体施加的力和引起的旋转效应。
这有助于他们在未来解决与磁场和力矩相关的问题。
希望以上信息能对您有所帮助。
如果您需要进一步的帮助,请随时告诉我。

恒定磁场磁力矩计算应用首先,让我们来了解一下恒定磁场和磁力矩的基本概念。
恒定磁场是指在空间中强度和方向都不随时间变化的磁场。
磁力矩是一个体系在磁场中受到的力矩。
磁力矩的大小和方向取决于磁场的强度和方向以及体系自身的性质。
在实际应用中,恒定磁场磁力矩计算有着广泛的应用。
以下将介绍一些具体的应用领域。
首先是磁共振成像技术。
磁共振成像是一种通过测量材料中原子核的磁性来获得材料内部结构的无创检测技术。
在磁共振成像中,恒定磁场磁力矩计算用于计算原子核在磁场中的力矩,从而确定其位置和性质。
这种技术在医学领域中广泛应用于人体影像检查,如MRI技术。
第二个例子是电动机的设计和计算。
电动机是一种将电能转化为机械能的设备,其中磁场和电流之间的相互作用是产生机械动力的基本原理。
在电动机的设计和计算中,恒定磁场磁力矩计算用于计算电动机转子的力矩,从而确定其输出功率。
这种技术在工业生产中广泛应用于电动机性能评估和优化设计。
第三个例子是磁性材料的力学性能评估。
磁性材料是一种具有特殊磁性性质的材料,如铁、钴、镍等。
在磁性材料的力学性能评估中,恒定磁场磁力矩计算用于计算材料中磁性粒子受到的力矩,从而确定其力学性能和磁性性能。
这种技术在材料科学和工程中广泛应用于磁性材料的选择和设计。
最后一个例子是磁悬浮交通技术。
磁悬浮交通是一种使用磁场和电流相互作用的原理来实现列车悬浮和推动的高速交通技术。
在磁悬浮交通技术中,恒定磁场磁力矩计算用于计算列车受到的力矩,从而确定其悬浮高度和运行速度。
这种技术在交通运输领域中广泛应用于高速铁路和磁悬浮列车的设计和运营。
综上所述,恒定磁场磁力矩计算是物理学中一个重要的应用领域,在许多技术领域都有广泛的应用。
通过测量电流、磁场强度等数据,可以计算磁力矩的大小和方向,从而确定物体的位置、性质和性能。
这为许多领域的科学研究和工程应用提供了关键的技术支持。
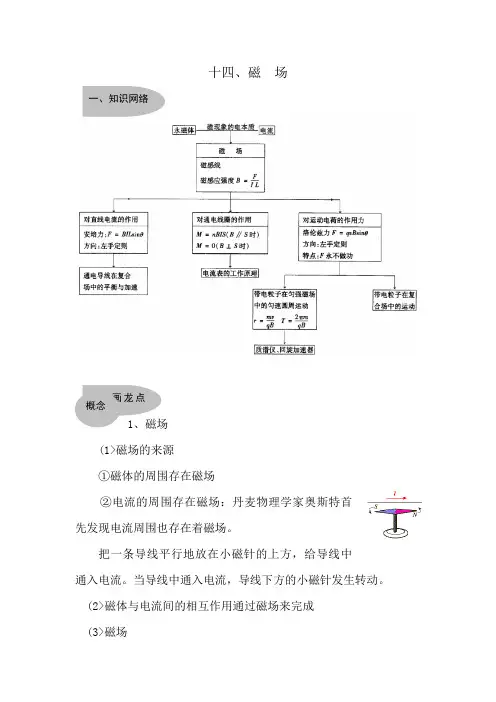
十四、磁 场1、磁场(1>磁场的来源①磁体的周围存在磁场②电流的周围存在磁场:丹麦物理学家奥斯特首先发现电流周围也存在着磁场。
把一条导线平行地放在小磁针的上方,给导线中通入电流。
当导线中通入电流,导线下方的小磁针发生转动。
(2>磁体与电流间的相互作用通过磁场来完成(3>磁场一、知识网络二、画龙点睛概念①磁场:磁体和电流周围,运动电荷周围存在的一种特殊物质,叫磁场。
②磁场的基本性质:对处于其中的磁极或电流有力的作用。
③磁场的物质性:虽然磁场看不见摸不着,对于我们初学者感到很抽象,其实磁场和电场一样是客观存在的,是物质存在的一种特殊形式。
b5E2RGbCAP2、磁场的方向磁感线(1>磁场的方向:物理学规定,在磁场中的任一点,小磁针北极受力的方向,亦即小磁针静止时北极所指的方向,就是该点的磁场方向。
p1EanqFDPw(2>磁感线:①磁感线所谓磁感线,是在磁场中画出的一些有方向的曲线,在这些曲线上,每一点的切线方向都在该点的磁场方向上。
DXDiTa9E3d②磁感线的可以用实验来模拟(3>几种典型磁体周围的磁感线分布①条形磁铁磁场的磁感线②条形磁铁磁场的磁感线③直线电流磁场的磁感线直线电流磁场的磁感线是一些以导线上各点为圆心的同心圆,这些同心圆都在跟导线垂直的平面上。
直线电流的方向和磁感线方向之间的关系可用安培定则(也叫右手螺旋定则>来判定:用右手握住导线,让伸直的大拇指所指的方向跟电流的方向一致,弯曲的四指所指的方向就是磁感线的环绕方向。
RTCrpUDGiT④环形电流磁场的磁感线环形电流磁场的磁感线是一些围绕环形导线的闭合曲线。
在环形导线的中心轴线上,磁感线和环形导线的平面垂直。
5PCzVD7HxA环形电流的方向跟中心轴线上的磁感线方向之间的关系也可以用安培定则来判定:让右手弯曲的四指和和环形电流的方向一致,伸直的大拇指所指的方向就是环形导线中心轴线上磁感线的方向。

第6章磁力的计算由理论力学可知,体系在某一方向的力和力矩等于在该方向的能量梯度,可表达为:式中,W 一为体系的能量,%—在i 方向的坐标,F —i 方向的力,作用在3方向的力 矩,。
一旋转角。
1. 吸引力的计算 1) 气隙能量有解的表达式:由上式得吸引力:B ;AA式中,F —吸引力(N),诳一气隙磁密气一板面积即"真空磁导率(4/rxlO-7%)2) 如果气隙较大,乩不均匀,能量表达式由(3)得引力应为:8式中,F —吸引力心),B 「G, A^-cm为了计算方便,将上式化为:式中,F —kgf, Bg —G , — cmdV 为气隙体积元,积分在全部气隙中进行,如果〃,工1时,〃u 应改为3,0,此式由计算dW F dw ——,T =—— F = ----- ,T = ---叫 8Q机求出W,再由—求出F/3) 也可不先求W,直接按下式求出磁吸引力户:户=jj 万石(6-7)F ——作用于磁体上的磁吸引力;5一一包国该物体的任意表而: P ——作用于该表面上的应力; P 的表达式为:p = l^(n-B )B- — B 2h(6-8)Ao 尸 2〃。
n ——沿积分表而s 法线方向的单位矢量: B ——磁感应强度矢量4) 下而介绍AC 。
、与铁氧体之间的磁吸引力。
试验证明,在永磁体直径D 等于高度时,吸引力最大。
故假定L in ^D = l,此时, 气隙磁密可用下列公式(注:此法由磁核积分法导出)。
ft在磁力试验中发现永磁体的H H C 也起作用,故将上式改为:例,求两个铁氧圆环之间的吸引力。
两环的磁特性和几何尺寸为:B r = 3500 G , H H c = 2250 O e , d 外=^5.0cni , c/*=<E>3.2c 〃7B^E B H C I(6-9)高度L m = 1.5cm可把圆环看成是直径0 = 1(〃外一〃内)和高度九,的圆柱绕z轴旋转而成的,故可用(6)2和(10)式联立求解。


第6章 磁力的计算由理论力学可知,体系在某一方向的力和力矩等于在该方向的能量梯度,可表达为:ii i WT q W F θ∂∂=∂∂=, (6-1) 式中,W —为体系的能量,i q —在i 方向的坐标,i F —i 方向的力,T —作用在θ方向的力矩,θ—旋转角。
1.吸引力的计算1) 气隙能量有解的表达式:22μgg g L A B W =或π82gg g L A B W =(6-2)由上式得吸引力:22μgg A B F =(6-3)式中,F —吸引力()N ,g B —气隙磁密()2mWb,gA —板面积()2m ,0μ—真空磁导率()mH7104-⨯π2) 如果气隙较大, g B 不均匀,能量表达式由(3)得引力应为:π82gg A B F =(6-4)式中,F —吸引力()yn d ,g B —G ,g A —2cm 。
为了计算方便,将上式化为:g g A B F 24965⎪⎪⎭⎫⎝⎛= (6-5)式中,F —kgf ,g B —G ,g A —2cm 。
dV B W g ⎰⎰⎰=0221μ (6-6)dV 为气隙体积元,积分在全部气隙中进行,如果1≠r μ时,0μ应改为0μ0r μ,此式由计算机求出W ,再由iq W∂∂求出i F 。
3) 也可不先求W ,直接按下式求出磁吸引力F:⎰⎰∇=s d p F(6-7)F——作用于磁体上的磁吸引力; s——包围该物体的任意表面; p——作用于该表面上的应力; p的表达式为:()n B B B n p 200211μμ-⋅= (6-8) n——沿积分表面s 法线方向的单位矢量;B——磁感应强度矢量4) 下面介绍05RC 与铁氧体之间的磁吸引力。
试验证明,在永磁体直径D 等于高度m L 时,吸引力最大。
故假定1=≠D L m ,此时,气隙磁密g B 可用下列公式(注:此法由磁核积分法导出)。
⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-=211D L D L B B g g r g 在磁力试验中发现永磁体的C B H 也起作用,故将上式改为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-=211D L D L H B B g g C B r g (6-9) 例,求两个铁氧圆环之间的吸引力。

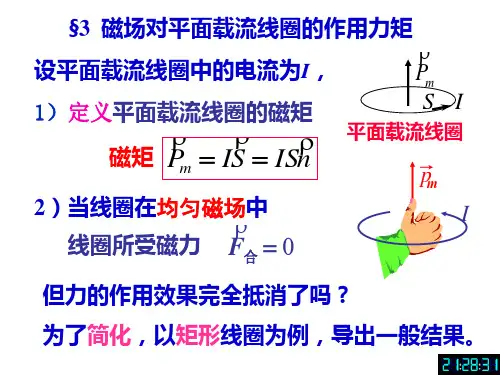
磁矩在磁场中的受力和受力矩磁矩是指物体在磁场中具有磁性的特性。
当磁矩与外部磁场相互作用时,会产生受力和受力矩。
磁矩的受力和受力矩涉及到物理学中的电磁学部分。
下面将从电流元的磁矩、磁场对磁矩的作用力和作用矩以及磁矩的力矩平衡等方面分别进行论述。
首先,让我们从电流元的磁矩开始探讨。
电流元是指电流通过的一个导线段。
当电流通过导线时,导线周围会形成一个磁场。
而电流元的磁矩则表示了这个磁场在空间上的分布情况。
具体来说,电流元的磁矩与电流元本身的长度和方向有关。
当电流元的长度增大时,磁矩也相应增大。
而电流元的方向则决定了磁矩的指向。
通过调整电流元的方向,可以改变磁矩在磁场中的受力和受力矩。
其次,我们来探讨磁场对磁矩的作用力和作用矩。
当磁矩在磁场中运动时,就会受到磁力的作用。
磁力是磁场对磁矩的作用力,其大小和方向取决于磁矩和磁场之间的相对关系。
根据库仑定律,磁力的大小和磁场强度以及磁矩的大小和磁场矢量的叉乘有关。
当磁矩与磁场平行时,磁力为零;当磁矩与磁场垂直时,磁力最大。
此外,磁场对磁矩的作用力还与磁场中的其他电流元的磁矩有关。
在磁场中,磁矩之间的作用力可能相互抵消,也可能相互增强。
除了作用力之外,磁场还会对磁矩产生作用矩。
作用矩是指磁场对磁矩的力矩。
在磁场中,磁矩受到的作用力会造成磁矩产生一个力矩,使其发生旋转。
根据安培定律,作用矩的大小和磁矩以及磁场的叉乘有关。
当磁矩与磁场垂直时,作用矩最大;当磁矩与磁场平行时,作用矩为零。
最后,我们来探讨磁矩的力矩平衡。
力矩平衡是指物体所受到的力和力矩之间的平衡关系。
在磁场中,磁矩的力矩平衡与磁矩所受到的作用力和作用矩有关。
当磁矩受到的作用力和作用矩平衡时,磁矩处于力矩平衡状态。
这时,磁矩所受到的磁场力和磁场作用矩相互抵消,使得磁矩保持平衡姿态。
力矩平衡的条件是作用矩的合力为零,即磁场对磁矩的合力矩为零。
只有当磁场对磁矩的合力矩为零时,磁矩才能保持在力矩平衡状态。
综上所述,磁矩在磁场中的受力和受力矩涉及到磁场对磁矩的作用力和作用矩。

非均匀磁场中磁感应强度的计算磁感应强度是描述磁场强弱和方向的物理量,用符号B表示。
在非均匀磁场中,磁感应强度会随着位置的变化而变化。
为了计算非均匀磁场中的磁感应强度,我们需要考虑磁场源、空间位置以及磁场分布等因素。
1.磁场源:磁场源可以是电流、磁铁等。
电流产生的磁场方向可以用右手螺旋定则确定,磁铁的磁场方向可以用磁铁的极性确定。
2.空间位置:在非均匀磁场中,空间位置对磁感应强度的影响很大。
通常我们需要根据空间位置的不同,分别计算磁感应强度。
3.磁场分布:非均匀磁场的分布可以用积分方法进行计算。
例如,利用毕奥-萨伐尔定律(Biot-Savart Law)可以计算非均匀直线电流产生的磁场分布。
4.磁感应强度的计算方法:(1)对于均匀磁场,磁感应强度B可以用公式B=μ₀I/2πr计算,其中μ₀为真空磁导率,I为电流,r为距离。
(2)对于非均匀磁场,我们需要根据具体情况选择合适的计算方法。
例如,对于直线电流产生的磁场,可以用毕奥-萨伐尔定律计算磁感应强度。
(3)在计算过程中,需要注意单位的转换。
磁感应强度的单位是特斯拉(T),真空磁导率的单位是亨利每米(H/m)。
5.磁感应强度的大小和方向:磁感应强度的大小表示磁场的强弱,方向表示磁场的方向。
在非均匀磁场中,磁感应强度的大小和方向都会随着位置的变化而变化。
6.磁感应强度的测量:磁感应强度可以通过磁感线、磁力线等方法进行可视化展示。
此外,还可以使用磁感应强度计等仪器进行测量。
7.磁感应强度在实际应用中的例子:磁感应强度在现代科技领域中有着广泛的应用,如磁悬浮列车、核磁共振成像(MRI)等。
综上所述,非均匀磁场中磁感应强度的计算涉及到磁场源、空间位置、磁场分布等多个因素。
在计算过程中,需要根据具体情况选择合适的计算方法,并注意单位的转换。
磁感应强度的大小和方向在非均匀磁场中会随着位置的变化而变化,可以通过磁感线、磁力线等方法进行可视化展示。
习题及方法:1.习题:一个长直导线通以电流I,距离导线距离为r处,求磁感应强度B。
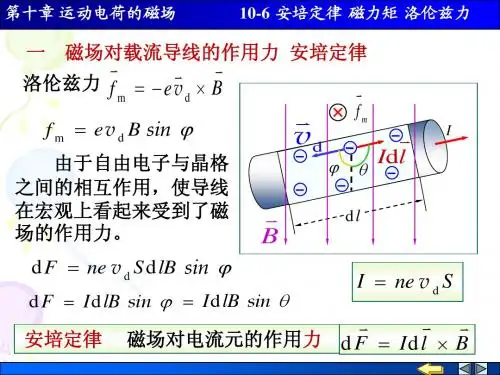

浅谈平面线圈在非均匀磁场中所受的磁力矩现今,平面线圈在非均匀磁场中所受的磁力矩一直是物理学、电子学、机械制造等学科领域的一个重要研究课题。
它与磁学方面涉及到的电机、变压器、磁性探测和强磁场测量等有关。
因此,研究平面线圈在非均匀磁场中所受的磁力矩,可以帮助我们更好地理解物理现象,并有助于实现新技术。
一、磁力矩的定义及计算磁力矩定义为平面线圈单位面积受到的磁力之积,它可以用矢量mathbf{U}来表示,是一个复数,由模象和象征组成。
磁力矩可以通过采用时域积分或频域积分的方法来计算,如下:mathbf{U}=int_0^ infty mathbf{B} times mathbf{A} , dt 其中,mathbf{B}磁场的强度,mathbf{A}线圈的面积向量,dt 时间步长。
二、磁力矩在非均匀磁场中的应用1、电机:电机是一种将电能转换为机械能的装置,是一种电动机。
它由绕组呈线圈形式组成。
当磁场经过绕组时,绕组受到磁力矩的作用,从而使绕组的每一细丝产生电流,此电流产生的磁场与外加的磁场相互作用,从而产生一种力,此力促使电机转动。
2、变压器:变压器是一种电器,能够将低电压变换成高电压,或者将高电压变换成低电压。
它是由若干绕组组成的电器,外加的磁场与绕组线圈中的磁力矩相互作用,使得当原绕组上流过电流时,在相邻的绕组上就可以产生相应的电压变化。
3、磁性探测:磁性探测是一种用来探测潜在磁体的物质,是一种磁学成像的技术。
磁性探测装置有检测器、放大器、分析仪等组成,当外加的磁场经过检测器时,检测器受到磁力矩的作用,从而使检测器产生电流,从而实现探测目标物体的磁性特征。
3、强磁场观测仪:强磁场观测仪是一种仪器,用来监测和记录强磁场或磁场变化的物理参量,如强磁场的强度、分布等,以研究磁场变化过程的物理规律。
它是由磁力矩放大器、磁学传感器、超声成像仪等组成的一个复杂的系统,它的关键是,绕组线圈受到外加的磁场,会受到磁力矩的作用,从而产生一定的电流,这种电流可以被放大器放大,然后通过磁学传感器转换,从而实现对强磁场的观测。
磁力矩公式在非均匀磁场中的应用
刘运;张良瑞
【期刊名称】《陕西科技大学学报(自然科学版)》
【年(卷),期】2003(021)002
【摘要】通过在非均匀磁场中载流线圈所受磁力矩的两个具体例子的计算,说明在非均匀磁场中计算载流线圈所受磁力矩方法的多样性及磁力矩公式M=Pm×B使用的灵活性.
【总页数】3页(P104-106)
【作者】刘运;张良瑞
【作者单位】陕西科技大学理学院,陕西,咸阳,712081;陕西科技大学理学院,陕西,咸阳,712081
【正文语种】中文
【中图分类】O441.2
【相关文献】
1.磁力矩器在磁洁净卫星平台中的应用技术研究 [J], 肖琦;张文彬;孟立飞
2.光纤陀螺在球面非均匀磁场中的磁敏感性研究 [J], 肖程;刘军;殷建玲;鲁军
3.非接触圆筒形推拉式磁偶合联轴器的磁力矩公式的推理及其分析 [J], 李廷占;张明成;于天池;王东升
4.带电粒子在非均匀磁场——磁瓶中的运动 [J], 沈犁理;钟寿仙
5.非均匀磁场中磁流体热磁对流的实验研究 [J], 李强;宣益民;李锐
因版权原因,仅展示原文概要,查看原文内容请购买。