模拟滤波器及IIR数字滤波器的设计

实验四 IIR 数字滤波器的设计及网络结构一、实验目的1．了解IIR 数字滤波器的网络结构。

2.掌握模拟滤波器、IIR 数字滤波器的设计原理和步骤。

3．学习编写数字滤波器的设计程序的方法。

二、实验内容数字滤波器：是数字信号处理技术的重要内容。

它的主要功能是对数字信号进行处理，保留数字信号中的有用成分，去除信号中的无用成分。

1．数字滤波器的分类滤波器的种类很多，分类方法也不同。

（1）按处理的信号划分：模拟滤波器、数字滤波器 （2）按频域特性划分；低通、高通、带通、带阻。

（3）按时域特性划分：FIR 、IIR2．IIR 数字滤波器的传递函数及特点数字滤波器是具有一定传输特性的数字信号处理装置。

它的输入和输出均为离散的数字信号，借助数字器件或一定的数值计算方法，对输入信号进行处理，改变输入信号的波形或频谱，达到保留信号中有用成分去除无用成分的目的。

如果加上A/D 、D/A 转换，则可以用于处理模拟信号。

设IIR 滤波器的输入序列为x(n)，则IIR 滤波器的输入序列x(n)与输出序列y(n)之间的关系可以用下面的方程式表示：1()()()M Ni j i j y n b x n i a y n j ===-+-∑∑（5-1）其中，j a 和i b 是滤波器的系数，其中j a 中至少有一个非零。

与之相对应的差分方程为：10111....()()()1....MM NN b b z b z Y z H Z X z a z a z ----++==++ （5-2）由传递函数可以发现无限长单位冲激响应滤波器有如下特点： （1） 单位冲激响应h(n)是无限长的。

（2） 系统传递函数H(z)在有限z 平面上有极点存在。

（3） 结构上存在着输出到输入的反馈，也就是结构上是递归型的。

3．IIR 滤波器的结构IIR 滤波器包括直接型、级联型和并联型三种结构：① 直接型：优点是简单、直观。

但由于系数bm 、a k 与零、极点对应关系不明显，一个bm 或a k 的改变会影响H(z)所有零点或极点的分布，所以一方面，bm 、a k 对滤波器性能的控制关系不直接，调整困难；另一方面，零、极点分布对系数变化的灵敏度高，对有限字长效应敏感，易引起不稳定现象和较大误差。

实验四IIR数字滤波器的设计与MATLAB实现一、实验目的：1、要求掌握IIR数字滤波器的设计原理、方法、步骤。

2、能够根据滤波器设计指标进行滤波器设计。

3、掌握数字巴特沃斯滤波器和数字切比雪夫滤波器的设计原理和步骤。

二、实验原理：IIR数字滤波器的设计方法：频率变换法、数字域直接设计以及计算机辅助等。

这里只介绍频率变换法。

由模拟低通滤波器到数字低通滤波器的转换，基本设计过程：1、将数字滤波器的设计指标转换为模拟滤波器指标2、设计模拟滤波器G(S)3、将G(S)转换为数字滤波器H（Z）在低通滤波器设计基础上，可以得到数字高通、带通、带阻滤波器的设计流程如下：1、给定数字滤波器的设计要求（高通、带通、带阻）2、转换为模拟（高通、带通、带阻）滤波器的技术指标3、转换为模拟低通滤波器的指标4、设计得到满足3步骤中要求的低通滤波器传递函数5、通过频率转换得到模拟（高通、带通、带阻）滤波器6、变换为数字（高通、带通、带阻）滤波器三、标准数字滤波器设计函数MATLAB提供了一组标准的数字滤波器设计函数，大大简化了滤波器设计过程。

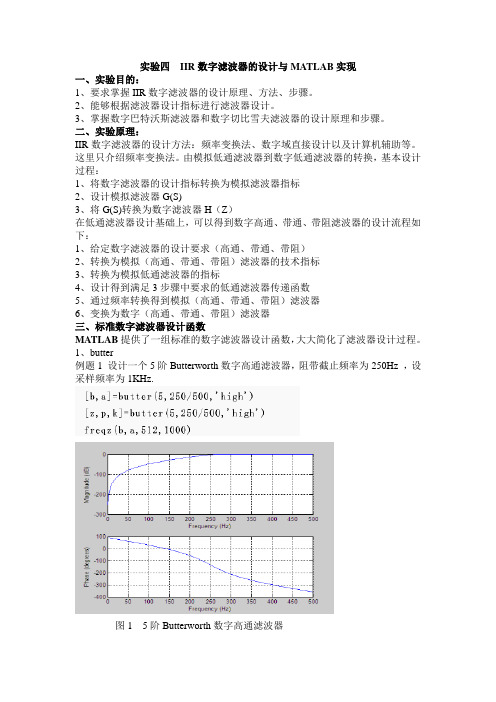
1、butter例题1 设计一个5阶Butterworth数字高通滤波器，阻带截止频率为250Hz ，设采样频率为1KHz.图1 5阶Butterworth数字高通滤波器2、cheby1和cheby2例题2 设计一个7阶chebyshevII型数字低通滤波器，截止频率为3000Hz，Rs=30dB,采样频率为1KHz。

图2 7阶chebyshevII型数字低通滤波器四、冲激响应不变法一般来说，在要求时域冲激响应能模仿模拟滤波器的场合，一般使用该方法。

冲激响应不变法一个重要的特点是频率坐标的变换时线性的，因此如果模拟滤波器的频响带限于折叠频率的话，则通过变换后滤波器的频率响应可不失真的反映原响应与频率的关系。

例题3 设计一个中心频率为500Hz，带宽为600 Hz的数字带通滤波器，采样频率为1K Hz。

实验三IIR数字滤波器设计实验报告一、实验目的：1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求：1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号，并对其滤波，对比滤波前后波形和频谱三、基本原理：㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础，常用的类型分为巴特沃斯（Butterworth）、切比雪夫（Chebyshev）Ⅰ型、切比雪夫Ⅱ型、贝塞尔（Bessel）、椭圆等多种。

在MATLAB信号处理工具箱里，提供了这些类型的IIR数字滤波器设计子函数。

（二）性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段，滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB，双线性变换法中T取1s.四、实验步骤：1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波，并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性：101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中，采用的带通滤波器为6000-7000Hz ，换算成角频率为4.47-0.55，在上图中可以清晰地看出到达了题目的要求。

冲击响应不变法后的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性，而在在幅频曲线上几乎没有差别，都能达到相同的结果。

由模拟滤波器设计IIR数字滤波器为了从模拟滤波器设计IIR数字滤波器，必须先设计一个满足技术指标的模拟滤波器，然后将其数字化，即从s平面映射到z平面，得到所需的数字滤波器。

虽然IIR数字滤波器的设计本质上并不取决于连续时间滤波器的设计，但是因为在许多应用中，数字滤波器就是用来模仿模拟滤波器功能的，所以由模拟滤波器转化为数字滤波器是很自然的是。

另外，模拟滤波器的设计技巧非常成熟，不仅有封闭形式的公式，而且设计系数已经表格化。

因此，有模拟滤波器设计数字滤波器的方法准确、简便，是目前最普遍采用的方法。

在模拟滤波器的设计中，低通滤波器是最基本的。

设计模拟滤波器的方法有多种，如巴特沃兹（Butterworth）型、切比雪夫型（Chebyshev）型、椭圆型（Elliptic）型滤波器。

为了能从模拟滤波器的低通原型设计各种IIR DF,一般需如下四个步骤：1. 把要求的低通（LP）、高通（HP）、带通（BP）、或带阻（BS）的特征频率参数转化为模拟低通滤波器低通原型的设计参数。

2. 用模拟逼近的方法获的巴特沃兹、切比雪夫或椭圆模拟低通原型的传递函数Hp(s)。

3. 通过s平面到z平面的映射关系，由Hp(s)求出相应的数字低通的系统函数Hp(z)。

4. 用数字域的频率变换，从Hp(z)求出所需的数字LP、HP、BP、或BS数字滤波器的系统函数H(z)。

下面将对上述四个步骤分别加以介绍。

5.2.1 模拟域的频率变换在模拟滤波器的设计中，巴特沃兹、切比雪夫以及椭圆滤波器的设计都是低通逼近。

所以，如果设计的滤波器不是低通，就需要将HP、BP、或BS的频率参数变换为低通原型的相应参数。

这个变换是在模拟域进行的，所以叫模拟频域变换。

1. 低通原型的设计参数设计一个低通滤波器需要给出4个参数：通带临界频率fp(Hz)，阻带临界频率fs(Hz)，通带最大衰耗αp(dB)，阻带最小衰耗αs(dB)。

这4个参数构成的低通样板图如图5.2所示。

实验四 IIR数字滤波器的设计与滤波一、巴特沃斯模拟滤波器的设计1．模拟滤波器的设计参数模拟滤波器的4个重要的通带、阻带参数为：或Omegap：通带截止频率或Omegas：阻带截至频率：通带内波动(dB)，即通带内所允许的最大衰减；：阻带内最小衰减通过以上参数就可以进行模拟滤波器的设计。

2．巴特沃斯模拟滤波器设计1）巴特沃斯滤波器阶数的选择：在已知设计参数，，，之后，可利用“buttord”命令可求出所需要的滤波器的阶数和3dB截止频率，其格式为：[N，Omegac]=buttord[fp，fs，Rp，Rs，’s’]，其中fp，fs，Rp，Rs分别为通带截止频率、阻带起始频率、通带内波动、阻带内最小衰减。

返回值N为滤波器的最低阶数，Wc为3dB截止频率。

2）巴特沃斯滤波器系数计算：由巴特沃斯滤波器的阶数N以及3dB截止频率Omegac可以计算出对应传递函数H(z)的分子分母系数，MATLAB提供的命令如下：巴特沃斯低通滤波器系数计算：[b，a]=butter(N,Omegac)，其中b为H(z)的分子多项式系数，a为H(z)的分母多项式系数巴特沃斯高通滤波器系数计算：[b，a]=butter(N,Omegac,’High’)巴特沃斯带通滤波器系数计算：[b，a]=butter(N，[Omega1，Omega2])，其中[Omega1，Omega2]为通带截止频率，是2元向量，需要注意的是该函数返回的是2N阶滤波器系数。

巴特沃斯带阻滤波器系数计算：[b，a]=butter(N，[Omega1，Omega2]，’stop’)，其中[Omega1，Omega2]为通带截止频率，是2元向量，需要注意的是该函数返回的也是2N阶滤波器系数。

二、巴特沃斯数字滤波器的设计1. 数字滤波器的设计参数滤波器的4个重要的通带、阻带参数为：：通带截止频率（Hz）：阻带起始频率（Hz）：通带内波动（dB），即通带内所允许的最大衰减；：阻带内最小衰减设采样速率（即奈奎斯特速率）为，将上述参数中的频率参数转化为归一化频率参数：：归一化通带截止频率，；：归一化阻带截至频率，通过以上参数就可以进行数字滤波器的设计。

IIR模拟低通滤波器设计IIR（Infinite Impulse Response）滤波器是一种数字滤波器，其输出信号的当前值取决于输入信号的当前值和一些先前的输出信号的值。

相比之下，FIR（Finite Impulse Response）滤波器的输出信号仅取决于一些先前的输入信号的值。

IIR低通滤波器是一种可以滤除高频信号成分的滤波器，同时保留低频信号的滤波器。

其设计的目标是，在给定的截止频率以下允许低频信号通过，而在截止频率以上滤除高频信号。

设计IIR低通滤波器的一种常见方法是使用巴特沃斯（Butterworth）滤波器。

巴特沃斯滤波器是IIR滤波器的一种特例，其特点是具有平坦的幅频特性和最小的群延迟。

IIR低通滤波器的设计步骤如下：1.选择滤波器的阶数：阶数决定了滤波器的复杂度和性能。

较高的阶数可以提供更陡峭的滤波特性，但也会增加计算复杂度。

2.选择截止频率：截止频率是滤波器的一个重要参数，用于确定滤波器的频率响应。

根据应用的需求，选择适当的截止频率。

3.归一化截止频率：将截止频率归一化为一个单位圆内的复频域值。

这是为了方便滤波器的设计和计算，可以使用以下公式进行归一化：normalized_cutoff_frequency = (2 * cutoff_frequency) / sampling_frequency4. 选择滤波器类型：根据实际需求，选择滤波器的类型。

巴特沃斯低通滤波器是最常见的选择，但也可以选择其他类型的滤波器，如Chebyshev和Elliptic滤波器。

5. 设计滤波器：通过使用滤波器设计工具或Matlab等数学软件，根据所选的滤波器类型和归一化截止频率设计出滤波器的传递函数。

6.转换为巴特沃斯形式：如果选择的滤波器类型不是巴特沃斯滤波器，则需要将其转换为巴特沃斯形式。

这可以通过对设计的滤波器进行变换和频率响应的调整来实现。

7.构造滤波器：将设计好的巴特沃斯滤波器转换为IIR数字滤波器的巴特沃斯形式，即为最终的IIR低通滤波器。

iir数字滤波器的设计matlab摘要：1.IIR数字滤波器简介2.MATLAB在IIR数字滤波器设计中的应用3.设计实例与分析4.结论正文：一、IIR数字滤波器简介IIR（无限脉冲响应）数字滤波器是数字信号处理中的重要组成部分，其设计方法与模拟滤波器设计密切相关。

在设计IIR数字滤波器时，需要确定采样间隔或采样频率，将数字滤波器的指标转化为模拟滤波器的指标，然后根据模拟滤波器的指标设计模拟滤波器。

最后，通过冲激响应不变法和双线性变换法，将模拟滤波器的冲激响应转化为数字滤波器的冲激响应。

二、MATLAB在IIR数字滤波器设计中的应用MATLAB以其强大的计算和仿真能力，在数字滤波器设计中得到了广泛的应用。

设计师可以利用MATLAB的函数和工具箱，方便地实现IIR数字滤波器的设计、仿真和分析。

三、设计实例与分析以下是一个基于MATLAB的IIR数字滤波器设计实例：1.确定设计指标：通带截止频率为1kHz，阻带截止频率为2kHz，通带波纹小于1dB，阻带衰减大于40dB。

2.利用MATLAB的函数，如freqz、butter等，设计模拟低通滤波器。

3.将模拟滤波器的参数转化为数字滤波器的参数，如采样频率、阶数等。

4.利用MATLAB的函数，如impulse、bode等，对数字滤波器进行仿真和分析。

四、结论通过以上实例，可以看出MATLAB在IIR数字滤波器设计中的重要作用。

它不仅提供了方便的设计工具，还能实时地展示滤波器的性能，大大提高了设计效率和精度。

此外，IIR数字滤波器的设计方法和MATLAB的应用也可以推广到其他数字信号处理领域，如音频处理、图像处理等。

iir数字滤波器的设计方法IIR数字滤波器的设计方法IIR数字滤波器是一种常用的数字信号处理工具，用于对信号进行滤波和频率域处理。

其设计方法是基于传统的模拟滤波器设计技术，通过将连续时间滤波器转换为离散时间滤波器来实现。

本文将介绍IIR数字滤波器的设计方法和一些常见的实现技巧。

一、IIR数字滤波器的基本原理IIR数字滤波器是一种递归滤波器，其基本原理是将输入信号与滤波器的系数进行加权求和。

其输出信号不仅与当前输入值有关，还与之前的输入和输出值有关，通过不断迭代计算可以得到最终的输出结果。

二、IIR数字滤波器的设计步骤1. 确定滤波器的类型：低通滤波器、高通滤波器、带通滤波器或带阻滤波器。

2. 确定滤波器的阶数：阶数决定了滤波器的陡峭度和性能。

3. 选择滤波器的截止频率或通带范围。

4. 根据所选的滤波器类型和截止频率，设计滤波器的模拟原型。

5. 将模拟原型转换为数字滤波器。

三、IIR数字滤波器的设计方法1. 巴特沃斯滤波器设计方法：- 巴特沃斯滤波器是一种最常用的IIR数字滤波器，具有平坦的通带特性和陡峭的阻带特性。

- 设计方法为先将模拟滤波器转换为数字滤波器，然后通过对模拟滤波器进行归一化来确定截止频率。

2. 阻带衰减设计方法：- 阻带衰减设计方法是一种通过增加滤波器的阶数来提高滤波器阻带衰减特性的方法。

- 通过增加阶数，可以获得更陡峭的阻带特性，但同时也会增加计算复杂度和延迟。

3. 频率变换方法：- 频率变换方法是一种通过对滤波器的频率响应进行变换来设计滤波器的方法。

- 通过对模拟滤波器的频率响应进行变换，可以得到所需的数字滤波器。

四、IIR数字滤波器的实现技巧1. 级联结构：- 将多个一阶或二阶滤波器级联起来，可以得到更高阶的滤波器。

- 级联结构可以灵活地实现各种滤波器类型和阶数的设计。

2. 并联结构：- 将多个滤波器并联起来，可以实现更复杂的频率响应。

- 并联结构可以用于设计带通滤波器和带阻滤波器。