著名的几何定理

初中数学竞赛几何中常用的24个必备定理1. 同位角定理：同位角互相相等或互补。

2. 对顶角定理：对顶角相等。

3. 同旁内角定理：同旁内角互补。

4. 外角定理：与一个多边形任意一内角相对的外角相等。

5. 内角和定理：n边形的内角和为180度×(n-2)。

6. 相关角定理：相邻角互补，对顶角互相相等。

7. 垂直直角定理：垂线与直线相交，形成直角。

8. 垂线定理：直线上任意一点向另一直线作垂线，垂线所在直线与原直线垂直。

9. 三角形内角和定理：三角形内角和为180度。

10. 等腰三角形定理：等腰三角形的底角相等。

11. 等边三角形定理：等边三角形的三个内角均为60度。

12. 直角三角形性质：直角三角形斜边平方等于其他两条边平方和。

13. 等角定理：两角相等的两个三角形全等。

14. 外接圆定理：三角形三个顶点到外接圆圆心的距离相等。

15. 中线定理：连接三角形两边的中线相等。

16. 中位线定理：连接三角形两边中点的线段平分第三边。

17. 高线定理：连接三角形顶点与对边垂直的线段相交于三角形内心。

18. 海伦公式：用三角形三条边的长度求其面积：S=sqrt[p(p-a)(p-b)(p-c)]，其中p=(a+b+c)/2。

19. 正多边形内角定理：正n边形的内角和为(180度×(n-2))/n。

20. 球面三角形定理：球面三角形三个顶点到球心的距离相等。

三条边为大圆弧。

21. 圆周角定理：圆周角等于对应的弧所夹的圆心角。

22. 切线定理：切线相切于圆，与该切点相切的直线垂直于切线。

23. 弦长定理：在同一圆上，两条弦所夹的圆心角相等，则它们的弦长相等。

24. 弧长定理：同一圆上，两个相等的圆心角所对应的弧长相等。

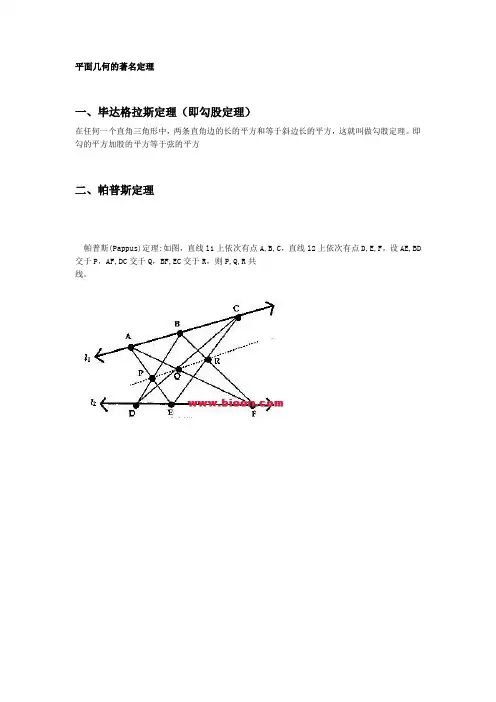
平面几何的著名定理一、毕达格拉斯定理（即勾股定理）在任何一个直角三角形中，两条直角边的长的平方和等于斜边长的平方，这就叫做勾股定理。

即勾的平方加股的平方等于弦的平方二、帕普斯定理帕普斯(Pappus)定理:如图，直线l1上依次有点A,B,C，直线l2上依次有点D,E,F，设AE,BD 交于P，AF,DC交于Q，BF,EC交于R，则P,Q,R共线。

三、影射定理（与相似三角形和比例有关）直角三角形射影定理（又叫欧几里德(Euclid)定理）：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。

每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC ,(3)(AC)^2;=CD·BC 。

等积式 (4)ABXAC=BCXAD(可用面积来证明)四、梅涅劳斯定理梅涅劳斯（Menelaus）定理（简称梅氏定理）是由古希腊数学家梅涅劳斯首先证明的。

它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

或：设X、Y、Z分别在△ABC的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。

证明一过点A作AG∥BC交DF的延长线于G，则AF/FB=AG/BD , CE/EA=DC/AG。

三式相乘得：(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二过点C作CP∥DF交AB于P，则BD/DC=FB/PF，CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立：若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/EA)=1，则F、D、E三点共线。

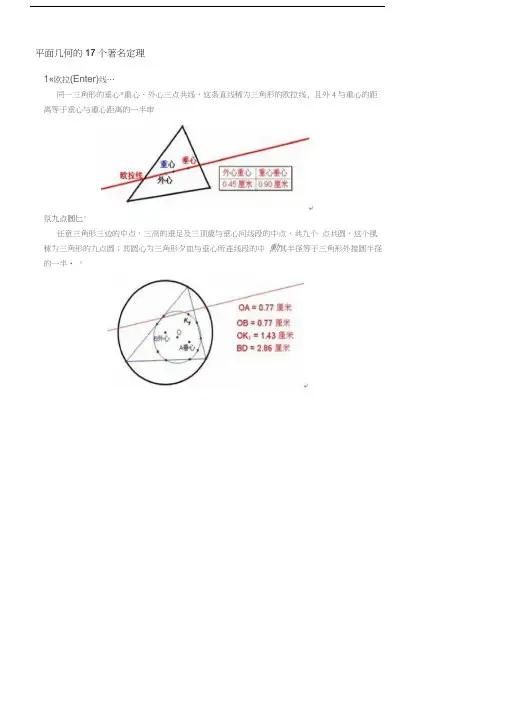
平面几何的17个著名定理1«欧拉(Enter)线…同一三角形的垂心*重心、外心三点共线，这条直线稀为三角形的欧拉线, 且外4与重心的距离等于垂心与重心距离的一半审氛九点圆匕*任意三角形三边的中点，三高的垂足及三顶歳与垂心问线段的中点，共九个点共圆，这个風秫为三角形的九点圆；其圆心为三角形夕皿与垂心所连线段的中勲其半径等于三角形外接圆半径的一半• *3.费尔马点…己知 P 为锐SAABC 内一点，当ZAPB = ZBPC= ZCPA= 120° 时，PA +PB + PC 的值最小，这个点P 称为AABC 的费尔马点。

心CP = 2.45 厘米AP = 1.64 厘米4、海伦(Heron)公式:：卩在ZXABC 中，边BC 、CA. AB 的长分别为a 、b 、c,若 严丄(a+b+c), “2则/XABC 的面积 S = Jp(p_a)(p_b)(p_c)，A7 p (p-AB>(p-BC)-(p-CA) = 8.96 殛米2BC AD = 8.96 J#米25、SK (Ceva)在AABC 中，过AABC 的顶点作相交于一点P 的直线，分别交边BC 、CA 、AB 与点D 、E 、F,则竺.—= 1；其逆亦真aDC EA FBBD = 2.78 MX DC = 1.95 厘米 CE = 1.64 厘米EA = 2.23 厘米 AF =2.31 厘米FB = 2.42 厘米 6、密格尔(Kfeuel)点=♦若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点，构成四个三角形，它们是AABF 、AAED . ABCE . ADCF ,贝I J 这四个三角形的外接圆共(韵借)备)"点，这个点称为密格尔点°卩A B DP （托动）7、葛尔刚（仙輙峻）点2A ABC 的内切圆分别切边AB 、BC 、C 為于点D 、E 、F,则AE 、BF 、CD 三线共点，这个点称为葛尔刚点。

立体几何的八个判定定理立体几何的八个判定定理是指由英国数学家约翰·威尔逊（John Wallis）在17th century所提出的一套定理。

其中包括：（1）贝瑟尔定理：任意一个平面三角形的内角之和等于180度。

（2）杨氏定理：任意一个对角相交的多边形，其内部角之和等于其外部角之和。

（3）特斯克定理：在同样边上的三个面有关的角相加等于180度。

（4）柯尔定理：在同样边上的四个面有关的角相加等于360度。

（5）高斯定理：任意一个多面体的角之和等于360度乘以面的数量。

（6）伯尔定理：任意一个多边形的角之和大于360度。

（7）双旋定理：任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。

（8）欧几里得定理：任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。

贝瑟尔定理是最重要的立体几何判定定理，表明任意一个平面三角形的三个内角之和都等于180度。

这个定理是用来表示平面三角形的构成的，而这个定理也被用来表示一个多边形的构成。

杨氏定理是贝瑟尔定理的推广，即任意一个对角相交的多边形，其内部角之和等于其外部角之和。

特斯克定理是杨氏定理的一个特殊情况，表示在同样边上的三个面有关的角相加等于180度。

柯尔定理也是杨氏定理的一个特殊情况，表示在同样边上的四个面有关的角相加等于360度。

高斯定理是一个重要的立体几何判定定理，即任意一个多面体的角之和等于360度乘以面的数量。

这个定理与贝瑟尔定理的相似之处在于，它们都可以用来表明多面体的构成，它们都表示了一个多面体的性质。

伯尔定理是高斯定理的一个推广，表明任意一个多边形的角之和大于360度。

双旋定理是一个重要的立体几何判定定理，表明任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。

欧几里得定理也是一个重要的立体几何判定定理，表明任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。

总的来说，立体几何的八个判定定理是一个重要的数学工具，它们不仅可以帮助人们更好地理解多面体和多边形的构造，还可以帮助人们解决一些复杂的问题，比如求解三角形的面积，求解多面体的体积等等。

几何中的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

6、三角形各边的垂直一平分线交于一点。

7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O，垂心为H，从O向BC边引垂线，设垂足不L，则AH=2OL9、三角形的外心，垂心，重心在同一条直线上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中心、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上12、库立奇*大上定理：（圆内接四边形的九点圆）圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

13、（内心）三角形的三条内角平分线交于一点，内切圆的半径公式：r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、（旁心）三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理：（巴布斯定理）设三角形ABC的边BC的中点为P，则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理：P将三角形ABC的边BC内分成m:n，则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，连接AB中点M和对角线交点E 的直线垂直于CD18、阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n（值不为1）的点P，位于将线段AB 分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形，21、爱尔可斯定理1：若△ABC和三角形△都是正三角形，则由线段AD、BE、CF的重心构成的三角形也是正三角形。

几何五大模型定理
几何学是一个古老的学科，并在数学领域发挥着不可替代的作用。

过去2000多年来，一些极具影响力的几何学家们有力地推动了几何学研究的发展，创造了许多引人注目的几何模型定理。

以下将介绍五大几何模型定理，它们是几何学的代表性研究成果。

第一个几何模型定理是欧几里得定理，也称为“欧几里得尺规定理”，这是古希腊数学家欧几里得著名的定理。

它声明：“三角形内角之和等于180度”。

它是数学基本概念的基础，借此可以证明各种几何图形的构成关系。

第二个几何模型定理是埃及人定理，也称为“埃及三角形定理”。

这是一个基本定理，它宣称：“正三角形的高等于它的底乘以三角形的高”。

第三个几何模型定理是勾股定理，这是古希腊数学家勾股第六世纪首次提出的定理。

它表明：“三角形的斜边的平方等于两常规边的平方之和”。

第四个几何模型定理是朱丽叶定理，由十八世纪法国数学家朱丽叶蒙德拉克提出。

它宣称：“在平面内，给定一个三角形与
它的外接圆，三角形内角周长和半径之比等于外角角度和圆周长的比之和”。

第五个几何模型定理是莱布尼茨定理，由德国数学家马克斯·莱布尼茨于1794年提出的定理。

它声明：“存在唯一的平行四边形，其面积等于任何给定四边形的面积之和”。

以上就是几何学五大模型定理的主要内容，它们的发现和推导象征着几何学的成熟，也为更深入研究几何学提供了基础。

立体几何经典定理概述(八大定理)立体几何经典定理概述（八大定理）本文将概述立体几何中的八大经典定理。

立体几何是研究三维空间中的图形和形体的数学学科，定理是在研究过程中得出的具有重要意义的数学命题。

1. 欧拉定理欧拉定理是立体几何中最著名的定理之一。

它规定了三维物体的面、顶点和边的关系。

具体来说，如果一个多面体满足面+顶点-边=2的关系，那么它就是一个封闭的多面体。

欧拉定理形象地描述了三维世界中多面体的特性。

2. 柯西定理柯西定理是关于立体几何中平行四边形的定理。

它指出，对于一个平行四边形，其对角线互相平分彼此。

这个定理在解决平行四边形的性质和关系时非常有用，能够帮助我们更好地理解平面几何的性质。

3. 形心定理形心定理是关于多边形形心的定理。

形心是多边形中所有顶点的连线的交点，该定理指出，任意多边形的形心一定在多边形的重心和质心连线的上面。

形心定理可以帮助我们确定多边形的形心位置，从而研究多边形的性质和变形。

4. 二等分线定理二等分线定理是关于立体几何中等分线的定理。

它规定了等分线在多面体中的特性，即等分线和相应的两个面以及它们的交点构成的平面垂直。

这个定理在解决多面体的等分线问题时非常有用，能够帮助我们进一步理解多面体的性质。

5. 范恩艾克线定理范恩艾克线定理是关于球面上切线和交角的定理。

它指出，在球面上，任意切线与相应交角的正弦值等于球心到交点的距离和切线长的比值。

这个定理在解决球面上的切线和交角问题时非常有用，能够帮助我们研究球面的性质和切线关系。

6. 斯坦纳定理斯坦纳定理是关于三维空间中图的生成树的定理。

生成树是一个无圈连通图的子图，其中包含了所有顶点并且边的数量最少。

斯坦纳定理指出，在三维空间中的图中，生成树的条数等于顶点数减去连通分量的数量。

这个定理在解决三维空间图的生成树问题时非常有用。

7. 勾股定理勾股定理是立体几何中最基础的定理之一。

它规定了直角三角形边长之间的关系，即直角三角形的两个直角边的平方和等于斜边的平方。

１勾股（毕达哥拉斯）定理*；*凡是容易找到内容及证明的，我们只记下他的名称，下同。

２射影（欧几里得定理）定理；３三角形中线共点（重心），并被该点分为２：１两部分；４四边形对边中点连线与两条对角线中点连线三线共点；５间隔连接六边形边的中点所得两三角形重心重合；６三角形三边中垂线交于一点（外心）；７三角形的三条高交于一点（垂心）；８三角形ABC外心为O，垂心为H，OL垂直BC于L，则AH=2OL；９三角形外心、垂心、重心三点共线；１０三角形各边中点、高的垂足、垂心与各顶点连线的中点，九点共圆（九点圆、欧拉圆或费尔巴哈圆*哲学家费尔巴哈的次兄，不要搞混）１１欧拉定理：三角形外心、重心、九点圆圆心、垂心依次共线（欧拉线）；１２库利奇（J.L.Coolidge）--大上（茂乔）定理：过圆上四点中任三点作三角形，这四个三角形九点圆圆心四点共圆，他被称作圆上四点构成四边形的九点圆；１３三角形三条内角平分线交于一点（内心），若三边为a、b、c，内切圆半径是（（s-a）*（s-b）*（s-c）/s）^0.5,面积是（（s-a）*（s-b）*（s-c）*s）^0.5--海伦公式，其中s是该三角形的半周长；１４三角形任一内角平分线与其余两顶点处的外角平分线三线共点（旁心，三个）；１５泰勒斯（Thales）定理：直径所对的圆周角为直角，（据说SAS、ASA、SSS也是泰勒斯发现的）；１６希波克拉茨（Hippocrates）定理：直角三角形ABC中，角C为直角，在斜边AB的同侧分别以BC、AC、AB为直径作半圆分别记为半圆AC、半圆AB和半圆BC，用半圆AC减去半圆AC与半圆AB公共部分得到月形AC，用半圆BC减去半圆BC与半圆AB公共部分得到月形BC，则月形BC与月形AC的面积之和与三角形ABC的面积相等；１７巴布斯定理（Pappus定理有两个，这是其一）：三角形ABC中，P为BC边中点，则AB^2+AC^2=2（AP^2+BP^2），这个定理又叫中线定理；１８斯图尔特定理（有些书翻译成斯特华特定理，Stewart）：三角形ABC中，P内分BC为m：n，则nAB^2+mAC^2=(m+n)AP^2+(mn/(m+n))BP^2，当m：n为1：1时，即为巴布斯定理；１９波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，AB中点M和对角线交点E两点确定的直线ME与CD垂直；２０阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n（≠1）的点P，位于将线段AB分成m:n的内分点C 和外分点D 两点所连线段CD为直径的定圆周上；２１托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC×BD，托勒密定理的逆定理也成立，托勒密定理推广：任意的四边形ABCD，有AB×CD+AD×BC≥AC×BD；２２以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形；２３爱尔可斯定理1（Echols）：若△A1B1C1和三角形△A2B2C2都是正三角形，则由线段A1A2、B1B2、C1C2的中心构成的三角形也是正三角形；２４爱尔可斯定理2：若△A1B1C1、△A2B2C2、△A3B3C3都是正三角形，则由三角形△A1A2A3、△B1B2B3、△C1C2C3的重心构成的三角形是正三角形；２５梅涅劳斯定理（Menelaus）：设△ABC的三边BC、CA、AB所在直线和一条不经过它们任一顶点的直线的分别交于为P、Q、R三点，则有(BP/PC)×(CQ/QA)×(AR/RB)=1,梅涅劳斯定理的逆定理也成立，若我们使用有向线段来描述这个问题，等式右侧的常数是-1；２６应用25，我们可以得到：设△ABC的∠A的外角平分线交边BC于P、∠C的平分线交边AB于R，∠B的平分线交边CA 于Q，则P、Q、R三点共线；２７应用25，我们可以得到：过任意△ABC的三个顶点A、B、C作它的外接圆的切线，分别和BC、CA、AB的延长线交于点P、Q、R，则P、Q、R三点共线；２８塞瓦定理（Ceva）：设△ABC的三个顶点A、B、C的与不在三边所在直线上一点S分别确定的三条直线AS、BS、C S分别与边BC、CA、AB所在直线交于P、Q、R三点，则(BP/PC)×(CQ/QA)×(AR/RB)=1,显然我们可以用它来证明三角形三条中线交于一点，塞瓦定理的逆定理也成立，这个定理写成有向线段的形式，等式不变；２９应用28，我们可以得到：设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E，BE和CD交于S，AS经过BC的中点M；３０△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T，则AR、BS、CT三线共点；３１西摩松定理（Simson，当然我们知道这个定理不应算在他的名下）：从△ABC的外接圆上任意一点P向三边BC、CA、AB 所在直线引垂线，垂足分别是D、E、R，则D、E、R三点共线（叫西摩松线）西摩松定理的逆定理也成立；３２史坦纳定理（Steiner）：设△ABC的垂心为H，其外接圆的任意点P，这时关于△ABC的点P的西摩松线通过线段PH的中点；３３应用32，我们可以得到：△ABC的外接圆上的一点P的关于三边BC、CA、AB的对称点和△ABC的垂心H四点共线（称作点P关于△ABC的镜象线，显然该直线与西摩松线平行）；３４波朗杰--藤下定理：P、Q、R在△ABC的外接圆上，则P、Q、R分别关于△ABC的三条西摩松线三线共点的充要条件是：弧AP+弧BQ+弧CR=0(mod2∏)，（书中没有注明波朗杰、藤下二人的来历）；３５波朗杰--藤下定理推论1：P、Q、R在△ABC的外接圆上，若P、Q、R关于△ABC的西摩松线交于一点S，则A、B、C 三点关于△PQR的的西摩松线也交于S；３６波朗杰--藤下定理推论2：在推论1（35）中，三条西摩松线的交点S是A、B、C、P、Q、R六点任取三点所作的三角形的垂心H1 和其余三点所作的三角形的垂心H2 所连线段H1H2的中点；３７波朗杰--藤下定理推论3，有贺(？)定理：由35，l是△ABC的外接圆上的一点P的关于△ABC的西摩松线，若弦QR 与ｌ互相垂直，则点P、Q、R的关于△ABC的西摩松线交于一点；３８波朗杰--藤下定理推论4：从△ABC的顶点向边BC、CA、AB引垂线，垂足分别是D、E、F，且BC、CA、AB的中点分别是L、M、N，则D、E、F、L、M、N六点共圆，这时L、M、N三点关于△DEF的三条西摩松线共点；３９△ABC的外接圆直径两个端点P、Q关于该三角形的西摩松线互相垂直，其交点在九点圆上；４０安宁定理：四点共圆，作每一点关于以其他三点为顶点三角形的西摩松线，此四线共点；４１卡诺（L.N.M.Carnot）定理：通过△ABC的外接圆的一点P，引与三边BC、CA、AB分别成同向的等角的直线PD、PE、PF，与三边的交点分别是D、E、F，则D、E、F三点共线；４２奥倍尔定理：通过△ABC的三个顶点引互相平行的三条直线，设它们与△ABC的外接圆的交点分别是A1、B1、C1，在△ABC的外接圆取一点P，则PA1、PB1、PC1与△ABC的三边BC、CA、AB所在直线的交点分别是D、E、F，则D、E、F三点共线；４３设P、Q为△ABC的外接圆的异于A、B、C的两点，P点的关于三边BC、CA、AB的对称点分别是U、V、W，这时，QU、QV、QW和三边BC、CA、AB所在直线的分别交于是D、E、F，则D、E、F三点共线；４４他拿定理：设P、Q为关于△ABC的外接圆的一对反点，点P的关于三边BC、CA、AB的对称点分别是U、V、W，这时，如果QU、QV、QW与边BC、CA、AB所在直线的交点分别为D、E、F，则D、E、F三点共线（反点：P、Q分别为圆O的半径OC和其延长线的两点，如果OC^2=OQ×OP，即OC是OQ、OP的比例中项，则称P、Q两点关于圆O互为反点）；４５朗古来定理：圆上四点，以其中任三点作三角形，在圆周取一点P，作P点的关于这四个三角形的西摩松线，再从P向这四条西摩松线引垂线，则四垂足共线；４６自三角形各边中点，分别向所对顶点处的外接圆切线引垂线，三条垂线交于九点圆圆心；４７ｎ点共圆，任ｎ－１点重心向其余一点处切线引垂线，此ｎ条垂线共点；４８康托尔（M.B.Cantor）定理1：一个圆周上有n个点，从其中任意n-2个点的重心向余下两点的连线所引的垂线共点;４９康托尔定理2：一个圆周上有A、B、C、D四点及M、N两点，作M和N分别关于三角形△BCD、△CDA、△DAB、△ABC中的两条西摩松线的交点，此四点共线（康托尔线）；５０康托尔定理3：一个圆周上有A、B、C、D四点及M、N、L三点，而l、m、n分别是M、N两点，L、N两点，M、L 两点的关于四边形ABCD的康托尔线，则l、m、n三线共点（康托尔点）；５１康托尔定理4：一个圆周上有A、B、C、D、E五点及M、N、L三点，则M、N、L三点关于四边形BCDE、CDEA、DEAB、EABC、ABCD的康托尔点五点共线（康托尔线），类似的这组定理可以无限迭代下去；５２费尔巴赫定理：三角形的九点圆与内切圆和旁切圆相切；５３莫利（F.Morley，通译莫莱）定理：任三角形的三个内角三等分，靠近边的两条三分角线相一个交点分别为ABC，则三角形ABC是正三角形（莫利正三角形）；５４牛顿（这个被苹果砸到头的第二任卢卡斯不必介绍了吧）定理1：四边形两组对边的延长线的交点所连线段的中点，两条对角线的中点，三点共线（牛顿线）；５６牛顿定理2：任一圆的圆心，外切四边形的两条对角线的中点，三点共线；58、笛沙格（G.Desargues）定理：两个三角形若对应点连线共点，则对应边交点（如果有）共线；５９巴布斯定理（这是第二个）：两条相异直线ａ、ｂ，ａ上有Ａｉ（ｉ＝１，２，３）三点，ｂ上有Ｂｉ（ｉ＝１，２，３）三点，则ＡｉＢｊ与ＢｉＡｊ（ｉ≠ｊ，ｉ，ｊ＝１，２，３）所交三点Ｃｉ（ｉ＝１，２，３）共线；６０巴斯加（Pascal）定理与布利安松（Brianchon）定理：圆内接六边形对边交点共线-圆外切六边形相对顶点连线共点.----------------------------------烟花绚烂，总算在除夕写完这篇《遗忘》的笔记（特意将书中第十三章调和点组扣掉，好给以后留个念想），满世温馨却独孤我一人，就把这篇笔记当作我送给自己的新年礼物吧，希望今年我可免去些执着，添几缕牵挂，余愿足矣。

【认识平面几何的61个著名定理，自行画出图形来学习，★部分要求证明出来】★1、勾股定理（毕达哥拉斯定理）★2、射影定理（欧几里得定理）★3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线和两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

★6、三角形各边的垂直平分线交于一点。

★7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC 的外心为O ，垂心为H ，从O 向BC 边引垂线，设垂足不L ，则AH=2OL9、三角形的外心，垂心，重心在同一条直线上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中心、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上12、库立奇大上定理：（圆内接四边形的九点圆） 圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

★13、（内心）三角形的三条内角平分线交于一点，内切圆的半径公式： ()()()s c s b s a s r ---=，s 为三角形周长的一半★14、（旁心）三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理：（巴布斯定理）设三角形ABC的边BC的中点为P，则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理：P将三角形ABC的边BC分成m和n两段，则有n×AB2+m×AC2=BC×（AP2+mn）17、波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，连接AB中点M和对角线交点E 的直线垂直于CD18、阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n（值不为1）的点P，位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上★19、托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC×BD★20、以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形，21、爱尔可斯定理1：若△ABC和△DEF都是正三角形，则由线段AD、BE、CF的重心构成的三角形也是正三角形。

初中数学竞赛几何中常用的24个必备定理在初中数学竞赛中，几何部分是一个重要的考察内容。

在几何题中，经常会涉及到一些常用的定理，掌握这些定理不仅能够帮助我们解题，还能够提高我们的解题速度和准确性。

下面列举了初中数学竞赛中常用的24个必备定理，希望能够帮助大家在竞赛中取得更好的成绩。

1. 垂径定理：直径是直角，半径垂直于弦。

2. 圆心角定理：圆心角是弦对圆心的角，两倍弦对圆心的角等于弧度。

3. 等腰三角形底角定理：等腰三角形的底角相等。

4. 等腰三角形等腰定理：等腰三角形的底边相等。

5. 等边三角形定理：等边三角形的三边相等。

6. 同位角定理：同位角相等。

7. 同旁内角定理：同旁内角相等。

8. 同旁外角定理：同旁外角相等。

9. 余角定理：余角相等。

10. 三角形内角和定理：三角形的内角和等于180度。

11. 三角形外角和定理：三角形的外角和等于360度。

12. 三角形角平分定理：角平分线把角分成两个相等的角。

13. 同角的角平分定理：同角的角平分线相等。

14. 三角形角平分线定理：角平分线相等。

15. 等角三角形角平分线定理：等角三角形角平分线相等。

16. 三角形中线定理：三角形的中线平行于底边，且等于底边的一半。

17. 三角形角平分线定理：角平分线交角的角度相等。

18. 三角形角平分线定理：角平分线角度相等。

19. 三角形角平分线定理：角平分线角度相等。

20. 三角形角平分线定理：角平分线角度相等。

21. 三角形角平分线定理：角平分线角度相等。

22. 三角形角平分线定理：角平分线角度相等。

23. 三角形角平分线定理：角平分线角度相等。

24. 三角形角平分线定理：角平分线角度相等。

这些定理是初中数学竞赛中常用的定理，掌握这些定理可以帮助我们更好地理解和解题。

希望大家在备战初中数学竞赛的过程中，能够充分掌握这些定理，提高自己的数学水平，取得理想的成绩。

祝大家都能在数学竞赛中取得好成绩！。

平面几何著名定理1、欧拉（Euler ）线：同一三角形的垂心、重心、外心三点共线，这条直线称为三角形的欧拉线；且外心与重心的距离等于垂心与重心距离的一半2、九点圆：任意三角形三边的中点，三高的垂足及三顶点与垂心间线段的中点，共九个点共圆，这个圆称为三角形的九点圆；其圆心为三角形外心与垂心所连线段的中点，其半径等于三角形外接圆半径的一半。

3、费尔马点：已知P 为锐角△ABC 内一点，当∠APB ＝∠BPC ＝∠CPA ＝120°时，PA ＋PB ＋PC 的值最小，这个点P 称为△ABC 的费尔马点。

4、海伦（Heron ）公式：在△ABC 中，边BC 、CA 、AB 的长分别为a 、b 、c ，若p ＝21（a ＋b ＋c ）， 则△ABC 的面积S ＝))()((c p b p a p p ---5、塞瓦（Ceva ）定理：在△ABC 中，过△ABC 的顶点作相交于一点P 的直线，分别交边BC 、CA 、AB 与点D 、E 、F ，则1=⋅⋅FBAFEA CE DC BD ；其逆亦真6、密格尔（Miquel ）点：若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点，构成四个三角形，它们是△ABF 、△AED 、△BCE 、△DCF ，则这四个三角形的外接圆共点，这个点称为密格尔点。

7、葛尔刚（Gergonne ）点:△ABC 的内切圆分别切边AB 、BC 、CA 于点D 、E 、F ，则AE 、BF 、CD 三线共点，这个点称为葛尔刚点。

8、西摩松（Simson ）线：已知P 为△ABC 外接圆周上任意一点，PD ⊥BC ，PE ⊥ACPF ⊥AB ，D 、E 、F 为垂足，则D 、E 、F 三点共线，这条直线叫做西摩松线。

9、黄金分割：把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项,这样的分割称为黄金分割11、笛沙格（Desargues）定理：已知在△ABC与△A'B'C'中，AA'、BB'、CC'三线相交于点O，BC与B'C'、CA与C'A'、AB 与A'B'分别相交于点X、Y、Z，则X、Y、Z三点共线；其逆亦真。

阿基米德折弦定理：AB和BC是⊙O的两条弦（即ABC是圆的一条折弦）,BC〉AB，M是弧ABC的中点，则从M向BC所作垂线之垂足D是折弦ABC的中点，即CD=AB+BD.从圆周上任一点出发的两条弦，所组成的折线,我们称之为该图的一条折弦.角平分线定理定理1：角平分线上的点到这个角两边的距离相等。

该命题逆定理成立：在角的内部到一个角的两边距离相等的点在这个角的角平分线上。

定理2：三角形一个角的平分线分其对边所成的两条线段与这个角的两边对应成比例。

该命题逆定理成立:如果三角形一边上的某个点分这条边所成的两条线段与这条边的对角的两边对应成比例，那么该点与对角顶点的连线是三角形的一条角平分线.xv=uy燕尾定理因此图类似燕尾而得名，是五大模型之一,是一个关于三角形的定理(如图△ABC，D、E、F 为BC、CA、AB 上点，满足AD、BE、CF 交于同一点O）。

S△ABC中,S△AOB：S△AOC=S△BDO:S△CDO=BD：CD；同理，S△AOC：S△BOC=S△AFO：S△BFO=AF：BF;S△BOC：S△BOA=S△CEO：S△AEO=EC：AE。

推论:共边比例定理：四边形ABCD（不一定是凸四边形)，设AC，BD相交于E，则有BE ：DE=S△ABC :S△ADC。

此定理是面积法最重要的定理.典型例题：如图三角形ABC的面积是10平方厘米，AE=ED,BD=2DC，则阴影部分的面积是_____平方厘米．答案：4解析:过D作DM‖BF交AC于M(如图)因为BD=2DC，因为AE=DE,所以△ABE的面积与△DBE的面积相等，所以阴影部分的面积为△DBE的面积+△AEF的面积，即三角形AFB的面积,由DM‖BF知道△DMC相似△CBF 所以CM：CF=CD：CB=1：3，即FM=CF，因为EF是△ADM的中位线，AF=MF，所以AF=AC，由此即可求出三角形AFB的面积，即阴影部分的面积．解：过D作DM‖BF交AC于M(如图）因为BD=2DC，因为AE=DE，所以△ABE的面积与△DBE的面积相等所以阴影部分的面积为△DBE的面积+△AEF的面积DM‖BF所以△DMC相似△CBF 所以CM:CF=CD：CB=1：3即FM=CF因为EF是△ADM的中位线，AF=MF，所以AF=AC所以△ABF的面积10×=4（平方厘米）即阴影部分的面积（即△DBE的面积加△AEF的面积）等于4平方厘米答：阴影部分的面积是4平方厘米,故答案为：4．共角定理：若两三角形有一组对应角相等或互补,则它们的面积比等于对应两边乘积的比。

数学史上著名的定理数学是人类的伟大创造之一，历史上有许多著名的数学定理和理论，它们为我们的认知和科技发展做出了巨大的贡献。

本文将介绍数学史上一些著名的定理，包括欧几里得定理、毕达哥拉斯定理、柏拉图定理、牛顿-莱布尼茨定理、柯西定理、笛卡尔定理、泰勒定理和欧拉公式。

1.欧几里得定理欧几里得（Euclid）是古希腊数学家，他的代表作《几何原本》是世界上最著名的数学著作之一。

欧几里得定理是平面几何中的一个基本定理，它指出：如果一个三角形的三条边分别等于另外两个三角形的三条边，那么这两个三角形必然相等。

这个定理的证明方法有很多种，其中最简单的是利用反证法。

2.毕达哥拉斯定理毕达哥拉斯（Pythagoras）是古希腊数学家，他的代表作也是《几何原本》。

毕达哥拉斯定理是直角三角形的一个重要性质，它指出：在一个直角三角形中，斜边的平方等于两直角边的平方和。

这个定理的证明方法很简单，只需要利用勾股定理即可。

3.柏拉图定理柏拉图（Plato）是古希腊哲学家，他的代表作之一是《对话录》。

柏拉图定理是指一个等腰三角形的底角等于它相对的顶角的一半。

这个定理的证明方法比较复杂，需要利用相似三角形的性质。

4.牛顿-莱布尼茨定理牛顿（Isaac Newton）是英国物理学家和数学家，他的代表作之一是《自然哲学之数学原理》。

莱布尼茨（Gottfried Wilhelm Leibniz）是德国数学家。

牛顿-莱布尼茨定理是指微积分学中的积分与求导是互逆的运算，这个定理的证明方法需要利用极限和导数的基本性质。

5.柯西定理柯西（Augustin-Louis Cauchy）是法国数学家，他的代表作之一是《分析教程》。

柯西定理是指任何一个周期函数都可以表示为傅里叶级数形式，这个定理的证明方法需要利用傅里叶级数的展开式。

6.笛卡尔定理笛卡尔（RenéDescartes）是法国哲学家和数学家，他的代表作之一是《几何原本》。

笛卡尔定理是指任何一条线段都可以被一个点分成两部分，其中一部分比另一部分长。

空间几何的八大定理空间几何有许多重要的定理，其中比较著名的有欧氏几何的五大公设，非欧几何的平行公设，以及一些基础定理，如勾股定理、锐角三角函数定理等。

以下是空间几何的八大定理：1. 欧氏几何的平行公设：在平面上，经过一点外一直线的直线只有一条与这条直线平行的直线。

这个公设是欧氏几何的基础，它确定了平面中直线的相互关系。

2. 勾股定理：三角形直角边的平方和等于斜边的平方。

这个定理是三角学中最基础的定理之一，也是空间几何中最重要的定理之一，它将三角形的长度关系与几何形状联系起来。

3. 圆锥曲线：圆锥曲线是平面上直线与圆锥相交而形成的曲线。

它包括圆、椭圆、双曲线和抛物线等多种形式，是空间几何中的基础概念之一。

4. 定比分点定理：在一条线段上，将其分为若干个部分，若知道其中某些部分的长度比例，则可以通过这些比例来确定这些部分的具体长度。

这个定理是空间几何中的基础定理之一，它可以用来解决许多关于长度和比例的问题。

5. 平面角的和定理：平面上两个相交直线所形成的相邻角之和等于180度。

这个定理是平面几何中的基础定理之一，它可以帮助我们理解平面上的角度关系。

6. 球面三角学：球面三角学研究的是球面上的三角形，其中包括球面上的角度、长度和面积等概念。

它是空间几何中的重要分支之一，与地理学、天文学等领域有着广泛的应用。

7. 平行四边形法则：平行四边形法则是指在平面上，任意两个平行四边形的对角线交点可以将它们分成四个全等的三角形。

这个法则是平行四边形的基础定理之一，它可以用来解决许多关于平行四边形的问题。

8. 空间中的直线和平面：在空间中，直线和平面之间有着重要的关系，它们可以相互垂直或平行，形成不同的几何形状。

这个定理是空间几何中的基础定理之一，它可以帮助我们理解空间中的几何结构。

关于平面几何的60条著名定理一些平面几何的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

6、三角形各边的垂直一平分线交于一点。

7、三角形的三条高线交于一点8、设三角形ABC的外心为O，垂心为H，从O向BC边引垂线，设垂足为L，则AH=2OL9、三角形的外心，垂心，重心在同一条直线（欧拉线）上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中心、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上12、库立奇*大上定理：（圆内接四边形的九点圆）圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

13、（内心）三角形的三条内角平分线交于一点，内切圆的半径公式：r=(s-a)(s-b)(s-c)s，s为三角形周长的一半14、（旁心）三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理：（巴布斯定理）设三角形ABC的边BC的中点为P，则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理：P将三角形ABC的边BC内分成m:n，则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n （值不为1）的点P，位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形，21、爱尔可斯定理1：若△ABC和△DEF都是正三角形，则由线段AD、BE、CF的中心构成的三角形也是正三角形。