蜗壳设计
- 格式：doc
- 大小：987.00 KB
- 文档页数：7
下载文档原格式
合集下载
蜗壳设计和优化
蜗壳设计和优化对于大多数径流式叶轮机械来说，蜗壳都是不可或缺的。
蜗壳一般需要定义多个横截面，这些横截面都是2D曲线并沿着圆周方向进行扫略。
一般而言，在泵和涡轮增压器中都包含蜗壳和叶轮。
对于泵和压气机而言，蜗壳的作用是，通过降低介质的速度，将其动能转化为压力势能，从而使其压力增加。
然而涡轮的蜗壳却有着相反的功能，即将废气的压力势能转化为动能（来驱动叶轮）。
CAESES是利用CFD进行自动化形状优化的先进的蜗壳设计优化工具。
其先进的参数化蜗壳模型，具有较高的稳定性，并通过高度自动化的流程能够节省您大量的工作时间。
在CAESES里创建的参数化蜗壳模型设计蜗壳的挑战系统的蜗壳流动优化是一项耗时的工作，通常这是一个反复迭代过程。
CFD 工程师会对一个之前由CAD部门设计创建的模型进行分析，得到分析结果后CFD工程师向CAD同事介绍如何改变形状，CAD工程师调整模型，并将其返回给CFD工程师。
这个循环可能需要花费几天甚至几周的时间，直到一个新的（性能改进的）蜗壳被开发出来。
考虑到（加入）其他部件（如叶轮和扩压器）能有更好的性能预测，那么情况将变得更加复杂。
理论上，CAESES能有效地将这项工作的耗时从几个月缩短到几天。
蜗舌模型这是主涡壳表面分别与入口（涡轮）或出口（压缩机）几何相交的区域。
CAESES提供各种技术和解决方案，为您解决这个棘手的工作。
这极大地加速了蜗舌几何的建模过程，并使得最终的蜗壳在自动化变形和优化期间绝对稳健。
稳健的蜗舌模型应用于自动化变形和优化过程横截面的定义CAESES中可以自定义横截面2D型线的形式，或导入现有数据以将其转换为参数化截面。
蜗壳通常由典型的分布规律控制，例如A/R比率，这些都可以在CAESES中进行设定。
CFD专家通常想要尝试自己的一些想法，并考虑更多与流动过程相符的形状控制。
这些想法和任意几何约束都可以在CAESES高度集成的蜗壳模型中直接考虑进去。
用户自定义2D横截面任意蜗壳模型的解决方案无论您使用的是何种设备或者您的蜗壳模型有多么复杂，对于全自动化模型优化，CAESES都是一个理想的选择，它可以节省您大量的时间和人力资源。
水轮机课程设计蜗壳设计
水轮机课程设计 蜗壳设计一、课程目标知识目标：1. 学生能理解水轮机蜗壳的基本结构及其在水力发电中的作用；2. 学生能够掌握蜗壳设计的基本原理，包括流速分布、水流角度和压力的计算；3. 学生能够了解并描述影响蜗壳效率的主要因素。
技能目标：1. 学生能够运用所学知识，进行蜗壳进出口直径、形状和长度的初步计算；2. 学生通过实际案例分析和模拟实验，培养解决蜗壳设计过程中遇到问题的能力；3. 学生能够运用CAD软件或其他绘图工具，绘制出符合技术要求的蜗壳结构图。
情感态度价值观目标：1. 学生通过课程学习，培养对水利工程学科的热爱和对水轮机蜗壳设计的兴趣；2. 学生在学习过程中，树立节能减排和可持续发展的观念，认识到蜗壳设计在环境保护和资源合理利用方面的重要性；3. 学生能够通过团队协作完成设计任务，培养沟通协调能力和集体荣誉感。
课程性质：本课程为应用实践性课程，结合理论知识和实际操作，提高学生的工程实践能力。
学生特点：学生为高中年级，具有一定的物理基础和数学计算能力，对工程设计和实践操作具有好奇心。
教学要求：注重理论与实践相结合，鼓励学生主动参与，培养其解决问题的能力和创新思维。
通过分解课程目标为具体学习成果，使学生在课程结束时能够达到预定的教学效果。
二、教学内容1. 引言：水轮机蜗壳的作用与结构简介，使学生了解蜗壳在水轮机中的重要性。
相关教材章节：第一章 水轮机概述2. 蜗壳设计原理：a. 流体力学基础，包括流速分布、水流角度和压力的计算；b. 蜗壳设计的基本参数及其相互关系；c. 影响蜗壳效率的因素。
相关教材章节：第二章 水轮机蜗壳设计原理3. 蜗壳设计计算：a. 蜗壳进出口直径、形状和长度的计算方法；b. 实际案例分析，以加深学生对蜗壳设计的理解；c. 模拟实验，锻炼学生解决实际问题的能力。
相关教材章节：第三章 蜗壳设计计算4. 蜗壳设计实践：a. 运用CAD软件或其他绘图工具进行蜗壳结构图的绘制；b. 团队协作完成蜗壳设计任务，培养学生的沟通协调能力；c. 针对设计方案进行评价和优化。
高比转离心风机速蜗壳设计
高比转离心风机速蜗壳设计1. 高比转离心风机的特点与优势高比转离心风机通常是指转速在10000转/分钟以上的离心风机，具有以下特点和优势：高效率：高比转离心风机采用高速旋转的转子，配以合理设计的蜗壳，能够产生较大的压力和流量，实现高效能的风动力转换。
小型化：相比传统离心风机，高比转离心风机在相同流量和压力下，可以通过提高转速和减小机身尺寸来实现风机的小型化，从而节省空间。
轻量化：高比转离心风机采用先进的材料和结构设计，减少风机的重量，便于悬挂和安装，适用于各种工业和商业场景的需求。
2. 转速蜗壳设计要考虑的因素在设计高比转离心风机的转速蜗壳时，需要考虑以下因素：流动性能：蜗壳的内部结构需要符合流动的要求，保证风气流的顺畅流动，减小损失。
压力扩散：蜗壳的设计应使风气流在进入蜗壳后能够进行适当的压力扩散，从而使得风压的分布更加合理，减小压力损失。
转向角度：在设计蜗壳的时候，需要考虑流体在转向过程中的能量转换和损失，通过合理的转向角度设计来减小能量损失。
材料选择：蜗壳需要采用具有良好机械性能、耐磨性和耐腐蚀性的材料，以保证蜗壳的使用寿命和性能稳定性。
噪音和振动：转速蜗壳的设计还需要考虑减小噪音和振动，通过合理的结构和材料设计来降低风机工作时的噪音和振动水平。
3. 设计方法和步骤高比转离心风机转速蜗壳的设计可以遵循以下步骤和方法：1.确定设计要求：根据风机的工作条件、流量和压力要求等，确定设计所需的参数和性能指标。
2.蜗壳的几何参数确定：确定蜗壳的进口直径、出口直径、导叶长度、导叶角度等几何参数，通过计算和模拟分析来得到最佳设计。
3.流动性能分析：利用CFD(ComputationalFluidDynamics)等工具对蜗壳内部风气流动进行数值模拟和分析，评估风机性能和流体损失。
4.优化设计：根据流动分析结果，对蜗壳进行优化设计，减小流体损失，提高风机效率。
5.结构和材料优化：优化蜗壳的结构和材料选择，以提高强度、降低噪音和振动，提高风机的可靠性和稳定性。
蜗壳及尾水管设计
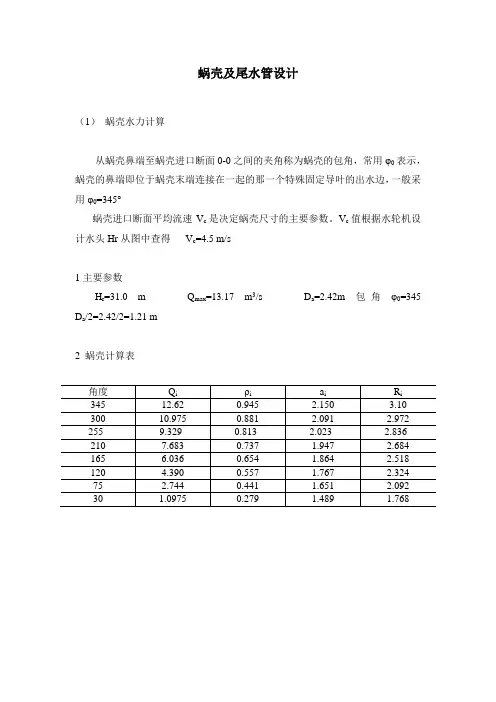
蜗壳及尾水管设计（1）蜗壳水力计算从蜗壳鼻端至蜗壳进口断面0-0之间的夹角称为蜗壳的包角，常用φ0表示，蜗壳的鼻端即位于蜗壳末端连接在一起的那一个特殊固定导叶的出水边，一般采用φ0=345°蜗壳进口断面平均流速V c是决定蜗壳尺寸的主要参数。
V c值根据水轮机设计水头Hr从图中查得V c=4.5 m/s1主要参数H r=31.0 m Q max=13.17 m3/s D a=2.42m 包角φ0=345 D a/2=2.42/2=1.21 m2 蜗壳计算表水轮机蜗壳单线图（2）尾水管设计根据以往经验,弯肘形尾说管不但可以减少开挖深度,而且具有良好的水力性能尾水管尺寸表弯肘型尾水管有进口直锥段.中间肘管段和出口扩散段和出口扩散段三部分组成.A 进口直锥段混流式水轮机单边扩散角009~7=θ,这里取 80.B 中间弯肘段是一段900转弯的变截面弯管,进口断面为圆形,出口断面为矩形.C 出口扩散段是一段水平放置,两侧平行,顶板上翘的矩形扩散管.起顶板仰角一般取0013~10=α,这里取13.应用第三种比例情况进行尺寸计算:h=2..6×1.4=3.64 m L=4.5×1.4=6.30 m B 5=2.72*1.4=3.808m D 4=1.35×1.4=1.89 m h 4=1.35×1.4=1.89 mh 6=0.675×1.4=0.945mL 1=0.94×1.4=2.548 m h 5=1.22×1.4=1.708m尾水管高度指水轮机底环平面至尾水管底版的高度.h=2.6*D 1=2.6*1.4=3.64m 满足最低要求,宽度B= 3.808m,同样满足要求. 尾水管长度指机组中心线至尾水管出口断面的距离. L=(3.5~4.5)D 1 这里取4 则L=4*1.4=5.6m。
《2024年基于Dynamo和AdvanceSteel的水轮机蜗壳快速设计方法》范文
《基于Dynamo和AdvanceSteel的水轮机蜗壳快速设计方法》篇一一、引言随着科技的不断进步，水力发电已成为绿色能源领域的重要一环。
水轮机作为水力发电的核心设备，其设计质量直接关系到发电效率和运行安全。
在众多水轮机设计环节中，蜗壳的设计尤为关键。
传统的蜗壳设计方法往往依赖于工程师的经验和手工计算，不仅效率低下，而且容易出现设计误差。
近年来，随着计算机辅助设计技术的发展，Dynamo和AdvanceSteel等软件在机械设计领域得到了广泛应用。
本文旨在探讨基于Dynamo和AdvanceSteel的水轮机蜗壳快速设计方法，以提高设计效率和精度。
二、Dynamo和AdvanceSteel简介1. DynamoDynamo是一款基于BIM（建筑信息模型）技术的可视化编程软件，可帮助设计师实现复杂模型的快速构建和优化。
在机械设计领域，Dynamo可实现参数化建模、几何形状的动态调整等功能，大大提高了设计效率。
2. AdvanceSteelAdvanceSteel是一款专为钢结构设计而开发的软件，具有强大的三维建模、结构分析和优化功能。
该软件可实现钢结构的快速建模、精确分析和优化设计，为水轮机蜗壳等钢结构的设计提供了有力支持。
三、基于Dynamo和AdvanceSteel的蜗壳快速设计方法1. 设计流程（1）需求分析：根据项目需求，确定蜗壳的尺寸、材料、性能等参数。
（2）参数化建模：利用Dynamo软件进行参数化建模，根据需求设定参数，自动生成蜗壳的三维模型。
（3）结构分析：将Dynamo生成的模型导入AdvanceSteel软件，进行结构分析和优化设计。
通过分析模型的应力、变形等数据，对模型进行优化，提高其结构强度和稳定性。
（4）模型优化与输出：根据结构分析结果，对模型进行优化调整，最终输出满足要求的蜗壳模型。
2. 具体步骤（1）在Dynamo中创建蜗壳的基本几何形状，如进口段、螺旋段和出口段等。
蜗壳设计 PPT
在实际设计计算中通常就是先假设一个蜗壳的截面形状求出bbr的关系带入下式中??将某一个已确定的r值带入就可求出一个对应的?值
离心式压气机蜗壳设计方 法的理论分析与研究
大家好
概述
• 传统的蜗壳设计方法主要有两种：
➢ 一种是基于蜗壳内速度为常值假设的周向平均速度法。 Vu=const
通过这一方法设计出来的蜗壳型线为一条阿基米德螺旋线。
➢ 一种是基于等环量法或者称为等速度矩法假设设计出来的 蜗壳。 VuR=const
通过这一方法设计出来的蜗壳型线为一条对数螺旋线。
大家好
2
周向平均速度法
•
大家好
3
周向平均速度法
•
大家好
4
周向平均速度法
• 确定蜗壳最大截面积，应设蜗壳的流量较计算值 略大10%，根据连续性方程：
• 最后根据公式
计算出各个截面的面积大小
大家好
7
参考文献
• [1] 潘地林,丁维龙,许云龙等.离心式通风机蜗壳型线设计方法的理论分析与试 验研究[J].流体机械,2002,30(4):4-7.DOI:10.3969/j.issn.1005-0329.2002.04.001.
• [2] 齐学义,赵强,马惠萍等.全蜗壳的非圆形断面水力设计及其CFD分析验证[J]. 兰州理工大学学报,2009,35(2):41-45.DOI:10.3969/j.issn.1673-5196.2009.02.011.
• [3] 赵德印,杨述华,李苏泷等.离心风机蜗壳设计优化[J].制冷与空调,2012,12(4):47,25.
• [4]王延生.车辆发动机废气涡轮增压. • [5]朱大鑫.涡轮增压与涡轮增压器.
大家好
8
结束
离心式压气机蜗壳设计方 法的理论分析与研究
大家好
概述
• 传统的蜗壳设计方法主要有两种：
➢ 一种是基于蜗壳内速度为常值假设的周向平均速度法。 Vu=const
通过这一方法设计出来的蜗壳型线为一条阿基米德螺旋线。
➢ 一种是基于等环量法或者称为等速度矩法假设设计出来的 蜗壳。 VuR=const
通过这一方法设计出来的蜗壳型线为一条对数螺旋线。
大家好
2
周向平均速度法
•
大家好
3
周向平均速度法
•
大家好
4
周向平均速度法
• 确定蜗壳最大截面积，应设蜗壳的流量较计算值 略大10%，根据连续性方程：
• 最后根据公式
计算出各个截面的面积大小
大家好
7
参考文献
• [1] 潘地林,丁维龙,许云龙等.离心式通风机蜗壳型线设计方法的理论分析与试 验研究[J].流体机械,2002,30(4):4-7.DOI:10.3969/j.issn.1005-0329.2002.04.001.
• [2] 齐学义,赵强,马惠萍等.全蜗壳的非圆形断面水力设计及其CFD分析验证[J]. 兰州理工大学学报,2009,35(2):41-45.DOI:10.3969/j.issn.1673-5196.2009.02.011.
• [3] 赵德印,杨述华,李苏泷等.离心风机蜗壳设计优化[J].制冷与空调,2012,12(4):47,25.
• [4]王延生.车辆发动机废气涡轮增压. • [5]朱大鑫.涡轮增压与涡轮增压器.
大家好
8
结束
风机蜗壳设计原理 -回复
风机蜗壳设计原理-回复这篇文章将探讨风机蜗壳的设计原理。
风机蜗壳是一种主要用于风机系统中的基础组件，它的主要功能是将进入风机的气体流线引导到风机叶轮，从而产生动力。
风机蜗壳的设计原理涉及流体力学、热力学和结构力学等多个领域，下面将一步一步地回答这个问题。
首先，我们需要了解蜗壳是什么以及它的作用。
蜗壳是一个环形结构，位于风机进气口和叶轮之间。
它的内壁具有蜗舌形状的导流面，能够将进入风机的气体流线引导到叶轮，从而提供驱动力。
蜗壳的主要作用是根据流体力学原理，将气体的输送效率最大化。
其次，我们来讨论蜗壳的设计原则。
蜗壳的设计主要依据两个原则：流动优先原则和能量转移原则。
第一、流动优先原则。
这个原则指的是在设计蜗壳时，需要考虑气体在蜗壳内的流动情况。
蜗壳的导流面应该设计成光滑的曲线，这样能够减少流体在流动过程中产生的湍流和阻力损失。
同时，蜗壳的流道应该是均匀、一致的，以保证气体在蜗壳内部的流速和压力分布的稳定性。
为了达到这个目标，在蜗壳的设计过程中通常采用数字仿真或试验来优化流道形状。
第二、能量转移原则。
这个原则指的是蜗壳应该尽可能地将气体的动能转化为机械能。
在进入蜗壳的气体首先遇到的是蜗壳的导向舌部分，导向舌的形状是关键因素之一。
导向舌的主要功能是改变气体的流向和速度，使其与叶轮的运动方向相匹配。
如果导向舌的设计不佳，会导致气体流动过程中的能量损失。
因此，蜗壳的导航舌部分需要通过灵活的设计和优化，以提高能量转移效率。
除了上述两个原则，蜗壳的设计还需要考虑结构强度和热耐受力。
由于风机运行时会有较大的气体压力和温度变化，蜗壳需要具备足够的强度和耐热性能，以确保其在长时间运行中的可靠性和稳定性。
最后，我们来讨论蜗壳的设计过程。
在实际的设计过程中，工程师通常会利用计算机辅助设计软件和数值仿真方法来进行蜗壳的设计和分析。
他们会根据实际工作条件和性能要求，确定蜗壳的尺寸、导流面曲线和导向舌的结构。
然后，利用数值仿真方法对蜗壳的流动特性进行模拟和优化，以达到最佳的性能。
风机蜗壳设计原理
风机蜗壳设计原理风机蜗壳是风机的重要部件之一，其设计原理对于风机的性能和效率有着重要的影响。
蜗壳的设计原理涉及到流体力学、结构设计和材料工程等多个领域。
本文将从这些方面详细介绍风机蜗壳的设计原理。
一、蜗壳的作用和特点风机蜗壳是用来将风机叶片吸入的气流引导至风机出口并增加风速的重要构件。
在风机中，蜗壳的作用主要体现在两个方面：一是通过蜗壳的设计优化，可以提高风机的效率和性能；二是蜗壳的结构设计能够保证风机在高速运转时的稳定性和安全性。
蜗壳的设计需要考虑到流体的运动规律、工程材料的性能、结构的强度等因素。
一个合理的蜗壳设计可以使得风机的风压损失减小，从而提高了风机的效率；合理的蜗壳结构设计可以减小风机在高速运转时的振动和噪音，提高了风机的稳定性和安全性。
二、蜗壳的流体力学设计原理在蜗壳的设计中，流体力学是至关重要的一环。
蜗壳能够通过特定的内部结构将进入的气流加速并引导至风机出口，其内部的几何形状和表面光滑度对气流运动和能量转换具有重要影响。
1. 蜗壳的截面设计蜗壳的截面设计直接影响了气流在蜗壳内部的运动规律和速度分布。
通常，蜗壳的截面呈渐变曲线型，从叶片进口到出口逐渐扩大。
这种设计能够使得气流在蜗壳中受到加速，从而提高了风机的效率。
截面的曲线形状还能够减小气流的阻力和损失，提高了风机的性能。
2. 蜗壳表面的光滑度设计蜗壳内部的表面光滑度对气流的摩擦阻力和流动分离有着重要的影响。
为了减小摩擦阻力和气流的能量损失，在蜗壳的内部表面通常采用光滑的表面处理技术，如抛光和涂层等。
这些表面处理技术可以降低摩擦阻力，使得气流在蜗壳内部能够更为顺畅地运动，从而提高了风机的效率。
三、蜗壳的结构设计原理蜗壳除了具有良好的流体力学性能外，其结构设计也十分重要。
合理的结构设计可以保证蜗壳在高速运转时的稳定性和安全性。
1. 蜗壳的叶片接口设计蜗壳与叶片的连接部分是蜗壳结构设计的重点。
这一区域需要保证叶片与蜗壳的良好连接，并且能够承受高速运转时的受力和振动。
风机蜗壳设计
0 引言蜗壳的作用是将离开叶轮的气体导向蜗壳出口，并将部分动压转变为静压。
蜗壳的结构是复杂的空间曲面体，理论上，蜗壳的型线是螺旋线，但是由于螺旋线结构较复杂，难于手工绘制。
因此，在生产中通常用简化的模型来近似。
由于蜗壳是离心通风机的关键部件，蜗壳型线的绘制不仅直接关系到蜗壳内的流动损失，还对叶轮的气动性能有很大影响，它直接影响风机的效率及输出流量、压力等性能参数，当工况变化时，需要重新计算并设计 , 使得产品设计周期延长。
本文应用三维建模工具CATIA，对蜗壳型线进行精确参数化建模，实现蜗壳的快速设计。
1 蜗壳的型线及结构参数1. 1 蜗壳的对数螺线型线及结构蜗壳的型线见图1。
图中R为蜗壳处半径，R 2 为叶道出口半径。
对于每一个角度φ值都可以得到一个R值，把各点连接起来就是蜗壳的型线。
其中：截面a-a 称为终了截面，A称为终了截面的张开度。
蜗壳的尺寸与张开度A有关，任意角度φ处的张开度Aφ为理论上，为了便于分析和计算，假定气流在蜗壳中为定常流动，忽略气体的粘性,气体沿着整个叶轮出口均匀地流出[1]。
图2表示在蜗壳型线起始段气体在蜗壳内的流动。
图中：R2为叶轮半径（即叶道出口半径），c为距离轮心R处的气流速度，a为气流角，c u、c m分别为R处的周向速度和径向速度。
c′2为叶道出口速度，c′2u、c′2m、a′2分别为叶道出口后的周向速度、径向速度及气流角(叶道出口后速度——刚出口时气流未充满截面，很快即互相混合，混合后的速度也即蜗壳的进口速度)。
蜗壳整个截面充满有效气流，由于忽略空气黏性，蜗壳内的流动满足动量守恒定律，当蜗壳宽度B为常数时，得任意截面处R与φ的函数关系式[1]为式中b 2 为叶片出口宽度，mm；α’ 2 为叶道出口后气流角，(°)；φ为该截面与起始截面之间的夹角，rad。
此式表明蜗壳型线为对数螺线。
将式（2）按照泰勒级数展开，并代入式（1），得任意角度φ处的张开度为式（3）即为按等环量法[4]设计的蜗壳型线模型。
《2024年基于Dynamo和AdvanceSteel的水轮机蜗壳快速设计方法》范文
《基于Dynamo和AdvanceSteel的水轮机蜗壳快速设计方法》篇一一、引言随着科技的进步和计算机辅助设计（CAD）工具的普及，工程设计的效率和精度得到了显著提升。
水轮机作为重要的清洁能源转换设备，其设计过程也日益依赖于先进的CAD软件。
本文将探讨如何利用Dynamo和AdvanceSteel这两个强大的工具，实现水轮机蜗壳的快速设计方法。
二、Dynamo与AdvanceSteel简介1. Dynamo：Dynamo是一款基于节点的可视化编程工具，它提供了强大的参数化建模能力，可以用于创建、分析和优化复杂的几何形状。
在工程设计领域，Dynamo被广泛应用于建筑、机械、电气等多个领域的设计和优化。
2. AdvanceSteel：AdvanceSteel是一款专为钢结构设计而开发的CAD软件，它提供了丰富的钢结构设计工具和材料库，支持参数化设计和三维建模。
三、水轮机蜗壳设计概述水轮机蜗壳是水轮发电机组的重要组成部分，其主要功能是将水流引入水轮机，并使其以最小的能量损失进入转轮。
因此，蜗壳的设计对于水轮机的性能和效率至关重要。
四、基于Dynamo的参数化建模在Dynamo中，我们可以利用其强大的参数化建模能力，根据水轮机蜗壳的设计要求，创建参数化的几何模型。
通过调整模型参数，可以快速生成多种不同的蜗壳设计方案，以便进行比选和优化。
此外，Dynamo还支持与其他CAD软件进行数据交换，方便将模型导入到AdvanceSteel中进行进一步的分析和优化。
五、利用AdvanceSteel进行钢结构设计将Dynamo生成的几何模型导入到AdvanceSteel中后，我们可以利用其丰富的钢结构设计工具和材料库，对蜗壳进行钢结构设计。
包括选择合适的材料、确定结构尺寸、进行强度和稳定性分析等。
此外，AdvanceSteel还支持与其他工程软件的协同工作，方便与其他设计团队进行沟通和协作。
六、快速设计流程基于Dynamo和AdvanceSteel的快速设计流程如下：1. 在Dynamo中创建参数化的水轮机蜗壳几何模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
17．1 进气蜗壳类型按通道数目划分，向心涡轮进气蜗壳可分为单通道和多通道两种。
图17-3 双通道串列进气蜗壳在图17-5中示出向心涡轮进气蜗壳常见的截面形状。
为今后叙述方便，每一种都取一个象形的名称。
图17-5 进气蜗壳常见截面形状17．2 蜗壳流动流动假定：不可压缩流体，稳定，等熵，等环量流动。
蜗壳进口处气流马赫数很低，可合理地假定为不可压缩流体。
在蜗壳出口处气流马赫数己很高，特别是无叶喷嘴环向心涡轮蜗壳出口，不可压缩流体必然导致较大误差。
内燃机出口气流是脉动的，稳定流动假定并不合理。
因非稳定流动的求解非常复杂，此假定是不得己而为之。
等熵流动假定意昧着计算中不考虑损失系数修正。
由于蜗壳中流体遵守动量距守恒规律，故等环量流动是比较符合实际的合理假定。
图17-1 单通道进气蜗壳图17-2双通道并列进气蜗壳图17-2图17-4 双通道串列进气蜗壳周向布置图17-6 进气蜗壳流动示意图进口流动：图17-6为进气蜗壳流动示意图。
在蜗壳进口处（O-O 截面）有，⎰=RCREi Ui dR b C G ρ0 (1)式中，0G 蜗壳进气流量。
ρ流体密度，不可压缩，故为常数。
i U C ,微流管周向分速。
i b 微流管宽度。
按气流流动是等环量分布的假定，Γ=i i U R C ,，可将上式改写成，⎰Γ=RCRE iidR R b G ρ0 ……………………………………….(2) 令 ⎰=RCREi dR b A 0，即蜗壳进口截面面积。
若设=0R A 0S dR R b RCRE ii=⎰，则 00S G Γ=ρ=0R A Γρ ……………………………………….(3) 式中，0R 是进口截面当量平均半径，由下式计算，⎰=RCRHiidR R b A R 00 ………………………………………. (4) 出口流动：蜗壳出口截面是宽度为b ，半径为h R 的圆柱面。
假定蜗壳出口气流沿周向均匀分布，即沿整个蜗壳出口截面的气流速度C 和气流角度α均为常数。
由此有气流分速U C 和R C 沿整个h R 圆周不变，是常数。
由等环量分布假定，有Γ=h U R C ，式（3）改写为，00S G Γ=ρ=0R A R C hU ρ ………………………………………. (5) 显然此假定同时假设了，从O-O 截面流进蜗壳的流量0G 将从蜗壳出口截面均匀地流出。
从整个出口截面流出的流量也是0G ，且有，b R C G h R πρ20= (6)合并式（5）和式（6）得，0022tan S bA b R C C R U ππα===………………………………. (7) 式（7）是一个获得广泛使用的公式。
切记，当量半径0R 按式（4）计算。
中间截面计算：首先，采用类似于式（2）的方法，从图17-6出口截面A-F-D 段流出蜗壳的流量φG 按下式计算,⎰Γ=iT h R R iidR R b G ,ρφ (8)式中，φ为计算截面的位置角。
令⎰=i T h R R i idR R b S ,φ，则式（8）改写为，φφρS G Γ= (9)然后，依据出口气流沿周向均匀流出的假定，流出蜗壳的流量与流出段的弧长成正比，从图17-6出口截面A-F-D 段流出的流量φG 也可按下式计算,πφφ20=G G ………………………………………. (10) 将由式(3)的0G 和式(9)的φG 代入式(10)，得位置角φ所确定的截面必须满足的几何条件：02S S πφφ=………………………………………. (11) 依据出口截面气流周向均匀假定所获得的式(11)表明，为保证出口气流周向均匀，φ截面应满足几何条件：⎰=iT hR R i i S dR R b ,02πφ ………………………………………. (12) 17．3 剖面型线设计计算蜗壳出口气流角度α是蜗壳设计计算最关键的参数。
一方面，由式(7) 可知，它控制蜗壳截面面积和外径大小。
另一方面，它直接控制喷嘴环或工作轮的进气角，间接控制喷嘴环叶片结构角。
由于向心涡轮工作轮叶片进口结构角一般为0度，因此无叶喷嘴环向心涡轮进气蜗壳的出口气流角度α，应该由工作轮设计参数确定。
笫二个关键参数是蜗壳出口宽度b 。
由式(7) 可知，在α确定之后，宽度b 是调整0S 的唯一手段。
可惜，多数情况下，宽度b 是由工作轮进口确定。
在出气角α和宽度b 确定之后，按式(7) 计算，0S 的大小随之被确定。
首要任务是设计蜗壳进口截面，其截面的形状和大小应满足要求的0S 值。
下面以Ω型蜗壳（图17-7）为例，为简化说明设定各圆角为0。
蜗壳进口处O-O 截面的剖面型线是封闭的，外半径为C R ，内外半径为E R 。
E R 应比h R 高一个蜗舌厚度V δ，即V h E R R δ+=。
令i i A dR b ∆=，采用分段数值积分公式，有⎰∑=∆==RCRE ni i i ii R AdR R b S 10 (13)本例中，=0S +∆11R A +∆22R A +∆33R A +∆44R A 55R A ∆。
例如求φ为30°时φS 的数值，使用式（11）有，0000694.036030S S S ==φ 以此类推，令φ值间距为30°，求出对应的φS 数值（见下表1）。
下一个任务是，依次设计φ截面的蜗壳剖面型线是不未封闭的，下面有一宽度b 的开口，外半径为i T R ,，内外半径为h R 。
剖面形状和大小应满足φS 值的要求。
以φ等于60°的剖面型线（图17-8）为例，⎰∑=∆==iT R Rhni ii i i R AdR R b S ,1φ ………………………………………. (14) 表1本例中，=60S +∆11R A +∆22R A +∆33R A +∆44R A 55R A ∆。
若0601667.0S S =，则所设计的蜗壳剖面型线满足φS 值的要求。
否则，修改i b 和（或）i T R ,数值，使60S 逐渐逼近01667.0S 。
注意到φS 逼近过程中，既可修改i b ，亦可修改i T R ,，因此逼近过程中应保证i b 和i T R ,数值变化按比例增大或减小。
即便如此，在所有截面设计完成之后，仍有必要将等间距φ的所有剖面型线绘制在同一图上（图17-5），检查各参数变化的协调性。
剖面型线设计计算的主要工作量在于大量重复进行的φS 积分计算。
17．4 剖面型线φS 数值积分计算除o 型，及不计及圆角的矩型剖面型线外，很难得到φS 积分的解析解。
采用分块（三角块，矩形块，扇形块，弓形块）手段，求解难度降低，复杂程度增高。
任何φS 积分的解析求解都没普遍性。
图17-8 蜗壳φ截面φS 计算示意图图17-7 蜗壳进口截面0S 计算示意图下面以M 型剖面型线(参数见图17-9)为例，介绍一种笔者采用的φS 分段数值积分方法。
它借助于AutoCAD 绘图软件和Autolisp 编程语言，实现半自动数值求解。
a) 依据图17-9 所示的M 型剖面型线参数，使用Autolisp 语言编制自动绘图程序，在AutoCAD 绘图界面上绘制出(如图17-10 所示)两外廓曲线，curL 和curR 。
两曲线起点和终点的Y 值均相等。
b) 设两曲线起点S Y 值和终点E Y 值之差为Y ∆。
用两条间距为n Y /∆的水平直线切割curL 和curR 两曲线，视切割带(如图17-10 所示)为一矩形，按式(17-14)计算iiR A ∆。
c) 重复b 步(1-n )次，获得和∑=∆ni iiR A 1，即φS 数值积分值。
图17-10 φS 分段数值积分法17．5 蜗壳设计注意事项在前述剖面型线设计计算中并未计及流量G 的影响。
在设计流量下，蜗壳进口处马赫数0C M 是恒量O-O 截面面积0A 大小是否适中的重要参数。
=G μ00)(A M q C **0TP (15)图17-9 M 型剖面型线参数示意图图17-11 某型蜗壳剖面型线式中，=μ11)12(-++k k k R k ，*0P 为进口总压，*0T 为进口总温。
式（15）求出的是平均马赫数。
例如，*0P =150 kPa ，*0T =650 C ，=0A 1650.5 2mm ，=0G 0.2 kg/s ，k =1.33，=R 287.0有=μ0.0397，)0.1000*150(*)5.1650*000001.0(*0397.02736502.0)(0+=C M q =0.618=0C M 0.39当=0G 0.3 kg/s 时，=)(0C M q 0.928，则=0C M 0.72。
显然，当=0G 0.3 kg/s 时，=0A 1650.5 2mm 似乎就显得小了。
根据图纸数据绘出的某型蜗壳剖面型线如图17-11所示。
由图可见，剖面型线沿周向的变化极不光滑，显然不满足前述沿周向均匀流动的设计要求。
叶轮进气周向不均匀，可能诱发气动激励的振动和噪音。
蜗壳多为铸件，图17-11所示的分隔肋又长又细，不利于液态金属流动分隔肋尖部，降低了铸件的成活率。
如果适当增大倒圆2r 和肋宽rib w ，将有助于降低铸件废品率。
同理，上述分析也适用于图17-6所示的蜗舌部分。
蜗壳与叶轮的最小间隙B h R R -=δ，δ太小易碰叶轮，太大则增大蜗壳重量。
蜗舌A 点处在有叶喷嘴环向心涡轮中，蜗壳剖面型线对性能的影响较小。
但在无叶喷嘴环向心涡轮中，它对性能的影响就很大。
因为剖面型线除影响叶轮进气均匀性外，还将直接影响叶轮进气速度和角度，间接影响叶轮做功能力和效率。