北航_机械振动基础_最全版
- 格式:pdf
- 大小:15.00 MB
- 文档页数:54

第9 章 机械振动基础人类生活在充满振动的自然界之中,固体物质中原子的振动、宇宙空间的电 磁振荡、机械钟表钟摆的摆动等,振动现象俯拾皆是。
而机械振动是机械工程和 日常生活普遍可见的力学现象,行驶交通工具的振动、人体脉搏不停息地跳动和 内燃机工作状态的振动等均属此类运动。
机械振动的传播便形成机械波,因此本 章是第10章波动的学习基础。
值得注意的是,机械振动和机械波的基本内容还是 电工学、无线电技术、自动控制技术等科学技术领域的理论基础。
本章将重点介 绍简谐振动及其规律,讨论简谐振动的合成,以及阻尼振动、受迫振动等更接近 客观实际的机械振动模型。
在本章学习过程中,应重视简谐振动的学习,掌握其 动力学方程的建立与求解,简谐振动合成复杂振动的研究等,为机械振动在专业 课程的学习和技术工程中的应用奠定扎实的理论基础。
9.1 简谐振动物体在其平衡位置附近往复运动称为机械振动,简谐振动属于最简单、最基 本的机械振动,是研究复杂振动的基础,因为复杂的振动可由若干简谐振动合成 获得。
由原长为l 、劲度系数为k 的轻弹簧和质量为m的物体构成的弹簧振子如图9.1所示,若不计空气阻力、水平桌面的摩擦力,则该力学系统做简谐振动,应用 牛顿第二定律可以求解其运动方程。
以下通过对弹簧振子的求解,详细介绍简谐 振动问题的求解方法。
以固定于地面的水平桌面为惯性系,选择如图9.1所示的坐 标系,取振动系统的平衡位置为坐标原点O,由胡克定律得到质量为m的振子所 受弹性力与其位移成正比得:=-F kx图9.1 弹簧振子如上式所述,将始终指向振子平衡位置、又与其位移成正比的力称为线性回2大学物理(下册)复力,受到此类力作用的系统一般为简谐振动系统。
由牛顿第二定律可得:22ddxm kxt=- (9.1.1)令 2kmw= (9.1.2) 由式(9.1.1)、(9.1.2)得到:222ddxxtw+= (9.1.3) 式(9.1.3)是振子简谐振动的动力学方程,求解该二阶线性齐次微分方程得 到振子简谐振动的运动方程为:()cos()x t A tw j=+ (9.1.4) 将式(9.1.4)对时间分别求一、二次导数得到振子简谐振动的速度、加速度为:00dsin()dxv A ttw w j==-+ (9.1.5)22000dcos()dva A t xtw w j w==-+=- (9.1.6) 由式(9.1.4)~(9.1.6)可知,物体做简谐振动时,其位移、速度和加速度 均为时间的周期性函数,图9.2给出了相应的函数图像。





第4章 机械振动基础4-1 图示两个弹簧的刚性系数分别为k 1 = 5 kN/m ,k 2 = 3 kN/m 。
物块重量m = 4 kg 。
求物体自由振动的周期。
解:根据单自由度系统自由振动的固有频率公式 mk =n ω 解出周期 nπ2ω=T图(a )为两弹簧串联,其等效刚度 2121eq k k k k k +=所以 )(2121n k k m k k +=ω2121n)(π2π2k k k k m T +==ω代入数据得s 290.0300050003000)4(5000π2=⨯+=T图(b )为两弹簧串联(情况同a ) 所以 T = 0.290 s图(c )为两弹簧并联。
等效刚度 k eq = k 1 + k 2 所以 mk k 21n +=ω21nπ2π2k k mT +==ω代入数据得 T = 0.140 s图(d )为两弹簧并联(情况实质上同(c ))。
所以 T = 0.140 s4-3 如图所示,质量m = 200 kg 的重物在吊索上以等速度v = 5 m/s 下降。
当下降时,由于吊索嵌入滑轮的夹子内,吊索的上端突然被夹住,吊索的刚度系数k = 400 kN/m 。
如不计吊索的重量,求此后重物振动时吊索中的最大张力。
解:依题意,吊索夹住后,重物作单自由度自由振动,设振幅为A ,刚夹住时,吊索处于平衡位置,以平衡位置为零势能点,当重物达到最低点时其速度v = 0。
根据机械能守恒,系统在平衡位置的动能与最低点的势能相等。
即 T max = V max 其中 2max 2v m T = , 2max 21kA V =v km A =吊索中的最大张力 mk v mg kA mg F +=+=max 代入数据得 kN 7.461040020058.92003max =⋅⋅+⋅=F4-5 质量为m 的小车在斜面上自高度h 处滑下,而与缓冲器相碰,如图所示。
缓冲弹簧的刚性系数为k ,斜面倾角为θ。


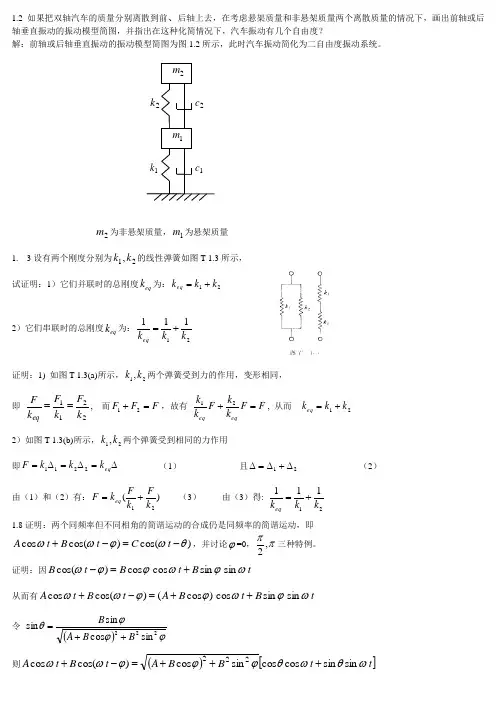
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。

机械振动基础课后习题答案1. 简谐振动的特点是什么?简述简谐振动的基本方程。
答:简谐振动是指振动系统在无外力作用下,自身受到弹性力作用而产生的振动。
其特点有以下几点:振动周期固定、振幅不变、振动轨迹为正弦曲线。
简谐振动的基本方程为x = A*cos(ωt + φ),其中x为振动的位移,A为振幅,ω为角频率,t为时间,φ为初相位。
2. 简述自由振动、受迫振动和阻尼振动的区别。
答:自由振动是指振动系统在无外力作用下,自身受到弹性力作用而产生的振动。
受迫振动是指振动系统在外力作用下,产生与外力频率相同的振动。
阻尼振动是指振动系统在有阻尼力作用下,产生的振动。
三者的区别在于外力的有无和阻尼力的存在与否。
3. 什么是振动的自由度?简述单自由度振动和多自由度振动的特点。
答:振动的自由度是指描述振动系统所需的独立坐标的个数。
单自由度振动是指振动系统所需的独立坐标只有一个,可以用一个坐标来描述整个振动系统。
多自由度振动是指振动系统所需的独立坐标大于一个,需要多个坐标来描述整个振动系统。
单自由度振动的特点是简单、容易分析,而多自由度振动具有更复杂的动力学特性。
4. 简述振动系统的自然频率和强迫频率。
答:振动系统的自然频率是指系统在无外力作用下自由振动时的频率。
自然频率只与系统的质量、刚度和几何形状有关。
强迫频率是指系统在受到外力作用下振动的频率。
强迫频率可以是任意频率,与外力的频率相同或不同。
5. 什么是共振?简述共振现象的发生条件。
答:共振是指振动系统在受到外力作用下,当外力的频率接近系统的自然频率时,振动幅度达到最大的现象。
共振现象发生的条件包括:外力的频率接近系统的自然频率,外力的幅度足够大,系统的阻尼较小。
6. 简述振动系统的阻尼对振动的影响。
答:阻尼对振动有以下几种影响:阻尼可以减小振幅,使振动逐渐衰减;阻尼可以改变振动的频率,使其偏离自然频率;阻尼可以引起相位差,使振动的相位发生变化。
7. 什么是振幅衰减?简述振幅衰减的特点。
