功和能

初中物理功和能的知识点总结一、功的概念：1.功是物体受到力作用而产生的效果，是力对物体做的有效作用。

2. 功的计算公式为W = F * s * cosθ，其中W为功，F为力，s为位移，θ为力和位移之间的夹角。

3.功的单位是焦耳（J）或牛·米（N·m）。

4.功的正负性：当力和位移的方向一致时，功为正；当力和位移的方向相反时，功为负。

5.功和能的关系：力对物体进行的功等于物体所具有的能量的变化，即功可以转化为能量。

二、能的概念：1.能是物体进行物理活动所具有的能力。

能是物体由于自身的一些特性而拥有的性质。

2.能的单位是焦耳（J）。

3.能的形式：能分为势能和动能两种形式。

-动能是物体运动时所具有的能量，与物体的质量和速度有关。

-势能是物体由于自身的位置或状态而具有的能量，与物体的位置和形状有关。

4.功和能的转化：当力对物体做功时，能可以转化为功；当物体消耗能量时，能可以转化为功。

三、能的转化与守恒：1.能的转化：能可以从一个物体转移到另一个物体，或者转化为其他形式的能。

2.能的守恒：能在宏观尺度上是守恒的，即能在不同形式之间转化时总量保持不变。

-机械能守恒：在不考虑摩擦阻力的情况下，机械系统中的势能和动能之和保持不变。

-动量守恒：在封闭系统中，系统的总动量在相互作用发生前后保持不变。

四、各种形式的能：1.动能：动能是物体由于运动所具有的能量，动能的大小与物体的质量和速度的平方成正比，动能公式为Ek=1/2*m*v^22.势能：势能是物体由于位置或状态而具有的能量，可分为重力势能、弹性势能等。

-重力势能：物体在重力作用下由高处移动到低处时，具有的能量，重力势能公式为Ep=m*g*h。

-弹性势能：物体在受力变形后恢复原状时所具有的能量，弹性势能公式为Ep=1/2*k*x^23.热能：热能是物体分子间热运动所具有的能量，与物体的温度有关。

4.电能：电能是由电荷所具有的能量，与电荷的大小和电势差有关。

初中物理功和能的关系1. 功和能的基本概念在我们的日常生活中，功和能就像一对儿好兄弟，密不可分。

说到功，大家可能会想起运动员在比赛中拼尽全力的样子，其实，功在物理学上有个简单的定义：就是力和物体移动的距离的乘积。

听起来有点枯燥？别急，我们来具体看看。

想象一下，你在推一个重重的箱子，如果你使劲推，它向前移动了，哎呀，那你就做了功！反之，如果你只是抱着它不动，哪怕你再使劲，也是没有功可言的，这就像你在努力减肥，却总是吃着零食一样，不见成效，真让人无奈。

能量嘛，就是一个物体做功的能力。

它有很多种类，比如动能、势能，简直就像是能量界的小明星，各有各的特点。

动能是物体运动时的能量，比如你骑着自行车风驰电掣，那你可就拥有了满满的动能。

而势能呢，想象一下，你把一块石头举高高的，它的能量就叫势能了。

简单说，能量就是让事情发生变化的“动力”，没有它，什么都动不了，大家都跟“僵尸”一样。

2. 功和能的关系2.1 功是能量转化的桥梁功和能就像小情侣，紧紧相连，互相依赖。

你做功，就意味着能量在转化。

当你推箱子的时候，你的力气转化为箱子的动能，哇，听起来是不是很浪漫？如果你不推，箱子就静静地待着，就像一位不愿意跳舞的女孩。

这里要注意的是，功和能的转化不是单向的，有时候能量也可以转化回功，比如当你刹车的时候，动能转化为热能，车子慢下来，这可真是个绝妙的演出。

2.2 能量守恒定律的奇妙之处讲到这儿，能量守恒定律就闪亮登场了！这条定律就像是宇宙中的“魔法”，告诉我们在一个封闭系统中，能量是不会消失的，只会转化。

想象一下，打个篮球，你把能量施加在球上，它就飞了出去；等球落地的时候，动能转化为势能，又从高处落下，又变回动能。

这种变化不断循环，真是个精彩的循环圈，感觉就像在玩一场无尽的游戏，让人心潮澎湃。

3. 日常生活中的应用3.1 功和能的生活实例在我们的日常生活中，功和能随处可见。

比如说，你每天早上起床，要不要先用力把被子扯开，啊，那就是在做功！然后你洗漱、吃早餐，满满的能量补充，准备好迎接一天的挑战。

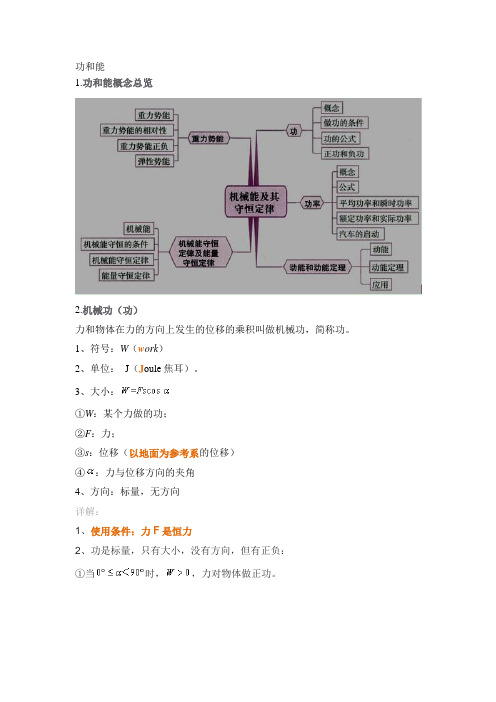
功和能1.功和能概念总览2.机械功（功）力和物体在力的方向上发生的位移的乘积叫做机械功，简称功。

1、符号：W（w ork）2、单位：J（J oule焦耳）。

3、大小：①W：某个力做的功；②F：力；③s：位移（以地面为参考系的位移）④：力与位移方向的夹角4、方向：标量，无方向详解：1、使用条件：力F是恒力2、功是标量，只有大小，没有方向，但有正负：①当时，，力对物体做正功。

②当时，，力对物体做负功，也称物体克服这个力做了功。

③当时，，力对物体不做功。

3、作用力与反作用力虽然等大、反向，但由于它们作用的对象不同，故位移关系不能确定。

因此，作用力做功时，反作用力可能做功，也可能不做功，可能做正功，也可能做负功，数值上也不一定相等。

4、编者的理解：某个力做的功等于这个力与位移的乘积，乘以这个力与位移之间夹角的余弦值。

研究某个力做的功即研究这个力对物体的运动是促进或是阻碍，与其他力的作用无关。

5.合力做功等于各力做功的代数和。

即。

实例：1、合力做的功，等于合力与位移的乘积，乘以合力与位移之间夹角的余弦值2、摩擦力做功，等于摩擦力与位移的乘积，乘以摩擦力与位移之间夹角的余弦值。

3、分析摩擦力做功严格按照功的公式进行分析，摩擦力阻碍的是相对接触面的运动，而不一定阻碍相对地面的运动，而做功公式中的位移是相对地面而言，所以摩擦力可以做正功，可以做负功，也可以不做功。

3.能量的转化能量守恒定律：能量既不能凭空产生，也不能凭空消失，它只能从一种形式转化为另一种形式，或者从一个物体转移到另一个物体，而在能量的转化或转移过程中，能的总量保持不变。

1.某种形式的能量减少，一定存在其他形式的能量增加，且减少量和增加量相等。

2.某个物体的能量减少，一定存在别的物体的能量增加，且减少量和增加量相等。

详解：1.能量守恒定律指出，能量不能被创造或消灭，只能从一个物体转移到另一个物体，或者从一种形式转化为另一种形式。

在大多数情况下，能量最终都转化为内能。

功和能知识点总结PPT一、功的概念及公式1.1 功的概念功是描述力对物体作用的效果的物理量，是衡量力的作用效果的大小。

当力使物体发生位移时，我们就说力对物体做了功。

1.2 功的公式在恒力作用下，物体在沿着力方向位移s的过程中所做的功W可以用下面的公式表示：\[ W = F \cdot s \cdot \cos\theta \]其中，F为作用力的大小，s为物体的位移，\(\theta\)为作用力与位移方向夹角的余弦值。

二、能的概念及分类2.1 能的概念能是物体由于自身的性质或者受到外力的作用而具有的做功能力，是物体的一种属性，是描写物体在某一过程中所具有的状态的物理量。

2.2 能的分类根据能量的形式和来源，能可以分为以下两类：（1）动能：物体由于运动而具有的能量。

（2）势能：物体由于位置关系而具有的能量。

三、能的转化和守恒3.1 能的转化在自然界和人类社会中，能的形式经常发生转化。

动能可以转化为势能，势能也可以转化为动能，而且能够相互转化。

3.2 能的守恒能量守恒定律是自然界中最基本的规律之一。

它表明在一个封闭系统中，系统内所有能量的代数和始终保持不变。

四、功率概念及计算4.1 功率的概念功率是描述力的作用速度的物理量，是衡量单位时间内所做功的大小。

公式如下：\[ P = \frac{W}{t} \]其中，P为功率，W为作用力在时间t内所做的功。

4.2 功率的计算在恒力作用下，力F对物体做功的功率可以用下面的公式表示：\[ P = F \cdot \cos\theta \cdot v \]其中，F为作用力的大小，v为物体的速度，\(\theta\)为作用力与速度方向夹角的余弦值。

五、应用实例5.1 计算功的应用在机械工程中，我们经常需要计算物体在受力作用下做的功，以便评估机械的性能。

5.2 能的转化应用在能源领域，我们需要掌握能量的转化原理，以便合理利用能源资源，减少能源消耗。

5.3 功率的应用在电气工程中，我们需要计算电路中的功率，以便设计安全可靠的电器设备。

高一物理功和能必会知识点能量是物理学中非常重要的一个概念，也是我们在生活中经常听到的一个词。

在高中物理中，学习和了解功和能是我们的重要课程之一。

在本文中，我们将深入研究功和能的概念及其必会的知识点。

首先，让我们来了解一下功的概念。

在物理学中，功是指一个力在作用下，物体沿着力的方向上做功的过程。

功的大小可以通过力的大小和物体在力的方向上移动的距离来计算。

用数学的方式来表达，功（W）等于力（F）与位移（s）的乘积，即W = F·s。

功的单位是焦耳（J）。

在这里，我们还需要了解一下能量的概念。

能量是物体所具有的能够产生物理变化的性质。

在物理学中一般将能量分为动能和势能两种形式。

动能是指物体由于运动而具有的能量，可以用1/2mv²来表示，其中m是物体的质量，v是物体的速度。

势能是指物体由于位置或状态而具有的能量，可以通过重力势能和弹性势能来进行具体的描述。

接下来，我们来看一下功和能之间的关系。

根据能量守恒定律，能量可以互相转换，但总能量保持不变。

当一个物体受到外力作用时，会发生功，这个功会改变物体的动能或势能。

例如，当我们把一个物体从地上抬高时，我们对物体施加的力会做功，将势能转变为重力势能。

又如，在一个斜面上推动一个物体时，我们所施加的力会做功，将动能转变为势能。

此外，我们还需要了解一些关于功和能的其他重要知识点。

首先是功率的概念。

功率是指单位时间内做功的多少，即功（W）与时间（t）的比值。

用数学的方式表达，功率（P）等于功（W）除以时间（t），即P = W/t。

功率的单位是瓦特（W）。

另一个重要的知识点是机械能守恒定律。

机械能是指动能和势能的总和。

在不发生摩擦和空气阻力的情况下，一个封闭系统中的机械能保持不变。

这个定律对于解决一些与能量转化有关的问题非常有用。

最后，我们还需要了解一些与摩擦有关的知识点。

在物体之间存在摩擦力时，功和能的转换将会受到影响。

当一个物体沿水平面移动时受到摩擦力，我们施加的外力将不再完全转化为物体的动能，而是被摩擦力消耗掉一部分。

【初中物理】初中物理功和能公式大全【—功和能】功和能公式：功率：p=w/t(定义式){p:功率[瓦(w)]，w:t时间内所做的功(j)，t:做功所用时间(s)}。

功和能(功是能量转化的量度)1.功：w=fscosα(定义式){w:功(j)，f:恒力(n)，s:加速度(m)，α：f、s间的夹角}w=fs2.重力做功：wab=mghab{m:物体的质量，g=9.8m/s2≈10m/s2，hab：a与b高度差(hab=ha-hb)}3.电场力作功：wab=quab{q:电量(c)，uab:a与b之间电势差(v)即uab=φa-φb}4.电功：w=uit(普适式){u：电压(v)，i:电流(a)，t:通电时间(s)}5.功率：p=w/t(定义式){p:功率[瓦(w)]，w:t时间内所搞的功(j)，t:作功所用时间(s)}6.汽车牵引力的功率：p=fv;p平=fv平{p:瞬时功率，p平：平均功率}7.汽车以恒定功率启动、以恒定加速度启动、汽车最小高速行驶速度(vmax=p额/f)8.电功率：p=ui(普适式){u：电路电压(v)，i：电路电流(a)}9.焦耳定律：q=i^2rt{q:电热(j)，i:电流强度(a)，r:电阻值(ω)，t:通电时间(s)}10.纯电阻电路中i=u/r;p=ui=u^2/r=i^2r;q=w=uit=u^2t/r=i^2rt11.动能：ek=mv^2/2{ek:动能(j)，m：物体质量(kg)，v:物体瞬时速度(m/s)}12.重力势能：ep=mgh{ep:重力势能(j)，g:重力加速度，h:竖直高度(m)(从零势能面起)}13.电势能：ea=qφa{ea:带电体在a点的电势能(j)，q:电量(c)，φa:a点的电势(v)(从零势能面起)}14.动能定理(对物体做正功，物体的动能增加)：w合=mvt^2/2-mv0方/2或w合=δek{w合：外力对物体做的总功，δek:动能变化δek=(mvt^2/2-mvo^2/2)}15.机械能守恒定律：δe=0或ek1+ep1=ek2+ep2也可以就是mv1^2/2+mgh1=mv2^2/2+mgh2知识拓展：重力做功与重力势能的变化(重力做功等于物体重力势能增量的负值)wg=-δep。

【高中物理】功能关系、能量守恒定律的知识点汇总，务必掌握！知识网络图一、功能关系1．功和能(1)功是能量转化的量度，即做了多少功，就有多少能量发生了转化。

(2)做功的过程一定伴随有能量的转化，而且能量的转化必须通过做功来实现。

2．力学中常用的四种功能对应关系(1)合外力做功等于物体动能的改变：即W(合)＝Ek2－Ek1＝ΔEk。

(动能定理)(2)重力做功等于物体重力势能的减少：即W(G)＝Ep1－Ep2＝－ΔEp。

(3)弹簧弹力做功等于弹性势能的减少：即W(弹)＝Ep1－Ep2＝－ΔEp。

(4)除了重力和弹簧弹力之外的其他力所做的总功，等于物体机械能的改变，即W(其他力)＝E2－E1＝ΔE。

(功能原理)二、能量守恒定律1．内容能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移的过程中，能量的总量保持不变。

2.表达式ΔE减＝ΔE增。

三、功能关系的应用1.对功能关系的进一步理解(1)做功的过程是能量转化的过程。

不同形式的能量发生相互转化是通过做功来实现的。

(2)功是能量转化的量度，功和能的关系，一是体现到不同的力做功，对应不同形式的能转化，具有一一对应关系；二是做功的多少与能量转化的多少在数量上相等。

2．不同的力做功对应不同形式的能的改变四、能量守恒定律的应用1.对定律的理解(1)某种形式的能量减少，一定有另外形式的能量增加，且减少量和增加量相等。

(2)某个物体的能量减少，一定有别的物体的能量增加，且减少量和增加量相等。

2．应用定律的一般步骤(1)分清有多少种形式的能(如动能、势能、内能、电能等)在变化。

(2)分别列出减少的能量ΔE减和增加的能量ΔE增的表达式。

(3)列恒等式：ΔE减＝ΔE增。

五、相对滑动物体的能量分析静摩擦力与滑动摩擦力做功特点比较。

功与能的关系功和能是物理学中两个重要的概念，它们描述了物体在运动中所具有的性质和变化。

功指的是物体受到的力在运动方向上所做的功或所消耗的能量，而能则是物体所具有的执行功的能力。

通过对功与能的深入探讨，可以更好地理解它们之间的关系。

一、功的定义和计算在物理学中，功的定义是指力对物体所作的做功或消耗的能量。

当一个力作用在一个物体上时，它可以改变物体的位置、速度或形状，从而产生功。

依据力的定义，力可以表示为：F = ma，其中F为力的大小，m为物体的质量，a为物体所受到的加速度。

为了计算功，我们需要考虑力的大小和物体在力的作用下所移动的距离。

根据物理学中计算功的公式，功可表示为：W = F·d·cosθ，其中W为功，F为力的大小，d为物体所移动的距离，θ为力和物体移动方向之间的夹角。

二、能的定义和分类能是指物体所具有的执行功的能力。

根据物理学的基本定律，能可以存在于不同的形式。

常见的能的形式包括机械能、热能、电能、化学能等。

这些能都是物体所拥有的，可以通过相应的方式进行转化或转移。

1. 机械能：机械能是指物体所具有的由于位置或运动而产生的能量，它可以分为动能和势能。

动能是指物体由于运动而具有的能量，可以用公式E_k = 0.5mv²来计算，其中E_k为动能，m为物体的质量，v为物体的速度。

势能是指物体由于所处的位置而具有的能量，可以用公式E_p = mgh来计算，其中E_p为势能，m为物体的质量，g为重力加速度，h为物体的高度。

2. 热能：热能是物体由于温度而具有的能量，它是物体内部分子与原子的运动与振动的总和。

热能可以通过热传导、热辐射等方式进行传递。

3. 电能：电能是指物体所具有的由于电荷的分布或电流所产生的能量，它可以通过电场或电流进行转移。

4. 化学能：化学能是指物体所具有的由于化学反应而产生的能量，常见的化学能包括燃烧能、化学键的能量等。

三、功和能是紧密相关的概念，它们之间存在着一定的关系。