。深圳市高级中学2019届高三12月模拟考试(理数)

深圳高级中学2019届高三年级12月模拟考试理 科 数 学一．选择题：本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，，则（ ） A ． B ． C ． D ．2.设α，β是两个不同的平面，m 是直线且m α⊂，“//m β”是“//αβ”的（ ）.A. 充分而不必要条件B.必要而不充分条件C. 充分必要条件D.既不充分也不必要条件3．若m 是2和8的等比中项，则圆锥曲线x 2+的离心率为（ ）A ．B ．C ． 或D ． 或4．《九章算术》中有“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则该竹子的容积为（ ）A ．升 B ．升 C ．升 D ．升5.已知向量a ，b 满足||2a =，||4b =，()a a b ⊥+，则向量a 在b 方向上的投影为（ ）A ．1-B ．2-C ．2D ．16.已知直线与相交于、两点，且120ACB ∠=︒，则实数的值为（ ）A ．B ． C. 或 D ．或7．已知某函数图象如图所示，则图象所对应的函数可能是（ ） {}230A x x x =-<(){}ln 2B x y x ==-AB =()2,+∞()2,3()3,+∞(),2-∞1001190112543320122430x y a -+=22:40C x y x ++=A B a 3101121313A ．2x x y =B ．22x y =-C ．e x y x =-D ．|2|2x y x =﹣ 8．若双曲线C ：()222210,0x y a b a b-=>>的一条渐近线被抛物线24y x =所截得的弦长为，则双曲线C 的离心率为（ ）A ．14B ．1C ．2D ．49.函数()()sin f x A x ωϕ=+（其中0,2A πϕ><）的图像如图所示，为了得到()cos 22g x x π⎛⎫=- ⎪⎝⎭的图像，只需将()f x 的图像( ) A.向左平移3π个长度单位 B.向右平移3π个长度单位 C.向左平移6π个长度单位 D.向右平移6π个长度单位10.如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为( )A.8+8+2+122411.记数列{}n a 的前n 项和为n S .已知11a =，1()2()n n n n S S a n N *+-=∈，则2018S =（ ）A ．10093(21)- B ．10093(21)2- C.20183(21)- D ．20183(21)2- 12. 若函数2()ln ln x f x ax x x x=+--有三个不同的零点，则实数a 的取值范围是( ) π7πxA. 1(1,)1e e e --B.1[1,]1e e e --C. 1(,1)1e e e ---D. 1[,1]1e e e --- 二．填空题：本大题4小题，每小题5分，满分20分．13．已知向量与的夹角为，，，则__________．14．若，，则__________． 15的等边三角形，若该几何体的外接球的体积为，则该几何体的体积为__________．16.ABC ∆中，角A ，B ，C 所对边分别为a ，b ，c .D 是BC 边的中点，且AD =8sin a B =，1cos 4A =-，则ABC ∆面积为 ． 三．解答题：本大题共8小题，满分70分，解答须写出文字说明、证明过程或演算步骤．17．已知数列的前项和为，且，，成等差数列，．（l ）求数列的通项公式；（2）若数列中去掉数列的项后余下的项按原顺序组成数列，求的值．18. 在ABC △中，内角A ，B ，C 的对边分别为a ，b ，c 且sin ()sin sin b B c b C a A +-=.（1）求角A 的大小；（2）若3sin sin 8B C =，且ABC △的面积为a .a b 60︒2=a 3=b 32-=a b tan 3α=π02α⎛⎫∈ ⎪⎝⎭，πcos 4α⎛⎫-= ⎪⎝⎭36π{}n a n n S n n a n S ()22log 11n n b a =+-{}n a {}n b {}n a {}n c 12100c c c +++19．如图，四棱锥P ABCD -中，PAD △为正三角形，//AB CD ，2AB CD =，90BAD ∠=︒，PA CD ⊥，E 为棱PB 的中点．（1）求证：平面PAB ⊥平面CDE ；（2）若直线PC 与平面PAD 所成角为45︒，求二面角A DE C --的余弦值．20．已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ，点P 在椭圆上，有124P P F F +=，椭圆的离心率为12e =； （1）求椭圆C 的标准方程；（2）已知()4,0N ，过点N 作直线l 与椭圆交于,A B 不同两点，线段AB 的中垂线为l '，线段AB 的中点为Q 点，记l '与y 轴的交点为M ，求MQ 的取值范围．21.已知函数21()ln(1)2f x x m x =+-，其中m R ∈． （1）求函数()f x 的单调区间；（2）若函数()f x 存在两个极值点1x ，2x ，且12x x <，证明：12()11ln 2042f x x -<<．22．在平面直角坐标系xOy 中，曲线C的参数方程是2cos x y θθ=⎧⎪⎨=⎪⎩（θ为参数），以射线Ox 为极轴建立极坐标系，直线l的极坐标方程为cos sin 0ρθρθ-=．（1）将曲线C 的参数方程化成普通方程，将直线l 的极坐标方程化成直角坐标方程；（2）求直线l 与曲线C 相交所得的弦AB 的长．。

2019届广东省深圳市高级中学高三12月模拟考试理科综合试题本试卷分选择题和非选择题，共15页，满分300分，考试时间150分钟（15：00-17：30）可能用到的相对原子质量：H1K39O16Cl35.5一、选择题：本题包括1-13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．生物表现一定的生命特征，与它们的结构以及分子组成密不可分。

下列相关叙述正确的是A.叶绿素、血红蛋白中含有N的一定是血红蛋白B.绿藻、黑藻、颤藻中没有叶绿体的一定是颤藻C.发菜和菠菜细胞内DNA均为链状的双螺旋结构D.核糖体、质粒、酶中没有核糖参与组成的一定是酶2．离子通过细胞膜进出细胞有两种方式，一种是通过离子通道，另一种是借助离子泵的搬运。

离子通道是由蛋白质复合物构成的，一种离子通道只允许一种离子通过，且只有在对特定刺激发生反应时才瞬时开放；离子泵是一种具有ATP水解酶活性的载体蛋白，能利用ATP水解释放的能量跨膜运输离子。

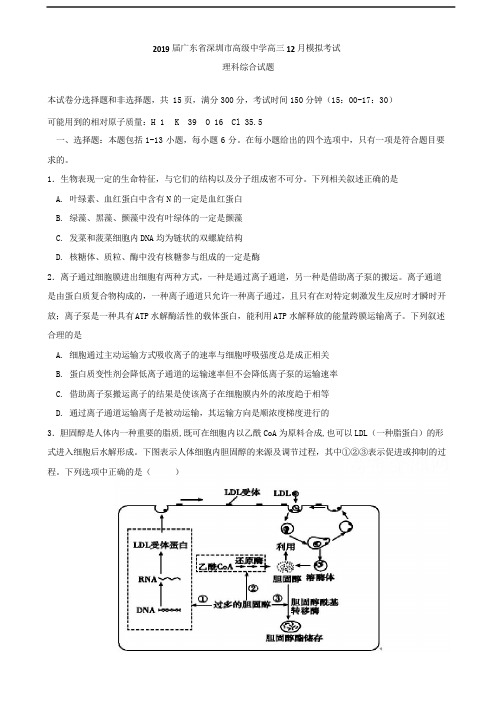
下列叙述合理的是A.细胞通过主动运输方式吸收离子的速率与细胞呼吸强度总是成正相关B.蛋白质变性剂会降低离子通道的运输速率但不会降低离子泵的运输速率C.借助离子泵搬运离子的结果是使该离子在细胞膜内外的浓度趋于相等D.通过离子通道运输离子是被动运输，其运输方向是顺浓度梯度进行的3．胆固醇是人体内一种重要的脂质,既可在细胞内以乙酰CoA为原料合成,也可以LDL（一种脂蛋白）的形式进入细胞后水解形成。

下图表示人体细胞内胆固醇的来源及调节过程，其中①②③表示促进或抑制的过程。

下列选项中正确的是（）A.CO2进入叶肉细胞的叶绿体基质后被转化为光合产物A．胆固醇在细胞中合成的场所是内质网,它是构成所有生物的细胞膜结构的重要成分B．细胞外液中的LDL与细胞膜上的受体结合,以胞吞方式进入细胞,这一过程与细胞膜的流动性性有关，需要消耗ATPC．从图中分析可知,如细胞内胆固醇过多，则会有①②③的反馈调节过程，①为抑制，②③为促进D．如果生物发生遗传性障碍，使LDL受体不能合成，则血浆中的胆固醇含量将下降4．在正常与遮光条件下向不同发育时期的豌豆植株供应14CO2，48h后测定植株营养器官和生殖器官中14C 的量。

深圳高级中学2019届高三年级12月模拟考试理科综合（物理）14.如图所示，甲图为光滑水平面上质量为M 的物体，用细线通过定滑轮与质量为m 的物体相连，m 所受重力为5N ；乙图为同一物体M 在光滑水平面上用细线通过定滑轮竖直向下受到拉力F 的作用，拉力F 的大小也是5N ，开始时M 距桌边的距离相等，则： A.M 到达桌边时的速度相等，所用的时间也相等 B.甲图中M 到达桌边用的时间较长，速度较大 C.甲图中M 到达桌边时的动能较大，所用时间较短 D.乙图中绳子受到的拉力较大15.如图所示，用传送带给煤车装煤，平均每5 s 内有5000kg 的煤粉落于车上，由于传送带的速度很小，可认为煤粉竖直下落．要使车保持以0.5 m/s 的速度匀速前进，则对车应再施以向前的水平力的大小为: A. 50N B. 250N C. 500ND.750N16.阻值均为R 的四个电阻、电容为C 的电容器及电动势为E 的电源（不计内阻）连接成如图所示的电路．开关K 闭合且电路稳定时，以下说法正确的是：A ．电容器两板间电压为E /3B ．电容器极板上的电荷量为2CE /5C ．减小电容器两极板正对面积，极板上的电荷量减小D ．减小电容器两极板间的距离，稳定后两板间电压比原来的更小17.如图所示，放在斜劈上的物块受到平行于光滑斜面向下的力F 作用，沿斜面向下运动，斜劈保持静止.下列说法中正确的是：A ．地面对斜劈的弹力大于斜劈和物块的重力之和B ．若F 增大，地面对斜劈的摩擦力也增大C ．若F 反向，地面对斜劈的摩擦力也反向D ．地面对斜劈作用力的方向一定与斜面不垂直18.如图所示，某极地轨道卫星的运行轨道平面通过地球的南北两极，已知该卫星从北纬60°的正上方，按图示方向第一次运行到南纬60°的正上方时所用时间为1 h ，则下列说法正确的是：A ．该卫星与同步卫星的运行半径之比为1:4B ．该卫星与同步卫星的运行速度之比为1:2C ．该卫星的运行速度一定大于7.9 km ／sD ．该卫星的机械能一定大于同步卫星的机械能 多选：19.如图所示，质量为m 、带电荷量为q 的带电微粒，以初速度v 0从A 点竖直向上射入真空中的沿水平方向的匀强电场中，微粒通过电场中B 点时速率v B =2v 0，方向与电场的方向一致，则下列说法中正确的是:A. 微粒所受的电场力大小是其所受重力的2倍B. 带电微粒的机械能增加了2mv 02C. A 、B 两点间的电势差为2mv 02/qD. A 、B 两点间的电势差为3mv 02/2q20.质量为400kg 的赛车在平直赛道上以恒定功率加速，受到的阻力不变，其加速度a 和速度的倒数1/v 的关系如图所示，则赛车: A ．速度随时间均匀增大 B ．加速度随时间均匀增大 C ．输出功率为160kW D ．所受阻力大小为1600N21.如图所示，斜劈B 固定在弹簧上，斜劈A 扣放在B 上，A 、B 相对静止，待系统平衡后用竖直向下的变力F 作用于A ，使A 、B 缓慢压缩弹簧，弹簧一直在弹性限度内，则下面说法正确的是:A ．压缩弹簧的过程中，B 对A 的摩擦力逐渐增大 B ．压缩弹簧的过程中，A 可能相对B 滑动C ．当弹簧压缩量为某值时，撤去力F ，在A 、B 上升的过程中，B 对A 的作用力先增大后减小2-a 11)s m --⋅-丙D ．当弹簧压缩量为某值时，撤去力F ，在A 、B 上升的过程中，A 、B 分离时，弹簧恢复原长 22. (6分）为测量动车起动过程中加速度的大小，某同学设计并实施了两个方案． 方案甲：观察发现铁轨旁相邻里程基座之间的距离为s ，用手表记录车厢从第1个里程基座运动到第2个里程基座的时间为t 1，车厢从第2个里程基座运动到第3个里程基座的时间为t 2． 方案乙：将细绳的一端系在行李架上，另一端悬挂一个钢球，测量钢球到悬点的距离L ，动车加速时，测出钢球偏离原平衡位置的水平距离d ．（1）用方案甲测得动车的加速度的表达式为a 1= ___________________；用方案乙测得动车的加速度的表达式为a 2= ___________________．（2）任选一个方案，简述该方案的误差主要来源：_________________________ ． 23.(9分)Ⅰ.如图为正在测量中的多用电表表盘，请完成下列问题：(1)如果用直流“50 V”挡测量电压，指针位置如图所示，读数为________ V.(2)图甲用多用电表测量电阻时，多用电表内部的电路可以等效为一电池、一个可变电阻和一表头相串联，电池电动势E ＝1.5 V ，选择开关在“×1”挡，把它的两表笔短接，旋转可变电阻R 1的旋钮，当指针指向“0”时，流过多用电表的电流为________ mA.(3)图乙是测量R x 阻值时的电路，欧姆表使用一段时间后，电池电动势变小，内阻变大，但此表仍能进行欧姆调零，按正确使用方法再测R x 的值，其测量结果与原结果相比较将________(选填“变大”、“变小”或“不变”)．(4)图丙是将表头G 改装成两个倍率挡(如“×1”、“×10”)的欧姆表电路原理图，则当开关S 合向________端(选填“a ”或“b ”)时，欧姆表是较大倍率挡．Ⅱ.某同学将量程为200 μA，内阻约为500 Ω的表头改装成量程为1 mA和10 mA的双量程电流表，设计电路如图甲所示．定值电阻R1＝500 Ω，R2＝250 Ω，S为单刀双掷开关，A、B 为接线柱．回下答下问题：(1)将开关S置于“1”挡时，量程为________ mA；(2)定值电阻的阻值R3＝________ Ω.(结果取3位有效数字)(3)利用改装的电流表进行某次测量时，S置于“2”挡，表头指示如图乙所示，则所测量电流的值为________ mA.24. (14分)如图甲所示,一根直杆AB与水平面成某一角度自定,在杆上套一个小物块,杆底端B 处有一弹性挡板,杆与板面垂直.现将物块拉到A点静止释放,物块下滑与挡板第一次碰撞前后的v-t图象如图乙所示,物块最终停止在B点. 重力加速度为取g=10 m/s2.求:(1)物块与杆之间的动摩擦因数μ.(2)物块滑过的总路程s.25.(18分)如图所示,半径R=1.6m的1/6光滑圆弧轨道位于竖直平面内，与长L=3m的绝缘水平传送带平滑连接，传送带以v=3m/s的速度顺时针转动，传送带右侧空间存在互相垂直的匀强电场和匀强磁场，电场强度E=20N/C,磁感应强度B=3.0T,方向垂直纸面向外．两个质量均为m=1.0×10-3Kg的物块a和b，物块a不带电，b带q=1.0×10-3C的正电并静止于圆弧轨道最低点，将a物块从圆弧轨道顶端由静止释放，运动到最低点与b发生正碰，碰撞时间极短，碰后粘合在一起，离开传送带后一起飞入复合场中，最后以与水平成600角落在地面上的P点（如图），已知两物块与传送带之间的动摩擦因数均为μ=0.1,取g=10m/s2,a、b均可看做质点．求：（1）物块a运动到圆弧轨道最低点时对轨道的压力；（2）传送带距离水平地面的高度;（3）两物块碰撞后到落地前瞬间的运动过程中，a、b系统机械能的变化量．33．[物理选修3-3]（15分）（1）（5分）下列说法不正确的是（）（选对1个得2分，选对2个得4分，选对3个得5分．每选错1个扣3分，最低得分为0分）A. 物体的温度为0℃时，物体的分子平均动能为零B. 两个分子在相互靠近的过程中其分子力逐渐增大，而分子势能先减小后增大C. 密封在容积不变的容器内的气体，若温度升高，则气体分子对器壁单位面积上的平均作用力增大D. 第二类永动机是不能制造出来的，尽管它不违反热力学第一定律，但它违反热力学第二定律E. 一定质量的理想气体，如果在某个过程中温度保持不变而吸收热量，则在该过程中气体的压强一定增大Ⅰ活塞刚好升到缸口时，气体的温度是多少？Ⅱ汽缸内气体对外界做多少功？Ⅲ气体内能的变化？12月18日月考物理答案：14. D 15.C 16. C 17.D 18. A 19. ABC 20.CD 21. AD22.【解析】试题分析：（1）对甲方案，根据位移时间公式求得加速度；对乙方案，通过受力分析利用牛顿第二定律求得加速度；（2）对甲方案，有与测量时间存在误差，故是主要误差来源（1）对甲方案：设加速度为a ，则，联立解得对乙方案通过受力分析可知，其中，解得（2）方案甲的误差主要来源是时间的测量；方案乙的误差主要来源是长度的测量． 23. Ⅰ(1)23.0 (2)100 (3)变大 (4)b Ⅱ(1)10 (2)25.5 (3)0.68 24.(1) 0.25 (2) 6m【解析】由图象可知,物块下滑的加速度a 1=vt ∆∆=4 m/s 2,上滑时的加速度大小a 2=vt ∆∆=8 m/s 2,杆AB 长L=2 m,设斜杆的倾角为θ,物块的质量为m,物块与杆间的动摩擦因数为μ, 由牛顿第二定律得F 合=mgsin θ-μmgcos θ=ma 1, F 合=mgsin θ+μmgcos θ=ma 2,代入数据,得μ=0.25, sin θ=0.6,cos θ=0.8.(2) 对物块整个过程分析,设物块运动的路程为s,由动能定理得 mgLsin θ-μmgcos θs=0,代入数据得,s=6m 25.. (共20分)（1）a 物块从释放运动到圆弧轨道最低点C 时，机械能守恒，221)cos 1(c mv mgR =-θ （2分） 得：s m v c /4= （1分）在C 点，由牛顿第二定律：Rmv mg F CN 2=- （2分）解得：N F N 2102-⨯= （1分）由牛顿第三定律，a 物块对圆弧轨道压力：N F N 2102-⨯=', 方向竖直向下 （1分）(2)ab 碰撞动量守恒：'=c c mv mv 2 s m v c /2='（2分） ab 在传送带上假设能与传送带达到共速时经过的位移为s ，ma mg 22=μ 得：2/1s m g a ==μ （2分）as v v c222='-得：m s 5.2=<L 所以ab 离开传送带时与其共速为v=3m/s （1分） 进入复合场后，N mg Eq 2102-==,所以做匀速圆周运动， （1分）由rmv Bqv 2= （2分）得：2qBmv2r ==（1分）由几何知识解得传送带与水平地面的高度：m r r h 321=+= （1分） （3）ab 系统在传送带上运动过程中，摩擦力对其做功：J mgs W f 31052-⨯==μ（1分） ab 系统在复合场运动过程中，电场力对其做功：J Eqh W 2106-⨯-=-=电 （1分） 所以，二者碰后一直到落地，系统机械能的变化量：△E=J W W f 2105.5--⨯=+电（1分）（或者： ab 在传送带上机械能的变化量：△E 1=△E k =J mv mv c 322105221221-⨯='-⨯ab 在复合场中机械能的变化量：△E 2=△E p = -J mgh 21062-⨯-= 所以，在二者碰后一直到落地，系统机械能的变化量：△E=△E 1+△E 2=J 2105.5-⨯-）33．（1）ABE （5分）（选对1个得2分，选对2个得4分，选对3个得5分．每选错1个扣3分，最低得分为0分）．（2）【解析】（10分）(2)（10）①封闭气体初态：V 1＝1 500 cm 3，T 1＝273 K ， 末态： V 2＝1 500 cm 3＋50×10 cm 3＝2 000 cm 3． 缓慢升高环境温度，封闭气体做等压变化． 由V 1T 1＝V 2T 2(2分)解出T2＝364 K (1分)②设封闭气体做等压变化的压强为p，对活塞：p0S＝pS＋G (2分)汽缸内气体对外界做功W＝pSh (1分)联立解得W＝25J (1分)③由热力学第一定律得，汽缸内气体内能的变化ΔU＝Q＋(－W) (2分) ΔU＝35J 故汽缸内的气体内能增加了35J． (1分)。

深圳高级中学2019届高三年级12月模拟考试 理 科 数 学一．选择题：本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}230A x x x =-<，(){}ln 2B x y x ==-，则A B =I （ ） A ．()2,+∞B ．()2,3C ．()3,+∞D ．(),2-∞2.设α，β是两个不同的平面，m 是直线且m α⊂，“//m β”是“//αβ”的（ ）. A. 充分而不必要条件 B.必要而不充分条件 C. 充分必要条件 D.既不充分也不必要条件 3．若m 是2和8的等比中项，则圆锥曲线x 2+的离心率为（ ）A ．B ．C ． 或D ． 或4．《九章算术》中有“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则该竹子的容积为（ ） A ．10011升 B ．9011升 C ．25433升 D ．20122升5.已知向量a r ，b r 满足||2a =r ，||4b =r ，()a a b ⊥+r r r，则向量a r 在b r 方向上的投影为（ ）A ．1-B ．2-C ．2D ．16.已知直线430x y a -+=与22:40C x y x ++=e 相交于A 、B 两点，且120ACB ∠=︒，则实数a 的值为（ ）A ．3B ．10 C. 11或21 D ．3或137．已知某函数图象如图所示，则图象所对应的函数可能是（ ）A ．2xx y =B ．22xy =-C ．e xy x =-D ．|2|2x y x =﹣8．若双曲线C ：()222210,0x y a b a b-=>>的一条渐近线被抛物线24y x =所截得的弦长为32，则双曲线C 的离心率为（ ） A ．14B ．1C ．2D ．49.函数()()sin f x A x ωϕ=+（其中0,2A πϕ><）的图像如图所示，为了得到()cos 22g x x π⎛⎫=-⎪⎝⎭的图像，只需将()f x 的图像( )A.向左平移3π个长度单位B.向右平移3π个长度单位 C.向左平移6π个长度单位 D.向右平移6π个长度单位10.如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为( ) A.88246++ B.88226++ C.2226++ D.126224++11.记数列{}n a 的前n 项和为n S .已知11a =，1()2()n n n n S S a n N *+-=∈，则2018S =（ ）A ．10093(21)- B ．10093(21)2- C.20183(21)- D ．20183(21)2-12. 若函数2()ln ln x f x ax x x x=+--有三个不同的零点，则实数a 的取值范围是( )π7πxA. 1(1,)1e e e -- B.1[1,]1e e e -- C. 1(,1)1e e e --- D. 1[,1]1e e e --- 二．填空题：本大题4小题，每小题5分，满分20分．13．已知向量a 与b 的夹角为60︒，2=a ，3=b ，则32-=a b __________． 14．若tan 3α=，π02α⎛⎫∈ ⎪⎝⎭，，则πcos 4α⎛⎫-= ⎪⎝⎭__________．15．某几何体的三视图如图所示，主视图是直角三角形，侧视图是等腰三角形，俯视图是边长为3的等边三角形，若该几何体的外接球的体积为36π，则该几何体的体积为__________．16.ABC ∆中，角A ，B ，C 所对边分别为a ，b ，c .D 是BC 边的中点，且10AD =，8sin 315a B c =，1cos 4A =-，则ABC ∆面积为 ．三．解答题：本大题共8小题，满分70分，解答须写出文字说明、证明过程或演算步骤． 17．已知数列{}n a 的前n 项和为n S ，且n ，n a ，n S 成等差数列，()22log 11n n b a =+-． （l ）求数列{}n a 的通项公式；（2）若数列{}n b 中去掉数列{}n a 的项后余下的项按原顺序组成数列{}n c ，求12100c c c +++L 的值．18. 在ABC △中，内角A ，B ，C 的对边分别为a ，b ，c 且sin ()sin sin b B c b C a A +-=. （1）求角A 的大小； （2）若3sin sin 8B C =，且ABC △的面积为3a .19．如图，四棱锥P ABCD -中，PAD △为正三角形，//AB CD ，2AB CD =，90BAD ∠=︒，PA CD ⊥，E 为棱PB 的中点．（1）求证：平面PAB ⊥平面CDE ；（2）若直线PC 与平面PAD 所成角为45︒，求二面角A DE C --的余弦值．20．已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ，点P 在椭圆上，有124P P F F +=，椭圆的离心率为12e =； （1）求椭圆C 的标准方程；（2）已知()4,0N ，过点N 作直线l 与椭圆交于,A B 不同两点，线段AB 的中垂线为l '，线段AB 的中点为Q 点，记l '与y 轴的交点为M ，求MQ 的取值范围．21.已知函数21()ln(1)2f x x m x =+-，其中m R ∈． （1）求函数()f x 的单调区间；（2）若函数()f x 存在两个极值点1x ，2x ，且12x x <，证明：12()11ln 2042f x x -<<．22．在平面直角坐标系xOy 中，曲线C 的参数方程是2cos 3x y θθ=⎧⎪⎨=⎪⎩（θ为参数），以射线Ox 为极轴建立极坐标系，直线l 的极坐标方程为cos sin 30ρθρθ--=．（1）将曲线C 的参数方程化成普通方程，将直线l 的极坐标方程化成直角坐标方程； （2）求直线l 与曲线C 相交所得的弦AB 的长．2019届高三年级12月模拟考试理科数学答 案1．B 2.B 3.D 4.D 5.A 6.D 7.D 8.C 9.D 10.A 11.A 12,A8．【解析】双曲线C ：()222210,0x y a b a b-=>>的一条渐近线方程不妨设为：0bx ay +=，与抛物线方程联立，24bx ay y x+=⎧⎨=⎩，消去y ，得240ax bx +=，所以121240b x x a x x ⎧+=-⎪⎨⎪=⎩，所以所截得的弦长为22223116b b a a ⎛⎫⎛⎫+= ⎪⎪⎝⎭⎝⎭，化简可得234bc a =，223bc a =，()222412c a c a -=，42120e e --=，得24e =或3-（舍），所以双曲线C 的离心率2e =．9.【解析】由图像知1A =，74123T T πππ=-⇒=，22ππωω=⇒=，7()112f π=-7322122k ππϕπ⇒⋅+=+，2πϕ<，得3πϕ=，所以()sin(2)3f x x π=+，为了得到()cos 2sin(2)2g x x x π⎛⎫=-= ⎪⎝⎭的图像，所以只需将()f x 的图象向右平移6π个长度单位即可，故选D ．10.该几何体为如图中的三棱锥C －A 1C 1E ，EC ＝EA 1＝25，A 1C ＝161616＋＋＝43， 三角形EA 1C 的底边A 1C 上的高为：22， 表面积为：S ＝12⨯2⨯4＋12⨯2⨯4＋12⨯42⨯4＋12⨯22⨯43＝88246++11π7πx12.ln ,(0,)ln x xa x x x x=-∈+∞-有3个不同解，令ln (),ln x xg x x x x=--22221ln 1ln ln (1ln )(2ln )(0,),'(),(ln )(ln )x x x x x x x g x x x x x x x ----∈+∞=-=--则当(0,)x ∈+∞时，令2ln y x x =-，则1211'2,(0,),'0,2x y x y y x x -=-=∈<当递减；当1(,),'0,2x y y ∈+∞>递增，则min 11ln1ln 20,(0,)2y x =-=+>∈+∞则当时，恒有2ln 0.'()0,x x g x ->=令得1x =或,(0,1),'()0,()x e x g x g x =∈<且时递减；(1,),'()0,()x e g x g x ∈>时递增；(,)x e ∈+∞时，'()0,()g x g x <递减，则()g x 的极小值为(1)1,()g g x =的极大值为1(),1e g e e e=--结合函数图象可得实数a 的取值范围是1(1,)1e e e--.[答案]A 二．填空题：本大题4小题，每小题5分，满分20分．13．【解析】2=Q a ，3=b ，a 与b 的夹角为60︒，1cos602332︒∴⋅=⋅⋅=⨯⨯=a b a b ， 又222329124361233636-=-⋅+=-⨯+=Q a b a a b b ，326∴-=a b ，故答案为6．14．【解析】由tan 3α=，可得sin 3cos αα=．又22sin cos 1αα+=，结合π02α⎛⎫∈ ⎪⎝⎭，，可得310sin α=，10cos α=．)π225cos cos sin 4ααα⎛⎫∴-=+=⎪⎝⎭25．15．根据几何体的三视图，得出该几何体如图所示，由该几何体的外接球的体积为36π，即34π36π3R =，3R ∴=，则球心O 到底面等边ABC △得中心O '的距离2233223OO R ⎛⎫'=-⨯= ⎪ ⎪⎝⎭，根据球心O 与高AD 围成的等腰三角形，可得三棱锥的高242h OO '==，故三棱锥的体积()21334263V =⨯⨯⨯=．即答案为6．16.三．解答题17．【解析】（1）因为n ，n a ，n S 成等差数列，所以2n n S n a +=，①·····2分 所以()()11122n n S n a n --+-=≥．②①－②，得1122n n n a a a -+=-，所以()()11212n n a a n -+=+≥．·····4分 又当1n =时，1112S a +=，所以11a =，所以112a +=，故数列{}1n a +是首项为2，公比为2的等比数列， 所以11222n n n a -+=⋅=，即21n n a =-．·····6分（2）根据（1）求解知，()22log 121121n n b n =+--=-，11b =，所以12n n b b +-=， 所以数列{}n b 是以1为首项，2为公差的等差数列．·····7分又因为11a =，23a =，37a =，415a =，531a =，663a =，7127a =，8255a =， 64127b =，106211b =，107213b =，·····9分 所以()()1210012107127c c c b b b a a a +++=+++-+++L L L ()()127107121322272⨯+⎡⎤=-+++-⎣⎦L ()72121072147212-⨯=-+- 2810729=-+11202=．·····12分 18.（1）由sin ()sin sin b B c b C a A +-=，由正弦定理得22()b c b c a +-=， 即222b c bc a +-=，·····3分所以2221cos 22b c a A bc +-==，∴3A π=.·····6分（2）由正弦定理simA sin sin a b c B C ==，可得sin sin a B b A =，sin sin a Cc A=，所以1sin 2ABCS bc A =△1sin sin sin 2sin sin a B a CA A A=⋅⋅2sin sin 2sin a B C A ==·····10分又3sin sin 8B C =，sin 2A =，∴28=4a =.·····12分19．【解析】（1）取AP 中点F ，连接EF ，DF ．E Q 为PB ，//=CD EF ∴， CDFE ∴为平行四边形，···········2分//DF CE ∴．又PAD △为正三角形，PA DF ∴⊥，从而PA CE ⊥，···········3分 又PA CD ⊥，CD CE C =I ，PA ∴⊥平面CDE ，···········4分 又PA ⊂平面PAB ，∴平面PAB ⊥平面CDE ．···········5分（2）//AB CD ，PA CD PA AB ⊥⇒⊥，又AB AD ⊥，PA AD A =I ，AB ∴⊥平面PAD ．CD ∴⊥平面PAD CPD ⇒∠为PC 与平面PAD 所成的角，即45CPD ∠=︒，CD AD ∴=．···········7分以A 为原点，建系如图，设4AD =，则()8,0,0B ，(0,2,23P ，()0,4,0D ，(3E ，···········8分()4,1,3AE ∴=u u u v ，()0,4,0AD =u u u v．设(),,x y z =n 为平面ADE 的法向量，则43040AE x y z AD y ⎧⋅=++=⎪⎨⋅==⎪⎩u u u r u u u r n n ，令4z =-，得)3,0,4=-n ，···········10分 由（1）知，(23AP =为平面CDE 的一个法向量．···········11分257cos<,>19AP AP AP ⋅∴==-u u u ru u u u u ru r n n n，即二面角A DE C --的余弦值为25719-， 即二面角A DE C --的余弦值为25719-．······12分 20．【解析】（1）因为124P P F F +=，所以24a =，所以2a =， 因为12e =，所以1c =， 所以222413b a c =-=-=， 所以椭圆C 的标准方程为22143x y +=．·······4分 （2）由题意可知直线l 的斜率存在，设l ：()4y k x =-，()11,A x y ，()22,B x y ，()00,Q x y ，联立直线与椭圆()221434x y y k x ⎧==-+⎪⎨⎪⎩，消去y 得()2222433264120k x k x k +-+-=，21223243k x x k +=+，2122641243k x x k -=+，·······5分 又()()()22223244364120kk k ∆=--+->，解得：1122k -<<，·····6分2120216243x x k x k +==+，()00212443k y k x k =-=-+，所以2221612,4343k k Q k k ⎛⎫- ⎪++⎝⎭，·······7分 所以l '：()001y y x x k -=--，即222121164343k k y x k k k ⎛⎫+=-- ⎪++⎝⎭，化简得：21443k y x k k =-++，·······8分 令0x =，得2443k m k =+，即240,43k M k ⎛⎫ ⎪+⎝⎭，·······9分 ()2224222222161616434343k k k k MQ k k k ⎛⎫+⎛⎫=+=⋅ ⎪ ⎪++⎝⎭⎝⎭+，·······10分 令243t k =+，则[)3,4t ∈，所以22222233231144161616321t t t t MQ t t t t --⎛⎫+ ⎪⎡⎤--⎛⎫⎝⎭=⋅=⋅=⋅-⋅-⋅+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦， 所以[)0,5MQ ∈．·······12分21.解：（1）函数()f x 定义域为(,1)-∞，且2'()11m x x mf x x x x-+-=-=--， 10x ->， 令20x x m -+-=，14m ∆=-，·····1分 当0∆≤，即14m ≥时，'()0f x ≤，∴()f x 在(,1)-∞上单调递减；·····2分 当0∆>，即14m <时，由20x x m -+=，解得1x =2x =，若104m <<，则121x x <<，∴1(,)x x ∈-∞时，'()0f x <，()f x 单调递减； 12(,)x x x ∈时，'()0f x >，()f x 单调递增；2(,1)x x ∈时，'()0f x <，()f x 单调递减；·····3分若0m ≤，则121x x <≤，∴1(,)x x ∈-∞时，'()0f x <，()f x 单调递减； 11(,1)x x ∈时，'()0f x >，()f x 单调递增；·····4分 综上所述：0m ≤时，()f x的单调递减区间为(-∞，单调递增区间为；104m <<时，()f x的单调递减区间为(-∞，，单调递增区间为11(22+； 14m ≥时，()f x 的单调递减区间为(,1)-∞．·····5分 （2）因为函数()f x 定义域为(,1)-∞，且2'()11m x x m f x x x x-+-=-=--， ∵函数()f x 存在两个极值点，∴'()0f x =在(,1)-∞上有两个不等实根1x ，2x ，记2()g x x x m =-+-，则140,11,2(1)(1)0,m g ⎧∆=->⎪⎪-<⎨⨯-⎪⎪<⎩∴104m <<， 从而由12121,,x x x x m +=⎧⎨=⎩且12x x <，可得11(0,)2x ∈，21(,1)2x ∈，·····7分 ∴22111122221ln(1)()12ln(1)2x m x f x x m x x x x x +-==⨯+-211111ln(1)2(1)x x x x =⨯+--，·8分 构造函数2()ln(1)2(1)x x x x x ϕ=+--，1(0,)2x ∈， 则22222'()ln(1)ln(1)2(1)12(1)x x x x x x x x x x ϕ-=+--=+----， 记22()ln(1)2(1)x p x x x =+--，1(0,)2x ∈，则231'()(1)3x x p x x h -+-=-， 令'()0p x =，得01(0,)2x =（12x =>，故舍去）， ∴()p x 在0(0,)x 上单调递减，在01(,)2x 上单调递增，·····10分又(0)0p =，11()ln 2022p =-<， ∴当1(0,)2x ∈时，恒有()0p x <，即'()0x ϕ<，∴()x ϕ在1(0,)2上单调递减，∴1()()(0)2x ϕϕϕ<<，即11ln 2()042x ϕ-<<，∴12()11ln 2042f x x -<<．·····12分 22．【解析】（1）曲线C 的参数方程化成直角坐标方程为22143x y +=，·····2分 因为cos x ρθ=，sin y ρθ=，所以l的直角坐标方程为0x y -=．·····4分（2）直线l 的倾斜角为4π，过点0)， 所以直线l化成参数方程为cos 4sin 4x t y t π⎧=⎪⎪⎨π⎪=⎪⎩，即2x y t ⎧=⎪⎪⎨⎪=⎪⎩，（t 为参数），5分 代入22143x y +=得，2760t +-=，247(6)3840∆-⨯⨯-=>， 设方程的两根是1t ，2t，则127t t +=-，1267t t =-，·····8分所以1277AB t t =-===．·····10分。

深圳市2019届高三第一次调研考试数学理试题第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复数的共轭复数是A. B. C. D.【答案】D【解析】【分析】根据复数的运算可知，再根据共轭复数的概念，即可求解。

【详解】由题意，根据复数的运算可知，所以，其共轭复数为：，故选D。

【点睛】本题主要考查了复数的运算，以及共轭复数的概念，其中解答中熟记复数的基本运算法则是解答的关键，着重考查了推理与运算能力，属于基础题。

2.已知集合，，则A. B. C. D.【答案】B【解析】【分析】由题意，求得集合，，再根据集合的交集的运算，即可求解。

【详解】由题意，求得集合，，所以，【点睛】本题主要考查了对数函数的图象与性质，以及集合的交集运算问题，其中解答中熟记对数函数的图象与性质，以及集合交集的运算是解答的关键，着重考查了运算与求解能力，属于基础题。

3.设为等差数列的前项和．若，，则的公差为A. -2B. -1C. 1D. 2【答案】A【解析】【分析】根据等差数列的前n项和公式和题设条件，求得，进而求解数列的公差，得到答案。

【详解】依题意，可得，解得，又，所以，所以公差，故选A。

【点睛】本题主要考查了等差数列的通项公式，以及前n项和公式的应用，其中解答中熟记等差数列的通项公式和前n项和公式，合理准确运算是解答的关键，着重考查了运算与求解能力，属于基础题。

4.己知某产品的销售额与广告费用之间的关系如下表：（单位：万元）（单位：万元）若求得其线性回归方程为，则预计当广告费用为6万元时的销售额为A. 42万元B. 45万元C. 48万元D. 51万元【答案】C【解析】【分析】根据上表中的数据，求得样本点中心，代入回归直线的方程，求得的值，得到回归直线的方程，即可求解。

【详解】由题意，根据上表中的数据，可得，，即回归方程经过样本点中心，又由线性回归方程为，所以，解得，所以，当时，，故选C.【点睛】本题主要考查了回归直线方程的应用问题，其中解答中熟记回归直线方程的性质，求得回归直线的方程是解答的关键，着重考查了运算与求解能力，属于基础题。

2019届广东省深圳市高级中学高三12月模拟考试理科综合试题2019届广东省深圳市高级中学高三12月模拟考试理科综合试题本试卷分选择题和非选择题，共15页，满分300分，考试时间150分钟（15：00-17：30）可能用到的相对原子质量：H1K39O16Cl35.5一、选择题：本题包括1-13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．生物表现一定的生命特征，与它们的结构以及分子组成密不可分。

下列相关叙述正确的是A.叶绿素、血红蛋白中含有N的一定是血红蛋白B.绿藻、黑藻、颤藻中没有叶绿体的一定是颤藻C.发菜和菠菜细胞内DNA均为链状的双螺旋结构D.核糖体、质粒、酶中没有核糖参与组成的一定是酶2．离子通过细胞膜进出细胞有两种方式，一种是通过离子通道，另一种是借助离子泵的搬运。

离子通道是由蛋白质复合物构成的，一种离子通道只允许一种离子通过，且只有在对特定刺激发生反应时才瞬时开放；离子泵是一种具有ATP水解酶活性的载体蛋白，能利用ATP水解释放的能量跨膜运输离子。

下列叙述合理的是A.细胞通过主动运输方式吸收离子的速率与细胞呼吸强度总是成正相关B.蛋白质变性剂会降低离子通道的运输速率但不会降低离子泵的运输速率C.借助离子泵搬运离子的结果是使该离子在细胞膜内外的浓度趋于相等D.通过离子通道运输离子是被动运输，其运输方向是顺浓度梯度进行的3．胆固醇是人体内一种重要的脂质,既可在细胞内以乙酰CoA为原料合成,也可以LDL（一种脂蛋白）的形式进入细胞后水解形成。

下图表示人体细胞内胆固醇的来源及调节过程，其中①②③表示促进或抑制的过程。

下列选项中正确的是（）A.CO2进入叶肉细胞的叶绿体基质后被转化为光合产物A．胆固醇在细胞中合成的场所是内质网,它是构成所有生物的细胞膜结构的重要成分B．细胞外液中的LDL与细胞膜上的受体结合,以胞吞方式进入细胞,这一过程与细胞膜的流动性性有关，需要消耗ATPC．从图中分析可知,如细胞内胆固醇过多，则会有①②③的反馈调节过程，①为抑制，②③为促进D．如果生物发生遗传性障碍，使LDL受体不能合成，则血浆中的胆固醇含量将下降4．在正常与遮光条件下向不同发育时期的豌豆植株供应14CO 2，48h后测定植株营养器官和生殖器官中14C 的量。

2019届高三年级适应性测试理科数学本试卷共6页，23小题，满分150分， 考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B 铅笔将试卷类型和考生号填涂在答题卡相应位置上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应的题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再填涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案，不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题组号的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

第Ⅰ卷(选择题 共60分)一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项符合要求．1．已知集合{|A x y ==，2{|log 1}B x x =≤，则AB =（A ）{|31}x x -≤≤ （B ）{|01}x x <≤ （C ）{|32}x x -≤≤ （D ）{|2}x x ≤2．已知3i1iz -=-（其中i 为虚数单位），则z 的虚部为 （A ）i - （B ）1- （C ） 1 （D ）23．在等比数列{}n a 中,12a =,前n 项和为n S ,若数列{}1n a +也是等比数列,则n S 等于(A)122n +- (B) 3n (C) 2n (D)31n -4．若4 cos5α=-，α是第三象限的角，则1tan21tan2αα+=-(A)12-(B)12(C) 2(D) 2-5．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形．现在勒洛三角形中随机取一点，则此点取自正三角形内的概率为(A)2π332(π3)--(B)32(π3)-(C)32(π3)+(D)2π332(π3)-+6．已知51(1)(2)axx x+-的展开式中各项系数的和为2，则该展开式中常数项为(A) 80-(B) 40-(C) 40(D) 807．现行普通高中学生在高一升高二时面临着选文理科的问题，学校抽取了部分男、女学生意愿的一份样本，制作出如下两个等高堆积条形图：根据这两幅图中的信息，下列统计结论是不．正确的是.(A)样本中的女生数量多于男生数量(B)样本中有理科意愿的学生数量多于有文科意愿的学生数量(C)样本中的男生偏爱理科(D)样本中的女生偏爱文科8．抛物线x y 42=的焦点为F ，准线为l ，经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ，l AK ⊥，垂足为K ，则△AKF 的面积是(A) 4 (B) 33 (C) 34 (D) 89．在平行四边形ABCD 中，113,2,,,32AB AD AP AB AQ AD ====若12,CP CQ ⋅= 则ADC ∠= 5()6A π 3()4B π 2()3C π ()2D π10．在平面直角坐标系xOy 中，已知点, A F 分别为椭圆2222:1(0)x y C a b a b+=>>的右顶点和右焦点，过坐标原点O 的直线交椭圆C 于, P Q 两点，线段AP 的中点为M ，若, , Q F M 三 点共线，则椭圆C 的离心率为 (A)13 (B) 23 (C) 83 (D) 32或8311． 设函数()y f x =的图像与2x ay +=的图像关于直线y x =-对称，且(2)(4)1f f -+-=，则a =（A ） 1- （B ）1 （C ）2 （D ）412． 设O 是正四面体P ABC -底面ABC 的中心，过O 的动平面与PC 交于,S 与,PA PB 的延长线分别交于,,Q R 则111||||||PQ PR PS ++ (A) 有最大值而无最小值 (B) 有最小值而无最大值 (C) 既有最大值又有最小值，且两者不相等 (D)是一个与平面QRS 无关的常数第II 卷（非选择题 共90分）本卷包括必考题和选考题两部分．第13-21题为必考题，每个试题考生都必须作答，第22-23题为选考题，考生根据要求作答．二、填空题:本大题共4小题,每小题5分,共20分． 13．在数列{}n a 中，1111,,(*)2019(1)n n a a a n N n n +==+∈+，则2019a 的值为______． 14. 已知函数sin 2cos ()()(()0)f x x x ϕϕϕ+=+<<π-的图象关于直线x =π对称，则cos2_____ϕ=．15．在三棱锥P ABC -中，平面PAB ⊥平面ABC ，ABC ∆是边长为的等边三角形，PAB ∆是以AB 为斜边的等腰直角三角形，则该三棱锥外接球的表面积为_________．16．已知函数22, 0,()e , 0,x x x f x x ⎧⎪=⎨>⎪⎩≤若方程2[()]f x a =恰有两个不同的实数根12,x x ，则12x x +的最大值是______．三、解答题：解答应写出文字说明，证明过程或演算步骤 17．（本小题满分12分）工程队将从A 到D 修建一条隧道，测量员测得图中的一些数据（,,,A B C D 在同一水平面内），求,A D 之间的距离.18．（本小题满分12分）已知四棱锥P ABCD -，底面ABCD 为菱形，PD PB =,H 为PC 上的点，过AH 的平面分别交PB ，PD 于点M ，N ，且BD ∥平面AMHN ． （1）证明：MN PC ⊥；（2）当H 为PC 的中点，PA PC AB ==，PA 与平面ABCD 所成的角为60︒，求AD 与平面AMHN 所成角的正弦值．HPABCDM N19. （本小题满分12分）在平面直角坐标系xOy 中，离心率为6的椭圆2222:1(0)x y C a b a b+=>>过点6(1,)M ． （1）求椭圆C 的标准方程；（2）若直线0x y m ++=上存在点G ，且过点G 的椭圆C 的两条切线相互垂直，求实数m 的取值范围．20. （本小题满分12分）某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数y （万人）与年份x 的数据：第x 年 12345678910旅游人数y （万人）300 283 321 345 372 435 486 527 622 800该景点为了预测2021年的旅游人数，建立了y 与x 的两个回归模型： 模型①：由最小二乘法公式求得y 与x 的线性回归方程50.8169.7y x =+；模型②：由散点图的样本点分布，可以认为样本点集中在曲线bx y ae =的附近．（1）根据表中数据，求模型②的回归方程bxy ae =． （a 精确到个位，b 精确到0．01）．（2）根据下列表中的数据，比较两种模型的相关指数2R ，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．回归方程①50.8169.7y x =+②bxy ae = 1021()iii y y =-∑ 3040714607①对于一组数据()()()1122,,,,,,n n v w v w v w ，其回归直线w v αβ=+的斜率和截距的最小二乘法估计分别为121()(),()niii nii w w v v w v v v βαβ==--==--∑∑．②刻画回归效果的相关指数22121()1()niii nii y y R y y ==-=--∑∑ ．③参考数据： 5.46235e≈， 1.43 4.2e ≈．表中1ln ,10i i i i u yu u ===∑．21．（本小题满分12分）已知函数()ln 2f x x x =--．（1）求曲线()y f x =在1x =处的切线方程；（2）函数()f x 在区间(,1)()k k k+∈N 上有零点，求k 的值； （3）若不等式()(1)()x m x f x x-->对任意正实数x 恒成立，求正整数m 的取值集合．请考生从第（22）、（23）两题中任选一题作答．如果多做，则按所做的第一个题目计分． 22．[选修4-4：坐标系与参数方程](10分）平面直角坐标系xOy 中，曲线1C 的方程为224x y +=，直线l 的参数 方程为2,,x t y t =--⎧⎪⎨=⎪⎩ （t 为参数），若将曲线1C 上的点的横坐标不变，纵坐标变为原来的32倍，得曲线2C ．（1）写出曲线2C 的参数方程;（2）设点(P -，直线l 与曲线2C 的两个交点分别为,A B ，求11PA PB+的值．23．[选修4-5：不等式选讲](10分）已知实数正数x , y 满足1x y +=． （1）解关于x 的不等式522x y x y ++-≤； （2）证明：2211119x y ⎛⎫⎛⎫--≥ ⎪ ⎪ ⎪⎝⎭⎝⎭2019届高三年级适应性测试理科数学参考答案及说明题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BBCABDDACCCD13．___1_________； 14．____35____； 15．__48π___； 16. ___3ln22-_____ .17．（本小题满分12分）工程队将从A 到D 修建一条隧道，测量员测得图中的一些数据（,,,A B C D 在同一水平面内），求,A D 之间的距离.AC 解：连接,在4154AC 中，ABC 22=+=∆....................................................3分414sin ,415cos =∠=∠ACB ACB .…………………………….5分.)32cos(cos ACB ACD ∠-=∠π=412534414*23415*)21(-=+-…….9分312-65412534*3*412-341AD 中，ACD 在2=-+=∆…….12分18．（本小题满分12分）已知四棱锥P ABCD -，底面ABCD 为菱形，PD PB =,H 为PC 上的点，过AH 的平面分别交PB ，PD 于点M ，N ，且BD ∥平面AMHN ． （1）证明：MN PC ⊥；（2）当H 为PC 的中点，3PA PC AB ==，PA 与平面ABCD 所成的角为60︒，求AD 与平面AMHN 所成角的正弦值．HPABCDM N【解析】（1）证明：连结AC 、BD 且ACBD O =，连结PO ．因为，ABCD 为菱形，所以，BD AC ⊥， 因为，PD PB =，所以，PO BD ⊥， 因为，ACPO O =且AC 、PO ⊂平面PAC ，所以，BD ⊥平面PAC ，因为，AC ⊂平面PAC ，所以，BD PC ⊥， 因为，//BD 平面AMHN ， 且平面AMHN平面PBD MN =，所以，//BD MN ，MN ⊥平面PAC ，所以，MN PC ⊥． ……………………………….5分 （2）由（I ）知BD AC ⊥且PO BD ⊥， 因为PA PC =，且O 为AC 的中点， 所以，PO AC ⊥，所以，PO ⊥平面ABCD ,所以PA 与平面ABCD 所成的角为PAO ∠，所以60PAO ∠=︒， 所以，12AO PA =，32PO PA =，因为，3PA AB =，所以，36BO PA =. 以OA ，OD ，OP 分别为x ，y ，z 轴，如图所示建立空间直角坐标系……….…..7分 记2PA =，所以，(0,0,0)O ，(1,0,0)A ，3(0,,0)3B -，(1,0,0)C -，3(0,,0)3D ，(0,0,3)P ，13(,0,)22H -，所以， 23(0,,0)BD =，33(,0,)2AH =-，3(1,,0)AD =-.……………..8分 记平面AMHN 的法向量为(,,)n x y z =，所以，00n BD n AH ⎧⋅=⎪⎨⋅=⎪⎩即23033022y x z ⎧=⎪⎨⎪-+=⎪⎩，令2x =，解得0y =，23z =，所以，(2,0,23)n =，.…………………….…..10分记AD 与平面AMHN 所成角为θ，所以，3sin |cos ,|||4||||n AD n AD n AD θ⋅=<>==. ………………………………………………………………………………………….…..11分 所以，AD 与平面AMHN 所成角的正弦值为34.………………………………..…..12分19. （本小题满分12分）如图：在平面直角坐标系xOy 中，离心率为63的椭圆2222:1(0)x y C a b a b+=>>过点6(1,)3M ．（1）求椭圆C 的标准方程；（2）若直线0x y m ++=上存在点G ，且过点G 的椭圆C 的两条切线相互垂直，求实数m 的取值范围．解：（1）由题意，2226,,c a a b c ⎧=⎪⎨⎪=+⎩解得223a b =，又221213a b +=，解得223,1,a b ⎧=⎪⎨=⎪⎩ 所以椭圆C 的标准方程为2213x y +=．------------------------------------------4分（2）①当过点G 的椭圆C 的一条切线的斜率不存在时，另一条切线必垂直于y 轴，易得(3,1)G ±；--------------------------------------------------------------6分②当过点G 的椭圆C 的切线的斜率均存在时，设000(,), 3G x y x ≠± 切线方程为00()y k x x y =-+，代入椭圆方程得2220000(31)6()3()30k x k kx y x kx y +--+--=，2220000[6()]4(31)[3()3]0k kx y k kx y ∆=--+--=，化简得：2200()(31)0kx y k --+=，由此得2220000(3)210x k x y k y --+-=，--------------------------------------8分设过点G 的椭圆C 的切线的斜率分别为12,k k ，所以20122013y k k x -=-．因为两条切线相互垂直，所以2020113y x -=--，即220004(3)x y x +=≠±，---------9分 由①②知G 在圆22004x y +=上，又点G 在直线0x y m ++=上， 所以直线0x y m ++=与圆224x y +=有公共点，所以211m +≤，所以2222m -≤≤．-------------------------11分综上所述，m 的取值范围为[22,22]-．---------------------------12分 20. （本小题满分12分）某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数y （万人）与年份x 的数据：第x 年 12345678910旅游人数y （万人）300 283 321 345 372 435 486 527 622 800 y x 模型①：由最小二乘法公式求得y 与x 的线性回归方程50.8169.7y x =+；模型②：由散点图的样本点分布，可以认为样本点集中在曲线bxy ae =的附近．（1）根据表中数据，求模型②的回归方程bxy ae =． （a 精确到个位，b 精确到0．01）．（2）根据下列表中的数据，比较两种模型的相关指数2R ，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．回归方程①50.8169.7y x =+②bxy ae = 1021()iii y y =-∑ 3040714607解：（1）对bxy ae =取对数，得ln ln y bx a =+，……1分 设ln u y =，ln c a =，先建立u 关于x 的线性回归方程。

绝密★启用前 试卷类型： A深圳市2019年高三年级第二次调研考试数 学（理科） 2019．4本试卷共6页，23小题，满分150分．考试用时120分钟．12iz +=−所对应的点位于 （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 3．2019年是新中国成立70周年，也是全面建成小康社会的关键之年．为喜迎祖国70周年生日，全民齐心奋力建设小康社会，某校特举办“喜迎国庆，共建小康”知识竞赛活动．下面的茎叶图是参赛两组选手的答题得分情况，则下列说法正确的是注意事项：1．答卷前，考生务必用黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号，并将条形码正向准确粘贴在答题卡的贴条形码区，请保持条形码整洁、不污损. 2．选择题每小题选出答案后，用2B 铅笔把答案涂在答题卷相应的位置上.3．非选择题必须用0.5毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液. 不按以上要求作答的答案无效.4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再做答. 5．考生必须保持答题卡的整洁，考试结束后，将答题卡交回.第Ⅰ卷一、 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{|0}M x x =>，2{|40}N x x =−≥，则M N =（A ）(,2](0,)−∞−+∞ （B ）(,2][2,)−∞−+∞ （C ）[2,+)∞ （D ）(0,)+∞2．在复平面内，复数i(1i)（第3题图）甲乙7895237373451（A ）甲组选手得分的平均数小于乙组选手得分的平均数 （B ）甲组选手得分的中位数大于乙组选手得分的平均数 （C ）甲组选手得分的中位数等于乙组选手得分的中位数（D ）甲组选手得分的方差大于乙组选手得分的方差 4．已知等比数列{}n a 满足112a =，且2434(1)a a a ⋅=−，则5a = （A ）8 （B ）16 （C ）32 （D ）64 5．已知函数22()(1)f x ax a x x=+−+是奇函数，则曲线()y f x =在1x = 处的切线的倾斜角为 （A ）π4 （B ）3π4 （C ）π3 （D ）2π36．在平行四边形ABCD 中，E 为CD 的中点，F 为AE 的中点．设AB =a ，AD =b ，则FB = （A ）3142−+a b （B ）1324+a b （C ）1324−a b （D ）3142−a b （第7题图）7．如图所示，网格纸上小正方形的边长为1，粗实线和粗虚线画出的是某几何体的三视图，则该几何体的表面积为 （A ）(842)π+ （B ）(942)π+ （C ）(882)π+ （D ）(982)π+8．十九世纪末，法国学者贝特朗在研究几何概型时提出了 “贝特朗悖论”，即“在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少？”贝特朗用“随机半径”、“随机端点”、“随机中点”三种方法求解，所得结果均不相同．该悖论的矛头直击概率概念本身，这极大地促进了概率论基础的严格化．已知“随机端点”的方法如下：设A 为圆O 上一个定点，在圆周上随机取一点B ，连结AB ，求所得弦长AB 大于圆O 的内接等边三角形边长的概率．记该概率为p ，则p =（A ）15 （B ）14 （C ）13 （D ）129．已知函数()ln 1af x x x=+−有且仅有一个零点，则实数a 的取值范围为 （A ）(,0]{1}−∞ （B ）[0,1] （C ）(,0]{2}−∞ （D ）[0,2]10．设点1F 、2F 分别为椭圆2222:1x y C a b+=的左、右焦点，点A 、B 分别为椭圆C 的右顶点和下顶点，且点1F 关于直线AB 的对称点为M ．若212MF F F ⊥，则椭圆C 的离心率为 （A）12（B）13 （C）12（D）211．已知函数()cos (0)f x x x ωωω=+>在区间ππ[,]43−上恰有一个最大值点和一个最小值点，则实数ω的取值范围为 （A ）8[,7)3 （B ）8[,4)3（C ）20[4,)3 （D ）20(,7)3（A（B）2 （C ）52 （D ）54第Ⅱ卷本卷包括必考题和选考题两部分. 第（13）题～第（21）题为必考题，每个试题考生都必须做答. 第（22）题～第（23）题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．A（第12题图）BCDFE12. 如图，在四面体ABCD 中，2AB CD ==，AC BD ==， AD BC ==E 、F 分别是AD 、BC 的中点.若用一个与 直线EF 垂直，且与四面体的每个面都相交的平面α去截该四面 体，由此得到一个多边形截面，则该多边形截面面积的最大值为13．设实数x ，y 满足23124x y x y ≤≤⎧⎪≤≤⎨⎪+≤⎩，，，则1y x −的最大值为___________．14．已知双曲线C ：22221x y a b−=，且圆E ：21x y −+=C E A BA n S {}na n 13a =2n ≥1122n n n n n S S S S na −−+−=2019m SS S ≥m ABC 2AB BC =25AC =13a =18．（本小题满分12分）在边长为D 的正方形AC 中，点2=AD CD 、2∠=∠A B D C B D 分别为边ABC ∠、AD 的中点，以CE ，CF 为折痕将△DFC 和△BCE 折起，使点B 、D 重合于点P ，连结PA ，得到如图所示的四棱锥P AECF −．（1）求证：EF PC ⊥；（2）求直线PA 与平面PEC 所成角的正弦值．CDFP22(2)1x y −+=的圆心是双曲线C 的右焦点，若圆E 与双曲线C 的渐近线相切，则双曲线C 的方程为___________．15．精准扶贫是全面建成小康社会、实现中华民族伟大“中国梦”的重要保障．某单位拟组成4男3女共7人的扶贫工作队，派驻到3个贫困地区A 、B 、C 进行精准扶贫工作．若每个地区至少派驻1男1女两位工作人员，且男性甲必须派驻到A地区，则不同的派驻方式有_______种．16．设n S 是数列{}n a 的前n 项和，且13a =，当2n ≥时，有1122n n n n n S S S S na −−+−=.则使得122019m S S S ⋅⋅⋅≥成立的正整数m 的最小值为_________. 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知△ABC 中，2AB BC =，25AC =，点D 在边AC 上，且2=AD CD ，2∠=∠ABD CBD ．（1）求ABC ∠的大小； （2）求△ABC 的面积．最小二乘法估计分别为121()()ˆ()niii nii w w v v v v ==−−=−∑∑β，ˆˆw v =−αβ． ②参考数据：月销售量/千件月售价/元10816201804122146024681210••••••••••19．（本小题满分12分）某网店销售某种商品，为了解该商品的月销量y （单位：千件）与月售价x （单位：元/件）之间的关系，对近几年的月销售量i y 和月销售价i x (1,2,3,,10)i =数据进行了统计分析，得到了下面的散点图：（1）根据散点图判断，ln y c d x =+ 与y bx a =+哪一个更适宜作为月销量y 关于月销售价x 的回归方程类型？（给出判断即可，不需说明理由），并根据判断结果及表中数据，建立y 关于x 的回归方程；（2）利用（1）中的结果回答问题：已知该商品的月销售额为z （单位：千元），当月销售量为何值时，商品的月销售额预报值最大？(月销售额=月销售量⨯当月售价) 参考公式、参考数据及说明： ①对一组数据1122(,),(,)(,)n n v w v w v w ，，，其回归直线w v αβ=+的斜率和截距的表中ln =i i u x ，110i i u u ==∑．③计算时，所有的小数都精确到0.01，如ln 4.06 1.40≈. 20．（本小题满分12分）已知抛物线2:4C xy =，过点(2,3)的直线l 交C 于A 、B 两点，抛物线C 在点A 、B处的切线交于点P ．（1）当点A 的横坐标为4时，求点P 的坐标；（2）若Q 是抛物线C 上的动点，当||PQ 取最小值时，求点Q 的坐标及直线l 的方程．21．（本小题满分12分）已知函数()e e (1)−=−−+xxf x a a x (a ∈R ).（其中常数e=2.718 28⋅⋅⋅，是自然对数的底数）.（1）求函数()f x 的极值点；（2）若对于任意01<<a ，关于x 的不等式21[()](e )λ−<−a f x a 在区间(1,)−+∞a 上存在实数解，求实数λ的取值范围.22．（本小题满分10分）选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，曲线1C 的参数方程为2cos ,sin ,αα=⎧⎨=⎩x y （α为参数），圆2C 的方程为22(2)4x y −+=，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，射线l 的极坐标方程为0θθ=(0)ρ≥．（1）求曲线1C 和圆2C 的极坐标方程； （2）当0π02θ<<时，射线l 与曲线1C 和圆2C 分别交于异于点O 的M 、N 两点，若||2||ON OM =，求△2MC N 的面积．23．（本小题满分10分）选修4－5：不等式选讲已知函数1()||||(1)f x x m x m m=−++>． （1）当2m =时，求不等式()3f x >的解集； （2）证明：1()3(1)f x m m +≥−．2019年深圳市高三第二次调研考试理科数学试题答案及评分参考第Ⅰ卷一．选择题1.A2.C3.D4.A5.B6.D7.A8.C9.A 10.C 11.B 12. B 二．填空题：13.214. 2213x y −= 15. 72 16. 100911. 解析：π()3sin cos 2sin()6f x x x x =+=+ωωω，x R ∈，令π6t x =+ω，()2sin f x t =. 若函数()f x 恰有一个最大值点和一个最小值点在区间ππ[,]43−上， 也即函数2sin y t =恰有一个最大值点和一个最小值点在区间ππππ[,]4636−++ωω上， ∴3ππππ,2462πππ3π,2362⎧−<−+≤−⎪⎪⎨⎪≤+<⎪⎩ωω，解得820,3314,⎧≤<⎪⎨⎪≤<⎩ωω，即843≤<ω， ∴ω的取值范围为8[,4)3，故应选B ．12. 解析：（法一）补成长，宽，高分别为3,2,1的长方体(如下图)， 由于EF α⊥，故截面为平行四边形MNKL ，可得5KL KN +=， 设异面直线BC 与AD 所成的角为θ，则sin sin sin HFB LKN θ=∠=∠， 算得26sin θ=，∴sin MNKL S NK KL NKL =⋅⋅∠四边形2266()2NK KL +≤=， 当且仅当NK KL =时取等号，故应选B ．（法二）()12FE AD FA FD AD ⋅=+⋅uur uuu r uu r uu u r uuu r ()14BA CA BD CD AD =+++⋅uu r uu r uu ur uu u r uuu r()()104BA AD CD AD CA AD BD AD ⎡⎤=⋅+⋅+⋅+⋅=⎣⎦uu r uuur uu u r uuu r uu r uuu r uu u r uuu r∴EF AD ⊥，同理可得EF BC ⊥，设异面直线BC 与AD 所成的角为θ，则sin sin sin HFB LKN θ=∠=∠，()321BC AD BA AC AD BA AD AC AD ⋅=+⋅=⋅+⋅=−+=−uu u r uuu r uu r uuu r uuu r uu r uuu r uuu r uuu rQ ，∴1cos ,5||||BC AD BC AD BC AD ⋅<>==−⋅uu u r uuu ruu u r uuu r uu u r uuu r ，sin ,sin BC AD θ∴<>==uu u r uuu r即sin NKL ∠=同法一可得sin MNKL S NK KL NKL =⋅⋅∠≤四边形， 当且仅当NK KL =时取等号，故应选B ． 16.解析：1122n n n n n S S S S na −−+−=，∴11122()n n n n n n S S S S n S S −−−+−=−， ∴112(21)(21)n n n n S S n S n S −−=+−−， ∴121212n n n n S S −+−−=， 令21n nn b S +=，则12n n b b −−=（2n ≥）， ∴数列{}n b 是以111331b S a ===为首项，公差2d =的等差数列， ∴21n b n =−，即2121n n n S +=−，∴2121n n S n +=−， ∴12521321321m m S S S m m +⋅⋅⋅=⨯⨯⋅⋅⋅⨯=+−， 由212019m +≥，解得1009m ≥，即正整数m 的最小值为1009，故应填1009． 三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知△ABC中，AB =，AC =点D 在边AC 上，且2=AD CD ，2∠=∠ABD CBD ． （1）求ABC ∠的大小； （2）求△ABC 的面积．解：（1）(法一)依题意设22θ∠=∠=ABD CBD ， ∵2=AD CD，AC =∴AD =，3CD =， …………………………………………2分 在△BAD 中，由正弦定理，可得sin sin AB ADADB ABD=∠∠ ，∴sin sin AB ABD ADB AD ∠∠==， ……………………………………4分同理，在△BCD 中，由正弦定理，可得sin sin BC CBD BDC CD ∠∠== ， ……………………………………6分∵πBDC BDA ∠+∠=，∴sin sin ∠=∠BDC BDA ，=∵AB =cos sin θθθ=， ∵0πθ<<，∴sin 0θ>，∴cos 2θ=，∴π4θ=， ∴3π34BC BC =+−⋅， 解得2BC =， …………………………………………………………10分∴213πsin3sin 224ABC S AB BC θ∆=⋅⋅==. …………………………………12分 (法二)2=AD CD ，∴12==BDC BDASCD SAD ，……………………………………2分 1sin 2BDC S BC BD θ∆=⋅⋅，1sin 22BDA S AB BD θ∆=⋅⋅，且AB =， 4ABC θ∠==. ……………………………………………………8分 （2）在△ABC 中，由余弦定理，得2222cos3AC AB AC AB BC θ=+−⋅， ∴2223π)cos∴2cos 2θ=，即4πθ=，∴334πθ∠=∠+∠==ABC ABD CBD 4ABCD E F ABAD CE CF DFC BCE B D P PAP AECF −EF PC ⊥PEC EFAC EF O AB BC ⊥AD CD ⊥PC PE⊥，…………………7分PC PF⊥，PE PF P =，设点PC ∴⊥到平面PEF 的距离为EF ⊂，EF PC ∴⊥，EF，解得AC EF⊥，…………………9分BE DF =OPE PF=O EF EF PO∴⊥AC EF⊥PO（第18题图）BE DF=OPE PF=O EFEF PO∴⊥AC EF⊥πθ∠=∠+∠==ABC ABD CBD ， ……………………………………8分 (以下同法一)【说明】本题主要考察正弦定理，余弦定理，二倍角公式及三角形面积计算公式等知识，意在考察考生数形结合、转化与化归思想，考察了学生的逻辑推理，数学运算等核心素养． 18．（本小题满分12分）在边长为4的正方形ABCD 中，点E 、F 分别为边AB 、AD 的中点，以CE ，CF 为折痕将△DFC 和△BCE 折起，使点B 、D 重合于点P ，连结PA ，得到如图所示的四棱锥P AECF −．（1）求证：EF PC ⊥；（2）求直线PA 与平面PEC 所成角的正弦值． 解析：（1）(法一)证明：连结EF ， 记AC 与EF 的交点为O ，在正方形ABCD 中，AB BC ⊥，AD CD ⊥， 翻折后PC PE ⊥，PC PF ⊥，……………………3分 又PE PF P =，PC ∴⊥平面PEF ，……………4分EF ⊂平面PEF ，EF PC ∴⊥；………………………5分(法二)证明：连结EF ，记AC 与EF 的交点为O ，在正方形ABCD 中，AC EF ⊥，BE DF =，O 为EF 的中点，翻折后，PE PF =，……………2分 O 是EF 的中点，EF PO ∴⊥， 而AC EF ⊥，PO 与AC 相交于O 点，EF ∴⊥平面PAC ，………………………4分又PC ⊂平面PAC ，EF PC ∴⊥；………………………5分 （2）(法一)由（1）可知△OPC 为直角三角形，2OP =，4PC =，32OC =， 设P 到AC的距离为h ，2432h ⋅=⋅，在Rt △POC 中，1cos 3PO POC OC ∠==，1cos 3POA ∴∠=−， 在△POA 中，222482cos 9PA OA OP OP OA POA =+−⋅⋅⋅∠=，PA ∴=PA 与平面PEC 所成角为θ，………………………10分sin h PA θ'∴==，………………………11分 ∴直线PA 与平面PEC所成角的正弦值为3．………………………12分 (法二)连结AC ，AC 与EF 交于O 点，以OA ，OE 所在的直线分别为x ，y 轴，过O 作垂直于面ABCD 的直线为z 轴，建立如图所示的空间直角坐标系，依题意有A，(C −，E ，………………………6分 过P 作PG AC ⊥，在Rt POC ∆中，OP =4PC =，OC = OP PC OC PG ∴⋅=⋅， 43PG ∴=，3OG ==，4(0)33P ∴−，，…………………8分 44()3PA ∴=−，24()24()33PF =−，…………………10分 设PA 与平面33PE =−所成角为C E =，则2PF PE ==，………………11分∴直线PA 与平面PEC 所成角的正弦值为3．……………………12分思路2：设平面22EF =的法向量为∴，PC P=3PE =−，CE =， 思路1：2PF PE ==，EF =∴PF PE ⊥，…………………9分显然PF PC ⊥，又PEPC P =，∴PF ⊥平面PEC ，易知(0,F ，∴平面PEC 的一个法向量CE PE ⎧⋅=⎪∴⎨⋅=⎪⎩n n，04033x z ⎧+=∴+−=⎩， 取1x =，则3y =−，z =−则(1,3,=−−n ，………………………10分 设PA 与平面PEC 所成角为θ，则||sin ||||PA PA θ⋅==⋅n n ，………………11分 ∴直线PA 与平面PEC 所成角的正弦值为11021()()27.54ˆ10.202.70()iii ii y y u u du u ==−−−===−−∑∑， 月销售量/千件月售价/元108162018041221462461210••••••••••C3．……………………12分 【说明】本题以翻折问题为载体考察空间中点，线，面的位置关系，异面直线垂直的判定，直线与平面所成角等知识，意在考察考生的空间想象能力，逻辑推理能力以及运算求解能力． 19．（本小题满分12分）某网店销售某种商品，为了解该商品的月销量y （单位：千件）与月售价x （单位：元/件）之间的关系，对近几年的月销售量i y 和月销售价i x (1,2,3,,10)i =数据进行了统计分析，得到了下面的散点图：（1）根据散点图判断，ln y c d x =+ 与y bx a =+哪一个更适宜作为月销量y 关于月销售价x 的回归方程类型？（给出判断即可，不需说明理由），并根据判断结果及表中数据，建立y 关于x 的回归方程； （2）利用（1）中的结果回答问题：已知该商品的月销售额为z （单位：千元），当月销售量为何值时，商品的月销售额预报值最大？解：（1）ln y c d x =+更适宜销量y 关于月销售价x 的回归方程类型．……1分 令ln u x =，先建立y 关于u 的线性回归方程，由于10122y x =+，…………1分 联立24,12,2x y y x ⎧=⎪⎨=+⎪⎩，解得2,1,x y =−⎧⎨=⎩，或4,4,x y =⎧⎨=⎩，(2,1)B ∴−，………………2分 由24x y =得2x y '=，所以2PA k =，直线PA 方程为24y x =−，…………3分同理可得直线PB 方程为1y x =−−，………………………4分 联立241=−⎧⎨=−−⎩y x y x ，可得12=⎧⎨=−⎩x y ，故点P 的坐标为(1,2)−. …………………5分（2）（法一）设11(,)4x A x ，22(,)4x B x ，由24x y =，2x y '=，所以12PA x k =，所以直线PA 的方程为2111()42x x y x x −=−，即21124x x y x =−，…………6分 ˆˆ 6.610.20 1.7524.45cy du =−=+⨯=， ………………………4分 所以y 关于u 的线性回归方程为ˆ24.4510.20yu =−， 因此y 关于x 的回归方程为ˆ24.4510.20ln yx =−. ………………………6分 （2）依题意得：(24.4510.20ln )z xy x x ==−， ………………………7分[(24.4510.20ln )]14.2510.20ln z xy x x x ''==−=−， ………………………8分令0z '=，即14.2510.20ln 0x −=，解得ln 1.40x ≈，所以 4.06x ≈， ………………………10分 当时(0,4.06)x ∈，z 递增，当(4.06,)x ∈+∞时，z 递减，故当 4.06x =，即月销售量10.17=y （千件）时，月销售额预报值最大. ……12分【命题意图】本题考查线性回归方程的知识和应用，通过散点图判断变量之间的关系建立回归模型，通过利用线性回归方程求非线性回归方程，通过建立函数模型利用导数求最大销售额问题．综合考查概率统计知识分析处理数据，解决实际问题的能力． 20．（本小题满分12分）已知抛物线2:4C x y =，过点(2,3)的直线l 交C 于A 、B 两点，抛物线C 在点A 、B 处的切线交于点P ．（1）当点A 的横坐标为4时，求点P 的坐标；（2）设Q 是抛物线C 上的动点，当||PQ 取最小值时，求点Q 的坐标及直线l 的方程． 解：（1）点A 的横坐标为4，(4,4)A ∴，易知此时直线l 的方程为同理PB 的方程为22224x x y x =−，联立解得1212(,)24x x x x P +，……………7分依题意直线l 的斜率存在，不妨设直线l 的方程为3(2)y k x −=−，由24,3(2),x y y k x ⎧=⎨−=−⎩得248120x kx k −+−=， 易知0∆>，因此124x x k +=，12812x x k =−，∴(2,23)P k k −，………………………8分∴点P 在直线1:30l x y −−=上，当||PQ 取最小值时，即抛物线2:4C x y =上的动点Q 到直线1l 的距离最小，…………………9分设200(,)4x Q x ，则Q 到1l的距离2220000|3||(1)2|(1)x x x x d 3,30,y x x y =−+⎧⎨−−=⎩解得(3,0)P ，32k =，∴直线l 的方程为32y x =，综上，点Q 的坐标为(2,1)，直线l 的方程为32y x =．…………12分 （法二）设11(,)A x y ，22(,)B x y ，00(,)P x y ，由24x y =，2xy '=，∴12PA x k =，直线PA 的方程为111()2x y y x x −=−，即112x y x y =−，同理PB 的方程为222x y x y =−，………………………7分 因为点P 在切线，PB 上，∴∴，∴11(,)A x y ，22(,)B x y 在直线02x =上，∴直线d 的方程为02x =，………………………8分又直线d 的过点2，∴(2,1)Q ，即点P 在直线1:30l x y −−=上．………………………9分−−−+−===，…………10分 ∴当02x =时，d ，此时(2,1)Q ，………………………11分易知过点Q 且垂直于1l 的直线方程为3y x =−+，由以下同法一．（法三）设00(,)P x y ，显然两条切线的斜率均存在，可设过点P 与C 相切的直线方程为00()y y k x x −=−，且切线PA ，PB 的斜率分别为1k ，2k ， 把00()y y k x x −=−与24x y =联立，并化简得，2004440x kx kx y −+−=，∴200(4)4(44)0k kx y ∆=−−=，即2000k x k y −+=，∴1k ，2k 是方程2000k x k y −+=的两根，120k k x +=，120k k y =，………………7分此时2004440x kx kx y −+−=的两根为12x k =或22x k =，即为切点A ，B 的横坐标，∴211(2,)A k k ，222(2,)B k k ，22211221222l k k k k k k k −+==−， 直线l 的方程为21211(2)2k k y k x k +−=−，即12122k k−−−'=+−+=x x xxxa f x a a ，…………………………………1分 ①当0≤a 时，∴函数()f x 的极小值点为0=x ，无极大值点； …………………………………………2分②当01<<a 时，y x k k +=−，…………8分 又直线l 过点(2,3)M ，则1212=3k k k k +−，即00=3x y −，∴点P 在直线1:30l x y −−=上．………………………9分以下同法一．【说明】本题以直线与抛物线为载体，及其几何关系为背景，利用方程思想解决几何问题，主要考察抛物线的切点弦，直线与抛物线的位置关系等知识，考查学生的逻辑推理，数学运算等数学核心素养及思辨能力. 21．（本小题满分12分）已知函数()e e(1)−=−−+xxf x a a x (a ∈R ).（其中常数e=2.718 28⋅⋅⋅，是自然对数的底数）（1）求函数()f x 的极值点；（2）若对于任意01<<a ，关于x 的不等式21[()](e )λ−<−a f x a 在区间(1,)−+∞a 上存在实数解，求实数λ的取值范围.解：（1）易知(e 1)(e )()e e (1)e∴函数的极大值点为，极小值点为；………………………………………3分③当1=a 时，2(e 1)()0e−'=≥x xf x 1()1'=−g a a，当01<<a 时，()0'>g a ， ∴()(1)0<=g a g ，即1ln −>a a ，显然10−<a ，∴ln 10<−<a a ， ……………………………………………6分∴由（1）可知当01<<a 时，()f x 在区间(1,0)−a 上递减，在区间(0,)+∞上递增，∴()f x 在区间(1,)−+∞a 上的最小值为(0)1=−f a ，关于x 的不等式21[()](e)λ−<−a f x a 在区间(1,)−+∞a 上存在实数解，∴只需当01<<a 时，关于a 的不等式21(1)(e )λ−−<−a a a 恒成立，……………………8分由上易知当01<<a 时，1e0−−>a a ，， ∴函数()f x 单调递增，即()f x 无极值点； ……………………………………………4分④当1>a 时，∴5分综上所述，当0≤a 时，函数()f x 的极小值点为0=x ，无极大值点； 当01<<a 时，函数()f x 的极大值点为ln =x a ，极小值点为0=x ； 当1=a 时，函数()f x 无极值点；当1>a 时，函数()f x 的极大值点为0=x ，极小值点为ln =x a .（2）以下需多次引用到如下不等式：e 1xx ≥+，当且仅当0=x 时取等号，证明略. 注意到当01<<a 时，有ln 10<−<a a . (法一)当01<<a 时，1e11−>+−=a a a ，∴ln 10<−<a a ， ……………6分(法二) 令()ln 1=−+g a a a ，则∴只需当01<<a 时，不等式21(1)e λ−−>−a a a恒成立即可，……………………………………9分 令函数21(1)()e −−=−x x F x x ，01≤<x ，则1112(1)(3e e 1)()(e )−−−−−−−'=−x x x x x x F x x ()Gx 01≤<x 1()(2)e 1−'=−−x G x x 01<<x 1e 2−>−x x ∴1(2)e 1−−<x x ()Gx ()0<G x ()(1)0>=G x G ()Gx ∴()0>G x 1()(3)e −=−x u x x 1()(2)e 0−'=−>x u x x (1)1'=u (1)2=u 1e 2−>−x x (1,2)T21−=−y x 1y x =+∴当01<<a 时，不等式1(3)e 1−−≥+x x x 恒成立，只需1=x ，综上，实数()0'<F x 的取值范围为()(0)e <=F x F . …………………………………………………………………12分 【命题意图】 本题以基本初等函数、不等式问题为载体，考查学生利用导数分析、解决问题的能力，分类讨论思想及逻辑推理、数学运算等数学核心素养，具有一定综合性. 22．（本小题满分10分）选修4－4：坐标系与参数方程在平面直角坐标系()e <F x 中，曲线1C 的参数方程为2cos ,sin ,αα=⎧⎨=⎩x y （α为参数），圆2C 的方程为22(2)4x y −+=，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，射线l 的极坐标方程为0θθ=(0)ρ≥． （1）求曲线1C 和圆2C 的极坐标方程；x ， (法一)令函数11()3e e 1−−=−−−x x G x x x ，01≤<x ，则1()(2)e 1−'=−−x G x x ， 当01<<x 时，1e 2−>−x x ，∴1(2)e 1−−<x x ，∴()0'<G x ， ∴()(1)0>=G x G ，即()0>G x ，……………………………………………………………11分(法二)令函数1()(3)e−=−x u x x ，01≤<x ，则1()(2)e 0−'=−>x ux x ，∴(1)1'=u ，又(1)2=u ， ∴函数1()(3)e −=−x u x x 在点(1,2)T 处的切线方程为21−=−y x ，即1y x =+，如图所示，易知1(3)e 1−−≥+x x x ，当且仅当1=x 时取等号， ∴当01<<x 时，()0>G x ，………………11分∴当01<<x 时，()0'<F x ， ∴()(0)e <=Fx F ，即()e <F x ，（2）当0π02θ<<时，射线l 与曲线1C 和圆2C 分别交于异于点O 的M 、N 两点，若||2||ON OM =，求△2MC N 的面积．解：（1）由2cos ,sin αα=⎧⎨=⎩x y ，得1C 的普通方程为2214x y +=，…………………………………1分把cos x ρθ=，sin y ρθ=代入，得22(cos )(sin )14ρθρθ+=，即222244cos 4sin 13sin ρθθθ==++， 所以1C 的极坐标方程为22413sin ρθ=+；………………………………………………………3分 由22(2)4x y −+=，把cos x ρθ=，sin y ρθ=代入，得4cos ρθ=，所以2C 的极坐标方程为4cos ρθ=； …………………………………………………………5分（2）把0θθ=代入22413sin ρθ=+，得22016(4cos )13sin θθ=+，解得， ………………………7分 202sin 3θ=，201cos 3θ=，又0π02θ<<，所以3ρ=M，04cos 3ρθ==N ， …………………8分 所以△2MC N 的面积222∆∆∆=−MC N C N C M O O S S S2011||()sin 222ρρθ=−⋅=⨯N M OC ． ……………………10分 【说明】本题主要考查了椭圆，圆的极坐标方程与直角坐标方程以及参数方程的互化、极坐标的几何意义与应用等知识点，重点考查数形结合思想，体现了数学运算、逻辑推理等核心素养．考察考生的化归与转化能力．23.（本小题满分10分）选修4－5：不等式选讲已知函数1()||||(1)f x x m x m m=−++>． （1）当2m =时，求不等式()3f x >的解集；413sin ρθ=+M， 把0θθ=代入4cos ρθ=，得04cos ρθ=N ， ………………………6分 由||2||ON OM =，得2N M ρρ=，即224N M ρρ=， 即202（2）证明：1()3(1)f x m m +≥−．解：（1）当2m =时，1()|2|||2f x x x =−++， ………………………1分 ①当12x ≤−时，原不等式等价于1(2)()32x x −−+>，解得34x <−， ……………2分 ②当122x −<<时，原不等式等价于532>，不等式无解，……………3分 ③当2x ≥时，原不等式等价于()12+32x x ⎛⎫−+> ⎪⎝⎭，解得94x >， ………………4分 综上，不等式()3f x >的解集为39(,)(,)44−∞−+∞； ………………5分 （2）由题11()||||||f x x m x m m m=−++≥+， ………………………6分 0m >，11||m m m m∴+=+， 1()f x m m ∴≥+， 当且仅当1,x m m ⎡⎤∈−⎢⎥⎣⎦时等号成立． ………………7分 11111()(1)1(1)(1)11f x m m m m m m m m m m ∴+≥++=+=−++−−−−，1m >，10m ∴−>，1(1)1131m m ∴−++≥+=−，…………………9分 1()3(1)f x m m ∴+≥−，当2m =，且1[,2]2x ∈−时等号成立．…………………………10分【说明】本题主要考查绝对值三角不等式以及不等式的解法，分段函数，基本不等式等知识点，重点考查分类讨论，数形结合的思想，体现了数学运算、逻辑推理等核心素养．。

2019届广东省深圳市高级中学高三12月模拟考试理科综合试题本试卷分选择题和非选择题，共 15页，满分300分，考试时间150分钟（15：00-17：30）可能用到的相对原子质量：H 1 K 39 O 16 Cl 35.5一、选择题：本题包括1-13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．生物表现一定的生命特征，与它们的结构以及分子组成密不可分。

下列相关叙述正确的是A. 叶绿素、血红蛋白中含有N的一定是血红蛋白B. 绿藻、黑藻、颤藻中没有叶绿体的一定是颤藻C. 发菜和菠菜细胞内DNA均为链状的双螺旋结构D. 核糖体、质粒、酶中没有核糖参与组成的一定是酶2．离子通过细胞膜进出细胞有两种方式，一种是通过离子通道，另一种是借助离子泵的搬运。

离子通道是由蛋白质复合物构成的，一种离子通道只允许一种离子通过，且只有在对特定刺激发生反应时才瞬时开放；离子泵是一种具有ATP水解酶活性的载体蛋白，能利用ATP水解释放的能量跨膜运输离子。

下列叙述合理的是A. 细胞通过主动运输方式吸收离子的速率与细胞呼吸强度总是成正相关B. 蛋白质变性剂会降低离子通道的运输速率但不会降低离子泵的运输速率C. 借助离子泵搬运离子的结果是使该离子在细胞膜内外的浓度趋于相等D. 通过离子通道运输离子是被动运输，其运输方向是顺浓度梯度进行的3．胆固醇是人体内一种重要的脂质,既可在细胞内以乙酰CoA为原料合成,也可以LDL（一种脂蛋白）的形式进入细胞后水解形成。

下图表示人体细胞内胆固醇的来源及调节过程，其中①②③表示促进或抑制的过程。

下列选项中正确的是（）A．胆固醇在细胞中合成的场所是内质网,它是构成所有生物的细胞膜结构的重要成分B．细胞外液中的LDL与细胞膜上的受体结合,以胞吞方式进入细胞,这一过程与细胞膜的流动性性有关，需要消耗ATPC．从图中分析可知,如细胞内胆固醇过多，则会有①②③的反馈调节过程，①为抑制，②③为促进D．如果生物发生遗传性障碍，使LDL受体不能合成，则血浆中的胆固醇含量将下降4．在正常与遮光条件下向不同发育时期的豌豆植株供应14CO2，48 h后测定植株营养器官和生殖器官中14C 的量。