第2讲 轴向拉压杆的内力和应力
- 格式:ppt
- 大小:4.90 MB
- 文档页数:27







材料力学Mechanics of Materials轴向拉压的内力与应力一、轴向拉压的受力和变形特征1 受力特征杆件受到的外力或其合力的作用线沿杆件轴线2 变形特征杆件沿轴线方向发生伸长或缩短3 工程实例二、轴向拉压横截面上的内力建立分离体的静力平衡方程求出内力。
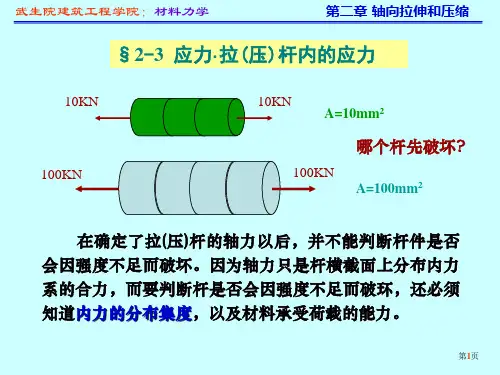
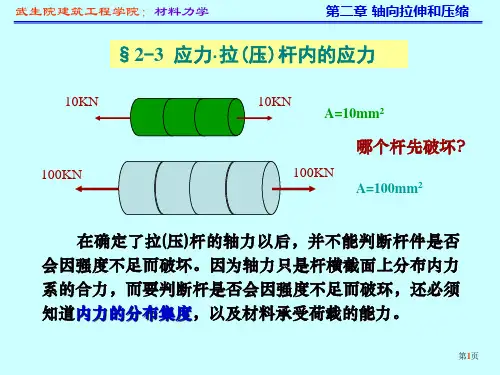
将杆件假想地沿某一横截面开取分离体,用内力表示去掉部分对保留部分的作用0N F F -=N F F∴=0xF=∑1 轴力FFmmFF NxmmF NF2 轴力的符号F N >0F N <拉力为正(方向背离杆件截面)压力为负(方向指向杆件截面)3 轴力图轴力沿杆件横截面的分布图称为轴力图2) 确定出最大轴力的数值及其所在位置,即确定危险截面位置,为强度计算提供依据。
1) 直观反映轴力与截面位置变化关系FF【例题1】一等直杆受力情况如图所示,试作杆的轴力图。
解:1)求约束力0:xF=∑RA 405525200F +-+-=RA 10kNF =2)截面法计算各段轴力AB 段:BC 段:0:xF =∑0:xF=∑N1RA 0F F -=N2RA 400F F --=N110kN F =N250kNF =F F F F N1CD 段:DE 段:0:xF=∑0:xF=∑N325200F +-=N4200F -=N35kNF =-N420kNF =3)绘制轴力图F 10kN5kN50kN+++20kN二、轴向拉压横截面上的应力1 实验现象横向线——仍为平行的直线,且间距增大。
纵向线——仍为平行的直线,且间距减小。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线3 推论轴向拉压时,横截面上只有正应力,且均匀分布N d AF A A σσ==⎰N F A σ=4 符号规定拉为正,压为负5 公式的使用条件1) 轴向拉压杆2) 除外力作用点附近以外其它各点处。
(范围:不超过杆的横向尺寸)F σ=αααA p F N =σαααp cos =ταααp sin=αA F /cos =σαcos 0=σαcos 02=ασ2sin 20二、轴向拉压斜截面上的应力有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)α斜截面正应力α斜截面切应力2cosασσα=022sinαστα=1) α:横截面外法线转到斜截面外法线所转的角度,逆时针转为正,反之为负。
第2讲教学方案——拉压杆的内力和应力第二章轴向拉伸与压缩§2-1轴向拉伸与压缩的概念与实例轴向拉伸和压缩的杆件在生产实际中经常遇到,虽然杆件的外形各有差异,加载方式也不同,但一般对受轴向拉伸与压缩的杆件的形状和受力情况进行简化,计算简图如图2-1。
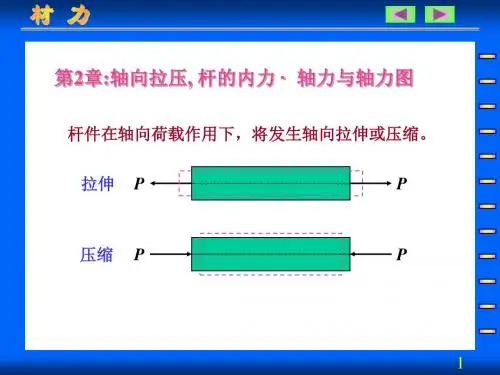
轴向拉伸是在轴向力作用下,杆件产生伸长变形,也简称拉伸;轴向压缩是在轴向力作用下,杆件产生缩短变形,也简称压缩。
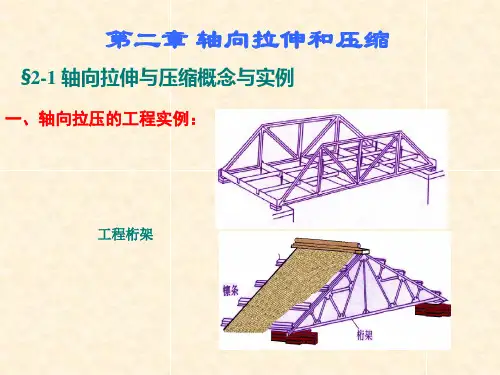
实例如图2-2所示用于连接的螺栓;如图2-3所示桁架中的拉杆;如图2-4所示汽车式起重机的支腿;如图2-5所示巷道支护的立柱。
通过上述实例得知轴向拉伸和压缩具有如下特点:1. 受力特点:作用于杆件两端的外力大小相等,方向相反,作用线与杆件轴线重合,即称轴向力。
2. 变形特点:杆件变形是沿轴线方向的伸长或缩短。
§2-2横截面上的内力和应力1.内力在图2-6所示受轴向拉力P 的杆件上作任一横截面m —m ,取左段部分,并以内力的合力N代替右段对左段的作用力。
由平衡条件0=∑X ,得0=-P N由于0>P (拉力),则0>=P N合力N 的方向正确。
因而当外力沿着杆件的轴线作用时,杆件截面上只有一个与轴线重合的内力分量,该内力(分量)称为轴力,一般用N 表示。
若取右段部分,同理0=∑X ,知0=N -P得0>=P N图中N 的方向也是正确的。
材料力学中轴力的符号是由杆件的变形决定,而不是由平衡坐标方程决定。
习惯上将轴力N 的正负号规定为:拉伸时,轴力N 为正;压缩时,轴力N 为负。
2.轴力图轴力图可用图线表示轴力沿轴线变化的情况。
该图一般以杆轴线为横坐标表示截面位置,纵轴表示轴力大小。
例2-1 求如图2-7所示杆件的内力,并作轴力图。
解:(1)计算各段内力AC 段:作截面1—1,取左段部分(图b )。
由0=∑X 得51=N kN (拉力)CB 段:作截面2-2,取左缎部分(图),并假设2N 方向如图所示。
由∑=0X 得KN N 102-=(2)绘轴力图选截面位置为横坐标;相应截面上的轴力为纵坐标,根据适当比例,绘出图线。