东南大学《工程矩阵理论》工程矩阵理论期终考试(A)

个人资料整理，仅供个人学习使用1 / 5东 南 大 学 考 试 卷（A 卷）课程名称 自动检测技术 考试学期 08-09--2得分 适用专业 自动化考试形式 闭卷 考试时间长度 100分钟个人资料整理，仅供个人学习使用一、填空题(共36分，每题6分)1、根据被测参量与时间的关系，测量误差可分为静态误差和动态误差两大类。

(2*3’)2、常见的被测参量可分为热工量、电工量、机械量、物性和成分量、光学量、状态量。

(6*1’)3、工业检测仪表（系统）常以最大引用误差作为判断其精度等级的尺度。

(6’)4、压力传感器常见的型式有应变式、压阻式、压电式、电容式等。

(4*1.5’)5、1989年7月第77届国际计量委员会批准建立了新的国际温标，简称ITS一90。

ITS一90基本内容为：（1）重申国际实用温标单位仍为K；（2）把水的三相点时温度值定义为0.01℃（摄氏度），同时相应把绝对零度修订为-273.15℃。

(3*2’)6、流量仪表的主要技术参数有流量范围、量程和量程比、允许误差和精度等级和压力损失。

(4*1.5’)二、问答题(共42分，每题14分)1、简述测量不确定度和测量准确度两者的异同点。

答：测量不确定度与测量准确度都是描述测量结果可靠性的参数。

(4’)其区别在于：测量准确度因涉及一般无法获知的“真值”而只能是一个无法真正定量表示的定性概念；测量不确定度的评定和计算只涉及已知量，因此，测量不确定度是一个可以定量表示的确定数值。

在实际工程测量中，测量准确度只能对测量结果和测量设备的可靠性作相对的定性描述，而作定量描述必须用测量不确定度。

(10’)共3 页第 1 页2、我国国家标准规定的工业用标准热电偶有几种？其中测温上限最高的热电偶其分度号是什么？它额定测温上限温度值是多少？热电偶具有哪些特点，使它成为是工业和武备试验中温度测量应用最多的器件？答：2 / 5个人资料整理，仅供个人学习使用3 / 5我国工业用标准热电偶有8种，(2’)其中分度号为S 、R 、B 的三种热电偶均由铂、铂铑合金制成，属贵金属热电偶；分度号为K 、N 、T 、E 、J 五种热电偶，由镍、铬、硅、铜、锰、镁、钴等金属的合金制成，属贱金属热电偶。

12东南大学考试卷（A）Array课程名称工程矩阵理论考试学期08-09-2 得分
适用范围工科硕士研究生考试形式闭卷考试时间长度150分钟
1．地子空间地一组基是；
2．若线性空间地线性变换在基下地矩阵是,则在基下地矩阵是；
3．如果矩阵满足,并且地秩为,则行列式；
4．若矩阵,则矩阵函数地行列式；
5．若是维单位列向量,是正定地,则参数满足条件.
二．（12%）设矩阵.讨论地可能地Jordan标准形.并问：当参数满足什么条件时,矩阵与是相似地.
三．（20%）记,上地变换定义为：对,.
1．证明：是上地线性变换；
2．求在地基下地矩阵；
3．求地特征值及相应地特征子空间地基；
4．问：是否存在地基,使得在这组基下地矩阵是对角阵？如存在,试给出这样地一组基及相应地对角阵；如不存在,请说明理由.
四．（10%）设.试将表示成关于地次数不超过2地多项式.
五．（8%）求地广义逆矩阵.
六．（15%）假设是有限维欧氏空间,是单位向量,上地线性变换定义如下：对任意,.
1.证明：是上地正交变换.
2.在中定义内积：对,.于是,成为欧氏空间.分别求中向量及地长度,并求正实数及单
位向量,使得如上地正交变换将变成.
七．证明题（20%）
1.假设是矩阵,分别是、酉矩阵.证明：.
2.假设是正规矩阵.若地特征值地模都等于1,证明：是酉矩阵.
3.假设是Hermite矩阵,其中,是地子矩阵,并且都是方阵.若是正定地.证明关于行列
式地不等式：.。

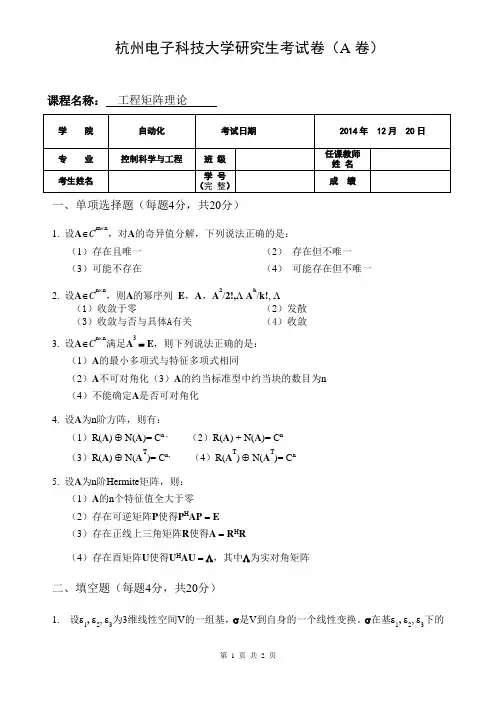
杭州电子科技大学研究生考试卷（A卷）课程名称：工程矩阵理论一、单项选择题（每题4分，共20分）1. 设A∈C m⨯n，对A的奇异值分解，下列说法正确的是：（1）存在且唯一（2）存在但不唯一（3）可能不存在（4）可能存在但不唯一2. 设A∈C n⨯n，则A的幂序列E，A，A2/2!, A k/k!,（1）收敛于零（2）发散（3）收敛与否与具体A有关（4）收敛3. 设A∈C n⨯n满足A3= E，则下列说法正确的是：（1）A的最小多项式与特征多项式相同（2）A不可对角化（3）A的约当标准型中约当块的数目为n（4）不能确定A是否可对角化4. 设A为n阶方阵，则有：（1）R(A) ⊕ N(A)= C n , （2）R(A) + N(A)= C n（3）R(A) ⊕ N(A T)= C n, （4）R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵，则：（1）A的n个特征值全大于零（2）存在可逆矩阵P使得P H AP=E（3）存在正线上三角矩阵R使得A=R H R（4）存在酉矩阵U使得U H AU=Λ，其中Λ为实对角矩阵二、填空题（每题4分，共20分）1. 设ε1, ε2, ε3为3维线性空间V的一组基，σ是V到自身的一个线性变换。

σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ，则σ在基ε3, 2ε2, 3ε1下的矩阵为。

2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。

3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭，则A 的最小多项式为 。

4. 设X = (x 1, x 2, , x n )T 为变向量，α = (a 1, a 2, , a n )T 为常向量，H = (h ij )n ⨯n 为常矩阵，则：，()=HX X XT D D。

5. 设A ∈C n ⨯n 为Hermite 矩阵，X ∈C n ，A 的n 个特征值为λ1，λ2， ，λn ，满足λ1 ≤ λ2 ≤ ≤ λn ，则： XX AXX H X H 0max ≠ =。

东 南 大 学 考 试 卷 （ A 卷 ） 课程名称 线性代数 考试学期 得分 使用专业 考试形式 闭 卷 考试时间长度 120分钟 题号 一 二 三 四 五 六 七 八 得分 一、（10%）选择题 1. 设3×2矩阵A =(A 1,A 2),B =(B 1,B 2)其中A 1,A 2,B 1,B 2是3维列向量. 若A 1,A 2线性无关, 则B 1,B 2线性无关的充要条件是( ). A.矩阵A 与B 等价 B. A 1,A 2能由B 1,B 2线性表示 C.向量组A 1,A 2与B 1,B 2等价 D. B 1,B 2能由A 1,A 2线性表示 2. 设A 为n 阶矩阵, E 为n 阶单位矩阵, 则下列叙述中, ( )是错误的. A. A 与E 合同的充分必要条件是A 正定 B. A 与E 相似的充分必要条件是A =E C. A 与E 相似的充分必要条件是行列式|A |=1 D. A 与E 等价的充分必要条件是行列式|A |≠0 3. 设A 为2×3矩阵, 交换A 的第一行和第二行得到矩阵B ,则( ). A. A (010100001)=B B. (010100001)A =B C. (0110)A =B D. A (0110)=B 4. 下列关于n 阶方阵A 的叙述中, 除了( )之外, 其余三个是相互等价的. A.齐次线性方程组Ax =0有非零解 B. A 的秩小于n C. A 是可逆矩阵 D.行列式|A |=0 5. 设A,B 都是m ×n 矩阵, 则下列矩阵中, ( )一定是对称矩阵.A. AB T +BA TB. A +BC. AB TD. AB T A二、（30%）判断题[ ] 6. (1234)的伴随矩阵为(4−3−21).[ ] 7. 设A,B 都是m ×n 矩阵, 则A 与B 等价的充分必要条件是它们的秩相等.[ ] 8. 设α1,α2,…,αs 为n 维列向量组, 若其中有一个向量αi 为零向量, 则α1,α2,…,αs 一定线性相关.[ ] 9. 若α,β为向量组α,β,γ的一个极大线性无关组, 而且β,γ也线性无关, 则β,γ也是学号姓名密封线α,β,γ的一个极大线性无关组.[ ] 10. 设A 为n 阶矩阵, 若对于任意的n 维列向量x , 有‖Ax ‖=‖x ‖则A 必为正交矩阵.[ ] 11. 设A 与B 都是n 阶正交矩阵, 则A +B 也是正交矩阵.[ ] 12. 设α与β都是非齐次线性方程组Ax =b 的解, 则α+β也是非齐次线性方程组Ax =b 的解.[ ] 13. 设α是非齐次线性方程组Ax =b 的解, β是齐次线性方程组Ax =0的解, 则α,β线性无关.[ ] 14. 若矩阵A 与B 相似, 则A 2与B 2相似.[ ] 15．矩阵A 与B 相似的充分必要条件是A 2与B 2相似.[ ] 16. 若矩阵A 与B 具有相同的特征多项式, 则A 与B 相似.[ ] 17. 设A 与B 都是n 阶实对称矩阵, 若A 与B 具有相同的特征多项式, 则A 与B 相似.[ ] 18. 二次型f (x 1,x 2)=(x 1,x 2)(1203)(x 1x 2)的矩阵为(1203). [ ] 19. 二次型f (x 1,x 2)=(x 1,x 2)(1203)(x 1x 2)是正定的. [ ] 20. 设多项式f (x )=2x 3−5x +7, A 为三阶方阵, 则f (A )=2A 3−5A +7.三、填空题（10%）21. 设A 为3×2矩阵, B =AA T 则B 的行列式|B |= _______.22. 设向量α=(123)与β=(1−2a)正交, 则 a = _______.23. 设α为非零的3维列向量, A =ααT , 则A 的正惯性指数= ________.24. 设A 为3阶矩阵,E 为3阶单位矩阵. 若A 2=E ,则r (A −E )+r (A +E )= ________.(注: 这里r (A −E )表示A −E 的秩,r (A +E )表示A +E 的秩.)25. 若向量组α,β,γ线性无关, α+β,β−γ,α+kγ线性相关, 则k = ________.四、（10%）设A =(a 11a 11111111a 11a ). 计算行列式|A |, 并针对a 的不同取值, 求A 的秩.五、（10%）设A =(0210),B =(12103410). 求矩阵X , 使得AX =B +X.六、（10%）设A =(20011000a )与B =(100010002) 相似. 求a 以及可逆矩阵P 使得 P −1AP =B .七、（10%）已知4阶方阵A=(α1,α2,α3,α4),其中α1,α2,α3,α4均为 4 维列向量, α2,α3,α4线性无关, 且α1=α2+α3−2α4.如果b=α1−α2+α3−α4, 求线性方程组Ax=b的通解.八、（10%）设二次型f(x1,x2,x3)=(x1+x2+x3)2.请写出该二次形的矩阵A,并写出该二次型在正交变换下的标准形.(不必写出所用的正交变换)。

共 ５ 页 第 页东南大学考试试卷课程名称 工程矩阵理论 考试学期 09-10-2得分适用专业工程硕士考试形式闭卷考试时间长度 120分钟）已知22⨯C的子空间1|,a a V x y C b b ⎧⎫⎛⎫=∈⎨⎬ ⎪⎝⎭⎩⎭， 2|,a b V x y C b a ⎧⎫⎛⎫=∈⎨⎬⎪--⎝⎭⎩⎭1V ，2V ，21V V ⋂，21V V +的一组基及它们的维数．（12%）在3R 的子空间{}(,,)|230W x y z x y z =-+=，(1,1,0)η=．求0W η∈，0min Wξηηηξ∈-=-．共 ５ 页 第 页四. （12%）已知矩阵101002101A ⎛⎫ ⎪= ⎪⎪⎝⎭．1. 求一个多项式()f λ，使得()Atf A Ae =；2. 求A 的广义逆矩阵+A ．五. （12%）已知矩阵,A B 的F-范数和算子2-范数分别是2,F A a A b==，2,FBc B d==，分别求分块矩阵A O M OB ⎛⎫= ⎪⎝⎭的F-范数和算子2-算子． 六. （12%）设矩阵102001b c A a ⎛⎫⎪= ⎪⎪⎝⎭，1000312B y x ⎛⎫ ⎪= ⎪⎪⎝⎭三. （14%）记11122122121101,,001111A A A A -⎛⎫⎛⎫⎛⎫====⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭．已知22⨯C 上的线性变换f 满足()ij ij f E A =(,1,2)i j =． 1． 求f 在基11122122,,,E E E E 下的矩阵；2． 分别求f 的值域()R f 和核子空间()K f 的基和维数； 3． 求f 的特征多项式和最小多项式．共 ５ 页 第 页．根据参数,,,,a b c x y 讨论,A B 可能的Jordan 标准形，并问：参数满足什么条件时，矩阵A 与B 是相似的？ 七. （10%）n 维欧氏空间V 上的线性变换f 定义如下：()(,)f x ax b x ωω=-，V x ∈∀。