线线平行垂直,线面平行垂直,面面平行垂直判定与性质

龙文教育个性化辅导授课案
教师：学生时间：年_ 月__日__段第__ 次课
四、平面与平面垂直的判定定理与性质定理 文字语言
图形表示
数学语言
判 定 定 理 一个平面过另一个平面的一条垂线，则这两个平面互相垂直。

性 质 定 理
两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面。

例1：下列命题中错误的是 （ ）
（A ）如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β
（B ）如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β （C ）如果平面α⊥平面γ，平面β⊥平面γ，=l αβ⋂，那么l ⊥平面γ （D ）如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
例2：已知直线l ⊥平面α，直线m ⊂平面β，下面有三个命题：①α∥β⇒l ⊥m ；
②α⊥β⇒l ∥m ；③l ∥m ⇒α⊥β.则真命题的个数为________．
例3：如图所示，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)
例4：在三棱柱ABC －A 1B 1C 1中，各棱长相等，侧棱垂直于底面，点D 是侧面BB 1C 1C 的中心，
则AD 与平面BB 1C 1C 所成角的大小是( )
A ．30°
B ．45°
C ．60°
D ．90°
龙文教育教务处制。

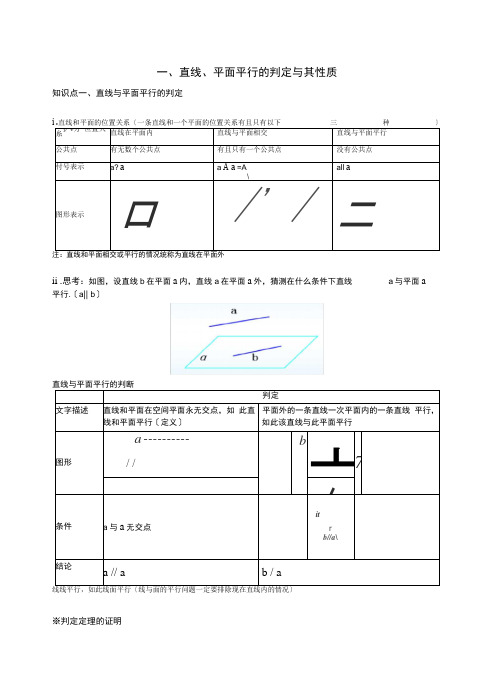
一、直线、平面平行的判定与其性质知识点一、直线与平面平行的判定ii .思考：如图，设直线b在平面a内，直线a在平面a外，猜测在什么条件下直线a与平面a 平行.〔a|| b〕※判定定理的证明特别提示证明直线和平面的平行通常采用如下两种方法：①利用直线和平面平行的判定定理，通过“线线平行，证得“线面〃平行；②利用两平面平行的性质定理，通过“面面〃平行，证得“线面〃平行. 知识点三、平面与平面平行的判定、直线、平面垂直的判定与其性质知识点一、直线和平面垂直的定义与判定要点诠释：定义中“平面-内的任意一条直线"就是指“平面二：内的所有直线"，这与“无数条直线〃不同〔线线垂直线面垂直〕知识点二、二面角I.二面角：：从一条直线出发的两个半平面所组成的图形叫二面角〔dihedral angle 〕.这条直线叫做二面角的棱，这两个半平面叫做二面角的面•记作二面角一AB —.〔简记P —AB —Q〕.面角的平面角的三个特征：i .点在棱上ii.线在面内iii.与棱垂直n .二面角的平面角：在二面角一I —的棱I上任取一点O ,以点O为垂足，在半平面，内分别作垂直于棱丨的射线OA和0B，如此射线OA和0B构成的AOB叫做二面角的平面角• 作用：衡量二面角的大小；X 围：0°180°.2能保证直线 a 与平面a 平行的条件是〔A 〕 A.a a ,b a ,a / bB .b a ,a / b知识点四、平面和平面垂直的定义和判定定义 判定文字描述 两个平面相交，如果它们所成的二面角是 直二面角，就说这两个平面垂直 .一个平面过另一个平面的垂线，如此这两 个平面垂直 图形 k z结果aAp = l a -l- B =90° 戸 a 丄 B 1 丄 cxj c a:丄 0〔垂直问题中要注意题目中的文字表述，特别是“任何〃“随意〃“无数〃等字眼〕 知识点五、平面和平面垂直的性质面面垂直 '线面垂直〔如果两个平面垂直，那么一个平面内垂直于它们交线的直线与一个面平垂直〕例题1.如图，假如 是长方体ABCD-ABCQ 被平面EFGH 截去几何体 EFGHBD 后得到的几 何体，其中E 为线段A i B i 上异于B i 的点，F 为线段BB 上异于B 的点，且EH// A i D i , 如此如下结论中不正确的答案是A. EH // FGB. 四边形EFGH 是矩形C. 是棱柱D.是棱台 C. b a ,c / a ,a / b,a / cD. b a ,A € a,B € a,C € b ,D € b 且 AC = BD3如下命题正确的答案是〔 DF 〕A. 平行于同一平面的两条直线平行B. 假如直线a / a ,如此平面a 内有且仅有一条直线与a 平行 C. 假如直线a / a ,如此平面a 内任一条直线都与a 平行 D. 假如直线a / a ,如此平面a 内有无数条直线与 a 平行E. 如果a 、b 是两条直线，且 a / b ，那么a 平行于经过b 的任何平面F. 如果直线a 、b 和平面a 满足 a / b , a / a ,b a,那么b /a4在空间，如下命题正确的答案是〔A 〕平行直线的平行投影重合〔B 〕平行于同一直线的两个平面平行〔C〕垂直于同一平面的两个平面平行A. m , n〔D〕垂直于同一平面的两条直线平行5m n为两条不同的直线，a、B为两个不同的平面，如此如下命题中正确的答案是B. a m , nm// nC. ml a,m 丄n n / aD. n / m,n丄a m± a〔A〕如果平面丄平面，那么平面内一定直线平行于平面〔B〕如果平面垂直于平面，那么平面内一定不存在直线垂直于平面〔C〕如果平面丄平面，平面丄平面，丨，那么丨丄平面〔D〕如果平面丄平面，那么平面内所有直线都垂直于平面设盘上是悔条直线, 血是两个平酣则a Lb的一个充分条件是(A) a ± a.bll(i.Q1 /J (B) □丄a少丄p(C) a c a,b丄(D)a c a.bll丄08. 求证：空间四边形相邻两边中点的连线，平行于经过另外两边的平面:空间四边形ABCD中, E、F分别是AB AD的中点求证：EF”平面BCD9. 如图，在椎体P-ABCD中，ABCD1边长为1的棱形,且/ DAB=60, ,PB=2,E,F分别是BC,PC的中点.⑴证明：AD丄平面DEF;(2)求二面角P-AD-B的余弦值.课堂练习A组1已知砌理是两条不冋宜线，a t j8,y是三个不同平面'下列命题中正确的是（）A•若fn\\ ay/II a,则加“舟 B.若c（一丁』丄人则口"0C*若卅队则伉//爪 D.若仍丄丄＜7,则朋“料4.已拓两荼直线,阳个平和。

平行和垂直认识平行线和垂直线的性质平行和垂直是几何学中常用的两个概念。

平行线和垂直线是直线的两种特殊情况，它们具有独特的性质和相互关系。

本文将分别介绍平行线和垂直线的定义、性质以及相关定理。

一、平行线的性质平行线是指在同一个平面上，永远不相交的两条直线。

平行线的性质包括以下几个方面：1. 平行线的定义：对于同一个平面上的两条直线，如果它们之间的任意两点都不重合并且永远不会相交，那么这两条直线就是平行线。

2. 平行线的判定方法：平行线有多种判定方法，常用的有以下几种：(1) 同位角相等定理：如果两条直线被一条直线所截，且同位角相等，则这两条直线是平行线。

(2) 逆否命题定理：如果两条直线与另一条直线的同位角不相等，则这两条直线不平行。

(3) 平行线性质的应用：如两直线分别与一条截它们的第三条线成等角，则这两条直线是平行线。

3. 平行线的性质：(1) 平行线与平行线之间相互平行，即如果线段AB与直线CD平行，而直线CD与直线EF平行，则线段AB与直线EF也平行。

(2) 平行线上的对应角相等，即平行线AB与CD之间的对应角都相等。

(3) 平行线截割平行线所得的交线上的对应线段成比例，即截割平行线所得的交线AB与CD上的线段AE与CF成比例。

等等。

二、垂直线的性质垂直线是指与另一条直线成直角的线段。

垂直线的性质包括以下几个方面：1. 垂直线的定义：如果两条直线相交且交角为90度，那么这两条直线是垂直线。

2. 垂直线的判定方法：垂直线有多种判定方法，常用的有以下几种：(1) 直角定理：如果两条直线互相垂直，则这两条直线上截取的线段为等腰直角三角形。

(2) 垂直线性质的应用：如直线AB与直线CD相交于点O，且AO与CO垂直，则直线AB与直线CD是垂直线。

3. 垂直线的性质：(1) 垂直线与垂直线之间相互垂直，即如果线段AB与线段CD垂直，而线段CD与线段EF垂直，则线段AB与线段EF也垂直。

(2) 垂直线上的对应角互补，即当线段AB与直线CD垂直时，由线段AB与直线CD所得到的对应角都是互补角。

面面垂直线面垂直的判定定理一、引言在几何学中，面面垂直是一个基本的概念。

当两个平面垂直时，我们称它们是面面垂直的。

本文将介绍面面垂直线面垂直的判定定理。

二、定义1. 面：在三维空间中，由无数条线段组成的平坦曲面。

2. 平行：两条线或两个平面在同一平面内，且不相交。

3. 垂直：两条线或两个平面相交于一个角度为90度的交点。

4. 面面垂直：当两个平面相互垂直时，它们被称为“面面垂直”。

三、定理如果一条直线同时与两个不同的平面相交，并且这条直线与其中一个平面的交线是另一个平面上的一条直线，则这两个平面是“面面垂直”的。

四、证明假设有两个不同的平面A和B，并且这两个平面相互垂直。

我们需要证明如果一条直线同时与这两个不同的平面相交，并且这条直线与其中一个平面A的交线是另一个平面B上的一条直线，则这两个平面是“ 面面垂直”的。

首先，我们需要证明这条直线存在。

假设这两个平面A和B相交于一条直线L。

因为这两个平面相互垂直，所以它们的交角为90度，因此直线L与平面A和平面B的交线都是垂直的。

接下来，我们需要证明这条直线与平面A和平面B的交线是垂直的。

假设这条直线与平面A的交点为P，与平面B的交点为Q，并且PQ 在平面B上。

我们需要证明AP和BQ是垂直的。

由于PQ在平面B上，所以PQ与平面A的交线PA也在平面B上。

因此，我们可以得到三角形APQ和三角形BPQ共享一个角度PQB，并且它们有一个共同边界PQ。

根据余弦定理：cos(APQ) = (AQ² + PQ² - AP²) / (2 * AQ * PQ)cos(BPQ) = (BQ² + PQ² - BP²) / (2 * BQ * PQ)由于AP = BQ（因为它们都等于L），所以AP² = BQ²。

将其代入上式中可得：cos(APQ) = cos(BPQ)因此，APQ = BPQ因此，AP和BP是垂直的。

线面平行垂直知识点一、线面平行的定义和性质1.定义：线面平行是指一条直线与一个平面内的所有直线都不相交。

2.性质：a.对于一个平面内的一条直线和平面外的任意一条直线，它们都不能同时与该平面平行。

b.平行线与同一平面内的另一条直线的关系：如果两条直线都与同一个平面平行，则这两条直线要么相交，要么重合。

c.平行线与不同平面内的直线的关系：如果两条直线分别与两个不相交平面平行，则这两条直线不相交。

二、线面垂直的定义和性质1.定义：线面垂直是指一条直线与一个平面内的所有直线都垂直相交。

2.性质：a.如果一条直线与一个平面垂直，则这条直线与平面内的任意一条直线都垂直。

b.平行于同一个平面内的两条直线不存在垂直关系。

c.如果两个平面垂直，则其法线向量互相垂直。

三、线面平行和垂直的判定方法1.平行判定：线面平行的判定可以通过向量的方法、斜率的方法和直线与平面的交点判定方法等。

例如，若两个平面的法线向量相等或平行，则这两个平面是平行的。

2.垂直判定：线面垂直的判定可以通过两条直线的方向向量相互垂直、用点法式判断直线与平面之间的关系等方法。

例如，若一条直线与一个平面垂直，则这条直线的方向向量与该平面的法线向量垂直。

四、线面平行和垂直的应用1.线面平行和垂直的知识可以用于建筑设计中，例如判断条墙与地面是否平行或垂直，从而影响建筑的结构布局。

2.在工程测量中，线面平行和垂直关系的知识可以用于量测一些平面的倾斜度和水平度等参数。

3.在图形的投影与透视等绘图问题中，线面平行和垂直关系的知识可以帮助我们正确地绘制出图形的形状和位置。

综上所述，线面平行和垂直是几何学中非常重要的概念，其涉及到线与面之间的相互关系。

了解线面平行和垂直的定义、性质以及判定方法，可以帮助我们更好地理解空间几何中的问题，并应用于实际生活和工作中。

一、直线、平面平行的判定及其性质知识点一、直线与平面平行的判定ⅰ.直线和平面的位置关系（一条直线和一个平面的位置关系有且只有以下三种）位置关系直线在平面内直线与平面相交直线与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a⊂αa∩α=A a||α图形表示注：直线和平面相交或平行的情况统称为直线在平面外ⅱ.思考：如图，设直线b在平面α内，直线a在平面α外，猜想在什么条件下直线a与平面α平行.（a||b）直线与平面平行的判断判定文字描述直线和平面在空间平面永无交点，则直线和平面平行（定义）平面外的一条直线一次平面内的一条直线平行，则该直线与此平面平行图形条件a与α无交点结论a∥αb∥α※判定定理的证明知识点二、直线与平面平行的性质图形条件a∥αa∥αa⊂βα∩β＝b 结论a∩α＝∅a∥b线面平行，则线线平行特别提示证明直线和平面的平行通常采用如下两种方法：①利用直线和平面平行的判定定理，通过“线线”平行，证得“质定理，通过“面面”平行，证得“线面”平行.知识点三、平面与平面平行的判定知识点四、平面与平面平行的性质二、直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定定义判定语言描述如果直线l和平面α内的任意一条直线都垂直，我们就说直线l与平面互相垂直，记作l⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直.图形条件b为平面α内的任一直线，而l对这一直线总有l⊥αl⊥m，l⊥n，m∩n＝B，mα，nα结论l⊥αl⊥α要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”知识点二、直线和平面垂直的性质性质语言描述一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线垂直于同一个平面的两条直线平行.图形条件知识点三、二面角Ⅰ.二面角：：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle）. 这条直线叫做二面角的棱，二面角ABαβ－－. （简记P AB Q－－）二面角的平面角的三个特征:ⅰ.点在棱上ⅱ.线在面内ⅲ.与棱垂直Ⅱ.二面角的平面角：在二面角αβ－l－的棱l上任取一点O，以点O为垂足，在半平面,αβ内分别作垂直于棱l的射成的AOB∠叫做二面角的平面角.作用：衡量二面角的大小；范围：000180θ<<.知识点四、平面和平面垂直的定义和判定定义判定文字描述两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.一个平面过另一个平面的垂线，则这两个平面垂直图形结果α∩β=l α-l-β=90o α⊥β（垂直问题中要注意题目中的文字表述，特别是“任何”“随意”“无数”等字眼）知识点五、平面和平面垂直的性质面面垂直线面垂直（如果两个平面垂直，那么一个平面内垂直于它们交线的直线与一个面平垂直1.如图，若Ω是长方体ABCD-A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中EBB 1上异于B 1的点，且EH ∥A 1 D 1，则下列结论中不正确的是A. EH ∥FGB.四边形EFGH 是矩形C. Ω是棱柱D. Ω是棱台2能保证直线a 与平面α平行的条件是（ A ）⊄α,b ⊂α,a ∥b B .b ⊂α,a ∥bC. b ⊂α,c ∥α,a ∥b,a ∥cD. b ⊂α,A ∈a,B ∈a,C ∈b ,D ∈b 且AC ＝BD3下列命题正确的是（ D F ）A. 平行于同一平面的两条直线平行B. 若直线a ∥α,则平面α内有且仅有一条直线与a 平行C. 若直线a ∥α,则平面α内任一条直线都与a 平行D. 若直线a ∥α,则平面α内有无数条直线与a 平行E. 如果a 、b 是两条直线，且a ∥b ，那么a 平行于经过b 的任何平面F. 如果直线a 、b 和平面α满足a ∥b ，a ∥α,b ⊄α，那么b ∥α4在空间，下列命题正确的是 （A ）平行直线的平行投影重合 （B ）平行于同一直线的两个平面平行 （C ）垂直于同一平面的两个平面平行 （D ）垂直于同一平面的两条直线平行5已知m 、n 为两条不同的直线，a 、β为两个不同的平面，则下列命题中正确的是A ．,,m n αα⊂⊂m ∥β，n ∥β⇒a ∥βB ．a ∥β，,m n αβ⊂⊂⇒m ∥nC ．m ⊥a,m ⊥n ⇒n ∥aD ．n ∥m,n ⊥a ⇒m ⊥a 6.下列命题中错误的是（A ）如果平面α⊥平面β，那么平面α内一定直线平行于平面β（B ）如果平面α垂直于平面β，那么平面α内一定不存在直线垂直于平面β （C ）如果平面α⊥平面γ，平面β⊥平面γ，l αβ⋂=，那么l ⊥平面γ （D ）如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β8.求证：空间四边形相邻两边中点的连线，平行于经过另外两边的平面． 已知：空间四边形ABCD 中，E 、F 分别是AB 、AD 的中点 求证：EF ‖平面BCD8题图 9题图9.如图，在椎体P-ABCD 中，ABCD 是边长为1的棱形， 且∠DAB=60 ， ,PB=2, E,F 分别是BC,PC 的中点. (1) 证明：AD ⊥ 平面DEF;(2) 求二面角P-AD-B 的余弦值.课堂练习A 组、n 是空间两条不同的直线，α、β是两个不同的平面，下面四个命题中，真命题的序号是________．①m ⊥α，n ∥β，α∥β⇒m ⊥n ； ②m ⊥n ，α∥β，m ⊥α⇒n ∥β； ③m ⊥n ，α∥β，m ∥α⇒n ⊥β； ④m ⊥α，m ∥n ，α∥β⇒n ⊥β.4.如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB 11111在长方体（1）作出过直线AC 且与直线BD1平行的截面，并说明理由.（2）设E 、F 分别是A1B 和B1C 的中点，求证直线6. 在图中所示的一块木料中，棱BC 平行于平面A ’C ’ ．（1）要经过平面内的一点P 和棱BC 将木料据开，应怎样画线 （2）所画的线和平面AC 是什么位置关系C A ''EABCFE 1 A 1B 1C 1D 1D。

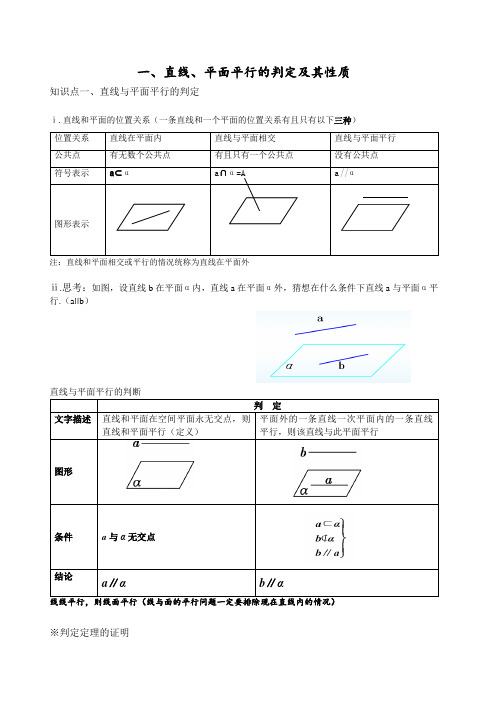
一、直线、平面平行的判定及其性质知识点一、直线与平面平行的判定ⅰ.直线和平面的位置关系（一条直线和一个平面的位置关系有且只有以下三种）位置关系直线在平面内直线与平面相交直线与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a⊂αa∩α=A a||α图形表示注：直线和平面相交或平行的情况统称为直线在平面外ⅱ.思考：如图，设直线b在平面α内，直线a在平面α外，猜想在什么条件下直线a与平面α平行.（a||b）判定文字描述直线和平面在空间平面永无交点，则直线和平面平行（定义）平面外的一条直线一次平面内的一条直线平行，则该直线与此平面平行图形条件a与α无交点结论a∥αb∥α※判定定理的证明知识点二、直线与平面平行的性质性质文字描述一条直线与一个平面平行，则这条直线与该平面无交点一条直线和一个平面平行，则过这条直线的任一平面与此平面相交，这条直线和交线平行．图形条件a∥αa∥αa⊂βα∩β＝b结论a∩α＝∅a∥b线面平行，则线线平行特别提示证明直线和平面的平行通常采用如下两种方法：①利用直线和平面平行的判定定理，通过“线线”平行，证得“线面”平行；②利用两平面平行的性质定理，通过“面面”平行，证得“线面”平行.判定文字描述如果两个平面无公共点，责成这两个平面平行一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行．如果两个平面同时垂直于一条直线，那么这两个平面垂直。

图形条件α∩β＝∅a，b⊂βa∩b＝Pa∥αb∥αl⊥αl⊥β结论α∥βα∥βα∥β性质文字描述如果两个平行平面同时和第三平面相交，那么他们的交线平行如果两个平面平行，那么其中一个平面内的直线平行于另一个平面图形条件α∥ββ∩γ＝bα∩γ＝a α∥β a⊂β结论a∥b a∥α二、直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定 定义 判定语言描述 如果直线l 和平面α内的任意一条直线都垂直，我们就说直线l 与平面互相垂直，记作l ⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直. 图形条件b 为平面α内的任一直线，而l 对这一直线总有l ⊥αl ⊥m ，l ⊥n ，m ∩n ＝B ，m ⊂α，n ⊂α 结论l ⊥α l ⊥α 要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”不同（线线垂直线面垂直）性质语言描述 一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线垂直于同一个平面的两条直线平行.图形条件结论知识点三、二面角Ⅰ.二面角：：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle ）. 这条直线叫做二面角的棱，这两个半平面叫做二面角的面. 记作二面角AB αβ－－. （简记P AB Q －－）二面角的平面角的三个特征:ⅰ. 点在棱上ⅱ. 线在面内 ⅲ.与棱垂直Ⅱ.二面角的平面角：在二面角αβ－l －的棱l 上任取一点O ，以点O 为垂足，在半平面,αβ内分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 作用：衡量二面角的大小；范围：00180θ<<.定义判定文字描述两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.一个平面过另一个平面的垂线，则这两个平面垂直图形结果α∩β=l α-l-β=90o α⊥β“任何”“随意”“无数”等字眼知识点五、平面和平面垂直的性质面面垂直线面垂直（如果两个平面垂直，那么一个平面内垂直于它们交线的直线与一个面平垂直）例题1.如图，若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1 D1，则下列结论中不正确的是A. EH∥FGB.四边形EFGH是矩形C. Ω是棱柱D. Ω是棱台2能保证直线a与平面α平行的条件是（ A ）A.a⊄α,b⊂α,a∥b B .b⊂α,a∥bC. b⊂α,c∥α,a∥b,a∥cD. b⊂α,A∈a,B∈a,C∈b ,D∈b且AC＝BD3下列命题正确的是（ D F ）A. 平行于同一平面的两条直线平行B. 若直线a∥α,则平面α内有且仅有一条直线与a平行C. 若直线a∥α,则平面α内任一条直线都与a平行D. 若直线a∥α,则平面α内有无数条直线与a平行E. 如果a、b是两条直线，且a∥b，那么a平行于经过b的任何平面F. 如果直线a、b和平面α满足a∥b，a∥α,b⊄α，那么b∥α4在空间，下列命题正确的是（A）平行直线的平行投影重合（B）平行于同一直线的两个平面平行（C）垂直于同一平面的两个平面平行（D ）垂直于同一平面的两条直线平行5已知m 、n 为两条不同的直线，a 、β为两个不同的平面，则下列命题中正确的是A ．,,m n αα⊂⊂m ∥β，n ∥β⇒a ∥βB ．a ∥β，,m n αβ⊂⊂⇒m ∥nC ．m ⊥a,m ⊥n ⇒n ∥aD ．n ∥m,n ⊥a ⇒m ⊥a 6.下列命题中错误的是（A ）如果平面α⊥平面β，那么平面α内一定直线平行于平面β（B ）如果平面α垂直于平面β，那么平面α内一定不存在直线垂直于平面β （C ）如果平面α⊥平面γ，平面β⊥平面γ，l αβ⋂=，那么l ⊥平面γ （D ）如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β8.求证：空间四边形相邻两边中点的连线，平行于经过另外两边的平面． 已知：空间四边形ABCD 中，E 、F 分别是AB 、AD 的中点 求证：E F ‖平面BCD8题图 9题图9.如图，在椎体P-ABCD 中，ABCD 是边长为1的棱形， 且∠DAB=60 ， ,PB=2, E,F 分别是BC,PC 的中点. (1) 证明：AD ⊥ 平面DEF;(2) 求二面角P-AD-B 的余弦值.课堂练习A 组3.m 、n 是空间两条不同的直线，α、β是两个不同的平面，下面四个命题中，真命题的序号是________．①m ⊥α，n ∥β，α∥β⇒m ⊥n ； ②m ⊥n ，α∥β，m ⊥α⇒n ∥β； ③m ⊥n ，α∥β，m ∥α⇒n ⊥β； ④m ⊥α，m ∥n ，α∥β⇒n ⊥β.4.如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB//CD ，AB=4, BC=CD=2, AA 1=2,E 、E 1、F 分别是棱AD 、AA 1、AB 的中点。

平行线与垂直线的判断与性质在几何学中，平行线与垂直线是非常重要的概念。

它们在我们日常生活中的应用广泛，例如在建筑设计、地理测量、工程规划等领域都起到了重要的作用。

本文将介绍平行线和垂直线的判断方法及其性质。

一、平行线的判断与性质平行线是指在同一个平面上永远不相交的两条直线。

判断两条线是否平行可以通过以下几种方法：1. 在平面上的两条直线，如果它们的斜率相等且不相交，则可以判定为平行线。

斜率的概念是直线上任意两点间纵坐标之差与横坐标之差的比值。

2. 如果两条直线上的任意一组对应角互相等于，则可以判定为平行线。

对应角是指两条直线上同位于相同位置的角度。

3. 如果两条直线之间的夹角为180度，则可以判定为平行线。

夹角是指两条直线相交时所形成的角度。

平行线具有以下性质：1. 平行线与一条截线形成的对应角互相等于。

2. 平行线上的任意一对内错角和外错角互相补角。

3. 平行线上的任意一对同位角相等。

二、垂直线的判断与性质垂直线是指与另一条线段或线相交时形成的直角的线。

判断两条线是否垂直可以通过以下几种方法：1. 如果两条直线的斜率互为倒数且乘积为-1，则可以判定为垂直线。

2. 如果两条直线上的任意一组对应角互为互补角，则可以判定为垂直线。

3. 如果两条直线的夹角为90度，则可以判定为垂直线。

垂直线具有以下性质：1. 垂直线与一条直线形成的内错角和外错角互为补角。

2. 垂直线上的任意一对同位角互相等于。

3. 垂直线与平面上的一条截线形成的对应角互为互补角。

三、平行线与垂直线的应用平行线和垂直线在日常生活中有广泛的应用。

以下是几个典型的例子：1. 建筑设计：在建筑设计中，平行线和垂直线起到了重要的作用。

例如，在绘制建筑图纸时，需要合理利用平行线和垂直线来确定各个建筑元素的位置和关系，以保证整体结构的稳定性和美观性。

2. 套房布局：在家居装修中，平行线和垂直线的应用也非常常见。

例如，在设计套房的布局时，通常会利用平行线和垂直线来划分房间的大小和位置，以确保每个房间的功能和空间利用率都达到最佳状态。

在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法（1）在同一平面内没有公共点的两条直线平行（定义）（2）先证在同一平面内，再用平面几何中的平行线的判定理或者相关图形的性质进行证明。

如①在同一平面内，两条直线被第三条直线所截，如果同位角或内错角相等，或同旁内角互补，则两直线平行。

②三角形、梯形中位线定理。

③平行四边形、矩形、菱形、正方形性质(对边平行)。

④在同一个平面内，同垂直于一条直线的两条直线平行（注意：此结论在空间不适合）。

（3）（线面平行的性质）如果一条直线和一个平面平行，则经过这条直线的一个平面与这个平面相交，那么这条直线和交线平行。

（4）如果两直线都平行于第三条直线，那么这两条直线互相平行（平行的传递性）。

（5）（面面平行的性质）如果两个平行平面分别和第三个平面相交，则它们的交线平行。

（6）（线面垂直的性质之一）如果两条直线垂直于同一个平面，那么这两条直线平行。

（7）用向量证明。

二、一条直线和一个平面平行的判定（1）如果一直线和一平面没有公共点，那么这条直线就和这个平面平行（定义）（2）平面外的一条直线，如果和这个平面内的一条直线平行，那么这条直线就和这个平面平行(线面平行的判定定理)。

（3）如果两个平面相互平行，那么在一个平面内的任何一条直线都平行于另一个平面.（线面平行的性质）。

（4）向量法。

三、两个平面平行的判定（1）如果两个平面没有公共点，那么这两个平面互相平行（定义）（2）如果一个平面内的两条相交直线分别和另一个平面平行，那么这两个平面平行。

（3）如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

（4）如果两个平面分别平行于第三个平面，那么这两个平面平行。

（5）如果两个平面垂直于同一条直线，那么这两个平面平行。

在空间“线线垂直、线面垂直、面面垂直”的判定方法一、 两条直线垂直的判定（1） 在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。

直线和平面平行、垂直的判定和性质1．在直线和平面的位置关系中，平行关系不仅应用较多，而且是学习平面和平面位置关系的基础，所以直线和平面平行的判定和性质是本单元的重点之一．判定定理说明要证一条直线和一个平面平行，只要在这个平面内找出一条直线和已知直线平行即可．对于直线和平面平行的性质定理、要注意避免“一条直线平行于一个平面，就平行于这个平面内的一切直线”的错误，线面平行和线线平行，是指过这条直线的任意一个平面和已知平面的交线与这条直线平行，尽管直线可以和平面内无数条直线平行，但不能说直线和平面内的任何直线平行．反证法是常用的一种证明方法．要会用反证法证明线面平行的判定定理．2．斜线和平面所成的角，定量地反映了斜线和平面的位置关系，它是通过转化为平面内的两条相交直线所成的角来度量的，它是这条斜线和平面内经过斜足的直线所成的一切角中的最小角．直线和平面所成的角，应分三种情形:(1)直线和平面斜交时，直线和平面所成的角是指直线和它在平面内的射影所成的锐角；(2)直线和平面垂直时，直线和平面所成的角就是直角；(3)直线和平面平行或直线在平面内时，直线和平面所成的角的度数是0°．综上所述，直线和平面所成角的范围是[0，].3．在应用三垂线定理及其逆定理时，重点在于先寻找平面的垂线，在引辅助线时，也应先作平面的垂线，这是因为垂线是确定斜线在平面内射影的关键．三垂线定理及其逆定理揭示了平面的斜线和它在这个平面上的射影必定同时垂直于平面内的直线的实质．在学习三垂线定理时，要注意处于各种位置的射影关系图形的识别和掌握，进而达到灵活应用的目的.典型题目分析例1．下列命题中①两条异面直线所成角α 的范围是0°＜α＜180°．②两条互相垂直的直线不一定相交．③分别和两条异面直线都垂直的直线叫做这两条异面直线的公垂线．④两条异面直线所成角的大小是惟一的，角的位置可以平移变化．⑤两条异面直线的公垂线有且只有一条．⑥若两条直线和第三条直线所成的角相等，则这两条直线平行．其中正确命题的个数是().A．1B．2 C 3D．4分析:对照有关概念，找出结论与条件不相符合的命题．解:由异面直线所成角的定义，公垂线定义知①③⑥错误，②④⑤正确，故选C．例2．如图所示，在长方体ABCD-A1B1C1D1中，BB1=3，BC=4，则异面直线A1B1与BC1的距离是________.分析:证A1B1⊥面BC1.解:在面BC1内作B1E⊥BC1于点E.长方体AC1中，A1B1⊥BB1，A1B1⊥B1C1，所以A1B1⊥面BC1，从而A1B⊥B1E，于是B1E的长就是异面直线A1B1和BC1间的距离.矩形BCC1B1中，BC1=，所以B1E=.即所求距离为.点评:本题将异面直线的距离问题转化为同一三角形内的点线距离问题.例3．E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AB、BC的中点，求EF到平面AA1C1C的距离.分析:转化为EF与AC间的距离.解:如图所示，连结BD分别交AC、EF于O、G，则BD⊥AC，BD⊥EF.正方体A1C中，AA1⊥平面ABCD，BD 平面ABCD.∴BD⊥AA1，而AA1、AC是平面AA1C1C内两条相交直线.∴BD⊥平面AA1C1C，又BD⊥EF，于是线段OG的长就是EF到平面AA1C1C的距离. 在正方形ABCD中，OG=.所以EF到平面AA1C1C的距离是.点评:将线面距离化为线线距离是一种常用转化方法，应注意正确使用这种方法.例4．点P在ΔABC所在平面上射影为O，如果PA⊥BC，PB⊥AC，则O为ΔABC的（）.A、垂心B、重心C、内心D、外心分析:作出PA在平面ABC上的射影，证明BC与之垂直.解:如图，连结OA，OB，则OA是PA在平面ABC上的射影.∵BC⊥PA，∴BC⊥OA.同理，AC⊥OB，∴O是ΔABC的垂心，故选A.点评:三角形的内心、外心、垂心、重心分别是三角形的三条角平分线、三条边的垂直平分线、三条高、三条中线的交点.课外练习：1．RtΔABC所在平面外一点P到直角顶点C的距离等于24，P到平面ABC的距离为12，若点P到AC和BC 的距离相等，求：点P到AC的距离.2．在空间四边形ABCD中，若AB⊥BC，BC⊥CD，CD⊥AB，且AB=BC=CD=a.则直线AD和BC所成角的正弦值为（）.A、B、C、D、3．在棱长为4的正方体，ABCD-A1B1C1D1中，A1到BD的距离等于_________.4．正方体ABCD-A1B1C1D1中，M、N、K分别是AD、DD1、DC的中点，求证：B1K⊥平面CMN.参考解答：1．如图，过P作PD⊥平面ABC，D为垂足，过D作DE⊥AC，DF⊥BC.分别连结PE和PF，则DE和DF分别是PE和PF在平面ABC内的射影.∵AC⊥DE，∴AC⊥PE，∵DF⊥BC，∴BC⊥DF，∵PE⊥AC，PF⊥BC，∴PE和PF是P到AC和BC的距离，∴PE=PF，∴DE=DF，∵CEDF是内角均为90°的四边形，∴CEPF是正方形，∴CD=´DE，在RtΔPCD中，PC=24，PD=12，∠PDC=90°，∴CD=，∴DE=，在RtΔPDE中，PD=12，DE=，∠PDE=90°，∴PE=，即P到AC、BC的距离均为.2．D3.4. 如图，分别连结BK和C1K，证明RtΔCDM≌RtΔBCK,证明RtΔCC1K≌RtΔCDN.设CM∩BK=P，∵∠KBC=∠PCK，∴∠PBC+∠BCP=90°，∴∠CPB=90°，∴CM⊥BK，∵BK是B1K在平面ABCD上的射影，∴B1K⊥CM.同理可证：B1K⊥CN，CN∩CM=C，∴B1K⊥平面MNC.在线测试选择题1．下列命题正确的是（）A、两个平面互相垂直，经过一个平面内一点垂直于交线的直线必垂直于另一个平面B、两条直线在两个相交平面内的射影都是平行直线，那么这两条直线互相平行C、一个二面角的两个面分别与另一个二面角的两个面垂直，那么这两个二面角相等或互补D、五边形中有两组不相邻的边平行，那么这个五边形是平面图形2．设P是正ΔABC所在平面外一点，PA=PB=PC=.若ΔABC的边长为1，则直线PC和平面ABC所成的角是（）.A、90°B、60°C、45°D、30°3．平面α内的∠MON=60°，PO是平面α的斜线段，PO=3，且PO与∠MON的两边均成45°角，那么点P到平面α的距离为（）.A、B、C、D、4．已知三个平面α、β、γ，一条直线l，要得到α//β，必须满足下列条件中的（）.A、l//α, l//β且l//γB、lγ, 且l//α，l//βC、α//γ且β//γD、l与α、β所成角相等5．已知a,b是两条直线，以下四个条件中：①α⊥γβ⊥γ②α内有不共线的三点到β的距离相等③aα, bα, a//β, b//β④a,b是异面直线且aα, a//β, b//β, b//α能推出α//β的是（）.A、④B、②，③C、②D、①，③答案与解析答案：1、D 2、D 3、A 4、C 5、A解析：1．答案：D．如A中α⊥β，α∩β=l, l'⊥β, l'⊥l, 但l'//α，矛盾.故排除A；B、C很容易否定.故本题应选D.2．答案：D．过P作PO⊥平面ABC，则垂足O为正ΔABC的中心.连结OC，则∠PCO为直线PC和平面ABC所成的角.在RtΔPOC中，OC=，PC=，则cos∠PCO=.从而∠PCO=30°，故选D.3．答案：A．如图，过P作PH⊥平面α，则垂足H在∠MON的平分线上，且PH的长为点P到平面α的距离.作HQ⊥OM，垂足为Q，在RtΔPQO中，PQ=OQ=.在RtΔOQH中，HQ=OQ·tan30°=.在RtΔPHQ中，PH=.选A.4．答案：C．平面与平面平行满足传递性.5．答案：A．当平面α、β是两个相交平面时，①不一定成立.当这三点在平面β两侧时，②不成立.当平面α、β是两个相交平面时，③不一定成立.因此选A.怎样学习立体几何我们学习每一门课，都应有不同的学法，学习《立体几何》时，应注意下面四点。

认识平行和垂直平行线和垂直线的特征认识平行和垂直线的特征平行线和垂直线是几何学中两个极为重要的概念。

它们在空间中描述物体位置和方向之间的关系，具有独特的特征和性质。

本文将介绍平行线和垂直线的定义、特征及其在几何学中的应用。

一、平行线的特征平行线是指在同一个平面内永不相交的两条直线。

平行线具有以下特征：1. 方向相同：平行线具有相同的方向，无论有多远，始终保持平行，永不相交。

2. 距离相等：平行线上任意两点到另一条平行线的距离始终相等。

这说明平行线之间的距离是保持恒定的，不会发生变化。

3. 角度特性：平行线之间不存在交角，它们的夹角为零度。

因此，平行线可以看作是一对交角为零的线。

4. 符号表示：在几何学中，平行线常常使用双竖杠“||”来表示，例如AB || CD，表示直线AB与直线CD平行。

平行线的概念在现实中有许多应用。

例如，在建筑设计中，平行线被广泛应用于墙体设计、道路布局等方面。

此外，在数学中，平行线也是解决几何问题的重要基础。

二、垂直线的特征垂直线是指在同一个平面内交于一点，相互之间成直角的两条直线。

垂直线具有以下特征：1. 相交于一点：垂直线在同一个平面内交于一点，该点被称为交点。

2. 直角特性：垂直线之间成直角，即两条垂直线之间的夹角为90度。

3. 符号表示：在几何学中，垂直线常常使用“⊥”来表示，例如AB⊥ CD，表示直线AB与直线CD垂直。

垂直线在几何学中的应用广泛而重要。

例如，在测量中，垂直线可以用来确定正北方向，用作建筑物和道路的基准线。

此外，在直角三角形中，垂直线是勾股定理的基础。

三、平行线与垂直线的关系平行线与垂直线在几何学中有重要的互补关系。

1. 平行线的垂线：当两条平行线遇到一条垂直线时，垂直线与平行线之间的夹角都是直角。

这就是说，垂直线是任意一条平行线的垂线。

2. 垂直线的平行线：当两条垂直线遇到一条直线时，直线与垂直线之间的夹角都是直角。

这就是说，任意一条垂直线都可以看作是两条平行线的垂线。

在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法（1）在同一平面内没有公共点的两条直线平行（定义）（2）先证在同一平面内，再用平面几何中的平行线的判定理或者相关图形的性质进行证明。

如①在同一平面内，两条直线被第三条直线所截，如果同位角或内错角相等，或同旁内角互补，则两直线平行。

②三角形、梯形中位线定理。

③平行四边形、矩形、菱形、正方形性质(对边平行)。

④在同一个平面内，同垂直于一条直线的两条直线平行（注意：此结论在空间不适合）。

（3）（线面平行的性质）如果一条直线和一个平面平行，则经过这条直线的一个平面与这个平面相交，那么这条直线和交线平行。

（4）如果两直线都平行于第三条直线，那么这两条直线互相平行（平行的传递性）。

（5）（面面平行的性质）如果两个平行平面分别和第三个平面相交，则它们的交线平行。

（6）（线面垂直的性质之一）如果两条直线垂直于同一个平面，那么这两条直线平行。

（7）用向量证明。

二、一条直线和一个平面平行的判定（1）如果一直线和一平面没有公共点，那么这条直线就和这个平面平行（定义）（2）平面外的一条直线，如果和这个平面内的一条直线平行，那么这条直线就和这个平面平行(线面平行的判定定理)。

（3）如果两个平面相互平行，那么在一个平面内的任何一条直线都平行于另一个平面.（线面平行的性质）。

（4）向量法。

三、两个平面平行的判定（1）如果两个平面没有公共点，那么这两个平面互相平行（定义）（2）如果一个平面内的两条相交直线分别和另一个平面平行，那么这两个平面平行。

（3）如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

（4）如果两个平面分别平行于第三个平面，那么这两个平面平行。

（5）如果两个平面垂直于同一条直线，那么这两个平面平行。

在空间“线线垂直、线面垂直、面面垂直”的判定方法一、 两条直线垂直的判定（1） 在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。