80
60
40
20
0.5
1.0
1.5
2.0
f[x_,y_]:=-0.4x^2/(120-35*2)-10; g[x_,y_]:=x; {x,y}={85.3977,78.2347}; h=0.1; t=2.1; Do[a=f[x,y];xa=x+h (a+f[x+h,y+h*a])/2; b=g[x,y];ya=y+h (b+g[x+h,y+h*b])/2; Print[k," ",t," ",xa," ",ya]; {t,x,y,xx[[20+k]],yy[[20+k]],tt[[20+k]]}={t+h,xa,ya,xa,ya,t+h},{k,1,50}]
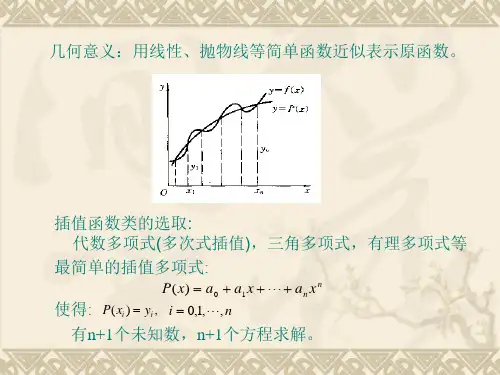
3、数值分析主要部分。 1各类插值方法我们讲过拉格朗日插值、牛顿插值、分段插值、 样条插值 2函数逼近及拟合3数值积分、欧拉法解常微分方程、龙格-库塔 法解常微分方程、方程组。
【1】插值 对于牛顿插值相对于拉氏插值增加一个节点,所有的插值基本多项式 要重新取、重新算.2而牛顿插值,节点增加,次数增加,即高次插值函数 计算量大,有剧烈震荡,数值稳定性较差(例如龙格现象);分段插值在 分段点上仅连续(即函数值相等),但是有尖点,不光滑(尖点导数不连 续);样条函数可以解决以上问题:使插值函数既是低次阶分段函数,又 是光滑的函数。 【2】理解逼近问题与拟合问题: 1)逼近问题:函数f(x)在区间[a,b]具有一阶光滑度,求多项式p(x)是 f(x)-p(x)在某衡量标准下最小的问题。 2)拟合问题:从理论上讲y=f(x)是客观存在的,但在实际中,仅仅从 一些离散的数据(xi,yi)(i=1,2…)是不可能求出f(x)的准确表达式,只能求 出其近似表达式φ(x)。 插值问题与逼近问题的特点和区别: 1)相同点:它们都是求某点值的算法。 2)不同点: A,被插值函数是未知的,而被逼近函数是已知的。 B,插值函数在节点处与被插值函数相等。而逼近函数的值只要满足很 好的均匀逼近即可。 C,求p(x)的方法不同。