康普顿散射朗伯定律

康普顿散射公式
康普顿散射公式是物理学中用于研究电磁波在某一物体表面上
反射或折射时，定义某种反射率或折射率的方程。

它是由美国物理学家Willard Harrison Cowperthwaite在1931年提出的，又被称为Cowperthwaite公式。

它的最大作用是可以用来预测某物体表面反射或折射的波的大小，也可以推断物体的表面属性。

康普顿散射公式的基本形式是：S=S0+S1(1-g)+S2(1+g)+S3，其中S为反射率或折射率，S0、S1、S2、S3为常数，g为微分系数。

该公式是根据反射或折射时光源和物体之间的位置和方向等条件来定
义的。

因为康普顿散射公式是一个多项式，在某种特定条件下，前4项可以认为是最重要的，所以可以简化为：S=S0+S1(1-g)+S2(1+g)。

康普顿散射公式计算的反射率或折射率会受到物体的表面属性
的影响，这就意味着，当物体的表面纹理凹凸不平时，其反射率会有所变化。

康普顿散射公式被广泛应用于多学科研究中，包括材料物理学、复合材料等。

它也被用于模拟某种物质表面反射或折射的光线，从而更好地了解物质的特性。

另外，康普顿散射公式也用于物理学的研究和机器视觉中，可以通过计算物体表面的反射率或折射率来模拟真实世界的物理现象，这有助于模拟特定的材料有关的参数和物理属性。

总之，康普顿散射公式是一个能够推断某物体表面反射或折射的
波的大小、推断物体表面属性以及模拟特定材料有关参数和物理属性的重要公式。

它已经在多学科研究中得到广泛应用，成为物理研究的重要工具。

康普顿散射公式推导过程康普顿散射是一种重要的散射现象，它是描述高能光子与自由电子相互作用的过程。

康普顿散射公式是描述康普顿散射现象的数学表达式，本文将从经典物理的角度出发，推导康普顿散射公式，并介绍其物理意义。

康普顿散射是指高能光子与自由电子相互作用时，光子的波长发生变化并改变方向的现象。

这个现象可以用经典电磁理论来解释。

首先，假设光子是粒子，具有能量E和动量p，自由电子也是粒子，具有质量m和速度v。

当光子与电子相互作用时，光子的能量和动量会转移给电子，从而改变光子的运动状态。

假设光子入射前的能量为E，动量为p，入射角为θ，光子入射后的能量为E'，动量为p'，散射角为φ。

根据能量守恒和动量守恒定律，可以得到以下关系式：1. 能量守恒：E + m0c^2 = E' + K (式1)2. 动量守恒：p = p'cosθ + p'sinθcosφ (式2)其中，m0c^2是电子的静止能量，K是电子获得的动能。

为了推导康普顿散射公式，我们首先需要做一些假设。

假设入射光子的能量远大于电子的静止能量，即 E >> m0c^2。

这样，我们可以忽略电子的静止能量，简化能量守恒式为：E = E' + K (式3)由于光子是电磁波，其动量可以表示为p = E/c。

根据这个关系，我们可以将动量守恒式转化为：E/c = E'/c + K'cosθ + K'sinθcosφ (式4)其中，K' = p'sinθ是入射光子的动量，K'cosθ和K'sinθcosφ是散射光子的动量。

接下来，我们需要利用康普顿效应的经验公式来推导康普顿散射公式。

根据实验结果，康普顿散射光子的波长变化量Δλ与入射光子的波长λ之间存在以下关系：Δλ = λ' - λ = λc(1 - cosφ) (式5)其中，λc是康普顿波长，它是与电子质量和光速相关的常数。

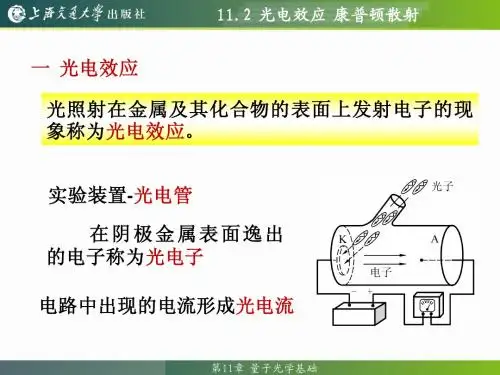
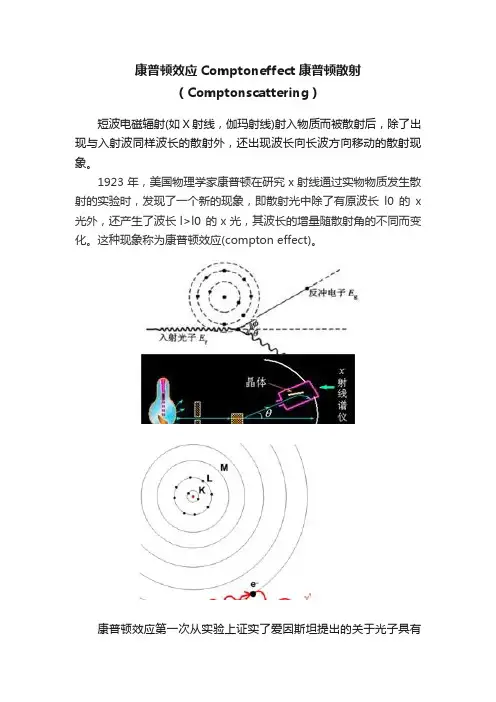
康普顿效应Comptoneffect康普顿散射（Comptonscattering）短波电磁辐射(如X射线，伽玛射线)射入物质而被散射后，除了出现与入射波同样波长的散射外，还出现波长向长波方向移动的散射现象。

1923年，美国物理学家康普顿在研究x射线通过实物物质发生散射的实验时，发现了一个新的现象，即散射光中除了有原波长l0的x 光外，还产生了波长l>l0 的x光，其波长的增量随散射角的不同而变化。

这种现象称为康普顿效应(compton effect)。

康普顿效应第一次从实验上证实了爱因斯坦提出的关于光子具有动量的假设。

这在物理学发展史上占有极端重要的位置。

吴有训对康普顿效应最突出的贡献在于测定了X射线散射中变线、不变线的强度比率R随散射物原子序数变化的曲线，证实并发展了康普顿的量子散射理论。

实验结果：(1)散射光中除了和原波长λ0相同的谱线外还有λ>λ0的谱线。

(2)波长的改变量Δλ=λ-λ0随散射角φ(散射方向和入射方向之间的夹角)的增大而增加.(3)对于不同元素的散射物质，在同一散射角下，波长的改变量Δλ相同。

波长为λ的散射光强度随散射物原子序数的增加而减小。

康普顿利用光子理论成功地解释了这些实验结果。

X射线的散射是单个电子和单个光子发生弹性碰撞的结果。

碰撞前后动量和能量守恒，化简后得到Δλ=λ-λ0=(2h/m0c)sin^2(/θ2)称为康普顿散射公式。

λ=h/(m0c)称为电子的康普顿波长。

康普顿散射只有在入射光的波长与电子的康普顿波长相比拟时，散射才显著，这就是选用X射线观察康普顿效应的原因。

而在光电效应中，入射光是可见光或紫外光，所以康普顿效应不明显。

康普顿散射仪的主体和实验时的状态康普顿散射谱仪的铅室内有光子的发射源137Cs康普顿效应与光电效应的区别：光电效应作用于内层电子，光子本身消失，能量完全转移给电子；康普顿效应发生在束缚最松的外层电子上，光子只损失一部分能量。

康普顿效应一、康普顿效应的实验及其规律康普顿效应(康普顿散射)：波长变长的散射光阑X 射线管探测器光谱仪晶体石墨体(散射物质)j1B2B1)散射光中不仅有原波长λ0的成分，还有 > 0的成分康普顿散射的实验规律2) 随散射角φ的增大而增加，与入射X 射线的波长无关。

4)原子量越小的物质，康普顿效应越显著3)与散射物质无关。

二、对实验结果的分析1、光的波动说解释电子做同频率的受迫振动辐射同一频率的电磁波电磁波通过物体光的波动理论只能说明波长不变的散射，而不能解释康普顿散射不应该出现与入射波波长不同的成分2. 康普顿效应的量子解释1) 波长改变的散射:X射线光子与原子外层电子的弹性碰撞入射光子被原子核束缚较弱的外层电子的束缚能，“X射线光子与静止自由电子的弹性碰撞”2)波长不变的散射是X射线光子与原子内层电子的弹性碰撞相当于与整个原子作弹性碰撞3)为什么原子量越小的物质，康普顿效应越显著?原子量越大的物质，内层束缚电子数相对越多，而外层电子数相对越少。

特别注意：按照康普顿的粒子碰撞模型的解释，似乎在碰撞中，电子吸收了入射光子的一部分能量，使光子能量减小，然后以较小的频率出现在散射方向。

其实这种理解是违反量子理论的基本观点的，爱因斯坦认为：光子不能再分割,而只能整个的被吸收或放出。

辐射电场的量子论也认为：在光子与电子相互作用时，电子是整个地吸收了入射光子，又整个地辐射出散射光子。

2200mc h c m h h h e e m c c 00 202m m 1c 康普顿效应公式001cos )(h m c j 000h p e c h 0三、康普顿散射的定量计算c (1cos ) j h p e ch j 0m 20m c m 2mc 1224310m .c o h m c 电子的康普顿波长处于X 射线波段理论结果与实验结果完全相一致波长的改变量与散射物的种类及入射光的波长无关，c (1cos ) j 1224310m .c o h m c康普顿散射只有在入射光的波长与电子的康普顿波长相比拟时，散射才显著πΔ2000486.c nm j ，波长改变最大电子获得的能量也最大0Δ0j ， 增大。

康普顿原理的应用什么是康普顿原理康普顿原理是根据美国物理学家康普顿（Arthur H. Compton）提出的一种物理现象，用来解释X射线和光子散射过程中的能量变化。

它揭示了光子在散射过程中能量和动量的守恒关系，成为现代物理学的重要基础原理之一。

康普顿散射是指X射线或γ射线与物质中的自由电子发生散射的现象。

在散射过程中，入射光子的能量会发生变化，同时光子会改变入射方向，这种现象被称为康普顿散射效应。

康普顿原理的基本公式康普顿原理可以用一个简单的数学公式来描述：$$\\Delta\\lambda = \\lambda' - \\lambda = \\frac{h}{m_e c} \\cdot (1-\\cos\\theta)$$其中，$\\Delta\\lambda$是散射光子的波长变化量，$\\lambda'$是散射光子的波长，$\\lambda$是入射光子的波长，ℎ是普朗克常量，m e是电子的质量，c是光速，$\\theta$是散射角。

这个公式显示了康普顿散射效应中入射光子波长变化的大小与散射角的关系。

通过测量散射光子的波长变化，可以推导出散射角，从而获得有关散射物质的信息。

康普顿原理在医学检查中的应用康普顿原理的应用非常广泛，尤其在医学检查中起着重要的作用。

下面列举了一些康普顿原理在医学检查中的具体应用：1.正电子发射断层扫描（PET）：PET技术利用正电子与电子湮灭产生两个能量相等的γ光子，这两个光子呈180度相对散射。

利用康普顿原理，通过测量这两个光子的能量和散射角度，可以得到有关内部器官的详细信息，用于癌症、心脏病等疾病的诊断和治疗。

2.计算机断层扫描（CT）：CT技术利用X射线进行扫描，康普顿原理被用于解释X射线与组织间的散射。

通过测量入射X射线和散射X射线的能量和散射角度，可以重建出体内的断层图像，用于疾病的早期检测和诊断。

3.核磁共振成像（MRI）：MRI技术利用强磁场和无线电波来生成图像，康普顿原理被用于解释无线电波与体内原子核的散射。

康普顿散射动量转移原则及能量方向康普顿散射是一种重要的粒子物理现象，它发生在高能光子与电子之间的相互作用过程中。

康普顿散射动量转移原则和能量方向是描述康普顿散射过程的重要规律和性质。

本文将详细介绍康普顿散射动量转移原则和能量方向的基本概念、原理以及相关应用。

首先，我们来了解一下康普顿散射的基本过程。

康普顿散射是由于高能光子与自由电子发生相互作用而引起的散射现象。

当高能光子碰撞到自由电子时，光子会失去一部分能量，并改变方向。

这个过程中，光子被散射到较大的角度，并且会转移一部分动量给电子。

在康普顿散射中，动量转移原则是指散射后的光子和电子之间交换的动量差。

根据动量守恒定律，散射前后的总动量应保持不变。

因此，光子失去的动量必然转移到了电子上。

动量转移原则描述了康普顿散射中光子和电子之间动量的转移关系。

接下来，让我们来了解一下康普顿散射中能量的转移方向。

根据能量守恒定律，散射前后的总能量应保持不变。

在康普顿散射中，光子失去的能量被转移给了电子，并且散射后的光子的能量减小，而电子的能量增加。

因此，能量的转移方向是从光子向电子转移。

康普顿散射动量转移原则和能量方向的研究不仅在理论物理领域具有重要地位，而且在实际应用中也有广泛的应用价值。

首先，深入研究康普顿散射的动量转移原则和能量方向有助于增强人们对基本粒子相互作用的理解。

通过研究康普顿散射过程，可以揭示物质内部微观结构的特征和性质。

其次，在医学领域，康普顿散射动量转移原则和能量方向的理论研究与实践应用相结合，可以为放射疗法和医学成像技术等提供重要的指导。

康普顿散射被广泛应用于医学成像技术中，如正电子发射断层扫描（PET）和单光子发射计算机断层扫描（SPECT）等。

这些技术利用康普顿散射过程中能量的转移方向来获取图像信息，从而实现对人体内部器官结构和功能的非侵入性检测。

此外，康普顿散射动量转移原则和能量方向的研究还对材料科学领域具有重要意义。

康普顿散射被用于通过测量散射光子的能量损失来研究材料的电子结构和晶格动力学行为。

康普顿散射实验康普顿散射实验是物理学中非常重要的实验之一，用于研究光的粒子性质。

在这篇文章中，我将详细解读康普顿散射实验的定律、实验准备和过程，并探讨其应用和其他专业性角度。

康普顿散射实验是由物理学家亚瑟·康普顿于20世纪20年代首次提出的，该实验验证了光的粒子性质，即光是由一束粒子组成的，这些粒子被称为光子。

实验证明，当光通过物质时，与物质内部的电子相互作用，发生能量和动量的交换，导致光的散射现象。

在康普顿散射实验中，我们主要关注入射光子的能量和散射光子的能量之间的关系，以及散射角度与入射角度之间的关系。

根据康普顿散射定律，入射光子的能量与散射光子的能量之差与散射角度正相关，而与入射角度无关。

在进行康普顿散射实验之前，我们需要准备以下实验设备和材料：1. 光源：用于发射光子的光源，通常使用X射线机或γ射线源。

2. 散射物质：用以散射光子的材料，通常选择高原子序数的物质，如铝或铜。

3. 探测器：用于测量散射光子的能量和角度的仪器，常用的探测器有闪烁体探测器、半导体探测器等。

具体的实验步骤如下：1. 将光源放置在实验室中的适当位置，并与探测器相连。

2. 在光源之前放置散射物质，确保光经过材料后发生散射。

3. 调整探测器的位置和角度，使其能够测量到散射光子的能量和散射角度。

4. 开始实验，测量入射光子的能量和入射角度，并记录下散射光子的能量和散射角度。

5. 重复实验多次，改变入射光子的能量和入射角度，以便得到更多的实验数据。

分析实验数据后，我们可以得出以下结论：1. 入射光子的能量与散射角度成正比，即入射光子能量增加，散射角度也增加。

2. 入射光子的能量与散射光子的能量之差与散射角度成正比，即入射光子能量增加，散射光子的能量减小，并且两者的差值随散射角度增大而增大。

康普顿散射实验在物理学和其他相关领域有着广泛的应用和深远的影响：1. 证实了光具有粒子性质，支持了量子力学的基本假设。

2. 应用于医学领域的断层扫描技术和放射治疗中，利用康普顿散射原理测量和分析散射光子的能量和散射角度，以获取有关人体组织结构和病变的信息。