中考相似三角形专题复习安徽中考相似压轴题

专题12难点探究专题：相似三角形中动点问题压轴题六种模型全攻略【考点导航】目录【典型例题】 (1)【考点一相似三角形动点中求时间多解问题（利用分类讨论思想）】 (1)【考点二相似三角形动点中求线段长多解问题（利用分类讨论思想）】 (2)【考点三相似三角形动点中求线段及线段和最值问题】 (4)【考点四相似三角形中的动点问题与函数图像问题】 (5)【考点五相似三角形中的动点问题与几何综合问题】 (7)【考点六相似三角形中的动点探究应用问题】 (9)【典型例题】【考点一相似三角形动点中求时间多解问题（利用分类讨论思想）】【变式训练】1．（2023秋·安徽安庆·九年级统考期末）如图，在钝角A出发运动到点B停止，动点E运动的速度为2cm/s．如果两点同时运动，那么当以点2．（2023·上海·九年级假期作业）如图，米/秒的速度同时开始运动，其中点直移动到点A为止．经过多长时间后，3．（2022·辽宁·灯塔市第一初级中学九年级期中）如图，在平面直角坐标系内，已知点0），动点P从点A开始在线段段BA上以每秒2个单位长度的速度向点(1)当t为何值时，△APQ与△AOB相似？(2)当t为何值时，△APQ的面积为24 5【考点二相似三角形动点中求线段长多解问题（利用分类讨论思想）】【变式训练】2．（2023春·江苏无锡·八年级宜兴市实验中学校考阶段练习）如图，在矩形连接BD，点M，N分别是边BC，终落在BD上，当PBM为直角三角形时，线段3．（2023·江苏盐城·校考一模）如图，在动点，过点E作DE⊥为等腰三角形时，当BCF4．（2023·山东济宁·统考一模）如图，在矩形点P是直线BC上的一个动点．若【考点三相似三角形动点中求线段及线段和最值问题】【变式训练】1．（2023·江苏苏州AE翻折得AFE△连接PF，则PQ2．（2023·湖北襄阳·统考模拟预测）如图，矩形△M，连接EM、BM，将BEM为．3．（2023春·安徽·九年级专题练习）如图，在正方形，上的动点，且BEG是AB CD为．4．（2023·江苏南通·统考三模）点C 的坐标为()0,3上一点，且3AQ PQ =【考点四相似三角形中的动点问题与函数图像问题】例题：（2023春·河南安阳·九年级统考期末）如图，正方形ABCD 一边AB 在直线l 上，P 是直线l 上点A 左侧的一点，24AB PA ==，E 为边AD 上一动点，过点P ，E 的直线与正方形ABCD 的边交于点F ，连接BE BF ，，若设DE x =，BEF △的面积为S ，则能反映S 与x 之间函数关系的图象是（）A ．B ．．．2023·山西运城·统考二模）如图中，36B ∠=︒，动点P 速运动至点C 停止．点P 的运动速度为，设点P 的运动时间为t （函数图像如图2所示．当AP 时，BP 的长为（）A ．252+B ．425-C ．4+2．（2023·河南焦作·统考二模）如图，在Rt ABC △中，过点P 作直线l AB ⊥，交折线ACB 于点Q ．设AP x =A ．．．．2023·安徽合肥·校联考二模）如图，在正方形ABCD 中，1AB =，动点P 从A 点出发沿和BC 上匀速移动，连接DP 交BC 或BC 的延长线于Q ，记点移动的距离为x ，的函数图像大致是（）A ．B ．C ．D ．4．（2023·黑龙江·模拟预测）如图，已知直线l 是线段AB 的中垂线，l 与AB 相交于点C ，D 是位于直线AB 下方的l 上的一动点（点D 不与点C 重合），连接AD BD ，，过点A 作AE BD ∥，过点B 作BE AE ⊥于点E ，若6AB =，设AD x =，AE y =，则y 关于x 的函数关系用图像可以大致表示为（）．A ．B ．C ．D ．【考点五相似三角形中的动点问题与几何综合问题】例题：（2023春·山东济宁·八年级统考期末）如图，在平面直角坐标系中，O 是坐标原点，矩形OABC 的两边分别在x 轴和y 轴上，点B 的坐标为()12,8，现有两动点P ，Q ，点P 以每秒3个单位的速度从点O 出发向终点A 运动，同时点Q 以每秒2个单位的速度从点A 出发向终点B 运动，连接PC ，PQ ，CQ ．设运动时间为t 秒()0t >．(1)点P 的坐标为______，点Q 的坐标为______（用含t 的代数式表示）；(2)请判断四边形APCQ 的面积是否会随时间t 的变化而变化，并说明理由；(3)若A ，P ，Q 为顶点的三角形与OCP △相似时，请求出t 的值．【变式训练】(1)BM =________；BN =__________．(2)若BMN 与ABC 相似，求t 的值；(3)连接AN CM ，，如图2，若AN CM ⊥BC=，点E是AD边上的一个动点，以CE为边在CE的右（2）如图2，四边形ABCD是矩形，2AB=，4CG CE=，连接DG，BE．判断线段DG与BE，有怎样的数量关系和位置关系，侧作矩形CEFG，且:1:2并说明理由；（3）如图3，在（2）的条件下，点E是从点A运动D点，则点G的运动路径长度为______；+的最小值为______．（4）如图3，在（2）的条件下，连接BG，则2BG BE【考点六相似三角形中的动点探究应用问题】【变式训练】【基础巩固】（1）参照小慧提供时思路，利用图（2）请证明上述结论；（2）A 、B 、C 、是同一直线l 上从左到右顺次的点，点P 是直线外一动点，【尝试应用】①若2AB =，1BC =，延长AB 至D ，使CD BC =【拓展提高】②拓展：若AB m =，BC n =，()m n ≠，P 点在长为___________（用含m 、n 的式子表示）．。

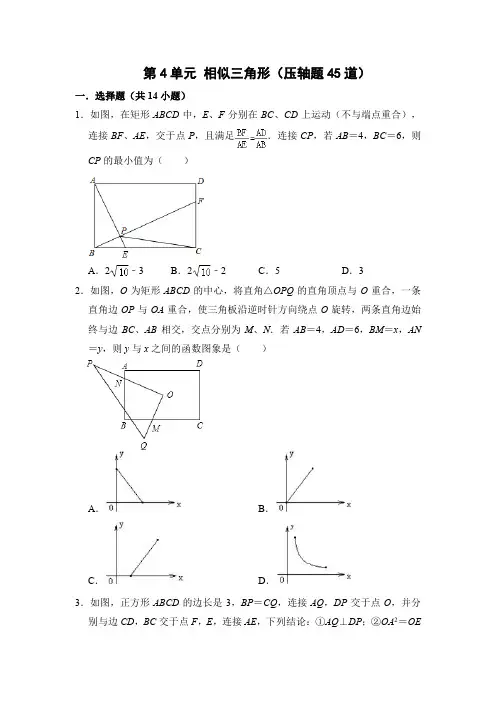
第4单元相似三角形（压轴题45道）一．选择题（共14小题）1．如图，在矩形ABCD中，E、F分别在BC、CD上运动（不与端点重合），连接BF、AE，交于点P，且满足．连接CP，若AB＝4，BC＝6，则CP的最小值为（）A．2﹣3B．2﹣2C．5D．32．如图，O为矩形ABCD的中心，将直角△OPQ的直角顶点与O重合，一条直角边OP与OA重合，使三角板沿逆时针方向绕点O旋转，两条直角边始终与边BC、AB相交，交点分别为M、N．若AB＝4，AD＝6，BM＝x，AN ＝y，则y与x之间的函数图象是（）A．B．C．D．3．如图，正方形ABCD的边长是3，BP＝CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA2＝OE•OP ；③S △AOD ＝S 四边形OECF ；其中正确结论的个数（ ）A ．1B ．3C ．2D ．04．如图，正方形ABCD 中，BE ＝EF ＝FC ，CG ＝2GD ，BG 分别交AE 、AF 于M 、N ，下列结论：①AF ⊥BG ；②；③S 四边形CGNF ＝S △ABN ；④．其中正确的有（ ）A ．①②③B ．②③④C ．①②④D ．①③④5．如图，在△ABC 中，∠ACB ＝90°，CD 、CE 分别是高和角平分线，已知△BEC 的面积是15，△CDE 的面积为3，则△ABC 的面积为（ ）A ．22.5或20B ．22.5C ．24或20D ．206．如图，在正方形ABCD 中，点E 、F 分别是BC 、DC 边上的两点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ．下列结论：①AB 2＝BN •DM ；②AF 平分∠DFE ；③AM •AE ＝AN •AF ；④．其中正确的结论是（ ）A．①②B．①③C．①②③D．①②③④7．如图，▱ABCD中，E为AD的中点．已知△DEF的面积为1，则▱ABCD的面积为（）A．9B．12C．15D．188．如图：把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中阴影部分）的面积是△ABC面积的一半，若AB＝，则此三角形移动的距离AA′是（）A．﹣1B．C．1D．9．如图，l1∥l2∥l3，直线a，b与l1、l2、l3分别相交于A、B、C和点D、E、F．若＝，DE＝4，则EF的长是（）A．B．C．6D．1010．如图，正方形ABCD的边长为25，内部有6个全等的正方形，小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上，则每个小正方形的边长为（）A．6B．5C．D．11．如图，D是等边△ABC边AB上的一点，且AD：DB＝1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF＝（）A．B．C．D．12．如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O 为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C和D的坐标分别为（）A．（2，2），（3，2）B．（2，4），（3，1）C．（2，2），（3，1）D．（3，1），（2，2）13．如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB＝6，AD＝5，则AE的长为（）A．2.5B．2.8C．3D．3.214．如图，正方形ABCD是一块绿化带，其中阴影部分EOFB，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为（）A．B．C．D．二．填空题（共11小题）15．如图，△ABC中，AB＝8，AC＝6，点E在AB上且AE＝3，点F在AC上，连接EF，若△AEF与△ABC相似，则AF＝．16．如图，线段AB为⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，点P是⊙O上一动点，连接CP，以CP为斜边在PC的上方作Rt△PCD，且使∠DCP＝60°，连接OD，则OD长的最大值为．17．如图Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点P为BC上任意一点，连接P A，以P A，PC为邻边作平行四边形P AQC，连接PQ，则PQ的最小值为．18．如图，四边形ABCD是平行四边形，E为BC边的中点，DE、AC相交于点F，若△CEF的面积为6，则△ADF的面积为．19．如图，在正方形ABCD中，AB＝2，M为CD的中点，N为BC的中点，连接AM和DN交于点E，连接BE，作AH⊥BE于点H，延长AH与DN交于点F，连接BF并延长与CD交于点G，则MG的长度为．20．如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为米．21．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H．给出下列结论：①△ABE≌△DCF；②＝；③DP2＝PH•PB；④＝．其中正确的是．（写出所有正确结论的序号）22．如图，矩形EFGH内接于△ABC，且边FG落在BC上．若BC＝3，AD＝2，EF＝EH，AD⊥BC，那么EH的长为．23．如图，矩形ABCD中，F是DC上一点，BF⊥AC，垂足为E，＝，△CEF的面积为S1，△AEB的面积为S2，则的值等于．24．如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A 和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是米．25．把标准纸一次又一次对开，可以得到均相似的“开纸”．现在我们在长为2、宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行，或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是．三．解答题（共20小题）26．如图，在△ABC中，∠C＝90°，点D在AC上，且CD＞DA，DA＝2，点P、Q同时从点D出发，以相同的速度分别沿射线DC、射线DA运动．过点Q作AC的垂线段QR，使QR＝PQ，连接PR，当点Q到达点A时，点P、Q 同时停止运动、设PQ＝x，△PQR与△ABC重叠部分的面积为S，当x＝时，点R恰好在AB边上．（1）填空：点R恰好经过AB边时，S的值为；（2）求S关于x的函数关系式，并写出x的取值范围．27．在△ABC中，∠ACB＝45°．点D（与点B、C不重合）为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB＝AC．如图①，且点D在线段BC上运动．试判断线段CF与BD之间的位置关系，并证明你的结论．（2）如果AB＞AC，如图②，且点D在线段BC上运动．（1）中结论是否成立，为什么？（3）若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC＝，BC＝3，CD＝x，求线段CP的长．（用含x的式子表示）28．如图，在矩形ABCD中对角线AC、BD相交于点F，延长BC到点E，使得四边形ACED是一个平行四边形，平行四边形对角线AE交BD、CD分别为点G和点H．（1）证明：DG2＝FG•BG；（2）若AB＝5，BC＝6，则线段GH的长度．29．如图，已知矩形OABC，以点O为坐标原点建立平面直角坐标系，其中A （2，0），C（0，3），点P以每秒1个单位的速度从点C出发在射线CO 上运动，连接BP，作BE⊥PB交x轴于点E，连接PE交AB于点F，设运动时间为t秒．（1）当t＝2时，求点E的坐标；（2）若AB平分∠EBP时，求t的值；（3）在运动的过程中，是否存在以P、O、E为顶点的三角形与△ABE相似．若存在，请求出点P的坐标；若不存在，请说明理由．30．已知：如图边长为2的正方形ABCD中，∠MAN的两边分别交BC、CD边于M、N两点，且∠MAN＝45°①求证：MN＝BM+DN；②若AM、AN交对角线BD于E、F两点．设BF＝y，DE＝x，求y与x的函数关系式．31．如图，已知ED∥BC，∠EAB＝∠BCF，（1）四边形ABCD为平行四边形；（2）求证：OB2＝OE•OF；（3）连接OD，若∠OBC＝∠ODC，求证：四边形ABCD为菱形．32．如图，在一块如图所示的三角形余料上裁剪下一个正方形，如果△ABC为直角三角形，且∠ACB＝90°，AC＝4，BC＝3，正方形的四个顶点D、E、F、G分别在三角形的三条边上．求正方形的边长．33．一块材料的形状是锐角三角形ABC，边BC＝120mm，高AD＝80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．（1）求证：△AEF∽△ABC；（2）求这个正方形零件的边长；（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？34．如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm．动点M从点B 出发，在BA边上以每秒3cm的速度向定点A运动，同时动点N从点C出发，在CB边上以每秒2cm的速度向点B运动，运动时间为t秒（0＜t＜），连接MN．（1）若△BMN与△ABC相似，求t的值；（2）连接AN，CM，若AN⊥CM，求t的值．35．如图，在四边形ABCD中，AB＝AD，AC与BD交于点E，∠ADB＝∠ACB．（1）求证：＝；（2）若AB⊥AC，AE：EC＝1：2，F是BC中点，求证：四边形ABFD是菱形．36．如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2＝CE•CA．（1）求证：BC＝CD；（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB＝OB，CD＝，求DF的长．37．等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．（1）若AE＝CF；①求证：AF＝BE，并求∠APB的度数；②若AE＝2，试求AP•AF的值；（2）若AF＝BE，当点E从点A运动到点C时，试求点P经过的路径长．38．如图，已知在矩形ABCD中，AD＝8cm，CD＝4cm，点E从点D出发，沿线段DA以每秒1cm的速度向点A方向移动，同时点F从点C出发，沿射线CD方向以每秒2cm的速度移动，当B、E、F三点共线时，两点同时停止运动．设点E移动的时间为t（秒），（1）求证：△BCF∽△CDE；（2）求t的取值范围；（3）连接BE，当t为何值时，∠BEC＝∠BFC？39．如图，△ABC中，AB＝AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．（1）求证：D是BC的中点；（2）若DE＝3，BD﹣AD＝2，求⊙O的半径；（3）在（2）的条件下，求弦AE的长．40．如图，△ABC中，∠BAC＝90°，AB＝AC＝1，点D是BC上一个动点（不与B、C重合），在AC上取E点，使∠ADE＝45度．（1）求证：△ABD∽△DCE；（2）设BD＝x，AE＝y，求y关于x的函数关系式；（3）当△ADE是等腰三角形时，求AE的长．41．【提出问题】（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边△AMN，连接CN．求证：∠ABC＝∠ACN．【类比探究】（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC＝∠ACN还成立吗？请说明理由．【拓展延伸】（3）如图3，在等腰△ABC中，BA＝BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰△AMN，使顶角∠AMN＝∠ABC．连接CN．试探究∠ABC与∠ACN的数量关系，并说明理由．42．在△ABC中，∠BAC＝90°，AB＝AC，点O在BC上（与B，C不重合），连接AO，F是线段AO上的点（与A，O不重合），∠EAF＝90°，AE＝AF，连接FE，FC，BE，BF．（1）如图1，若AO⊥BC，求证：BE＝BF；（2）如图2，若将△AEF绕点A旋转，使边AF在∠BAC的内部，延长CF 交AB于点G，交BE于点K．①求证：△AGC∽△KGB；②当△BEF为等腰直角三角形时，请你直接写出AB：BF的值．43．在矩形ABCD中，AB＝6cm，BC＝8cm．（1）如图①，若动点Q从点C出发，在对角线CA上以每秒3cm的速度向A 点匀速移动，同时动点P从点B出发，在BC上以每秒2cm的速度向点C匀速移动，运动时间为t秒（0≤t＜3），t取何值时，四边形ABPQ的面积最小？（2）如图②，若点Q在对角线CA上，CQ＝4cm，动点P从点B出发，以每秒1cm的速度沿BC运动至点C停止．设点P运动了t秒，当t为何值时，以Q、P、C为顶点的三角形是等腰三角形？44．数学课上，王老师出示问题：如图1，将边长为5的正方形纸片ABCD折叠，使顶点A落在边CD上的点P处（点P与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．（1）观察操作结果，在图1中找到一个与△DEP相似的三角形，并证明你的结论；（2）当点P在边CD的什么位置时，△DEP与△CPG面积的比是9：25？请写出求解过程；（3）将正方形换成正三角形，如图2，将边长为5的正三角形纸片ABC折叠，使顶点A落在边BC上的点P处（点P与B、C不重合），折痕为EF，当点P在边BC的什么位置时，△BEP与△CPF面积的比是9：25？请写出求解过程．45．已知：如图，△ABC中，AD⊥BC，过点D作DE⊥AB，DF⊥AC，连接EF，（1）若AD2＝BD•DC，①求证：∠BAC＝90°．②AB＝4，DC＝6，求EF．（2）如图2，若AD＝4，BD＝2，DC＝4，求EF．。

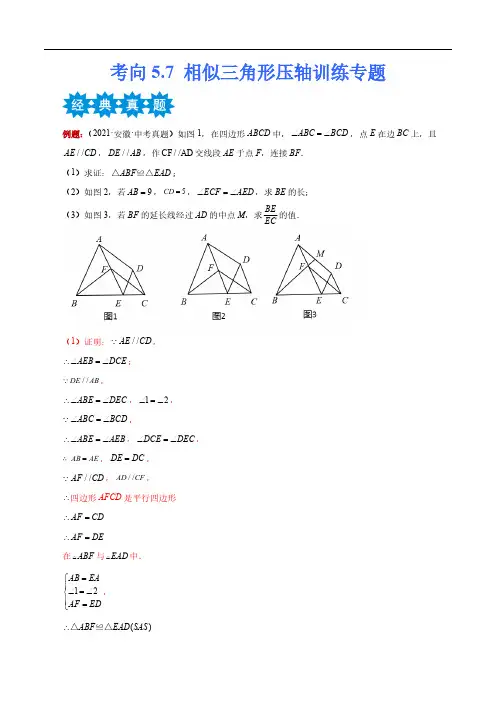
考向5.7 相似三角形压轴训练专题例题：（2021·安徽·中考真题）如图1，在四边形ABCD 中，ABC BCD ∠=∠，点E 在边BC 上，且//AE CD ，//DE AB ，作CF //AD 交线段AE 于点F ，连接BF ．（1）求证：ABF EAD △≌△；（2）如图2，若9AB =，5CD =，ECF AED ∠=∠，求BE 的长；（3）如图3，若BF 的延长线经过AD 的中点M ，求BE EC的值．（1）证明：//AE CD ，AEB DCE ∴∠=∠；//DE AB ，ABE DEC ∴∠=∠，12∠=∠，ABC BCD ∠=∠ ，ABE AEB ∴∠=∠，DCE DEC ∠=∠，AB AE =∴，DE DC =，//AF CD ，//AD CF ，∴四边形AFCD 是平行四边形AF CD∴=AF DE∴=在ABF 与EAD 中．12AB EA AF ED =⎧⎪∠=∠⎨⎪=⎩，()ABF EAD SAS ∴△≌△（2）ABF EAD △≌△，BF AD ∴=，在AFCD □中，AD CF =，BF CF ∴=，FBC FCB ∴∠=∠，又2FCB ∠=∠ ，21∠=∠，1FBC ∴∠=∠，在EBF △与EAB 中．1EBF BEF AEB ∠=∠⎧⎨∠=∠⎩，EBF EAB ∴△∽△；EBEFEA EB ∴=；9AB = ，9AE ∴=；5CD = ，5AF ∴=；4EF ∴=，49EBEB ∴=，6BE ∴=或6-（舍）；（3）延长BM 、ED 交于点G ．ABE 与DCE 均为等腰三角形，ABC DCE ∠=∠，ABE DCE ∴△∽△，AB AE BE DC DE CE∴==，设1CE =，BE x =，DC DE a ==，则AB AE ax ==，AF CD a ==，(1)EF a x ∴=-，//AB DG ，3G ∴∠=∠；在MAB △与MDG 中，345G MA MD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()MAB MDG AAS ∴△≌△；DG AB ax ∴==．(1)EG a x ∴=+；//AB EG ，FAB FEG ∴△∽△，FA AB FE EG∴=，(1)(1)a ax a x a x ∴=-+，(1)1x x x -∴=+，2210x x ∴--=，2(1)2x ∴-=，1x ∴=11x ∴=，21x =+，1BE EC∴=一、单选题1．（2018·山东聊城·中考真题）如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且OA=5，OC=3．若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的A 1处，则点C 的对应点C 1的坐标为（ ）A ．（﹣91255，）B ．（﹣12955，）C ．（﹣161255，）D ．（﹣121655，）2．（2020·四川遂宁·中考真题）如图，在正方形ABCD 中，点E 是边BC 的中点，连接AE 、DE ，分别交BD 、AC 于点P 、Q ，过点P 作PF ⊥AE 交CB 的延长线于F ，下列结论：①∠AED +∠EAC +∠EDB ＝90°，②AP ＝FP ，③AE ，④若四边形OPEQ 的面积为4，则该正方形ABCD 的面积为36，⑤CE •EF ＝EQ •DE ．其中正确的结论有（ ）A ．5个B ．4个C ．3个D ．2个3．（2018·广西桂林·中考真题）如图，在平面直角坐标系中，M 、N 、C 三点的坐标分别为（12，1），（3，1），（3，0），点A 为线段MN 上的一个动点，连接AC ，过点A 作AB AC ⊥交y 轴于点B ，当点A 从M 运动到N 时，点B 随之运动，设点B 的坐标为（0，b ），则b 的取值范围是（ ）A ．114b -≤≤B ．514b -≤≤C ．9142b -≤≤D ．914b -≤≤二、填空题4．（2017·贵州黔南·中考真题）如图，在ABC 中，AB ＝2，AC ＝4，ABC 绕点C 按逆时针方向旋转得到A B C ''△，使CB '∥AB ，分别延长AB ，CA '相交于点D ，则线段BD 的长为__．5．（2016·四川资阳·中考真题）如图，在等腰直角△ABC 中，∠ACB=90°，CO ⊥AB 于点O ，点D 、E 分别在边AC 、BC 上，且AD=CE ，连结DE 交CO 于点P ，给出以下结论：①△DOE 是等腰直角三角形；②∠CDE=∠COE ；③若AC=1，则四边形CEOD 的面积为14；④22222AD BE OP DP PE +-=⋅，其中所有正确结论的序号是___________．三、解答题6．（2019·广西梧州·中考真题）如图，在矩形ABCD 中，4,3AB BC ==，AF 平分DAC ∠，分别交,DC BC 的延长线于点,E F ；连接DF ，过点A 作AH DF ∕∕，分别交,BD BF 于点,G H ．（1）求DE 的长；（2）求证：1DFC ∠=∠．7．（2012·浙江金华·中考真题）在锐角△ABC 中，AB=4，BC=5，∠ACB=45°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△ABA 1的面积为4，求△CBC 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转过程中，点P 的对应点是点P 1，求线段EP 1长度的最大值与最小值．8．（2013·江苏盐城·中考真题）阅读材料：如图①，△ABC 与△DEF 都是等腰直角三角形，∠ACB=∠EDF=90°，且点D 在AB 边上，AB 、EF 的中点均为O,连结BF 、CD 、CO ，显然点C 、F 、O 在同一条直线上，可以证明△BOF ≌△COD ，则BF=CD解决问题：（1）将图①中的Rt △DEF 绕点O 旋转得到图②，猜想此时线段BF 与CD 的数量关系，并证明你的结论；（2）如图③，若△ABC 与△DEF 都是等边三角形，AB 、EF 的中点均为O,上述（1）中结论仍然成立吗？如果成立，请说明理由；如果不成立，请求出BF 与CD 之间的数量关系；（3）如图④，若△ABC 与△DEF 都是等腰三角形，AB 、EF 的中点均为O,且顶角∠ACB=∠EDF=α，请直接写出BF CD的值（用含α的式子表示出来）．9．（2018·浙江舟山·中考真题）已知，ABC ∆中，B C ∠=∠，P 是BC 边上一点，作CPE BPF ∠=∠，分别交边AC ，AB 于点E ，F .（1）若CPE C ∠=∠（如图1），求证：PE PF AB +=.（2）若CPE C ∠≠∠，过点B 作CBD CPE ∠=∠，交CA （或CA 的延长线）于点D .试猜想：线段PE ，PF 和BD 之间的数量关系，并就CPE C ∠>∠情形（如图2）说明理由.（3）若点F 与A 重合（如图3），27C ∠= ，且PA AE =.①求CPE ∠的度数；②设PB a =，PA b =，AB c =，试证明：22a cb c-=.10．（2015·四川成都·中考真题）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB 的延长线相交于点D，E，F，且BF=BC，⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．（1）求证：△ABC≌△EBF；（2）试判断BD与⊙O的位置关系，并说明理由；（3）若AB=1，求HG•HB的值．一、单选题BC＝2，M为1．（2021·广西百色·中考真题）如图，矩形ABCD各边中点分别是E、F、G、H，AB＝AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S．设AM＝x，则S关于x的函数图象大致是（）A ．B ．C ．D ．2．（2019·辽宁鞍山·中考真题）如图，正方形ABCD 和正方形CGFE 的顶点C ，D ，E 在同一条直线上，顶点B ，C ，G 在同一条直线上．O 是EG 的中点，∠EGC 的平分线GH 过点D ，交BE 于点H ，连接FH 交EG于点M ，连接OH ．以下四个结论：①GH ⊥BE ；②△EHM ∽△GHF ；③BC CG1；④HOM HOG S S △△＝2，其中正确的结论是（ ）A ．①②③B ．①②④C ．①③④D ．②③④3．（2015·广西贵港·中考真题）如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC 于点F ，连接DF ，分析下列五个结论：①△AEF ∽△CAB ；②CF=2AF ；③DF=DC ；④tan ∠⑤S 四边形CDEF =52S △ABF ，其中正确的结论有（ ）A ．5个B ．4个C ．3个D ．2个二、填空题4．（2017·湖北十堰·中考真题）如图，正方形ABCD 中，BE=EF=FC ，CG=2GD ，BG 分别交AE ，AF 于M ，N ．下列结论：①AF ⊥BG ；②BN=NF ；③38MB MG =；④S 四边形CGNF =S 四边形ANGD ．其中正确的结论的序号是_______．5．（2015·四川南充·中考真题）如图，正方形ABCD 边长为1，以AB 为直径作半圆，点P 是CD 中点，BP 与半圆交于点Q ，连结DQ ．给出如下结论：①DQ ＝1；②；③S △PDQ ＝；④cos ∠ADQ=．其中正确结论是_________．（填写序号）三、解答题6．（2021·内蒙古赤峰·中考真题）数学课上，有这样一道探究题．如图，已知ABC 中，AB =AC =m ，BC =n ，()0180BAC αα∠=︒<<︒，点P 为平面内不与点A 、C 重合的任意一点，将线段CP 绕点P 顺时针旋转a ，得线段PD ，E 、F 分别是CB 、CD 的中点，设直线AP 与直线EF 相交所成的较小角为β，探究EF AP 的值和β的度数与m 、n 、α的关系，请你参与学习小组的探究过程，并完成以下任务：（1）填空：【问题发现】小明研究了60α=︒时，如图1，求出了EF PA =___________，β=___________；小红研究了90α=︒时，如图2，求出了EF PA =___________，β=___________；【类比探究】他们又共同研究了α=120°时，如图3，也求出了EF PA ；【归纳总结】最后他们终于共同探究得出规律：EF PA =__________(用含m 、n 的式子表示)；β=___________ (用含α的式子表示)．（2）求出120α=︒时EF PA的值和β的度数．7．（2021·湖南岳阳·中考真题）如图，在Rt ABC 中，90ACB ∠=︒，60A ∠=︒，点D 为AB 的中点，连接CD ，将线段CD 绕点D 顺时针旋转()60120αα︒<<︒得到线段ED ，且ED 交线段BC 于点G ，CDE ∠的平分线DM 交BC 于点H ．（1）如图1，若90α=︒，则线段ED 与BD 的数量关系是________，GD CD=________；（2）如图2，在（1）的条件下，过点C 作//CF DE 交DM 于点F ，连接EF ，BE ．①试判断四边形CDEF 的形状，并说明理由；②求证：BE FH =；（3）如图3，若2AC =，()tan 60m α-︒=，过点C 作//CF DE 交DM 于点F ，连接EF ，BE ，请直接写出BE FH的值（用含m 的式子表示）．8．（2021·四川乐山·中考真题）在等腰ABC 中，AB AC =，点D 是BC 边上一点（不与点B 、C 重合），连结AD ．（1）如图1，若60C ∠=°，点D 关于直线AB 的对称点为点E ，结AE ，DE ，则BDE ∠=________；（2）若60C ∠=°，将线段AD 绕点A 顺时针旋转60︒得到线段AE ，连结BE ．①在图2中补全图形；②探究CD 与BE 的数量关系，并证明；（3）如图3，若AB AD k BC DE==，且ADE C ∠=∠，试探究BE 、BD 、AC 之间满足的数量关系，并证明．9．（2020·湖北省直辖县级单位·中考真题）实践操作：第一步：如图1，将矩形纸片ABCD 沿过点D 的直线折叠，使点A 落在CD 上的点A '处，得到折痕DE ，然后把纸片展平．第二步：如图2，将图1中的矩形纸片ABCD 沿过点E 的直线折叠，点C 恰好落在AD 上的点C '处，点B 落在点B '处，得到折痕EF ，B C ''交AB 于点M ，C F '交DE 于点N ，再把纸片展平．问题解决：（1）如图1，填空：四边形AEA D '的形状是_____________________；（2）如图2，线段MC '与ME 是否相等？若相等，请给出证明；若不等，请说明理由；（3）如图2，若2cm,'4cm AC DC '==，求:DN EN 的值．10．（2020·四川内江·中考真题）如图，正方形ABCD 中，P 是对角线AC 上的一个动点（不与A 、C 重合），连结BP ，将BP 绕点B 顺时针旋转90︒到BQ ，连结QP 交BC 于点E ，QP 延长线与边AD 交于点F ．（1）连结CQ ，求证：AP CQ =；（2）若14AP AC =，求:CE BC 的值；（3）求证：PF EQ =．11．（2021·湖北十堰·中考真题）已知抛物线25y ax bx =+-与x 轴交于点()1,0A -和()5,0B -，与y轴交于点C ，顶点为P ，点N 在抛物线对称轴上且位于x 轴下方，连AN 交抛物线于M ，连AC 、CM ．（1）求抛物线的解析式；（2）如图1，当tan 2ACM ∠=时，求M 点的横坐标；（3）如图2，过点P 作x 轴的平行线l ，过M 作MD l ⊥于D ，若MD =，求N 点的坐标．1．A【解析】【分析】直接利用相似三角形的判定与性质得出△ONC1三边关系，再利用勾股定理得出答案．【详解】过点C1作C1N⊥x轴于点N，过点A1作A1M⊥x轴于点M，由题意可得：∠C1NO=∠A1MO=90°，∠1=∠2=∠3，则△A1OM∽△OC1N，∵OA=5，OC=3，∴OA1=5，A1M=3，∴OM=4，∴设NO=3x，则NC1=4x，OC1=3，则（3x）2+（4x）2=9，解得：x=±35（负数舍去），则NO=95，NC1=125，故点C的对应点C1的坐标为：（-95，125）．故选A．【点拨】此题主要考查了矩形的性质以及勾股定理等知识，正确得出△A1OM∽△OC1N是解题关键．2．B【解析】【分析】①正确:证明∠EOB=∠EOC=45°，再利用三角形的外角的性质即可得出答案；②正确：利用四点共圆证明∠AFP=∠ABP=45°即可；③正确：设BE=EC=a，求出AE，OA即可解决问题；④错误：通过计算正方形ABCD的面积为48；⑤正确：利用相似三角形的性质证明即可.【详解】①正确：如图，连接OE，∵四边形ABCD是正方形，∴AC⊥BD，OA=OC=OB=OD，∴∠BOC=90°，∵BE=EC，∴∠EOB=∠EOC=45°，∵∠EOB＝∠EDB+∠OED，∠EOC=∠EAC+∠AEO，∴∠AED+∠EAC+∠EDO=∠EAC+∠AEO+∠OED+∠EDB=90°，故①正确；②正确：如图，连接AF，∵PF⊥AE，∴∠APF=∠ABF=90°，∴A，P，B，F四点共圆，∴∠AFP=∠ABP＝45°，∴∠PAF=∠PFA＝45°，∴PA=PF，故②正确；③正确：设BE=EC=a，则AE，OA＝OC＝OB＝OD a，∴AE AO AE ，故③正确；④错误：根据对称性可知，OPE OQE ≅△△，∴OEQ S △=12OPEQ S 四边形=2，∵OB =OD ，BE =EC ，∴CD =2OE ，OE ⊥CD ，∴ EQ OE 1==DQ CD 2， OEQ CDQ △△，∴ODQ S =4△， CDQ S =8△，∴CDO S =12△，∴ABCD S =48正方形，故④错误；⑤正确：∵∠EPF =∠DCE =90°，∠PEF =∠DEC ，∴EPF ECD △△，∴EF PE =ED EC，∴EQ =PE ，∴CE•EF =EQ•DE ，故⑤正确；综上所诉一共有4个正确，故选：B ．【点拨】本题主要考查了三角形外角性质、四点共圆问题、全等与相似三角形的综合运用，熟练掌握相关概念与方法是解题关键.3．B【解析】【分析】延长NM 交y 轴于P 点，则MN ⊥y 轴．连接CN ．证明△PAB ∽△NCA ，得出PB PA NA NC=，设PA=x ，则NA=PN-PA=3-x ，设PB=y ，代入整理得到22393()24y x x x =-=--+，根据二次函数的性质以及12≤x≤3，求出y 的最大与最小值，进而求出b 的取值范围．【详解】解：如图，延长NM 交y 轴于P 点，则MN ⊥y 轴．连接CN ．在△PAB 与△NCA 中，9090APB CNA PAB NCA CAN ∠∠︒⎧⎨∠∠︒-∠⎩＝＝＝＝，∴△PAB ∽△NCA ，∴PB PA NA NC=，设PA=x ，则NA=PN-PA=3-x ，设PB=y ，∴31y x x =-，∴22393()24y x x x =-=--+，∵-1＜0，12≤x≤3，∴x=32时，y 有最大值94，此时b=1-94=-54，x=3时，y 有最小值0，此时b=1，∴b 的取值范围是-54≤b≤1．故选：B ．【点拨】本题考查了相似三角形的判定与性质，二次函数的性质，得出y 与x 之间的函数解析式是解题的关键．4．6.【解析】【详解】试题分析：∵将△ABC 绕点C 按逆时针方向旋转得到△A′B′C ，AB ＝2，AC ＝4，∴A′B′＝AB ＝2，AC′＝AC ＝4，∠CA′B′＝∠A.又∵CB′∥AB ，∴∠A′CB′＝∠A. ∴△A′CB′∽△DAC.∴CA A B AD AC'''=，即4284AD AD =⇒=. ∴BD=6.考点：1.旋转的性质；2.平行的性质；3.相似三角形的判定和性质.5．①②③④．【解析】【详解】试题分析：①正确．如图，∵∠ACB=90°，AC=BC ，CO ⊥AB∴AO=OB=OC ，∠A=∠B=∠ACO=∠BCO=45°，在△ADO 和△CEO 中，∵OA=OC ，∠A=∠ECO ，AD=CE ，∴△ADO ≌△CEO ，∴DO=OE ，∠AOD=∠COE ，∴∠AOC=∠DOE=90°，∴△DOE 是等腰直角三角形．故①正确．②正确．∵∠DCE+∠DOE=180°，∴D 、C 、E 、O 四点共圆，∴∠CDE=∠COE ，故②正确．③正确．∵AC=BC=1，∴S △ABC =12×1×1=12，S 四边形DCEO =S △DOC +S △CEO =S △CDO +S △ADO =S △AOC =12S △ABC =14，故③正确．④正确．∵D 、C 、E 、O 四点共圆，∴OP•PC=DP•PE ，∴22OP +2DP•PE=22OP +2OP•PC=2OP （OP+PC ）=2OP•OC ，∵∠OEP=∠DCO=∠OCE=45°，∠POE=∠COE ，∴△OPE ∽△OEC ，∴OP OE OE OC =，∴OP•OC=2OE ，∴22OP +2DP•PE=22OE =2DE =22CD CE +，∵CD=BE ，CE=AD ，∴22222AD BE OP DP PE +=+⋅，∴22222AD BE OP DP PE +-=⋅．故④正确．考点：勾股定理；四点共圆．6．（1）32=DE ；（2）见解析.【解析】【分析】（1）由AD CF ∕∕，AF 平分DAC ∠，可得FAC AFC ∠=∠，得出5AC CF ==，可证出ADE FCE ∆∆∽，则AD DE CF CE =，可求出DE 长；（2）由ADG HBG ∆∆∽，可求出DG ，则DE DC DG DB=，可得EG BC ∕∕，则1AHC ∠=∠，根据DF AH ∕∕，可得AHC DFC ∠=∠，结论得证．【详解】（1）解：∵矩形ABCD 中， AD CF ∕∕，∴DAF ACF ∠=∠，∵AF 平分DAC ∠，∴DAF CAF ∠=∠，∴FAC AFC ∠=∠，∴AC CF =，∵4,3AB BC ==，∴5AC ==，∴5CF =，∵AD CF ∕∕，∴ADE FCE ∆∆∽，∴AD DECF CE =，设DE x =，则354xx =-，解得32x =∴32=DE ；（2）∵,AD FH AF DH ∕∕∕∕，∴四边形ADFH 是平行四边形，∴3AD FH ==，∴2,5CH BH ==∵AD BH ∕∕，∴ADG HBG ∆∆∽，∴DGADBG BH =，∴355DGDG =-，∴158DG =，∵32=DE ，∴45DE DCDG DB ==，∴EG BC ∕∕，∴1AHC ∠=∠，又∵DF AH ∕∕，∴AHC DFC ∠=∠，1DFC ∠=∠．【点拨】考核知识点：相似三角形综合运用.证明相似三角形，运用相似三角形性质是关键.7．（1）∠CC 1A 1=90°．（2）S △CBC1=254．（3）最小值为：EP 12．最大值为：EP 1= 7．【解析】【分析】（1）由旋转的性质可得：∠A 1C 1B=∠ACB=45°，BC=BC 1，又由等腰三角形的性质，即可求得∠CC 1A 1的度数．（2）由旋转的性质可得：△ABC ≌△A 1BC 1，易证得△ABA 1∽△CBC 1，利用相似三角形的面积比等于相似比的平方，即可求得△CBC 1的面积．（3）由①当P 在AC 上运动至垂足点D ，△ABC 绕点B 旋转，使点P 的对应点P 1在线段AB 上时，EP 1最小；②当P 在AC 上运动至点C ，△ABC 绕点B 旋转，使点P 的对应点P 1在线段AB 的延长线上时，EP 1最大，即可求得线段EP 1长度的最大值与最小值．【详解】解：（1）∵由旋转的性质可得：∠A 1C 1B=∠ACB=45°，BC=BC 1，∴∠CC 1B=∠C 1CB=45°．∴∠CC 1A 1=∠CC 1B+∠A 1C 1B=45°+45°=90°．（2）∵由旋转的性质可得：△ABC ≌△A 1BC 1，∴BA=BA 1，BC=BC 1，∠ABC=∠A 1BC 1．∴11BA BA BC BC =，∠ABC+∠ABC 1=∠A 1BC 1+∠ABC 1∴∠ABA 1=∠CBC 1．∴△ABA 1∽△CBC 1∴1122ABA CBC S AB 416S CB 525∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭．∵S△ABA1=4，∴S△CBC1=254．（3）过点B作BD⊥AC，D为垂足，∵△ABC为锐角三角形，∴点D在线段AC上．在Rt△BCD中，①如图1，当P在AC上运动至垂足点D，△ABC绕点B旋转，使点P的对应点P1在线段AB上时，EP1最小．最小值为：EP1=BP1﹣BE=BD﹣2．②如图2，当P在AC上运动至点C，△ABC绕点B旋转，使点P的对应点P1在线段AB的延长线上时，EP1最大．最大值为：EP1=BC+BE=5+2=7．8．（1）根据等腰直角三角形和旋转的性质，由SAS证出△BOF≌△COD，即可得出结论.（2）不成立.根据等边三角形和旋转的性质，证出△BOF∽△COD，即可得出结论.（3）BFtan CD2α=.【解析】【详解】分析：（1）根据等腰直角三角形和旋转的性质，由SAS证出△BOF≌△COD，即可得出结论.（2）根据等边三角形和旋转的性质，证出△BOF∽△COD，即可得出结论.（3）如图，连接CO、DO，仿（2）可证△BOF∽△COD，从而BF BO CD CO=.由点O是AB的中点，可得CO⊥AB，∴BOtan2COα=.∴BFtanCD2α=.解：（1）相等.证明如下：如图，连接CO、DO，∵△ABC是等腰直角三角形，点O是AB的中点，∴BO=CO，CO⊥AB.∴∠BOC=900.同理，FO=DO，∠DOF=900.∴∠BOF=900＋∠COF，∠COD=900＋∠COF.∴∠BOF=∠COD.∴△BOF≌△COD（SAS）.∴BF=CD.（2）不成立.如图，连接CO、DO，∵△ABC 是等边三角形，∴∠CBO=600.∵点O 是AB 的中点，∴CO ⊥AB ，即∠BOC=900.∴在Rt △BOC 中，CO tan CBO BO ∠==同理，∠DOF=900，DO FO =.∴CO DO BO FO=.又∵∠BOF=900＋∠COF ，∠COD=900＋∠COF.∴∠BOF=∠COD.∴△BOF ∽△COD.∴CD CO BF BO==∴CD =.（3）BF tan CD 2α=.9．（1）证明见解析；（2）猜想：BD PE PF =+，理由见解析；（3）①51CPE ∠= ；②证明见解析.【解析】【详解】【分析】（1）根据平行线的判定，得到//PE AF ，//PF AE ，证明PE AF =.即可证明PE PF AB +=. （2）过点B 作DC 的平行线交EP 的延长线于点G ，证明FBP ∆≌()GBP ASA ∆，得到PF PG =.证明四边形BGED 是平行四边形，即可得到BD EG PG PE PE PF ==+=+.（3）①设CPE BPF x ∠=∠=，27APE PEA C CPE x ∠=∠=∠+∠=+ ，根据三角形的内角和列出方程，求解即可.②延长BA 至M ，使AM AP =，连结MP ,证明 ABP PBM ∆~∆.根据相似三角形的性质得到BP BM AB BP=，即可证明.【解答】（1）∵B C ∠=∠，CPE BPF ∠=∠，CPE C ∠=∠，∴B BPF CPE ∠=∠=∠，BPF C ∠=∠，∴PF BF =，//PE AF ，//PF AE ，∴PE AF =.∴PE PF AF BF AB +=+=.（2）猜想：BD PE PF =+，理由如下：过点B 作DC 的平行线交EP 的延长线于点G ，则ABC C CBG ∠=∠=∠，∵CPE BPF ∠=∠，∴BPF CPE BPG ∠=∠=∠，又BP BP =，∴FBP ∆≌()GBP ASA ∆，∴PF PG =.∵CBD CPE ∠=∠，∴//PE BD ，∴四边形BGED 是平行四边形，∴BD EG PG PE PE PF ==+=+.（3）①设CPE BPF x ∠=∠=，∵27C ∠= ，PA AE =，∴27APE PEA C CPE x ∠=∠=∠+∠=+ ，又180BPA APE CPE ∠+∠+∠= ，即27180x x x +++= ，∴51x = ，即51CPE ∠= .②延长BA 至M ，使AM AP =，连结MP ，∵27C ∠= ，51BPA CPE ∠=∠= .∴180BAP B BPA ∠=-∠-∠ 102M MPA ==∠+∠ ，∵AM AP =，∴1512M MPA BAP ∠=∠=∠= ，∴M BPA ∠=∠，而B B ∠=∠，∴ABP PBM ∆~∆.∴BP BM AB BP=，∴2BP AB BM =⋅.∵PB a =，PA AM b ==，AB c =，∴()2a c b c =+，∴22a cb c-=.【点评】考查平行四边形的判定与性质，全等三角形的判定与性质，相似三角形的判定与性质， 综合性比较强，对学生综合能力要求较高.10．（1）证明见试题解析；（2）相切，理由见试题解析；（3）2．【解析】【分析】（1）由∠ABC=90°和FD ⊥AC ，得到∠ABF=∠EBF ，由∠DEC=∠BEF ，得到∠DCE=∠EFB ，从而得到△ABC ≌△EBF （ASA ）；（2）BD 与⊙O 相切．连接OB ，只需证明∠DBE+∠OBE=90°，即可得到OB ⊥BD ，从而有BD 与⊙O 相切；（3）连接EA ，EH ，由DF 为线段AC 的垂直平分线，得到AE=CE ，由△ABC ≌△EBF ，得到AB=BE=1，进而得到=故1BF BC ==即可得出结论24EF =+又因为BH 为角平分线，易证△EHF 为等腰直角三角形，故222EF HF =，得到22122HF EF ==△GHF ∽△FHB ，得到2HG HB HF ⋅=．【详解】解：（1）∵∠ABC=90°，∴∠CBF=90°，∵FD ⊥AC ，∴∠CDE=90°，∴∠ABF=∠EBF ，∵∠DEC=∠BEF ，∴∠DCE=∠EFB ，∵BC=BF ，∴△ABC ≌△EBF （ASA ）；（2）BD 与⊙O 相切．理由：连接OB ，∵DF 是AC 的垂直平分线，∴AD=DC ，∴BD=CD ，∴∠DCE=∠DBE ，∵OB=OF ，∴∠OBF=∠OFB ，∵∠DCE=∠EFB ，∴∠DBE=∠OBF ，∵∠OBF+∠OBE=90°，∴∠DBE+∠OBE=90°，∴OB ⊥BD ，∴BD 与⊙O 相切；（3）连接EA ，EH ，∵DF 为线段AC 的垂直平分线，∴AE=CE ，∵△ABC ≌△EBF ，∴AB=BE=1，∴=，∴1BF BC ==+∴(2222114EF BE BF =+=+=+，又∵BH 为角平分线，∴∠EBH=∠EFH=45°，∴∠HEF=∠HBF=45°，∠HFG=∠EBG=45°，∴△EHF 为等腰直角三角形，∴222EF HF =，∴22122HF EF ==∵∠HFG=∠FBG=45°，∠GHF=∠GHF ，∴△GHF ∽△FHB ，∴HF HGHB HF =，∴2HG HB HF ⋅=，∴22HG HB HF ⋅==．【点拨】本题考查了全等三角形的判定和性质，相似三角形的判定和性质，圆周角定理，勾股定理，线段的垂直平分线的性质，直角三角形的性质，等腰直角三角形的判定和性质，熟练掌握这些定理是解题的关键．1．D【解析】【分析】把M 点的运动过程分为AE 段（0x ≤≤）和BE x ≤≤可知在AE 段HAE GHD EOM GPS S S S S S =+--△△△△，分别表示出四个三角形的面积即可用x 表示出S ；同理当在BE 段时1111HAE GHD EO M GP S S S S S S =+++△△△△，分别表示出四个三角形的面积即可用x 表示出S ；最后根据x与S 的函数关系式对图像进行判断即可【详解】解：如下图所示，当M 点的运动过程在AE 段则由题意可知HAE GHD EOM GPSS S S S S =+--△△△△∵四边形ABCD 是矩形，直线l ⊥AB ，H 、E 、F 、G 为AD 、AB 、BC 、CD 的中点∴=HAE GHD S S △△，=EOM GPSS S △△∴22HAE EOMS S S =-△△∵1=2HAE S AE AH △，11122AH AD BC ===，12AE AB ==∴1=2HAE S AE AH △∵直线l ⊥AB∴∠OME =∠A =90°∴△HAE ∽△OME ∴AH OM AE ME=∴OM =又∵ME AE AM x=-=∴)OM x ==∴)212EOM S OM ME x ==- △∴)222HAE EOM S S S x =-=△△如下图所示，当M 点的运动过程在BE 段同理当在BE 段时1111HAE GHD EO M GP S S S S S S =+++△△△△即1122HAE EO M S S S =+△△同理可以得到111O M E =11M E AM AE x =-=∴111O M E x ==∴11211112EO M S O M M E x ==- △∴11222HAE EO MS S S x=+=△△综上所述当M点的运动过程在AE段时)222HAE EOMS S S x=-=--△△，二次函数开口向下；当M 点的运动过程在BE段时2S x=，二次函数开口向上故选D.【点拨】本题主要考查了二次函数图像，矩形的性质，相似三角形等等知识点，解题的关键在于能够熟练掌握相关知识点进行求解运算.2．A【解析】【分析】由四边形ABCD和四边形CGFE是正方形，得出△BCE≌△DCG，推出∠BEC+∠HDE=90°，从而得GH⊥BE；由GH是∠EGC的平分线，得出△BGH≌△EGH，再由O是EG的中点，利用中位线定理，得HO∥BG 且HO=12BG；由△EHG是直角三角形，因为O为EG的中点，所以OH=OG=OE，得出点H在正方形CGFE 的外接圆上，根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°，∠HEG=∠HFG，从而证得△EHM∽△GHF；设HN=a，则BC=2a，设正方形ECGF的边长是2b，则NC=b，CD=2a，由HO∥BG，得出△DHN∽△DGC，即可得出DN HNDC CG=，得到b2a a2a2b-=，即a2+2ab-b2=0，从而求得BC1CG-，设正方形ECGF的边长是2b，则，得到，通过证得△MHO∽△MFE，得到OM OHEM EF===1OMOE===，进一步得到1HOM HOMHOE HOGS SS S∆∆∆∆==.【详解】解：如图，∵四边形ABCD 和四边形CGFE 是正方形，∴BC ＝CD ，CE ＝CG ，∠BCE ＝∠DCG ，在△BCE 和△DCG 中，BC CD BCE DCGCE CG =⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△DCG （SAS ），∴∠BEC ＝∠BGH ，∵∠BGH+∠CDG ＝90°，∠CDG ＝∠HDE ，∴∠BEC+∠HDE ＝90°，∴GH ⊥BE ．故①正确；∵△EHG 是直角三角形，O 为EG 的中点，∴OH ＝OG ＝OE ，∴点H 在正方形CGFE 的外接圆上，∵EF ＝FG ，∴∠FHG ＝∠EHF ＝∠EGF ＝45°，∠HEG ＝∠HFG ，∴△EHM ∽△GHF ，故②正确；∵△BGH ≌△EGH ，∴BH ＝EH ，又∵O 是EG 的中点，∴HO ∥BG ，∴△DHN ∽△DGC ，DN HN DC CG∴=设EC 和OH 相交于点N ．设HN ＝a ，则BC ＝2a ，设正方形ECGF 的边长是2b ，则NC ＝b ，CD ＝2a ，222b a a a b-∴=即a 2+2ab ﹣b 2＝0，解得：a ＝b ＝（﹣b ，或a ＝（﹣1b （舍去），212ab ∴=1BCCG ∴=故③正确；∵△BGH ≌△EGH ，∴EG ＝BG ，∵HO 是△EBG 的中位线，∴HO ＝12BG ，∴HO ＝12EG ，设正方形ECGF 的边长是2b ，∴EG ＝，∴HOb ，∵OH ∥BG ，CG ∥EF ，∴OH ∥EF ，∴△MHO △MFE ，∴OM OH EM EF ===∴EMOM ，∴1OMOE ===，∴1HOMHOES S ∆∆=-∵EO ＝GO ，∴S △HOE ＝S △HOG ，∴1HOMHOGS S ∆∆=-故④错误，故选A ．【点拨】本题考查了正方形的性质，以及全等三角形的判定与性质，相似三角形的判定与性质，正确求得两个三角形的边长的比是解决本题的关键．3．B【解析】【详解】过D 作DM ∥BE 交AC 于N ，∵四边形ABCD 是矩形，∴AD ∥BC ，∠ABC=90°，AD=BC ，∵BE ⊥AC 于点F ，∴∠EAC=∠ACB ，∠ABC=∠AFE=90°，∴△AEF ∽△CAB ，故①正确；∵AD ∥BC ，∴△AEF ∽△CBF ，∴AE AF BC CF =，∵AE=12AD=12BC ，∴12AF CF =，∴CF=2AF ，故②正确，∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM=DE=12BC ，∴BM=CM ，∴CN=NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF=DC ，故③正确；设AD=a ，AB=b ，易知△BAE ∽△ADC ，有A D AD B AE C =，即2a b a b=∵tan ∠CAD==CD b AD a ，∴tan ∠④错误；∵△AEF ∽△CBF ，∴12EF AE BF BC ==，∴S △AEF =12S △ABF ，S △ABF =16S 矩形ABCD ，∵S △ABE =14S 矩形ABCD ，S △ACD =12S 矩形ABCD ，∴S △AEF =112S 四边形ABCD ，又∵S 四边形CDEF =S △ACD ﹣S △AEF =12S 矩形ABCD ﹣112S 矩形ABCD =512S 矩形ABCD ，∴S 四边形CDEF =52S △ABF ，故⑤正确；故选B ．考点：1．相似三角形的判定与性质；2．矩形的性质；3．综合题．4．①③.【解析】【详解】试题分析：①易证△ABF ≌△BCG ，即可解题；②易证△BNF ∽△BCG ，即可求得的值，即可解题；③作EH⊥AF，令AB=3，即可求得MN，BM的值，即可解题；④连接AG，FG，根据③中结论即可求得S四边形CGNF和S四边形ANGD，即可解题．①∵四边形ABCD为正方形，∴AB=BC=CD，∵BE=EF=FC，CG=2GD，∴BF=CG，∵在△ABF和△BCG中，，∴△ABF≌△BCG，∴∠BAF=∠CBG，∵∠BAF+∠BFA=90°，∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；②∵在△BNF和△BCG中，，∴△BNF∽△BCG，∴,∴BN=NF；②错误；③作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，AF=，∵S△ABF=AFBN=ABBF，∴BN=，NF=BN=，∴AN=AF﹣NF=，∵E是BF中点，∴EH是△BFN的中位线，∴EH=，NH=，BN∥EH，∴AH=，，解得：MN=，∴BM=BN﹣MN=，MG=BG﹣BM=，∴,③正确；④连接AG，FG，根据③中结论，则NG=BG﹣BN=，∵S四边形CGNF=S△CFG+S△GNF=CGCF+NFNG=1+，S四边形ANGD=S△ANG+S△ADG=ANGN+ADDG=,∴S四边形CGNF≠S四边形ANGD，④错误；故答案为①③．考点：全等三角形的判定和性质，相似三角形的判定和性质.5．①②④【解析】【分析】①连接OQ，OD，如图1．易证四边形DOBP是平行四边形，从而可得DO∥BP．结合OQ=OB，可证到∠AOD=∠QOD，从而证到△AOD≌△QOD，则有DQ=DA=1；②连接AQ，如图2，根据勾股定理可求出BP．易证Rt△AQB∽Rt△BCP，运用相似三角形的性质可求出BQ，从而求出PQ的值，就可得到PQBQ的值；③过点Q作QH⊥DC于H，如图3．易证△PHQ∽△PCB，运用相似三角形的性质可求出QH，从而可求出S△DPQ的值；④过点Q作QN⊥AD于N，如图4．易得DP∥NQ∥AB，根据平行线分线段成比例可得32DN PQAN BQ==，把AN=1-DN代入，即可求出DN，然后在Rt△DNQ中运用三角函数的定义，就可求出cos∠ADQ的值．【详解】解：①连接OQ，OD，如图1．易证四边形DOBP是平行四边形，从而可得DO∥BP．结合OQ=OB，可证到∠AOD=∠QOD，从而证到△AOD≌△QOD，则有DQ=DA=1．故①正确；②连接AQ，如图2．则有CP=12，=．易证Rt△AQB∽Rt△BCP，运用相似三角形的性质可求得则=，∴32 PQBQ=．故②正确；③过点Q作QH⊥DC于H，如图3．易证△PHQ∽△PCB，运用相似三角形的性质可求得QH=35，∴S△DPQ=12DP•QH=12×12×35=320．故③错误；④过点Q作QN⊥AD于N，如图4．易得DP ∥NQ ∥AB ，根据平行线分线段成比例可得32DN PQ AN BQ ==，则有312DN DN =-，解得：DN=35．由DQ=1，得cos ∠ADQ=35DN DQ =．故④正确．综上所述：正确结论是①②④．故答案为：①②④．【点拨】本题主要考查了圆周角定理、平行四边形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质、平行线的性质、锐角三角函数的定义、勾股定理等知识，综合性比较强，常用相似三角形的性质、勾股定理、三角函数的定义来建立等量关系，应灵活运用．6．（1）【问题发现】12，60°，45°；【类比探究】见（2）题的解析；【归纳总结】2n m ，1802a ︒-；（2），30°【解析】【分析】（1）当60α=︒时，△ABC 和△PDC 都是等边三角形，可证△ACP ∽△ECF ，从而有12EF AP =，∠Q ＝β＝∠ACB ＝60°；当90α=︒时，△ABC 和△PDC 都是等腰直角三角形，同理可证△ACP ∽△ECF 即可解决，依此可得出规律；（2）当120α=︒，可证CE AC =，CF CP =CE CA CF CP =，由∠ECF ＝∠ACP ，可得△PCA ∽△FCE 即可解决问题．【详解】（1）【问题发现】如图1，连接AE ，PF ，延长EF 、AP 交于点Q ，当60α=︒时，△ABC 和△PDC 都是等边三角形，∴∠PCD ＝∠ACB ＝60°，PC ＝CD ，AC ＝CB ，∵F 、E 分别是CD 、BC 的中点，∴12CF PC =，12CE AC =，∴CF CE PC AC=，又∵∠ACP ＝∠ECF ，∴△ACP ∽△ECF ，∴12EF AP =，∠CEF ＝∠CAP ，∴∠Q ＝β＝∠ACB ＝60°，当90α=︒时，△ABC 和△PDC 都是等腰直角三角形，如图2，连接AE ，PF ，延长EF 、AP 交于点Q ，∴∠PCD ＝∠ACB ＝45°，PC CD ，AC ，∵F 、E 分别是CD 、BC 的中点，∴CE AC =，CF PC =∴CF CE PC AC=，又∵∠ACP＝∠ECF，∴△ACP∽△ECF，∴EFAP==，∠CEF＝∠CAP，∴∠Q＝β＝∠ACB＝45°，【归纳总结】由此，可归纳出22nEF CE nAP AC m m===，β＝∠ACB＝1802a︒-；（2）当120α=︒，连接AE，PF，延长EF、AP交于点Q，∵AB＝AC，E为BC的中点，∴AE⊥BC，∠CAE＝60°∴sin60°＝CEAC=，同理可得：CFCP=∴CE CFAC CP=，∴CE CACF CP=，又∵∠ECF＝∠ACP，∴△PCA∽△FCE，∴EF ECAP AC==∠CEF＝∠CAP，∴∠Q＝β＝∠ACB＝30°．【点拨】本题主要考查了三角形相似的判定与性质，通过解决本题感受到：图形在变化但解决问题的方法不变，体会“变中不变”的思想．7．（1）ED BD =（2）①正方形，理由见解析；②见解析；（3【解析】【分析】（1）根据“斜中半”定理可得CD AD BD ==，然后根据旋转的性质可得CD ED =，从而得出ED BD =，再结合题意推出30B DCG ∠=∠=︒，从而根据正切函数的定义求出GD CD即可；（2）①通过证明CDF EDF △≌△，并综合条件//CF DE ，推出四边形CDEF 是正方形；②首先根据CFH DGH △△∽推出DH DG FH CD ==GBE GDH △≌△得到BE DH =，即可得出结论；（3）根据题意可首先证明四边形CDEF 是菱形，然后证明出EBG HFC △△∽，即可推出结论BE BG FH FC =，再作DK CG ⊥，通过解直角三角形，求出BG 的长度，从而得出结论．【详解】（1）∵点D 为Rt ABC 中斜边AB 的中点，∴CD AD BD ==，∵线段CD 绕点D 顺时针旋转得到线段ED ，∴CD ED =，∴ED BD =，∵Rt ABC 中，90ACB ∠=︒，60A ∠=︒，∴30B ∠=︒，∵CD BD =，∴30B DCG ∠=∠=︒，∴在Rt DCG 中，tan tan 30GD DCG CD =∠=︒=故答案为：ED BD =（2）①正方形，理由如下：∵90α=︒，DM 平分CDE ∠，∴90CDE ∠=︒，CDF EDF ∠=∠，∵CD ED =，DF DF =，∴()CDF EDF SAS △≌△，∴DCF DEF ∠=∠，∵//CF DE ，∴180FCD CDE ∠+∠=︒，∴90FCD ∠=︒，∴90DCF DEF CDE ∠=∠=∠=︒，∴四边形CDEF 为矩形，又∵CD ED =，∴四边形CDEF 为正方形；②显然，在正方形CDEF 中，CFH GDH △△∽，∴DH DG FH CF=，又∵CD CF =，∴DH DG FH CD ==由（1）得：60,,A CD AD ∠=︒=则ACD △为等边三角形，∴60ADC ∠=︒，∵90CDE ∠=︒，∴30GDB ∠=︒，∴GDB GBD ∠=∠，GD GB =，又∵DE DB =，∴()1180752DBE DEB GDB ∠=∠=︒-∠=︒，∴753045GBE ∠=︒-︒=︒，∵45GDH ∠=︒，∴GBE GDH∠=∠在GBE 与GDH 中，GDH GBE GD GBDGH BGE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()GBE GDH ASA △≌△，∴BE DH =，∴BE DH DG FH FH CD ===（3）同（2）中①理，CDF EDF △≌△，∴CDF EDF ∠=∠，CFD EFD ∠=∠，∵//CF DE ，∴CFD EDF ∠=∠，∴CFD CDF ∠=∠，EDF EFD ∠=∠，∴CF CD =，ED EF =，∴四边形CDEF 为菱形，∵ACD △为等边三角形，∴2AC CD AD BD ====，菱形的边长也为2，由题意，2HDG α∠=，13022DEB DBE ADE α∠=∠=∠=︒+，∵30DBG ∠=︒，∴2EBG α∠=，即：HDG EBG ∠=∠，∴EBG HDG △△∽，∵在菱形CDEF 中，HFC HDG △△∽，∴EBG HFC △△∽，∴BE BG FH FC=，如图，作DK CG ⊥，∵30DCK ∠=︒，∴60CDK ∠=︒，60KDG α∠=-︒，∵2CD =，∴1DK =，CK =在Rt KDG △中，()tan tan 60GK KDG m DKα=∠=-︒=，∴GK m =，∴CG m =，在Rt ABC 中，BC ==∴BG BC CG m m =-==，∵2CF CD ==，∴BE BG FH FC ==．【点拨】本题考查相似三角形的判定与性质，特殊平行四边形的判定与性质，以及锐角三角函数等，综合性较强，掌握基本图形的性质，灵活运用相似三角形以及锐角三角函数是解题关键．8．（1）30°；（2）①见解析；②CD BE =；见解析；（3）()AC k BD BE =+，见解析【解析】【分析】（1）先根据题意得出△ABC 是等边三角形，再利用三角形的外角计算即可（2）①按要求补全图即可②先根据已知条件证明△ABC 是等边三角形，再证明AEB ADC △≌△，即可得出CD BE=（3）先证明AC BC AD DE=，再证明ACB ADE △∽△，得出BAC EAD ∠=∠，从而证明AEB ADC △≌△，得出BD BE BC +=，从而证明()AC k BD BE =+【详解】解：（1）∵AB AC =，60C ∠=°∴△ABC 是等边三角形∴∠B =60°∵点D 关于直线AB 的对称点为点E∴AB ⊥DE ，∴BDE ∠=30︒故答案为：30︒；（2）①补全图如图2所示；②CD 与BE 的数量关系为：CD BE =；证明：∵AB AC =，60BAC ∠=︒．∴ABC 为正三角形，又∵AD 绕点A 顺时针旋转60︒，∴AD AE =，60EAD ∠=︒，∵60BAD DAC ∠+∠=︒，60BAD BAE ∠+∠=︒，∴BAE DAC ∠=∠，∴AEB ADC △≌△，∴CD BE =．（3）连接AE ．∵AB AD k BC DE ==，AB AC =，∴AC AD BC DE =．∴AC BC AD DE=．又∵ADE C ∠=∠，∴ACB ADE △∽△，∴BAC EAD ∠=∠．∵AB AC =，∴AE AD =，∴BAD DAC BAD BAE ∠+∠=∠+∠，∴DAC BAE ∠=∠，∴AEB ADC △≌△，CD BE =．∵BD DC BC +=，∴BD BE BC +=．又∵AC k BC=，∴()AC k BD BE =+．【点拨】本题考查相似三角形的证明及性质、全等三角形的证明及性质、三角形的外角、轴对称，熟练进行角的转换是解题的关键，相似三角形的证明是重点9．（1）正方形；（2）MC ME '=，见解析；（3）25【解析】【分析】（1）有一组邻边相等且一个角为直角的平行四边形是正方形；（2）连接EC '，由（1）问的结论可知，90AD BC EAC B '=∠=∠=︒，，又因为矩形纸片ABCD 沿过点E 的直线折叠，可知折叠前后对应角以及对应边相等，有B B '∠=∠，B C BC ''=，90AE B C EAC B ''''=∠=∠=︒，，可以证明Rt EC A ' 和Rt C EB '' 全等，得到C EA EC B '''∠=∠，从而有MC ME '=；（3）由Rt EC A Rt C EB ''' ≌，有AC B E ''=；由折叠知，AC BE '=，可以计算出()8cm AB =；用勾股定理计算出DF 的长度，再证明DNF ENG ∽得出等量关系，从而得到:DN EN 的值．【详解】（1）解：∵ABCD 是平行四边形，∴'////AD BC EA ，'//AE DA ∴四边形'AEA D 是平行四边形∵矩形纸片ABCD 沿过点D 的直线折叠，使点A 落在CD 上的点A '处∴'AED A ED≌∴'AE A E=∵90A ∠=∴四边形AEA D '的形状是正方形故最后答案为：四边形AEA D '的形状是正方形；（2）MC ME'=理由如下：如图，连接EC '，由（1）知：AD AE=∵四边形ABCD 是矩形，∴90AD BC EAC B '=∠=∠=︒，由折叠知：B C BC B B'''=∠=∠，∴90AE B C EAC B ''''=∠=∠=︒，。

4.4相似三角形［过关演练］（40分钟90分)1。

已知,那么的值为（B）A.B。

C.D。

【解析】因为,设a=2k，则b=3k,则原式=.2。

若△ABC∽△DEF,相似比为3∶2,则对应高的比为(A）A.3∶2B.3∶5 C。

9∶4 D.4∶9【解析】因为△ABC∽△DEF,根据相似三角形的性质“相似三角形对应高之比等于相似比”可得对应高的比为3∶2.3.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D，E,F.已知AB=1,BC=3,DE=2，则EF的长为(C)A。

4 B。

5 C.6 D。

8【解析】∵AD∥BE∥CF，∴,∵AB=1,BC=3，DE=2，∴,解得EF=6.4。

如图,以点O为位似中心，将△ABC放大得到△DEF.若AD=OA，则△ABC与△DEF的面积之比为（B）A.1∶2 B。

1∶4C.1∶5D.1∶6【解析】∵以点O为位似中心，将△ABC放大得到△DEF，AD=OA，∴OA∶OD=1∶2，∴△ABC 与△DEF的面积之比为1∶4.5。

(2018·哈尔滨）如图，在△ABC中,点D在BC边上,连接AD，点G在线段AD上,GE∥BD，且交AB于点E，GF∥AC,且交CD于点F,则下列结论一定正确的是(D）A。

B。

C.D。

【解析】∵GE∥BD，GF∥AC，∴△AEG∽△ABD，△DFG∽△DCA,∴,∴.6.（2018·浙江绍兴)学校门口的栏杆如图所示，栏杆从水平位置BD绕点O旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B，D,AO=4 m，AB=1。

6 m，CO=1 m，则栏杆C端应下降的垂直距离CD为（C）A.0.2 mB.0。

3 mC.0.4 mD.0.5 m【解析】∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°，又∵∠AOB=∠COD,∴△ABO∽△CDO,则，∵AO=4 m,AB=1。

6 m，CO=1 m，∴,解得CD=0.4 m.7。

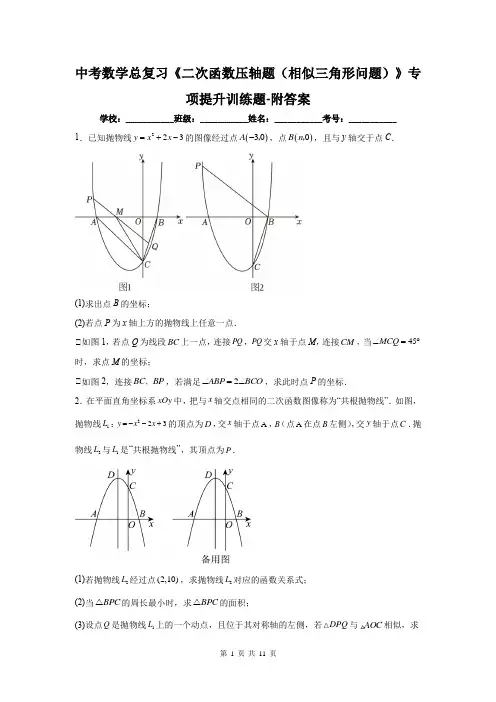
中考数学总复习《二次函数压轴题（相似三角形问题）》专项提升训练题-附答案学校：___________班级：___________姓名：___________考号：___________1．已知抛物线223y x x =+-的图像经过点()30A -，，点()0B n ，，且与y 轴交于点C ．(1)求出点B 的坐标；(2)若点P 为x 轴上方的抛物线上任意一点．①如图1，若点Q 为线段BC 上一点，连接PQ ，PQ 交x 轴于点M ，连接CM ，当45MCQ ∠=︒时，求点M 的坐标；①如图2，连接BC BP 、，若满足2ABP BCO ∠=∠，求此时点P 的坐标．2．在平面直角坐标系xOy 中，把与x 轴交点相同的二次函数图像称为“共根抛物线”．如图，抛物线1L ：223y x x =--+的顶点为D ，交x 轴于点A ，B （点A 在点B 左侧），交y 轴于点C ．抛物线2L 与1L 是“共根抛物线”，其顶点为P ．(1)若抛物线2L 经过点(2,10)，求抛物线2L 对应的函数关系式； (2)当BPC △的周长最小时，求BPC △的面积；(3)设点Q 是抛物线1L 上的一个动点，且位于其对称轴的左侧，若DPQ 与AOC 相似，求其“共根抛物线”2L 的顶点P 的坐标．3．如图：抛物线244y ax ax =-+与x 轴交于A 、B 两点，点A 的坐标是（1，0），与y 轴交于点C ．（1）求抛物线的对称轴和点B 的坐标；（2）过点C 作CP ①对称轴于点P ，连接BC 交对称轴于点D ，连接AC 、BP ，且①BPD =①BCP ，求抛物线的解析式；（3）在（2）的条件下，设抛物线的顶点为G ，连接BG 、CG 、求①BCG 的面积．4．如图，在平面直角坐标系中，抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点C ．若线段OA OB OC 、、的长满足2OC OA OB =⋅，则这样的抛物线称为“黄金”抛物线，如图，抛物线22(0)y ax bx a =++≠为“黄金”抛物线，其与x 轴交点为A ，B （其中B 在A 的右侧），与y 轴交于点C ．且4OA OB =；(1)求抛物线的解析式；(2)若P 为AC 上方抛物线上的动点，过点P 作PD AC ⊥，垂足为D ． ①连接PC ，当ACO CPD ∽△△时，求点P 的坐标． ①求PD 的最大值．5．抛物线y ＝ax 2﹣2x +c 经过点A (3，0)，点C (0，﹣3)，直线y ＝﹣x +b 经过点A ，交抛物线于点E ．抛物线的对称轴交AE 于点B ，交x 轴于点D ，交直线AC 于点F ．(1)求抛物线的解析式；(2)如图①，点P为直线AC下方抛物线上的点，连接P A，PC，△BAF的面积记为S1，△P ACS1时．求点P的横坐标；的面积记为S2，当S2＝38(3)如图①，连接CD，点Q为平面内直线AE下方的点，以点Q，A，E为顶点的三角形与△CDF 相似时（AE与CD不是对应边），请直接写出符合条件的点Q的坐标．A-、B两点，交y轴于C；直线AD交抛物线于第6．抛物线224=--交x轴于(2,0)y ax ax一象限内点D，且D的横坐标为5(1)求抛物线解析式；S=，求点E的坐标；(2)点E为直线AD下方抛物线上一动点，且21ADE∠+∠=∠，若存在，请求出此时点P的坐标；(3)抛物线上是否存在点P，使PCO DAO CBO若不存在，请说明理由．7．如图所示，平面直角坐标系中，二次函数y＝a（x+2k）（x﹣k）图象与x轴交于A、B两点，抛物线对称轴为直线x＝﹣2；(1)求k的值；(2)点C为抛物线上一点，连接BC、AC，作CD①x轴于D，当①BCA＝90°时，设CD长度为d，求d与a的函数关系式；(3)抛物线顶点为S，作S T垂直AB于T，点Q为第一象限抛物线上一点，连接AQ交S T于点P，过B作x轴的垂线交AQ延长线于点E，连接OE交BQ于点G，过O作OE的垂线交AQ于点F，若OF＝OG，tan①ABQ＝2时，连接S Q，求证：S Q＝S P．8．如图，抛物线y= x2+bx+c的顶点D坐标为（1，4），且与x轴相交于A，B两点(点A 在点B的左侧)，与y轴相交于点C，点E在x轴上方且在对称轴左侧的抛物线上运动，点F在抛物线上并且和点E关于抛物线的对称轴对称，作矩形EFGH，其中点G，H都在x轴上．(1)求抛物线解析式；(2)设点F横坐标为m①用含有m的代数式表示点E的横坐标为________（直接填空）；①当矩形EFGH为正方形时，求点G的坐标；①连接AD，当EG与AD垂直时，求点G的坐标；(3)过顶点D作DM①x轴于点M，过点F作FP①AD于点P，直接写出△DFP与△DAM相似时，点F的坐标．9．如图，抛物线28y ax bx =++与x 轴交于()2,0A -和点()8,0B ，与y 轴交于点C ，顶点为D ，连接AC ，BC 和BC 与抛物线的对称轴l 交于点E ．(1)求该抛物线的函数表达式；(2)点P 是第一象限内抛物线上的动点，连接PB ，PC ，设四边形PBOC 和AOC 的面积分别为PBOC S 四边形和AOCS，记AOC PBOC S S S =-△四边形，求S 最大值点P 的坐标及S 的最大值；(3)点N 是对称轴l 右侧抛物线上的动点，在射线ED 上是否存在点M ，使得以点M ，N 和E 为顶点的三角形与BOC 相似？若存在，求点M 的坐标；若不存在，请说明理由． 10．如图1，抛物线()20y ax bx c a =++≠与直线443y x =-+的交点分别位于x 轴、y 轴上的AB 两点，与x 轴的另一交点为()2,0C -．(1)求抛物线的解析式；(2)如图2，连接BC ，点P为AB 上方抛物线上一动点，过点P 作PQ BC ∥交AB 于点Q ，过点P 作PR x ⊥轴交AB 于点R ，求①PQR 周长最大值及此时点P 的坐标；(3)在（2）问条件下，当①PQR 面积最大时，将①PQR 绕点R 顺时针旋转n °（090n <<），当旋转过程中，PR AB ⊥时，记此时三角形为111PQ R ∆，再将111PQ R ∆沿直线AB 进行翻折得到222P Q R ∆，将222P Q R ∆沿直线AB 进行平移，在平移过程中，若点2P 恰好在抛物线上，记此时的三角形为333PQ R ∆，请直接写出此时3P 的坐标．11．如图，在平面直角坐标系中，点O 为坐标原点，抛物线22y ax x c =-+与x 轴交于点(1,0)A ，点(3,0)B -，与y 轴交于点C ，连接BC ，点P 在第二象限的抛物线上，连接PC 和PO ，线段PO 交线段BC 于点E ．(1)求抛物线的表达式；(2)若PCE 的面积为1S ，OCE △的面积为2S ，当1223S S =时，求点P 的坐标； (3)已知点C 关于抛物线对称轴的对称点为点N ，连接BN ，点H 在x 轴上，当HCB NBC ∠=∠时①求满足条件的所有点H 的坐标①当点H 在线段AB 上时，点Q 是平面直角坐标系内一点，保持1QH =，连接BQ ，将线段BQ 绕着点Q 顺时针旋转90°，得到线段QM ，连接MH ，请直接写出线段MH 的取值范围．12．如图，抛物线2y x bx c =++与x 轴交于A （10-，），B （4，0），过点A 的直线=1y x --与该抛物线交于点C ，点P 是该抛物线上不与A ，B 重合的动点，过点P 作PD ①x 轴于点D ，交直线AC 于点E ．(1)求抛物线的解析式；(2)当点P在直线AC的下方，且2PE DE=时，求点P的坐标；(3)当直线PD为1x=时，在直线PD上是否存在点Q，使①ECQ与①EDA相似？若存在，请求出点Q坐标；若不存在，请说明你的理由．13．已知抛物线228y x x=-++与x轴交于点A、B（点A在点B的左侧），与y轴交于点C．(1)求点B、C的坐标；(2)连接BC，若BC的中点为点D，请你求经过点A和点D的直线表达式；(3)设点C'与点C关于该抛物线的对称轴对称．在y轴上是否存在点P，使PCC'△与POB 相似，若存在，求出所有P点坐标；若不存在，请说明理由．14．如图1，平面直角坐标系xOy中，直线y＝－12x－2与x轴交于点A，与y轴交于点C．抛物线y＝14x2＋bx＋c经过点A、点C，且与x轴交于另一点B，连接BC．(1)求抛物线的解析式； (2)点P 是抛物线上一动点．①当点P 在直线AC 下方的抛物线上运动时，如图2，连接AP ，CP ．求四边形ABCP 面积的最大值及此时点P 的坐标；①当点P 在x 轴上方的抛物线上运动时，过点P 作PM ①x 轴于点M ，连接BP ．是否存在点P ，使①PMB 与①AOC 相似？若存在，请直接写出点P 的坐标；若不存在，请说明理由． 15．如图，在平面直角坐标系中，已知抛物线顶点A 的坐标为()2,4-，且经过坐标原点，与x 轴负半轴交于点B ．(1)求抛物线的函数表达式并直接写出点B 的坐标；(2)过点A 作AC x ⊥轴于点C ，若点D 是y 轴左侧的抛物线上一个动点（点D 与点A 不重合），过点D 作DE x ⊥轴于点E ，连接AO ，DO ，当以A ，O ，C 为顶点的三角形与以D ，O ，E 为顶点的三角形相似时，求点D 的坐标；(3)在（2）的条件下，当点D 在第二象限时，在平面内存在一条直线，这条直线与抛物线在第二象限交于点F ，在第三象限交于点G ，且点A ，点B ，点D ，到直线FG 的距离都相等，请直接．．写出线段FG 的长． 参考答案：1．(1)()10B ， (2)①,302 ⎛⎫- ⎪⎝⎭M ；①155741, 6⎛⎫- ⎪⎝⎭P2．(1)抛物线2L 对应的函数关系式为2246y x x =+-； (2)2BPCS=；(3)点P 的坐标为(1,3)P -或(1,2)-．3．（1）B （3，0）；（2）2343333y x x =-+-；（3）3 4．(1)213222y x x =--+(2)①P 坐标为(3,2)-；①PD 的最大值为4555．(1)y ＝x 2﹣2x ﹣3 (2)P 点的横坐标为352+或352 (3)Q 点坐标为(﹣7，5)或(﹣12，5)或(3，﹣10)或(3，﹣5) 6．(1)2142y x x =-- (2)191,2E ⎛⎫- ⎪⎝⎭；E 2（2，-4）(3)存在，（8，20）7．(1)k ＝4 (2)1d a=-8．(1)223y x x =-++ (2)①2m -；①G 点坐标为()5,0；①G 点坐标为（1172+，0）(3)F 点坐标为（73，209）9．(1)21382y x x =-++(2)()4,12P ，最大值为56(3)存在 ()3,8 ()3,515+ ()3,1110．(1)222433y x x =-++(2)PQR 周长最大值为459520+，此时点37(,)22P(3)3326146(,)223P +--或326146(,)223--+11．(1)y =-x 2-2x +3；(2)点P 的坐标是（-2，3）或（-1，4）；(3)①点H 的坐标是（-1，0）或（-9，0）；①2-2≤MH ≤2+2．12．(1)234y x x =-- (2)(1，-6)(3)存在，点Q 的坐标为（1，-4）或（1，-6）13．(1)(4,0)B ；(0,8)C (2)2y x =+(3)存在，1(0,16)P 或2160,3P ⎛⎫⎪⎝⎭或3(0,422)P +或4(0,422)P -或5(0,426)P +或6(0,426)P -14．(1)211242y x x =+- (2)①四边形ABCP 面积的最大值为8，此时点P 为（－2，－2）；①存在符合条件的点P ，点P 坐标为（－6，4）或（－12，28）或（4，4）第 11 页 共 11 页 15．(1)24y x x =--，点B （-4，0）；(2)()6,12--或99,24⎛⎫-- ⎪⎝⎭或77,24⎛⎫- ⎪⎝⎭． (3)553。

2023年安徽中考总复习　与相似三角形有关的模型（１）平行线型基本图形图形演化一图形演化二２０１８．２３考查说明：ＤＥ∥ＢＣ．结论：△ＡＤＥ∽△ＡＢＣ２０１７．２３考查说明：ＤＥ∥ＡＢ．结论：△ＤＥＣ∽△ＢＡＣ说明：构造平行相似；背景：平行四边形ＡＢＣＤ中，点Ｅ，Ｇ分别在ＢＣ，ＣＤ上，ＡＥ交ＢＧ于点Ｆ；辅助线：过点Ｅ作ＥＨ∥ＣＤ交ＢＧ于点Ｈ；结论：△ＢＥＨ∽△ＢＣＧ，△ＥＨＦ∽△ＡＢＦ（２）共角型（不含平行线和直角）基本图形图形演化一图形演化二说明：∠ＡＤＥ＝∠Ｂ．结论：△ＡＤＥ∽△ＡＢＣ２０２１．２３考查２０１７．２３考查２０１２．２３考查说明：∠ＡＣＤ＝∠Ｂ．结论：△ＡＣＤ∽△ＡＢＣ说明：已知∠ＥＡＢ＝∠ＣＡＤ，∠Ｄ＝∠Ｂ，由共夹角相等可知∠ＢＡＣ＝∠ＤＡＥ．结论：△ＡＤＥ∽△ＡＢＣ（３）直角三角形斜边高线型基本图形图形演化一图形演化二说明：在△ＡＢＣ中，∠ＢＡＣ＝９０°，ＡＤ⊥ＢＣ于点Ｄ．结论：△ＡＢＤ∽△ＣＡＤ∽△ＣＢＡ，ＡＤ２＝ＢＤ·ＣＤ，ＡＢ２＝ＢＤ·ＢＣ，ＡＣ２＝ＣＤ·ＢＣ说明：ＤＥ⊥ＢＣ交ＡＣ于点Ｅ．结论：△ＣＤＥ∽△ＣＡＢ，ＤＣＡＣ＝ＣＥＣＢ＝ＤＥＡＢ说明：在矩形ＡＢＣＤ中，ＡＥ⊥ＢＤ于点Ｅ，ＡＥ的延长线交ＢＣ于点Ｆ．结论：图中与△ＢＥＦ相似（除过本身）的三角形有５个（４）一线三等角型图形一图形二图形三说明：点Ｅ在线段ＢＣ上，∠Ｂ＝∠Ｃ＝∠ＡＥＤ，由∠Ｂ＋∠ＢＡＥ＝∠ＡＥＤ＋∠ＥＣＤ，得∠ＢＡＥ＝∠ＣＥＤ．结论：△ＡＢＥ∽△ＥＣＤ，ＡＢＥＣ＝ＢＥＣＤ＝ＡＥＥＤ说明：在矩形ＡＢＣＤ中，ＡＥ⊥ＥＦ，由互余角相等可得∠ＢＡＥ＝∠ＣＥＦ，∠ＡＥＢ＝∠ＥＦＣ．结论：△ＡＢＥ∽△ＥＣＦ，ＡＢＥＣ＝ＢＥＣＦ＝ＡＥＥＦ说明：在等腰△ＡＢＣ中，ＡＢ＝ＡＣ，点Ｄ在ＢＣ上，且∠ＡＤＥ＝∠Ｂ，由三角形内外角关系可知，∠ＡＤＣ＝∠Ｂ＋∠ＢＡＤ＝∠ＡＤＥ＋∠ＣＤＥ．结论：∠ＢＡＤ＝∠ＣＤＥ，得△ＡＢＤ∽△ＤＣＥ，ＡＢＤＣ＝ＡＤＤＥ＝ＢＤＣＥ８８（５）旋转相似型图形一图形二图形三２０１５．２３考查说明：在△ＡＢＣ中，ＡＢ＝ｋＡＣ，△ＡＤＥ由△ＡＢＣ旋转得到．结论：△ＡＢＤ∽△ＡＣＥ，ＢＤＣＥ＝ＡＢＡＣ＝ＡＤＡＥ＝ｋ２０１５．２３考查说明：在等腰Ｒｔ△ＡＢＣ中，∠ＡＣＢ＝９０°，在等腰Ｒｔ△ＡＤＥ中，∠ＡＥＤ＝９０°．结论：△ＡＣＥ∽△ＡＢＤ，ＣＥＢＤ＝ＡＣＡＢ＝槡２２，直线ＣＥ与ＢＤ的夹角为４５°说明：∠ＡＣＢ＝９０°，∠ＡＢＣ＝３０°，ＤＥ是中位线，△Ｄ′ＢＥ′由△ＤＢＥ旋转得到．结论：△ＡＤ′Ｂ∽△ＣＥ′Ｂ，ＡＤ′ＣＥ′＝ＡＢＣＢ＝ＢＤ′ＢＥ′＝槡２３３，直线ＣＥ′与ＡＤ′的夹角为３０°综合集训１．如图，在矩形ＡＢＣＤ中，ＡＢ＝２，ＢＣ＝３，若点Ｅ是边ＢＣ的中点，连接ＡＥ，过点Ｄ作ＤＦ⊥ＡＥ交ＡＥ于点Ｆ，求ＤＦ的长．第１题图解：在矩形ＡＢＣＤ中，ＡＢ＝２，ＢＣ＝３，∠ＢＡＤ＝∠Ｂ＝９０°，∵点Ｅ是边ＢＣ的中点，∴ＢＥ＝１２ＢＣ＝１．５，∴ＡＥ＝ＡＢ２＋ＢＥ槡２＝２．５．∵ＤＦ⊥ＡＥ，∴∠ＢＡＥ＋∠ＤＡＦ＝∠ＤＡＦ＋∠ＦＤＡ＝９０°，∴∠ＢＡＥ＝∠ＦＤＡ．∵∠Ｂ＝∠ＡＦＤ＝９０°，∴△ＡＢＥ∽△ＤＦＡ，∴ＤＦＡＢ＝ＡＤＥＡ，∴ＤＦ２＝３２．５，∴ＤＦ＝２．４．２．如图，在矩形ＡＢＣＤ中，Ｅ为ＢＣ上一点．若ＡＢ＝１２，ＡＤ＝２５，ＢＥ＝１６，求证：△ＡＢＥ∽△ＥＣＤ．第２题图证明：在矩形ＡＢＣＤ中，ＡＤ＝ＢＣ＝２５，ＡＢ＝ＣＤ＝１２，∠Ｂ＝∠Ｃ＝９０°．∵ＢＥ＝１６，∴ＣＥ＝２５－１６＝９．∴ＡＢＥＣ＝１２９＝４３，ＢＥＣＤ＝１６１２＝４３，∴ＡＢＥＣ＝ＢＥＣＤ．又∵∠Ｂ＝∠Ｃ＝９０°，∴△ＡＢＥ∽△ＥＣＤ．３．如图，在锐角△ＡＢＣ中，ＡＢ＝４，ＢＣ＝５，将△ＡＢＣ绕点Ｂ按逆时针方向旋转，得到△Ａ１ＢＣ１，连接ＡＡ１，ＣＣ１，若△ＡＢＡ１的面积为４，求△ＣＢＣ１的面积．第３题图解：由旋转的性质可得∠Ａ１ＢＣ１＝∠ＡＢＣ，ＢＡ＝ＢＡ１，ＢＣ＝ＢＣ１，∴ＢＡＢＣ＝ＢＡ１ＢＣ１，∠ＡＢＣ＋∠ＡＢＣ１＝∠Ａ１ＢＣ１＋∠ＡＢＣ１，∴∠ＡＢＡ１＝∠ＣＢＣ１，∴△ＡＢＡ１∽△ＣＢＣ１，∴Ｓ△ＡＢＡＳ△ＣＢＣ＝（ＡＢＢＣ）２＝（４５）２＝１６２５，∵Ｓ△ＡＢＡ＝４，∴Ｓ△ＣＢＣ＝２５４．９８４．如图，在锐角△ＯＡＢ中，点Ｍ，Ｎ分别在边ＯＢ，ＯＡ上，ＯＧ⊥ＡＢ于点Ｇ，ＯＨ⊥ＭＮ于点Ｈ，∠ＮＯＨ＝∠ＯＡＢ．（１）求证：△ＯＭＮ∽△ＧＯＢ；（２）若ＯＭ＝３，ＯＡ＝７，求ＯＨＯＧ的值．第４题图（１）证明：在△ＯＨＮ和△ＯＧＢ中，∵∠ＯＨＮ＝∠ＯＧＢ＝９０°，∠ＮＯＨ＝∠ＢＯＧ，∴△ＯＨＮ∽△ＯＧＢ，∴∠ＯＮＨ＝∠Ｂ，∵∠ＡＯＢ＝∠ＭＯＮ，∴△ＯＭＮ∽△ＯＡＢ；（２）解：由（１）得△ＯＭＮ∽△ＯＡＢ，∵ＯＭ＝３，ＯＡ＝７，∴ＯＨＯＧ＝ＯＭＯＡ＝３７．５．如图①，在等边△ＡＢＣ中，点Ｄ是边ＢＣ上的动点（不与点Ｂ、Ｃ重合），点Ｅ、Ｆ分别在ＡＢ和ＡＣ边上，且∠ＥＤＦ＝６０°．（１）如图①，求证：△ＢＤＥ∽△ＣＦＤ；（２）若点Ｄ移至ＢＣ的中点，如图②，求证：ＦＤ平分∠ＥＦＣ．第５题图证明：（１）∵△ＡＢＣ是等边三角形∴∠Ｂ＝∠Ｃ＝６０°，∵∠ＢＥＤ＋∠Ｂ＝∠ＥＤＦ＋∠ＦＤＣ．∠ＥＤＦ＝６０°，∴∠ＢＥＤ＝∠ＣＤＦ，∴△ＢＤＥ∽△ＣＦＤ；（２）由（１）知△ＢＤＥ∽△ＣＦＤ，∴ＢＤＣＦ＝ＤＥＤＦ，∵ＢＤ＝ＣＤ，∴ＣＤＣＦ＝ＤＥＤＦ，∵∠ＥＤＦ＝∠Ｃ＝６０°，∴△ＤＦＥ∽△ＣＦＤ，∴∠ＥＦＤ＝∠ＣＦＤ，∴ＦＤ平分∠ＣＦＥ．６．如图，在平行四边形ＡＢＣＤ中，点Ｅ是ＡＣ上一点，射线ＢＥ与ＣＤ的延长线交于点Ｐ，与边ＡＤ交于点Ｆ，连接ＦＣ．（１）若∠ＡＢＦ＝∠ＡＣＦ，求证：ＣＥ２＝ＥＦ·ＥＰ；（２）若点Ｄ是ＣＰ的中点，ＢＥ＝２槡３，求ＥＦ的长．第６题图（１）证明：∵四边形ＡＢＣＤ是平行四边形，∴ＡＢ∥ＣＤ，∴∠ＡＢＦ＝∠Ｐ，∵∠ＡＢＦ＝∠ＡＣＦ，∴∠ＡＣＦ＝∠Ｐ，∵∠ＣＥＦ＝∠ＰＥＣ，∴△ＣＥＦ∽△ＰＥＣ，∴ＣＥＰＥ＝ＥＦＣＥ，即ＣＥ２＝ＥＦ·ＥＰ；（２）解：∵四边形ＡＢＣＤ是平行四边形，∴ＡＢ∥ＣＤ，ＡＢ＝ＣＤ，ＡＤ∥ＢＣ，∴∠ＡＢＦ＝∠Ｐ，∵∠ＡＥＢ＝∠ＣＥＰ，∴△ＢＥＡ∽△ＰＥＣ，∴ＢＥＰＥ＝ＡＢＣＰ，∵点Ｄ是ＣＰ的中点，∴ＣＰ＝２ＣＤ＝２ＡＢ，∴２槡３ＰＥ＝１２，解得ＰＥ＝４槡３，∴ＰＢ＝６槡３．∵ＡＢ＝ＣＤ＝ＤＰ，∠ＢＡＦ＝∠ＰＤＦ，∠ＡＦＢ＝∠ＤＦＰ，∴△ＡＢＦ≌△ＤＰＦ，∴ＢＦ＝ＰＦ，∴ＢＦ＝１２ＰＢ＝３槡３，∴ＥＦ＝ＢＦ－ＢＥ＝槡３．０９。

中考数学总复习《相似三角形综合压轴题》专项提升练习(附答案）学校:___________班级：___________姓名：___________考号：___________1．三个等角的顶点在同一条直线上，称一线三等角模型（角度有锐角、直角、钝角，若为直角，则又称一线三垂直模型）．解决此模型问题的一般方法是利用三等角关系找全等或相似三角形所需角的相等条件，利用全等或相似三角形解决问题．【证明体验】如图1，在四边形ABCD 中点P 为AB 上一点90DPC A B ∠=∠=∠=︒，求证：AD BC AP BP ⋅=⋅． 【思考探究】（2）如图2，在四边形ABCD 中点P 为AB 上一点，当DPC A B β∠=∠=∠=时，上述结论是否依然成立？说明理由． 【拓展延伸】（3）请利用（1）（2）获得的经验解决问题：如图3，在ABC 中22AB =45B ∠=︒以点A 为直角顶点作等腰Rt ADE △，点D 在BC 上，点E 在AC 上，点F 在BC 上，且45EFD ∠=︒，若5CE =CD 的长．2．综合实践问题背景：借助三角形的中位线可构造一组相似三角形，若将它们绕公共顶点旋转，对应顶点连线的长度存在特殊的数量关系，数学小组对此进行了研究．如图1，在ABC 中90,4B AB BC ∠=︒==分别取AB ，AC 的中点D ，E ，作ADE ．如图2所示，将ADE 绕点A 逆时针旋转，连接BD ，CE ．(1)探究发现旋转过程中线段BD 和CE 的长度存在怎样的数量关系？写出你的猜想，并证明． (2)性质应用如图3，当DE 所在直线首次经过点B 时，求CE 的长． (3)延伸思考如图4，在Rt ABC △中90,8,6ABC AB BC ∠=︒==，分别取AB ，BC 的中点D ，E ．作BDE ，将BDE 绕点B 逆时针旋转，连接AD ，CE ．当边AB 平分线段DE 时，求tan ECB ∠的值．3．如图，M 为线段AB 的中点，AE 与BD 交于点C ，DME A B α∠=∠=∠=且DM 交AC 于F ，ME 交BC 于G ．(1)写出图中两对相似三角形；(2)连接FG ，如果45α=︒，42AB =3AF =，求FG 的长．4．如图，在ABC 中6cm AB =，12cm BC =和90B ．点P 从点A 开始沿AB 边向点B 以1cm /s 的速度移动，点Q 从点B 开始沿BC 边向点C 以2cm /s 的速度移动，如果P 、Q 分别从A 、B 同时出发，设移动时间为()s t ．(1)当2t =时，求PBQ 的面积； (2)当t 为多少时，PBQ 的面积是28cm ？ (3)当t 为多少时，PBQ 与ABC 是相似三角形？5．下面是小新同学在“矩形折叠中的相似三角形”主题下设计的问题，请你解答．如图，已知在矩形ABCD 中点E 为边AB 上一点（不与点A 、点B 重合），先将矩形ABCD 沿CE 折叠，使点B 落在点F 处，CF 交AD 于点H ．(1)观察发现：写出图1中一个与AEG △相似的三角形：______．（写出一个即可）(2)迁移探究：如图2，若4AB =，6BC =当CF 与AD 的交点H 恰好是AD 的中点时，求阴影部分的面积． (3)如图③，当点F 落在边AD 上时，延长EF ，与FCD ∠的角平分线交于点M ，CM 交AD 于点N ，当FN AF ND =+时，请直接写出ABBC的值．6．【阅读】如图1，若ABD ACE ∽，且点B 、D 、C 在同一直线上，则我们把ABD △与ACE △称为旋转相似三角形．(1)【理解】如图2，ABC 和ADE 是等边三角形，点D 在边BC 上，连接CE ．求证：ABD △与ACE △是旋转相似三角形．(2)【应用】如图3，ABD △与ACE △是旋转相似三角形AD CE ，求证：③ABC ADE △△∽；③AC DE =；(3)【拓展】如图4，AC 是四边形ABCD 的对角线90,D B ACD ∠=︒∠=∠，25,20BC AC ==和16AD =，试在边BC 上确定一点E ，使得四边形AECD 是矩形，并说明理由．7．综合与实践如图1，已知纸片Rt ABC △中90BAC ∠=︒，AD 为斜边BC 上的高（AD BC ⊥于点D ）． 观察发现（1）请直接写出图中的一组相似三角形．（写出一组即可）实践操作第一步：如图2，将图1中的三角形纸片沿BE 折叠（点E 为AC 上一点），使点A 落在BC 边上的点F 处； 第二步：BE 与AD 交于点G 连接GF ，然后将纸片展平． 猜想探究（2）猜想四边形AEFG 是哪种特殊的四边形，并证明猜想． （3）探究线段GF ，BE ，GE 之间的数量关系，并说明理由．8．如图1，已知AD 是ABC 的角平分线，可证AB BDAC CD=．证明思路是如图2，过点C 作CE AB ∥，交AD 的延长线于点E ，构造相似三角形来证明AB BDAC CD=．(1)利用图2证明AB BDAC CD=； (2)如图3，在Rt ABC △中90BAC ∠=︒，D 是边BC 上一点．连接AD ，将ACD 沿AD 所在直线折叠，点C 恰好落在边AB 上的E 点处．若1AC =，AB=2，求DE 的长．9．【教材原题】如图③，在ABC 中DE BC ∥，且3AD =，2DB =图中的相似三角形是__________，它们的相似比为__________ ；【改编】将图③中的ADE 绕点A 按逆时针方向旋转到如图③所示的位置，连接BD 、CE ．求证：ABD ACE ∽△△；【应用】如图③，在ABC 和ADE 中90BAC DAE ∠=∠=︒，30ABC ADE ∠=∠=︒点D 在边BC 上，连接CE ，则ACE △与ABD △的面积比为__________．10．问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD 是ABC 的角平分线，可证AB BDAC CD=小慧的证明思路是：如图2，过点C 作CE AB ∥，交AD 的延长线于点E ，构造相似三角形来证明．(1)尝试证明：请参照小慧提供的思路，利用图2证明AB BDAC CD=； (2)基础训练：如图3，在Rt ABC △中90BAC ∠=︒，D 是边BC 上一点．连接AD ，将ACD 沿AD 所在直线折叠，点C 恰好落在边AB 上的E 点处．若1AC =，2AB =求DE 的长；(3)拓展升华：如图4，ABC 中6AB = ，AC=4，AD 为BAC ∠的角平分线，AD 的中垂线EF 交BC 延长线于F ，当3BD =时，求AF 的长．11．定义：两个相似三角形，如果它们的一组对应角有一个公共的顶点，那么把这两个三角形称为“阳似三角形”、如图1，在ABC 与AED △中ABC AED ∽△△．所以称ABC 与AED △为“阳似三角形”，连接EB DC ，，则DCEB为“阳似比”．(1)如图1，已知R ABC 与Rt AED △为“阳似三角形”，其中90CBA DEA ∠=∠=︒，当30BAC ∠=︒时，“阳似比”DCEB=______； (2)如图2，二次函数234y x x =-++交x 轴于点A 和B 两点，交y 轴于点C ．点M 为直线12y x =在第一象限上的一个动点，且OMB △与CNB 为“阳似三角形”，连接CM ③当点N 落在二次函数图象上时，求出线段OM 的长度； ③若32CN =34BM MC +的最小值．12．已知在Rt ABC △中90ACB ∠=︒，CD AB ⊥于点D ．(1)在图1中写出其中的两对相似三角形．(2)已知1BD =，DC=2，将CBD △绕着点D 按顺时针方向进行旋转得到C BD '，连接AC '，BC ． ③如图2，判断AC '与BC 之间的位置及数量关系，并证明； ③在旋转过程中当点A ，B ，C '在同一直线上时，求BC 的长．13．定义：若一个四边形能被其中一条对角线分割成两个相似三角形，则称这个四边形为“和谐四边形”，这条对角线叫“和谐线”．(1)如图1，在44⨯的正方形网格中有一个网格Rt ABC △和两个网格四边形ABCD 与四边形ABCE ，其中是被AC 分割成的“和谐四边形”的是______．(2)如图2，BD 平分ABC ∠，43BD =10BC =，四边形ABCD 是被BD 分割成的“和谐四边形”，求AB 长； (3)如图3，A 为抛物线24y x =-+的顶点，抛物线与x 轴交于点B ，C ．在线段AB 上有一个点P ，在射线BC 上有一个点Q ．P 、Q 5/秒，5个单位/秒的速度同时从B 出发分别沿BA ，BC 方向运动，设运动时间为t ，当其中一个点停止运动时，另一个点也随之停止运动．在第一象限的抛物线上是否存在点M ，使得四边形BQMP 是以PQ 为和谐线分割的“和谐四边形”，若存在，请直接写出t 的值；若不存在，请说明理由．14．【阅读理解】小白同学遇到这样一个问题：ABC 中D 是BC 的中点，E 是AB 上一点，延长DE 、CA 交于点F ，DE=EF ，AB=5，求AE 的长．小白的想法是：过点E 作EH BC ∥交AC 于H ，再通过相似三角形的性质得到AE 、BE 的比，从而得出AE 的长．请你按照小白的思路完成解答．【解决问题】请借助小白的解题经验，完成下面问题：ABC 中AD 平分BAC ∠交BC 于D ，E 为AB 边上一点，AE=AD ，H 、Q 为BC 上两点，CQ DH =和DQ mDH =，G 为AC 上一点，连接EQ 交HG 、AD 于F 、P ，180EFG EAD ∠+∠=︒猜想并验证EP 与GH的数量关系．15．【温故知新】（1）九（1）班数学兴趣小组认真探究了课本P 91第13题：如图1，在正方形ABCD 中E 是AD 的中点，F 是CD 上一点，且3CF DF =，图中有哪几对相似三角形?把它们表示出来，并说明理由．③小华很快找出ABE DEF △△∽，他的思路为：设正方形的边长4AB a =，则2,AE DE a DF a ===，利用“两边分别成比例且夹角相等的两个三角形相似”即可证明，请你结合小华的思路写出证明过程； ③小丽发现图中的相似三角形共有三对，而且可以借助于ABE 与DEF 中的比例线段来证明EBF △与它们都相似．请你根据小丽的发现证明其中的另一对三角形相似；【拓展创新】（2）如图2，在矩形ABCD 中E 为AD 的中点，EF EC ⊥交AB 于F ，连结FC ．()AB AE > ③求证：AEF ECF ∽△△；③设2,BC AB a ==，是否存在a 值，使得AEF △与BFC △相似．若存在，请求出a 的值；若不存在，请说明理由．参考答案：1．（3）52．(1)2BD CE =(2)6CE =(3)1tan 2ECB ∠=3．(1)DMG ③DBM △，EMF ③EAM △ (2)53FG =4．(1)8(2)2秒或4秒(3)当t 为3或1.2秒钟，使PBQ 与ABC 相似．5．(1)FHG △或DHC （写出一个即可）(2)阴影部分的面积是23 (3)AB BC 的值为357．（1）ABC DBA ∽ ABC CAD ∽ DBA DAC ∽（其中一个即可，答案不唯一）；（2）四边形AEFG是菱形，（3）212GF GE BE =⋅ 8． 5 9．【教材原题】ADE ABC △△∽，35【应用】13 10．5(3)611．23105337 12．(1)BCD ACD ∽ BCD BAC ∽△△ CAD BAC △∽△（任写两对即可）(2)③2AC BC '= AC BC '⊥ ③BC 2595+2595-+13．(1)四边形ABCE ；(2)10AB =或245； (3)1118t = 2881t = 1825t = 180169t =．14．阅读理解 54AE =；解决问题，猜想：12EP m GH m +=+． 15．③存在 3。

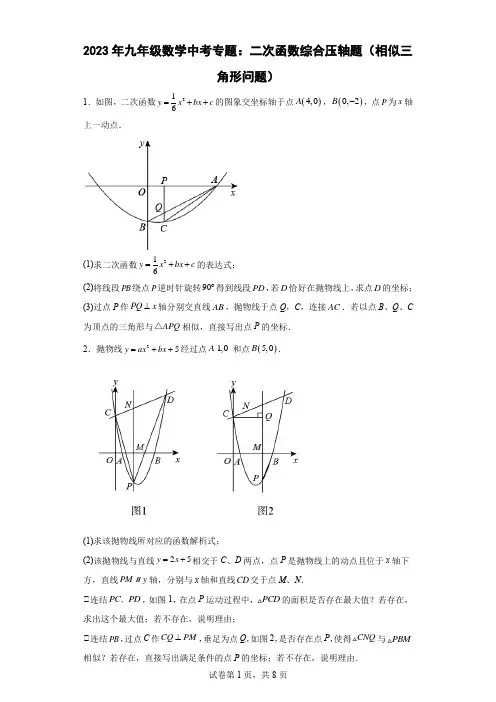
2023年九年级数学中考专题：二次函数综合压轴题（相似三角形问题）1．如图，二次函数216y x bx c =++的图象交坐标轴于点()4,0A ，()0,2B -，点P 为x 轴上一动点．(1)求二次函数216y x bx c =++的表达式； (2)将线段PB 绕点P 逆时针旋转90︒得到线段PD ，若D 恰好在抛物线上，求点D 的坐标； (3)过点P 作PQ x ⊥轴分别交直线AB ，抛物线于点Q ，C ，连接AC ．若以点B 、Q 、C 为顶点的三角形与APQ △相似，直接写出点P 的坐标． 2．抛物线25y ax bx =++经过点1,0A 和点()5,0B ．(1)求该抛物线所对应的函数解析式；(2)该抛物线与直线25y x =+相交于C 、D 两点，点P 是抛物线上的动点且位于x 轴下方，直线PM y ∥轴，分别与x 轴和直线CD 交于点M 、N ．①连结PC PD 、，如图1，在点P 运动过程中，PCD 的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；①连结PB ，过点C 作CQ PM ⊥，垂足为点Q ，如图2，是否存在点P ，使得CNQ 与PBM 相似？若存在，直接写出满足条件的点P 的坐标；若不存在，说明理由．3．已知抛物线24y ax ax b =-+与x 轴交于A ，B 两点，（A 在B 的左侧），与y 轴交于C ，若OB OC =，且03C （，）．(1)求抛物线的解析式；(2)设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标； (3)在抛物线上是否存在一点M ，过M 作MN x ⊥轴于N ，以A 、M 、N 为顶点的三角形与AOC ∆相似，若存在，求出所有符合条件的M 点坐标，若不存在，请说明理由． 4．如图．在平面直角坐标系中．抛物线212y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ．点A 的坐标为()1,0-，点C 的坐标为()0,2-．已知点(),0E m 是线段AB 上的动点（点E 不与点A ，B 重合）．过点E 作PE x ⊥轴交抛物线于点P ，交BC 于点F ．(1)求该抛物线的表达式；(2)若:1:2EF PF =，请求出m 的值；(3)是否存在这样的m ，使得BEP △与ABC 相似？若存在，求出此时m 的值；若不存在，请说明理由；(4)当点E 运动到抛物线对称轴上时，点M 是x 轴上一动点，点N 是抛物线上的动点，在运动过程中，是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，请直接写出点M 的坐标．5．如图，二次函数212y x bx c =-++图像交x 轴于点A ，B （A 在B 的左侧），与y 轴交于点(0,3)C ，CD y ⊥轴，交抛物线于另一点D ，且5CD =，P 为抛物线上一点，PE y轴，与x 轴交于E ，与BC ，CD 分别交于点F ，G ．(1)求二次函数解析式；(2)当P 在CD 上方时，是否存在点P ，使得以C ，P ，G 为顶点的三角形与FBE 相似，若存在，求出CPG △与FBE 的相似比，若不存在，说明理由．(3)点D 关于直线PC 的对称点为D ，当点D 落在抛物线的对称轴上时，此时点P 的坐标为________．6．如图，抛物线22y ax bx =++与x 轴交于点A ，B ，与y 轴交于点C ，已知A ，B 两点坐标分别是(1,0)A ，(4,0)B -，连接,AC BC ．(1)求抛物线的表达式；(2)将ABC ∆沿BC 所在直线折叠，得到DBC ∆，点A 的对应点D 是否落在抛物线的对称轴上？若点D 在对称轴上，请求出点D 的坐标；若点D 不在对称轴上，请说明理由；(3)若点P 是抛物线位于第二象限图象上的一动点，连接AP 交BC 于点Q ，连接BP ，BPQ ∆的面积记为1S ，ABQ ∆的面积记为2S ，求12S S 的值最大时点P 的坐标． 7．已知，二次函数23y ax bx =+-的图象与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于C 点，点A 的坐标为()1,0-，且OB OC =．(1)求二次函数的解析式；(2)当04x ≤≤时，求二次函数的最大值和最小值分别为多少？(3)设点C '与点C 关于该抛物线的对称轴对称．在y 轴上是否存在点P ，使PCC '△与POB 相似，且PC 与PO 是对应边？若存在，求出点P 的坐标；若不存在，请说明理由．8．已知菱形OABC 的边长为5，且点(34)A ，，点E 是线段BC 的中点，过点A ，E 的抛物线2y ax bx c =++与边AB 交于点D ，(1)求点E 的坐标；(2)连接DE ，将BDE △沿着DE 翻折痕．①当B 点的对应点B '恰好落在线段AC 上时，求点D 的坐标；①连接OB ，BB '，若BB D '△与BOC 相似，请直接写出此时抛物线二次项系数=a ______． 9．如图，抛物线22(0)y ax x c a =-+≠与x 轴交于A 、()3,0B 两点，与y 轴交于点()0,3C -，抛物线的顶点为D ．(1)求抛物线的解析式；(2)已知点M 是x 轴上的动点，过点M 作x 轴的垂线交抛物线于点G ，是否存在这样的点M ，使得以点A 、M 、G 为顶点的三角形与BCD △相似，若存在，请求出点M 的坐标；若不存在，请说明理由．(3)在直线BC 下方抛物线上一点P ，作PQ 垂直BC 于点Q ，连接CP ，当CPQ 中有一个角等于ACO ∠时，求点P 的坐标．10．如图，抛物线顶点D 在x 轴上，且经过(0,3)-和(4,3)-两点，抛物线与直线l 交于A 、B 两点．(1)直接写出抛物线解析式和D 点坐标；(2)如图1，若()03A ，-，且 94ABDS ＝，求直线l 解析式； (3)如图2，若90ADB ∠=︒，求证：直线l 经过定点，并求出定点坐标．11．如图1，已知抛物线2=23y x x --与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接BC ，点P 是线段BC 下方抛物线上一动点，过点P 作∥PE BC ，交x 轴于点E ，连接OP 交BC 于点F ．(1)直接写出点A ，B ，C 的坐标以及抛物线的对称轴； (2)当点P 在线段BC 下方抛物线上运动时，求BFPE取到最小值时点P 的坐标； (3)当点P 在y 轴右边抛物线上运动时，过点P 作PE 的垂线交抛物线对称轴于点G ，是否存在点P ，使以P 、E 、G 为顶点的三角形与①AOC 相似？若存在，来出点P 的坐标；若不存在，请说明理由．12．如图，抛物线212ax ax b =-+y 经过()1,0A -，32,2C ⎛⎫⎪⎝⎭两点，与x 轴交于另一点B ．(1)求此抛物线的解析式；(2)若抛物线的顶点为M ，点P 为线段OB 上一动点(不与点B 重合)，点Q 在线段MB 上移动，且2PM MQ MB =⋅，设线段OP x =，2MQ y =，求2y 与x 的函数关系式，并直接写出自变量x 的取值范围；并直接写出PM APPQ BQ-的值；(3)在同一平面直角坐标系中，两条直线x m =，x n =分别与抛物线交于点E ，G ，与（2）中的函数图象交于点F ，.H 问四边形EFHG 能否为平行四边形？若能，求m ，n 之间的数量关系；若不能，请说明理由．13．已知抛物线213222y x x =-++交x 轴于A 、B 两点，A 在B 的左边，交y 轴于点C ．(1)求抛物线顶点的坐标；(2)如图1，若10,2E ⎛⎫- ⎪⎝⎭，P 在抛物线上且在直线AE 上方，PQ AE ⊥于O ，求PQ 的最大值；(3)如图2，点(),3D a （32a <）在抛物线上，过A 作直线交抛物线于第四象限另一点F ，点M 在x 轴上，以M 、B 、D 为顶角的三角形与AFB △相似，求点M 的坐标． 14．如图，抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ，与y 轴交于点C ，联结AC 、BC ．(1)求该抛物线的表达式及顶点D 的坐标；(2)如果点P 在抛物线上，CB 平分ACP ∠，求点P 的坐标：(3)如果点Q 在抛物线的对称轴上，DBQ 与ABC 相似．求点Q 的坐标．15．如图，抛物线23y ax x c =-+与x 轴交于(4,0)A -，B 两点，与y 轴交于点(0,4)C ，点D 为x 轴上方抛物线上的动点，射线OD 交直线AC 于点E ，将射线OD 绕点O 逆时针旋转45︒得到射线OP ，OP 交直线AC 于点F ，连接DF ．(1)求抛物线的解析式； (2)当点D 在第二象限且34DE EO =时，求点D 的坐标； (3)当ODF △为直角三角形时，请直接写出点D 的坐标．16．如图①，抛物线与x 轴交于A ，B 两点，与y 轴交于点C （0，3），顶点为D （4，-1），对称轴与直线BC 交于点E ，与x 轴交于点F ．(1)求二次函数的解析式；(2)点M 在第一象限抛物线的对称轴上，若点C 在BM 的垂直平分线上，求点M 的坐标； (3)如图①，过点E 作对称轴的垂线在对称轴的右侧与抛物线交于点H ，x 轴上方的对称轴上是否存在一点P ，使以E ，H ，P 为顶点的三角形与EFB △相似，若存在，求出P点坐标；若不存在，请说明理由．17．如图，在平面直角坐标系xOy 中，已知抛物线2y ax x c =++经过()2,0A -，()0,4B 两点，直线3x =与x 轴交于点C ．(1)求a ，c 的值；(2)经过点O 的直线分别与线段AB ，直线3x =交于点D ，E ，且BDO △与OCE △的面积相等，求直线DE 的解析式；(3)P 是抛物线上位于第一象限的一个动点，在线段OC 和直线3x =上是否分别存在点F ，G ，使B ，F ，G ，P 为顶点的四边形是以BF 为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．18．如图1，抛物线2y ax bx c =++与x 轴交于A ，B （点A 在点B 左侧），与y 轴负半轴交于C ，且满足2OA OB OC ===．(1)求抛物线的解析式；(2)如图2，D 为y 轴负半轴上一点，过D 作直线l 垂直于直线BC ，直线l 交抛物线于E ，F 两点（点E 在点F 右侧），若3DF DE =，求D 点坐标； (3)如图3，点M 为抛物线第二象限部分上一点，点M ，N 关于y 轴对称，连接MB ，P 为线段MB 上一点（不与M 、B 重合），过P 点作直线x t =（t 为常数）交x 轴于S ，交直线NB 于Q ，求QS PS -的值（用含t 的代数式表示）．参考答案：1．(1)211266y x x =-- (2)()3,1D -或()8,10D -(3)点P 的坐标为()011-，或()10，．2．(1)265y x x =-+ (2)37,24⎛⎫- ⎪⎝⎭或()3,4-3．(1)243y x x =-+ (2)()2,2P 或()2,2-(3)存在符合条件的M 点，且坐标为：110(3M ，7)9-，()26,15M ，38(3M ，5)9-4．(1)213222y x x =--； (2)2m =；(3)存在，m 的值为0或3；(4)存在，M 点的坐标为()7,0或()1,0M 或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭．5．(1)215322y x x =-++；(2)存在点P ，使得以C ，P ，G 为顶点的三角形与FBE 相似，CPG △与FBE 的相似比为2或25；(3)P 点横坐标55．6．(1)213222y x x =--+(2)点D 不在抛物线的对称轴上， (3)(2,3)-7．(1)2=23y x x --(2)函数的最大值为5，最小值为4- (3)存在，(0,9)P -或9(0,)5P -8．(1)13(2)2E ， (2)①11(4)2D ，或23(4)6D ，；①47-9．(1)2=23y x x --(2)()0,0，()6,0，8,03⎛⎫ ⎪⎝⎭，10,03⎛⎫⎪⎝⎭(3)57,24⎛⎫- ⎪⎝⎭或者315,24⎛⎫- ⎪⎝⎭10．(1)()2324y x =--，()2,0D (2)334y x =-或1534y x =- (3)证明见解析，定点坐标为423⎛⎫- ⎪⎝⎭，11．(1)A （﹣1，0），B （3，0），C （0，﹣3），对称轴为直线x ＝1(2)当t ＝32时，BF PE 最小，最小值为47，此时P （32，﹣154）．(3)存在，点P 的坐标为（2，﹣3）12．(1)211322y x x =-++(2)22150322y x x x =-+≤<（），PM AP PQ BQ -的值为0 (3)m 、n 之间的数量关系是2(1)m n m +=≠13．(1)（32，258）答案第3页，共3页(3)（2，0）或（-5，0）或13,07⎛⎫ ⎪⎝⎭或2205⎛⎫- ⎪⎝⎭，14．(1)2=+43y x x --，(21)D ， (2)111639⎛⎫ ⎪⎝⎭，- (3)(2，−2)或12,3⎛⎫ ⎪⎝⎭15．(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)(3,4)-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭16．(1)21234y x x =-+(2)(4,3(3)存在P 1)或(4,1)，使以E ，H ，P 为顶点的三角形与EFB △相似，17．(1)12a =-，4c = (2)23y x =- (3)存在这样的点F ，点F 的坐标为(2,0)或18．(1)2122y x =- (2)()0,1D -或190,8D ⎛⎫- ⎪⎝⎭， (3)24QS PS t -=-+。

中考数学压轴题因动点产生的相似三角形问题专项练习1．如图，在平面直角坐标系xOy中，将抛物线y=x2的对称轴绕着点P（0，2）顺时针旋转45° 后与该抛物线交于A、B两点，点Q是该抛物线上一点．（1）求直线AB的函数表达式；（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；（3）如图②，若点Q在y轴左侧，且点T（0，t）（t＜2）是射线PO上一点，当以P、B、Q 为顶点的三角形与△PAT相似时，求所有满足条件的t的值．2．如图，已知BC是半圆O的直径，BC=8，过线段BO上一动点D，作AD⊥BC 交半圆O于点A，联结AO，过点B作BH⊥AO，垂足为点H，BH的延长线交半圆O于点F．（1）求证：AH=BD；（2）设BD=x，BE•BF=y，求y关于x的函数关系式；（3）如图2，若联结FA并延长交CB的延长线于点G，当△FAE与△FBG相似时，求BD的长度．3．如图，在平面直角坐标系xOy中，直线AB过点A（3，0）、B（0，m）（m＞0），tan∠BAO=2．（1）求直线AB的表达式；（2）反比例函数y=的图象与直线AB交于第一象限内的C、D两点（BD＜BC），当AD=2DB 时，求k1的值；（3）设线段AB的中点为E，过点E作x轴的垂线，垂足为点M，交反比例函数y=的图象于点F，分别联结OE、OF，当△OEF∽△OBE时，请直接写出满足条件的所有k2的值．4．如图，在Rt△ABC中，∠ACB=90°，AC=1，BC=7，点D是边CA延长线的一点，AE⊥BD，垂足为点E，AE的延长线交CA的平行线BF于点F，连结CE交AB 于点G．（1）当点E是BD的中点时，求tan∠AFB的值；（2）CE•AF的值是否随线段AD长度的改变而变化？如果不变，求出CE•AF的值；如果变化，请说明理由；（3）当△BGE和△BAF相似时，求线段AF的长参考答案一．解答题（共36小题）【分析】（1）根据题意易得点M、P的坐标，利用待定系数法来求直线AB的解析式；（2）如图①，过点Q作x轴的垂线QC，交AB于点C，再过点Q作直线AB的垂线，垂足为D，构建等腰直角△QDC，利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答；（3）根据相似三角形的对应角相等推知：△PBQ中必有一个内角为45°；需要分类讨论：∠ PBQ=45°和∠PQB=45°；然后对这两种情况下的△PAT是否是直角三角形分别进行解答．另外，以P、B、Q为顶点的三角形与△PAT相似也有两种情况：△Q″PB∽△PAT、△Q″BP∽△PAT．【解答】解：（1）如图①，设直线AB与x轴的交点为M．∵∠OPA=45°，∴OM=OP=2，即M（﹣2，0）．设直线AB的解析式为y=kx+b（k≠0），将M（﹣2，0），P（0，2）两点坐标代入，得解得．，故直线AB的解析式为y=x+2；22（2）如图①，过点Q 作x 轴的垂线QC ，交AB 于点C ，再过点Q 作直线AB 的垂线，垂足为D ，根据条件可知△QDC 为等腰直角三角形，则QD=QC ．设Q （m ，m 2），则C （m ，m+2）．∴QC=m+2﹣m 2=﹣（m﹣ ）+ ，QD= QC= [﹣（m﹣ ）+ ]．故当m= 时，点Q 到直线AB的距离最大，最大值为；（3）∵∠APT=45°，∴△PBQ 中必有一个内角为45°，由图知，∠BPQ=45°不合题意．①如图②，若∠PBQ=45°，过点B 作x 轴的平行线，与抛物线和y 轴分别交于点Q′、F ．此时满足∠PBQ′=45°．∵Q′（﹣2，4），F （0，4），∴此时△BPQ′是等腰直角三角形，由题意知△PAT 也是等腰直角三角形．（i ）当∠PTA=90°时，得到：PT=AT=1，此时t=1；（ii ）当∠PAT=90°时，得到：PT=2，此时t=0．②如图③，若∠PQB=45°，①中是情况之一，答案同上；先以点F 为圆心，FB 为半径作圆，则P 、B 、Q′都在圆F 上，设圆F 与y 轴左侧的抛物线交于另一点Q″．则∠PQ″B=∠PQ′B=45°（同弧所对的圆周角相等），即这里的交点Q″也是符合要求．设Q″（n ，n 2）（﹣2＜n ＜0），由FQ″=2，得n 2+（4﹣n 2）2=22，即n 4﹣7n 2+12=0．解得n 2=3或n 2=4，而﹣2＜n ＜0，故n=﹣，即Q″（﹣，3）．可证△PFQ″为等边三角形，所以∠PFQ″=60°，又PQ″=PQ″，所以∠PBQ″=∠PFQ″=30°．则在△PQ″B中，∠PQ″B=45°，∠PBQ″=30°．（i）若△Q″PB∽△PAT，则过点A作y轴的垂线，垂足为E．则ET= AE= ，OE=1，所以OT=﹣1，解得t=1﹣；（ii）若△Q″BP∽△PAT，则过点T作直线AB垂线，垂足为G．设TG=a，则PG=TG=a，AG= TG= a，AP=，∴ a+a= ，解得PT= a=﹣1，∴OT=OP﹣PT=3﹣，∴t=3﹣．综上所述，所求的t的值为t=1或t=0或t=1﹣或t=3﹣．2．【分析】（1）由AD⊥BC，BH⊥AO，利用垂直的定义得到一对直角相等，再由一对公共角，且半径相等，利用AAS得到三角形ADO与三角形BHO全等，利用全等三角形对应边相等得到OH=OD，利用等式的性质化简即可得证；（2）连接AB，AF，如图1所示，利用HL得到直角三角形ADB与直角三角形BHA全等，利用全等三角形对应角相等得到一对角相等，再由公共角相等得到三角形ABE与三角形AFB相似，由相似得比例即可确定出y与x的函数解析式；（3）连接OF，如图2所示，利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似，由相似得比例求出BD的长即可．【解答】（1）证明：∵AD⊥BC，BH⊥AO，∴∠ADO=∠BHO=90°，在△ADO与△BHO中，，∴△ADO≌△BHO（AAS），∴OH=OD，又∵OA=OB，∴AH=BD；（2）解：连接AB、AF，如图1所示，∵AO是半径，AO⊥弦BF，∴∴AB=AF，∴∠ABF=∠AFB，在Rt△ADB与Rt△BHA中，，∴Rt△ADB≌Rt△BHA（HL），∴∠ABF=∠BAD，∴∠BAD=∠AFB，又∵∠ABF=∠EBA，∴△BEA∽△BAF，∴= ，∴BA2=BE•BF，∵BE•BF=y，∴y=BA2，∵∠ADO=∠ADB=90°，∴AD2=AO2﹣DO2，AD2=AB2﹣BD2，∴AO2﹣DO2=AB2﹣BD2，∵直径BC=8，BD=x，∴AB2=8x，则y=8x（0＜x＜4）；方法二：∵BE•BF=y，BF=2BH，∴BE•BH=y，∵△BED∽△BOH，∴= ，∴OB•BD=BE•BH，∴4x=y，∴y=8x（0＜x＜4）；（3）解：连接OF，如图2所示，∵∠GFB是公共角，∠FAE＞∠G，∴当△FAE∽△FBG时，∠AEF=∠G，∵∠BHA=∠ADO=90°，∴∠AEF+∠DAO=90°，∠AOD+∠DAO=90°，∴∠AEF=∠AOD，∴∠G=∠AOD，∴AG=AO=4，∵∴∠AOD=∠AOF，∴∠G=∠AOF，又∵∠GFO是公共角，∴△FAO∽△FOG，∴= ，∵AB 2=8x ，AB=AF ，∴，∴AF=2x，=解得：x=3±，∵3+＞4，舍去，∴BD=3﹣．3．【分析】（1）先通过解直角三角形求得A 的坐标，然后根据待定系数法即可求得直线AB 的解析式；（2）作DE ∥OA ，根据题意得出= = ，求得DE ，即D 的横坐标，代入AB 的解析式求得纵坐标，然后根据反比例函数图象上点的坐标特征即可求得k 1；（3）根据勾股定理求得AB 、OE ，进一步求得BE ，然后根据相似三角形的性质求得EF 的长，从而求得FM 的长，得出F 的坐标，然后根据反比例函数图象上点的坐标特征即可求得k 2．【解答】解：（1）∵A （3，0）、B （0，m ）（m ＞0），∴OA=3，OB=m ，∵tan ∠BAO==2，∴m=6，设直线AB 的解析式为y=kx+b ，代入A （3，0）、B （0，6）得：解得：b=6，k=﹣2∴直线AB的解析式为y=﹣2x+6；（2）如图1，∵AD=2DB，∴= ，作DE∥OA，∴==，∴DE=OA=1，∴D的横坐标为1，代入y=﹣2x+6得，y=4，∴D（1，4），∴k1=1×4=4；（3）如图2，∵A（3，0），B（0，6），∴E（，3），AB==3，∵OE是Rt△OAB斜边上的中线，∴OE= AB=，BE=，∵EM⊥x轴，∴F的横坐标为，∵△OEF∽△OBE，∴=，∴，∴EF=，∴FM=3﹣=．∴F（，），∴k2=×=．。

专题04相似三角形的性质压轴题型全攻略【考点导航】目录【典型例题】 (1)【考点一相似三角形有关线段的计算】 (1)【考点二相似三角形有关面积的计算】 (2)【考点三相似三角形性质的应用】 (2)【考点四相似三角形性质的拓展提高】 (3)【过关检测】 (4)【典型例题】【考点一相似三角形有关线段的计算】A．252+【答案】A【分析】根据全等三角形的判定得出及相似三角形的判定和性质求解即可．A．254B．【答案】A【分析】证明ABE ECFV:VA ．12AF EF =B ．12AF EF =【答案】D 【分析】先证明ADG ECG ≌得到AD =【考点二相似三角形有关面积的计算】【例题2】如图，在ABC 中，D 、E 分别是AB 和AC 的中点，15BCED S =四边形，则ABC S = ()A ．30B ．25C ．22D ．20【答案】D 【分析】根据题意得出DE 是ABC 的中位线，进而可得ADE ABC △△∽，根据面积比等于相似比的平方，A ．2.4B ．3【答案】B 【分析】证明ABE CDE ∽△△可求A．2:3B．3:【答案】D【分析】根据平行四边形的性质得到【考点三相似三角形性质的应用】【答案】22【分析】设EF x =分米，判断出AEF △和DEG △可求出AE ，即可得到正方体礼品盒的棱长．【详解】解：如图，在正方形ABCD 中，AD设EF x =分米，由此裁剪可得：AEF △和∴AEF DEG ∽ ，∴AE EF DE EG =，即10AE AE =-解得：2AE =分米，∴222EF AE ==分米，∴正方体礼品盒的棱长为故答案为：22．【点睛】本题考查了相似三角形的判定和性质，解题的关键是理解题意，读懂裁剪的方法，找到相似三角形．【变式2】魏朝时期，刘微利用下图通过令出入相补，各从其类”证明了勾股定理．BF 交CD 于E ，若2DE =【答案】117【分析】根据已知条件得到CD DE CE =+到结论．【详解】解：4CE = ，2DE =，A．4B．13 3【答案】B【分析】首先根据正方形的性质，得出()SASABF DAE△≌△，则AFB∠A ．23B ．192【答案】B 【分析】证CDJ 是等边三角形，DCI ∠∵菱形ABCD 和菱形CEFG 在同一条直线上，∴60DCJ JDC ∠=∠=︒，ICJ ICE ∠=∠∴CDJ 是等边三角形，60JIC ∠=︒-∠∴1JI JC CD ===，90DCI ∠=︒，A．2个∴90BPG BQG PGQ ∠=∠=∠=︒，∴四边形PBQG 是矩形，∴90PBQ ∠=︒，∵90ABC ∠=︒，∴NPB QBE ∠=∠，由①得DEC CNB ≌，∴EC NB =，∵E 是BC 的中点，∴EC BE =，∴BE BN =，∴90NBP EBQ NPB EBQ BN BE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴NBP EBQ AAS ≌（），∴BP BQ =，∴四边形PBQG 是正方形，∴45BGN ∠=︒，故④正确；如图所示，连接NE ，设BN x =，则2BE EC x BC CD AB x =====，，【过关检测】一、选择题1.如图，ABO CDO ∽，2BO OD =，CDO 的周长为4，则ABO 的周长为（）A ．2B ．4【答案】C 【分析】根据相似三角形的周长比等于相似比，即可得出结果．【详解】解：∵ABO CDO ∽，A ．32B ．48【答案】B 【分析】根据平行四边形的性质可得A．2B．3【答案】A【分析】根据角平分线的定义及平行线的性质可知【点睛】本题考查了平行线的性质，相似三角形的判定与性质，角平分线的定义，中点的定义，等腰三角形的判定与性质，掌握相似三角形的判定与性质是解题的关键．4.如图，在Rt ABC △中，AB =点G 在CD 上，且1DG GC =::A ．22cm B ．24cm 【答案】B 【分析】连接DE ，首先得到DE ∥12DF DE BF AB ==，然后利用三角形面积公式求出∵D 、E 分别为AC BC 、中点，∴DE AB ∥，13cm 2DE AB ==，∴ABD EDF ∠=∠，BAF DEF ∠=∠∴ABF EDF ∽，1DF DE 二、填空题【答案】16【答案】733【分析】作2⊥AE l 于E 点，CF∴AE CF ∥，AED CFD ∽，∴12AE DE AD CF DF CD ===，设AD x =，则3AC x =，由“三线合一【答案】8⊥轴于点【分析】过点A作AE x求出D点的坐标，最后利用设,k A m m ⎛⎫ ⎪⎝⎭，则,OE m AE ==∵23OA AB =，25AO OB ∴=，,AOE BOC AEO BCO ∠=∠∠=∠ AOE BOC ∴ △△，【答案】6【分析】通过四边形EFGH 为矩形推出AEH △的高，可得出AM EH AD BC=，再将数据代入即可得出答案．∵四边形EFGH 是矩形，∴EH ∥BC ，∴AEH ABC ∽△△，∴点H是AD的中点，∥，∵AB DG∴点F是BG的中点，【答案】4.5【分析】根据等边对等角和折叠的性质证明计算求出 3.5GF =，则CG =【详解】解：∵16AC BC ==【答案】25【分析】在正方形ABCD 中，EM AD ⊥于M ，可得EMF △222AD AG DG +=，解得a DE EF =，1122DM FM DF a∴===，90ADG HFD MEF ∠+∠=︒=∠+∠ ADG MEF ∴∠=∠，11PN AC ∥ ，11PM BC ∥，11BPN BAC ∴ ∽，11APM ABC ∽，则11112P N BP x AC AB ==，同理得到1111PM AP x BC AB==，两式相加得到11x x +=，【答案】17.5m【分析】依题意，四边形CBDE ==，证明AEC15mFC BM【答案】213【分析】记ADC α∠=，则CAB CMD ∽，求得DM 【详解】解：如图．记ADC ∠则CD CM =，ACB ∠=∠∵2CD AC =，∴22CM AC BC ==，∴CAB CMD ∽，∴2MD CM AB AC==；∴24DM AB ==，∵ADM ADC ∠=∠+∠∴246BD AM ==+故答案为：213．【点睛】本题考查了旋转的性质，相似三角形的判定和性质，勾股定理，证明18．如图，在正方形连接DF ，则DF 的长为【答案】3104【分析】如图，过F 作FM ⊥可得四边形CMFN 是正方形，则FM ME AB BE =，即2332a a -=，解得∵CF 平分DCE ∠，∴45FCM FCN ∠=∠=︒，∴=CM FM ，∴四边形CMFN 是正方形，【答案】12/0.5【分析】如图，延长AF 、点，可得12BE CE B E '===由折叠的性质可得，AEB AEB '∠=∠∵E 为BC 中点，∴12BE CE B E BC '===，由菱形的性质可得，AD BC =，AD【答案】7【分析】根据题意，过E 作用ABD ADC S S = 得到BD CD =求解．∴EM AN ∥，∴BEM BAN △∽△，∴BE EM BA AN=，∵3AB BE =，即1BE =，5BED EDC S S ∴==△△，3AB BE = ，BD CD =，EF ∴AEF ABD ∽△△，EFO △23EF AE BD AB ∴==，【答案】14【分析】由菱形的性质及ECF ∠FDG CBG ∠=∠，DFG BCG ∠=∠【详解】∵60ECF ACB ∠=∠=∴ECF ACE ACB ACEÐ-Ð=Ð-Ð∴FCA ECB∠=∠∵四边形ABCD 是菱形，∴AD BC ∥，12FAC BAD Ð=Ð∴180120BAD ABC =︒-=︒∠∠∴160FAC BAD Ð=Ð=°【答案】3m 2【分析】先通过证明ABM86 1.6FN FN +=求解即可．【详解】解：∵EF AB∥,【答案】245【分析】过点D 作DE BC ⊥于点再由三角形面积公式即可得出答案．【详解】解：如图，过点D 作由折叠可知12ACD A CD '∠=∠=∠∴45CDE A CD '∠=∠=︒，∴DE CE =，设DE x =，则6BE x =-，。

相似三角形（8大题型）（48道压轴题专练） 压轴题型一 相似形压轴题型1．（20-21九年级上·重庆渝中·期末）如图，△ABC 三个顶点的坐标分别是A （－2，2），B （－4，1），C （－1，－1）．以点C 为位似中心，在x 轴下方作△ABC 的位似图形△A'B'C ．并把△ABC 的边长放大为原来的2倍，那么点A'的坐标为( )A ．（1，－6）B ．（1，－7）C ．（2，－6）D ．（2，－7）2．（23-24八年级下·山东淄博·(2)ABCD AD AB AD <<纸片，以它的一边为边长剪去一个菱形，在余下的平行四边形中，再以它的一边为边长剪去一个菱形．若剪去两个菱形后余下的平行四边形与原平行四边形ABCD 相似，则平行四边形ABCD 的相邻两边AD 与AB 的比值是 ．3．（2024·湖北武汉·一模）如图是由小正方形组成的网格，四边形ABCD的顶点都在格点上，仅用无刻度的直尺在所给定的网格中按要求完成下列画图，画图过程用虚线表示，画图结果用实线表示．(1)在图1中，先以点A为位似中心，将四边形ABCD缩小为原来的12，画出缩小后的四边形111AB C D，再在AB上画点E，使得DE平分四边形ABCD的周长；(2)在图2中，先在AB上画点F，使得CF BC=，再分别在AD，AB上画点M，N，使得四边形BCMN 是平行四边形．4．（23-24九年级上·江苏南京·阶段练习）形状相同（即长与宽之比相等）的矩形是相似矩形，已知一个矩形长为()1a a³，宽为1．一分为二（1）如图1，将矩形分割为一个正方形（阴影部分）和小矩形，小矩形恰与原矩形相似，则a的值为______．（2）如图2，将矩形分割为两个矩形，使每个小矩形均与原矩形相似，则a的值为______．一分为多（3）有同学说“无论a为何值，该矩形总可以分割为几个小矩形，这几个小矩形都与原矩形相似”，你同意这个说法吗？若同意，在图3中画出一种可行的分割方案；若不同意，举出反例．一分为三（4）将矩形分割为三个矩形，使每个小矩形均与原矩形相似．画出所有可能的分割方案的示意图，并在每个示意图下方直接写出对应的a 的值．5．（20-21八年级下·山东淄博·期末）如图，四边形ABCD ∽四边形A B C D ¢¢¢¢，且62A Ð=°，75B Ð=°，140D Т=°，9AD =，11A B ¢¢=，6A D ¢¢=，8B C ¢¢=．(1)请直接写出：C Ð= 度；(2)求边AB 和BC 的长．6．（23-24九年级上·广西南宁·阶段练习）如图，在平面直角坐标系中，ABC V 的三个顶点坐标分别为()1,1A ，()3,2B ，()2,3C （每个方格的边长均为1个单位长度），请按下列要求画图：(1)111A B C △与ABC V 关于原点O 成中心对称，画出111A B C △并写出点1A 的坐标；(2)以原点O 为位似中心，相似比为2，在第一象限内将ABC V 放大，画出放大后的222A B C △并写出点2B 的坐标；(3)根据信息回答问题：已知ABC V 的面积为32，AB ，请直接写出222A B C △的面积和22A B 边上的高的值．压轴题型二 比例线段压轴题型1．（2020古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底0.618≈，称为黄金分割比例），如图，著名的“断臂维纳斯”便是如此．此外，．若某人满足上述两个黄金分割比例，且腿长为105cm ，头顶至脖子下端的长度为26cm ，则其身高可能是（ ）A ．165cmB ．175cmC ．185cmD ．190cm2．（2024·四川乐山·一模）古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将线段MN 分为两线段MG ，GN ，使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项，即满足MG GN MN MG ==这个数称为“黄金分割”数，把点G 称为线段MN 的“黄金分割”点．如图，在ABC V 中，已知3AB AC ==，4BC =，若D ，E 是边BC 的两个“黄金分割”点，则ADE V 的面积为 ．3．（23-24八年级下·贵州六盘水·期末）已知a ，b ，c ，d ，e ，f 六个数，如果()0a c e k b d f b d f ===++¹，那么a c e k b d f++=++．理由如下：∵()0a c e k b d f b d f===++¹∴a bk =，c dk =，e fk =（第一步）∴()k b d f a c e bk dk fk k b d f b d f b d f++++++===++++++（第二步）(1)解题过程中第一步应用了______的基本性质；在第二步解题过程中，()k b d f k b d f ++=++应用了______的基本性质；(2)应用此解题过程中的思路和方法解决问题：①如果22567a b c ===，则218a b c ++=______；②已知0345x y z ==¹，求23x y z x y z -++-的值．4．（23-24九年级上··的矩形叫黄金矩形．如图①，已知黄金矩形ABCD 的宽1AB =．(1)黄金矩形ABCD 的长BC = ；(2)如图②，将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ，得到新的矩形DCEF ，猜想矩形DCEF 是否为黄金矩形，并证明你的结论；(3)在图②中，连接AE ，求点D 到线段AE 的距离．5．（22-23九年级上·浙江·周测）若实数a b c ，，满足a b c b c a a c b c a b +-+-+-==，求()()()a b b c a c abc+×+×+的值．6．（23-24九年级下·山东淄博·期末）已知a ，b ，c ，d 为四个不为0的数．(1)如果3a b =，求a b b +与a b a b -+的值；(2)如果(),a c a b c d b d =¹¹，求证a c b a d c =--；(3)如果a c a b d b +=+，求证a c b d=．压轴题型三 相似三角形的判定压轴题型1．（21-22九年级上·陕西咸阳·期中）如图，在矩形ABCD 中，E 是AD 边的中点，BE ^F ，连接DF ，分析下列四个结论，①AEF CAB △∽△，②CF 2AF =；③DF DC =；④CD AC =．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个2．（2024·广东深圳·二模）如图，在等腰直角ABC V 中，4AB BC ==，D 为BC 上一点，E 为BC 延长线上一点，且45DAE =°∠，2AE AD =，则BD = ．3．（2024·广东梅州·模拟预测）（1）如图1，在矩形ABCD 中，点C ，D 分别在边DC ，BC 上，AB AB ^，垂足为点G ．求证：ADE DCF ∽V V ．【问题解决】（2）如图2，在正方形ABCD 中，点E ，F 分别在边DC ，BC 上，AE DF =，延长BC 到点H ，使CH DE =，连接DH ．求证：ADF H Ð=Ð．【类比迁移】（3）如图3，在菱形ABCD 中，E F 分别在边DC ，BC 上，10AE DF ==，7DE =，60AED Ð=°，求CF 的长．4．（2024·山西晋中·二模）综合与实践问题情境：数学活动课上，老师要求同学们以正方形为背景探索几何图形运动变化中的数学结论．如图1，正方形ABCD 中，4AB =，点E ，F 分别是边AB ，AD 的中点，连接EF ，点G 是线段EF 上的一个动点，连接AG ，将线段AG 绕点A 逆时针方向旋转90°，得到AH ，连接HD ，GB ．猜想证明：（1）针对老师给出的问题背景，“智慧小组”发现GB HD =，请你证明这一结论；操作探究：（2）“善思小组”提出问题：如图2，当点G 为线段EF 的中点时，连接FH ，试判断四边形AGFH 的形状，并说明理由；深入探究：（3）“创新小组”BG 与直线DH 交于点M ，当AHD V 为直角三角形时，请直接写出四边形AGMH 的面积．5．（2024·安徽蚌埠·一模）如图1，在四边形ABCD 中，120ABC Ð=°，60ADC Ð=°，对角线AC ，BD 相交于点O ，且AC AD =，BD 平分ABC Ð．(1)求证：DB AB CB =+；(2)如图2，过点D 作DE AB ∥，使DE BC =，连接AE ，取AE 中点 F ，连接DF ，求证：22AC DF OD =×．6．（23-24九年级上·湖南常德·期中）（1）如图1，在四边形ABCD 中，90BAD BCD Ð=Ð=°，连接AC BD ，，过点A 作AE AC ^交CB 的延长线于点E ，求证：E ACD Ð=Ð．（2）如图2，在四边形ABCD 中，AB AD =，（1）中的其它条件不变，点M ，N 分别是BD EC ，的中点，连接AN AM ，，MN ．①求证：AE AC =﹔②求证：N ABE AM ∽△△．压轴题型四 相似三角形的性质压轴题型1．（22-23九年级上·上海长宁·期中）已知点D 在ABC V 的边BC 上，联结AD ，如果ABD △与ACD V 相似，那么下列四个说法：①BAD C Ð=Ð；②AD BC ^；③2AD BD CD =×；④22AB BD AC CD =．一定成立的是（ ）．A ．②④B ．①③C ．①②③D ．②③④2．（2024·上海浦东新·三模）如图，在ABC V 中，3AC BC ==，90C Ð=°，点D 在边BC 上（不与点B ，点C 重合），连接AD ，点E 在边AB 上，EDB ADC Ð=Ð．已知点H 在射线AC 上，连接EH 交线段AD 于点G ，当1CH =，且AEH BED Ð=Ð时，则BE AB = ．3．（23-24八年级下·山东威海·期末）如图1，矩形ABCD ，点E ，点F 分别为AD ，BC 上的点，将矩形沿EF 折叠，使点B 的对应点B ¢落在CD 上，连接BB ¢．(1)如图2，当点B ¢与点D 重合时，连接BE ，试判断四边形BEB F ¢的形状，并说明理由；(2)若6AB =，8BC =，求折痕EF 的最大值．4．（23-24八年级下·山东东营·期末）综合与探究(1)如图1，在正方形ABCD 中，点E ，F 分别在边BC CD ，上，且AE BF ^，则线段AE 与BF 的之间的数量关系为_____________；(2)【类比探究】如图2，在矩形ABCD 中，35AB AD ==，，点E ，F 分别在边BC ，CD 上，且AE BF ^，请写出线段AE 与BF 的数量关系，并证明你的结论．(3)【拓展延伸】如图3，在Rt ABC V 中，9046ABC AB BC Ð=°==，，，D 为BC 上一点，且2BD =，连接AD ，过点B 作BE AD ^于点F ，交AC 于点E ，求BE 的长．5．（23-24九年级下·广西南宁·阶段练习）已知等边ABC V ，以AC 为斜边向外作Rt ACD △，定义Rt ACD △为等边ABC V 的“关联直角三角形”，连接BD 交AC 于点E ，下面我们来研究与DE BE的值有关的问题．(1)如图①，当“关联直角三角形”是等腰直角三角形时，DE BE的值为______；(2)如图②，当“关联直角三角形”是含30°的直角三角形时，求DE BE的值；(3)如图③，当“关联直角三角形”是一般的直角三角形时，若16,3DE AB BE ==，求BD 的值．6．（2024·安徽·中考真题）如图1，ABCD Y 的对角线AC 与BD 交于点O ，点M ，N 分别在边AD ，BC 上，且AM CN =．点E ，F 分别是BD 与AN ，CM 的交点．(1)求证：OE OF =；(2)连接BM 交AC 于点H ，连接HE ，HF ．（ⅰ）如图2，若HE AB ∥，求证：HF AD ∥；（ⅱ）如图3，若ABCD Y 为菱形，且2MD AM =，60EHF Ð=°，求AC BD 的值．压轴题型五 相似三角形的应用压轴题型1．（2024·浙江温州·三模）图1是《九章算术》中记载的“测井深”示意图，译文指出：“如图2，今有井直径CD 为5尺，不知其深AD ．立5尺长的木CE 于井上，从木的末梢E 点观察井水水岸A 处，测得“入径CF ”为4寸，问井深AD 是多少？（其中1尺10=寸）”根据译文信息，则井深AD 为（ ）A ．500寸B ．525寸C ．550寸D ．575寸2．（2022·浙江金华·一模）将一本高为17cm （即17cm EF =）的词典放入高（AB ）为16cm 的收纳盒中（如图1）．恰好能盖上盒盖时，测得底部F 离收纳盒最左端B 处8cm ，若此时将词典无滑动向右倒，书角H 的对应点H ¢恰为CD 中点．（1）收纳盒的长BC = ；（2）现将若干本同样的词典放入此有盖的收纳盒中，如图2放置，则最多有本书可与边BC 有公共点．3．（2024·江苏南京·一模）在光学中，由实际光线会聚成的像，称为实像，而光线能会聚的是因为折射．图中，凸透镜EF 的焦距为f ，主光轴l EF ^，A ，B ，C ，D 都在l 上，其中O 是光心，2OB OD f ==，蜡烛PQ l ^（蜡烛可移动，且OQ f >），光线PG l ∥，其折射光线GC 与另一条经过光心的光线PP ¢相交于点P ¢（P Q l ¢¢^）即为蜡烛在光屏上所成的实像．图中所有点都在同一平面内．记物高()PQ 为h ，像高()P Q ¢¢为h ¢，物距()OQ ，像距()OQ ¢为v ．(1)若10cm f =，10cm h =，15cm u =，=v cm ．(2)求证111u v f+=．(3)当f 一定时，画出v 与u 之间的函数图象()u f >，并结合图象描述v 是怎么随着u 的变化而变化的？4．（23-24九年级上·河北邢台·1，小红家的阳台上放置了一个晒衣架，图2是晒衣架的侧面示意图，立杆AB 、CD 相交于点O ，B 、D 两点在地面上，经测量得到136cm AB CD ==，51cm OA OC ==，34cm OE OF ==，现将晒衣架完全稳固张开，扣链EF 成一条线段．发现：连接AC ．则AC 与EF 有何位置关系?并说明理由；探究：若32cm EF =，求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时，连衣裙才不会拖在地面上?5．（22-23九年级上·浙江·单元测试）如图，Rt ABC V 为一块铁板余料，90B Ð=°，6cm BC =，8cm AB =，要把它加工成正方形小铁板，有如图所示的两种加工方案，请你分别计算这两种加工方案的正方形的边长．6．（2022九年级·全国·专题练习）阅读理解：如图1，AD 是△ABC 的高，点E 、F 分别在AB 和AC 边上，且EF //BC ，可以得到以下结论：AH EF AD BC=．拓展应用：(1)如图2，在△ABC 中，BC ＝3，BC 边上的高为4，在△ABC 内放一个正方形EFGM ，使其一边GM 在BC 上，点E 、F 分别在AB 、AC 上，则正方形EFGM 的边长是多少？(2)某葡萄酒庄欲在展厅的一面墙上，布置一个腰长为100cm ，底边长为160cm 的等腰三角形展台．现需将展台用隔板沿平行于底边，每间隔10cm 分隔出一排，再将每一排尽可能多的分隔成若干个无盖正方体格子，要求每个正方体格子内放置一瓶葡萄酒．平面设计图如图3所示，将底边BC 的长度看作是0排隔板的长度．①在分隔的过程中发现，当正方体间的隔板厚度忽略不计时，每排的隔板长度（单位：厘米）随着排数（单位：排）的变化而变化．请完成下表：排数/排0123…隔板长度/厘米160__________________…若用n 表示排数，y 表示每排的隔板长度，试求出y 与n 的关系式；②在①的条件下，请直接写出该展台最多可以摆放多少瓶葡萄酒？压轴题型六 重心的性质压轴题型1．（23-24九年级上·浙江宁波·期末）如图，点G 是ABC V 的重心，过点G 作MN BC ∥分别交AB AC ，于点M ，N ，过点N 作ND AB ∥交BC 于点D ，则四边形BDNM 与ABC V 的面积之比是（ ）A ．1:2B ．2:3C ．4:9D ．7:92．（2023·上海·一模）在Rt ABC △中，9030B BAC BC Ð=°Ð=°=，，1，以AC 为边在ABC V 外作等边ACD V ，设点E 、F 分别是ABC V 和ACD V 的重心，则两重心E 与F 之间的距离是 ．3．（2024·江苏盐城·中考真题）如图1，E 、F 、G 、H 分别是平行四边形ABCD 各边的中点，连接AF CE 、交于点M ，连接AG 、CH 交于点N ，将四边形AMCN 称为平行四边形ABCD 的“中顶点四边形”．(1)求证：中顶点四边形AMCN 为平行四边形；(2)①如图2，连接AC BD 、交于点O ，可得M 、N 两点都在BD 上，当平行四边形ABCD 满足________时，中顶点四边形AMCN 是菱形；②如图3，已知矩形AMCN 为某平行四边形的中顶点四边形，请用无刻度的直尺和圆规作出该平行四边形．（保留作图痕迹，不写作法）4．（23-24七年级下·江苏扬州·阶段练习）作图．(1)直尺作图：如图1，已知D 、E 分别为AB 、AC 中点，过点A 作AF 平分ABC V 面积；(2)直尺作图：如图2，已知AD BC ∥，在四边形ABCD 中作一点O ，使AOB COD S S =△△；(3)尺规作图：如图3，已知D 为AC 中点，点M 在BC ，在AC 上作点N 使MN 平分ABC V 面积．5．（2024·辽宁丹东·二模）阅读与思考：三角形的重心定义：三角形三条中线相交于一点，这个交点叫做三角形的重心．三角形重心的一个重要性质：重心与一边中点的连线的长是对应中线长的13．下面是小明证明性质的过程．如图，在ABC V 中，D 、E 分别是边BC 、AC 的中点，AD 、BE 相交于点G ，求证：13GE GD BE AD ==证明：连接ED ，∵D ，E 是边BC ，AC 的中点，∴DE AB ∥，12DE AB =（依据1）∴ABG DEGV V ∽∴12GE GD DE GB GA AB ===（依据2）∴13GE GD BE AD ==(1)任务一，在小明的证明过程中，依据1和依据2的内容分别是：依据1：______________________依据2：______________________(2)应用①如图，在ABC V 中，点G 是ABC V 中的重心，连接AG 并延长交BC 与点E ，若 3.5GE =，求AG 长．②在ABC V 中，中线AD 、BE 相交于点O ，若ABC V 的面积等于30，求BOD V 的面积．6．（2024·河南周口·三模）（1）古往今来，人们在生产和生活中对三角形的应用层出不穷，三角形也是我们平时研究的重点，如图1，已知ABC V 是等边三角形． P 是ABC V 的重心，连接BP CP ，并延长分别交边AC AB ，于点E ，D ．试判断：①BPD Ð的度数为 ；②线段PB PD PE ，，之间的数量关系：PB PD PE +；（填写“>”“<”或“=”）（2）如图2，若在等边ABC V 中，点E 是射线AC 上一动点（其中点E 不与点A 重合，且12CE AC <），连接BE ，作边BA 关于直线 BE 的对称线段 BD ，直线CD ，BE 相交于点 P ，试探究线段PB PC PD ，，的数量关系，并说明理由．压轴题型七 平面向量的线性运算压轴题型1．（23-24九年级上·上海·期中）下列判断不正确的是（ ）A ．()222a b a b +=+r r r r ；B ．如果向量a r 与b r 均为单位向量，那么a b =r r 或a b =-r r ；C ．如果a b =r r ，那么a b =r r ；D ．对于非零向量b r ，如果()0a k b k =×¹r r ，那么a b r r P ．2．（2024·上海普陀·二模）如图，梯形ABCD 中，AD BC ∥，过点A 作AE DC ∥分别交BD 、BC 于点F 、E ，23BE BC =，设AD a =uuu r r ，AB b =uuu r r ，那么向量FE uuu r 用向量a r 、b r 表示为 ．3．（23-24八年级下·上海崇明·期末）如图，点E 在平行四边形ABCD 的对角线BD 的延长线上．(1)填空：BA AB +uuu r uuu r ＝ ，BA AE ED DC +++uuu r uuu r uuu r uuu r ＝ ；(2)图中与AB uuu r 相等的向量是 ，与AD uuu r 相反的向量是 ；(3)求作：DC DE +uuu r uuu r （不写作法，保留作图痕迹，写出结论）．4．（23-24八年级下·上海·期末）如图，在四边形ABCD 中，AD BC ∥，点O 是对角线AC 的中点，DO 的延长线与BC 相交于点E ，设AB a uuu r r =，AD b =uuu r r ，BE c =uuu r r ．(1)试用向量a r 、b r 、c r 表示向量：ED =uuu r ______；(2)写出图中所有与AD uuu r 互为相反向量的向量：______；(3)求作：AD OC +uuu r uuu r．（画出所求向量，并直接写出结论）5．（23-24八年级下·上海闵行·期末）如图，已知梯形ABCD 中，AB DC P ，点E 在AB 上，ED BC ∥．(1)填空：BE ED DC CB +++=uuu r uuu r uuu r uuu r ，(2)填空：BA AD DC EA ++-=uuu r uuu r uuu r uuu r ；(3)在图中直接作出AE ED AB +-uuu r uuu r uuu r ．（不写作法，写结论）6．（2022八年级下·上海·专题练习）如图，已知点M 是△ABC 边BC 上一点，设AB uuu r ＝a r ，AC uuu r ＝b r ．(1)当BM MC＝2时，AM uuuu r ＝______；（用a r 与b r 表示）(2)当AM uuuu r ＝4377a b +r r 时，BM MC ＝______；(3)在原图上作出AM uuuu r 在AB uuu r 、AC uuu r 上的分向量．压轴题型八 相似三角形的动点问题1．（2020·山西·一模）如图，在ABC V 中，8AB AC ==，6BC =，点P 从点B 出发以1个单位长度/秒的速度向点A 运动，同时点Q 从点C 出发以2个单位长度/秒的速度向点B 运动，其中一点到达另一点即停．当以B ，P ，Q 为顶点的三角形与ABC V 相似时，运动时间为（ ）A ．2411秒B ．95秒C ．2411秒或95秒D ．以上均不对2．（2023八年级上·江苏·专题练习）如图，在ABC V 中，90C Ð=°，3AC =，4BC =，动点P 从点B 出发以每秒1个单位长度的速度沿B A ®匀速运动；同时点Q 从点A 出发同样的速度沿A C B ®®匀速运动．当点P 到达点A 时，P 、Q 同时停止运动，设运动时间为t 秒，当t 为 时，以B 、P 、Q 为顶点的三角形是等腰三角形．3．（2024·吉林长春·三模）如图，在Rt ABC △中，90ABC Ð=°，8AB =，6BC =，点D 为AC 中点，动点P 从点A 出发，沿边AB 以每秒5个单位长度的速度向终点B 运动，连结DP ，将线段DP 绕点D 逆时针旋转90°得线段DE ，连结PE ．设点P 运动的时间为t 秒．(1)用含t 的代数式表示点P 到AC 的距离为________；(2)当点E 落在ABC V 内部（不包括边界）时，求t 的取值范围；(3)当PE 与ABC V 的一边平行时，求线段PE 的长度；(4)当经过点E 与ABC V 的一个顶点的直线平分ABC V 面积时，直接写出t 的值．4．（2024·江苏苏州·二模）如图，矩形ABCD 中，4AB ＝厘米，3BC ＝厘米，点E 从A 出发沿AB BC -匀速运动，速度为1厘米/秒；同时，点F 从C 出发沿对角线CA 向A 匀速运动，速度为1厘米/秒，连接DE DF EF 、、，设运动时间为t 秒．请解答以下问题：(1)当0 2.5t ＜＜时①t 为何值时，EF AD ∥；②设DEF V 的面积为y ，求y 关于t 的函数；5．（2023·吉林松原·模拟预测）已知ABC V 中，90C Ð=°，3cm AC =，4cm CD =，BD AD =．点F 从点A 出发，沿AC CD -运动，速度为1cm/s ，同时点E 从点B 出发，沿BD DA -运动，运动速度为1cm/s ，一个点到达终点，另一点也停止运动．设AEF △ 的面积为S 2cm ，点E ，F 运动时间为t s ．(1)求BD 的长；(2)用含t 的代数式表示DE ；(3)求S 与t 的函数关系式，并写出t 的取值范围．6．（23-24九年级下·河北邯郸·阶段练习）如图1和2，在矩形ABCD 中，6,8AB BC ==，点K 在CD 边上．且73CK =．点M N ，分别在,AB BC 边上，且2AM CN ==．点P 从点M 出发沿折线MB BN -匀速运动，点E 在CD 边上随P 移动，且始终保持^PE AP ；点Q 从点D 出发沿DC 匀速运动，点P Q ，同时出发，点Q 的速度是点P 的一半，点P 到达点N 时停止，点Q 随之停止．设点P 移动的路程为x ．(1)当点Q 与点K 重合时，通过计算确定点P 的位置；(2)若点P 在BN 上，当BP CE =时，如图2，求x 的值；(3)在点P 沿折线MB BN -运动过程中，求点Q ，E 的距离（用含x 的式子表示）；(4)已知点P 从点M 到点B 再到点N 共用时20秒，请直接写出点K 在线段QE 上（包含端点）的总时长．。

希望教育 2019年中考数学一轮复习讲义学生：全慧 第一讲 相似三角形1、比例对于四条线段a ，b ，c ，d ，如果其中两条线段的比(即它们长度的比)与另两条线段的比相等，如(即ab ＝bc )，我们就说这四条线段是成比例线段，简称比例线段． 1.若, 则；2．以下列长度（同一单位）为长的四条线段中，不成比例的是（ ）A ．2，5，10，25B ．4，7，4，7C ．2，0.5，0.5，4D ．，，，3．若∶3 =∶4 =∶5 , 且, 则； 4．：若, 则5、已知，求代数式的值．2、平行线分线段成比例定理：平行线分线段成比例定理指的是两条直线被一组平行线（不少于3条）所截，截得的对应线段的长度成比例。

推论：平行于三角形一边的直线，截其他两边（或两边延长线）所得的对应线段成比例。

练习1，如下图，EF∥BC ，若AE∶EB=2∶1,EM=1,MF=2,则AM∶AN=____,BN∶NC=_____2、已知：如图，ABCD ，E 为BC 的中点，BF ︰FA ＝1︰2，EF 与对角线BD 相交于G ，求BG ︰BD 。

3、如图，在ΔABC 中，EF//DC ，DE//BC ，求证： （1）AF ︰FD ＝AD ︰DB ； （2）AD 2＝AF·AB。

3 、相似三角形的判定方法判定0.平行于三角形一边的直线与其他两边或两边延长线相交，所截得的三角形与 判定1. 两个角对应相等的两个三角形__________．a cb d =322=-y y x _____=y x 255225a bc 6=-+c b a ___________,____,===c b a 43===f e d c b a ______=++++f d b e c a 023a b =≠()225224a ba b a b -⋅--判定2. 两边对应成_________且夹角相等的两个三角形相似． 判定3. 三边对应成比例的两个三角形___________． 判定4.斜边和 对应成比例的两个直角三角形相似 常见的相似形式：1. 若DE∥BC（A 型和X 型）则______________．2.子母三角形（1） 射影定理：若CD 为Rt△ABC 斜边上的高（双直角图形） (2)∠ABD=∠c则Rt△ABC∽Rt△ACD∽Rt△CBD 且AC 2=________，CD 2=_______，BC 2=__ ____．（1）练习1、如图，已知∠ADE=∠B ，则△AED ∽__________2、如图，在Rt △ABC 中，∠C=90°，DE ⊥AB 于D ，则△ADE ∽_________3、如图；在∠C=∠B ，则_________ ∽_________,__________ ∽_________4.如图，具备下列哪个条件可以使⊿ACD∽⊿BCA （ ）A B C D 5.下列四个三角形，与右图中的三角形相似的是（ ）6、如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3、4及x ，那么x 的值（ ） A. 只有1个 B. 可以有2个 C. 可以有3个 D. 有无数个4 、相似三角形的性质与应用1. 相似三角形的对应边_________，对应角________．2. 相似三角形的对应边的比叫做________，一般用k 表示．3. 相似三角形的对应边上的_______•线的比等于_______比，周长之比也等于________比，面积比等于_________．练习1、如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O ）20米的A 处，则小明的影子AM 长为 米．E A D CBEA DCBAD CBBC AB CD AC =CD BDAC AB =CB CD AC •=2BD AD CD •=2第3题第2题第1题OAC BACBA BE CDE E DDABCD3、如图，在△ABC 中，M 、N 分别是边AB 、AC 的中点，则△AMN 的面积与 四边形MBCN 的面积比为( )．(A) (B) (C) (D)4、如图，△ABC 中，E 、F 分别是AB 、AC 上的两点，且，若△AEF 的面积为2，则四边形EBCF 的面积为 ．5、如图，在边长为9的正三角形ABC 中，BD=3，∠ADE=60°， 则AE 的长为 ．6.如图，点M 是△ABC 内一点，过点M 分别作直线平行于△ABC 的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分） 的面积分别是4，9和49．则△ABC 的面积是 ．7.如图，在□ABCD 中，E 为CD 上一点，连接AE 、BD ，且AE 、BD 交于点F ，S △DEF ：S △ABF =4：25，则DE ：EC=（ ） A ． 2：5 B ． 2：3 C ． 3：5 D ． 3：28、如图，Rt △ABC 中，∠ACB=90°，∠ABC=60°，BC=2cm ，D 为BC 的中点，若动点E 以1cm/s 的速度从A 点出发，沿着A→B→A 的方向运动，设E 点的运动时间为t 秒（0≤t ＜6），连接DE ，当△BDE 是直角三角形时，t 的值为（ ） A ． 2 B ． 2.5或3.5 C ． 3.5或4.5 D ． 2或3.5或4.55、相似多边形（1）对应边成比例，对应角相等的两个多边形叫做相似多边形． （2）相似多边形的对应角相等，对应边的比相等.（3）相似多边形对应边的比称为相似比． 相似多边形面积的比等于相似比的平方．练习1.如图，在长为8 cm 、宽为4 cm 的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（ ）A. 2 cm 2B. 4 cm 2C. 8 cm 2D. 16 cm 22.（2011.潍坊）已知矩形ABCD 中，AB=1,在BC 上取一点E ,沿AE 将△ABE 向上折叠，使B 点落在AD 上的F 点，若四边形EFDC 与矩形ABCD 相似，则AD=（ ） A ．B ．C ．D ．24、将一个长为a ，宽为b 的矩形，（1）分为相同的两个矩形，且与原矩形相似，求a:b(2) 分为相同的三个矩形，且与原矩形相似，求a:b (3) 割掉一个正方形，剩余的矩形与原矩形相似，求a:b12131423215-215+35、如图，AB∥EF∥CD，（1）AB＝10，CD＝15，AE∶ED＝2∶3，求EF的长。

相似九年级安徽试卷难题专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个省份的九年级学生参加的数学考试中，包含了相似这一章节的难题？A. 安徽省B. 浙江省C. 广东省D. 湖北省答案：A2. 在相似图形中，如果两个三角形的对应角相等，那么它们是：A. 全等三角形B. 相似三角形C. 直角三角形D. 难以确定答案：B3. 下列哪个比例可以表示两个相似三角形的边长比？A. 1:2B. 2:3C. 3:4D. 4:5答案：B4. 如果两个相似三角形的边长比是2:3，那么它们的面积比是：A. 2:3B. 4:9C. 6:9D. 8:27答案：B5. 在相似图形中，如果两个三角形的对应边成比例，那么它们的：A. 面积相等B. 面积成比例C. 角度相等D. 角度成比例答案：B二、判断题（每题1分，共5分）1. 相似图形的面积比等于它们对应边长的平方比。

（√）2. 两个全等三角形的对应边长必须相等。

（√）3. 相似三角形的对应角度必须相等。

（√）4. 两个相似三角形的面积比等于它们对应边长的比。

（×）5. 相似图形的周长比等于它们对应边长的比。

（√）三、填空题（每题1分，共5分）1. 相似图形的面积比等于它们对应边长的____比。

2. 如果两个相似三角形的边长比是3:4，那么它们的面积比是____。

3. 在相似图形中，如果两个三角形的对应边成比例，那么它们的____相等。

4. 相似三角形的对应角度必须____。

5. 两个相似三角形的周长比等于它们对应边长的____。

四、简答题（每题2分，共10分）1. 简述相似图形的定义。

2. 解释相似三角形的性质。

3. 说明相似图形的面积比与边长比的关系。

4. 举例说明相似三角形在实际生活中的应用。

5. 解释全等三角形与相似三角形的区别。

五、应用题（每题2分，共10分）1. 两个相似三角形的边长比是2:3，如果一个三角形的边长是6cm，那么另一个三角形的边长是多少？2. 如果两个相似三角形的面积比是4:9，如果一个三角形的面积是36cm²，那么另一个三角形的面积是多少？3. 两个相似三角形的边长比是3:4，如果一个三角形的周长是18cm，那么另一个三角形的周长是多少？4. 如果两个相似三角形的边长比是5:7，那么它们的面积比是多少？5. 两个相似三角形的边长比是2:5，如果一个三角形的面积是20cm²，那么另一个三角形的面积是多少？六、分析题（每题5分，共10分）1. 分析相似三角形在实际生活中的应用，并举例说明。