2016年数学建模题目
- 格式:docx
- 大小:135.06 KB
- 文档页数:3

2016年数学建模题目
2016年数学建模题目有很多,这里提供几个供参考:
1. 微积分题目:某地区由于气候变化,连续三年遭受了严重的干旱。
该地区有三个水库,每个水库的容量和进水量都不同。
每年干旱季节,该地区需要从这三个水库中抽取一定量的水来满足农业灌溉和居民生活需求。
请设计一个数学模型,根据每年水库的容量、进水量和需求量,确定每年从每个水库中抽取的水量,以确保三年的总抽取量最小。
2. 线性代数题目:某地区有若干个村庄,每个村庄都有一定的居民数量。
这些村庄之间有一定的交通路线,每条路线都有一定的距离和运输成本。
请设计一个数学模型,找出最优的路线和运输方式,使得所有村庄之间的运输成本最小。
3. 概率论与数理统计题目:某地区有若干个工厂,每个工厂都有一定的生产能力和生产成本。
这些工厂之间有一定的物流关系,每条物流都有一定的运输成本和运输时间。
请设计一个数学模型,找出最优的物流方案,使得所有工厂之间的总运输成本最小。
希望这些题目能够给您一些启示。
如需更多信息,建议访问数学建模论坛或请教数学专业人士。

2016数学建模国赛赛题
2016年数学建模国赛赛题一般是指《数学建模入门教程》中的赛题,主要
有以下三类:
1. 问题一:水深测量与海洋动力现象模拟。
要求:使用集中质量法将系统中的各个物体视为一个质点,对各个物体建立静力平衡方程,在水深18m时给定浮标在海水中所受浮力,从而根据建
立的平衡方程求出各物体的倾斜角度,再根据几何关系求出海域的模拟深度。
通过不断修正浮标的浮力,使得海域的模拟深度等于18m,最终求得风速
分别为12m/s和24m/s时浮标的吃水深度和各节钢管的倾斜角度。
2. 问题二:交通流模型与小区开放对周边道路通行的影响。
要求:利用元胞自动机的方法,分别分析不同道路车量位置与车流量变化、负荷系数以及基于交通流的车速。
先对不同小区进行划分,再利用问题一的方法和结论,分别模拟不同小区、不同路段开放小区对车辆通行情况的分析。
最后根据第一问选取出的六个指标,依据其计算公式,分别得出所有样本的所有指标值。
再根据这些指标值,利用投影寻踪法,得到不同小区、不同路段下,开放小区对周围道路通行的影响。
3. 问题三: Braess 悖论。
要求:对于这个问题没有给出具体的要求,因为这是一个理论问题,主要探讨的是网络流理论中的一个著名悖论。
请注意,由于题目较为复杂,建议在数学建模课程或相关论坛中寻找更详细的解答。

全国大学生数学建模竞赛真题试卷复习材料2016年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
C题电池剩余放电时间预测
铅酸电池作为电源被广泛用于工业、军事、日常生活中。
在铅酸电池以恒定电流强度放电过程中,电压随放电时间单调下降,直到额定的最低保护电压(Um,本题中为9V)。
从充满电开始放电,电压随时间变化的关系称为放电曲线。
电池在当前负荷下还能供电多长时间(即以当前电流强度放电到Um的剩余放电时间)是使用中必须回答的问题。
电池通过较长时间使用或放置,充满电后的荷电状态会发生衰减。
问题1 附件1是同一生产批次电池出厂时以不同电流强度放电测试的完整放电曲线的采样数据。
请根据附件1用初等函数表示各放电曲线,并分别给出各放电曲线的平均相对误差(MRE,定义见附件1)。
如果在新电池使用中,分别以30A、40A、50A、60A和70A电流强度放电,测得电压都为9.8伏时,根据你获得的模型,电池的剩余放电时间分别是多少?
问题2 试建立以20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型,并用MRE评估模型的精度。
用表格和图形给出电流强度为55A时的放电曲线。
问题3 附件2是同一电池在不同衰减状态下以同一电流强度从充满电开始放电的记录数据。
试预测附件2中电池衰减状态3的剩余放电时间。


2016数学建模竞赛题目
我国未来5年粮油产量等预测(2人完成)粮食是一个国家稳定的基础。
我国长期重视粮食生产。
随着城镇化建设,我国未来粮食生产情况是涉及国计民生的大问题。
请研究以下问题:
1.搜集1975年-2015年每隔5年全国小麦,水稻,玉米,棉花,油料,杂粮以下农作物的种植面积、产量和进口量数据(例如1975,1980,1985,…,或1976,1981,….,),并进行数据分析和述评,探讨我国农业生产存在的问题,提出保障我国居民生活安全的意见和建议。
2. 预测未来5年我国主要农产品(小麦、水稻、玉米、油菜籽)的产量、需求和对外依存度。
3. 据国家统计局统计,2014年全国玉米产量21567.3万吨,2014年1~12月中国玉米进口259.8万吨,2015年我国玉米产量22458.0,同时进口玉米720万吨(2016拟计划进口720万吨)。
由于玉米供大于求,2015年国家发改委取消了2007年以来实施的东北三省和内蒙古自治区实行玉米临时收储政策,玉米收购价格由2014年的1.2元/斤下降到0.70元/斤,全国玉米种植户减少收入1000亿元。
试分析这些情况对未来我国玉米和其它农作物生产的影响,并为我国农业管理部门提出意见和建议。

2016数学建模d题摘要:一、数学建模简介1.数学建模的定义2.数学建模的重要性3.数学建模的应用领域二、2016 数学建模D 题背景及内容1.题目背景2.题目内容3.题目难度及挑战三、解题思路及方法1.问题分析2.解题思路3.常用数学建模方法四、2016 数学建模D 题案例分析1.案例一2.案例二3.案例三五、总结与反思1.2016 数学建模D 题的启示2.数学建模能力的培养3.对未来数学建模比赛的展望正文:数学建模是一种运用数学方法解决实际问题的过程,它涉及到多个学科领域,如统计学、计算机科学、经济学等。
数学建模在现代社会具有很高的实用价值,可以帮助我们更好地理解世界、预测未来和优化决策。
在我国,数学建模竞赛是一项重要的赛事,吸引了大量的高校学生参与。
2016 年的数学建模D 题以“飞行器航迹优化问题”为背景,要求参赛者针对给定的飞行器、目标和航路约束条件,设计出一种飞行器航迹优化算法。
该题目具有一定的难度和挑战性,需要参赛者具备较强的数学功底和实际问题解决能力。
在解题过程中,首先要对题目进行深入分析,明确问题的关键信息和隐含条件。
然后根据问题特点,选择合适的解题思路和方法。
常用的数学建模方法有:线性规划、动态规划、遗传算法、模拟退火算法等。
为了更好地理解2016 数学建模D 题,我们可以通过以下三个案例进行分析:案例一:采用线性规划方法求解飞行器航迹优化问题。
通过建立线性目标函数和约束条件,求解最优航迹。
该方法简单易行,但对于复杂问题可能无法得到全局最优解。
案例二:利用动态规划方法解决飞行器航迹优化问题。
通过将问题拆分为子问题,并采用动态规划的思想,逐步求解子问题,最终得到全局最优解。
该方法在时间复杂度上具有优势,但在空间复杂度上可能较高。
案例三:采用遗传算法求解飞行器航迹优化问题。
通过模拟自然界的生物进化过程,对飞行器航迹进行迭代优化。
遗传算法具有全局搜索能力,能够较快地找到最优解,但可能受初始种群和参数设置的影响。

用方格因子影响模型探究小区开放对道路通行的影响摘要目前我国人口增长,各种大型小区增多,各小区家庭拥有小汽车量也在增多,根据我国的道路交通设计和城市规划设计,我国的道路交通存在着严重问题,所以对交通的通行能力有着较大需求,本题将要分析的是,如果常规的封闭性小区开放,那周边道路通行会出现怎样的变化。
关于第一问,本文选取五个交通参数,道路通行能力、道路网的饱和度、车道交通流量比、车辆的延误时间、饱和流量;可以由各个指标来衡量小区开放以后对周围道路的交通状况的影响。
关于第二问,先将城市交通道路网格化,再建立方形小区内点对之间的最优路径寻模型,通过分析交通网格化下的封闭性小区开放之后,小区内的各个点对之间的各个路径中,最优路径是否存在,同时可以计算得出小区的面积及位置对点对间交通便捷度影响因子的影响,通过因子分析法来计算并寻找最优路径,从而判断周边道路的交通状态,是否会因为小区的开放而得到缓解。
关于第三问,分析其开放前后小区对周边道路的交通通行带来的影响;从参考资料中选取一个城市小区,通过对小区结构以及道路结构对其道路通行能力的分析。
同时构建一个方形小区,通过假设其开放前和开放后的各类数据,进行一个辅助比较,通过这两种类型的小区,并应用第一问与第二问中的模型,发现打破一个封闭小区,可以使得周边道路上车辆的通行能力增加,即使得交通状况有所改善。
第四问要求从交通通行的角度提出建议,通过以上三问对开放性小区评价指标、周边道路交通体系、长沙市某具体小区与构建的虚拟小区等的研究结果,向相关部门提出了对小区开放的合理建议。
关键字:小区开放;道路通行能力;最优路径;饱和流量;交通便捷度影响因子一、问题重述近几年,我国经济飞速发展,在GDP上升的同时,封闭型的小区也越来越多,政府、开发商、居民等也越来越多的居住于封闭型小区,同时私家车在我国城市居民家庭中的数量越来越多,逐步普及。
这给各个道路的交通,以及小区周边的道路交通造成了巨大压力,可以说城市道路交通拥堵的问题变得不容忽视。

风电场运行状况分析及优化模型摘要在充分理解题意及合理假设的基础上,通过对问题的深入分析,利用Excel 对数据处理分析,建立了风能资源利用情况模型并对其进行评估;对实测风速和功率的拟合,建立了最优风机选择模型;最后从经济效益最大化为主要目标,通过多目标规划,建立人员分配模型,进行人员排班优化。
·问题一:为了研究该风电场的风能资源和风能资源的利用情况,对附件1的数据处理及分析,然后对原始数据的完整性和合理性进行判断,选择合理数据,计算出年、月、日的平均风速和各时期的平均功率。
根据平均风功率密度公式311()()2nwp i i D v n ρ==∑计算出平均风功率密度为290.39/wp D W m =。
然后对其进行评估,根据wp D 和风的功率wp =n P D S ⋅⋅风计算出风能利用率为40.92%。
根据贝茨极限得出大型风力发电机对风能的最高利用率为59.3%,从而得出该风电场的风能利用率相对合理,进而可以判断该风电场的风能资源利用情况较好。
·问题二:从风能资源与风机匹配角度出发,根据附件2风速信息,对数据进行聚类分析,并绘制频率分布直方图,并得出一期和二期工程风机的年平均风速均为6/m s 。
根据附件3的数据,通过最小二乘法对各期风速和功率进行数据拟合,得出系数k 越大,发电效果越好。
对附件4中新型电机的参数分析,计算出系数k 值。
最终,得出新型风机功效略好于二期工程,相较一期工程功效略差,因此新型风机比二期风机更适合此风力发电厂,应使一期工程与新型风机作为发电厂设备。
·问题三:以风电场经济效益最大化为主要目标,通过分析风电场的效能为出发点,先确立风机停机维护时段的基础上,再运用“0-1”规划建立人员分配模型,用枚举法得到人员排班方案,从而得到每组两天轮班工作并由在3月4日至5日、8月20日至21日值班人员进行停机维护的工作排班方案。
本文还进一步建立了多目标规划的人员分配模型,并进一步检验,得到值班与提及维护分立进行的模式以每组一天轮流值班并分别于每年的三月上旬和八月下旬进行停机维护,每年两组轮换进行维护。
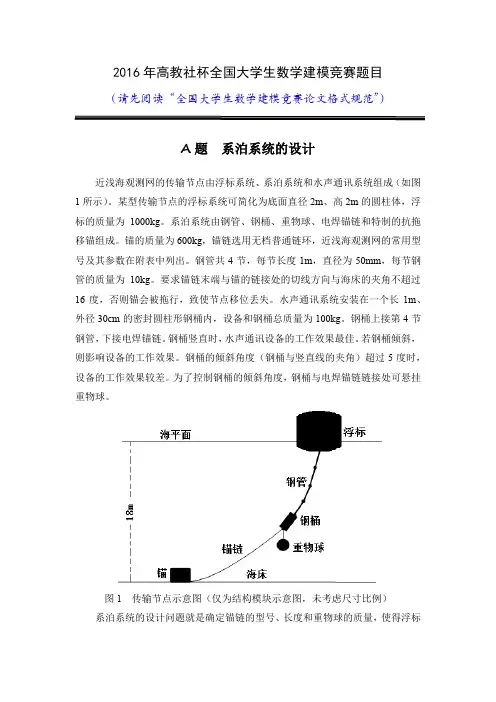
2016年高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。

2016年高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。

2016数学建模d题一、题目背景介绍2016年数学建模D题背景涉及我国某地区交通规划问题。
为了缓解交通拥堵,提高道路利用率,需要对交通信号灯的控制策略进行优化。
题目给出了某地区一段时间内的车辆流量数据,要求我们设计一种合适的信号灯控制策略,使得车辆等待时间最短,道路利用率最高。
二、数学建模方法概述针对这道题目,我们可以采用以下数学建模方法:1.建立车辆等待时间模型:根据车辆到达时间、离去时间和绿灯时长,计算每辆车的等待时间。
2.建立道路利用率模型:根据道路上车流量和时段,计算道路的利用率。
3.优化模型:通过调整信号灯的控制策略,使得车辆等待时间和道路利用率达到最优。
三、解题思路与步骤1.数据预处理:对给出的车辆流量数据进行整理,提取关键参数。
2.构建车辆等待时间模型:根据关键参数,使用排队论方法建立车辆等待时间模型。
3.构建道路利用率模型:结合车辆等待时间模型,建立道路利用率模型。
4.设计优化算法:采用遗传算法、粒子群算法等优化方法,求解最优信号灯控制策略。
5.模型检验与优化:通过仿真实验,检验模型效果,并对模型进行优化。
四、具体计算过程与结果分析1.数据预处理:将给出的车辆流量数据进行排序,提取出各个时段的车流量。
2.车辆等待时间模型:根据车流量和绿灯时长,计算每辆车的等待时间。
3.道路利用率模型:根据车流量和时段,计算道路的利用率。
4.优化模型:通过调整绿灯时长和绿闪时间,使得车辆等待时间和道路利用率达到最优。
5.模型检验与优化:通过仿真实验,对比不同信号灯控制策略下的车辆等待时间和道路利用率,找出最优策略。
五、结论与启示1.通过数学建模方法,成功解决了交通信号灯控制策略优化问题。
2.最优信号灯控制策略可以有效降低车辆等待时间,提高道路利用率。
3.本次建模过程中,掌握了数据处理、模型构建、优化求解等关键步骤。
4.在实际应用中,可以进一步结合实际情况,对模型进行调整和优化。
综上,通过数学建模方法,我们可以为交通信号灯控制策略优化提供有力支持。
2016年数学建模考试题一.(本题满分50分)设E 为位移算子,I 为恒等算子(也称单位算子)1. (15分) 求解初值问题:243,3(0)1,(1).2()()3k E I y y y E k -+==⎧=⎪⎨⎪⎩ 2. (15分)设1302Q -⎛⎫= ⎪-⎝⎭,求如下线性差分方程组的通解: ()()E k Q k ψψ=3. (20分)考虑方程322(2)(4)(26)()()k E I E I y k k k EI k -+=+++,(1)给出对应齐次方程的通解: (2)写出非齐次方程的特解形式,二.(本题满分25分)设甲、乙两个种群,当它们独自在个自然环境中生存时,数量的演变遵从Logistic 方程,而当这两个种群在同一个自然环境中生存时, 为了争夺有限的同一种食物来源,它们之间存在生存竞争关系。
在适当假设下,甲乙两个种群的数量1()x t ,2()x t 满足如下模型1211112()(1)x x x t r x N N α=--,22121221()(1)x x x t r x N N α=--- 其中12,r r 为种群固有增长率,12,N N 为最大容纳量,,(11)ααα≠是竞争同一种食物来源时对另外一方增长产生影响的相关参数,以上参数均为正常数。
求该模型平衡点,并讨论平衡点稳定性。
三(本题满分25分)设渔场鱼量的自然增长服从Gompertz 模型; ()ln N x t rx x=.其中()x t 是渔场鱼量,r 是固有增长率,N 是最大容纳量。
现考虑捕捞,设单位时间捕捞量为()h Cx t =,其中C 是捕捞强度,(1)建立具有捕捞的渔场鱼量变化模型,并讨论平衡点及其稳定性;(2)求最大持续产量h ∞及获得最大产量时的捕捞强度C ∞,。
2016数学建模d题摘要:1.题目背景介绍2.数学建模D题分析3.解题思路与方法4.具体步骤详解5.模型检验与优化6.结论与启示正文:一、题目背景介绍数学建模D题是2016年数学建模竞赛的一个题目,题目背景涉及我国城市交通规划与管理。
参赛者需要根据题目要求,构建一个数学模型,对城市交通进行优化,以提高道路通行能力和减少拥堵现象。
二、数学建模D题分析数学建模D题主要涉及以下几个方面:城市交通网络、车辆路径规划、交通拥堵、道路拓宽、公交线路优化等。
为了更好地解决这些问题,我们需要对城市交通网络进行深入分析,找出拥堵的原因,并提出合理的解决方案。
三、解题思路与方法1.数据收集:收集城市交通相关数据,如道路网络、交通流量、出行时间、公交线路等。
2.数据预处理:对收集的数据进行清洗、整理和转换,以便于后续建模分析。
3.建立模型:根据题目背景和分析结果,选择合适的数学模型,如图论模型、网络优化模型、动态规划模型等。
4.模型求解:利用编程工具或数学软件,求解所建立的模型,得到优化结果。
5.模型检验与优化:检验模型的有效性,根据实际情况对模型进行调整和优化。
四、具体步骤详解1.数据收集:通过网络、文献、政府部门等渠道获取城市交通相关数据。
2.数据预处理:将原始数据转化为可用于建模的格式,如道路网络表示为有向图、交通流量表示为邻接矩阵等。
3.建立模型:根据题目要求,选择合适的数学模型。
例如,利用图论模型求解最短路径问题,利用网络优化模型求解最大流问题,利用动态规划模型求解公交线路优化问题等。
4.模型求解:利用编程工具或数学软件,如MATLAB、Python等,求解所建立的模型。
5.模型检验与优化:检验模型的有效性,如道路拓宽、公交线路优化等。
根据实际情况,对模型进行调整和优化。
五、结论与启示通过对2016年数学建模D题的分析和求解,我们可以得出以下结论:1.城市交通优化是一个复杂的问题,需要综合考虑多种因素。
2.数学建模是一种有效的解决交通优化问题的方法,可以帮助我们更好地理解城市交通现象。
关于联想时滞反馈神经网络的设计和研究大脑是人体最为复杂的信息处理系统. 联想记忆(Associative Memory, AM) 是人脑的重要认知功能之一。
联想记忆神经网络是模拟大脑, 能将一些样本模式存储在神经网络的权值中,通过大规模的并行计算, 使不完整的(损坏的)、受到噪声“污染”的畸变模式恢复到原有的模式。
自联想记忆是指由受损的输入模式恢复到完整的模式本身;异联想记忆是指由输入模式获得与之相关的其他模式。
例如, 听到1 首歌曲的一部分便可以联想到整个曲子, 看到某人的名字会联想到他( 她) 的相貌等特点。
前者称为自联想( Self-Association) , 而后者称为异联想(Hetero- Association)。
在联想记忆中,神经网络的渐近稳定的平衡点被用来产生稳定的记忆。
总的说来,基于递归神经网络的联想记忆设计中通常有两种联想模式方法[1]。
在第一种方法中,一个提示信息被设定为初始条件且激活状态收敛到一个渐近稳定的平衡点。
因为每一个平衡点有一个吸引区域,所以如果这个模式用相应的平衡点编码且初始条件位于吸引区域中,那么称这个模式被联想记住了。
外积方法、特征结构方法、奇异值分解方法、感知器训练方法和伪逆技巧都是用于这种设计[5]。
在第二种方法中,提示信息被用作输入而不是初始条件(基于外部输入),这时要求神经网络有一个全局渐近稳定的平衡点(或全局指数稳定的平衡点),不同的输入对应于不同的平衡点[1]。
问题如下:1. 输出记忆模式为(1)(2)(3)(4)(5),,,,p p p p p (如图1) ,构造自联想连续型神经网络建立数学模型. 给出设计过程,实现自联想设计。
进行仿真,给出5组随机噪声条件下(或有畸变的)的输入模式能得到自联想输出模式(例如图2给出了一组由随机噪声的输入模式恢复到正确的自联想模式) 。
(注:问题1-4可以考虑激励函数1,1(),111,1x f x x x x -<-⎧⎪=-≤≤⎨⎪>⎩或其他激励函数来设计)。
2016数学建模d题摘要:I.引言A.背景介绍B.问题描述C.目的和意义II.传染病传播模型A.SIR 模型B.SEIR 模型C.传播速度和影响因素III.控制策略分析A.隔离措施B.疫苗接种C.药物干预D.综合控制策略IV.模型建立与求解A.模型参数设定B.数学模型建立C.求解方法和过程V.结果与讨论A.疫情传播趋势分析B.控制策略有效性分析C.结果的启示和意义VI.结论A.主要发现和结论B.研究局限与展望正文:I.引言A.背景介绍:随着全球化的发展,传染病的传播速度和范围不断扩大,给人类健康带来了严重威胁。
因此,对传染病传播的建模和控制策略研究具有重要的现实意义。
B.问题描述:2016 数学建模d 题要求参赛者针对某一传染病,建立数学模型,分析疫情传播的速度、影响因素和控制策略。
C.目的和意义:通过对传染病传播的数学建模,为政府和相关部门制定传染病防控政策提供理论依据。
II.传染病传播模型A.SIR 模型:SIR 模型由易感者(Susceptible)、感染者(Infected)和康复者(Recovered)三个部分组成,描述了疫情在人群中的传播过程。
B.SEIR 模型:SEIR 模型在SIR 模型的基础上增加了潜伏期(Exposed)的概念,使得模型更能反映实际情况。
C.传播速度和影响因素:传染病传播的速度受到感染率、隔离措施、人群流动性等因素的影响。
III.控制策略分析A.隔离措施:隔离措施是控制传染病传播的重要手段,包括居家隔离、集中隔离、限制出行等。
B.疫苗接种:疫苗接种可以提高人群免疫力,降低感染率,是预防传染病传播的重要措施。
C.药物干预:针对病毒或细菌的药物干预,可以降低感染者的传染性,加速康复过程。
D.综合控制策略:结合多种控制策略,从多个角度遏制疫情传播。
IV.模型建立与求解A.模型参数设定:根据题目所给信息,设定模型参数,如感染率、康复率等。
B.数学模型建立:根据SIR 或SEIR 模型,建立传染病传播的数学模型。
2016年数模国赛题目
2016年数学建模国赛共有多道题目,以下是其中一道题目的详
细描述:
题目,城市交通网络规划。
背景,某城市的交通网络规划需要进行优化,以提高交通效率
和减少交通拥堵。
要求,设计一个合理的交通网络规划方案,使得城市内的交通
流畅,同时最小化交通拥堵和行驶时间。
问题一,基于已有的道路和交通流量数据,确定各个路段的通
行能力和拥堵情况,并构建一个合适的交通网络模型。
问题二,根据问题一中的交通网络模型,通过合理的交通信号
灯控制策略,优化交通信号灯的配时方案,以最大程度地提高交通
流畅性。
问题三,考虑到城市交通网络的日常变化和特殊事件(如事故、
施工等),设计一套自适应的交通管理系统,能够及时调整交通信号灯配时方案,并提供实时的交通信息给驾驶员和交通管理部门。
问题四,对于未来城市交通发展,结合人口增长和城市规划,提出相应的交通网络扩建和改造方案,以适应未来的交通需求。
以上仅是2016年数学建模国赛的其中一道题目,其他题目的具体描述可能会有所不同。
在比赛中,参赛者需要结合数学建模方法和工程实践,综合运用数学、计算机科学、交通规划等知识,提出创新性的解决方案,并进行模型验证和结果分析。
关于联想时滞反馈神经网络的设计和研究
大脑是人体最为复杂的信息处理系统. 联想记忆(Associative Memory, AM) 是人脑的重要认知功能之一。
联想记忆神经网络是模拟大脑, 能将一些样本模式存储在神经网络的权值中,通过大规模的并行计算, 使不完整的(损坏的)、受到噪声“污染”的畸变模式恢复到原有的模式。
自联想记忆是指由受损的输入模式恢复到完整的模式本身;异联想记忆是指由输入模式获得与之相关的其他模式。
例如, 听到1 首歌曲的一部分便可以联想到整个曲子, 看到某人的名字会联想到他( 她) 的相貌等特点。
前者称为自联想( Self-Association) , 而后者称为异联想(Hetero- Association)。
在联想记忆中,神经网络的渐近稳定的平衡点被用来产生稳定的记忆。
总的说来,基于递归神经网络的联想记忆设计中通常有两种联想模式方法[1]。
在第一种方法中,一个提示信息被设定为初始条件且激活状态收敛到一个渐近稳定的平衡点。
因为每一个平衡点有一个吸引区域,所以如果这个模式用相应的平衡点编码且初始条件位于吸引区域中,那么称这个模式被联想记住了。
外积方法、特征结构方法、奇异值分解方法、感知器训练方法和伪逆技巧都是用于这种设计[5]。
在第二种方法中,提示信息被用作输入而不是初始条件(基于外部输入),这时要求神经网络有一个全局渐近稳定的平衡点(或全局指数稳定的平衡点),不同的输入对应于不同的平衡点[1]。
问题如下:
1. 输出记忆模式为(1)(2)(3)(4)(5),,,,p p p p p (如图1) ,构造自联想连续型神经网络建立数
学模型. 给出设计过程,实现自联想设计。
进行仿真,给出5组随机噪声条件下(或有畸变的)的输入模式能得到自联想输出模式(例如图2给出了一组由随机噪声的输入模式恢
复到正确的自联想模式) 。
(注:问题1-4可以考虑激励函数1,1(),111,1x f x x x x -<-⎧⎪=-≤≤⎨⎪>⎩
或
其他激励函数来设计)。
图1(黑色的为-1,白色为
1)
图2
2. 给定输入模式: (1)(2)(3),,u u u (图3),对应的输出记忆模式为: (1)(2)(3),,p p p (图4), 构造
异联想神经网络建立数学模型,给出参数分类条件和设计过程,使得状态变量收敛到平衡点,实现异联想设计; 进行仿真, 实现无噪声(或无畸变)的输入模式得到异联想输出模式,即()(),1,2,3i i u p i →= (如图5). a.要求模型中考虑时间延迟对神经网络的影响
图3
图4
图5
3. 利用问题二中模型, 实现给出5组随机噪声条件下(或有畸变的)的输入模式能得到异联
想输出模式(例如图6给出了一组由随机噪声的输入模式恢复到正确的异联想模式) 。
a.分析存储容量。
b.分析加入不同程度噪声(或畸变)是否能实现联想记忆。
图6
4. 在1971年c 蔡少棠就预言有第四种基本的无源性电路元件存在。
他指出忆阻[2]是连接
电荷和磁通之间的关系量,而且忆阻能够记住流过它的电流和断电时本身的阻值。
直到2008年,Williams 和他的同事们宣称他们制造出了纳米级的固体忆阻并把他们的结果发表在《自然》杂志上。
至此忆阻得到了广泛的研究和应用. 要求建立忆阻递归神经网络模型实现异联想记忆(()(),1,2,3i i u p i →=)。
5. 考虑运用不同的激励函数(例如墨西哥帽子[4] 1,1,11()2,131,
3x x x f x x x x -<-⎧⎪-≤≤⎪=⎨-+≤≤⎪⎪>⎩), 寻找一个实际应用,实现多模式分类,并加以实现.
参考文献:
1. Zhigang Zeng and Jun Wang. Design and analysis of high-capacity associative memories
based on a class of discrete-time recurrent neural networks. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on 38.6 (2008): 1525-1536
2. 鲍 刚. 基于忆阻递归神经网络的联想记忆分析与设计 (2012)
3. 周开利, 康耀红. 神经网络模型及其MATLAB 仿真程序设计. 北京:清华大学出版社
(2011)
4. Xiaobing Nie , Wei Xing Zheng , Jinde Cao. Multistability of memristive Cohen –Grossberg
neural networks with non-monotonic piecewise linear activation functions and time-varying delays(2015):27-36
5. Zheng P, Tang W, Zhang J. Efficient continuous-time asymmetric Hopfield networks for
memory retrieval[J]. Neural computation, 2010, 22(6): 1597-1614。