中考数学 弧长和扇形的面积、圆锥的侧面积和全面积辅导练习(无答案)

2.7-2.8弧长及扇形的面积与圆锥的侧面积【推本溯源】因此，半径为R 的圆中360°的圆心角所对的弧长(圆的周长)公式：n °的圆心角所对的圆的弧长公式：l=180rn π(弧是圆的一部分)。

注：（1）对于弧长公式，关键是要理解1°的圆心角所对的弧长是圆周长的，即；（2）公式中的ｎ表示1°圆心角的倍数，故ｎ和180都不带单位，R 为弧所在圆的半径；（3）弧长公式所涉及的三个量：弧长、圆心角度数、弧所在圆的半径，知道其中的两个量就可以求出第三个量.扇形面积：（1）定义：由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形（2）面积公式：半径为R 的圆中360°的圆心角所对的扇形面积(圆面积)公式：；n °的圆心角所对的扇形面积公式：注：（1）对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即；（2）在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.（3）扇形面积公式，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；（4）扇形两个面积公式之间的联系：.2.回顾小学时候学习的圆锥（1）圆锥的概念：由一个底面和一个侧面围成的几何体，圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周所形成的几何体。

（2）圆锥的母线：连接圆锥顶点和底面圆上任意一点的线段；（3）圆锥的高：连接圆锥顶点与底面圆心的线段叫做圆锥的高。

我们通常令圆锥的母线长为，底面半径为r，侧面展开图中的扇形圆心角为n°，所以圆锥的侧面积2360lS rlππ=扇n=；圆锥的全面积.【解惑】A ．20cm πB ．10cm π【答案】B【分析】根据弧长公式求解即可．【详解】解：弧的半径20cm OA =，圆心角∴»902010180AB ππ⨯==，A ．12183π-B ．1236π-【答案】A【分析】根据折叠，ACB AOB ≌△△6OC OB BC ===得到OBC △是等边三角形；最后阴影部分面积面积，即可求解．【详解】依题意：ACB AOB ≌△△∴6AC BC AO BO ====∴四边形OACB 是菱形∵6OC OB ==∴6OC OB BC ===∴OBC △是等边三角形同理：OAC 是等边三角形故120AOB ∠=︒由三线合一，在Rt OBD △中：∵1302OBD OBC ∠=∠=︒，∴132OD OB ==，3BD OD =【答案】15π【分析】由几何体的主视图和左视图都是等腰三角形，俯视图是圆，圆锥，结合图形可得出圆锥的高及底面半径，继而可求出圆锥侧面展开图的半径，求解．106.8m【答案】2【分析】根据扇形面积公式求出圆锥的侧面积，柱的侧面积，即可求解．【详解】解：由题意，得圆锥的侧面积为：圆柱的侧面积为：4π【摩拳擦掌】上的点，且直线AB与CD夹1．（2023·浙江·九年级假期作业）如图，A，B，C，D为O的半径是（）角为45︒．若 AB， AC， CD的长分别为π，π和3π，则OA．4B．4.5C．5D．5.5【答案】A【分析】延长BA，与直线CD交于E，连接BD，设弧长为π所对的圆周角为α，根据题意【点睛】本题考查弧长的计算，圆周角定理，同弧或等弧所对的圆周角相等，三角形内角和定理，求得弧长为π所对的圆心角是解题的关键．2．（2023·浙江·九年级假期作业）如图，四边形=，若130AC AD∠=︒，ABC【点睛】弧长公式等知识，综合运用这些知识是解题的关键．3．（2023·内蒙古赤峰·统考中考真题）图，这个圆锥的底面圆周长为带进行装饰，其中需要粘贴一条从点vA．30cm【答案】B【分析】根据圆锥的底面圆周长求得半径为120︒，进而即可求解．【详解】解：∵这个圆锥的底面圆周长为故选：B．【点睛】本题考查了圆锥侧面展开图的圆心角的度数，开图的圆心角为120︒解题的关键．【答案】20010033π⎛⎫+ ⎪⎝⎭【分析】根据题意，先找到圆心O ，然后根据B ．60P ∠=︒可以得到AOB ∠的度数，然后即可得到优弧图的面积为PAO PBO AMB S S S ++扇形△△计算即可．【详解】解：设圆心为O ，过O 作AO PA ⊥如图，∵PA ，PB 分别与扇形AOB中，6OA=，∴==，OC OA6将扇形AOB翻折，使点A与圆心∴==，CD AOAD OD3⊥，∴=，OC AC∴===，6OC AC AO【答案】5π【分析】把半径和圆心角代入弧长公式即可；【详解】150********n r l πππ⨯⨯===故填：5π．【点睛】本题考查弧长公式的应用，准确记忆公式，并正确代入公式是解题的关键．【答案】24π-/42π-+【分析】连接OE OC ，，15BCE ∠=︒，证得BOE ∠可得面积．【详解】解：连接OE ，由旋转知AC AD CAD =∠，∴60BOC ACE ∠=︒∠，∴90BCE ACE ∠=-∠=︒∴230BOE BCE ∠=∠=∴90EOC ∠=︒，(1)计算这个圆锥侧面展开图的面积；(2)求这个圆锥的底面半径．【答案】(1)2π(1)若2r =，求 BD的长．(2)若,AB CD AB =∥【答案】(1)149π(2)见解析【分析】（1）连接OB 140BOD ∠=︒，根据弧长的公式即可得到结论；（2）根据AB DB =，得260COD DBC ∠=∠= 四边形ABCD 内接于70A ∴∠=︒，140BOD ∴∠=︒，∴ BD 的长为1402180π⨯（2）证明：AB DB = 70A ADB ∴∠=∠=︒，40ABD ∴∠=︒AB CD ∥ ，40BDC ABD ∴∠=∠=︒，1801104030DBC ∴∠=︒-︒-︒=︒，260COD DBC ∴∠=∠=︒，OC OD = ，OCD ∴△为等边三角形，CD OC r ∴==．【点睛】本题考查的是圆周角定理、弧长的计算、圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键．【知不足】1．（2023·湖南·统考中考真题）如图，圆锥底面圆的半径为4，则这个圆锥的侧面展开图中 AA '的长为（）A ．4πB ．6πC ．8πD ．16π【答案】C 【分析】根据底面周长等于 AA '，即可求解．【详解】解：依题意， AA '2π48π=⨯=，故选：C ．【点睛】本题考查了圆锥的侧面展开图的弧长，熟练掌握圆锥底面周长等于 AA '是解题的关键．2．（2023·河北保定·统考模拟预测）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问积及为米几何？”译文：屋内墙角处的米堆为一个圆锥的四分之一（如图），米堆底部的弧长为8尺，米堆的高为5尺，那么这个米堆遮挡的墙面面积为（）A ．80π平方尺B ．160π平方尺C ．128π平方尺【答案】A【分析】设米堆底部的扇形半径为r ，则由米堆底部的弧长为出方程，求出该米堆的底面半径，再根据三角形的面积公式，面积．【详解】解：设米堆底部的扇形半径为r ，则由米堆底部的弧长为2π84r =，A ．223m πB ．23m π【答案】A∵,AO BO =∴1,2AD BD AB ==∵302m,OAB OA ∠=︒=，∴11m,2OD OA ==∵PM 、PN 分别与 ∴OM PM ⊥，ON ⊥∴OMP ONP ∠∠==∴360MON ∠∠=︒-∠①AB为直径；②ACD(1)从三条信息中选择两条作为条件，另一条作为结论，组成一个真命题．你选择的条件是___________(2)在（1）的条件下，若（2）解：由（1）可知，如图所示，连接OD ，∴22AOD ACD ∠=∠=⨯∵ AD 的长为43π，设 1204r π【点睛】本题考查圆的基本性质，圆周角定理，弧长计算，等腰三角形的判定和性质，三角形外角的性质等，理解直径所对的圆周角为直角及其推论，掌握弧长计算公式是解题关键．9．（2022秋·江苏宿迁·一条圆弧经过网格点A 、(1)请在图中确定该圆弧所在圆心(2)连接AD CD 、，则D 的半径为(3)若扇形DAC 是某一个圆锥的侧面展开图，求该圆锥的底面半径．【答案】(1)画图见解析，(2（3）解：由题意得，该圆锥的底面半径为【点睛】本题考查了垂径定理的推论以及圆锥的有关计算，到的知识点为：非直径的弦的垂直平分线经过圆心；长．10．（2023·安徽安庆·统考一模）如图，圆锥侧面展开得到扇形，此扇形半径【答案】22【分析】设圆锥底面圆的半径为底面圆的半径，再根据勾股定理即可求出结果【详解】解：设圆锥底面圆的半径为∵3AC ACB =∠，【一览众山小】1.（2023·江苏南通·统考二模）如图为某几何体的三视图，则该几何体的侧面积是（）A ．36πB ．48πC ．60πD ．96π【答案】C 【分析】根据三视图有圆，有三角形，由此可判断该几何体是圆锥；从图可看出该圆锥的底A．π【答案】B【分析】根据圆锥底面圆的周长等于它侧面展开图扇形的弧长，周长即可．【详解】解：∵圆锥底面圆的半径为A．3B．6【答案】B【分析】求得扇形的弧长，进而求出圆锥的底面周长，即可求出圆锥的底面半径．【详解】解：∵圆形纸片的半径为9cm制作这种外包装需要用如图所示的等腰三角形∠=︒，将扇形DOE围成圆锥时，ODAOB90锥底面的直径．∵弧DE 与AB 相切，∴90OFB ∠=︒，∵12cm AO BO ==，AOB ∠222+12+12AB AO BO ==【答案】10π【分析】利用弧长公式π180n r l =直接计算即可．【详解】∵半径15m OA =，圆心角AOB ∠∴AB l 120π1510π180⨯⨯==，【答案】245π【答案】28cm π/8π平方厘米【分析】根据圆周角定理由∠三角形的性质得42AB =，然后用圆的面积减去扇形的面积即可求解．【详解】∵90ABC ∠=︒，∴AC 为O 的直径，即AC =【点睛】本题考查了扇形的面积计算以及圆周角定理，式．11．（2023秋·河南周口·九年级校考期末）图图2），制作这种外包装雷要用如图将扇形EAF 围成圆锥时，AE ，12AD =cm ．(1)求这种加工材料的顶角BAC ∠的大小．(2)求加工材料剩余部分（图中阴影部分）的面积．（结果保留π）【答案】(1)90BAC ∠=︒(2)14436π-(1)若该圆弧所在圆的圆心为(2)连接AD 、CD ，则D 的半径长为(3)若扇形ADC 是一个圆锥的侧面展开图，求该圆锥的底面圆的半径长．（结果保留根号）【答案】(1)()4,0-；(2)45，90；(3)5．【分析】（1）连接BC 、AB 结合网格得到D 点坐标；（2）利用勾股定理求出AD 为直角三角形，从而得到∠（3）设该圆锥的底面圆的半径长为程即可．【详解】（1）解：连接BC 由各点坐标可知，网格中1利用网格特点，作线段BC 、如图所示，则点D 的坐标为()4,0-，故答案为：()4,0-；（2）连接AC ，如图，224845AD =+=，即D 的半径长为45；2280AD CD == 222412160AC =+=222AD CD AC ∴+=，ADC ∴ 为直角三角形，ADC ∠故答案为：45；90；（3）设该圆锥的底面圆的半径长为由题意可得：90·452180r ππ=，解得：5r =，即该圆锥的底面圆的半径长为5【点睛】本题考查了圆锥的计算：∠；(1)求证：BD平分ABC(2)若点E恰好是AO的中点，求扇形【答案】(1)见解析(2)2π3相切于点D，AC与O=6AB ，E 是AO 的中点，2AE OE OB \===，在Rt AOD 中，12DE AO OE ==DE OD OE ∴==，DOE ∴△为等边三角形，相切；(1)求证：CD与O=，求扇形(2)若2AD=，CD CB【答案】(1)见解析(2)2π∠=∠=（2）由（1）可得：ACD B =，∵CD CB∴D B∠=∠，∠=∠=∠=∠，∴ACD B OCB D。

圆的计算问题中考演练1.圆锥的底面半径为4cm ，高为5cm ，则它的表面积为（ ）A ．12πcm 2B ．26πcm 2C ．πcm 2D ．（4+16）πcm 22.已知圆锥的母线长是12，它的侧面展开图的圆心角是120°，则它的底面圆的直径为（ ） A ．2 B ．4 C ．6 D ．83.如图，圆锥的底面半径r 为6cm ，高h 为8cm ，则圆锥的侧面积为（ ）A ．30πcm 2B ．48πcm 2C ．60πcm 2D ．80πcm 24.如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小A ．90°B ．120°C ．135°D ．150° 5.已知圆锥的底面半径为4cm ，母线长为6cm ，则它的侧面展开图的面积等于（ ） A ．24cm 2 B ．48cm 2 C ．24πcm 2 D ．12πcm 26.如图，从一张腰长为60cm ，顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（ ）A ．10cmB ．15cmC ．10cm D ．20cm 7.如图，已知圆锥的高为，高所在直线与母线的夹角为30°，圆锥的侧面积为 ．3题4题7题9题10题8.若一个圆锥的底面半径为2，母线长为6，则该圆锥侧面展开图的圆心角是 ． 9.在Rt △ABC 中，∠ACB=90°，AC=2，以点B 为圆心，BC 的长为半径作弧，交AB 于点D ，若点D 为AB 的中点，则阴影部分的面积是___________10.如图，AB 是圆O 的直径，弦CD ⊥AB ，∠BCD=30°，CD=4，则阴影面积是__________11.如图，PA 、PB 是⊙O 的切线，切点分别为A 、B ，若OA=2，∠P=60°，则的长为 _____________________12.如图，一扇形纸扇完全打开后，外侧两竹条BD 和AC 的夹角为120°，长为25cm ，贴纸部分的宽BD 为15cm ，若纸扇两面贴纸，则贴纸的面积为______________________ 13.如图，在矩形ABCD 中，AB=5，BC=10，一圆弧过点B 和点C ，且与AD 相切，则图中阴影部分面积为 ．14.如图，扇形OAB 中，∠AOB ＝60°，OA ＝6cm ，则图中阴影部分的面积是 .15如图，在Rt ABC ∆中，90ACB ∠=，AC =以点C 为圆心，CB 的长为半径画弧，与AB 边交于点D ,将BD 绕点D 旋转0180后点B 与点A 恰好重合，则图中阴影部分的面积为___ .11题 12题15题 16题 17题 C16.如图，半圆O 的直径AB=2，弦CD ∥AB ，∠COD=90°，则图中阴影部分的面积为 ．17.如图，△ABC 的外接圆O 的半径为2，∠C=40°，则的长是． 18.如图，C 为半圆内一点，O 为圆心，直径AB 长为2cm ，∠BOC=60°，∠BCO=90°，将△BOC 绕圆心O 逆时针旋转至△B ′OC ′，点C ′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为 cm 2．19.如图，AB 是⊙O 的直径，AC 是⊙O 的弦，过点C 的切线交AB 的延长线于点D ，若∠A=∠D ，CD=3，则图中阴影部分的面积为 ．20.如图，⊙O 的半径为2，点A 、C 在⊙O 上，线段BD 经过圆心O ，∠ABD=∠CDB=90°，AB=1，CD=，则图中阴影部分的面积为 ．21.如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC ，已知圆锥的高h 为12cm ，OA=13cm ，则扇形AOC 中AC ⋂的长是 cm ；（结果保留π）22.已知⊙O 的半径为2，A 为⊙O 外一点，过点A 作⊙O 的一条切线AB ，切点是B ，AO 的延长线交⊙O 于点C ，若∠BAC=30°，则劣弧的长为 ．23.如图，在⊙O 中，半径OA ⊥OB ，过点OA 的中点C 作FD ∥OB 交⊙O 于D 、F 两点，且CD=，以O 为圆心，OC 为半径作，交OB 于E 点． （1）求⊙O 的半径OA 的长；（2）计算阴影部分的面积．20题 21题 22题23.如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．（1）求证：DE是⊙O的切线；（2）若AE=6，∠D=30°，求图中阴影部分的面积．24.如图，在Rt△ABC中，∠ABC=90°，以CB为半径作⊙C，交AC于点D，交AC的延长线于点E，连接ED，BE．（1）求证：△ABD∽△AEB；（2）当= 时，求tanE；（3）在（2）的条件下，作∠BAC的平分线，与BE交于点F，若AF=2，求⊙C的半径．4 3。

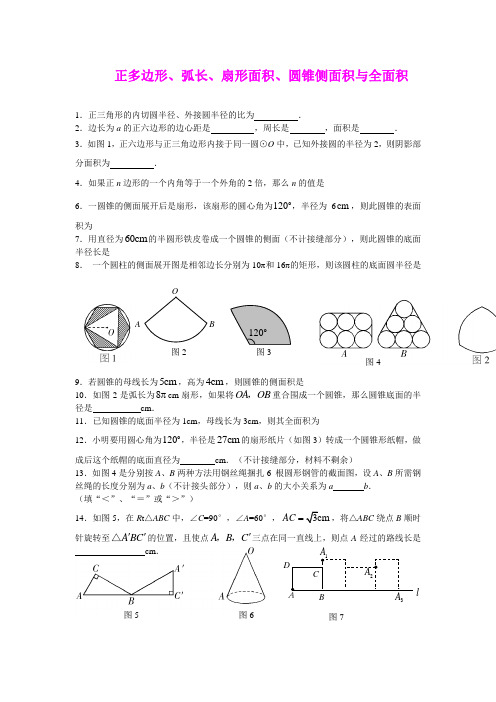
3l图2 图7正多边形、弧长、扇形面积、圆锥侧面积与全面积1．正三角形的内切圆半径、外接圆半径的比为 ．2．边长为a 的正六边形的边心距是 ，周长是 ，面积是 ． 3．如图1，正六边形与正三角边形内接于同一圆⊙O 中，已知外接圆的半径为2，则阴影部分面积为 ．4．如果正n 边形的一个内角等于一个外角的2倍，那么n 的值是__________6．一圆锥的侧面展开后是扇形，该扇形的圆心角为120，半径为6cm ，则此圆锥的表面积为_____________7．用直径为60cm 的半圆形铁皮卷成一个圆锥的侧面（不计接缝部分），则此圆锥的底面半径长是_______________8． 一个圆柱的侧面展开图是相邻边长分别为10π和16π的矩形，则该圆柱的底面圆半径是____________9．若圆锥的母线长为5cm ，高为4cm ，则圆锥的侧面积是____________10．如图2是弧长为8πcm 扇形，如果将OA OB ，重合围成一个圆锥，那么圆锥底面的半径是 cm ．11．已知圆锥的底面半径为1cm ，母线长为3cm ，则其全面积为____________12．小明要用圆心角为120，半径是27cm 的扇形纸片（如图3）转成一个圆锥形纸帽，做成后这个纸帽的底面直径为 cm ．（不计接缝部分，材料不剩余）13．如图4是分别按A 、B 两种方法用钢丝绳捆扎6 根圆形钢管的截面图，设A 、B 所需钢丝绳的长度分别为a 、b （不计接头部分），则a 、b 的大小关系为a b ． （填“＜”、“＝”或“＞”）14．如图5，在R t △ABC 中，∠C =90°，∠A =60°，AC =，将△ABC 绕点B 顺时针旋转至A BC ''△的位置，且使点A B C '，，三点在同一直线上，则点A 经过的路线长是________________cm ．O AB 120 图4图3 图5图6CB '15．如图6，已知圆锥的母线长OA ＝8，地面圆的半径r ＝2．若一只小虫从A 点出发，绕圆锥的侧面爬行一周后又回到A 点，则小虫爬行的最短路线的长是 ________ 16．已知扇形的圆心角为120︒，半径为2cm ，则扇形的弧长是 cm ，面积是____ 2cm ． 17．钟表的分针的长为5cm ，那么经过25分钟，分针针端转过的弧长是_________cm 18．如图7，矩形ABCD 中，86AB AD ==，，将矩形ABCD 在直线l 上按顺时针方向不滑动的每秒转动90，转动3秒后停止，则顶点A 经过的路线长为 ．19．如图8将ABC △绕点C 顺时针旋转得到A B C '''△，已知903ACA BC '∠==，，则点B 旋转经过的路线长是 ．20．若圆锥的底面半径为4cm ，圆锥的全面积为2cm S ，母线长为x cm ，则S 与x 的函数关系式为 ，且S 随x 的减小而 ．21．如图9，ABC △的边长都大于2，分别以它的顶点为圆心，1为半径画弧（弧的端点分别在三角形的相邻两边上），则这三条弧的长的和是___________________22．如图10，半圆的直径10AB =，P 为AB 上一点，点C D ，为半圆的三等分点，则阴影部分的面积等于_______． 23．在半径为18的圆中，24．如图11，将ABC △绕点C 旋转60得到A B C ''△，已知6AC =，4BC =，则线段AB 扫过的图形面积为___________25．如图12，在△ABC 中，∠A =90，分别以B 、C 为圆心的两个等圆外切，两圆的半径都为1cm ，则图中阴影部分的面积为 cm 2．26．如图13，PA PB ，切⊙O 于A B ，两点，若60APB =∠，⊙O 的半径为3，则阴影部分的面积为________．C A 'P图8图10图14图13图12图11图18 B图16 27． 如图14，⊙A ，⊙B ，⊙C ，⊙D 相互外离，它们的半径都是1，顺次连结四个圆心得到四边形ABCD ，则图中四个扇形（阴影部分）的面积之和等于28． 如图15，AB =O 为AB 的中点，AC BD ，都 是半径为3的⊙O 的切线，C D ，为切点，则弧CD 的长为 ．29．如图16将边长为8cm 的正方形ABCD 的四边沿直线l 向右 滚动（不滑动），当正方形滚动两周时，正方形的顶点A 所经过的路线的长是 cm ．30．如图17，以BC 为直径，在半径为2圆心角为90的扇形内作半圆，交弦AB 于点D ，连接CD ，则阴影部分的面积是_____________ 31．如图18，四边形ABCD 是一个矩形，⊙C 的半径是2cm ，4cm 2cm CF EF ==，．则图中阴影部分的面积为 2cm ．32．一个滑轮起重装置如图5所示，滑轮的半径是10cm ，当重物上升10cm 时， 滑轮的一条半径OA 绕轴心O 按逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动，π取3.14，结果精确到1°)（ ）A ．115° B ．60° C ．57° D ．29°33．如图6(1)，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图6(2)所示的一个圆锥模型．设圆的半径为r ，扇形半径为R ，则圆的半径与扇形半径之间的关系为（ ） A ．2R r =B ．94R r =C ．3R r =D ．4R r =34．如图7，边长为12m 的正方形池塘的周围是草地，池塘边A 、B 、C 、D 处各有一棵树，且AB ＝BC ＝CD ＝3m ．现用长4m 的绳子将一头羊拴在其中的一棵数上，为了使羊在草地上活动区域的面积最大，应将绳子拴在________处35．在半径为27m 的圆形广场中央点O 的上空安装了一个照明光源S ，S 射向地面的光束呈圆锥形，如图8所示，若光源对地面的最大张角（即图中∠ASB 的度数）是120°时效果最好，试求光源离地面的垂直高度SO 为多少时才符合要求?(精确到0.1m)B (D )C B C l AB C D A B36. 如右图所示，它是一个用厚度为0.15cm 不锈钢薄片制作的上部分是圆锥下部分是圆柱的储水设备，若不锈钢的密度为31079.0⨯3/m kg ,问制作100个这样的储水设备用的不锈钢薄片的重量为多少？（结果精确到0.01kg ）37．如图5(1)有一个宝塔，它的地基边缘是周长为24m 的正六边形ABCDEF (如图5(2))，点O 为中心（下面各题结果精确到0.1m)． （1）求地基的中心到边缘的距离；（2）己知塔的墙体宽为1m ，现要在塔的底层中心建一圆形底座的塑像，并且留出最窄处为1.6m 的观光通道，问塑像底座的半径最大是多少？38．一位小朋友在粗糙不打滑的“Ｚ”字形平面轨道上滚动一个半径为10cm 的圆盘，如图所示，AB 与CD 是水平的，BC 与水平面的夹角为60，其中60cm 40cm AB CD ==，，40cm BC =，请你作出该小朋友将圆盘从A 点滚动到D 点其圆心所经过的路线的示意图，并求出此路线的长度．ABD60cm答案1． 1：2 2。

2019-2020年中考数学总复习考点跟踪训练35圆的弧长与扇形面积、圆锥的侧面积与全面积一、选择题1. (xx黑龙东)一圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠一圈彩带回到A点，则彩带最少用多少厘米(接口处重合部分忽略不计)( )A. 10πcmB. 102cmC. 5πcmD. 52cm2. (xx舟山)一个圆锥的侧面展开图是半径为6的半圆，则这个圆锥的底面半径为( )A. 1.5B. 2C. 2.5D. 33. (xx义乌)一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是( )A. 5∶4B. 5∶2C. 5∶2D. 5∶ 24. (xx泰安)如图，半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为( )A. (π2－1)cm 2 B. (π2＋1)cm 2C. 1cm 2D. π2cm 2二、填空题5. (xx 呼和浩特)一个底面直径是80cm ，母线长为90cm 的圆锥的侧面展开图的圆心角的度数为________．6. (xx 河北)如图，将长为8cm 的铁丝首尾相接围成半径为2cm 的扇形，则S 扇形＝________cm 2.7. (xx 南京)如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r ＝2cm ，扇形的圆心角θ＝120°，则该圆锥的母线长l 为________cm .8. (xx 牡丹江)如图，如果从半径为3cm 的圆形纸片上剪去13圆周的一个扇形，将留下的扇形围成一个圆锥(接缝处不重叠)，那么这个圆锥的底面半径是________cm .三、解答题9. (xx佛山)如图，圆锥的侧面展开图是一个半圆，求母线AB与高AO的夹角．(参考公式：圆锥的侧面积S＝πrl，其中r为底面半径，l为母线．)10. (xx丽水)如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中，画出△AB′C′；(2)计算线段AB在变换到AB′的过程中扫过区域的面积．B组能力提升练1. (xx南充)如图，矩形ABCD中，AB＝5，AD＝12，将矩形ABCD按如图所示的方式在直线l上进行两次旋转，则点B在两次旋转过程中经过的路径的长是( )A. 252π B. 13πC. 25πD. 25 22. (xx杭州)点A、B、C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线AC，垂足为E，直线AD与BE相交于点H.若BH＝3AC，则∠ABC所对的弧长等于________(长度单位)．3. (xx江西)如图1，一辆汽车的背面有一种特殊形状的刮雨器，忽略刮雨器的宽度可抽象为一条折线OAB，如图2所示，量得连杆OA长为10cm，雨刮杆AB长为48cm，∠OAB＝120°.若启动一次刮雨器，雨刮杆AB正好扫到水平线CD的位置，如图3所示．(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离；(结果精确到0.01)(2)求雨刮杆AB扫过的最大面积．(结果保留π的整数倍)(参考数据：sin60°＝32，cos60°＝12，tan60°＝3，721≈26.851，可使用科学计算器)4. (xx黔西南)如图，点B、C、D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B＝∠A＝30°，BD＝2 3.(1)求证：AC是⊙O的切线；(2)求由线段AC、AD与弧CD所围成的阴影部分的面积．(结果保留π)21716 54D4 哔24310 5EF6 延N34133 8555 蕕26011 659B 斛29668 73E4 珤 # ! @K,。

初三数学弧长和扇形面积公式、圆锥的侧面积和全面积人教实验版本卷贰O 贰贰年贰月捌日编写； 出题人：令狐学复；欧阳化语；令狐理总。

【本讲教育信息】一. 教学内容：弧长和扇形面积公式、圆锥的侧面积和全面积教学目的1. 使学生掌握弧长和扇形面积公式、圆锥及其特征，使学生掌握圆锥的轴截面图及其特点。

2. 使学生掌握弧长和扇形面积公式、圆锥侧面展开图的画法及侧面积计算公式。

3. 使学生比拟纯熟地应用弧长和扇形面积公式、圆锥的根本性质和轴截面解决有关圆锥外表积的计算问题。

4. 培养学生空间观念及空间图形与平面图形的互相转化思想，培养学生空间想象才能和计算才能。

教学重点和难点：教学重点是弧长和扇形面积公式，圆锥及其特征，圆锥的侧面积计算难点是圆锥侧面展开图〔扇形〕中各元素与圆锥各元素之间的关系 教学过程 1. 圆周长：r 2C π= 圆面积：2r S π=2. 圆的面积C 与半径R 之间存在关系R 2C π=，即360°的圆心角所对的弧长，因此，1°的圆心角所对的弧长就是360R2π。

n °的圆心角所对的弧长是180Rn π 180Rn π=∴l P 120*这里的180、n 在弧长计算公式中表示倍分关系，没有单位。

3. 由组成圆心角的两条半径和圆心角所对的弧所围成的圆形叫做扇形。

发现：扇形面积与组成扇形的圆心角的大小有关，圆心角越大，扇形面积也就越大。

4. 在半径是R 的圆中，因为360°的圆心角所对的扇形的面积就是圆面积2R S π=，所以圆心角为n °的扇形面积是： R 21360R n S 2l =π=扇形〔n 也是1°的倍数，无单位〕5. 圆锥的概念观察模型可以发现：圆锥是由一个底面和一个侧面围成的。

其中底面是一个圆，侧面是一个曲面，假如把这个侧面展开在一个平面上，展开图是一个扇形。

如图，从点S 向底面引垂线，垂足是底面的圆心O ，垂线段SO 的长叫做圆锥的高，点S 叫做圆锥的顶点。

第2课时圆锥的侧面积和全面积知识要点基础练知识点1圆锥的相关概念和侧面展开图1.【教材母题变式】若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是(C)A.90°B.100°C.120°D.60°2.(南通中考)如图所示的扇形纸片半径为5 cm,用它围成一个圆锥的侧面,该圆锥的高是4 cm,则该圆锥的底面周长是(D)A.3π cmB.4π cmC.5π cmD.6π cm3.已知扇形的圆心角为120°,面积为300π cm2.(1)求扇形的弧长;(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?解:(1)20π cm.(2)20 cm.知识点2圆锥的侧面积和全面积4.(无锡中考)已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于(C)A.24 cm2B.48 cm2C.24π cm2D.12π cm25.如图,一个直角三角板,两直角边长分别是AC=7 cm,BC=24 cm,∠ACB=90°,把直角三角板△ABC绕BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为(B)A.160π cm2B.175π cm2C.120π cm2D.135π cm26.小刚用一张半径为12 cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5 cm,那么这张扇形纸板的面积是60πcm2.综合能力提升练7.一个圆锥形的圣诞帽底面半径为12 cm,母线长为13 cm,则圣诞帽的表面积为(B)A.312π cm2B.156π cm2C.78π cm2D.60π cm28.(齐齐哈尔中考)一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是(A)A.120°B.180°C.240°D.300°9.将直径为40 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为(A)A. cmB.10 cmC.45 cmD. cm10.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π=3),则圆柱底周长约为(注:圆柱体的体积=底面积×高)(B)A.1丈3尺B.5丈4尺C.9丈2尺D.48丈6尺11.已知圆锥的母线长是35,它的侧面展开图是圆心角为216°的扇形,那么这个圆锥的(D)A.底面半径是15B.高是26C.侧面积是700πD.底面积是441π12.现有一张圆心角为108°,半径为40 cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10 cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是(A)A.18°B.36°C.72°D.90°13.小杰生日的前一天,妈妈让小杰用学过的数学知识做一顶生日帽,小杰先从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥侧面,小杰做的帽子高为4 cm,则求出帽子的直径为(C)A.26 cmB.30 cmC.32 cmD.24 cm14.如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为2 m,母线长为8 m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米12元钱,那么购买油毡所需要的费用是603元(结果保留整数).15.如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是40 cm.【变式拓展】如图,小红同学在半径为4的圆中剪去一个圆心角为60°的扇形,并将剩下部分(图中阴影部分)制成一个无缝隙且不重合的圆锥,则这个圆锥的高为.16.如图所示,已知圆锥底面半径r=10 cm,母线长为40 cm.(1)求它的侧面展开图的圆心角和表面积.(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线的长是多少?为什么?解:(1)=2π×10,解得n=90,即侧面展开图的圆心角是90°.圆锥的表面积=π×102+π×10×40=500π(cm2).(2)如图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B 所走的最短路线是线段AB的长.在Rt△ASB中,SA=40,SB=20,∴AB=20(cm).∴甲虫走的最短路线的长是20 cm.17.如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6 cm,下底面直径为4 cm,母线长EF=9 cm,求扇形OAB 的圆心角及这个纸杯的表面积.(结果保留根号和π)解:扇形OAB的圆心角是40°,纸杯的表面积为49π cm2.拓展探究突破练18.铁匠王老五要制作一个圆锥体模型,操作规则是:在一块边长为16 cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)请你帮助他算一算可以吗?(1)请说明方案一不可行的理由;(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.解:连接AC,E为两圆的切点,(1)理由如下:∵扇形的弧长=16×=8π,圆锥底面周长=2πr,∴圆的半径O1E=4 cm.过O1作O1F⊥CD,∴△CO1F为等腰直角三角形,∴O1C=O1F=O1E=4 cm.又∵AE=AB=16 cm,而制作这样的圆锥实际需要正方形纸片的对角线长为AE+EO1+O1C=16+4+4=20+4 cm.∵20+4>16,∴方案一不可行.(2)方案二可行.求解过程如下:设圆锥底面圆的半径为r cm,圆锥的母线长为R cm,∵在一块边长为16 cm的正方形纸片上,∴正方形对角线长为16 cm,则(1+)r+R=16①,2πr=②.由①②,可得R=,r=.故所求圆锥的母线长为 cm,底面圆的半径为 cm.。

弧长及扇形的面积、圆锥的侧面积一、请准确填空(每小题3分，共24分)1.两个同心圆的半径差为5，其中一个圆的周长为15π，则另一个圆的周长为_____.2.已知a 、b 、c 分别是正六边形的一边、最短对角线和最长对角线，则a ∶b ∶c 为_____.3.已知Rt △ABC ，斜边AB =13 cm ，以直线BC 为轴旋转一周，得到一个侧面积为65π cm 2的圆锥，则这个圆锥的高等于_____.4.已知在同一平面内圆锥两母线在顶点最大的夹角为60°，母线长为8，则圆锥的侧面积为_____.5.已知圆柱的底面半径长和母线长是方程4x 2－11x +2=0的两个根，则该圆柱的侧面展开图的面积是_____.6.圆内接正方形的一边切下的一部分的面积等于2π－4，则正方形的边长是_____，这个正方形的内切圆半径是_____.7.要制造一个圆锥形的烟囱帽，如图1，使底面半径r 与母线l 的比r ∶l =3∶4，那么在剪扇形铁皮时，圆心角应取_____.8.将一根长24 cm 的筷子，置于底面直径为5 cm ，高为12 cm 的圆柱形水杯中(如图2).设筷子露在杯子外面的长为h cm ，则h 的取值范围是_____.图1 图2二、相信你的选择(每小题3分，共24分)9.已知正三角形的边长为a ，其内切圆的半径为r ，外接圆的半径为R ，则r ∶a ∶R 等于 A.1∶23∶2B.1∶2∶23C.1∶2∶3D.1∶3∶210.如图3，△ABC 是正三角形，曲线ABCDEF …叫做“正三角形的渐开线”，其中、 、、… 圆心依次按A 、B 、C 循环，它们依次相连接，如果AB =1，那么曲线CDEF 的长是A.8πB.6πC.4πD.2π11.如图4，一扇形纸扇完全打开后，外侧两竹条AB 、AC 的夹角为120°，AB 长为30 cm ，贴纸部分BD 长为20 cm ，贴纸部分的面积为A.800π cm 2B.500π cm 2C.3800π cm 2 D.3500π cm 212.已知如图5，两同心圆中大圆的半径OA 、OB 交小圆于C 、D ，OC ∶CA =3∶2，则和的长度比为A.1∶1B.3∶2C.3∶5D.9∶2513.如图6，AB 为半圆O 的直径，C 是半圆上一点，且∠COA =60°，设扇形AOC 、△COB 、弓形BmC 的面积为S 1、S 2、S 3，则它们之间的关系是A.S 1<S 2<S 3B.S 2<S 1<S 3C.S 1<S 3<S 2D.S 3<S 2<S 1DE EFABCDEFACDBO图3 图4 图5 图614.如图7中，正方形的边长都相等，其中阴影部分面积相等的有(1)(2)(3)(4)图7A.(1)(2)(3)B.(2)(3)(4)C.(1)(3)(4)D.(1)(2)(3)(4) 15.如果圆锥的母线长为5 cm ，底面半径为3 cm ，那么圆锥的表面积为A.39π cm 2B.30π cm 2C.24π cm 2D.15π cm 2 16.一个圆台形物体的上底面积是下底面积的41.如图8，放在桌面上，对桌面的压强是200 帕，翻过来放，对桌面的压强是A.50帕B.80帕C.600帕D.800帕图8三、考查你的基本功(共14分)17.(6分)如图9，圆锥底面半径为r ，母线长为3r ，底面圆周上有一蚂蚁位于A 点，它从A 点出发沿圆锥面爬行一周后又回到原出发点，请你给它指出一条爬行最短的路径，并求出最短路径.AABCDOEF图9图1018.(8分)如图10，等腰Rt △ABC 中斜边AB =4，O 是AB 的中点，以O 为圆心的半圆分别与两腰相切于点D 、E ，图中阴影部分的面积是多少？请你把它求出来.(结果用π表示)四、生活中的数学(共18分)19.(8分)铅球比赛要求运动员在一固定圆圈内投掷，推出的铅球必须落在40°角的扇形区域内(以投掷圈的中心为圆心).如果运动员最多可投7 m ，那么这一比赛的安全区域的面积至少应是多少？(结果精确到0.1 m 2)20.(10分)如图11，有一直径是1 m 的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形CAB . (1)被剪掉的阴影部分的面积是多少？(2)若用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？(结果可用根号表示)ABCOA BO图11图12图13五、探究拓展与应用(共20分)21.(10分)现有总长为8 m 的建筑材料，用这些建筑材料围成一个扇形的花坛(如图12)，当这个扇形的半径为多少时，可以使这个扇形花坛的面积最大？并求最大面积.22.(10分)如图13，正三角形ABC 的中心恰好为扇形ODE 的圆心，且点B 在扇形内，要使扇形ODE 绕点O 无论怎样转动，△ABC 与扇形重叠部分的面积总等于△ABC 的面积的31，扇形的圆心角应为多少度？说明你的理由.弧长和扇形面积练习题1. 某中学的铅球场如图所示，已知扇形AOB 的面积是362m ，弧AB 的长度为9m ，求半径OA 是多少？2. 已知圆锥的侧面积为π82cm ，侧面展开图的圆心角为45°，求该圆锥的母线长3．如图小华为参加毕业晚会演出，准备制一顶圆锥形纸帽，纸帽的底面半径为9cm ，母线长为30cm ，制作这个纸帽至少需要纸板的面积至少为多少cm 2．（结果保留π）4．如图已知扇形AO B 的半径为6cm ，圆心角的度数为120°，若将此扇形围成一个圆锥，求围成的圆锥的侧面积5. 将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），求每个圆锥容器的底面半径6．如图，一把遮阳伞撑开时母线长为2米，底面半径为1米，则做这把遮阳伞需用布料的面积是多少120︒B O A 6cm7.如图，将一个含有45°且直角边为1的三角板绕顶点C 顺时针旋转135°，分别求顶点A 所经过的路线长和顶点B 所经过的路线长8．三角板ABC 中，︒=∠90ACB ，︒=∠30B ，6=BC ．三角板绕直角顶点C 逆时针旋转，当点A 的对应点'A 落在AB 边的起始位置上时即停止转动，求B 点转过的路径长9. 如图所示，PA ，PB 切⊙O 于A ，B 两点，若∠APB=60°，⊙O 的半径为3，求阴影部分的面积10.如图，线段AB 与⊙O 相切于点C ，连结OA ，OB ，OB 交⊙O 于点D ，已知6O A O B ==，63AB =． （1）求⊙O 的半径；（2）求图中阴影部分的面积．11.一个圆锥的高为33，侧面展开图是半圆，求圆锥的侧面积12．如图，圆锥的轴截面是边长为6cm 的正三角形ABC ，P 是母线AC 的中点．求在圆锥的侧面上从B 点到P 点的最短路线的长．COABDB 'A 'C A B。