当前位置：文档之家 › 空间解析几何课件

空间解析几何课件

  • 格式：ppt
  • 大小：7.15 MB
  • 文档页数：152

下载文档原格式

  / 152

合集下载

高等数学Ⅰ第一章课件：空间解析几何

高等数学Ⅰ第一章课件：空间解析几何

练习题答案
一、1、Ⅳ,Ⅴ,Ⅷ,Ⅲ；
2、(-3,2,1),(3,2,-1),(-3,-2,-1),
(-3,-2,1),(3,2,1),(3,-2,-1)；
3、(-4,3,0),(0,3,5),(-4,0,5),
(-4,0,0),(0,3,0),(0,0,5)；
4、(a, a,a), (a, a, a),(a,a, a),(a,a, a) ；
(2) 空间直角坐标系 （轴、面、卦限）
（注意它与平面直角坐标系的区别）
空间两点间距离公式
M1M2 x2 x1 2 y2 y1 2 z2 z1 2
思考题
1. 在空间直角坐标系中，指出下列 各点在哪个卦限？
A(1,2,3), B(2,3,4), C(2,3,4), D(2,3,1) .
b
3a
2
5
解
a
b
5
1
b
b
3a
2
5
(1
3)a
1
5 2
1 5
5
b
2a
5
b.
2
例2 试用向量方法证明：对角线互相平分的
四边形必是平行四边形.
证 AM MC BM MD
D b
A
a
C
M
B
AD AM MD MC BM BC
AD 与 BC 平行且相等, 结论得证.
1.2 空间直角坐标系
3、点 A ( 4 , 3 , 5 )在xoy 平面上的射影点为_____ ______,在 yoz 面上的射影点为__________，在 zox轴上的射影点为_________，在x 轴上 的射影 点为________，在x 轴上 的射影点为______，在 z 轴上 的射影点为_______ ;

空间解析几何28965-PPT文档资料25页

空间解析几何28965-PPT文档资料25页
§7．7 平面及其方程
一、平面的点法式方程
法线向量、 平面的点法式方程
二、平面的一般方程
平面的一般方程、特殊的平面、截距式方程
三、两平面的夹角
两平面的夹角、两平面夹角的余弦 两平面平行与垂直的条件 点到平面的距离公式
一、平面的点法式方程
法线向量： 如果一非零向量垂直于一平面，
这向量就叫做该平面的法线向量．
或
C3B．
将其代入所设方程并除以B(B 0)，便得所求的平面方程为 y3z0．
例4 设一平面与x、y、z轴的交点依次为P(a, 0, 0)、Q(0, b, 0)、 R(0, 0, c)三点， 求这平面的方程(其中a 0，b 0，c 0)．
z R (0, 0, c)
n
Q (0, b, 0)
| n 1 | { A x 0 B y 0 C z 0 ( A x 1 B y 1 C z 1 ) } ，
又因Ax1By1Cz1D0，| n | A 2 B 2 C 2 ， 所以 P r j n P 1 P 0 A 0 A 2 B 0 B 2 C x C 0 2 D y ． z
O
y
P (a, 0, 0) x
例4 设一平面与x、y、z轴的交点依次为P(a, 0, 0)、Q(0, b, 0)、 R(0, 0, c)三点， 求这平面的方程(其中a 0，b 0，c 0)．
解 设所求平面的方程为
A x B yC zD0．
因P(a, 0, 0)、Q(0, b, 0)、R(0, 0, c)三点都在这平面上，所以点P、
解 先求出这平面的法线向量 n ．

M 1M 2{3， 4， 6}， n

M 1M3{2， 31}， 可取

高等数学-01空间解析几何(课件

高等数学-01空间解析几何(课件
向量的数量积
表示两个向量的夹角。
向量的向量积与向量的混合积
向量的向量积
表示两个向量的垂直程度。
向量的混合积
表示三个向量的空间关系。
向量在空间几何中的应用
力的合成与分解
在物理中，力可以表示为向量，力的 合成与分解可以通过向量的加法、数 乘和向量积进行计算。
速度和加速度的分析
在运动学中，速度和加速度可以表示 为向量，通过向量的加法、数乘、向 量积和混合积进行计算和分析。
空间解析几何在计算机图形学中 用于三维建模、动画制作和虚拟 现实技术。
空间解析几何的基本概念
空间向量
表示空间中具有大小和方向的 量。
向量积
表示两个向量的外积，是一个 向量运算，结果是一个向量。
空间点
表示空间中一个位置的点。
向量运算
包括加法、数乘、向量的模等 基本运算。
混合积
表示三个向量的内积，结果是 一个标量。
习题三
总结词
向量的数量积、向量积和混合积
详细描述
习题三主要涉及向量的数量积、向量积和混合积的计算和性质。通过这些练习题，学生 可以深入理解向量的数量积、向量积和混合积的概念和计算方法，掌握其性质和应用，
提高解题能力。
THANKS
感谢观看
曲线方程
通过给定的方程，可以描 述曲线的形状和路径。
常见曲线
圆、椭圆、抛物线、双曲 线等。
曲面与曲线的应用
工程设计
在机械工程、航空航天、船舶制造等领域，曲面与曲线被广泛应 用于产品设计和优化。
数学建模
在物理、化学、生物等学科中，曲面与曲线可以用来描述自然现 象和规律，建立数学模型。
数据分析
在统计学和数据分析领域，曲面与曲线可以用来可视化数据和探 索数据之间的关系。

空间解析几何教育课件

空间解析几何教育课件

例.题 设 P是球内 ,A ,B 一 ,C 是 定 球 点 面上 , A三 P B 个 BP 动 CC点 P A,
2 以 P,A P,B P为 C 棱作平 ,记行 P 与 相六 对面 的 Q 体 ,求 顶 Q 点 点 的 为 轨
－－ (北 － 京 2大 0考 0学 7研 ) 题
参考解答 : 设球面的半径为
由 (1 ), ( 2 ), 得
cos
AB , AC

b2 c2 a2 ,
(2)
2 bc

2S bc
2


b2
c2 2 bc
a2
2


1,
即
16 S 2 ( 2 bc ) 2 ( b 2 c 2 a 2 ) 2
[ 2 bc ( b 2 c 2 a 2 )][ 2 bc ( b 2 c 2 a 2 )]
[( b c ) 2 a 2 ][ a 2 ( b c ) 2 ]
( b c a )( b c a )( a b c )( a b c )
2 p ( 2 p 2 a )( 2 p 2 b )( 2 p 2 c ),
即
S 2 p ( p a )( p b )( p c ).
其中 a,b,c为三角形的 ,p三 1(a边 b长 c),S为三角形.的面积 2
参考解答 : 设 | AB | c , | AC | b , | BC | a . 由 S 1 | AB AC |, 得 2
sin AB , AC 2 S ,
(1)
bc
由 CB AB AC , 得 CB CB AB AC AB AC , 即

《高数空间解析几何》PPT课件

《高数空间解析几何》PPT课件
类似地， 方程 f( y , z)= 0在空间表示以 yoz 坐标面上的 曲线为准线，平行于 x 轴的直线为母线的柱面. 方程 f( x , z)= 0在空间表示以 xoz 坐标面上的曲线为准线， 平行于 y 轴的直线为母线的柱面.
8
椭圆柱面：
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周，求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
曲面讨论的两个基本问题： （1）已知曲面的形状，建立这曲面的方程； （2）已知方程 F(x, y, z) =0，研究这方程的图形；
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面，称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2

空间解析几何基础34页PPT

空间解析几何基础34页PPT
Q Ny
M 1 M 2 x 2 x 1 2 y 2 y 1 2 z 2 z 1 2 .
空间两点间距离公式
特殊地：若两点分别为 M (x,y,z),O(0,0,0)
d OM x2y2z2.
例 1 求 证 以 M 1(4 ,3 ,1 )、 M 2(7 ,1 ,2 )、 M 3(5 ,2 ,3 )
特殊点的表示: 坐标轴上的点 P , Q , R , 坐标面上的点 A , B , C , O(0,0,0)
z
R(0,0,z)
B(0,y,z)
C(x,o,z)
o x P(x,0,0)
•M(x,y,z)
y
Q(0,y,0) A(x,y,0)
空间两点间的距离
设 M 1 (x 1,y 1,z1)、 M 2(x 2,y 2,z2)为 空 间 两 点
以下给出两例常见的曲面.
例 1 建 立 球 心 在 点 M 0 (x 0 ,y 0 ,z 0 )、 半 径 为 R
的 球 面 方 程 .
解 设 M (x ,y ,z )是 球 面 上 任 一 点 ，
根据题意有 |M0M |R
x x 0 2 y y 0 2 z z 0 2 R 所求方程为 x x 0 2 y y 0 2 z z 0 2 R 2
a1x2+a2y2+a3z2+b1xy+b2yz+b3zx+c1x+c2y+c3z+d=0 (7.5)
所表示的空间曲面称为二
次曲面,其中ai,bi,ci(i=1,2,3) 和d均为常数,且ai,bi不全 为零.
(1)球面 x2+y2+z2=R2 (R>0) (7.6)
面垂直与xOy平面,且z轴在该平面上.

空间解析几何-第2章-空间的平面与直线ppt

空间解析几何-第2章-空间的平面与直线ppt
(2) L // Am Bn Cp 0.
例 1 设直线L : x 1 y z 1，平面 2 1 2
: x y 2z 3，求直线与平面的夹角.
解
n (1,1, 2), s (2,1, 2),
sin
| Am Bn Cp |
A2 B2 C 2 m2 n2 p2
M0M { x x0 , y y0 , z z0 }
A( x x0 ) B( y y0 ) C(z z0 ) 0
平面的点法式方程
其中法向量
n
{ A, B,C},
已知点
( x0 ,
y0 ,
z0 ).
平面上的点都满足上方程，不在平面上的 点都不满足上方程，上方程称为平面的方程， 平面称为方程的图形．
化简得 2x 3 y z 6 0.
例3 已知两点M(1,-2,3)与N(3,0,-1)，求线段 MN的垂直平分面方程。
二、平面的一般式方程
由平面的点法式方程
A( x x0 ) B( y y0 ) C(z z0 ) 0
Ax By Cz ( Ax0 By0 Cz0 ) 0
z
s
L
M
M0
M0 ( x0 , y0 , z0 ), M ( x, y, z), o
y
M L,
M0M // s
x
s (m, n, p), M0M { x x0 , y y0 , z z0 }
x x0 m
y y0 z z0
n
p
直线的对称式方程 （标准方程、点向式
方程）
注: 当方向向量的某个坐标 为零时，比如
解析几何
第2章 空间的平面与直线
10/26/2024
§2.1.1 平面的方程

空间解析几何初步_ppt课件

空间解析几何初步_ppt课件

第二节 曲面及其方程
一、曲面方程的概念
二、旋转曲面
三、柱面 四、二次曲面
第七章
机动 目录 上页 下页 返回 结束
一、曲面方程的概念
引例: 求到两定点A(1,2,3) 和B(2,-1,4)等距离的点的 轨迹方程. 解:设轨迹上的动点为 M AM BM ,即 ( x ,y ,z ) ,则
( x 1 ) ( y 2 ) ( z 3 )
定义1. 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系:
(1) 曲面 S 上的任意点的坐标都满足此方程; (2) 不在曲面 S 上的点的坐标不满足此方程,
则 F( x, y, z ) = 0 叫做曲面 S 的方程,
曲面 S 叫做方程 F( x, y, z ) = 0 的图形.
证:
2 2 2 14 M M ( 7 4 ) ( 1 3 ) ( 2 1 ) 1 2
2 M M )2 6 1 )2 (32 2 3 (57) (2 2 2 2 6 ( 2 3 ) ( 5 4 ) ( 3 1 ) M M 1 3
M M M M 2 3 1 3
M1
M2
M3
M M M 即 1 2 3为等腰三角形 .
机动 目录 上页 下页 返回 结束
及B 等距 例5. 在 z 轴上求与两点 A ( 4 , 1 , 7 ) ( 3 , 5 , 2 ) 离的点 .
解: 设该点为 M ( 0 , 0 ,z ) ,因为 M A M B ,
( x , y , z ) , ( x ,y , z ) 对两点 A 与B 2 2 2 1 1 1
A
B
两点间的距离公式: 2 2 2 |AB| ( x x ) ( y y ) ( z z ) 21 21 21

《空间解析几何》课件

《空间解析几何》课件
了解空间解析几何在计算机图形 学中的应用，如3D建模、动画制 作等。
THANKS
感谢观看
通过参数方程表示曲面的形式，如x = x(u, v)，y = y(u, v)，z = z(u, v)。
曲面方程
表示三维空间中曲面的方程形式，如z = f(x, y)。
空间曲线的方程
1 2
参数曲线
通过参数方程表示曲线的形式，如x = x(t)，y = y(t)，z = z(t)。
空间曲线
表示三维空间中曲线的方程形式，如F(x, y, z) = 0。
空间解析几何的应用领域
总结词
空间解析几何在许多领域都有广泛的应用。
详细描述
在物理学中，空间解析几何用于描述物理现象的空间关系，如力学、电磁学和光学等领 域。在计算机图形学中，空间解析几何用于建模和渲染三维场景。在工程学中，空间解 析几何用于设计和分析机械、建筑和航空航天等领域中的物体和结构。此外，空间解析
03
空间平面与直线
空间平面的方程
平面方程的基本形式
Ax + By + Cz + D = 0
特殊平面
平行于坐标轴的平面、过原点的平面、与坐标轴垂直的平面
参数方程
当平面过某一定点时，可以用参数方程表示平面的方程
空间直线的方程
直线方程的基本形式
Ax + By + Cz = 0
特殊直线
与坐标轴平行的直线、过原点的直线、与坐标轴垂直的直线
利用代数方法，如向量运算、线性代数等， 求解空间几何问题。
几何意义
将代数解转化为几何意义，解释其实际意义 。
如何理解空间几何中的概念？
向量的概念
理解向量的表示、向量的加法、数乘以及向量的模 等基本概念。

《空间解析几何基础》PPT课件

《空间解析几何基础》PPT课件

24
(5)二次锥面
x2 a2
y2 b2
z2 c2
0
(6)椭圆抛物面
x2 a2
y2 b2
2z
0
(a,b,c 0) (a,b 0)
(7.10) (7.11)
25
(7)双曲抛物面(马鞍面) x2 y2 2z 0 (a,b 0) a2 b2
(7.12)
26
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
(1) x 2;
(2) x2 y2 4;
(3) y x 1.
27
思考题解答
方程
平面解析几何中 空间解析几何中
x2
平行于y 轴的直线 平行于 yoz 面的平面
圆心在(0,0) ，
x2 y2 4
半径为2 的圆
以z 轴为中心轴的圆柱面
y x 1 斜率为1的直线 平行于z 轴的平面
பைடு நூலகம்
28
三、平面区域的概念及其解析表示 设P0(x0,y0)是xOy平面上的一定点,δ>0为一实
4
空间两点间的距离
设M1 ( x1 , y1 , z1 )、M 2 ( x2 , y2 , z2 )为空间两点
zR
M1•
P o
d M1M2 ?
• M2
Q N
在直角M1 NM 2 及 直 角 M1 PN
中，使用勾股定
y 理知
x
d 2 M1P 2 PN 2 NM 2 2 ,
5
M1P x2 x1 , PN y2 y1 , NM 2 z2 z1 ,
(7.4)
其 中 a,b,c,d 为 常 数 , 且 a,b,c 不 全 为 零 . 例 如 , 当

空间解析几何精ppt课件

空间解析几何精ppt课件
记作－a ; 因平行向量可平移到同一直线上, 故两向量平行又称
两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k
个向量共面 .
.
机动 目录 上页 下页 返回 结束
二、向量的线性运算
1. 向量的加法 平行四边形法则:
b ab
(ab)c
c
bc
a(bc)
a 三角形法则: ab
b
过空间一定点 o ,由三条互相垂直的数轴按右手规则
组成一个空间直角坐标系.
• 坐标原点
Ⅲ
zz 轴(竖轴)
Ⅱ
• 坐标轴
Ⅳ
• 坐标面
• 卦限(八个) Ⅶ x
x轴(横轴)
Ⅷ
yoz面 oxoy面
Ⅴ
Ⅰ
y
y轴(纵轴)
Ⅵ
.
机动 目录 上页 下页 返回 结束
在直角坐标系下
点 M 1 1有序数组 (x, y, z) 1 1向径 r
M2
零向量: 模为 0 的向量, 记 0 ， 或 作 0 . M 1
.
机动 目录 上页 下页 返回 结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等,
记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行,记作
a∥b ; 规定: 零向量与任何向量平行 ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量,
ab b a
a
运算规律 : 交换律 a b b a
结合律 (ab)ca(bc)a.
.
机动 目录 上页 下页 返回 结束
s a 1 a 2 a 3 a 4 a 5
a4
a5
a3 s

空间解析几何简介课件

空间解析几何简介课件

一点 M 的线速度 的表示式 .
解: 在轴 l 上引进一个角速度向量 , 使 , 其
方向与旋转方向符合右手法则 , 在 l 上任取一点 O, 作
向径
它与 的夹角为 , 则
点 M离开转轴的距离
a r sin
a M
且
符合右手法则
l
v r
O
*三、向量的混合积
1. 定义 已知三向量 a , b , c , 称数量
设 P是 中3一个平面， VP 定义如上，则 中3 与二维子
空间VP 正交的非零向量称为平面P的法向量；平面 P的
所有法向量添上零向量组成 的3 一个一维子空间， 中3
以平面 的P法向量为方向向量的直线称为平面 的法P 线 。
a b c c Pr jc a b c Prjc a Prjc b
c Pr jc a c Pr jc b a c b c
4. 数量积的坐标表示
设 a ax e1 ay e2 az e3 , b bx e1 by e2 bz e3 ,则
( ax e1 ay e2 az e3 ) (bx e1 by e2 bz e3 )
内容小结
设 a (ax , ay , az ) , b (bx ,by ,bz ), c (cx , cy , cz )
1. 向量运算
加减: 数乘: 点积:
a b (ax bx , ay by , az bz )
a (ax ,ay ,az )
a b axbx ayby azbz
叉积:
i jk ab ax ay az
bx by bz
ax ay az
混合积: a b c ( a b ) c bx by bz
2. 向量关系:

高等数学教学课件-09空间解析几何

高等数学教学课件-09空间解析几何
向量的模(两点距离 ) 公式：
aOM x12y12z12
N M a b ( x 1 x 2 ) 2 ( y 1 y 2 ) 2 ( z 1 z 2 ) 2 两 向 量 夹 角 ： c o s ( a ,b ) x 1 x 2 y 1 y 2 z 1 z 2
整 理 得 zy 1 例 求 到 P 1 ( 1 , 1 , 2 ) , P 2 ( 2 , 2 , 1 ) 距 离 相 等 点 的 轨 迹 . 解 设 M ( x , y , z ) 为 轨 迹 任 一 点 ， 则 P 1 M P 2 M
( x 1 ) 2 ( y 1 ) 2 ( z 2 ) 2 ( x 2 ) 2 ( y 2 ) 2 ( z 1 ) 2 整 理 得 6 x 6 y 2 z 3
( 记 ,,) 为 向 量 的 方 向 角 .
因 为 a i a x a i c o s a c o s , 所 以
在xy面下部与第一 卦限相对应的称为 第Ⅴ卦限;以后依次 称为第Ⅵ、Ⅶ、Ⅷ 卦限.
任 给 向 量 r , 空 间 对 应 有 点 M , 使 O M r . 以 O M 为
对 角 线 作 长 方 体 ,与 坐 标 轴 重 合 的 棱 为 O P, O Q ,
O R ,则
r O P O Q O R
高等数学
微积分
西南财经大学经济数学系 孙疆明
精
空间解析几何与向量代数
向量及其线性运算
数量积、向量积、混合积
曲面及其方程
平面
空间曲线及其方程
一、向量及其线性运算
向量概念 有大小、有方向的量称为向量. 用 符 号 a 、 b 、 v 、 F 、 … 等 标 记 . 如 果 强 调 起 点 A 、 终 点 B ,也 记 A B . 向 量 的 大 小 叫 做 向 量 的 模 .记 为A B、 a… 等 . 模 为 1的 向 量 叫 做 单 位 向 量 . 模 为 0的 向 量 叫 零 向 量 .记 为 0.

空间解析几何PPT

空间解析几何PPT

应的分子也为0
2、平行向量的坐标表示式
a // b b a
(bx , by , bz ) (ax , ay , az )
bx ax
by ay
bz az
例3 求解以向量为未 知元的线性方程组
xx
4 2
y y
a b
其中 a = (3,1,2),b = (5,-1,4).
在空间直角坐标系Oxyz的三条轴的正方向分别取三个 单位向量 i, j, k 称为基本单位向量.
1、向量的加减法与数乘
a
(a
x
,
ay,
az ) axi ay j azk;
b (bx , by , bz ) bxi by j bzk;
⑴加法 a b (ax bx , ay by, az bz )
结果是一个与原向量同方向的单位向量.
(3) 两个向量的平行关系（共线定理）
定理 设向量 a 0，那么向量 b 平行于 a 的充分必要条件
是：存在唯一的实数 ，使 b a.
证设:b充// a分, 取性显然b；, 当下b面与证a 同明向必时要性取正值，
当
b
与
a
a
反向时 取负值，
则此时
b
与
a
同向.
又
a
a
b
a
b,
故有 b a.
a
再证明 的唯一性. 设 b
两式相减，得
(
)a
a0，，又设即ba，a
0，
a 0， 故 0， 即 .
证毕
注：此定理是建立数轴和坐标的理论依据. 设点O及单位向量i 确定了数轴Ox,
对于轴上任一点P, 对应一个向量OP,
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a b c c Pr jc a b c Prjc a Prjc b
c Pr jc a c Pr jc b a c b c
机动 目录 上页 下页 返回 结束
例1. 证明三角形余弦定理
c2 a2 b2 2abcos
证: 如图 . 设
CB a, C A b, AB c
作业 P300 3 , 5, 13, 14,
15, 18, 19
第二节 目录 上页 下页 返回 结束
备用题
41k.设, 求m向量3 ia54j m
8k 3
, n
n
p
2i
在
x
4
j
7k
,
p
5i
轴上的投影及在
y
j
轴上的分向量.
解: 因
故在 x 轴上的投影为 a x 13 在 y 轴上的分向量为 ay j 7 j
则
Ab
c
C
Ba
c 2 (a b)(a b) aa bb2ab
a 2 b 2 2 a b cos
a a ,b b ,c c
c2 a2 b2 2abcos
机动 目录 上页 下页 返回 结束
4. 数量积的坐标表示
设 a ax i ay j az k , b bx i by j bz k , 则 ( ax i ay j az k ) (bx i by j bz k )
第七章
空间解析几何与向量代数
第一部分 向量代数 第二部分 空间解析几何
在三维空间中: 空间形式 — 点, 线, 面
数量关系 — 坐标, 方程（组） 基本方法 — 坐标法; 向量法
第一节
第七章
向量及其线性运算
一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影
ab b a
a 运算规律 : 交换律 a b b a
结合律 ( a b ) c a (b c ) a b c
三角形法则可推广到多个向量相加 .
机动 目录 上页 下页 返回 结束
s a1 a2 a3 a4 a5
a4
a5
a3 s
a2 a1
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
第二节
第七章
数量积 向量积 *混合积
一、两向量的数量积 二、两向量的向量积 *三、向量的混合积
机动 目录 上页 下页 返回 结束
一、两向量的数量积
引例. 设一物体在常力 F 作用下, 沿与力夹角为
的直线移动, 位移为 s , 则力F 所做的功为
WF
s
cos
1. 定义
例6. 已知两点
和
求
解: AB AB 1 (3 , 1 , 2)
AB
14
3 , 1 , 2
14 14 14
机动 目录 上页 下页 返回 结束
2. 方向角与方向余弦
设有两非零向量
称 =∠AOB
任取空间一点 O
(0≤ ≤ ) 为向量
,
a
,
b 的夹角.
记作
类似可定义向量与轴, 轴与轴的夹角 .
OM
1
1
(OA
OB
B
1
1
(x1 x2 , y1 y2 , z1 z2 )
M
机动 目录 上页 下页 返回 结束
说明: 由
1
1
(x1 x2 , y1 y2 , z1 z2 )
得定比分点公式:
A
x1 x2 1
,
y1 y2 1
,
z1 z2
1
M B
o
A
当 1时, 点 M 为 AB 的中点 ,于是得
a 0, b 0 则 ab 0
机动 目录 上页 下页 返回 结束
3. 运算律
(1) 交换律 (2) 结合律
b a
a ( b)
( a ) ( b) a ( b)
(ab)
(3) 分配律
(a b) c
Pr jc a Pr jc b Pr jc ( a b)
事实上, 当 c 0 时, 显然成立 ; 当c 0时
平行向量对应坐标成比例:
当
a
0
时,
bx ax by ay
bx by bz ax ay az
bz az
机动 目录 上页 下页 返回 结束
例2. 求解以向量为未知元的线性方程组
其中
a
5x 3x
3 2
y y
a b
（2，1，2）, b （1，1，
2）.
① ②
解:
2×①
x
－23a× ②3b,得
机动 目录 上页 下页 返回 结束
2. 设 m i j, n 2 j k, 求以向量 m , n 为边的平
行四边形的对角线的长度 .
解：对角线的长为
|mn|
m n ( 1, 1,1)
m n (1,3, 1)
|mn 3
| m n 11
n m
该平行四边形的对角线的长度各为 3, 11
2. 向量的减法 三角不等式
a
机动 目录 上页 下页 返回 结束
3. 向量与数的乘法
是一个数
,
与
a
的乘积是一个新向量,
记作
a
.
规定 :
总之:
a
a
运算律 : 结合律
(
a)
(
a)
a
11可aa见a;a ;
分配律
(a
b)
a
b
则有单位向量
a
1 a
a.
因此
a
a
a
机动 目录 上页 下页 返回 结束
M1M3 (5 4)2 (2 3)2 (3 1)2 6
M 2M3 M1M3
M1
M3
即 M1M 2M3 为等腰三角形 .
M2
机动 目录 上页 下页 返回 结束
例5. 在 z 轴上求与两点
及
离的点 .
等距
解: 设该点为M (0,0, z), 因为 M A M B ,
(4)2 12 (7 z)2 32 52 (2 z)2
的坐标为 M (x , y , z), 则
z OM ON NM OA OB OC C
r
x
i
y
j
z
k
(x
,
y
,
z
)
此式称为向量 r 的坐标分解式 ,
ko i
j
r
M B y
A
x
N
沿三个坐标轴方向的分向量.
机动 目录 上页 下页 返回 结束
设四、a 利(aa用x,坐baay标,((aa作zx)a,向x b,b量xa, (a的yby,x线,baby性zy,),ba运zz),算bz为) 实数，则
(7
,
1,10)
代入②得
y
1
(3
x
b)
(11,
2
,16)
2
机动 目录 上页 下页 返回 结束
例3. 已知两点 在AB直线上求一点 M , 使
及实数 1,
解: 设 M 的坐标为
如图所示
AM MB
AM OM OA MB OB OM
OM O A (OB OM )
A
M B
o
A
得 即
r
o
y
x
机动 目录 上页 下页 返回 结束
例7. 已知两点
和
的模 、方向余弦和方向角 .
计算向量
解: M1M 2 ( 1 2, 3 2 , 0 2 ) (1, 1, 2 )
(1)2 12 ( 2)2 2
cos 1 , cos 2
2
2
2 ,
,
3
3
3
4
机动 目录 上页 下页 返回 结束
i j jk ki 0源自a b axbx ayby azbz
两向量的夹角公式 当 为非零向量时, 由于
a b cos , 得
cos
axbx ayby azbz
ab
a
2 x
a
2 y
az2
bx2 by2 bz2
机动 目录 上页 下页 返回 结束
例2. 已知三点 M (1,1,1), A( 2, 2,1), B( 2,1, 2), 求
)
MD
1 2
(b
a
)
机动 目录 上页 下页 返回 结束
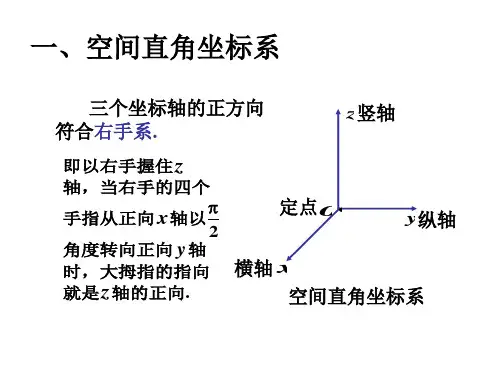
三、空间直角坐标系
1. 空间直角坐标系的基本概念
过空间一定点 o ,由三条互相垂直的数轴按右手规则
组成一个空间直角坐标系.
• 坐标原点
Ⅲ
z z 轴(竖轴)
Ⅱ
• 坐标轴
Ⅳ
• 坐标面
• 卦限(八个) Ⅶ
x
x轴(横轴)
Ⅷ
yoz面 o xoy面
Ⅴ
Ⅰ
y
y轴(纵轴)
M2 M1
机动 目录 上页 下页 返回 结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ;
若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行,记作 a∥b ; 规定: 零向量与任何向量平行 ;
与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作－a ;
设向量 a , b 的夹角为 , 称
记作
ab
M1 s
M2
W F s
为a与b的数量积 (点积) .
机动 目录 上页 下页 返回 结束
b
在
a
上的投影为
b
记作 Pr ja b