金字塔算法模型初识

数学金字塔模型公式金字塔模型是一种常见的数学图形，它具有金字塔形状的特征。

在数学中，我们可以使用公式来计算金字塔的各种属性。

首先，让我们来看一下金字塔的基本构成。

金字塔由一系列的水平层级组成，每一层都比上一层多一个单位的方块。

例如，第一层只有一个方块，第二层有四个方块，第三层有九个方块，以此类推。

这种构成方式形成了一个等差数列。

根据金字塔的结构，我们可以推导出两个关键的数学公式。

第一个公式用于计算金字塔的总方块数量，称为总数公式。

第二个公式用于计算金字塔的层数，称为层数公式。

总数公式可以表达为：总数 = (层数 * (层数 + 1) * (2 * 层数 + 1)) / 6。

这个公式基于等差数列的求和公式，将每一层的方块数量相加得出总数。

层数公式可以表达为：层数 = （sqrt(8 * 总数 + 1) - 1）/ 2。

这个公式基于总数公式的逆推，通过解一元二次方程可以得出层数。

举个例子来说明这两个公式的使用。

假设我们要计算一个金字塔的总数和层数，已知总数为36。

首先，我们可以使用层数公式计算出金字塔的层数：层数 =（sqrt(8 * 36 + 1) - 1）/ 2 = （sqrt(289) - 1）/ 2 = (17 - 1) / 2 = 8。

接下来，我们可以使用总数公式计算金字塔的总方块数量：总数 = (层数 * (层数 + 1) * (2 * 层数 + 1)) / 6 = (8 * (8 + 1) * (2 * 8 + 1)) / 6 = 36。

通过这两个公式，我们可以方便地计算金字塔的总数和层数，从而更好地理解和掌握金字塔模型在数学中的应用。

数学公式的运用使得我们能够更高效地解决问题，并且扩展了我们对数学概念的理解。

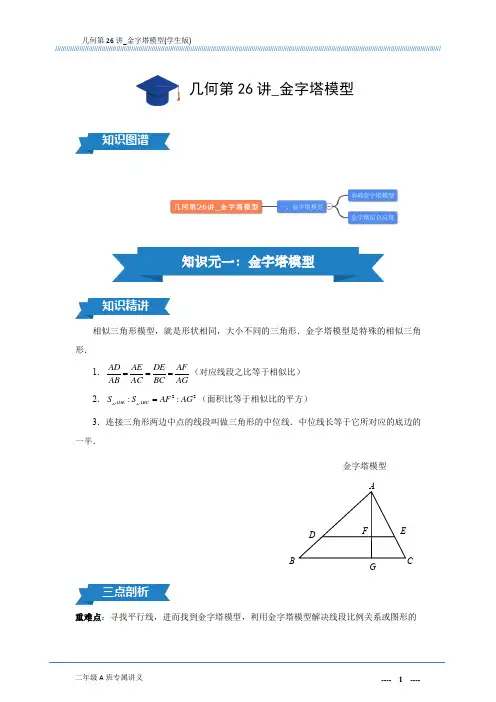
相似三角形模型，就是形状相同，大小不同的三角形．金字塔模型是特殊的相似三角形．1．AD AE DE AFAB AC BCAG===（对应线段之比等于相似比）2．22::ADEABCS SAF AG =（面积比等于相似比的平方）3．连接三角形两边中点的线段叫做三角形的中位线．中位线长等于它所对应的底边的一半．重难点：寻找平行线，进而找到金字塔模型，利用金字塔模型解决线段比例关系或图形的几何第26讲_金字塔模型F E D GCBA金字塔模型面积比例关系．题模一：基础金字塔模型例1.1.1如图所示，BC 与DE 平行．已知4AD =，5BD =，16DE =，则BC =__________．例1.1.2如图所示，DE 与BC 平行，已知4AD =，5BD =，△ADE 的面积为32，则四边形DECB 面积为_________．例1.1.3如图，DE 平行BC ，若:2:3AD DB =，那么:ADE ECB S S =△△________．例 1.1.4如图， ABC △中，DE ，FG ，MN ，PQ ，BC 互相平行，AD DF FM MP PB====，则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形___________．题模二：金字塔综合应用例1.2.1如图，已知三角形ADE 的面积为1平方厘米，D 、E 分别是AB 、AC 边的靠近A 点的三等分点．那么三角形OBC 的面积是_______平方厘米．A ED CBQ E GNMF PA D CB例1.2.2如图，三角形ABC 的面积为60，D 、E 分别为AB 、AC 的中点，F 、G 是BC 边上的三等分点，三角形DOE 的面积是______．例1.2.3如图，在三角形ABC 中，D 、E 为AB 、AC 的三等分点，DF 、EG 分别垂直BC 于F 、G ，矩形DEGF 面积为6，那么三角形ABC 面积为__________．例1.2.4如图，在正方形ABCD 中，E 是BC 边上靠近B 点的三等分点，F 是DC 边上靠近D 点的三等分点，已知正方形ABCD 的面积为20平方厘米，则阴影部分的面积是________平方厘米．例1.2.5如右图，已知D 是BC 中点，E 是CD 的中点，F 是AC 的中点．三角形ABC 由①~⑥这6部分组成，其中②比⑥多12平方厘米．那么三角形ABC 的面积是______________平方厘米．OCBEDAOGFCBEDACGFBED AACD EFBPR随练1.1如图是一个边长为4的正方形ABCD ，E 、H 分别是AB 和BG 的中点，3AG =．阴影部分的面积是____________．随练1.2长方形ABCD 的面积是40，E 、F 、G 、H 分别为AD 、AH 、DH 、BC 的中点，三角形EFG 的面积是__________．随练1.3如图，三角形ABE 中，AB 平行DC ，BD 交AC 于O ，AD =2DE ，三角形AB0的面积为4，求三角形ABE 的面积等于_____________．作业1如图，EF 和BC 平行，:1:2AE EB =．已知2AF =，3EF =，那么CF的长度是多HGF EDCBAAFED C B ①② ③④⑤⑥HG E DC BA ABCDEO少？AC 的长度是多少？BC 的长度是多少？作业2如图，已知AC 与ED 平行，三角形ABC 被分成三块区域，其中两块区域的面积已标出那么三角形ACD 的面积是__________．作业3如图，ABC △中，DE ，FG ，BC 互相平行，AD DF FB ==，则::ADE DEGF FGCB S S S =△四边形四边形_______________．作业4如图，三角形ABE 中，AB 平行CD ,AC =5厘米，CE =15厘米．如果已知三角形CDE 的面积是90平方厘米，那么梯形ABDC 的面积是__________平方厘米．作业5如图，在△ABC 中，若AF FB =，AG GC =，152DE BC ==，BC 边上的高为12，EGF A D CBBFEC AEDCBA96ABC D EEF 与DG 相交于点H ，则图中阴影面积是__________．作业6如图，三角形ABE 中，AB 平行DC ，BD 交AC 于O ，AD =DE ，三角形ABE 面积为36，求三角形OCD 的面积等于____________．作业7如图，已知D 是BC 的中点，E 是AC 的中点．三角形ABC 由①至⑤这5部分组成，其中①的面积比④多6平方厘米．请问：三角形ABC 的面积是多少平方厘米？ABCDEOABCD E①②③④⑤。

学习《知识转化的金字塔模型》心得体会学习金字塔学习法心得体会（陈慧玲）美国学者埃德加.戴尔（Edgar Dale）1946年提出了“学习金字塔”（Cone of Learning）的理论。

金字塔的内容主要包括：第一种：“听讲”，最熟悉最常用的方式，学习效果却是最低的，两周以后学习的内容只能留下5％。

第二种：通过“阅读”方式学到的内容，可以保留10％。

第三种：用“声音、图片”的方式学习，可以达到20％。

第四种：是“示范”，采用这种学习方式，可以记住30％。

第五种：“小组讨论”，可以记住50％的内容。

第六种：“做中学”或“实际演练”，可以达到75％。

第七种：是“教别人”或者“马上应用”，可以记住90％的学习内容。

从中我们可以看出学习效果在30%以下的几种传统方式，都是个人学习或被动学习；而学习效果在50％以上的，都是团队学习、主动学习和参与式学习。

主动学习应该是课堂学习的主旋律。

如果我们的课堂照本宣科、单向灌输是主流，老师带张嘴，学生带双耳朵，一堂课效率是很低的，纯属浪费学生的时间。

学生学得轻松，一定要提高学习的效率。

像英语科，要学生们充分利用自己的全部感官，通过体验式的学习，给孩子们留下“刻骨铭心”的记忆，激发起孩子们的好奇心和探究欲，会利用各种方式，读书，看视频等，继续关注和探究所学知识，实现由“知”到“行”的转变。

这种“我要学”的主动学习才是最有效率的学习。

因此，教师要学会调整甚至改变教学方式和角色，充分尊重学生在学习活动中的主体地位。

引导学生自觉地参加合作学习，学生要努力转变学习方法，要由被动听转到主动学，要多种器官综合使用，要耳、眼、脑、口、手并用。

在教学中，要大力提倡小组合作学习，在参与中掌握知识，生成能力，从而真正实现了从知识到能力的转化，更使学生们真正将老师传授的知识记得多，记得准，记得牢。

让学生在合作探究学习中展示自我，体验成功，从而提升学习兴趣，这样我们的课堂教学就会变得高效，学生的学习也会变得高效，从而培养了学生的能力，提高了学生素质，为学生的终生发展奠定了坚实的基础作为英语老师要转变教学观念，少在课堂上讲“大道理”。

金字塔算法公式金字塔算法，也叫金字塔模型，是一种常见的数据挖掘算法，主要用于分类、聚类和回归等大数据处理与分析工作中。

该算法利用了数据的自相似性，将数据层层分解，从而得出数据的特征与规律。

本文将从金字塔算法的定义、基本原理、应用场景以及相关实例四个方面进行阐述。

一、金字塔算法的定义金字塔算法是一种基于树状结构的数据处理算法，其核心在于对数据进行多层次的分解和重组。

在金字塔模型中，原始数据被分解为多个层次的模型，每一层次都包含了原始数据的一部分信息。

在预测与分析过程中，使用金字塔模型可以通过自相似性进行数据的预测和分类，从而为决策提供支持和依据。

二、金字塔算法的基本原理金字塔算法的基本原理是分层与重组。

分层是将原始数据逐层分解，每一层次都包含原始数据的一部分信息，且信息量越来越少；重组是将分解后的数据逐级重组，通过特定的分析模型和算法，得出目标数据的特征和规律。

通过不断迭代这一过程，最终得出准确率较高的分析结果。

三、金字塔算法的应用场景1.语音识别：金字塔算法可以将原始语音信号分解为多个层次的信号模型，并通过这些信号模型来识别不同的语音信号，从而实现语音识别。

2.图像处理：金字塔算法能够将图像进行分层处理，并通过多尺度分析和比较，实现图像分类和识别。

在医学图像处理中也被广泛应用。

3.物体识别：金字塔算法可以将物体分解为多个尺度和特征，并通过比较特征之间的相似度，实现对不同物体的识别和分类。

四、相关实例1.图像分割实例在图像分割中，金字塔算法将图像逐级分解，得到不同比例和分辨率的图像。

通过分析每一层次的图像特征，最终实现对目标图像的分割和识别。

2.语音信号去噪实例在语音信号去噪中，金字塔算法将语音信号分解为多个频带信号，并通过对比不同频带信号特征，去除其中的噪声信号，从而实现对纯净语音的提取。

综上所述，金字塔算法不仅是一种常见的数据处理算法，也是一种基于树状结构的数据挖掘算法。

金字塔算法适用于多种领域，如图像分析、物体识别和语音信号处理等。

特征金字塔公式介绍如下：
特征金字塔是一种用于计算机视觉中的目标检测和图像识别的技术。

特征金字塔公式是用来描述特征金字塔的计算过程的数学公式。

特征金字塔公式如下：
对于每个尺度$s_i$，计算图像的高斯金字塔$G_i$ 和拉普拉斯金字塔$L_i$：
$G_i(x,y) = \mathrm{Gaussian}(I(x,y), s_i)$
$L_i(x,y) = G_i(x,y) - \mathrm{expand}(G_{i+1}(x,y),2)$
其中，$I(x,y)$ 表示输入图像，$\mathrm{Gaussian}(I(x,y), s_i)$ 表示对输入图像$I(x,y)$ 进行高斯模糊操作，并使用尺度参数$s_i$ 进行缩放。

$\mathrm{expand}(G_{i+1}(x,y),2)$ 表示将尺度为$s_{i+1}$ 的高斯金字塔图像$G_{i+1}$ 进行双线性插值放大两倍，以与$G_i$ 相同的尺寸。

然后，对于每个尺度$s_i$，将$G_i$ 和$L_i$ 连接在一起形成特征金字塔$P_i$：
$P_i = {G_i} \cup {L_{i,j}}_{j=1}^{n}$
其中，${L_{i,j}}_{j=1}^{n}$ 表示拉普拉斯金字塔$L_i$ 的$n$ 个层级。

特征金字塔的主要目的是在不同尺度上检测目标或识别图像。

因为图像中的目标可以具有不同的尺度，使用特征金字塔可以帮助算法更好地适应这些不同的尺度，并提高检测或识别的准确性。

数学金字塔模型公式摘要：一、引言1.数学金字塔模型的背景与意义2.文章的目的与结构二、数学金字塔模型的基本概念1.数学金字塔模型的定义2.金字塔模型的基本元素三、数学金字塔模型的公式推导1.数学金字塔模型的基本公式2.公式推导的过程与方法四、数学金字塔模型的应用领域1.数学教育领域的应用2.实际问题解决中的运用3.对其他模型的启示与借鉴五、结论1.数学金字塔模型的重要性和价值2.对未来研究的展望正文：一、引言数学金字塔模型是一种用于描述数学知识结构和认知过程的理论模型，通过金字塔模型，我们可以更好地理解数学知识的层次性和相互关联性。

本文旨在详细介绍数学金字塔模型的基本概念、公式推导及其在数学教育和其他领域的应用，以期为相关研究和实践提供有益的参考。

二、数学金字塔模型的基本概念数学金字塔模型是一个描述数学知识结构和认知过程的理论框架，由美国数学教育家布鲁诺·博特纳（Bruno Bortner）于1980 年代提出。

该模型将数学知识分为四个层次：具体实例、概念、原则和元认知。

这四个层次按照从具体到抽象、从简单到复杂的顺序排列，形成一个金字塔形状。

1.具体实例：这一层次主要是指具体的数学问题、公式、定理等，是数学知识的起点，也是学生最初接触到的数学内容。

2.概念：在具体实例的基础上，学生需要理解和掌握相应的数学概念，例如函数、集合、概率等。

概念是对一类具体实例的抽象和概括，具有较高的抽象性。

3.原则：原则是数学知识中的基本原理和规律，如交换律、结合律等。

原则是对多个概念之间关系的阐述，具有更高的抽象性。

4.元认知：元认知是最高层次的数学知识，涉及到对数学知识本身的认知、思考和反思。

这一层次包括数学思维方法、问题解决策略等。

三、数学金字塔模型的公式推导数学金字塔模型并没有具体的数学公式，而是一个描述数学知识结构和认知过程的理论框架。

布鲁诺·博特纳通过实证研究，发现了数学知识结构和认知过程之间的相互关联，从而提出了这个模型。

金字塔模型与沙漏模型①ADAB=AEAC=DEBC=AFAG② S△ADE:S△ABC =AF2:AG2所谓的相似三角形,就就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变她们都相似),与相似三角形相关,常用的性质及定理如下: (1) 相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;(2) 相似三角形面积的比等于它们相似比的平方;(3) 连接三角形两边中点的线段我们叫做三角形的中位线;三角形中位线定理:三角形的中位线长等于她所对应的底边长的一半。

相似三角形对应角相等、对应边成比例的两个三角形叫做相似三角形。

如果三边分别对应A,B,C与a,b,c:那么:A/a=B/b=C/c,即三边边长对应比例相同。

判定方法定义对应角相等,对应边成比例的两个三角形叫做相似三角形。

预备定理平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似。

(这就是相似三角形判定的定理,就是以下判定方法证明的基础。

这个引理的证明方法需要平行线与线段成比例的证明)1判定定理常用的判定定理有以下6条:判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。

(简叙为:两角对应相等,两个三角形相似。

)(AA) 判定定理2:如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似。

(简叙为:两边对应成比例且夹角相等,两个三角形相似。

)(SAS)判定定理3:如果两个三角形的三组对应边成比例,那么这两个三角形相似。

(简叙为:三边对应成比例,两个三角形相似。

)(SSS)判定定理4:两个三角形三边对应平行,则个两三角形相似。

(简叙为:三边对应平行,两个三角形相似。

)判定定理5:如果一个直角三角形的斜边与一条直角边与另一个直角三角形的斜边与一条直角边对应成比例,那么这两个直角三角形相似。

(简叙为:斜边与直角边对应成比例,两个直角三角形相似。

)(HL)判定定理6:如果两个三角形全等,那么这两个三角形相似(相似比为1:1)(简叙为:全等三角形相似)。

ncc模板匹配算法金字塔-回复NCC模板匹配算法金字塔：从理论到实践引言：在计算机视觉领域中，模板匹配算法是一种常见而重要的图像处理方法。

它可以用于在一个图像中寻找到与给定模板最相似的区域，并进行识别、跟踪、检测等任务。

然而，由于图像中的物体可能存在尺度变化、旋转、光照变化等问题，传统的模板匹配算法往往会受到影响，导致匹配结果不准确。

为了解决这些问题，NCC（Normalized Cross-Correlation）模板匹配算法金字塔应运而生。

第一部分：NCC模板匹配算法的基本原理NCC模板匹配算法是基于互相关运算的。

在模板匹配过程中，首先需要获取到待匹配图像和模板图像。

然后，通过在待匹配图像上滑动模板，计算模板与图像之间的相似度。

1.1 归一化互相关运算归一化互相关运算是NCC模板匹配算法的关键。

它使得模板和图像之间的相似度可以在不同的尺度下进行比较。

1.2 互相关运算公式互相关运算可以通过模板和图像的像素值进行计算。

在NCC模板匹配算法中，互相关运算的公式如下所示：NCC(x, y) = 1/n * Σ[(T(i, j) - μ_T) * (I(x + i, y + j) - μ_I)]其中，T(i, j)表示模板图像中坐标为(i, j)的像素值，I(x, y)表示待匹配图像中坐标为(x, y)的像素值。

μ_T和μ_I分别表示模板图像和待匹配图像的均值。

1.3 归一化互相关运算归一化互相关运算通过计算互相关值之间的相似度，来确保模板匹配算法在不同的尺度下能够得到一致的结果。

具体公式为：NCC(x, y) = Σ[(T(i, j) - μ_T) * (I(x + i, y + j) - μ_I)] / [σ_T * σ_I]第二部分：金字塔的概念及其应用为了解决尺度变化的问题，NCC模板匹配算法引入了金字塔的概念。

金字塔是一种多尺度的图像表示方法，它通过对图像进行不同分辨率的缩放，使得算法能够在不同尺度下进行匹配。

第1篇一、引言金字塔模型作为一种经典的系统架构模型，被广泛应用于各个领域，特别是在软件开发领域。

金字塔模型实践教学是指将金字塔模型的基本原理、层次结构和实践方法融入到实际教学过程中，以培养学生的系统思维、实践能力和创新意识。

本文将从金字塔模型的基本概念、实践教学方法和实践案例三个方面进行探讨。

二、金字塔模型的基本概念金字塔模型是一种将系统分为三个层次的模型，分别是：业务层、应用层和基础层。

1. 业务层：业务层是金字塔模型的最底层，主要描述了系统的业务需求、业务规则和业务流程。

在这一层，我们需要分析业务需求，确定业务规则，并设计业务流程。

2. 应用层：应用层位于金字塔模型的中间层，主要描述了系统的功能模块、用户界面和数据处理。

在这一层，我们需要根据业务需求，设计功能模块，实现用户界面，并处理数据。

3. 基础层：基础层是金字塔模型的最顶层，主要描述了系统的技术架构、硬件设备和软件平台。

在这一层，我们需要选择合适的技术架构，配置硬件设备，并搭建软件平台。

三、金字塔模型实践教学方法1. 理论教学与实践教学相结合在金字塔模型实践教学过程中，我们需要将理论教学与实践教学相结合。

首先，通过理论教学，使学生了解金字塔模型的基本概念、层次结构和实践方法。

然后，通过实践教学，让学生在实际项目中应用金字塔模型，提高学生的实践能力和创新能力。

2. 案例教学与项目教学相结合金字塔模型实践教学过程中，我们可以采用案例教学与项目教学相结合的方式。

首先，通过案例教学，让学生了解金字塔模型在实际项目中的应用场景和解决方法。

然后，通过项目教学，让学生在项目实践中运用金字塔模型，提高学生的实践能力和团队合作能力。

3. 分层次教学与分层评价相结合金字塔模型实践教学过程中，我们需要根据学生的实际情况，实施分层次教学和分层评价。

首先，针对不同层次的学生，设计不同的教学内容和方法。

然后，通过分层评价，了解学生的学习成果，及时调整教学策略。

四、实践案例以下是一个基于金字塔模型的实践教学案例：项目背景：某公司希望开发一个在线购物系统，满足用户在线浏览、搜索、购买和支付等功能。

逻辑金字塔思考方式
逻辑金字塔思考方式
逻辑金字塔思考法（Logical Pyramid Thinking），也被称为“逻辑拓展思考法”，是一种能够深入分析解决问题的思考方式，它采用一个由上到下、由宽到窄的逻辑结构，围绕一个核心主题，把其拓展成为多层逻辑关系，在思考的过程中挖掘更深层次的联系，以求得问题的根本性原因和有效的解决方案。

1、理解主题
首先，理解和把握主题是最基本的环节，只有彻底明白主题，才能够开始有效的拓展思考，也能够形成一个逻辑金字塔思维模型。

2、归纳主题
接下来的步骤是归纳主题，即是把主题归纳成一个简单的句子或概念，而这句话或概念就是拓展思考的核心。

3、拓展思考
在归纳主题的基础上，从核心主题出发，深入思考，并联系实际情况，把主题联系到其他相关的概念，形成多层次的逻辑关系。

4、推理分析
最后一步是对前面拓展出来的思路和逻辑关系进行推理分析，以寻求问题的根本性原因和可行的解决方案。

逻辑金字塔思考方式是一种深入分析解决问题的有效方法，能够帮助人们从大量的信息中挖掘更有价值的思路和见解，用于实现更好的解决方案。

在实践中，逻辑金字塔思考方式能够更好的整合现有知
识，让思考和决策更加趋于合理。

数学金字塔模型公式(一)数学金字塔模型公式1. 引言数学金字塔模型是一种常用于解决具有递归结构的问题的数学模型。

它通过将问题分解成更小的子问题，并将子问题的解合并起来得到原问题的解。

本文将介绍数学金字塔模型的相关公式，并通过例子进行解释说明。

2. 公式1：递推公式递推公式是数学金字塔模型中最基本的公式，它描述了将一个问题分解为更小的子问题的过程。

递推公式通常使用递归的方式表示，形式如下：f(n) = f(n-1) + f(n-2)其中，f(n)表示第n个问题的解，f(n-1)和f(n-2)表示第n-1个和第n-2个子问题的解。

递推公式的含义是，要求解第n个问题，需要先求解第n-1个和第n-2个子问题。

例子：斐波那契数列斐波那契数列是一个经典的递归序列，它的递推公式为：f(n) = f(n-1) + f(n-2)。

其中，f(1) = 1，f(2) = 1。

根据递推公式，我们可以计算出斐波那契数列的前几项：1, 1, 2, 3, 5, 8, 13, …3. 公式2：合并公式合并公式描述了如何将子问题的解合并起来得到原问题的解。

合并公式通常根据具体的问题而定，形式各异。

例子：归并排序归并排序是一种经典的排序算法，它的合并公式为：将两个有序子数组合并为一个有序数组。

具体实现过程如下：def merge(arr, l, m, r):n1 = m - l + 1n2 = r - m# 创建临时数组L = [0] * (n1)R = [0] * (n2)# 复制数据到临时数组 L[] 和 R[]for i in range(0, n1):L[i] = arr[l + i]for j in range(0, n2):R[j] = arr[m + 1 + j]# 合并临时数组返回到 arr[l..r]i = 0 # 初始化第一个子数组的索引 j = 0 # 初始化第二个子数组的索引 k = l # 初始归并子数组的索引while i < n1 and j < n2:if L[i] <= R[j]:arr[k] = L[i]i += 1else:arr[k] = R[j]j += 1k += 1# 复制剩余元素到 arr[]while i < n1:arr[k] = L[i]i += 1k += 1while j < n2:arr[k] = R[j]j += 1k += 1def mergeSort(arr, l, r):if l < r:# 计算中间位置m = (l+(r-1))//2# 将数组拆分为两个子数组mergeSort(arr, l, m)mergeSort(arr, m+1, r)# 合并两个子数组merge(arr, l, m, r)在归并排序算法中，我们使用合并公式将两个排好序的子数组合并为一个有序数组。

数学金字塔模型公式
【原创实用版】
目录
1.数学金字塔模型公式概述
2.数学金字塔模型公式的构成
3.数学金字塔模型公式的应用
4.数学金字塔模型公式的优缺点
正文
【数学金字塔模型公式概述】
数学金字塔模型公式，是一种用于描述数学问题的特殊模型，它的构成包括了金字塔形状的各个层面上的数值。

这种模型能够直观地反映出数学问题的内在逻辑关系，因此在解决一些复杂的数学问题时，具有非常高的实用价值。

【数学金字塔模型公式的构成】
数学金字塔模型公式通常由两部分组成，一部分是金字塔的底层，也就是公式的基础部分，另一部分则是金字塔的塔尖部分，也就是公式的高阶部分。

这两部分通过一系列的数学运算，如加减乘除、指数运算、对数运算等，相互联系起来，构成了整个金字塔模型公式。

【数学金字塔模型公式的应用】
数学金字塔模型公式在实际应用中，通常用于解决一些复杂的数学问题，如微积分、概率论、线性代数等。

通过这种模型，可以将复杂的问题分解为若干个简单的问题，从而简化了解题的过程。

同时，这种模型还能够帮助人们更直观地理解数学问题的内在逻辑关系，提高了解题的效率。

【数学金字塔模型公式的优缺点】
数学金字塔模型公式的优点在于其直观性和逻辑性，能够帮助人们更好地理解和解决数学问题。

然而，这种模型也存在一些缺点，如公式的构建过程较为复杂，需要具有一定的数学基础和逻辑思维能力。

金字塔原理，不止是MECE，更重要的是SCQA序言周末和一个客户进行了一场近9个小时的研讨，对金字塔原理的理解，又更深了一层。

在这场研讨会中，有些人甚至是第一次接触金字塔原理，第一次听说MECE法则、第一次听说SCQA模型，但令人佩服的时，不愧都是一些博士，1个小时的理论介绍后，人家对MECE、SCQA理解就已经出口成章了。

比如，讲完结论先行，就有人分享了下面这个故事：公交车上，一个中年人对一个时髦小伙子说：“我今天早上8点就从玉溪坐大巴来了，人太多了，到现在都还晕车，我要去一个亲戚家做客，他家生了一个大胖小子，今天刚好满100天，请我们老乡一起庆祝一下，我老乡可有钱了，在昆明有3套房子呢，他今天让我们去的这个地方，是他在昆明买的第一套房子，说是这路公交车有个站离他们家比较近，小伙子，我想问一下，我要到红山小区，在哪个站下车比较好？”，话还未说完，公交车到了到站了，小伙子歉意的一笑，“大叔，我到站了，你问一下别人吧”。

中年大叔大约说了2分钟，最后小伙子才知道他的需求，可惜公交车不等人，小伙子来不及帮他就下车了，那么，如果这个中年大叔懂得金字塔原理的结论先行，会怎么做呢？“您好，小伙子，我要到红山小区，请问在哪个站下车比较好？”既有礼貌，又在10秒钟内说出需求，不超过10秒，他就可以获得答案。

金字塔原理是什么？金字塔原理是麦肯锡公司一位叫芭芭拉·明托(Barbara Minto)的顾问提出的一个方法论，她也是麦肯锡公司有史以来第一位女性顾问，金字塔原理是训练人们逻辑思维、逻辑表达最有效的工具之一，金字塔原理拥有四大核心思想：1.结论先行2.MECE法则3.4个逻辑结构4.结构化我们先看一张典型的金字塔结构图：图1、典型的的金字塔结构结论先行为什么要结论先行呢？结论先行的最大价值在于：（1）让对方第一时间听到你的结论，即便对方因为有事打扰或中途离开（2）对方听到你的结论后，接下来的所有内容，他的大脑会自动将接下来的讯息关联到这个结论上，这是一种吸引力。

金字塔模型结论及证明
金字塔模型结论：
1. 金字塔结构是一种清晰展现思路的有效方法，其核心是一个模型，即背景、冲突、疑问、答案（S-C-Q-A）。

2. 金字塔结构中的信息组织遵循了演绎推理和归纳推理两种推理方式。

演绎推理是从一个大前提推导到一个小前提，然后得出结论的过程。

归纳推理则是将信息按照金字塔结构进行归纳分组，以便理解和记忆。

3. 金字塔结构的特点包括结论先行、以上统下、归类分组和逻辑推进。

这些特点有助于组织信息，使其更加易于理解和记忆。

4. 掌握金字塔原理的核心思想，运用它去构思自己的写作和演讲，可以提高思考、沟通、表达和解决问题的能力。

证明：
金字塔原理的证明可以通过实验和实证研究来进行。

例如，可以设计一些实验来测试人们在不同信息组织方式下的理解和记忆能力，以此来验证金字塔原理的有效性。

此外，也可以通过对比研究的方法，比较使用金字塔结构和不使用金字塔结构的信息组织方式在沟通和表达方面的效果差异。

总之，金字塔原理是一种有效的信息组织方法，其结论可以通过实验和实证研究来证明。

掌握金字塔原理的核心思想，并将其应用于实际工作和生活中，可以提高个人的逻辑思维和表达能力。

金字塔模型公式及图形
金字塔模型公式是：1+2+3+...+n=n(n+1)/2。

n=9，一共有9*10/2=45。

金字塔模型是一种简单的几何图形，其模型的制作和试验都很简便。

可采取底边长12厘米，棱长11.4厘米，高8厘米或底边9厘米，棱长8.55厘米，高6厘米两种比例。

模型的大小可根据被试验物情况，从8厘米至2.3米高。

金字塔模型的内涵
金字塔模型是由美国匹兹堡大学商学院John E·Prescott教授提出的一种模型，主要用于对竞争对手的跟踪分析，是企业开展竞争对手跟踪工作的指导工具，Prescott的金字塔模型提供了一条“竞争信息，竞争决策”的工作线索。

金字塔模型强调信息如何形成竞争决策，金字塔模型分为三层。

分析模型中塔的底层是各种基础数据库，主要存放竞争对手的基本信息和关键数据。

中层的更新数据库定期对竞争对手的基本信息进行更新，及时反映竞争对手的新举措和新动向。

上层的分析、预测和决策，是企业在综合分析竞争信息的基础上形成的竞争决策。

除此之外，还有分散在金字塔外部的“零散信息点”，是企业获得的突发的竞争对手信息，对这些信息进行必要的分析处理后，既可以形成对竞争对手的新认识，也可以激活上层的评估与预测。