2016-2017年全国中考二次函数与平行四边形压轴题

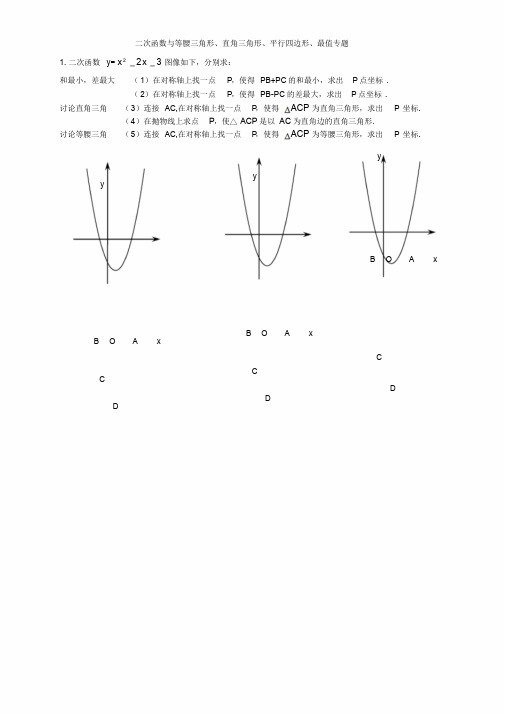
二次函数与等腰三角形、直角三角形、平行四边形、最值专题1. 二次函数y= x2 2x 3图像如下，分别求：和最小，差最大（1）在对称轴上找一点P，使得PB+PC的和最小，求出P 点坐标.（2）在对称轴上找一点P，使得PB-PC的差最大，求出P 点坐标.讨论直角三角（3）连接AC,在对称轴上找一点P，使得ACP 为直角三角形，求出P坐标.（4）在抛物线上求点P，使△ACP是以AC为直角边的直角三角形．讨论等腰三角（5）连接AC,在对称轴上找一点P，使得ACP 为等腰三角形，求出P坐标.yyyB O A xB O A xB O A xCCCDDD122.已知抛物线y＝ax ＋bx＋c 经过A( －1，0) 、B(3 ，0) 、C(0 ，3) 三点，直线l 是抛物线的对称轴．(1) 求抛物线的函数关系式；(2) 设点P是直线l 上的一个动点，当△PAC的周长最小时，求点P的坐标；(3) 在直线l 上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．2. 已知：如图一次函数y＝1x＋1 的图象与x 轴交于点A，与y 轴交于点B；二次函数y＝2 1 x22＋bx＋c 的图象与一次函数y＝（1）求二次函数的解析式；1x＋1 的图象交于B、C两点，与x 轴交于D、E两点且D点坐标为（1，0）2（2）求四边形BDEC的面积S；（3）在x 轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．yC 2BxA O D E22、（2013?连云港）如图，抛物线y=-x 2+mx+n与x 轴分别交于点A（4，0），B（-2 ，0），与y 轴交于点C．（1）求该抛物线的解析式；（2）M为第一象限内抛物线上一动点，点M在何处时，△ACM的面积最大；（3）在抛物线的对称轴上是否存在这样的点P，使得△PAC为直角三角形？若存在，请求出所有可能点P 的坐标；若不存在，请说明理由．4、(西宁）在平面直角坐标系中，现将一块等腰直角三角板A BC 放在第二象限，斜靠在两坐标轴上，点C 为（-1，0）．如图所示， B 点在抛物线y=12 x2+2+12x-2 图象上，过点 B 作BD ⊥x 轴，垂足为D，且B 点横坐标为-3．（1）求证：△BDC ≌△COA；（2）求BC 所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P，使△ACP 是以AC 为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由．39、（潼南）如图，在平面直角坐标系中，△ABC 是直角三角形，∠ACB=90 °，AC=BC ，OA=1，OC=4，抛物线y=x 2+bx+c 经过A，B 两点，抛物线的顶点为D．（1）求b，c 的值；（2）点 E 是直角三角形ABC 斜边AB 上一动点（点A、B 除外），过点 E 作x 轴的垂线交抛物线于点F，当线段EF 的长度最大时，求点 E 的坐标；（3）在（2）的条件下：①求以点E、B、F、D 为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP 是以EF 为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，说明理由．2 bx c a6．如图，已知抛物线y ax ( 0)的顶点坐标为Q 2, 1 ，且与y 轴交于点 C 0,3 ，与x轴交于A、B 两点（点A在点 B 的右侧），点P 是该抛物线上一动点，从点C沿抛物线向点 A 运动（点P 与A不重合），过点P作PD∥y 轴，交AC于点D．(1) 求该抛物线的函数关系式；(2) 当△ADP是直角三角形时，求点P 的坐标；(3) 在问题(2) 的结论下，若点E在x轴上，点 F 在抛物线上，问是否存在以A、P、E、F 为顶点的平行四边形？若存在，求点 F 的坐标；若不存在，请说明理由．4。

1.如图，抛物线的顶点为P （1，0），一条直线与抛物线相交于A （2，1），B （－21，m ）两点．（1）求抛物线和直线AB 的解析式；（2）若M 为线段AB 上的动点，过M 作MN ∥y 轴，交抛物线于点N ，连接NP 、AP ，试探究四边形MNP A 能否为梯形，若能，求出此时点M 的坐标；若不能，请说明理由．2.如下列图，在平面直角坐标系中，抛物线y ＝ax2＋bx ＋c （a ≠0）．经过A （－1，0）、B （3，0）、C （0，3）三点，其顶点为D ，连接BD ，点P 是线段BD 上一个动点（不与B 、D 重合），过点P 作y 轴的垂线，垂足为E ，连接BE ．（1）求抛物线的解析式，并写出顶点D 的坐标；（2）假设P 点的坐标为（x ，y ），△PBE 的面积为s ，求s 与x 的函数关系式，写出自变量x 的取值范围，并求出s 的最大值；（3）在（2）的条件下，当s 取得最大值时，过点P 作x 轴的垂线，垂足为F ，连接EF ，把△PEF 沿直线EF折叠，点P 的对应点为P ′ ，请直接写出P ′点坐标，并判断点P ′是否在该抛物线上．3．如图，抛物线与x轴交于A（x1，0），B（x2，0）两点，且x1＞x2，与y轴交于点C（0，4），其中x1，x2是方程x2－2x－8＝0的两个根．（1）求这条抛物线的解析式；（2）点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；（3）探究：若点Q是抛物线对称轴上的点，是否存有这样的点Q，使△QBC成为等腰三角形，若存有，请直接写出所有符合条件的点Q的坐标；若不存有，请说明理由．4．已知：如下列图，关于x的抛物线y＝ax2＋x＋c（a≠0）与x轴交于点A（－2，0），点B（6，0），与y 轴交于点C．（1）求出此抛物线的解析式，并写出顶点坐标；（2）在抛物线上有一点D，使四边形ABDC为等腰梯形，写出点D的坐标，并求出直线AD的解析式；（3）在（2）中的直线AD交抛物线的对称轴于点M，抛物线上有一动点P，x轴上有一动点Q．是否存有以A、M、P、Q为顶点的平行四边形？假设存有，请直接写出点Q的坐标；假设不存有，请说明理由．5．如图，矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上，A （－3，0），过点C 的直线y ＝－2x ＋4与x 轴交于点D ，二次函数y ＝－21x2＋bx ＋c 的图象经过B 、C 两点． （1）求B 、C 两点的坐标； （2）求二次函数的解析式；（3）若点P 是CD 的中点，求证：AP ⊥CD ；（4）在二次函数的图象上是否存有这样的点M ，使以A 、P 、C 、M 为顶点的四边形为矩形？若存有，求出点M 的坐标；若不存有，请说明理由．6．已知：抛物线y ＝ax2＋bx ＋c （a ≠0）的对称轴为x ＝－1，与x 轴交于A 、B 两点，与y 轴交于点C ，其中A （－3，0）、C （0，－2）．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存有一点P ，使得△PBC 的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE ∥PC 交x 轴于点E ，连接PD 、PE ．设CD 的长为m ，△PDE 的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存有最大值，若存有，请求出最大值；若不存有，请说明理由．7.如图，已知抛物线y＝x2－1与x轴交于A、B两点，与y轴交于点C．（1）求A、B、C三点的坐标．（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．（3）在x轴上方的抛物线上是否存有一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存有，请求出M点的坐标；否则，请说明理由．8．如图，抛物线y＝ax2＋bx－3与x轴交于A，B两点，与y轴交于C点，且经过点（2，－3a），对称轴是直线x＝1，顶点是M．（1）求抛物线对应的函数表达式；（2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存有这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存有，请求出点P的坐标；若不存有，请说明理由；（3）设直线y＝－x＋3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E 三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；（4）当E是直线y＝－x＋3上任意一点时，（3）中的结论是否成立？（请直接写出结论）9．如图，已知抛物线y＝ax2＋bx＋c与y轴交于点A(0，3)，与x轴分别交于B(1，0)、C(5，0)两点．（1）求此抛物线的解析式；（2）若点D为线段OA的一个三等分点，求直线DC的解析式；（3）若一个动点P自OA的中点M出发，先到达x轴上的某点（设为点E），再到达抛物线的对称轴上某点（设为点F），最后运动到点A．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．10．如图，在平面直角坐标系中，以点A(－3，0)为圆心、5为半径的圆与x轴相交于点B、C两点（点B在点C的左边），与y轴相交于D、M两点（点D在点M的下方）．（1）求以直线x＝－3为对称轴、且经过D、C两点的抛物线的解析式；（2）若点P是这条抛物线对称轴上的一个动点，求PC＋PD的取值范围；（3）若点E为这条抛物线对称轴上的点，则在抛物线上是否存有这样的点F，使得以点B、C、E、F 为顶点的四边形是平行四边形？若存有，求出点F的坐标；若不存有，说明理由．11．如图，已知抛物线y＝ax2＋bx－4与直线y＝x交于点A、B两点，A、B的横坐标分别为－1和4．（1）求此抛物线的解析式．（2）若平行于y轴的直线x＝m（0＜m＜5＋1）与抛物线交于点M，与直线y＝x交于点N，交x轴于点P，求线段MN的长（用含m的代数式表示）．（3）在（2）的条件下，连接OM、BM，是否存有m的值，使得△BOM的面积S最大？若存有，请求出m 的值，若不存有，请说明理由．12．如图，抛物线经过A（4，0），B（1，0），C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存有P点，使得以A、P、M为顶点的三角形与△OAC相似？若存有，请求出符合条件的点P的坐标；若不存有，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．13. 如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y 轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .b ；若不存有，说明理由.14.如图，已知抛物线212y x bx c x =++与轴交于点A （-4，0）和B （1，0）两点，与y 轴交于C 点. (1)求此抛物线的解析式；(2)设E 是线段AB 上的动点，作EF ∥AC 交BC 于F ，连接CE ，当△CEF 的面积是△BEF 面积的2倍时，求E 点的坐标；(3)若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P 点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标.x15.如图，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ， 那么是否存有点P ，使四边形POP /C 为菱形？若存有，请求出此时点P 的坐标；若不存有，请说明理由．（3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.16.在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ，点A 的坐标为(30)-，，若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线2x =-．（1）求直线AC 及抛物线的函数表达式；（2）假如P 是线段AC 上一点，设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆，且:2:3ABP BPC S S ∆∆=，求点P 的坐标；（3）设Q 的半径为l ，圆心Q 在抛物线上运动，则在运动过程中是否存有Q 与坐标轴相切的情况？若存有，求出圆心Q 的坐标；若不存有，请说明理由．并探究：若设⊙Q 的半径为r ，圆心Q 在抛物线上运动，则当r 取何值时，⊙Q 与两坐轴同时相切？。

中考数学分类汇编二次函数压轴题1.（ 2016?成都第 28 题）如图，在平面直角坐标系xOy 中，抛物线y=a（ x+1）2﹣ 3 与 x 轴交于 A， B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C（ 0，﹣），顶点为D ，对称轴与x 轴交于点H，过点 H 的直线 l 交抛物线于P， Q 两点，点Q 在 y 轴的右侧．（ 1）求 a 的值及点A，B 的坐标；（ 2）当直线l 将四边形ABCD 分为面积比为3： 7 的两部分时，求直线l 的函数表达式；（ 3）当点 P 位于第二象限时，设PQ的中点为M，点 N 在抛物线上，则以 DP 为对角线的四边形DMPN 能否为菱形？若能，求出点N 的坐标；若不能，请说明理由．2.（ 2016?扬州第 28 题）如图 1，二次函数y = ax2 + bx 的图像过点A（-1， 3），顶点 B 的横坐标为 1.（ 1）求这个二次函数的表达式；（ 2）点 P 在该二次函数的图像上，点Q 在 x 轴上，若以A、B、P、Q 为顶点的四边形是平行四边形，求点P 的坐标；（ 3）如图 3，一次函数y = kx （k＞0）的图像与该二次函数的图像交于O、 C 两点，点T 为该二次函数图像上位于直线 OC 下方的动点，过点 T 作直线 TM⊥ OC，垂足为点M ，且 M 在线段 OC 上（不与 O、C 重合），过点 T 作直线 TN∥ y 轴交 OC 于点 N。

若在点 T 运动的过程中，ON 2 为常数，试确定k 的值。

OMy y yA3 AN C1 M T-1 O x O x O xBB图1 图 2（备用图）图 3二、与轴对称和等腰三角形性质有关的综合题3.（ 2016?益阳第 21 题）如图，顶点为A( 3,1) 的抛物线经过坐标原点O，与x轴交于点B．（1）求抛物线对应的二次函数的表达式；（2）过 B 作 OA 的平行线交y轴于点 C，交抛物线于点D，求证：△ OCD ≌△ OAB ；（ 3）在x轴上找一点P ，使得△PCD的周长最小，求出P 点的坐标．4.（ 2016?哈尔滨第27 题）如图，二次函数y＝ ax 2＋bx（ a≠0）的图象经过点 A（ 1， 4），对称轴是直线 x＝－3，线2段 AD 平行于 x 轴，交抛物线于点D．在 y 轴上取一点 C（ 0，2），直线 AC 交抛物线于点B，连结 OA，OB，OD，BD ．（ 1）求该二次函数的解析式；（ 2）设点 F 是 BD 的中点，点 P 是线段 DO 上的动点，将△BPF 沿边 PF 翻折，得到△′′B PF ，使△ B PF 与△ DPF 重叠部分的面积是△BDP 的面积的 1 ′上方，求线段 PD 的长度 ;4 ，若点 B在 OD（ 3）在（ 2）的条件下，过′′H⊥PF 于H ′H交于点 M，点 G 在线段B 作 B ，点 Q 在 OD 下方的抛物线上，连接 AQ 与 BAM 上，使∠ HPN+∠ DAQ =135 °，延长 PG 交 AD 于 N．若′M= 5AN+ B 求点 Q 的坐标．2y y yD A D A D AC C CO x O x O xB B B三、与图形的平移与旋转变换性质有关的综合题5.（ 2016?重庆第 26 题）如图 1，二次函数y1 x 2- 2x 1的图象与一次函数y=kx+b(k≠0)的图象交于A，B两点，点2A 的坐标为（ 0,1），点B 在第一象限内，点交点，过点 B 作 x 轴的垂线，垂足为 N，且（1）求直线 AB 和直线 BC 的解析式；（2）点 P 是线段 AB 上一点，点 D 是线段C 是二次函数图象的顶点，点M 是一次函数y=kx+b(k≠ 0)的图象与 x 轴的S△AMO︰ S 四边形AONB =1︰48。

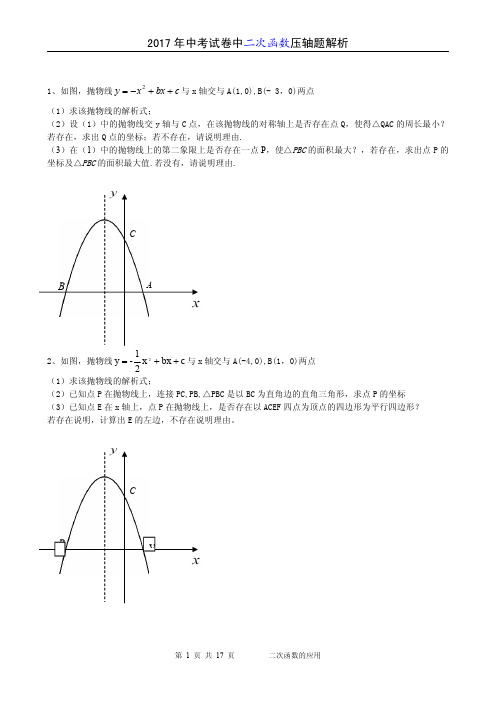
1、如图，抛物线c bx x y ++-=2与x 轴交与A(1,0),B(-3，0)两点（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由.（3）在（1）中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.2、如图，抛物线c bx x 21-y 2++=与x 轴交与A(-4,0),B(1，0)两点（1）求该抛物线的解析式；（2）已知点P 在抛物线上，连接PC,PB,△PBC 是以BC 为直角边的直角三角形，求点P 的坐标（3）已知点E 在x 轴上，点P 在抛物线上，是否存在以ACEF 四点为顶点的四边形为平行四边形？若存在说明，计算出E的左边，不存在说明理由。

ABC A B CV3、如图①，已知抛物线32++=bx ax y （a ≠0）与x 轴交于点A (1，0)和点B (－3，0)，与y 轴交于点C ．（1）求抛物线的解析式；(2)设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．(3)如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．4．如图，抛物线y =ax 2+bx +4与x 轴的两个交点分别为A （－4，0）、B （2，0），与y 轴交于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ．（1）求抛物线的函数解析式，并写出顶点D 的坐标；（2）在直线EF 上求一点H ，使△CDH 的周长最小，并求出最小周长；（3）若点K 在x 轴上方的抛物线上运动，当K 运动到什么位置时，△EFK的面积最大？并求出最大面积．C E D G A xy O B F7、如图，抛物线y=ax2﹣8ax+12a（a＞0）与x轴交于A、B两点（A在B的左侧），与y轴交于点C，点D的坐标为（﹣6，0），且∠ACD=90°．（1）请直接写出A、B两点的坐标；（2）求抛物线的解析式；（3）抛物线的对称轴上是否存在点P，使得△PAC的周长最小？若存在，求出点P的坐标及周长的最小值；若不存在，说明理由；（4）平行于y轴的直线m从点D出发沿x轴向右平行移动，到点A停止．设直线m与折线DCA的交点为G，与x轴的交点为H（t，0）．记△ACD在直线m左侧部分的面积为s，求s关于t的函数关系式及自变量t的取值范围．8、如图，抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．（1）求A、B、C的坐标；（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2DQ，求点F的坐标．9、如图①，在平面直角坐标中，点A 的坐标为（1，﹣2），点B 的坐标为（3，﹣1），二次函数y=﹣x 2的图象为l 1．（1）平移抛物线l 1，使平移后的抛物线经过点A，但不过点B．①满足此条件的函数解析式有个．②写出向下平移且经点A 的解析式．（2）平移抛物线l 1，使平移后的抛物线经过A，B 两点，所得的抛物线l 2，如图②，求抛物线l 2的函数解析式及顶点C 的坐标，并求△ABC 的面积．（3）在y 轴上是否存在点P，使S △ABC =S △ABP ？若存在，求出点P 的坐标；若不存在，请说明理由．10、如图，已知抛物线223y x x =-++与x 轴交于A 、B 两点（点A 在点B的左边），与y 轴交于点C ，连接BC 。

中考数学总复习《二次函数与平行四边形综合压轴题》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________1．如图，已知抛物线y=ax2+3ax+c(a>0)与y轴交于点C，与x轴交于A，B两点，点A在点B左侧，点B 的坐标为(1,0)(1)求抛物线的函数关系式；(2)若点D是x轴上的一点，在抛物线上是否存在点E，使以A，C，D，E为顶点且以AC为一边的四边形是平行四边形？若存在，请求出点E的坐标；若不存在，请说明理由．2．如图，在平面直角坐标系中，已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(−1,0)，B(3,0)两点，与y轴交于点C，连接BC．(1)求该抛物线的解析式；(2)点P为直线BC上方的抛物线上一点，过点P作y轴的垂线交线段BC于M，过点P作x轴的垂线交线段BC 于N，求△PMN的周长的最大值．(3)若点N为抛物线对称轴上一点，抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请求出所有满足条件的点M的坐标；若不存在，请说明理由．3．如图，已知抛物线y=12x2−32x−n(n>0)与x轴交于A，B两点（A点在B点的左边），与y轴交于点C．(1)如图1，若AB=5，则n的值为______（直接写出结果）；(2)如图1，在（1）的条件下，点P在抛物线上，点Q在抛物线的对称轴上，若以BC为边，以点B、C、P、Q为顶点的四边形是平行四边形，求P点的坐标；(3)如图2，过点A作直线BC的平行线交抛物线于另一点D，交y轴于点E，若AE:ED=1:4，求n．4．抛物线y=ax2−4经过A、B两点，且OA=OB，直线EC过点E(4，−1)，C(0，−3)点D是线段OA（不含端点）上的动点，过D作PD⊥x轴交抛物线于点P，连接PC、PE．(1)求抛物线与直线CE的解析式；(2)求证：PC+PD为定值；(3)在第四象限内是否存在一点Q，使得以C、P、E、Q为顶点的平行四边形面积最大，若存在，求出Q点坐标；若不存在，请说明理由．5．如图1 抛物线y=−23x2−23x+4与x轴交于A B．两点（点A在点B的左边）与y轴交于点C直线y=kx+b经过点A C．(1)求直线AC的解析式；(2)点P为直线AC上方抛物线上的一个动点过点P作PD⊥AC于点D过点P作PE∥AC交x轴于点E 求PD+AE的最大值及此时点P的坐标；(3)在（2）问PD+AE取得最大值的情况下将该抛物线沿射线AC方向平移103个单位后得到新抛物线点M为新抛物线对称轴上一点在新抛物线上确定一点N使得以点P C M N为顶点的四边形是平行四边形写出所有符合条件的点M的坐标并写出求解点M的坐标的其中一种情况的过程．6．在平面直角坐标系中抛物线y=−x2−4x+c与x轴交于点A B（点A在点B的左侧）与y轴交于点C且点A的坐标为(−5,0)．(1)求点C的坐标；(2)如图1 若点P是第二象限内抛物线上一动点求点P到直线AC距离的最大值并求出此时点P的坐标；(3)如图2 若点M是抛物线上一点点N是抛物线对称轴上一点是否存在点M使以A C M N 为顶点的四边形是平行四边形？若存在请直接写出点M的坐标；若不存在请说明理由．7．如图1 抛物线y=−x2+3x+4与x轴交于A B两点（A在B的左侧）与y轴交于点C连接AC,BC．(1)求△ABC的面积；(2)如图2 点P为直线上方抛物线上的动点过点P作PD∥AC交直线BC于点D过点P作直线PE∥x轴交直线BC于点E求PD+PE的最大值及此时P的坐标；(3)在（2）的条件下将原抛物线y=−x2+3x+4向右平移2个单位再向上平移8个单位点M是新抛物线与原抛物线的交点N是平面内任意一点若以P B M N为顶点的四边形是平行四边形请直接写出点N的坐标．8．如图抛物线y=ax2+bx−4(a≠0)与x轴交于A(4,0)和B(−1,0)两点与y轴交于点C点P是直线AC下方的抛物线上一动点．(1)求抛物线的解析式；(2)过点P作PD⊥x轴于点D交直线AC于点E求线段PE的最大值及此时点P的坐标；(3)取（2）中PE最大值时的P点在坐标平面内是否存在点Q使得以点A C P Q为顶点的四边形为平行四边形？若存在直接写出点Q的坐标若不存在请说明理由．9．如图抛物线与x轴交于A(x1，0)，B(x2，0)两点且x1<x2与y轴交于点C(0，−5)其中x1，x2是方程x2−4x−5=0的两个根．(1)求这条抛物线的解析式；(2)点M是线段AB上的一个动点过点M作MN∥BC交AC于点N连接CM当△CMN的面积最大时求点M的坐标；(3)点D(4，k)在（1）中抛物线上点E为抛物线上一动点在x轴是否存在点F使以A D E F 四点为顶点的四边形是平行四边形？如果存在直接写出所有满足条件的点F的坐标；如果不存在请说明理由．x2+bx+c与直线AB交于点A(0，−4)B(4，0)．10．如图在平面直角坐标系中抛物线y=12(1)求该抛物线的函数表达式；(2)点P是直线AB下方抛物线上的一动点过点P作x轴的平行线交AB于点C过点P作y轴的平行线交x轴于点D求PC+PD的最大值及此时点P的坐标；(3)在（2）中PC+PD取得最大值的条件下将该抛物线沿水平方向向左平移5个单位点E为点P的对应点平移后的抛物线与y轴交于点F M为平移后的抛物线的对称轴上一点．在平移后的抛物线上确定一点N使得以点E F M N为顶点的四边形是平行四边形直接写出所有符合条件的点N的坐标．11．如图已知抛物线y=−x2+bx+c与一直线相交于A(−1,0)C(2,3)两点与y轴交于点N其顶点为D．(1)求抛物线及直线AC的解析式．(2)设点M(3,m)求使MN+MD的值最小时m的值．(3)若抛物线的对称轴与直线AC相交于点B E为直线AC上的任意一点过E作EF∥BD交抛物线于点F 以B D E F为顶点的四边形能否为平行四边形？若能求出点E F的坐标；若不能请说明理由．12．综合与探究x+如图在平面直角坐标系中直线y=4x+4与x轴交于A点与y轴交于C点抛物线y=ax2+83c(a≠0)）经过A C两点与x轴相交于另一点B连接BC．点P是线段BC上方抛物线上的一个动点过点P作PQ⊥BC交线段BC于点Q．(1)求抛物线的解析式；(2)点D为抛物线对称轴上的一个动点则|DC−DB|的最大值是___________；(3)求PQ的最大值并写出此时点P的坐标；(4)在x轴上找一点M抛物线上找一点N使以点B,C,M,N为顶点的四边形是平行四边形请直接写出点M的坐标．13．如图1 在平面直角坐标系中抛物线y=ax2+bx+√3(a≠0)与x轴交于点A(−1，0)点B(3，0)与y轴交于点C．(1)求该抛物线的解析式；(2)点P为直线BC上方抛物线上的一点过点P作x轴的平行线交BC于点D过点P作y轴的平行线交BC 于点E求PD+PE的最大值以及此时点P的坐标；(3)如图2 将抛物线沿射线CB的方向平移使得平移后的抛物线经过线段CB的中点且平移后抛物线的对称轴与x轴交于点M N R是直线BC上任意两点Q为新抛物线上一点直接写出所有使得以点M N R Q为顶点的四边形是平行四边形的点Q的横坐标并把求其中一个点的横坐标过程写出来．14．抛物线y=ax2+bx+c（a≠0）与x轴交于点A(−3,0)B(1,0)两点与y轴交于点C(0,3)点P 是抛物线上的一个动点．(1)求抛物线的函数表达式；(2)如图1 点P在线段AC上方的抛物线上运动（不与A C重合）过点P作PD⊥AB垂足为D PD 交AC于点E．作PF⊥AC垂足为F若点P的横坐标为t请用t的式子表示PE并求△PEF的面积的最大值；(3)如图2 点Q是抛物线的对称轴l上的一个动点在抛物线上存在点P使得以点A P C Q为顶点的四边形是平行四边形请直接写出所有符合条件的点P的坐标并把求其中一个点P的坐标的过程写下来．15．综合与探究如图1 在平面直角坐标系中二次函数y=x2+bx+c的图象与x轴交于A B两点与直线l交于B C两点其中点A的坐标为(−2,0)点C的坐标为(−1,−4)．(1)求二次函数的表达式和点B的坐标．(2)若P为直线l上一点Q为抛物线上一点当四边形OBPQ为平行四边形时求点P的坐标．(3)如图2 若抛物线与y轴交于点D连接AD,BD抛物线上是否存在点M使∠MAB=∠ADB？若存在请直接写出点M的坐标；若不存在请说明理由．x2+bx+c(a≠0)与x轴交于A B两点．其中点A(−2,0)点B(4,0)．16．在直角坐标系中抛物线y=12(1)求抛物线的解析式．x+n经过A点与y轴交于D．在直线l下方的抛物线上有一个动点P连接(2)如图1 在直线l:y=−12PA PD求△PAD面积的最大值及其此时P的坐标．(3)将抛物线y向右平移1个单位长度后得到新抛物线y1点E是新抛物线y1的对称轴上的一个动点点F是原抛物线上的一个动点取△PAD面积最大值时的P点．若以点P D E F为顶点的四边形是平行四边形直接写出点F的坐标并写出求解其中一个F点的过程．17．如图已知抛物线y=−x2−2x+3的顶点为D点且与x轴交于B A两点（B在A的左侧）与y轴交于点C．点E为抛物线对称轴上的一个动点：(1)当点E在x轴上方且CE∥BD时求sin∠DEC的值；(2)若点Р在抛物线上是否存在以点B E C P为顶点的四边形是平行四边形﹖请求出点Р的坐标；DE取得最小值连接AE并延长交第二象限抛物线为点M请(3)若抛物线对称轴上有点E使得AE+√55直接写出AM的长度．18．图1 在平面直角坐标系xOy中已知抛物线y=−x2+bx+c经过A(−1,0)B(3,0)两点．P是抛物线上一点且在直线BC的上方．(1)求抛物线的解析式；(2)如图2 点E为OC中点作PQ∥y轴交BC于点Q若四边形CPQE为平行四边形求点P的横坐标；(3)如图3 连结AC、AP AP交BC于点M作PH∥AC交BC于点H．记△PHM△PMC△CAM的面积分别为S1,S2,S3．判断S1S2+S2S3是否存在最大值若存在求出最大值；若不存在请说明理由．19．如图在平面直角坐标系中抛物线y=−12x2+bx+c与x轴交于A(−2,0),B(4,0)两点（点A在点B 的左侧）与y轴交于点C连接AC、BC点P为直线BC上方抛物线上一动点连接OP交BC于点Q．(1)求抛物线的函数表达式；(2)当PQOQ 的值最大时求点P的坐标和PQOQ的最大值；(3)把抛物线y=−12x2+bx+c向右平移1个单位再向上平移2个单位得新抛物线y′M是新抛物线上一点N是新抛物线对称轴上一点当以M N B C为顶点的四边形是平行四边形时写出所有符合条件的N点的坐标并写出求解点N的坐标的其中一种情况的过程．20．抛物线y=ax2+bx+3(a≠0)与x轴交于A(−1，0)、B(3，0)与y轴交于点C．(1)求抛物线的表达式；(2)如图1 M 为抛物线对称轴l 上一动点 连接MA 、MC 求MA +MC 的最小值及此时M 点的坐标； (3)如图2 抛物线的对称轴l 与x 轴交于点E 点F(2，1) P 为抛物线上一动点 Q 为抛物线对称轴l 上一动点 以点E F P Q 为顶点的四边形为平行四边形时 直接写出所有可能的点Q 的坐标．参考答案1．（1）解：∵点B的坐标为(1,0)∵OB=1∵OC=3OB∵OC=3∵C(0,−3)∵抛物线y=ax2+3ax+c(a>0)过点B,C∵{a+3a+c=0，c=−3，解得{a=34，c=−3，∵抛物线的函数关系式为y=34x2+94x−3；（2）在抛物线上存在点E使以A C D E为顶点且以AC为一边的四边形是平行四边形；理由：①如图1 当点E在x轴下方时则：CE∥AD∵点E的纵坐标为−3令y=−3则34x2+94x−3=−3解得x1=−3x2=0∵点E的坐标为(−3,−3)；②如图2 当点E在x轴上方时∵平行四边形的对角线分平行四边形为面积相等的两个三角形点C到x轴的距离为3∵点E 到x 轴的距离为3 令y =3 则34x 2+94x −3=3解得x =−3±√412∵E 2(−3−√412,3) E 3(−3+√412,3)综上可得 在抛物线上存在点E 使以A C D E 为顶点且以AC 为一边的四边形是平行四边形 点E 的坐标为(−3,−3)或(−3−√412,3)或(−3+√412,3)．2．（1）解：（1）∵抛物线y =ax 2+bx +2(a ≠0)过A (−1,0) B (3,0)两点∴{a −b +2=09a +3b +2=0解得{a =−23b =43 ∴抛物线的解析式为y =−23x 2+43x +2； （2）当x =0时 y =2 即：C (0,2) 则OC =2 OB =3 BC =√13设BC 的解析式为：y =kx +b 1 将B (3,0) C (0,2)代入可得： {b 1=23k +b 1=0 解得：{k =−23b 1=2∵BC 的解析式为：y =−23x +2设P (t,−23t 2+43t +2)∵点P 为直线BC 上方的抛物线上一点 过点P 作y 轴的垂线交线段BC 于M 过点P 作x 轴的垂线交线段BC 于N∵{t>0 t<3−23t2+43t+2≤2则2≤t<3当x=t时点N的纵坐标为：y=−23t+2则PN=−23t2+43t+2−(−23t+2)=−23t2+2t=−23(t−32)2+32(2≤t<3)∵当t=2时PN有最大值为：−23×(2−32)2+32=43由题意可知∠BOC=∠P=90°PN∥y轴则∠PNM=∠OCB ∵△BOC∽△MPN则OCPN =OBPM=BCMN则PM=32PN MN=√132PN△PMN的周长为PN+PM+MN=PN+32PN+√132PN=5+√132PN则当PN最大时△PMN的周长有最大值即：△PMN的周长的最大值为5+√132×43=10+2√133；（3）存在点M使得以B C M N为顶点的四边形是平行四边形①以BC为对角线过C作CM∥x轴交抛物线与M点N在x轴上NB=2=MC M(2,2)；②以BC为边过M作MG垂直抛物线对称轴于G当MG=OB=3且OC=GN时四边形CNMB为平行四边形M点横坐标x=3+1=4纵坐标y=−23×42+43×4+2=−103M(4,−103)；③过N 作NH ∥x 轴 与过M 作MH ∥y 轴交于H 当MH =CO =2 NH =BO =3时 四边形CMNB 为平行四边形 M 点横坐标为x =1−3=−2 纵坐标y =−23×(-2)2+43×(-2)+2=−103 M(−2,−103)；综上所述：点M 的坐标为(2,2)或(4,−103)或(−2,−103)．3．（1）解：∵抛物线与x 轴交于A B 两点 ∵x A +x B =−(−32)÷12=3 x A ⋅x B =−2n ∵AB =5 即x B −x A =5 ∵x B −x A =√(x B −x A )2=√(x B +x A )2−4x B x A =√32−4(−2n )=5解得：n =2；（2）由（1）当12x 2−32x −2=0时解得x 1=−1 x 2=4 ∴OA =1 OB =4 ∴B(4,0) C(0,−2)∵抛物线对称轴为直线x =−b2a =−−322×12=32∴设点Q 坐标为(32 b) 由平行四边形性质可知当BQ CP 为平行四边形对角线时 点P 坐标为(112 b +2)代入y =12x 2−32x −2 解得b =238则P 点坐标为(112398)当CQ PB 为为平行四边形对角线时 点P 坐标为(−52 b −2) 代入y =12x 2−32x −2解得b =558则P 坐标为(−52 398)综上点P 坐标为(112 398),(−52 398)；（3）设点D 坐标为(a,b)∵AE:ED =1:4则OE =15b OA =14a∵AD∥BC ∴△AEO ∽△BCO∵OC =n∴OB OC=OA OE∴OB =5an4b由一元二次方程根与系数关系x 1x 2=−n 12=−14a ⋅5an4b ∴b =532a 2将点A(−14a0)D(a,532a2)代入y=12x2−32x−n{0=12×(−14a)2−32⋅(−14a)−n532a2=12a2−32a−n解得a=6或a=0（舍去）则n=278．4．（1）解：令x=0则y=−4∵B(0，−4)∵OA=OB∵OA=OB=4∵A(4，0)将点A(4，0)代入y=ax2−4得：0=16a−4解得：a=14∵抛物线的解析式为：y=14x2−4；设直线CE为y=mx+n将点E(4，−1)C(0，−3)的坐标代入y=mx+n得{4m+n=−1n=−3解得：{m=12 n=−3∵直线CE的解析式是：y=12x−3；（2）证明：设点P(t，14t2−4)0<t<4如图过点P作PF⊥y轴于点F则PF=t则FC=|14t2−4+3|=|14t2−1|PD=4−14t2PC=√t2+(14t2−1)2=14t2+1∵CP+PD=(14t2+1)+(4−14t2)=5为定值；（3）解：存在理由：①当CE是平行四边形的边时如下图：设直线CE交x轴于点M DP交CE于点H令y=0则0=12x−3解得x=6；令x=0则y=−3∵OM=6OC=3则CM=√32+62=3√5∵tan∠OMC=OCOM =12cos∠OMC=OMCM=2√5过点P作PN⊥CE于点N则∠NPD=∠OMC则PN=PHcos∠NPD=2√5PH则以C P E Q为顶点的平行四边形面积=PN⋅CE=2√5CE⋅PH其中2√5CE为常数故当PH最大时平行四边形的面积最大设点P(x，14x2−4)则点H(x，12x−3)则PH=(12x−3)−(14x2−4)=−14(x−1)2+54≤54即PH的最大值为54此时点P(1，−154)；②当CE是平行四边形的对角线时如下图同理可得：以C P E Q为顶点的平行四边形面积=2√5×CE⋅PH此时PH =14(x 2−2x −4)∵当x >1时 PH 的值随x 最大而增大 而x <4 当x =4时 PH 最大值为1<54 故该种情况 不符合题设要求 综上 点P (1，−154) 即四边形CPQE 为平行四边形时 符合题设要求设点Q(s ，t)由中点坐标公式得：{4+1=s−1−154=t −3 解得：{s =5t =−74故点Q (5，−74)．5．（1）解：当x =0时 y =4 ∵点C (0,4)当y =0时 −23x 2−23x +4=0 解得：x 1=−3,x 2=2 ∵点A (−3,0),B (2,0)设直线AC 的解析式为y =kx +b 把点A (−3,0) C (0,4)代入得： {−3k +b =0b =4 解得：{k =43b =4 ∵直线AC 的解析式为y =43x +4；（2）解：如图 过点P 作PF ⊥x 轴于点F 交AC 于点G∵A (−3,0) C (0,4) ∵OA =3,OC =4∵AC =√OA 2+OC 2=5设点P (m,−23m 2−23m +4) 则点G (m,43m +4)∵OF =−m PF =−23m 2−23m +4 PG =(−23m 2−23m +4)−(43m +4)=−23m 2−2m ∵PE ∥AC ∵∠PEF =∠CAO ∵∠PFE =∠AOC =90° ∵△PEF∽△CAO ∵EF OA=PF OC即EF 3=−23m 2−23m+44解得：EF =−12m 2−12m +3 ∵AE =EF +OF −OA =−12m 2−32m∵PD ⊥AC∵∠PDG =∠AOC =90° ∵∠PGD +∠DPG =90°∵∠AGF +∠OAC =90°,∠AGF =∠PGD ∵∠DPG =∠OAC ∵△DPG∽△OAC ∵PG AC=PD OA即−23m 2−2m5=PD 3解得：PD =−25m 2−65m∵PD +AE =(−12m 2−32m)+(−25m 2−65m)=−910m 2−2710m =−910(m +32)2+8140 ∵当m =−32时 PD +AE 有最大值 最大值为8140；此时点P (−32,72)；（3）解：∵y =−23x 2−23x +4=−23(x +12)2+256∵原抛物线的顶点坐标为(−12,256)∵将该抛物线沿射线AC 方向平移103个单位后得到新抛物线∵相当于原抛物线沿x 轴向右平移2个单位 再沿y 轴向上平移83个单位后得到新抛物线 ∵新抛物线的解析式为y =−23(x +12−2)2+256+83=−23(x −32)2+416=−23x 2+2x +163∵新抛物线的对称轴为直线x=32设点M(32,s)N(t,−23t2+2t+163)若以对角线CM,PN为对角线有{t−322=0+322−2 3t2+2t+163+722=4+s2解得：{s=296t=3此时点M的坐标为(32,296)；若以对角线CN,PM为对角线有{0+t2=−32+3224−23t2+2t+1632=72+s2解得：{s=356t=0此时点M的坐标为(32,356)；若以对角线CP,MN为对角线有{0−322=t+322−2 3t2+2t+163+s2=72+42解得：{s=856t=−3此时点M的坐标为(32,856)；综上所述点M的坐标为(32,296)或(32,356)或(32,856)．6．（1）解：将点(−5,0)代入y=−x2−4x+c得：0=−25+20+c解得：c=5∵抛物线的表达式为：y=−x2−4x+5把x=0代入得：y=5∵点C的坐标为(0,5)；（2）解：过点P作PD⊥x轴于点D交AC于点F过点P作PE⊥AC于点E ∵A(−5,0)C(0,5)∵OA=OC=5∵∠OAC=45°∵PE⊥AC PD⊥x轴∵∠PEF=∠ADF=90°∵∠PFE =∠AFD ∵△PFE ∽△AFD∵∠EPF =∠OAC =45°在Rt △PEF 中 PE =PF ⋅cos45°=√22PF 设直线AC 的函数表达式为：y =kx +b将点A (−5,0) C (0,5)代入得：{0=−5k +b 5=b 解得：{k =1b =5∵直线AC 的函数表达式为：y =x +5设点P (t,−t 2−4t +5) 则F (t,t +5)∵PF =(−t 2−4t +5)−(t +5)=−t 2−5t =−(t +52)2+254 ∵当t =−52时 PF 有最大值 最大值为254∵PE =√22×254=25√28． 把x =−52代入y =−x 2−4x +5得：y =−254+10+5=354 ∵P (−52,354) 综上：点P 到直线AC 距离为25√28 此时P (−52,354)；（3）解：由（1）可得 抛物线的表达式为：y =−x 2−4x +5∵该抛物线是对称轴为直线x =−b2a =−2∵点N 再抛物线对称轴上 点M 在抛物线上∵设点N (−2,n ) M (m,−m 2−4m +5)①当AC 为平行四边形的对角线时∵A(−5,0)C(0,5)∵AC中点为(−52,5 2 )∵N(−2,n)M(m,−m2−4m+5)∵−2+m2=−52解得：m=−3∵−m2−4m+5=−(−3)2−4×(−3)+5=8∵M(−3,8)；②当AN为平行四边形的对角线时∵A(−5,0)N(−2,n)∵AN中点为(−72,n 2 )∵M(m,−m2−4m+5)C(0,5)∵m 2=−72解得：m=−7∵−m2−4m+5=−(−7)2−4×(−7)+5=−16∵M(−7,−16)③当AM为平行四边形的对角线时∵A(−5,0)M(m,−m2−4m+5)∵AN中点为(−5+m2,−m2−4m+52)∵N(−2,n)C(0,5)∵−2 2=−5+m2解得：m=3∵−m2−4m+5=−(3)2−4×3+5=−16∵M(3,−16)综上：点M的坐标为(−3,8)或(−7,−16)或(3,−16)．7．（1）解：令y=0则−x2+3x+4=0解得x=−1或4∵A(−1,0),B(4,0)∵OA=1,BO=4令x=0则y=4∵C(0,4)∵OC=4∵S△ABC=12×5×4=10；（2）解：∵OA=1,BO=4OC=4∵AB=5,AC=√17∵PE∥x轴∵∠PED=∠CBA∵PD∥AC∵∠EPD=∠CAB∵△ABC∽△PED∵ABPE =ACPD 即5PE =√17PD∵PD =√175PE 设直线BC 的解析式为y =kx +b∵{b =44k +b =0 解得{k =−1b =4∵直线BC 的解析式为y =−x +4设P (t,−t 2+3t +4) 则E (t 2−3t,−t 2+3t +4)∵PE =−t 2+4t∵PE +PD =(1+√175)(−t 2+4t )=−(1+√175)(t −2)2+4(1+√175) ∵当t =2时 PE +PD 的值最大 最大值为4+4√175此时P (2,6)； （3）解：∵原抛物线y =−x 2+3x +4向右平移2个单位 再向上平移8个单位得到新抛物线 ∵平移后的抛物线的解析式为y =−(x −72)2+574 联立方程组{y =−x 2+3x +4y =−x 2+7x +2 解得{x =12y =14∵M (12,214) 设N (x,y )①当PB 为平行四边形的对角线时{6=x +126=y +214 解得{x =112y =34∵N (112,34)；②当PM 为平行四边形的对角线时{2+12=x +46+214=y 解得{x =−32y =454∵N (−32,454)）；③当PN 为平行四边形的对角线时{x +2=4+126+y =214解得{x =52y =34∵N (52,−34)； 综上所述：N 点坐标为(112,34)或(−32,454)或(52,−34)．8．（1）解：把A (4,0) B (−1,0)代入y =ax 2+bx −4得：{16a +4b −4=0a −b −4=0解得{a =1b =−3∴抛物线的函数表达式为y =x 2−3x −4；（2）由题意可得C (0,−4) 则OC =4由题意可得直线AC 过点A (4,0) C (0,−4) 则设函数解析式为：y =kx +b 1依题意得：{0=4k +b 1−4=b 1解得：{k =1b 1=−4AC 的函数关系式为y =x −4令P (m,m 2−3m −4) 则E (m,m −4)∴PE =(m −4)−(m 2−3m −4)=−m 2+4m =−(m −2)2+4∵当m =2时 PE 的最大值为4．∵P (2,−6)；（3）存在．点Q 的坐标为(2,2)或(2,−2)或(−2,−10)．解：设Q (x,y ) 又A (4,0) C (0,−4) P (2,−6)当AC PQ 为平行四边形的对角线时 AC 与PQ 的中点重合∵{x +2=4+0y −6=0−4解得：{x =2y =2∵Q (2,2)；当AP CQ 为平行四边形的对角线时 AP 与CQ 的中点重合∵{x +0=0+2y −4=0−6解得：{x =2y =−2∵Q (2,−2)；当AQ CP 为平行四边形的对角线时 AQ 与CP 的中点重合∵{x +4=0+2y +0=−4−6解得：{x =−2y =−10∵Q (−2,−10)；综上所述 点Q 的坐标为(2,2)或(2,−2)或(−2,−10)．9．（1）解：解方程x 2−4x −5=0得x 1=−1，x 2=5 则A(−1，0)，B(5，0) 设抛物线解析式为y =a (x +1)(x −5)把C(0，−5)代入得−5=a ×1×(−5)解得a =1∵抛物线解析式为y =x 2−4x −5；（2）解：作NH ⊥x 轴于H 如图1设M(t ，0)∵MN ∥BC∴△AMN ∽△ABC∴AM ：AB =NH ：CO 即(x +1)：6=NH ：5∴NH =56(x +1) ∴S △CMN =S △ACM −S △AMN =12(x +1)⋅5−12⋅(x +1)⋅56(x +1)=−512x2+53x+2512=−512(x−2)2+154当x=2时△CMN的面积最大此时M点的坐标为(2，0)；（3）解：当x=4时y=x2−4x−5=−5则D(4，−5)如图2 当AF∥DE则E(0，−5)，CD=4∵AF=4∵此时F点坐标为(3，0)或(−5，0)；当EF∥AD，AD=EF时则点E和点D的纵坐标互为相反数即点E的纵坐标为5当y=5时x2−4x−5=5解得x1=2+√14，x2=2−√14若E点坐标为(2+√14，5)由于点A(−1，0)向右平移5个单位向下平移5个单位得到D点则E 点向右平移5个单位向下平移5个单位得到F点此时F点坐标为(7+√14，0)；若E点坐标为(2−√14，5)同样方法得到此时F点坐标为(7−√14，0)；总上所述满足条件的F点坐标为(3，0)或(−5，0)或(7+√14，0)或(7−√14，0)．10．（1）解：将点A(0，−4)B(4，0)代入y=12x2+bx+c得：{c=−48+4b+c=0解得：{c =−4b =−1∵该抛物线的函数表达式为：y =12x 2−x −4；（2）解：如图 设PD 交BC 于H∵A(0，−4) B(4，0)∵OA =OB =4∵∠OBA =∠OAB =45°∵PC∥OB PD∥OA∵∠BCP =∠OBA =45° ∠PHC =∠BHD =∠OAB =45° ∵PC =PH设直线AB 的解析式为y =kx +b 1则{b 1=−44k +b 1=0 解得：{b 1=−4k =1∵直线AB 的解析式为y =x −4设P (t ，12t 2−t −4) 则H(t ，t −4) D(t ，0)∵PC +PD =PH +PD=t −4−(12t 2−t −4)+(−12t 2+t +4)=−t 2+3t +4=−(t −32)2+254∵当t =32时 PC +PD 取得最大值254 此时P (32，−358)；（3）解：由题意得：平移后抛物线解析式为y =12(x +5)2−(x +5)−4=12x 2+4x +72E (−72，−358)∵F (0，72)∵抛物线y =12x 2+4x +72的对称轴为x =−4∵设M(−4，m) N (n ，12n 2+4n +72)分情况讨论：①当EF 为对角线时则−4+n =−72解得：n =12 此时12n 2+4n +72=458∵点N 的坐标为(12，458)；②当EM 为对角线时则−72−4=n 即n =−152此时12n 2+4n +72=138∵点N 的坐标为(−152，138)；③当EN 为对角线时则−72+n =−4 即n =−12此时12n 2+4n +72=138∵点N 的坐标为(−12，138)综上所述 点N 的坐标为(12，458)或(−152，138)或(−12，138)．11．（1）解；将A (−1,0) C (2,3)两点代入y =−x 2+bx +c 得 {0=−1−b +c 3=−4+2b +c 解得{b =2c =3∵y =−x 2+2x +3设直线AC 的解析式为y =kx +b将A (−1,0) C (2,3)两点代入得 {0=−k +b 3=2k +b 解得{k =1b =1∵y =x +1∵抛物线的解析式为y=−x2+2x+3直线AC的解析式为y=x+1；（2）解：当x=0y=3当x=1y=4当y=0x1=−1或x2=3∵N(0，3)D(1，4)抛物线与x轴的另一个交点坐标为(3，0)∵M(3，m)如图作直线l=3平行于y轴则M在直线l上作D关于直线l的对称点D′连接ND′与直线l交点为M连接DM由题意知D′(5，4)MD=MD′∵MN+MD=MN+MD′∵当N，M，D′三点共线时MN+MD的值最小且为ND′设直线ND′的解析式为y=px+q将N、D′点坐标代入得{3=q4=5p+q解得{p=15 q=3∵直线ND′的解析式为y=15x+3将M(3，m)代入得m=15×3+3=185∵m的值为185；（3）解：将x=1代入y=x+1得y=2∵B(1，2)BD=2设E(n，n+1)则F(n，−n2+2n+3)∵以B D E F 为顶点的四边形为平行四边形∵EF =BD∵|EF |=|n 2−n −2|=2①当n 2−n −2=−2 解得n 1=0 n 2=1（与B 重合 舍去） ∵n =0 则E(0，1) F(0，3)②当n 2−n −2=2 解得n 3=1+√172 n 4=1−√172∵n =1+√172 则E (1+√172，3+√172) F (1+√172，√17−12)n =1−√172 则E (1−√172，3−√172) F (1−√172，−√17−12)综上所述 以B D E F 为顶点的四边形能为平行四边形 E(0，1)F(0，3)或E (1+√172，3+√172) F (1+√172，√17−12)或E (1−√172，3−√172) F (1−√172，−√17−12)．12．（1）解：∵直线y =4x +4与x 轴交于A 点 与y 轴交于C 点∵A(−1，0) B(0，4)∵抛物线y =ax 2+83x +c (a ≠0)）经过A C 两点∵{a (−1)2+83×(−1)+c =0c =4解得{a =−43c =4∵抛物线的解析式为：y =−43x 2+83x +4（2）解：取C 关于对称轴的对称点C ′ 对称轴x =−b2a =1∵C ′(2，4)解方程−43x 2+83x +4=0得到x 1=−1，x 2=3∵B(3，0)∵CD =C ′D∵当D 、C ′、B 共线时 |CD −BD |有最大值BC ′∵BC ′=√(3−2)2+42=√17∵故答案为：√17；（3）解：过点P做PM⊥x轴交BC于点M 设直线BC的解析式为：y=kx+4∵B(3，0)∵k=−43∵直线BC的解析式为y=−43x+4设P(m，−43m2+83m+4)则M(m，−43m+4)∵PM=−43m2+83m+4+43m−4=−43m2+4m=−43(m−32)2+3∵当m=32时PM有最大值3∵y P=−43×(32)2+83×32+4=5∵PM∥y轴∵∠PMQ=∠OCB∵BC=√OB2+OC2=5∵sin∠PMQ=PQPM =OBBC=sin∠OCB∵PQ=PM⋅OBBC =35PM∵当PM最大时PQ最大∵此时P(32，5)；（4）解：①BC为对角线∵BM∥CN BM在x轴上∵CN∥x轴N为C的对称点∵N(2，4) CN =2∵BM =2∵M(1，0)②BC 为边 BN 为对角线 设M(m ，0) N (n ，−43n 2+83n +4)∵{3+n =m +00−43n 2+83n +4=4+0∵n =2或n =0（舍去）∵m =5∵M(5，0)③BC 为边 CN 为对角线 设M(m ，0) N (n ，−43n 2+83n +4) ∵{3+m =n +00+0=−43n 2+83n +4+4∵n =1±√7∵m =−2±√7∵M(−2+√7，0)或M(−2−√7，0)综上可得到：M 1(1,0) M 2(5,0) M 3(−2−√7,0) M 4(√7−2,0)．13．（1）解：将A(−1， 0) 点B(3，0)代入y =ax 2+bx +√3(a ≠0)得{a −b +√3=09a +3b +√3=0解得{a =−√33b =2√33∴该抛物线的解析式为y =−√33x 2+2√33x +√3； （2）解：∵ tan∠CBO =CO BO =√33∴ ∠CBO =30°∵DP∥x 轴∴ ∠PDE =∠CBO =30°．又由题知△PDE 是直角三角形 ∠DPE =90°∴ PD =PEtan30°=√3PE∴ PD +PE =(√3+1)PE当PE 最大时 PD +PE 的长最大设直线BC 的解析式为：y =kx +b (k ≠0)∵直线BC 经过点B(3，0) C(0，√3)代入y =kx +b (k ≠0)得：{0=3k +b b =√3解得{k =−√33b =√3∴y =−√33x +√3 设P (m ，−√33m 2+2√33m +√3) 则E (m ，−√33m +√3) ∴PE =−√33m 2+√3m =−√33(m −32)2+3√34∵−√33<0 ∴当m =32时 PE 有最大值 PE max =3√34 ∴(PD +PE )max =9+3√34 此时P (32，5√34)； （3）解：由（2）得B(3，0) C(0，√3)∵BC 中点的坐标为(32，√32) ∵可以看作点C 向右移动32个单位长度 向下移动√32个单位长度∵抛物线经过点C 平移后的抛物线经过中点∵y =−√33x 2+2√33x +√3=−√33(x −1)2+4√33 ∵平移后的抛物线的解析式为：y=−√33(x −1−32)2+4√33−√32=−√33(x −52)2+5√36对称轴为x =52∵与x 轴的交点坐标为M (52，0)设点Q 的坐标为：(m ，−√33(m −52)2+5√36)当MQ 为平行四边形的对角线时 如图所示：对角线的交点仍在直线BC 上∵MQ 的中点为(52+m 2,−√33(m−52)2+5√362) 代入直线解析式得：−√33(x −52)2+5√362=−√33(52+x 2)+√3 解得：m 1=6+√72 m 2=6−√72；当MQ 为平行四边形的边时 MQ∥BC设直线MQ 的解析式为y =cx +d 且c =−√33 将点M (52，0)代入得0=−√33×52+d 解得：d =5√36∵直线MQ 的解析式为y =−√33x +5√36 将点Q 代入得：−√33(m −52)2+5√36=−√33m +5√36解得：m 3=6+√112综上可得：点Q 的横坐标为：6+√112或6−√112或6+√72或6−√72．14．（1）解：将A(−3,0) B(1,0) C(0,3)三点代入解析式得{a +b +c =09a −3b +c =0c =3解得：a =−1 b =−2 c =3∵y =−x 2−2x +3；（2）解：设AC 解析式为y =kx +b将A(−3,0) C(0,3)代入解析式可得{−3k +b =0b =3解得：{k =1b =3∵y =x +3∵点P 的横坐标为t∵P(t,−t 2−2t +3)∵PD ⊥AB∵E(t,t +3)∵PE =−t 2−2t +3−(t +3)=−t 2−3t =−(t +32)2+94 ∵A(−3,0) C(0,3)∵∠CAB =∠ACB =45°∵PD ⊥AB PF ⊥AC∵∠CAB =∠AED =∠PEF =∠FPE =45°∵△PEF 是等腰直角三角形过F 作FG ⊥PE∵FG ⊥PE∵FG =12PE∵S △PEF =12×PE ×FG =14PE 2∵当t =−32时 面积最大S△PEF最大=14×(94)2=8164；（3）解：由（1）得x 对=−−22×(−1)=−1设Q(−1,m)∵点A P C Q为顶点的四边形是平行四边形①当AC为对角线时P点坐标为P(−2,3−m)∵3−m=−(−2)2−2×(−2)+3=3解得：m=0P1(−2,3)；②当AQ为对角线时P点坐标为P(−4,m−3)∵m−3=−(−4)2−2×(−4)+3=−5解得：m=−2P2(−4,−5)；③当CQ为对角线时P点坐标为P(2,3+m)∵3+m=−22−2×2+3=−5解得：m=−8P3(2,−5)；综上所述：P 1(−2,3) P 2(−4,−5) P 3(2,−5)；15．（1）解：∵点A 的坐标为(−2,0) 点C 的坐标为(−1,−4) ∵{4−2b +c =01−b +c =−4 解得：{b =−1c =−6∵二次函数的表达式为y =x 2−x −6；令y =0 则x 2−x −6=0解得：x 1=3,x 2=−2∵点B 的坐标为(3,0)；（2）解：如图∵点B 的坐标为(3,0)∵OB =3设直线l 的解析式为y =k 1x +b 1把点(3,0) (−1,−4)代入得：{0=3k 1+b 1−4=−k 1+b 1 解得：{k 1=1b 1=−3∵直线l 的解析式为y =x −3∵四边形OBPQ 为平行四边形∵PQ ∥OB,PQ =OB =3∵PQ ∥x 轴设点P 的坐标为(m,m 2−m −6) 则点Q 的坐标为(m,m −3) ∵PQ =(m −3)−(m 2−m −6)=−m 2+2m +3∵−m 2+2m +3=3解得：m =2或0（舍去）∵点P 的坐标为(2,−1)；（3）解：对于y=x2−x−6令x=0y=−6∵点D的坐标为(0,−6)∵OD=6∵点A(−2,0),B(3,0)∵AB=5,BD=√32+62=3√5AD=√22+62=2√10如图过点A作AE⊥BD于点E∵S△ABD=12OD×AB=12AE×BD∵AE=2√5∵DE=√AD2−AE2=2√5∵AE=DE∵△ADE是等腰直角三角形∵∠ADB=45°∵∠MAB=∠ADB∵∠MAB=45°过点M作MF⊥x轴于点F∵△AFM是等腰直角三角形∵AF=FM设点M的坐标为(t,t2−t−6)∵FM=|t2−t−6|,AF=t+2∵|t2−t−6|=t+2解得：t=−2（舍去）或2或4∵点M的坐标为(2,−4)或(4,6)．16．解:（1）∵抛物线y=12x2+bx+c(a≠0)与x轴交于A B两点．其中点A(−2,0)点B(4,0)∵y=12(x+2)(x−4)=12x2−x−4（2）将A(−2,0)代入l:y=−12x+n得：0=−12×(−2)+n解得：n=−1∵y=−12x−1令x=0解得：y=−1∵D(0,−1)如图所示过点P作PE⊥x轴交l于点E设P(t,−12t2−t−4)则E(t,−12t−1)∵PE=−12t−1−(−12t2−t−4)=−12t2+12t+3∵S△PAD=12|x D−x A|⋅PE=12×2×(−12t2+12t+3)=−12t2+12t+3=−12(t−12)2+258∵对称轴为t=12且−2<t<3∵△PAD面积最大值为258此时P(12,−358)；（3）∵点A(−2,0)点B(4,0)关于x=1对称则抛物线y=12x2−x−4的对称轴为直线x=1∵将抛物线y向右平移1个单位长度后得到新抛物线y1∵则平移后新抛物线y1的对称轴为直线x=2设E(2,m)F(t,12t2−t−4)①若以PF为对角线时{12+t=2+0−358+12t2−t−4=m−1解得：t=32∵F(32,−358)②PE为对角线时2+12=t+0解得：t=52当t=52时12t2−t−4=−278∵F(52,−278)③若以PD为对角线时12+0=2+t解得：t=−32当t=−32时12t2−t−4=118∵F(−32,−118)综上所述F(32,−358)或F(52,−278)或F(−32,−118)．17．（1）解：∵y=−x2−2x+3令y=−x2−2x+3=0解得x1=1x2=−3即A(1,0)B(−3,0)把x=0代入y=−x2−2x+3中得y=−3即C(0,−3)∵y=−x2−2x+3=−(x+1)2+4∵对称轴是直线x=−1顶点D(−1,4)设对称轴与x轴交于点F∵BF=2DF=4BD=2√5∵CE∥BD∵∠BDE=∠CED在Rt△BDF sin∠DEC=sin∠BDF=BFBD =22√5=√55．（2）解：存在∵点P在抛物线上点E在对称轴上∵可设P(m,−m2−2m+3)E(−1,n)B(−3,0)①以BC为对角线时由平行四边形的对角线互相平分；则x B+x C=x P+x E∵−3+0=−1+m解得m=−2即P(−2,3)；同理②以BE为对角线时−3+(−1)=0+m解得m=−4即P(−4,−5)；③以BP为对角线时−3+m=0+(−1)解得m=2即P(2,−5)；综上所述存在P(−2,3)P(−4,−5)P(2,−5)使得点B E C P为顶点的四边形是平行四边形；（3）解：如图所示过点A作AH⊥DB于点H交对称轴于点E连接AE并延长交第二象限抛物线为点M在Rt △DHE 中 sin∠HDE =HE DE ∵HE =sin∠HDE ×DE =√55DE ∵AE +√55DE =AE +HE∵要AE +√55DE 取得最小值 即要AE +HE 最小 ∵当点A E H 三点共线且AH 垂直BD 时AE +HE 最小此时AE +√55DE 最小 在Rt △DHE Rt △EFA 中 ∠HDE =∠FAE∵tan∠BDE =tan∠FAE =24=EF AF =EF2∵EF =1 即E (−1,1)∵A (1,0)设直线AE 的解析式为：y =kx +b则{−k +b =1k +b =0解得：{k =−12b =12∵AE 的解析式为：y =−12x +12 联立{y =−12x +12y =−x 2−2x +3解得{x =−52y =74或{x =1y =0 （舍去）∵M (−52,74)∵AM =√(1+52)2+(74)2=7√54．18．解:（1）∵抛物线y =−x 2+bx +c 经过A (−1,0) B (3,0)∵{−1−b +c =0−9+3b +c =0解得{b =2c =3∵y =−x 2+2x +3（2）当x =0时 y =−x 2+2x +3=3∵点C 的坐标是(0,3)∵OC =3∵四边形CPQE 为平行四边形 E 为OC 中点∵PQ =CE =32设直线BC 的解析式为y =kx +b则{3k +b =0b =3∵直线BC 的解析式为y =−x +3设P(m ，−m 2+2m +3)∵Q(m ，−m +3)∴PQ =−m 2+3m =32∴m =3±√32 ∵点P 的横坐标为3±√32； （3）∵PH ∥AC∵S 1S 2=MH CM =PHAC∴S 1S 2+S 2S 3=2PH AC作AN ∥BC 交y 轴于N 作PQ ∥y 轴交BC 于Q∵∠PQH =∠NCB =∠ANC ∠PHC =∠ACH,ON OC =AO BO ∵ON3=13 ∵ON =1,CN =ON +CO =4,∵∠PHC =∠HPQ +∠PQH ∠ACH =∠NCB +∠ACN∵∠HPQ =∠ACN∵△CAN ∽△PHQ设P (n,−n 2+2n +3) 则Q (n,−n +3)∵PQ =−n 2+3n∴S 1S 2+S 2S 3=2PH AC =2PQCN =2PQ4=−n 2+3n2=−12(n −32)2+98． ∵S 1S 2+S 2S 3最大值98． 即S 1S 2+S 2S 3存在最大值 最大值为98． 19．（1）解：∵抛物线y =−12x 2+bx +c 与x 轴交于A (−2,0) B (4,0)两点（点A 在点B 的左侧）∴{−12×(−2)2−2b +c =0−12×42+4b +c =0 解得：{b =1c =4∴抛物线的函数表达式为y =−12x 2+x +4；（2）解：∵抛物线y =−12x 2+x +4与y 轴交于点C∴C (0,4)∴OC =4设直线BC 的解析式为y =kx +d 把B (4,0) C (0,4)代入 得：{4k +d =0d =4解得：{k =−1d =4∴直线BC 的解析式为y =−x +4如图1 过点P 作PD∥y 轴交BC 于点D设P (m,−12m 2+m +4) 则D (m,−m +4)∴PD =−12m 2+m +4−(−m +4)=−12m 2+2m ∵PD∥OC∴△PDQ∽△OCQ∴PQ OQ =PD OC =−12m 2+2m 4=−18(m −2)2+12∴当m =2时 PQOQ 取得最大值12 此时 P (2,4)； （3）解：∵向右平移1个单位 再向上平移2个单位得新抛物线y ′∴新抛物线解析式为y ′=−12(x −2)2+132=−12x 2+2x +92 对称轴为直线x =2 设M (t,−12t 2+2t +92) N (2,s )①当BC 为▱BCN 1M 1的边时则BC∥MN BC =MN∴{t −2=4s =−12t 2+2t +92+4 解得：{t =6s =52∴N 1(2,52)；②当BC 为▱BCM 2N 2的边时则BC∥MN BC =MN{t −2=−4s =−12t 2+2t +92−4解得：{t =−2s =−112∴N 2(2,−112)；③当BC 为▱BM 3CN 3的对角线时则{t +2=4−12t 2+2t +92+s =4解得：{t =2s =−52∴N 3(2，−52)；综上所述 N 点的坐标为： (2,52)或(2,−112)或(2，−52)．20．（1）解：将A(−1，0)、B(3，0)代入y =ax 2+bx +3(a ≠0)得{0=a −b +30=9a +3b +3解得 {a =−1b =2∵抛物线的表达式为y =−x 2+2x +3；（2）解：如图1 连接CB 交l 于M ′ 连接AM ′由题意知 抛物线的对称轴为直线x =1 MA +MC =M ′A +M ′C =M ′B +M ′C∵当C ，M ′，B 三点共线时 MA +MC =BC 此时值最小当x =0时 y =3∵C(0，3)在Rt △BOC 中 由勾股定理得BC =√OB 2+OC 2=3√2∵MA +MC 值最小为3√2；设直线BC 的解析式为y =kx +b将(0，3) (3，0)代入得 {3=b 0=3k +b解得 {k =−1b =3∵直线BC 的解析式为y =−x +3当x =1时 y =2∵M(1，2)∵MA +MC 的最小值为3√2 M(1，2)；（3）解：设Q(1，m) 以点E F P Q 为顶点的四边形为平行四边形时 分两种情况求解： ①EF 为平行四边形的边；如图2 四边形EFP 1Q 1为平行四边形∵FP1∥EQ1FP1=EQ1∵P1(2，3)EQ1=FP1=2∵Q1(1，2)；如图3 四边形EFQ2P2为平行四边形)则P2(0，m−1)∵EQ2的中点坐标为(1，m2当x=0时y=3则P2(0，3)∵m−1=3解得m=4∵Q2(1，4)；②EF为平行四边形的对角线；如图4 四边形EQ3FP3为平行四边形。

中考数学总复习《二次函数压轴题（特殊四边形）》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________1．如图，已知抛物线232y a x k ⎛⎫=-+ ⎪⎝⎭经过()1,0A -，()0,4C -两点，直线m 是抛物线的对称轴．(1)求抛物线的解析式．(2)设E 是直线m 上的一个动点，当点E 到点A ，C 的距离之和最短时，求点E 的坐标．(3)已知P 为抛物线的顶点，在平面直角坐标系中是否存在一点Q ，恰好使得P ，Q ，B ，C 为顶点平行四边形，若存在，写出所有符合条件的Q 点坐标，并写出求解点Q 的坐标的其中一种情况的过程，若不存在，说明理由． 2．如图，抛物线232yax bx与x 轴交于()1,0A -和()3,0B ，与y 轴交于C 点，点C 关于抛物线的对称轴的对称点为点D ．抛物线顶点为H ．(1)求抛物线的解析式．(2)如图1，在抛物线上是否存在一点M （异于点B ）使得ACB ACM S S =△△？若存在，请求出M 的坐标，不存在，说明理由；(3)如图2，当点E 在抛物线上运动时，在直线AD 上是否存在点F ，使得以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．3．如图，已知抛物线23y ax bx =+-（a ，b 为常数，且0a ≠）与x 轴交于()30A B ，，两点，且3OB OA =，与y 轴交于点C ，点D 为第四象限内抛物线上的动点，DE y ∥轴交BC 所在直线于点E ．(1)求抛物线的函数表达式和点C '的坐标；(2)若点F 为y 轴上一点，是否存在点D ，使得以点C ，D ，E ，F 为顶点的四边形是菱形？若存在，求出所有符合条件的点D 的坐标：若不存在，请说明理由．4．如图，在平面直角坐标系中，抛物线24y ax bx =++与x 轴分别交于()4,0A -，()2,0B 两点，与y 轴交于C 点．(1)求抛物线的解析式；(2)点P 为直线AC 上方抛物线上任意一点，过点P 作PD y ∥轴交直线AC 于点D ，过点D 作DH x ∥轴，交y 轴于点H ，求PD DH +的最大值及此时点P 的坐标；(3)将抛物线沿着水平方向向右平移2个单位长度得到新的抛物线，点E 为原抛物线与平移后的抛物线的交点，点M 为平移后的抛物线对称轴上一动点，点N 为坐标平面内一点，直接写出所有使得以点B ，E ，M ，N 为顶点的四边形是菱形的点N 的坐标，并把求其中一个点N 的坐标的求解过程写出来．5．如图，已知直线1y x =+与抛物线2y x mx n =-++交于A 、D 两点且A 点在x 轴上，抛物线与x 轴另一个交点为B ，与y 轴交于点()0,3C ．(1)求抛物线的解析式；(2)如图，直线AD 上方的抛物线上有一点F ，过点F 作FG AD ⊥于点G ，求线段FG 的最大值；(3)点M 是抛物线的顶点，点P 是y 轴上一点，点Q 是坐标平面内一点，以A ，M ，P ，Q 为顶点的四边形是以AM 为边的矩形，求点Q 的坐标．6．如图，已知直线24y x =-+分别交x 轴、y 轴于点B ．抛物线过A ，B 两点． P 是线段AB 上一动点，过点P 作PC ⊥x 轴于点C ，交抛物线于点D ．(1)若抛物线的顶点M 的坐标为19,22⎛⎫⎪⎝⎭，其对称轴交AB 于点N ．⊥求抛物线的解析式．⊥在抛物线的对称轴上找一点Q ，使AQ BQ -的值最大，试求出点Q 的坐标． ⊥是否存在点P ，使四边形MNPD 为平行四边形？若存在，求出此时点P 的坐标．(2)当点P 的横坐标为1时，是否存在这样的抛物线，使得以B ，P ，D 为顶点的三角形与AOB 相似？若存在，直接写出满足条件的抛物线的解析式；若不存在，请说明理由．7．如图1，在平面直角坐标系中，抛物线22y ax bx =++与x 轴交于()40A -，和()10B ，，与y 轴交于点C ，连接AC BC ，．(1)求该抛物线的解析式；(2)如图1，在x 轴上有一动点D ，平面内是否存在一点E ，使以点A 、D 、C 、E 为顶点的四边形是菱形？若存在，请求出点E 的坐标，若不存在，请说明理由． (3)如图2，点M 为抛物线上的一动点：⊥若点M 为直线AC 上方的抛物线上任意一点，过点M 作y 轴的平行线，交AC 于点N ，过点M 作x 轴的平行线，交直线AC 于点Q ，求MNQ △周长的最大值；⊥若点M 为抛物线上的任意一动点，且45ACM BAC ∠=︒-∠，请直接写出满足条件的点M 的坐标． 8．如图，直线443y x =+与x 轴交于点A ，与y 轴交于点C ，抛物线2)83(0y ax x c a =-+≠经过A ，C 两点，交x 轴的正半轴于点B ，连接BC ．(1)求抛物线的解析式．(2)点P 在抛物线上，连接PB ，当45PBC ∠=︒时，求点P 的坐标；(3)已知点M 从点B 出发，以每秒1个单位长度的速度沿BA 运动，同时点N 从点O 出发，以每秒3个单位长度的速度沿OC CA ，运动．当点M ，N 运动到某一时刻时，在坐标平面内是否存在点D ，使得以A ，M ，N ，D 为顶点的四边形是矩形?若存在，请直接写出点D 的坐标；若不存在，请说明理由．9．如图1，平面直角坐标系xOy 中，抛物线()230y ax bx a =++<与x 轴分别交于点()30A -,和点()10B ,，与y 轴交于点C ，P 为抛物线上一动点．(1)写出抛物线的对称轴为直线______，抛物线的解析式为______；(2)如图2，连结AC ，若P 在AC 上方，作PQ y ∥轴交AC 于Q ，把上述抛物线沿射线PQ 的方向向下平移，平移的距离为h ()0h >，在平移过程中，该抛物线与直线AC 始终有交点，求h 的最大值；(3)若P 在AC 上方，设直线AP ，BP 与抛物线的对称轴分别相交于点F ，E ，请探索以A ，F ，B ，G （G 是点E 关于x 轴的对称点）为顶点的四边形面积是否随着P 点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．(4)设M 为抛物线对称轴上一动点，当P ，M 运动时，在坐标轴上是否存在点N ，使四边形PMCN 为矩形？若存在，直接写出点P 的横坐标；若不存在，请说明理由．10．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象与x 轴交于()30A ，，()10B -，两点，与y 轴交于点()03C ，．(1)求这个二次函数的解析式；(2)已知点D 是直线AC 上方的抛物线上一动点．⊥当点D 运动到什么位置时，四边形ABCD 的面积最大？求此时D 点的坐标和四边形ABCD 的最大面积； ⊥连接DO DC ，，并把DOC △沿CO 翻折，得到四边形DOD C '，那么是否存在点D ，使四边形DOD C '为菱形？若存在，请求出此时点D 的坐标；若不存在，请说明理由．11．如图，抛物线23y ax ax c =-+与x 轴交于A ，()4,0B 两点（A 在B 的左侧），与y 轴交于点(0,4)C -，直线l 是地物线的对称轴，直线l 与x 轴交于点D ．(1)求抛物线的函数表达式；(2)点M 在直线l 上，且12DM =，点P ，Q 是抛物线上的动点，点P 在点Q 的左侧，是否存在点P ，Q 使得以点D 、M 、P 、Q 为顶点的四边形是菱形？若存在，请求出点P ，Q 的坐标；若不存在，请说明理由． 12．如图，二次函数的图象交x 轴于点()2,0A -和()8,0B ，交y 轴于点()0,4C ，连接AC ，BC ，点P 是线段OB 上一动点，过点P 作直线PD AC ∥，交y 轴于点D ，交线段BC 于点E ，交x 轴上方二次函数的图象于点F ．(1)求二次函数的表达式．(2)当点P 为线段DE 的三等分点时，求点P 的坐标．(3)在线段OB 上是否存在点P ，使得四边形AEFC 为平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由． 13．综合与探究如图，直线4y x =-+与x 轴交于点B ，与y 轴交于点C ，经过B ，C 两点的抛物线212y x bx c =-++与x 轴的另一个交点为点A ，连接AC ．(1)求抛物线的解析式以及点A 的坐标；(2)若点P 是直线BC 上方抛物线上的一个动点，过点P 作PQ AC ∥交直线4y x =-+于点Q ，求线段PQ 的最大值；(3)若点M 在直线BC 上运动，在坐标平面内是否存在另一个点N ，使得以A ，C ，M ，N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．14．如图，已知抛物线()230y ax ax c a =++>与x 轴交于A 、B 两点，与y 轴交于点C ，点A 在点B 左侧，点B 的坐标为()1,0，点C 的坐标为为()0,3-．(1)求抛物线的函数关系式；(2)若点D 是x 轴上的一点，在抛物线上是否存在点E ，使以A 、C 、D 、C 为顶点且以AC 为一边的四边形是平行四边形﹖若存在，请求出点E 的坐标；若不存在，请说明理由． 15．综合与探究：如图，抛物线248433y x x =+-与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ．(1)求点A ，B ，C 的坐标；(2)点D 是第三象限内抛物线上的动点，设点D 的横坐标为m ，求四边形ABCD 面积S 的最大值及此时点D 的坐标；(3)若点P 在抛物线对称轴上，点Q 是平面内一点，试探究，是否存在点P ，Q ，使以点A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形？若存在，请求出点P 的坐标；若不存在，请说明理由．参考答案：1．(1)232524y x ⎛⎫=-- ⎪⎝⎭(2)35,22E -⎛⎫⎪⎝⎭(3)59,24Q ⎛⎫ ⎪⎝⎭或145,24Q -⎛⎫- ⎪⎝⎭或119,24Q -⎛⎫ ⎪⎝⎭2．(1)21322y x x =-++．(2)存在，M 点的坐标为214,2⎛⎫-- ⎪⎝⎭(3)存在，点F 的坐标为10,2⎛⎫ ⎪⎝⎭或317517,24⎛⎫++ ⎪⎝⎭或317517,24⎛⎫-- ⎪⎝⎭或12,2⎛⎫-- ⎪⎝⎭3．(1)抛物线的函数表达式为223y x x =--，点C 的坐标为()03-，(2)存在点D ，使得以点C ，D ，E ，F 为顶点的四边形是菱形，点D 的坐标为()23-，或()32,242--4．(1)2142y x x =--+ (2)92 53,2P ⎛⎫- ⎪⎝⎭(3)()1,419-+或()1,419--或()3,19或()3,19-5．(1)223y x x =-++(2)928(3)72,2Q ⎛⎫ ⎪⎝⎭或12,2Q ⎛⎫- ⎪⎝⎭6．(1)⊥2224y x x =-++；⊥1,62Q ⎛⎫⎪⎝⎭；⊥存在 3,12P ⎛⎫ ⎪⎝⎭(2)存在，2224y x x =-++或25342y x x =-++7．(1)213222y x x --=+(2)存在 ()10,2E - ()225,2E ()325,2E - 45,22E -⎛⎫⎪⎝⎭(3)⊥625+ ⊥1(5,3)M -- 22375(,)749M -8．(1)248433y x x =--+(2)51213,20100⎛⎫- ⎪⎝⎭(3)71311362⎛⎫+-- ⎪ ⎪⎝⎭，或()33-，或11355⎛⎫-- ⎪⎝⎭，9．(1)=1x - 223y x x =--+ (2)h 的最大值为169(3)不变，这个四边形的面积为16 (4)存在，点P 的横坐标为51456-± 1-10．(1)二次函数的解析式为223y x x =-++；(2)⊥点D 的坐标为31524⎛⎫ ⎪⎝⎭，时，四边形ABCD 的最大面积值为758；⊥点D 的坐标为210322⎛⎫+ ⎪ ⎪⎝⎭，．11．(1)234y x x =--(2)存在，点P 、Q 的坐标分别是()2,6- ()5,6或()1,6- ()2,6-12．(1)213442y x x =-++(2)点P 的坐标为8011⎛⎫ ⎪⎝⎭，或1607⎛⎫⎪⎝⎭，； (3)不存在，理由见解析13．(1)抛物线的解析式为2142y x x =-++ ()20A -，； (2)PQ 的最大值为253； (3)点N 的坐标为()21010--，或()21010-+-，或()46，或()75-，．14．(1)239344y x x =+- (2)()3,3--或341,32⎛⎫-- ⎪ ⎪⎝⎭或341,32⎛⎫-+ ⎪ ⎪⎝⎭15．(1)()30A -，()10B ， ()04C -， (2)当点D 坐标为352⎛⎫-- ⎪⎝⎭，时，四边形ABCD 面积S 的最大值为252； (3)存在，P 的坐标为1318⎛⎫-- ⎪⎝⎭，。

1．如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c经过A，B两点．（1）求抛物线的解析式；（2）点E是直角△ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E、F的坐标；（3）在（2）的条件下：在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，请求出所有点P的坐标；若不存在，请说明理由．2．如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）D与点M M、N同时32）三点．（1（2）点（3）点E、F，若△PEB4．如图A（4，0）（1（2）点C2）（3P 为5（1（2ACD沿x （3点Q6．如图1，在平面直角坐标系中，O是坐标原点，抛物线y=﹣x2﹣x+8与x轴正半轴交于点A，与y轴交于点B，连接AB，点M，N分别是OA，AB的中点，Rt△CDE≌Rt△ABO，且△CDE始终保持边ED经过点M，边CD经过点N，边DE与y轴交于点H，边CD与y轴交于点G．（1）填空：OA的长是，∠ABO的度数是度；（2）如图2，当DE∥AB，连接HN．①求证：四边形AMHN是平行四边形；②判断点D是否在该抛物线的对称轴上，并说明理由；（3）如图3，当边CD经过点O时，（此时点O与点G重合），过点D作DQ∥OB，交AB延长线上于点Q，延长ED到点K，使DK=DN，过点K作KI∥OB，在KI上取一点P，使得∠PDK=45°（点P，Q 在直线ED的同侧），连接PQ，请直接写出PQ的长．7．如图，抛物线y=x2+x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6，）在抛物线上，直线AC与y轴交于点D．（1）求c的值及直线AC的函数表达式；（2）点P在x轴正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．①求证：△APM∽△AON；②设点M的横坐标为m，求AN的长（用含m的代数式表示）．8．抛物线y=4x2﹣2ax+b与x轴相交于A（x1，0），B（x2，0）（0＜x1＜x2）两点，与y轴交于点C．（1）设AB=2，tan∠ABC=4，求该抛物线的解析式；（2）在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；（3）是否存在整数a，b使得1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．9．如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（点A在点B的左侧），直线l与抛物线交于A，C两点，其中点C的横坐标为2．（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ的周长最小？若存在，求出这个最小值及点M，N的坐标；若不存在，请说明理由．（4）点H是抛物线上的动点，在x轴上是否存在点F，使A、C、F、H四个点为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的F点坐标；如果不存在，请说明理由．10．如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到点C的位置，一条抛物线正好经过点O，C，A三点．（1）求该抛物线的解析式；（2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分别过点P，点M作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．（3）如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点构成以OC为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．11．如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y=x2+bx+c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，与抛物线y=x2+bx+c交于第四象限的F点．（1）求该抛物线解析式与F点坐标；（2）如图（2），动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；同时，动点M从点A出发，沿线段AE以每秒个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒．①问EP+PH+HF是否有最小值？如果有，求出t的值；如果没有，请说明理由．②若△PMH是等腰三角形，请直接写出此时t的值．12．如图，已知直线y=kx﹣6与抛物线y=ax2+bx+c相交于A，B两点，且点A（1，﹣4）为抛物线的顶点，点B在x轴上．（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．13．如图1，在平面直角坐标系xOy中，直线l：与x轴、y轴分别交于点A和点B（0，﹣1），抛物线经过点B，且与直线l的另一个交点为C（4，n）．（1）求n的值和抛物线的解析式；（2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l 上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；（3）M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．14．如图，四边形ABCD是边长为4的正方形，动点P、Q同时从A点出发，点P沿AB以每秒1个单位长度的速度向终点B运动．点Q沿折线ADC以每秒2个单位长度的速度向终点C运动，设运动时间为t秒．（1）当（2）当（3ABCD面15．如图x与A在点B（1（2）点过点E作90°，点F，P F′处，再沿Q（31个单位长度向点N运动到H y 轴于点I求t16．如图，直线与x轴的另（﹣1，0）．（1）求（2）P E，交x 轴于点F①求S与②求S（3）过点P作直线b∥x轴（图2），交AC于点Q，那么在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，请求出点R的坐标；若不存在，请说明理由．17．已知正方形OABC的边OC、OA分别在x、y轴的正半轴上，点B坐标为（10，10），点P从O 出发沿O→C→B运动，速度为1个单位每秒，连接AP．设运动时间为t．（1）若抛物线y=﹣（x﹣h）2+k经过A、B两点，求抛物线函数关系式；（2）当0≤t≤10时，如图1，过点O作OH⊥AP于点H，直线OH交边BC于点D，连接AD，PD，设△APD的面积为S，求S的最小值；（3）在图2中以A为圆心，OA长为半径作⊙A，当0≤t≤20时，过点P作PQ⊥x轴（Q在P的上方），且线段PQ=t+12：①当t在什么范围内，线段PQ与⊙A只有一个公共点？当t在什么范围内，线段PQ与⊙A有两个公共点？②请将①中求得的t的范围作为条件，证明：当t取该范围内任何值时，线段PQ与⊙A总有两个公共点．18．如图，二次函数y=x2﹣4x的图象与x轴、直线y=x的一个交点分别为点A、B，CD是线段OB 上的一动线段，且CD=2，过点C、D的两直线都平行于y轴，与抛物线相交于点F、E，连接EF．（1）点A的坐标为，线段OB的长= ；（2）设点C的横坐标为m①当四边形CDEF是平行四边形时，求m的值；②连接AC、AD，求m为何值时，△ACD的周长最小，并求出这个最小值．19．如图，已知二次函数y=﹣x2+bx+c（c＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB=OC=3，顶点为M．（1）求二次函数的解析式；（2）点ACPQ的面积为S（320x x AC，BC，已知（1）P P 使得以A（2）设，连接以每秒个单位的速度运动到时，点M21．A（0，2），直线y=x C，交x 轴于点G Q，△PCQ（1（2（3（4M+22抛物线y=x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．问题解决如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．（1）写出点C的坐标，并说明∠ECF=90°；（2）在△PEF中，M为EF中点，P为动点．①求证：PE2+PF2=2（PM2+EM2）；②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．23．已知抛物线经过A（﹣3，0），B（1，0），C（2，）三点，其对称轴交x轴于点H，一次函数y=kx+b（k≠0）的图象经过点C，与抛物线交于另一点D（点D在点C的左边），与抛物线的对称轴交于点E．（1）求抛物线的解析式；（2）如图1，当S△EOC =S△EAB时，求一次函数的解析式；（3）如图2，设∠CEH=α，∠EAH=β，当α＞β时，直接写出k的取值范围．24．如图1，已知直线EA与x轴、y轴分别交于点E和点A（0，2），过直线EA上的两点F、G分别作x轴的垂线段，垂足分别为M（m，0）和N（n，0），其中m＜0，n＞0．（1）如果m=﹣4，n=1，试判断△AMN的形状；（2）如果mn=﹣4，（1）中有关△AMN的形状的结论还成立吗？如果成立，请证明；如果不成立，请说明理由；（3）如图2，题目中的条件不变，如果mn=﹣4，并且ON=4，求经过M、A、N三点的抛物线所对应的函数关系式；（4）在（3）的条件下，如果抛物线的对称轴l与线段AN交于点P，点Q是对称轴上一动点，以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似，求符合条件的点Q的坐标．25．如图，二次函数与x轴交于A、B两点，与y轴交于C点，点P从A点出发，以1个单位每秒的速度向点B运动，点Q同时从C点出发，以相同的速度向y轴正方向运动，运动时间为t秒，点P到达B点时，点Q同时停止运动．设PQ交直线AC于点G．（1）求直线AC的解析式；（2）设△PQC的面积为S，求S关于t的函数解析式；（3）在y轴上找一点M，使△MAC和△MBC都是等腰三角形．直接写出所有满足条件的M点的坐标；（4）过点P作PE⊥AC，垂足为E，当P点运动时，线段EG的长度是否发生改变，请说明理由．26．如图，在平面直角坐标系xOy中，二次函数的图象与x轴交于A（﹣1，0）、B（3，0）两点，顶点为C．（1）求此二次函数解析式；（2）点D为点C关于x轴的对称点，过点A作直线l：交BD于点E，过点B作直线BK∥AD交直线l于K点．问：在四边形ABKD的内部是否存在点P，使得它到四边形ABKD四边的距离都相等？若存在，请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，若M、N分别为直线AD和直线l上的两个动点，连结DN、NM、MK，求DN+NM+MK 和的最小值．27．如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．（1）求经过A、B、C三点的抛物线的解析式；（2）当（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ=1，要使四边形BCPQ的周长最小，求出P、Q两点的坐标．28．如图，已知抛物线与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C（0，）．（1）求抛物线的解析式及其顶点D的坐标；（2）设直线CD交x轴于点E，过点B作x轴的垂线，交直线CD于点F，在直线CD的上方，y轴及y轴的右侧的平面内找一点G，使以点G、F、C为顶点的三角形与△COE相似，请直接写出符合要求的点G的坐标；（3）如图，抛物线的对称轴与x轴的交点M，过点M作一条直线交∠ADB于T，N两点，①当∠DNT=90°时，直接写出的值；②当直线TN绕点M旋转时，试说明：△DNT的面积S=DN?DT；△DNT并猜想：的值是否是定值？说明理由．29．如图①，Rt△ABC中，∠B=90°∠CAB=30°，AC⊥x轴．它的顶点A的坐标为（10，0），顶点B的坐标为，点P从点A出发，沿A→B→C的方向匀速运动，同时点Q从点D（0，2）出发，沿y轴正方向以相同速度运动，当点P到达点C时，两点同时停止运动，设运动的时间为t 秒．（1）求∠BAO的度数．（直接写出结果）（2）当点P在AB上运动时，△OPQ的面积S与时间t（秒）之间的函数图象为抛物线的一部分（如图②），求点P的运动速度．（3）求题（2）中面积S与时间t之间的函数关系式，及面积S取最大值时，点P的坐标．（4）如果点P，Q保持题（2）中的速度不变，当t取何值时，PO=PQ，请说明理由．30．如图，已知直线l：y=x+2与y轴交于点D，过直线l上一点E作EC丄y轴于点C，且C点坐标为（0，4），过C、E两点的抛物线y=﹣x2+bx+c交x轴于A、B两点（点A在点B的左侧）．（1）求抛物线的解析式：（2）动点Q从点C出发沿线段CE以1单位/秒的速度向终点E运动，过点Q作QF⊥ED于点F，交BD于点H，设点Q运动时间为t秒，△DFH的面积为S，求出S与t的函数关系式（并直接写出自变量t的取值范围）；（3）若动点P为直线CE上方抛物线上一点，连接PE，过点E作EM⊥PE交线段BD于点M，当△PEM 是等腰直角三角形时，求四边形PMBE的面积．31．已知在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0，且a，b，c为常数）的对称轴为：直线x=，与x轴分别交于点A、点B，与y轴交于点C（0，﹣），且过点（3，﹣5），D为x轴正半轴上的动点，E为y轴负半轴上的动点．（1）求该抛物线的表达式；（2）如图1，当点D为（3，0）时，DE交该抛物线于点M，若∠ADC=∠CDM，求点M的坐标；（3）如图2，把（1）中抛物线平移使其顶点与原点重合，若直线ED与新抛物线仅有唯一交点Q 时，y轴上是否存在一个定点P使PE=PQ？若存在，求出点P的坐标；若不存在，请说明理由．参考答案与试题解析一．解答题（共31小题）1．（2017秋?上杭县期中）如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c经过A，B两点．（1）求抛物线的解析式；（2）点E是直角△ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E、F的坐标；（3）在（2）的条件下：在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，请求出所有点P的坐标；若不存在，请说明理由．【考点】HF：二次函数综合题．【专题】151：代数综合题；32：分类讨论．【分析】（1）根据AC=BC，求出BC的长，进而得到点A，B的坐标，利用待定系数法即可求得抛物线的解析式；（2）利用待定系数法求出直线AB的解析式，用含m的式表示出E，F的坐标，求出EF的长度最大时m的值，即可求得E，F的坐标；（3）分两种情况：∠E﹣90°和∠F=90°，分别得到点P的纵坐标，将纵坐标代入抛物线解析式，即可求得点P的值．【解答】解：（1）∵OA=1，OC=4，AC=BC，∴BC=5，∴A（﹣1，0），B（4，5），抛物线y=x2+bx+c经过A，B两点，∴，解得：，∴y=x2﹣2x﹣3；（2）设直线AB解析式为：y=kx+b，直线经过点A，B两点，∴，解得：，∴直线AB的解析式为：y=x+1，设点E2∴EF=m+1﹣m2+2m+3=﹣m2+3m+4=﹣（m﹣）2+，∴当EF最大时，m=，∴点E（，），F（，）；（3）存在．①当∠FEP=90°时，点P的纵坐标为，即x2﹣2x﹣3=，解得：x1=，x2=，∴点P1（，），P2（，），②当∠EFP=90°时，点P的纵坐标为，即x2﹣2x﹣3=，解得：x1=，x2=（舍去），∴点P3（，），综上所述，P1（，），P2（，），P3（，）．【点评】本题主要考查二次函数的综合题，其中第（3）小题要注意分类讨论，分∠E=90°和∠F=90°两种情况．2．（2017秋?鄂城区期中）如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）代入A（1，0）和C（0，3），解方程组即可；（2）求出点B的坐标，再根据勾股定理得到BC，当△PBC为等腰三角形时分三种情况进行讨论：①CP=CB；②BP=BC；③PB=PC；（3）设AM=t则DN=2t，由AB=2，得BM=2﹣t，S△MNB=×（2﹣t）×2t=﹣t2+2t，运用二次函数的顶点坐标解决问题；此时点M在D点，点N在对称轴上x轴上方2个单位处或点N在对称轴上x 轴下方2个单位处．【解答】解：（1）把A（1，0）和C（0，3）代入y=x2+bx+c，解得：b=﹣4，c=3，∴二次函数的表达式为：y=x2﹣4x+3；（2）令y=0，则x2﹣4x+3=0，解得：x=1或x=3，∴B（3，0），∴BC=3，点P在y轴上，当△PBC为等腰三角形时分三种情况进行讨论：如图1，①当CP=CB时，PC=3，∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1（0，3+3），P2（0，3﹣3）；②当BP=BC时，OP=OB=3，∴P3（0，﹣3）；③当PB=PC时，∵OC=OB=3∴此时P与O重合，∴P4（0，0）；综上所述，点P的坐标为：（0，3+3）或（0，3﹣3）或（0，﹣3）或（0，0）；（3）如图2，设A运动时间为t，由AB=2，得BM=2﹣t，则DN=2t，∴S△MNB=×（2﹣t）×2t=﹣t2+2t=﹣（t﹣1）2+1，即当M（2，0）、N（2，2）或（2，﹣2）时△MNB面积最大，最大面积是1．【点评】本题是二次函数的综合题型，其中涉及到运用待定系数法求二次函数，等腰三角形的性质，轴对称的性质等知识，运用数形结合、分类讨论及方程思想是解题的关键．3．（2017?泸州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过A（﹣1，0）、B（4，0）、C （0，2）三点．（1）求该二次函数的解析式；（2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；（3）点P是该二次函数图象上位于第一象限上的一动点，连接PA分别交BC、y轴于点E、F，若△PEB、△CEF的面积分别为S1、S2，求S1﹣S2的最大值．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）当点D在x轴上方时，则可知当CD∥AB时，满足条件，由对称性可求得D点坐标；当点D 在x轴下方时，可证得BD∥AC，利用AC的解析式可求得直线BD的解析式，再联立直线BD和抛物线的解析式可求得D点坐标；（3）过点P作PH∥y轴交直线BC于点H，可设出P点坐标，从而可表示出PH的长，可表示出△PEB的面积，进一步可表示出直线AP的解析式，可求得F点的坐标，联立直线BC和PA的解析式，可表示出E点横坐标，从而可表示出△CEF的面积，再利用二次函数的性质可求得S1﹣S2的最大值．【解答】解：（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+x+2；（2）当点D在x轴上方时，过C作CD∥AB交抛物线于点D，如图1，∵A、B关于对称轴对称，C、D关于对称轴对称，∴四边形ABDC为等腰梯形，∴∠CAO=∠DBA，即点D满足条件，∴D（3，2）；当点D在x轴下方时，∵∠DBA=∠CAO，∴BD∥AC，∵C（0，2），∴可设直线AC解析式为y=kx+2，把A（﹣1，0）代入可求得k=2，∴直线AC解析式为y=2x+2，∴可设直线BD解析式为y=2x+m，把B（4，0）代入可求得m=﹣8，∴直线BD解析式为y=2x﹣8，联立直线BD和抛物线解析式可得，解得或，∴D（﹣5，﹣18）；综上可知满足条件的点D的坐标为（3，2）或（﹣5，﹣18）；（3）过点P作PH∥y轴交直线BC于点H，如图2，设P（t，﹣t2+t+2），由B、C两点的坐标可求得直线BC的解析式为y=﹣x+2，∴H（t，﹣t+2），∴PH=yP ﹣yH=﹣t2+t+2﹣（﹣t+2）=﹣t2+2t，设直线AP的解析式为y=px+q，∴，解得，∴直线AP的解析式为y=（﹣t+2）（x+1），令x=0可得y=2﹣t，∴F（0，2﹣t），∴CF=2﹣（2﹣t）=t，联立直线AP和直线BC解析式可得，解得x=，即E点的横坐标为，∴S1=PH（xB﹣xE）=（﹣t2+2t）（4﹣），S2=??，∴S1﹣S2=（﹣t2+2t）（4﹣）﹣??=﹣t2+4t=﹣（t﹣）2+，∴当t=时，有S1﹣S2有最大值，最大值为．【点评】本题为二次函数的综合应用，涉及待定系数法、平行线的判定和性质、三角形的面积、二次函数的性质、方程思想汲分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中确定出D点的位置是解题的关键，在（3）中用P点的坐标分别表示出两个三角形的面积是解题的关键．本题考查知识点较多，综合性较强，计算量大，难度较大．4．（2017?南充）如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣，直线l的解析式为y=x．（1）求二次函数的解析式；（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P 为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）由题意抛物线的顶点坐标为（2，﹣），设抛物线的解析式为y=a（x﹣2）2﹣，把（0，0）代入得到a=，即可解决问题；（2）如图1中，设E（m，0），则C（m，m2﹣m），B（﹣m2+m，0），由E、B关于对称轴对称，可得=2，由此即可解决问题；（3）分两种情形求解即可①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．②当N′=N′B′时，设P（m，m﹣3），列出方程解方程即可；【解答】解：（1）由题意抛物线的顶点坐标为（2，﹣），设抛物线的解析式为y=a（x﹣2）2﹣，把（0，0）代入得到a=，∴抛物线的解析式为y=（x﹣2）2﹣，即y=x2﹣x．（2）如图1中，设E（m，0），则C（m，m2﹣m），B（﹣m2+m，0），∵E′在抛物线上，易知四边形EBE′C是正方形，抛物线的对称轴也是正方形的对称轴，∴E、B关于对称轴对称，∴=2，解得m=1或6（舍弃），∴B（3，0），C（1，﹣2），∴直线l′的解析式为y=x﹣3．（3）如图2中，①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．②当N′=N′B′时，设P（m，m﹣3），则有（m﹣）2+（m﹣3﹣）2=（3）2，解得m=或，∴P2（，），P3（，）．综上所述，满足条件的点P坐标为（0，﹣3）或（，）或（，）．【点评】本题考查二次函数综合题、待定系数法、等腰三角形的判定和性质、两点间距离公式等知识，解题的关键是学会用分类讨论的思想思考问题，学会根据方程，属于中考压轴题．5．（2017?宜宾）如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．（1）求抛物线的解析式；（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x 轴向右平移m个单位，当点C落在抛物线上时，求m的值；（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）由A、B的坐标，利用待定系数法可求得抛物线的解析式；（2）由题意可求得C点坐标，设平移后的点C的对应点为C′，则C′点的纵坐标为8，代入抛物（3为平行四Q 由B、E【解答】（1∴，（2）∵∴OD=6∴C（﹣6∵C（﹣6∴当点C∴m（3）∵∴可设P由（2①当BE垂线，垂足为N，如图，则∠BEF=∠BMP=∠QPN，在△PQN和△EFB中∴△PQN≌△EFB（AAS），∴NQ=BF=OB﹣OF=5﹣1=4，设Q（x，y），则QN=|x﹣2|，∴|x﹣2|=4，解得x=﹣2或x=6，当x=﹣2或x=6时，代入抛物线解析式可求得y=﹣7，∴Q点坐标为（﹣2，﹣7）或（6，﹣7）；②当BE为对角线时，∵B（5，0），E（1，8），∴线段BE的中点坐标为（3，4），则线段PQ的中点坐标为（3，4），设Q（x，y），且P（2，t），∴x+2=3×2，解得x=4，把x=4代入抛物线解析式可求得y=5，∴Q（4，5）；综上可知Q点的坐标为（﹣2，﹣7）或（6，﹣7）或（4，5）．【点评】本题为二次函数的综合应用，涉及待定系数法、平移的性质、全等三角形的判定和性质、平行四边形的性质、方程思想及分类讨论思想等知识．在（1）注意待定系数法的应用，在（2）中求得平移后C点的对应点的坐标是解题的关键，在（3）中确定出Q点的位置是解题的关键．本题考查知识点较多，综合性较强，难度适中．6．（2017?沈阳）如图1，在平面直角坐标系中，O是坐标原点，抛物线y=﹣x2﹣x+8与x轴正半轴交于点A，与y轴交于点B，连接AB，点M，N分别是OA，AB的中点，Rt△CDE≌Rt△ABO，且△CDE G．（1（2②判断点（3点Q P，Q 在直线【考点】【专题】【分析】（2）②如图12，由﹣=（3的坐标即可解决问题；【解答】y=8，∴B（0，∴OB=8当y=0﹣x﹣x8=0x2+4x﹣（x﹣8）x 1=8，x2=∴A（8，∴OA=8，在Rt△AOB中，tan∠ABO===，∴∠ABO=30°，故答案为：8，30；（2）①证明：∵DE∥AB，∴，∵OM=AM，∴OH=BH，∵BN=AN，∴HN∥AM，∴四边形AMHN是平行四边形；②点D在该抛物线的对称轴上，理由是：如图1，过点D作DR⊥y轴于R，∵HN∥OA，∴∠NHB=∠AOB=90°，∵DE∥AB，∴∠DHB=∠OBA=30°，∵Rt△CDE≌Rt△ABO，∴∠HDG=∠OBA=30°，∴∠HGN=2∠HDG=60°，∴∠HNG=90°﹣∠HGN=90°﹣60°=30°，∴∠HDN=∠HND，∴DH=HN=OA=4，∴Rt△DHR中，DR=DH==2，∴点D的横坐标为﹣2，∵抛物线的对称轴是直线：x=﹣=﹣=﹣2，∴点D在该抛物线的对称轴上；（3）如图3中，连接PQ，作DR⊥PK于R，在DR上取一点T，使得PT=DT．设PR=a．∵NA=NB，∴HO=NA=NB，∵∠ABO=30°，∴∠BAO=60°，∴△AON是等边三角形，∴∠NOA=60°=∠ODM+∠OMD，∵∠ODM=30°，∴∠OMD=∠ODM=30°，∴OM=OD=4，易知D（﹣2，﹣2），Q（﹣2，10），∵N（4，4），∴DK=DN==12，∵DR∥x轴，，∴∠KDR=∠OMD=30°∴RK=DK=6，DR=6，∵∠PDK=45°，∴∠TDP=∠TPD=15°，∴∠PTR=∠TDP+∠TPD=30°，∴TP=TD=2a，TR=a，∴a+2a=6，∴a=12﹣18，可得P（﹣2﹣6，10﹣18），∴PQ==12．【点评】本题考查二次函数综合题、平行四边形的判定和性质、锐角三角函数、30度角的直角三角形的性质、等边三角形的判定和性质、勾股定理、平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．7．（2017?宁波）如图，抛物线y=x2+x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6，）在抛物线上，直线AC与y轴交于点D．（1）求c的值及直线AC的函数表达式；（2）点P在x轴正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．①求证：△APM∽△AON；②设点M的横坐标为m，求AN的长（用含m的代数式表示）．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）把C点坐标代入抛物线解析式可求得c的值，令y=0可求得A点坐标，利用待定系数法可求得直线AC的函数表达式；（2）①在Rt△AOB和Rt△AOD中可求得∠OAB=∠OAD，在Rt△OPQ中可求得MP=MO，可求得∠MPO=∠MOP=∠AON，则可证得△APM∽△AON；②过M作ME⊥x轴于点E，用m可表示出AE和AP，进一步可表示出AM，利用△APM∽△AON可表示出AN．【解答】解：（1）把C点坐标代入抛物线解析式可得=9++c，解得c=﹣3，∴抛物线解析式为y=x2+x﹣3，令y=0可得x2+x﹣3=0，解得x=﹣4或x=3，∴A（﹣4，0），设直线AC的函数表达式为y=kx+b（k≠0），把A、C坐标代入可得，解得，∴直线AC的函数表达式为y=x+3；（2）①∵在Rt△AOB中，tan∠OAB==，在RtAOD中，tan∠OAD==，∴∠OAB=∠OAD，∵在Rt△POQ中，M为PQ的中点，∴OM=MP，∴∠MOP=∠MPO，且∠MOP=∠AON，∴∠APM=∠AON，∴△APM∽△AON；②如图，过点M作ME⊥x轴于点E，则OE=EP，∵点M的横坐标为m，∴AE=m+4，AP=2m+4，∵tan∠OAD=，∴cos∠EAM=cos∠OAD=，∴=，∴AM=AE=，∵△APM∽△AON，∴=，即=，∴AN=．【点评】本题为二次函数的综合应用，涉及待定系数法、三角函数的定义、相似三角形的判定和性质、等腰三角形的性质、直角三角形的性质及方程思想等知识．在（1）中注意函数图象上的点的坐标满足函数解析式，以及待定系数法的应用，在（2）①中确定出两对对应角相等是解题的关键，在（2）②中用m表示出AP的长是解题的关键，注意利用相似三角形的性质．本题考查知识点较多，综合性较强，难度较大．8．（2017?自贡）抛物线y=4x2﹣2ax+b与x轴相交于A（x1，0），B（x2，0）（0＜x1＜x2）两点，与y轴交于点C．（1）设AB=2，tan∠ABC=4，求该抛物线的解析式；（2）在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；（3）是否存在整数a，b使得1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）由tan∠ABC=4，可以假设B（m，0），则A（m﹣2，0），C（0，4m），可得抛物线的解析式为y=4（x﹣m）（x﹣m+2），把C（0，4m）代入y=4（x﹣m）（x﹣m+2），求出m的值即可解决问题；（2）设P（m，4m2﹣16m+12）．作PH∥OC交BC于H，根据S△PBC =S△PHC+S△PHB构建二次函数，利用二次函数的性质解决问题；（3）不存在．假设存在，由题意由题意可知，且1＜﹣＜2，首先求出整数a的值，代入不等式组，解不等式组即可解决问题．【解答】解：（1）∵tan∠ABC=4∴可以假设B（m，0），则A（m﹣2，0），C（0，4m），∴可以假设抛物线的解析式为y=4（x﹣m）（x﹣m+2），把C（0，4m）代入y=4（x﹣m）（x﹣m+2），得m=3，∴抛物线的解析式为y=4（x﹣3）（x﹣1），∴y=4x2﹣16x+12，（2）如图，设D（m，4m2﹣16m+12）．作DH∥OC交BC于H．∵B（3，0），C（0，12），∴直线BC的解析式为y=﹣4x+12，∴H（m，﹣4m+12），∴S△DBC =S△DHC+S△DHB=?（﹣4m+12﹣4m2+16m﹣12）?3=﹣6（m﹣）2+，∵﹣6＜0，∴m=时，△DBC面积最大，此时D（，﹣3）．（3）不存在．理由：假设存在．由题意可知，且1＜﹣＜2，∴4＜a＜8，∵a是整数，∴a=5或6或7，当a=5时，代入不等式组，不等式组无解．当a=6时，代入不等式组，不等式组无解．当a=7时，代入不等式组，不等式组无解．综上所述，不存在整数a、b，使得1＜x1＜2和1＜x2＜2同时成立．【点评】本题考查二次函数综合题、待定系数法、三角形的面积，不等式组等整数，解题的关键是灵活运用待定系数法确定函数解析式，学会构建二次函数，利用二次函数的性质解决问题，学会利用不等式组解决问题，属于中考压轴题．9．（2017?日照模拟）如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（点A在点B的左侧），直线l与抛物线交于A，C两点，其中点C的横坐标为2．（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ的周长最小？若存在，求出这个最小值及点M，N的坐标；若不存在，请说明理由．（4）点H是抛物线上的动点，在x轴上是否存在点F，使A、C、F、H四个点为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的F点坐标；如果不存在，请说明理由．【考点】HF：二次函数综合题．【专题】16：压轴题．【分析】（1）令抛物线y=x2﹣2x﹣3=0，求出x的值，即可求A，B两点的坐标，根据两点式求出直线AC的函数表达式；（2）设P点的横坐标为x（﹣1≤x≤2），求出P、E的坐标，用x表示出线段PE的长，求出PE的最大值，进而求出△ACE的面积最大值；（3）根据D点关于PE的对称点为点C（2，﹣3），点Q（0，﹣1）点关于x轴的对称点为M（0，1），则四边形DMNQ的周长最小，求出直线CM的解析式为y=﹣2x+1，进而求出最小值和点M，N的坐标；（4）结合图形，分两类进行讨论，①CF平行x轴，如图1，此时可以求出F点两个坐标；②CF不平行x轴，如题中的图2，此时可以求出F点的两个坐标．【解答】解：（1）令y=0，解得x1=﹣1或x2=3，∴A（﹣1，0），B（3，0）；将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3，∴C（2，﹣3），∴直线AC的函数解析式是y=﹣x﹣1，（2）设P点的横坐标为x（﹣1≤x≤2），则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3），∵P点在E点的上方，PE=（﹣x﹣1）﹣（x2﹣2x﹣3）=﹣x2+x+2，∴当x=时，PE的最大值=，△ACE的面积最大值=PE[2﹣（﹣1）]=PE=，（3）D点关于PE的对称点为点C（2，﹣3），点Q（0，﹣1）点关于x轴的对称点为K（0，1），连接CK交直线PE于M点，交x轴于N点，可求直线CK的解析式为y=﹣2x+1，此时四边形DMNQ 的周长最小，。

2017年中考压轴题——二次函数、动点综合题1．（本小题满分13分）如图，二次函数32-+=bx ax y 的图象与x 轴交于A （-1，0），B （3，0）两点，与y 轴交于点C .该抛物线的顶点为M . （1）求该抛物线的解析式； （2）判断△BCM 的形状，并说明理由.（3）探究坐标轴上是否存在点P ，使得以点P ，A ，C 为顶点的三角形与△BCM 相似？若存在，请求出点P 的坐标，若不存在，请说明理由.2．（13分）如图，已知抛物线y=x 2+bx+c 经过△ABC 的三个顶点，其中点A （0，1），点B （﹣9，10），AC ∥x轴，点P 时直线AC 下方抛物线上的动点． （1）求抛物线的解析式； （2）过点P 且与y 轴平行的直线l 与直线AB 、AC 分别交于点E 、F,当四边形AECP 的面积最大时,求点P 的坐标； （3）当点P 为抛物线的顶点时，在直线AC 上是否存在点Q ，使得以C 、P 、Q 为顶点的三角形与△ABC 相似，若存在，求出点Q 的坐标，若不存在，请说明理由．(第26题图)3．（13分）如图1，抛物线y=ax 2+bx +3（a ≠0）与x 轴交于点A 、点B （点A 在点B 左侧），与y 轴交于点C ，点D 为抛物线的顶点，已知点A 、点B 的坐标分别为A （﹣1，0）、B （3，0）． （1）求抛物线的解析式；（2）在直线BC 上方的抛物线上找一点P ，使△PBC 的面积最大，求P 点的坐标；（3）如图2，连接BD 、CD ，抛物线的对称轴与x 轴交于点E ，过抛物线上一点M 作MN ⊥CD ，交直线CD 于点N ，求当∠CMN=∠BDE 时点M 的坐标．4．（本小题满分13分） 如图，已知抛物线232y ax x c =-+与x 轴相交于A 、B 两点，并与直线122y x =-交于B 、C 两点，其中点C 是直线122y x =-与y 轴的交点，连接AC ． ⑴求抛物线的解析式； ⑵证明：△ABC 为直角三角形；⑶△ABC 内部能否截出面积最大的矩形DEFG ？（顶点D 、E、F 、G 在△ABC 各边上）若能，求出最大面积；若不能，请说明理由．（第26题图）5．（本小题满分13分）如图，二次函数32-+=bx ax y 的图象与x 轴交于A （-1，0），B （3，0）两点，与y 轴交于点C .该抛物线的顶点为M .（1）求该抛物线的解析式；（2）判断△BCM 的形状，并说明理由.（3）探究坐标轴上是否存在点P ，使得以点P ，A ，C 为顶点的三角形与△BCM 相似？若存在，请求出点P 的坐标，若不存在，请说明理由.6.（本题满分13分）如图，已知二次函数y =﹣x 2+bx +c 的图象交x 轴于点A （4，0）和点B ，交y 轴于点C （0，4）． （1）求这个二次函数的表达式；（2）若点P 在第一象限内的抛物线上，求四边形AOCP 面积的最大值和此时点P 的坐标；（3）在平面直角坐标系内，是否存在点Q ，使A ，B ，C ，Q 四点构成平行四边形？若存在，直接写出点Q 的坐标；若不存在，说明理由．7．（13分）如图，已知抛物线与x 轴交于A （﹣1，0）、B （5，0）两点，与y 轴交于点C （0，5）． （1）求该抛物线所对应的函数关系式；（2）D 是笫一象限内抛物线上的一个动点（与点C 、B 不重合），过点D 作DF ⊥x 轴于点F ，交直线BC 于点E ，连结BD 、CD ．设点D 的横坐标为m ，△BCD 的面积为S ．①求S 关于m 的函数关系式及自变量m 的取值范围；②当m 为何值时,S 有最大值,并求这个最大值； ③直线BC 能否把△BDF 分成面积之比为2:3的两部分？若能,请求出点D 的坐标；若不能,请说明理由．（第26题8．（13分）如图，隧道的截面由抛物线和长方形构成，长方形的长是12m ，宽是4m ．按照图中所示的直角坐标系，抛物线可以用y=﹣x 2+bx +c 表示，且抛物线的点C 到墙面OB 的水平距离为3m 时，到地面OA 的距离为m ．（1）求该抛物线的函数关系式，并计算出拱顶D 到地面OA 的距离；（2）一辆货运汽车载一长方体集装箱后高为6m ，宽为4m ，如果隧道内设双向行车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m ，那么两排灯的水平距离最小是多少米？9．（13分）如图，已知抛物线与x 轴交于A （﹣1，0）、E （3，0）两点，与y 轴交于点B （0，3）． （1）求抛物线的解析式；（2）设抛物线顶点为D ，求四边形AEDB 的面积；（3）△AOB 与△DBE 是否相似？如果相似，请给以证明；如果不相似，请说明理由．26. (满分13分) 如图，抛物线经过A （﹣1，0），B （5，0），C （0，25）三点． （1）求抛物线的解析式； （2）在抛物线的对称轴上有一点P ，使PA+PC 的值最小，求点P 的坐标； （3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求点N 的坐标；若不存在，请说明理由．。

二次函数压轴题面积类1．如图，抛物线经过点A〔﹣1，0〕、B〔3，0〕、C〔0，3〕三点．〔1〕求抛物线的解析式．〔2〕点M是线段上的点〔不及B，C重合〕，过M作∥y轴交抛物线于N，假设点M的横坐标为m，请用m的代数式表示的长．〔3〕在〔2〕的条件下，连接、，是否存在m，使△的面积最大？假设存在，求m的值；假设不存在，说明理由．2．如图，抛物线的图象及x轴交于A、B两点，及y轴交于C点，B点坐标为〔4，0〕．〔1〕求抛物线的解析式；〔2〕摸索究△的外接圆的圆心位置，并求出圆心坐标；〔3〕假设点M是线段下方的抛物线上一点，求△的面积的最大值，并求出此时M点的坐标．平行四边形类3．如图，在平面直角坐标系中，抛物线2经过点A〔3，0〕、B〔0，﹣3〕，点P是直线上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．〔1〕分别求出直线和这条抛物线的解析式．〔2〕假设点P在第四象限，连接、，当线段最长时，求△的面积．〔3〕是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？假设存在，请干脆写出点P的横坐标；假设不存在，请说明理由．4．如图，在平面直角坐标系中放置始终角三角板，其顶点为A 〔0，1〕，B〔2，0〕，O〔0，0〕，将此三角板绕原点O逆时针旋转90°，得到△A′B′O．〔1〕一抛物线经过点A′、B′、B，求该抛物线的解析式；〔2〕设点P是在第一象限内抛物线上的一动点，是否存在点P，使四边形′A′B的面积是△A′B′O面积4倍？假设存在，恳求出P的坐标；假设不存在，请说明理由．〔3〕在〔2〕的条件下，试指出四边形′A′B是哪种形态的四边形？并写出四边形′A′B的两条性质．5．如图，抛物线2﹣2的顶点A在直线l：﹣5上．〔1〕求抛物线顶点A的坐标；〔2〕设抛物线及y轴交于点B，及x轴交于点C、D〔C点在D点的左侧〕，试推断△的形态；〔3〕在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？假设存在，求点P的坐标；假设不存在，请说明理由．周长类6．如图，△的两直角边、分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为〔﹣3，0〕、〔0，4〕，抛物线2经过点B，且顶点在直线上．〔1〕求抛物线对应的函数关系式；〔2〕假设把△沿x轴向右平移得到△，点A、B、O的对应点分别是D、C、E，当四边形是菱形时，试推断点C和点D是否在该抛物线上，并说明理由；〔3〕在〔2〕的条件下，连接，对称轴上存在一点P使得△的周长最小，求出P点的坐标；〔4〕在〔2〕、〔3〕的条件下，假设点M是线段上的一个动点〔点M及点O、B不重合〕，过点M作∥交x轴于点N，连接、，设的长为t，△的面积为S，求S和t的函数关系式，并写出自变量t 的取值范围，S是否存在最大值？假设存在，求出最大值和此时M点的坐标；假设不存在，说明理由．等腰三角形类7．如图，点A在x轴上，4，将线段绕点O顺时针旋转120°至的位置．〔1〕求点B的坐标；〔2〕求经过点A、O、B的抛物线的解析式；〔3〕在此抛物线的对称轴上，是否存在点P，使得以点P、O、B 为顶点的三角形是等腰三角形？假设存在，求点P的坐标；假设不存在，说明理由．8．在平面直角坐标系中，现将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，且点A〔0，2〕，点C〔﹣1，0〕，如下图：抛物线2﹣2经过点B．〔1〕求点B的坐标；〔2〕求抛物线的解析式；〔3〕在抛物线上是否还存在点P〔点B除外〕，使△仍旧是以为直角边的等腰直角三角形？假设存在，求全部点P的坐标；假设不存在，请说明理由．9．在平面直角坐标系中，现将一块等腰直角三角板放在第一象限，斜靠在两坐标轴上，且点A〔0，2〕，点C〔1，0〕，如下图，抛物线2﹣﹣2经过点B．〔1〕求点B的坐标；〔2〕求抛物线的解析式；〔3〕在抛物线上是否还存在点P〔点B除外〕，使△仍旧是以为直角边的等腰直角三角形？假设存在，求全部点P的坐标；假设不存在，请说明理由．综合类10．如图，抛物线2的图象及x轴的一个交点为B〔5，0〕，另一个交点为A，且及y轴交于点C〔0，5〕．〔1〕求直线及抛物线的解析式；〔2〕假设点M是抛物线在x轴下方图象上的一动点，过点M作∥y轴交直线于点N，求的最大值；〔3〕在〔2〕的条件下，获得最大值时，假设点P是抛物线在x 轴下方图象上随意一点，以为边作平行四边形，设平行四边形的面积为S1，△的面积为S2，且S1=6S2，求点P的坐标．11．如图，抛物线2〔a≠0〕的图象过点C〔0，1〕，顶点为Q〔2，3〕，点D在x轴正半轴上，且．〔1〕求直线的解析式；〔2〕求抛物线的解析式；〔3〕将直线绕点C逆时针方向旋转45°所得直线及抛物线相交于另一点E，求证：△∽△；〔4〕在〔3〕的条件下，假设点P是线段上的动点，点F是线段上的动点，问：在P点和F点挪动过程中，△的周长是否存在最小值？假设存在，求出这个最小值；假设不存在，请说明理由．12．如图，抛物线及x轴交于A〔1，0〕、B〔﹣3，0〕两点，及y轴交于点C〔0，3〕，设抛物线的顶点为D．〔1〕求该抛物线的解析式及顶点D的坐标．〔2〕试推断△的形态，并说明理由．〔3〕探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形及△相像？假设存在，请干脆写出点P的坐标；假设不存在，请说明理由．13．如图，抛物线23及x轴交于A、B两点，过点A的直线l及抛物线交于点C，其中A点的坐标是〔1，0〕，C点坐标是〔4，3〕．〔1〕求抛物线的解析式；〔2〕在〔1〕中抛物线的对称轴上是否存在点D，使△的周长最小？假设存在，求出点D的坐标，假设不存在，请说明理由；〔3〕假设点E是〔1〕中抛物线上的一个动点，且位于直线的下方，试求△的最大面积及E点的坐标．14．如图，抛物线﹣x24及x轴相交于A、B两点，及y轴相交于点C，假设A点的坐标为A〔﹣2，0〕．〔1〕求抛物线的解析式及它的对称轴方程；〔2〕求点C的坐标，连接、并求线段所在直线的解析式；〔3〕试推断△及△是否相像？并说明理由；〔4〕在抛物线的对称轴上是否存在点Q，使△为等腰三角形？假设存在，求出符合条件的Q点坐标；假设不存在，请说明理由．15．如图，在坐标系中，△是等腰直角三角形，∠90°，A〔1，0〕，B〔0，2〕，抛物线2﹣2的图象过C点．〔1〕求抛物线的解析式；〔2〕平移该抛物线的对称轴所在直线l．当l挪动到何处时，恰好将△的面积分为相等的两部分？〔3〕点P是抛物线上一动点，是否存在点P，使四边形为平行四边形？假设存在，求出P点坐标；假设不存在，说明理由．山水是一部书，枝枝叶叶的文字间，声声鸟鸣是抑扬顿挫的标点，在茂密纵深间，一条曲径，是整部书最芳香的禅意。